Current Research
A good presentation of general-purpose ALS classification is in [
12]. Our work relates to some of the contour and TIN -based ground filtering algorithms mentioned in [
13], since all of our methods either directly or indirectly use or produce a tailor-made ground model. Methods described in [
13] are usually more generic accommodating to infrastructure signatures etc. It is possible, that methods described in our paper have to be combined with existing generic ground model algorithms, where an assembly of methods would use e.g., a voting arrangement at the approximity of constructed environment.
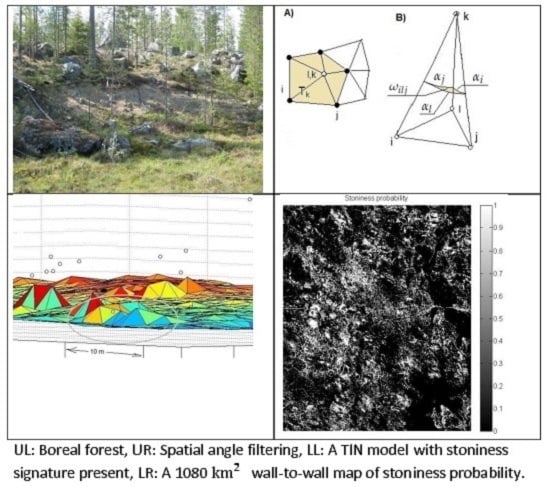
Solid angle filtering (SAF) in
Section 2.4 resembles the despike algorithm presented in [
14]. Two problems are mentioned in [
14]: Unnecessary corner removals (rounding off the vertices of e.g., block-like structures) and effects of negative blunders (false points dramatically below the real surface level). Our routine was specifically designed to eliminate these problems. SAF can also be used in canopy removal. An interesting new technique in limiting the ground return points is min-cut based segmentation of k-nearest neighbors graph (k-NNG) [
15]. The graph is fast to compute with space partitioning, and it could have served as a basis for stoniness analysis directly e.g., by fast local principal components analysis (PCA) and local normal estimation with vector voting procedure, as in [
16]. The literature focuses mostly on laser clouds of technological environment, where the problem of eliminating the canopy (noise) and finding the ground returns (a smooth technical surface) are not combined. Our experiments with local normal approximation and vector voting were inferior to results presented in this paper. There is great potential in local analysis based on k-NNG, though.
There seems to be no research concerning the application of ALS data to stoniness detection in forest areas. Usually target areas have no tree cover [
17], objects are elongated (walls, ditches, archaeological road tracks, etc.) [
17,
18] and often multi-source data like photogrammetry or wide-spectrum tools are used. curbstones which separate the pavement and road in [
18]. Their data has the sample density
which produces geometric error of size
m which is larger than the observed shapes (curbstones) and thus not practical. Effects of foliage and woody debris are discussed in [
19]. They mention that even a high-density ALS campaign is not able to get a dense sampling of the ground surface in a non-boreal forest (Pennsylvania, U.S.). They reported ground return ratio is 40% with the ground sample density
, which is much higher than
in our study. The distribution of the local ground sample density was not reported in [
19] but is probably much higher than in our case.
DEM in
Figure 1) is a standard data type used by geographic information systems (GIS). Many implementations and heuristics exist (see e.g., [
20]) to form DEM from ALS format
.las defined by [
21]. Usually, the smallest raster grid size is dictated by the sample density and in this case DEM grid size
is possible, and
already suffers from numerical instability and noise.
A rare reference to DEM based detection of a relatively small local ground feature (cave openings) in forest circumstances is presented in [
22]. In that paper the target usually is at least partially exposed from canopy and the cave opening is more than 5 m in diameter. On the other hand, the forest canopy was denser than at our site in general. Another application is detecting karst depressions, where slope histograms [
23] and local sink depth [
24] were used to detect karst depressions. There are similarities with our study, e.g., application of several computational steps and tuning of critical parameters (e.g., the depression depth limit in [
23]), although the horizontal micro-topology feature size is much larger than in our study (diameter of doline depressions is 10–200 m vs. 1.5–6 m diameter of stones in our study). The vertical height differences are at the same range, 0.5–1.5 m in our study and in [
23,
24], though. A similar study of [
25] uses higher density LiDAR data with
to detect karst depressions of size 26 m and more. The vertical height difference (depth) was considerably larger than in in [
23,
24]. The high density point cloud and a carefully designed multi-step process results in quantitative analysis of sinkholes in [
25], unlike in our study, where the stoniness likelihood of a binary classifier is the only output.
One reference [
19] lists several alternative LiDAR based DEM features, which could be used in stone detection, too. These include fractal dimension, curvature eigenvectors, and analyzing variograms generated locally over multiple scales. Some of the features are common in GIS software, but most should be implemented for stoniness detection.
Hough method adapted to finding hemispherical objects is considerably slower than previous ones, although there is a recent publication about various possible optimizations, see e.g., [
26]. These optimizations are mainly about better spatial partitioning.
Minimum description length (MDL) is presented in [
27] with an application to detect planes from the point cloud. The approach is very basic, but can be modified to detect spherical gaps rather easily. MDL formalism can provide a choice between two hypotheses:
a plain spot/a spot with a stone. Currently, there is no cloud point set with individual stones tagged to train a method based on MDL. MDL formalism could have been used without such an annotated data set, but we left this approach for further study. In addition, probably at least 4..8 returns per stone is needed and thus a higher ground return density than is currently available.
This paper presents two methods based on ALS data and one method using DEM and acting as a baseline method. The DEM method was designed according to the following considerations: It has to be easy to integrate to GIS and it would start from a DEM raster file, then generate one or many texture features for the segmentation phase. The possible texture features for this approach are the following:
local height difference, see Laplace filtering
Section 2.7. This feature was chosen as the baseline method since it is a typical and straightforward GIS technique for a problem like stoniness detection.
various roughness measures, e.g., rugosity (related trigonometrically to the average slope), local curvature, standard deviation of slope, standard deviation of curvature, mount leveling metric (opposite to a pit fill metric mentioned in [
19]).
multiscale curvature presented in [
28]. It is used for dividing the point cloud to ground and non-ground returns, but could be modified to bring both texture information and curvature distribution information. The latter could then be used for the stoninesss prediction like in this study. The methods, possibly excluding interpolation based on TIN, seem to be numerically more costly than our approach.
Possible GIS -integrated texture segmentation methods would be heavily influenced on the choices made above. Most of the features listed are standard tools in GIS systems or can be implemented by minimal coding. An example is application of the so called mount leveling metric to stoniness detection, which would require negating the height parameter at one procedure.
Terrain roughness studied in [
19] is a concept which is close to stoniness. Authors mention that the point density increase from
to
did not improve the terrain roughness observations considerably. This is understandable since the vertical error of the surface signal is at the same range as the average nearest point distance of the latter data set. The paper states that algorithms producing the terrain roughness feature have importance to success. This led us to experiment with various new algorithms.
Point cloud features based on neighborhoods of variable size are experimented with in [
29]. Many texture recognition problems are sensitive to the raster scale used, thus we tested a combination of many scales, too. According to [
16], curvature estimation on triangulated surfaces can be divided to three main approaches:
surface fitting methods: a parametric surface is fitted to data. Our local linear fit LLC falls on this category, yet does not necessarily require triangularization as a preliminary step.
total curvature methods: curvature approximant is derived as a function of location. Our local triangular curvature LTC is of this category of methods.
curve fitting methods.
LLC has a performance bottleneck in local linear fit procedure described in
Section 2.5. This problem has been addressed recently in [
30], where an algebraic-symbolic method is used to solve a set of total least squares problems with Gaussian error distribution in a parallelizable and efficient way. That method would require modification and experimentations with e.g., a gamma distributed error term due to asymmetric vegetation and canopy returns.
The vector voting method presented in [
16] decreases noise and achieves good approximative surface normals for symmetrically noisy data sets of point clouds of technological targets. Our target cloud has asymmetrical noise (vegetation returns are always above the ground), and returns under the ground (e.g., reflection errors) are extremely rare. Usually vector voting methods are used in image processing. They are based on triangular neighborhood and any similarity measure between vertices, focusing signal to fewer points and making it sometimes easier to detect. Neighborhood voting possibilities are being discussed int
Section 4.
General references of available curvature tensor approximation methods in case of triangulated surfaces are [
31,
32]. A derivation of Gaussian curvature
and mean curvature
is in [
33]:
where
are the two eigenvalues of the curvature tensor. Perhaps the best theoretical overview of general concepts involved in curvature approximation on discrete surfaces based on discrete differential geometry (DDG) is [
34].
We experimented with methods which can produce both mean and Gaussian curvatures, giving access to curvature eigenvalues and eigenvectors. Our experiments failed since the mean curvature
seems to be very noise-sensitive to compute and would require a special noise filtering post-processing step. Difficulties in estimating the mean curvature from a noisy data have been widely noted, see e.g., [
29].
In comparison to previous references, this paper is an independent study based on the following facts: point cloud density is low relative to the field objects of interest (stones), ratio of ground returns amongst the point cloud is high providing relatively even coverage of the ground, a direct approach without texture methods based on regular grids was preferred, individual stones are not tagged in the test data, and the methods are for a single focused application. Furthermore, we wanted to avoid complexities of segmentation-based filtering described in [
35] and the method parameters had to be tunable by cross-validation approach.