Modulation Model of High Frequency Band Radar Backscatter by the Internal Wave Based on the Third-Order Statistics
Abstract
:1. Introduction
2. Modulation Model of Radar Backscatters by Internal Wave Based on Third-Order Statistics
2.1. Radar Backscatters of Ocean Surface Based on Third-Order Statistics
2.2. Modulation Transfer Function of Radar Backscatter by Internal Wave
3. Experimental Validation of the Model
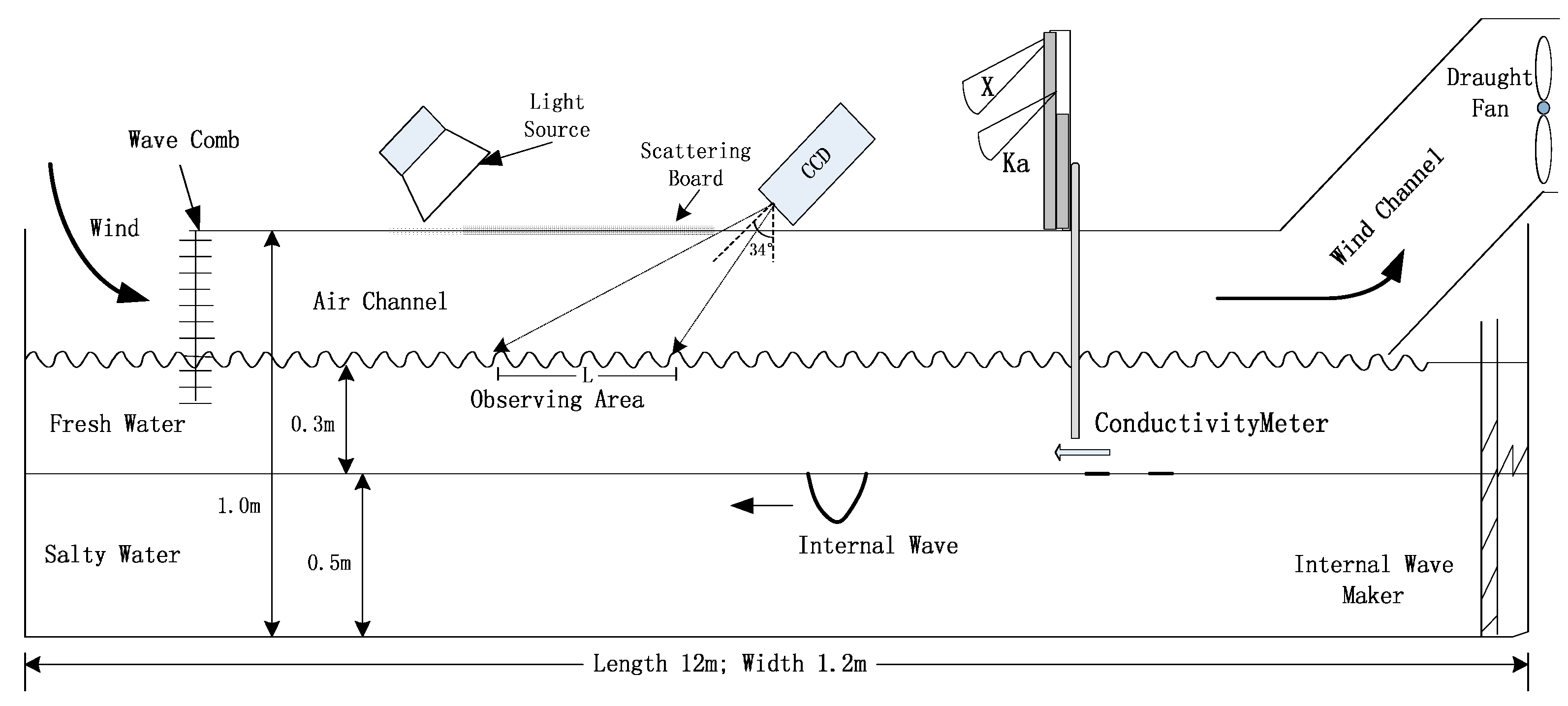
3.1. Experiment Description
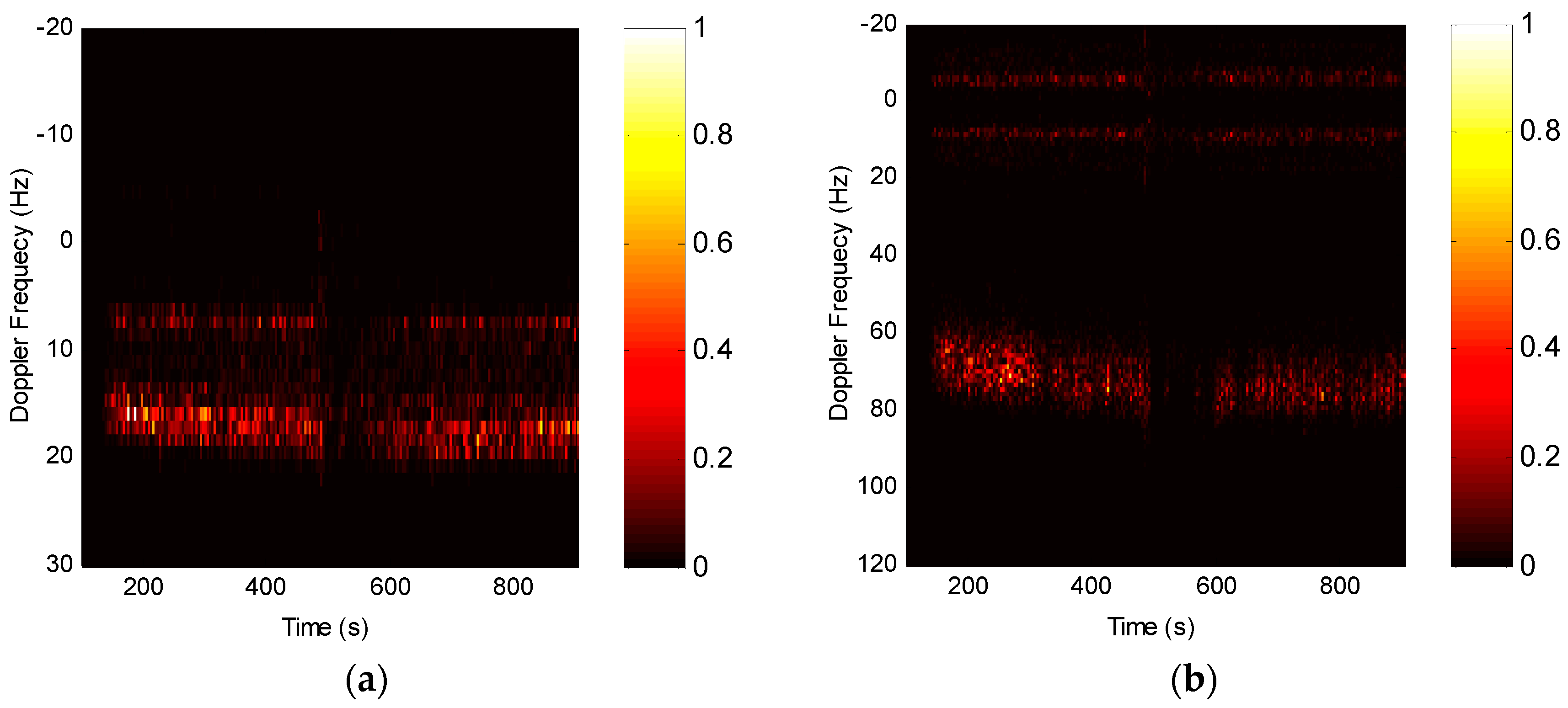
3.2. Experimental Data Processing
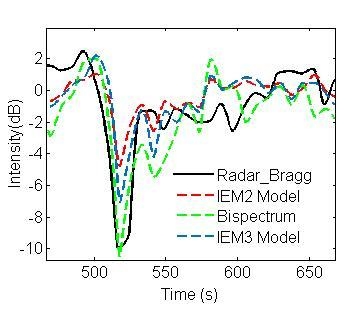
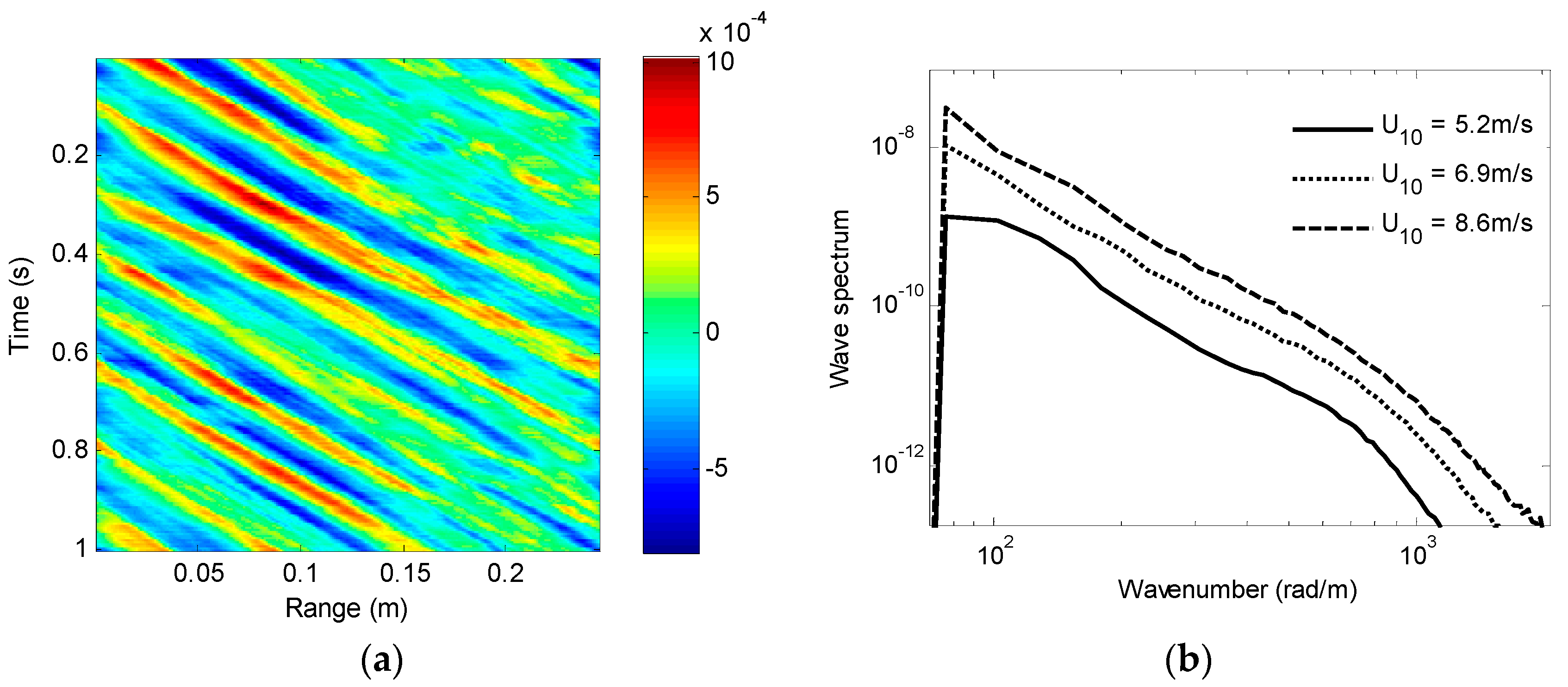
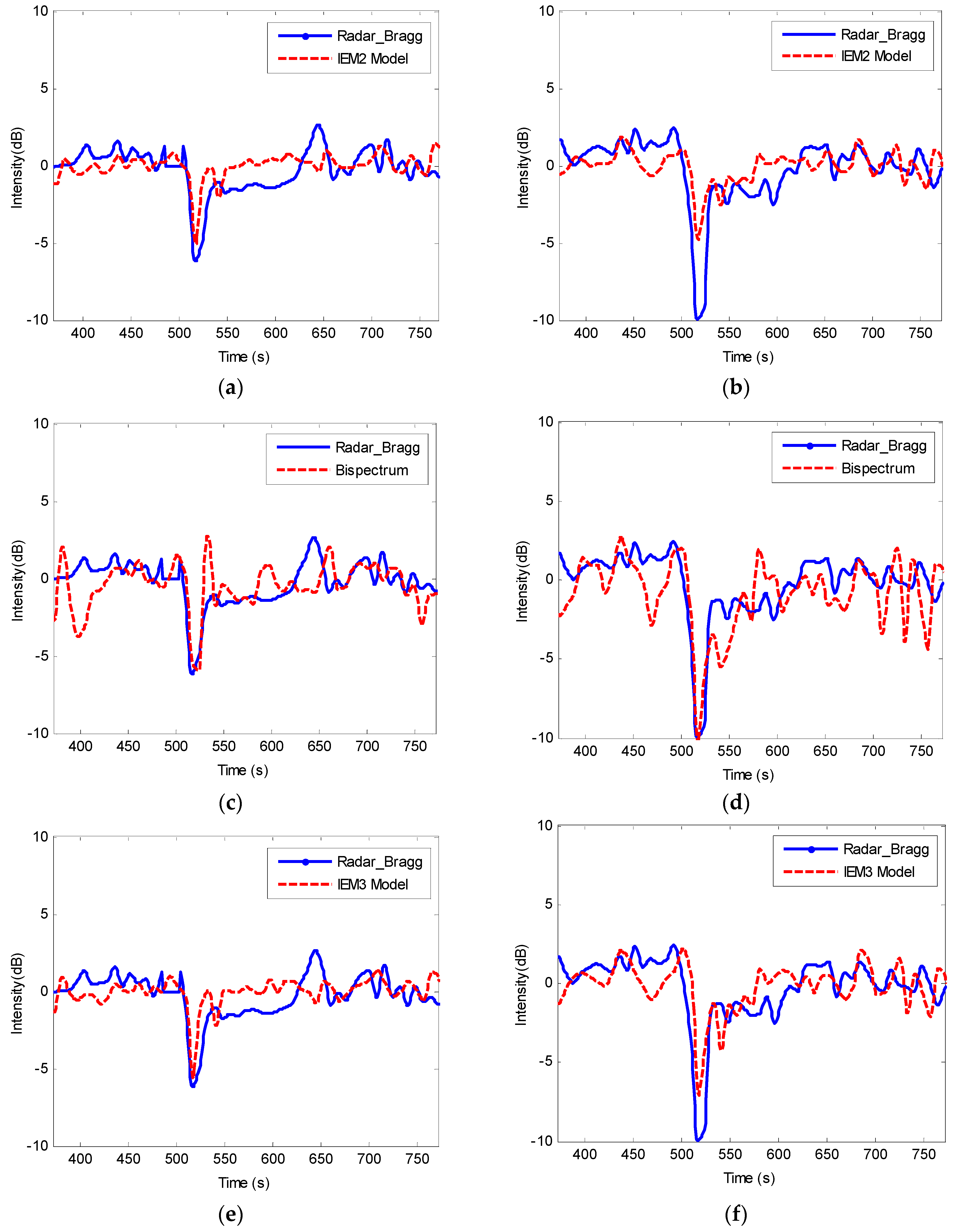
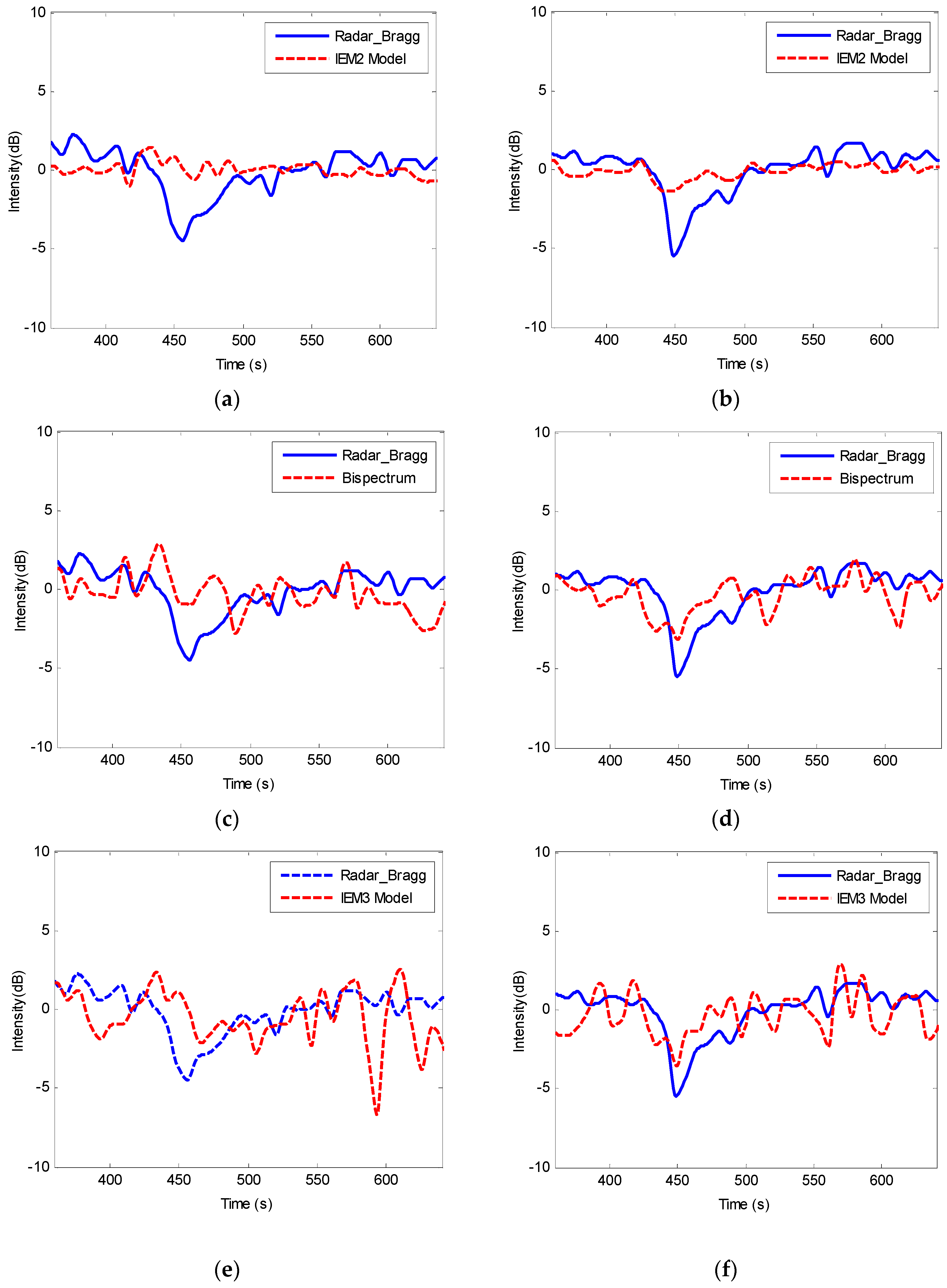
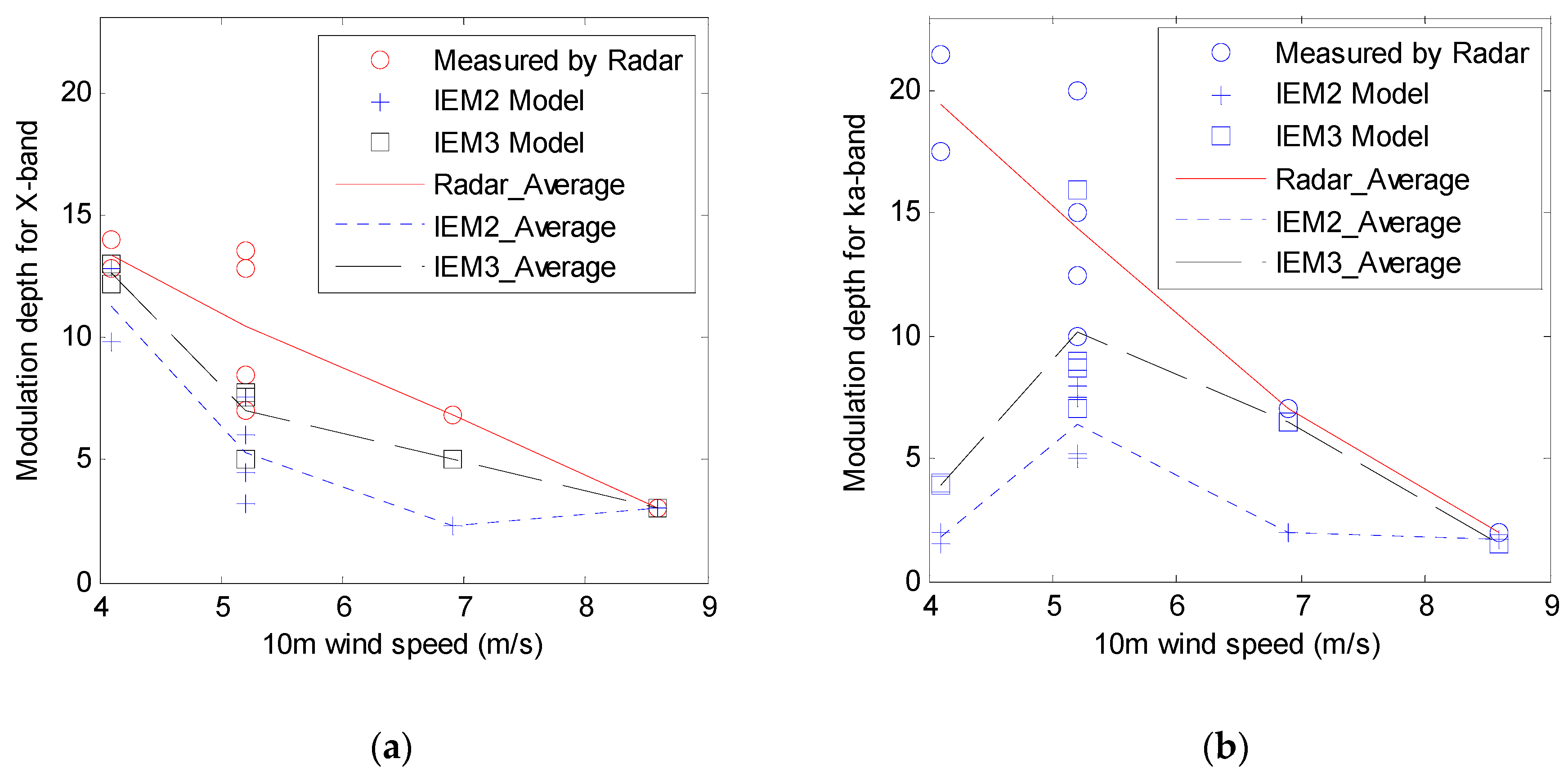
4. Results of Experiments and Discussion
4.1. Comparison between Radar Measurements and Values Calculated by Models
4.2. Relation between Modulation Depth of Radar Backscatter and Wind Speeds
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Radar Backscatter Coefficient Function
References
- Jackson, C.R.; Apel, J.R. Syntheic Aperture Radar Marine User’s Manual; NOAA/NESDIS: Washington, DC, USA, 2004.
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Plant, W.J.; Alpers, W. The Saxon-FPN Experiment. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Remote Sensing: Global Monitoring for Earth Management, Espoo, Finland, 3–6 June 1991; IEEE: New York, NY, USA, 1991; pp. 1983–1987. [Google Scholar]
- Hughes, B.A.; Dawson, T.W. Joint Canada-U.S. Ocean wave investigation project: An overview of the Georgia Strait experiment. J. Geophys. Res. Oceans 1988, 93, 12219–12234. [Google Scholar] [CrossRef]
- Gasparovic, R.F.; Apel, J.R.; Kasischke, E.S. An overview of the sar internal wave signature experiment. J. Geophys. Res. Oceans 1988, 93, 12304–12316. [Google Scholar] [CrossRef]
- Johanessen, J.A.; Korsbakken, E.; Samuel, P.; Jenkins, A.; Espedal, H. Coast watch: Using SAR imagery in an operational system for monitoring coastal currents, wind, surfactants and oil spills. In Operational Oceanography: The Challenge for European Co-Operation; Stel, J.H., Ed.; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Plant, W.J.; Keller, W.C.; Hayes, K.; Chatham, G.; Lederer, N. Normalized radar cross section of the sea for backscatter: 2. Modulation by internal waves. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Bai, X.; Liu, Z.; Li, X.; Chen, Z.; Hu, J.; Sun, Z.; Zhu, J. Observations of high-frequency internal waves in the Southern Taiwan Strait. J. Coast. Res. 2013, 29, 1413–1419. [Google Scholar] [CrossRef]
- Li, X.; Jackson, C.R.; Pichel, W.G. Internal solitary wave refraction at Dongsha Atoll, South China Sea. Geophys. Res. Lett. 2013, 40, 3128–3132. [Google Scholar] [CrossRef]
- Bai, X.; Liu, Z.; Li, X.; Hu, J. Generation sites of internal solitary waves in the Southern Taiwan Strait revealed by MODIS true-colour image observations. Int. J. Remote Sens. 2014, 35, 4086–4098. [Google Scholar] [CrossRef]
- Liu, B.; Yang, H.; Zhao, Z.; Li, X. Internal solitary wave propagation observed by tandem satellites. Geophys. Res. Lett. 2014, 41, 2077–2085. [Google Scholar] [CrossRef]
- Dong, D.; Yang, X.; Li, X.; Li, Z. SAR observation of eddy-induced mode-2 internal solitary waves in the South China Sea. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6674–6686. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R. Radiation stresses in water waves; a physical discussion, with applications. In Deep Sea Research and Oceanographic Abstracts; Elsevier: Amsterdam, The Netherlands, 1964; pp. 529–562. [Google Scholar]
- Whitham, G. A general approach to linear and non-linear dispersive waves using a lagrangian. J. Fluid Mech. 1965, 22, 273–283. [Google Scholar] [CrossRef]
- Bretherton, F.P. A note on hamilton’s principle for perfect fluids. J. Fluid Mech. 1970, 44, 19–31. [Google Scholar] [CrossRef]
- Thompson, D.R. Calculation of radar backscatter modulations from internal waves. J. Geophys. Res. Oceans 1988, 93, 12371–12380. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Bennett, J.R. Full-spectrum modelling of synthetic aperture radar internal wave signatures. J. Geophys. Res. Oceans 1988, 93, 12345–12354. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Akimov, D.; Johanessen, J.A.; Chapron, B. On radar imaging of current features: 1. Model and comparison with observations. J. Geophys. Res. Oceans 2005, 110. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean, 2nd ed.; Cambridge University Press: Cambridge, UK, 1977; pp. 37–81. [Google Scholar]
- Fung, A.K. Microwave Scattering and Emission Models and Their Applications; Artech House: London, UK, 1994. [Google Scholar]
- Wright, J. A new model for sea clutter. IEEE Trans. Antennas Propag. 1968, 16, 217–223. [Google Scholar] [CrossRef]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and ocean waves—A review. Bound. Layer Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Chen, K.S.; Fung, A.K.; Weissman, D.A. A backscattering model for ocean surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 811–817. [Google Scholar] [CrossRef]
- Plant, W.J. A new interpretation of sea-surface slope probability density functions. J. Geophys. Res. Oceans 2003, 108. [Google Scholar] [CrossRef]
- Plant, W.J. A stochastic multiscale model of microwave backscatter from the ocean. J. Geophys. Res. Oceans 2002, 107, 3120. [Google Scholar] [CrossRef]
- Plant, W.J.; Wright, J.W. Phase speeds of upwind and downwind traveling short gravity waves. J. Geophys. Res. Oceans 1980, 85, 3304–3310. [Google Scholar] [CrossRef]
- Hughes, B.A. The effect of internal waves on surface wind waves 2. Theoretical analysis. J. Geophys. Res. Oceans 1978, 83, 455–465. [Google Scholar] [CrossRef]
- Plant, W.J. A relationship between wind stress and wave slope. J. Geophys. Res. Oceans 1982, 87, 1961–1967. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C.; Hayes, K.; Chatham, G. Normalized radar cross section of the sea for backscatter: 1. Mean levels. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]

| Specifications | Values | |
|---|---|---|
| Band | X | Ka |
| Frequency | 9.4 GHz | 35 GHz |
| Beam Width | 9° × 9° | 6° × 6° |
| Incidence Angle | 50° | 57° |
| Specifications | Values |
|---|---|
| Swath Width | 36 cm |
| Resolution (Geometrical) | 0.3 mm |
| Frame Repetition | 300 Hz |
| Analog-to-Digital Convert Frequency | 300 KHz |
| Uw (m/s) | U10 (m/s) | D (m/s) | F (m) | Di (m) | |
|---|---|---|---|---|---|
| No. 1 | 3.2 | 4.1 | 0.8 | 5 | 0.3 |
| No. 2 | 4 | 5.2 | 0.8 | 5 | 0.3 |
| No. 3 | 5 | 6.9 | 0.8 | 5 | 0.3 |
| No. 4 | 6 | 8.6 | 0.8 | 5 | 0.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Liu, L.; Wang, X.; Chong, J.; Zhang, X.; Yu, X. Modulation Model of High Frequency Band Radar Backscatter by the Internal Wave Based on the Third-Order Statistics. Remote Sens. 2017, 9, 501. https://doi.org/10.3390/rs9050501
Chen P, Liu L, Wang X, Chong J, Zhang X, Yu X. Modulation Model of High Frequency Band Radar Backscatter by the Internal Wave Based on the Third-Order Statistics. Remote Sensing. 2017; 9(5):501. https://doi.org/10.3390/rs9050501
Chicago/Turabian StyleChen, Pengzhen, Lei Liu, Xiaoqing Wang, Jinsong Chong, Xin Zhang, and Xiangzhen Yu. 2017. "Modulation Model of High Frequency Band Radar Backscatter by the Internal Wave Based on the Third-Order Statistics" Remote Sensing 9, no. 5: 501. https://doi.org/10.3390/rs9050501