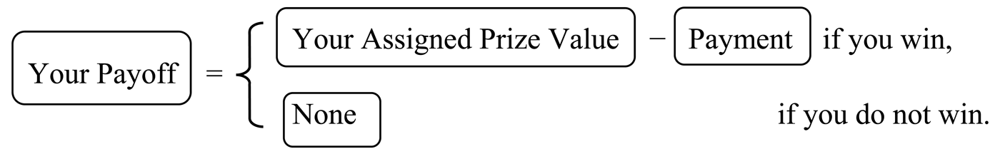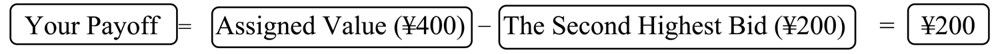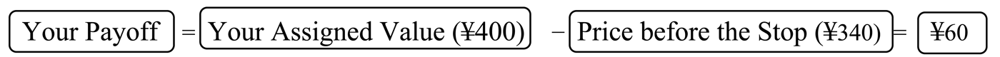Spite and Reciprocity in Auctions
Abstract
: The paper presents a complete information model of bidding in second price sealed-bid and ascending-bid (English) auctions, in which potential buyers know the unit valuation of other bidders and may spitefully prefer that their rivals earn a lower surplus. Bidders with spiteful preferences should overbid in equilibrium when they know their rival has a higher value than their own, and bidders with a higher value underbid to reciprocate the spiteful overbidding of the lower value bidders. The model also predicts different bidding behavior in second price as compared to ascending-bid auctions. The paper also presents experimental evidence broadly consistent with the model. In the complete information environment, lower value bidders overbid more than higher value bidders, and they overbid more frequently in the second price auction than in the ascending price auction. Overall, the lower value bidder submits bids that exceed value about half the time. These patterns are not found in the incomplete information environment, consistent with the model.1. Introduction
One of the most basic and apparently innocuous assumptions about behavior in games is that players will adopt dominant strategies. One reason why players may avoid dominant strategies, as expressed in monetary payoffs, is because they have social preferences such as spite or conditional Results and Discussion cooperation. Recent laboratory research in public good mechanism design, for example, has documented extensive failure by subjects to follow dominant strategies even in fairly simple environments, perhaps due to a desire to cooperate with others who are also cooperative (Attiyeh et al. [1]; Kawagoe and Mori [2]; Cason et al. [3]). Mixed results also exist in experiments assessing the incentive-compatibility of second price (Vickrey) auctions. For example, Kagel and Levin [4] find that 58 to 67 percent of bids exceed value, and Harstad [5] reports that severe overbidding does not decline over time, while others such as Coppinger et al. [6], Cox et al. [7], Kagel et al. [8], and Chew and Nishimura [9] report consistency with value-revealing bidding.
Overbidding is much less pronounced in the English, ascending-bid auction. Especially in the “Japanese” version of ascending-bid auction [10,11], which is isomorphic to the second price auction, the equilibrium bidding strategy is more transparent, which has led some researchers to conclude that the subtlety of the dominant strategy in the sealed bid second-price auction is a primary reason some bidders fail to follow it. Learning is also difficult in the second price auction because the use of a weakly dominated strategy may often not cause any loss in actual payoff (Kagel and Levin [4]). Moreover, even with standard (own-payoff maximizing) preferences, many Nash equilibria exist in these auction formats other than the dominant strategy equilibrium.
This paper explores the importance of alternative, spiteful preferences as an explanation for overbidding in second price and ascending-bid auctions. A spiteful agent has utility that increases when the earnings of her rivals decrease, and so she may be willing to sacrifice some monetary payoff in order to reduce the other agent's monetary payoff (Saijo and Nakamura [12]). The following section contains our formal definition, which features a reciprocal motive; i.e., subjects feel more spiteful towards others who treat them spitefully. The key design feature of second price and ascending-bid auctions that make them incentive-compatible under standard preferences makes them particularly prone to manipulation by bidders who have spiteful preferences. Because an individual's monetary payoff conditional on winning the auction is independent of her bid, if she cares only about her monetary payoff has no incentive to change her bid to lower her price. But if she fails to win her bid may determine the payoff of the winner. Therefore, if she is spiteful she can increase her bid to increase her (spiteful) utility. Agents who have spiteful preferences would not consider a bid equal to value to be a dominant strategy.
We construct a two-bidder, intention-based reciprocal decision model which belongs to the class of reciprocity models including Rabin [13] and Segal and Sobel [14], and extend it to the sequential decision making of the ascending-bid auction in the spirit of Dufwenberg and Kirchsteiger [15] and Falk and Fischbacher [16]. Intention is measured by the distance between a buyer's bid choice and her standard value-revealing bid which we consider as the intention neutral reference. A bidder with a low value for the object may behave spitefully when her opponent expects to win a positive surplus. This can be interpreted as part of the disutility of losing the auction, since she is in a disadvantageous position. This may prompt her to place a spiteful bid higher than her value, hoping to reduce her opponent's winning surplus. For example, suppose it is common knowledge that bidder 1 values the object at 800 yen, while bidder 2 values the object at 700 yen. A spiteful bidder 2 could bid, say, 750 rather than her value 700 in a second-price auction to reduce bidder 1's winning surplus from 800 – 700 = 100 to 800 – 750 = 50. A novelty of our analysis is in incorporating retaliation by the bidder who has a higher value. The higher value bidder may place a deliberately low bid in order to penalize the spiteful conduct by the lower value bidder, even though such a retaliatory bid reduces his chance of winning. Continuing the example, bidder 1 could bid less than his value of 800, such as 760, in order to limit the spiteful actions of bidder 2. Bidder 1 could even penalize a spiteful bidder 2 by bidding lower than 750.
Another novel feature of our analysis is that we consider a complete information environment, which strengthens the impact of social preferences such as spite and reciprocity. This is intended to approximate conditions in which bidders have some information about rivals' values or costs, such as in local government procurement settings with repeated competition between the same set of bidders. In the incomplete information environment typically employed in the auction literature, adding spiteful and reciprocal preferences as we have modeled them still results in bids equal to value in the unique (but not dominant strategy) symmetric equilibrium. By contrast, bidders with spiteful and reciprocal preferences should overbid in equilibrium when they have complete information about their rival's value and they know their rival has a higher value than their own.
Spiteful and reciprocal preferences also make the second price and the ascending-bid auction forms non-isomorphic. In an ascending-bid auction, an auctioneer or clock raises a calling price until there remains only one active bidder. A climbing calling price gradually reduces the winner's payoff. Taking this effect into account, in our sequential decision model the bidders are more aware of the extent of the other's spitefulness when they reach each new, higher calling price, because they can infer that their rival did not drop out. This makes the bidder with the higher value willing to retaliate at an earlier stage. Consequently, for the same level of spiteful preferences, in response the lower value bidders should overbid less in the ascending-bid auction than in the second price auction. Thus, the upper bound of the set of equilibria in ascending-bid auctions is likely to be lower.
The second part of the paper presents experimental evidence that provides some qualified support for the predictions of this model. In the complete information environment, lower value bidders overbid more than higher value bidders, and they overbid more frequently in the second price auction than in the ascending price auction. Overall, the lower value bidder submits bids that exceed value about one-half the time. These patterns are not found in the data we collected for the incomplete information environment, consistent with the model. Similar to most of the literature on incomplete information second price and ascending bid auctions, bids are near values for both low-and high-value bidders.
Researchers have recently measured and explored the impact of social preferences that include reciprocity and spite in a variety of environments, but often in non-competitive contexts such as public good provision, two-agent bargaining and simple games. A small amount of research has studied the impact of spite in auctions, starting with Morgan et al.'s [17] theoretical analysis. Their model, which we discuss below in more detail, features non-reciprocal spite and does not predict differences between the second price and ascending price auctions for the two-bidder setting we employ. Cooper and Fang's [18] experimental study also considers (like us) a two-bidder environment for simplicity, but only second price auctions. They provide bidders with noisy information about their rival's value, with varying degrees of accuracy, and find that overbidding is consistent both with spite and “joy-of-winning” motivations. Andreoni et al. [19] also report a laboratory experiment in which bidders may have information about rivals' value draws. They consider first and second price auctions, all with four competing bidders, and test predictions regarding equilibrium strategies in three different information structures. Their results provide strong support for theory, but they also observe overbidding by lower value bidders in their second price auctions that is consistent with a spite motive. Herrmann and Orzen [20] identify spiteful behavior in two-bidder contests that share some strategic similarities to auctions.
Our results are also consistent with spiteful bidder preferences, and we observe overbidding and underbidding in a pattern consistent with our model of reciprocal spite. Lower value bidders overbid relative to their values, but in response the higher value bidders underbid to punish this overbidding (or at least make overbidding risky). In equilibrium these spiteful social preferences substantially reduce the size of the set of Nash equilibria. Moreover, this combination of spite and reciprocity is the reason that isomorphism fails for the second price and ascending price auction, and the particular pattern of larger and more frequent overbids in the second price auction predicted by the model is also observed in the experimental data.
2. The Model: Spite Bidding with and without Reciprocity
2.1. Known Values (Complete Information)
Consider, for simplicity, the case of two buyers with unit demand of values {v1,v2}, with v1 > v2. In this subsection, we assume that both buyers know each other's values. Although this assumption of complete information about a rival bidder's values is unusual, we consider it for two reasons. First, complete information is a reasonable approximation of auction markets that take place repeatedly between the same set of bidders, such as procurement auctions where bid histories provide information about values (Arora et al. [21]; Cason et al. [22]), and other settings with repeated bidding such as for internet search auctions (Edleman et al. [23]). Second, spiteful motivations are more likely to be triggered in the complete information environment, since bidders know their relative value position. This allows the model to highlight the effect of spiteful reciprocity while eliminating the complexity arising from value uncertainty. This view is also consistent in spirit with the increased information about rivals studied in Andreoni et al. [19] and Cooper and Fang [18] that also consider implications of spite in auctions. Thus, our complete information model provides a useful benchmark for the case of well-informed bidders, which presents the starkest contrast to the more standard incomplete information context, considered below in Section 2.2. As will be seen, an analysis of this complete information context reveals new implications for bidder behavior in auctions.
We consider all values and bids in terms of minimum transaction unit ε > 0, corresponding for example to a minimum currency unit. Let vi ∈ V, i ∈ {1,2}, where V = {0, ε,2ε, ⋯, v̅−ε, v̅},v̅ = u̅ε, and u̅ is a finite positive integer greater than 1. Each buyer chooses a bid bi ∈ Bi = B, i ∈ {1,2}, where Bi = B = {0, ε, 2ε, ⋯, b̅ − ε, b̅}, i ∈ {1,2}, a set of bids commonly available to the two buyers, where b̅ = c̅ε > v̅ and c̅ is a finite positive integer greater than 1. In what follows, we consider only pure bid strategies.
A. Second Price Auction
In the second price auction with two buyers, the winner's payment is equal to the loser's bid. Thus, buyer i's monetary payoff is given by πi : Bi × Bj → ℜ, i, j ∈ {1,2}, i ≠ j, such that
Case 1: The Conventional Model
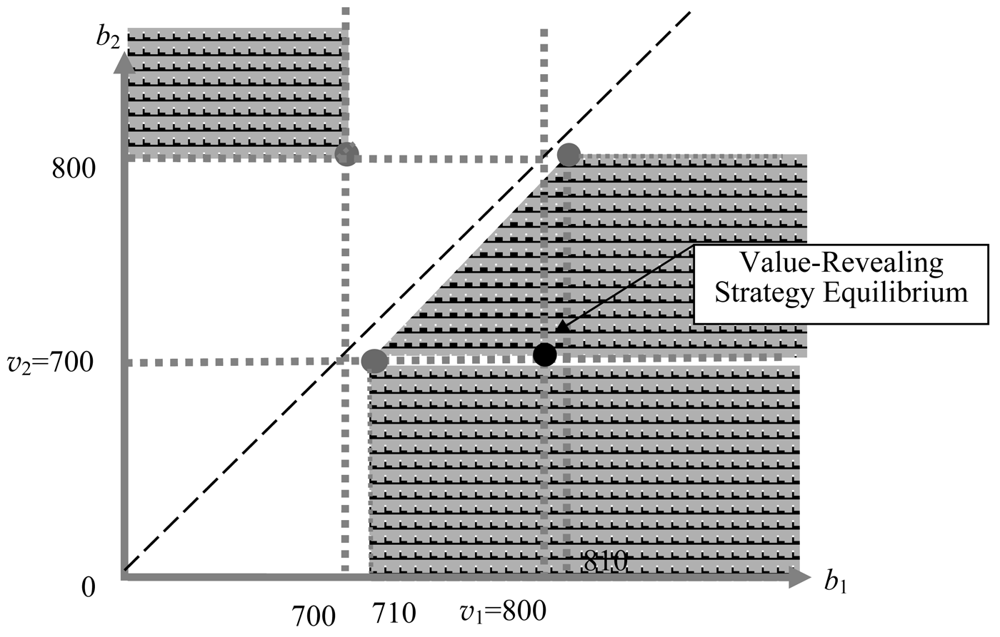
It is well known that the second price auction has multiple Nash equilibria. Figure 1 shows the set of Nash equilibria with two buyers who receive payoff (1) when (v1, v2) = (800, 700). The upper left shaded area is the set of inefficient equilibria where buyer 2 with the lower value wins. The efficient lower right area includes a value-revealing dominant strategy Nash equilibrium [24,25].
In the following, we show that introducing spiteful motivations narrows the set of Nash equilibria and that the equilibrium set also differs between when bidders are spiteful with and without reciprocity.
Case 2: Spite-without-Reciprocity
Morgan et al. [17] present a model of two spiteful buyers who obtain a utility loss when they lose that depends on their rival's amount of monetary winning payoff [26]. There is no element of reciprocity in their model, since buyers become unconditionally spiteful whenever they lose. So we call this case the spite-without-reciprocity model. In their model, buyer i's utility can be represented by
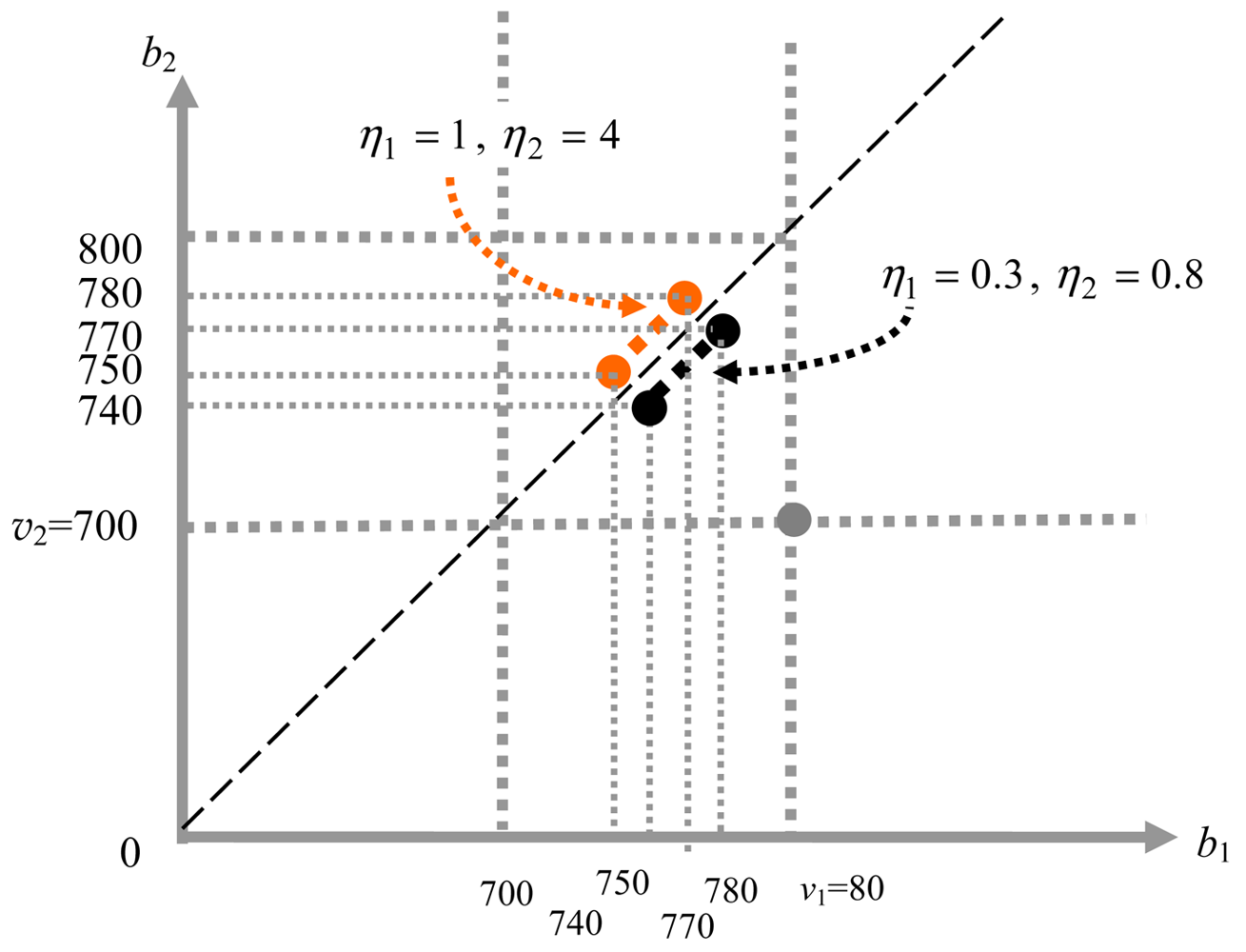
The black dotted line in Figure 2 shows, the set of Nash equilibria for the case with (v1, v2) = (800, 700), ε = 10, η1 = 0.3, and η2 = 0.8. The equilibrium set is much smaller compared to Figure 1, and all of its elements are efficient. When spiteful preferences are stronger, however, as shown by the orange dotted line with η1 = 1 and η2 = 4, all elements of the equilibrium set are inefficient. The condition that determines whether the equilibrium set is efficient is η1η2 < 1. Two points should be noted; one is that the lower bound of the equilibrium set is strictly above (b1, b2) = (v2 + ε, v2) or (b1, b2) = (v2, v2 + ε). The other is that the value-revealing strategy (b1, b2) = (v1, v2) is no longer an equilibrium and there is no equilibrium bid strategy that generates the equivalent monetary outcome of the value-revealing strategy.
Case 3: Spite-with-Reciprocity
The main innovation of our model is to incorporate the possibility of retaliation against a bidder's spiteful behavior. We label this spite-with-reciprocity model. We construct buyers' utility in the spirit of the reciprocity model proposed by Segal and Sobel [14] with some modifications on the specific functional forms [27–31]:
Specifically, consider the case of buyer 1. If b2 ∈ {v2, ⋯, v1 − ε}, buyer 1 should speculate what makes buyer 2 place a bid b2 > v2 since such bids increase the likelihood of a negative monetary payoff if buyer 2's purpose is to win. It is reasonable for buyer 1 to perceive buyer 2's bid deviation from v2 as spiteful, because buyer 2 reduces buyer 1's winning surplus to v1 − b2 from v1 − v2. Hence, the size of bid deviation v2 − b2 corresponds to buyer 1's lost surplus. How much damage the lost surplus means to buyer 1 must be measured relative to the range of buyer 1's potential winning payoff possible with buyer 2's spite bid, which is v1 − v2. Thus, we define buyer 1's weight such that [34]. Recognizing buyer 2's spiteful intention, buyer 1 may reciprocate by placing a deliberately low bid in order to let buyer 2 win with negative winning surplus of v2 − b1.
Consider next the case of buyer 2. The size of bid deviation v1 − b1 reflects the minimum winning surplus that buyer 1 claims. The larger payoff buyer 1 claims, the more spiteful buyer 2 becomes. The size of bid deviation v1 − b1 also corresponds to buyer 1's maximum potential winning surplus that she is willing to forego to retaliate against buyer 2. The impact of bid deviation v1 − b1 should be measured relative to the payoff range v1 − v2. Thus, we define buyer 2's weight by . With these specifications for weights, it is easy to check that the losing payoff of each buyer i, i ∈ {1,2} is increasing in her own bid bi.
Segal and Sobel [14] showed that the Nash equilibrium concept is directly applicable to their general reciprocity model (see [27]). Accordingly, we define the equilibrium of the second price auction as follows.
Definition 1 (Equilibrium in the second price auction)
A strategy profile generates an equilibrium in the second price sealed-bid auction, if for each i, j ∈ {1,2}, i ≠ j, , where BRi : Bj → Bi is buyer i's best response correspondence defined by
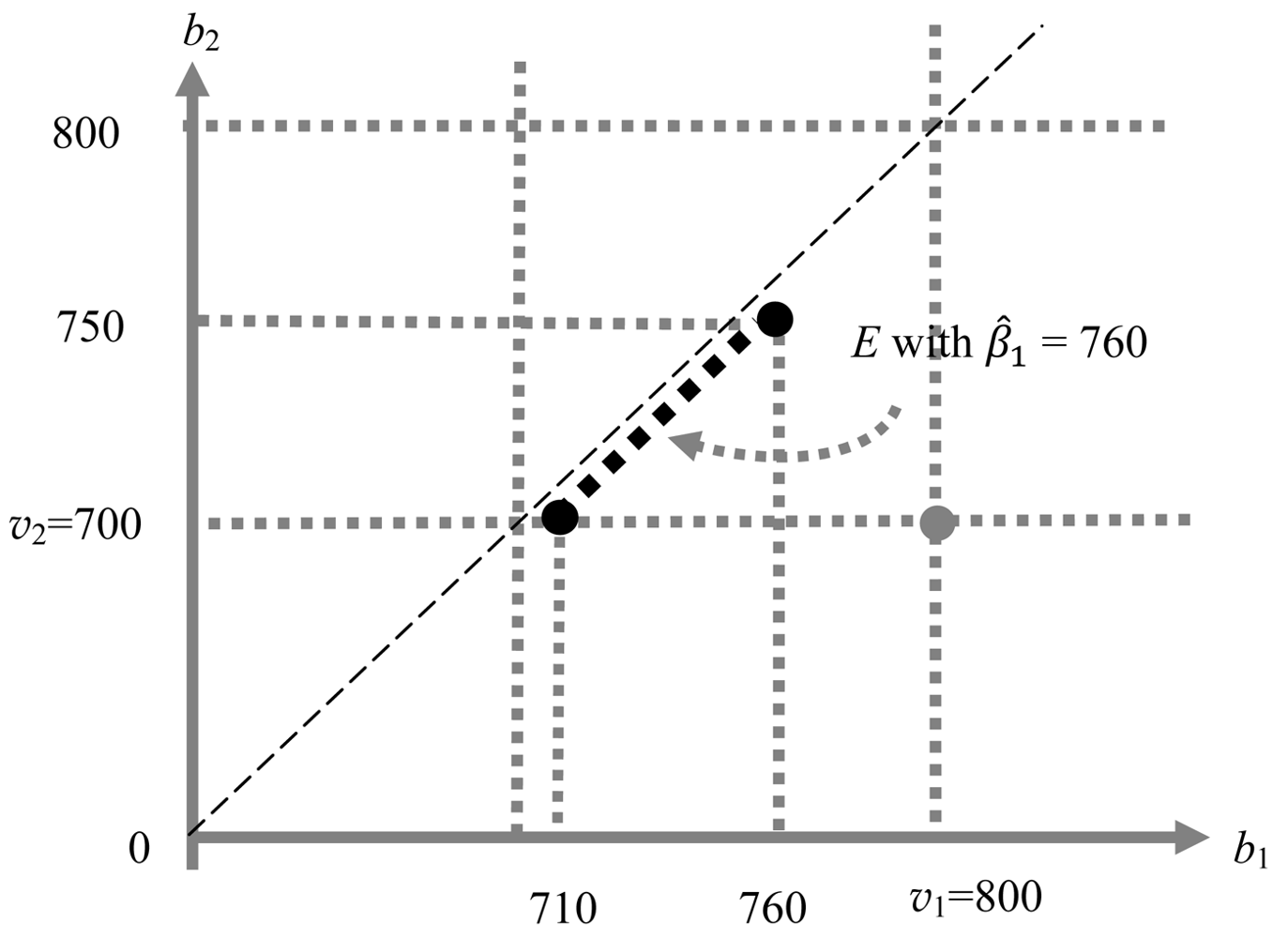
Thus, we can identify the equilibrium set for any (v1, v2) ∈ V × V, v1 > v2, and γ1 ∈ ℜ+, which is formally stated in Proposition 1 below. (Proofs of all propositions and lemmas are collected in Appendices A and B.) Figure 3 shows an example when (v1, v2) = (800, 700) and γ1 = 2. The equilibrium set is represented by a dotted line segment whose lower bound is (b1, b2) = (v2 + ε, v2) = (710, 700) and upper bound is (b1, b2) = (β̂1 + ε, β̂1)= (760, 750), where β̂1 ∈ B1 is the threshold bid for buyer 1 in the following sense [35]; when her rival bids above β̂1, buyer 1 strictly prefers to lose, and weakly prefers to win otherwise. Lemma 1 below summarizes the property of β̂i, i ∈ {1,2} (For details about β̂i and the proof of Lemma 1, see Appendix A-1.) [36].
Lemma 1
(i) There exists a unique threshold bid β̂i ∈ B, for each i ∈ {1,2}. (ii) β̂1 ∈ {v2, ⋯, v1 − ε} and β̂2 = v2.
Proposition 1
The equilibrium set with buyers of the spite-with-reciprocity type is given by
The boundaries of equilibrium set are defined by the two buyers' threshold bids, and the equilibrium set in Figure 3 is much smaller than the one in Figure 1 [37]. Unlike the conventional and the spite-without-reciprocity models, the equilibrium set is always efficient. We can conclude that introducing buyers of spite-with-reciprocity type does not impede efficiency, and it even potentially improves the performance of second price auction, since it eliminates inefficient outcomes from the equilibrium set [38]. Although the value-revealing bid strategy is no longer an equilibrium, the equilibrium bid strategy (b1, b2) = (v2 + ε, v2) = (β̂2 + ε, β̂2), the lower bound of E, generates the equivalent outcome.
B. Ascending-Bid Auction
In an ascending-bid auction the calling price rises by unit ε, and this increase occurs in each unit of time in the clock version. We assume that the initial price is low enough so that both buyers are active at the start. The auction terminates when either buyer withdraws from bidding. If both buyers withdraw simultaneously, the winner is chosen randomly with equal probabilities, and the winner has to pay her own withdrawal bid.
Let r ∈ B denote the calling price, with r = 0 corresponding to the initial stage before the auction starts. At each r, each buyer chooses a bid at which she plans to withdraw. Such a planned withdrawal bid of buyer i at decision point r is denoted by bi,r ∈ Br, where Bi,r = Br = {r, r + ε, −, b̅}, i ∈ {1,2} for all r ∈ B. Note that the decision problem at r = 0 is equivalent to that in the second price auction. Each buyer makes sequential decision at each decision point r as the calling price rises, until she arrives at the actual withdrawal point where bi,r = r. Those sequential decisions of planned withdrawal bids (hereafter bids) {bi,r} are behavioral strategies. Since the ascending-bid auction does not allow buyers to reenter after they withdraw, our analysis focuses on the buyers' behavioral strategies. The auction terminates at the decision point where min{b1,r, b2,r} = r.
We are particularly interested in buyers' behavior when r climbs past v2. When this occurs there is no doubt that buyer 2's bid exceeds v2, which means to buyer 1 that buyer 2 is spiteful. By letting r go beyond v2, buyer 2 eliminates the upper part of possible payoff range of buyer 1 located above v1 − r. The extent of spitefulness toward buyer 1 of the same size of bid deviation v2 − b2 must be different for different range of buyer 1's possible winning payoffs, and so must be the effect of the bid deviation v1 − b1 on buyer 2. We extend our model (3) to the extensive form in the spirit of Dufwenberg and Kirchsteiger [15] based on the behavioral strategies, through modifying the weight , i, j ∈ {1,2}, i ≠ j, of (3) in the following way. The new weight depends on a behavioral strategy bj,r at each decision point r, and especially when r ∈ {v2 + ε, ⋯, v1 − ε}, the weight is updated with the new, smaller denominator v1 − max{v2, r} + ε. Buyer i's utility at r is therefore given by
For each r, we consider the equilibrium set analogous of E in Proposition 1, which we call interim equilibrium set, denoted by Er.
Definition 2 (Interim equilibrium)
At each r ∈ B, let BRi,r(bj,r) denote buyer i's best response correspondence against a given bj,r ∈ Br such that, for i, j ∈ {1,2}, i ≠ j. A bid strategy profile at given r ∈ B is an interim equilibrium, if , i, j ∈ {1,2}, i ≠ j.
For a given r, an interim equilibrium set can be stated as Er = {(b1,r, b2,r) ∈ Br × Br ∣ bi,r ∈ BRi,r(bj,r), i ={1,2}, i ≠ j}. The set E0 at r = 0 is the same as E in the second price auction. Let us call Ernull, if its only element is (b1,r, b2,r) = (r, r). Proposition 2 below describes the properties of non-null interim equilibrium sets. Each non-null Er has its lower bound (b1,r, b2,r) = (max{r, v2} + ε, max{r, v2}) and its upper bound (b1,r, b2,r)=(β̂1,r + ε, β̂1,r), where β̂1,r ∈ Br is the threshold bid for buyer 1 at decision point r, which is the counterpart of β̂1 in the second price auction [41]. Lemma 2 summarizes the properties of β̂i,r, i ∈ {1,2}. By the rule of the ascending-bid auction that prohibits reentry, if Er is null for some, r = r′, then Er is null for all r ∈ {r′ + ε, ⋯, b̅}. Lemma 3 shows that the calling price r̂ identified in Lemma 2 (i) is the lowest r beyond which Er becomes null. Consequently, the auction will never continue beyond r̂.
Lemma 2
There exists r̂ ∈ {v2, ⋯, v1 − ε} such that r̂ = min{r ∈ B∣r = β̂1,r}.
β̂2,r = v2 when r ∈ {0, ⋯, v2}, otherwise no buyer 2's threshold bid exists. There exists unique β̂1,r ∈ {max{v2, r}, ⋯, v1 − ε} for each r ∈ {0, ⋯, r̂} with β̂1,0 = β̂1. No buyer 1's threshold bid exists for r ∈ {r̂ + ε, ⋯, b} except r = v1 where β̂1,r = v1.
β̂1,r = β̂1 for all r ∈ {0, ε, ⋯,v2} and β̂1,r is non-increasing in r, for all r ∈ {v2 + ε, ⋯, r̂}.
Lemma 3
Er is not null for all r ∈ {0, ⋯, r̂} and Er is null otherwise.
Buyer i does not prefer to win against any of her rival's possible bids bj,r ∈ Br, when r falls in the range where no β̂i,r exists (see Appendix A-4). Based on Lemma 2 and 3, we can derive buyers' best response correspondences. (The list of the best response correspondences is available in Appendix (A-5.). By Lemma 3, we can restrict our equilibrium analyses to the case r ∈ {0, ⋯, r̂}.
Proposition 2
The interim equilibrium set Er for all r ∈ {0, ε, ⋯, r̂ − ε} is given by Er = {(b + ε, b) ∈ Br × Br∣max{v2, r} ≤ b ≤ β̂1,r}.
For r = r̂ = β̂1,r, Er̂ = {(r̂ + ε, r̂), (r̂, r̂)} if β̂1, r̂ = β̂1,r̂, and Er̂ = {(r̂ + ε, r̂)} otherwise.
Let Br denote the set of bid profiles whose lower bid is greater than r, defined by Br = {(b1, b2)∣min{b1, b2} ∈ {r + ε, r + 2ε, ⋯, b̅}}. Then, for a given r ∈ {0, ε, ⋯, r̂}, the set Er\(Er ∩ Br) consists of interim equilibrium bid profiles that terminate the auction at r. Thus, these bid strategy profiles constitute equilibrium that ultimately determine the price in the ascending-bid auction. Hence, we define the equilibrium as follows.
Definition 3 (Equilibrium in the ascending-bid auction)
A bid strategy profile is an equilibrium in the ascending-bid auction, if [42].
Proposition 2 together with Lemma 2 implies that we have an inclusion relation among all non-null interim equilibrium sets of the following sort: Er̂ ⊂ Er̂−ε ⊂⋯⊂Ev2 =⋯=E0 = E [43]. The next proposition identifies the equilibrium set in the ascending-bid auction.
Proposition 3
The bid strategy profile is equilibrium in the ascending-bid auction if and only if .
It is immediate that the equilibrium set E \ (E ∩ Br̂) ⊆ E. The upper bound of the equilibrium set of the ascending-bid auction coincides with the upper bound of the set Er̂ which is (b1,r, b2,r) = (r̂ + ε, r̂). It is bounded by the upper bound of the equilibrium set E in the second price auction (b1, b2) = (β̂1 + ε, β̂1), since β̂1,r ≤ β̂1. Furthermore, (β̂1 + ε, β̂1) is bounded by the upper bound of the equilibrium set in the conventional model (v1, v1 − ε).
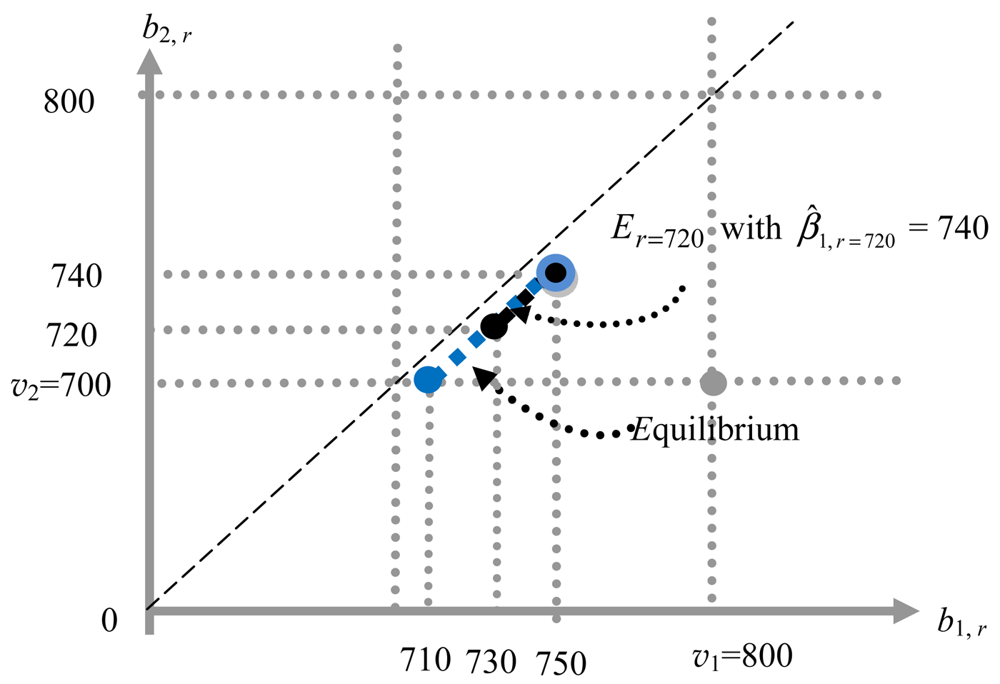
Figure 4 depicts an interim equilibrium set Er when v1 = 800, v2 = 700, γ1 = 2, ε = 10, r = 720, and β̂1,r=720 = 740 as the dark dotted line between (b1, b2) = (r + ε, r) = (730, 720) and (b1,r, b2,r) = (β̂1,r + ε, β̂1,r) = (750, 740). The set E720 in Figure 4 is the proper subset of the equilibrium set E in the second price auction of Figure 3. In this example, since the threshold bid β̂1,r ∈ Br remains the same at 740 for r = 730 and 740 (due to the discreteness of Br [44]), r̂ = 740. Consequently, the equilibrium set of the ascending-bid auction comes down to the blue dotted line connecting between (710, 700) and (750, 740).
The analysis up to this point boils down to the following testable hypothesis: if the bidders are all self-regarding money-maximizing preference types, it is known that the prices observed in the ascending-bid auction should coincide in distribution with those in the second price auction. This also is the case when bidders are the type of spite-without-reciprocity, because the upper bound of corresponding interim equilibrium sets remains the same, which is easy to check. But if some bidders are the type of spite-with-reciprocity, it immediately follows from Proposition 3 that higher prices should be less frequent in the ascending-bid auction than in the second price auction.
2.2. Unknown Values (Incomplete Information)
In the incomplete information case, there are two main differences compared to the complete information case. First, the two players are now perceived as symmetric buyers (ex ante), so that we omit the subscript when there is no risk of confusion. Second, we no longer have a reason to restrict buyers' value sets and bid sets to be discrete with the minimum bid unit ε to ensure the existence of equilibrium.
Let V̅ = [0, v̅] be a closed interval from which each buyer's value is drawn independently. Let G:V̅ → [0, 1] be the cumulative probability distribution of each buyer's value with density function g:V̅ → [0,1], which is common knowledge. In what follows, we consider a buyer whose private value is v ∈V̅, and she perceives her opponent's value as a random variable z ∈ V̅ that follows the cumulative probability distribution G with density function g.
We consider the second price auction as the special case of the ascending-bid auction where the calling price is zero. Thus, our analysis focuses on the ascending-bid auction. Let B̅r = [r, b̅] ⊆ B̅, with b̅ > v̅, and r ∈ B̅0 = B̅ denote buyer's bid set at decision point when the calling price is r. Consider a continuous and continuously differentiable function br : V̅ → B̅r, with br(0) = 0 to represent buyer's withdrawal bid strategy, (hereafter bid strategy for short) at a given decision point r. We focus on a symmetric equilibrium where both buyers employ the same bid strategy br(·), for all r ∈ B̅. Since such a symmetric equilibrium bid function must be strictly increasing in its argument [45,46], each buyer can construct the probability distribution of her opponent's bid from G via the inverse bid strategy function . As the calling price r increases, the possibility of the opponent's bid being less than r is eliminated, so that each buyer updates G conditional on .
Suppose that at a given r, a buyer with value v makes a bid br (x) as if her value is x ∈ V̅. She expects that her opponent with value z will make a withdrawal bid br(z). For a given z, we can construct buyer i's deterministic utility U(br(x), br(z), r) based on the utility (4), where bi,r, bj,r, vi, and vj correspond to br (x), br (z), v, and z, respectively. Then the buyer's expected utility is obtained by taking expectation of U(br (x), br (z), r) with respect to random variable z, denoted by EUz(x, r) ≡ Ez[U(br(x), br(z), r)]. The exact form of buyer's expected utility EUz(x, r) is provided by (B2) in Appendix B-1. Buyer's decision problem at each r is to choose a bid strategy function br(x) that maximizes EUz(x, r) when x = v, for every v ∈ V̅.
Following the same steps in the preceding subsection 2.1B, let us define symmetric interim equilibrium as follows.
Definition 4
Let a function be continuous, continuously differentiabe, and strictly increasing bid strategy for a given r ∈ B̅. Then, the function generates a symmetric interim equilibrium at r if it maximizes EUz ( x, r) ∣x=v for all v ∈ V̅.
For each buyer, her ultimate withdrawal decision point is given by , where her optimal bid coincides with the current calling price.
Definition 5
Let a function b* : V̅ → B̅ be continuous, continuously differentiable, and strictly increasing bid strategy. Then, the function b*(·) generates a symmetric equilibrium in the ascending-bid auction if it maximizes for all v ∈ V̅.
Then the symmetric equilibrium bid function is sequentially rational if it also generates symmetric interim equilibrium at each r ∈ [0, b*−1(v)] ⊂ B̅for all v ∈ V̅.
Proposition 4
There exists a unique symmetric interim equilibrium strategy b*(·) such that b*(v) = v, for all relevant r ∈ [0, b*−1(v)] ⊂ B̅ and for all v ∈ V̅.
Proposition 4 asserts that the value-revealing bid strategy is a unique symmetric equilibrium bid strategy (but not a dominant strategy) in both the second price and ascending-bid auctions. The intuition behind Proposition 4 is simple. In the incomplete information environment, buyers are no longer aware of their relative value position, which is the driving force for their spiteful bids in the complete information case. This result contrasts with Morgan et al. [17] who predict overbidding by all buyers with the spite-without-reciprocity type. Moreover, in contrast to the complete information case considered in the previous section, the incomplete information case with buyers of the spite-with-reciprocity type does not generate any differences in bidding or winning prices between the second price and ascending-bid auctions.
3. Experimental Design
The theoretical model in the previous section generates a range of empirical implications that we evaluated in a controlled laboratory experiment. The experiment consisted of seven sessions of 12 subjects each (84 total subjects), all conducted with undergraduate econ major students at Shinshu University. Subjects bid in a series of two-bidder auctions with one item for sale. Motivated by the differing testable implications derived above, the principal treatment variables were the auction format (ascending-bid versus second price sealed-bid) and information conditions (complete versus incomplete). Both of these treatment variables were varied within sessions, and in four sessions all subjects bid in both formats and both information conditions. In the remaining three sessions subjects only bid in complete information, sealed-bid auctions. Subjects submitted bids for 6 to 10 consecutive periods within each treatment configuration.
A secondary treatment variable was the matching rule. This was also varied within sessions, so sometimes subjects bid against the same opponent for 6 to 10 periods, and at other times subjects bid against randomly-changing opponents every period. We included fixed pairings in some sessions because the multiple equilibria (cf Figures 1–4) may require some coordination. Fixed pairings make this coordination more plausible. The matching rule was common knowledge. The presentation order of both the principal and secondary treatment variables was varied across sessions to control for order effects.
In the complete information treatment, the two possible resale values for the two bidders were 700 and 800 yen. These two values were randomly assigned each period, and this was common knowledge. Therefore, after a bidder learned that her resale value was 800 yen, for example, she knew with certainty that the other bidder's resale value was 700 yen. In the incomplete information treatment, resale values were drawn independently for each bidder each period from the discrete uniform distribution between 500 and 800 yen. The uniform distribution is the most commonly-used distribution in the extensive literature on independent private value auctions (Kagel, [47]). This probability distribution was common knowledge, but individuals only learned their own value draw. Bids were constrained to 10-yen increments, but value draws could be any whole yen amount in the feasible range. In all ascending-bid auction treatments the clock price increased in 10-yen increments.
Subjects received the difference between their resale value and their price paid when they won the auction. The price was determined by the lowest bid or the first drop-out price, depending on the auction format, with the highest or the remaining bidder winning the auction. (Consistent with the theoretical model, ties were resolved randomly.) Subjects received written instructions to describe the auction rules and procedures, which they first read in silence before the experimenter read them aloud. The instructions included both equation and payoff table explanations describing the relationship between bidder actions, allocations, and payoffs. A translation of the instructions is shown in Appendix C. At the conclusion of the session subjects received their cumulative auction earnings in cash, along with a 1,000 yen show-up payment. Payments (including this show-up payment) averaged about 4,500 yen, and ranged between 1,590 and 10,788 yen. Sessions typically lasted about 150 min.
4. Experimental Results
4.1. Overview
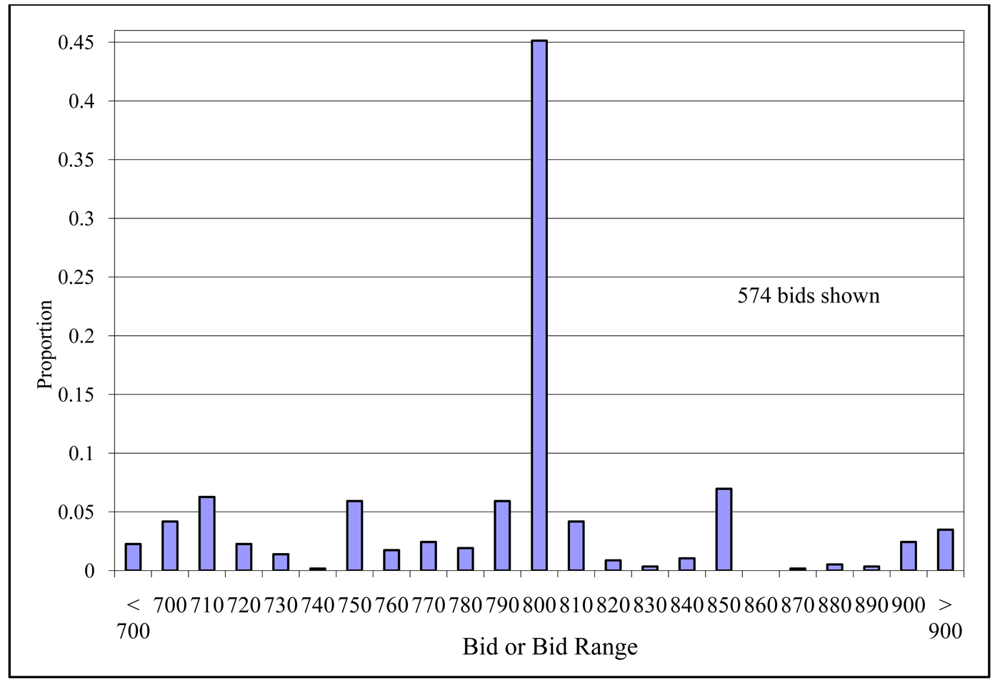
In order to orient the reader, we first summarize the data using a series of figures before turning to formal hypothesis testing. Recall that in the complete information environment, the valuations are either 700 or 800 yen. Figures 5 and 6 display the frequency distribution of bids for the low-value (700) and high-value (800) bidder, respectively [48]. In the ascending-bid auction, 30 of the 291 bids for the low value bidder are not observed directly, since the low-value bidder won the auction when the high-value bidder dropped out. These censored bids are at least as high as this drop-out price, so the minimum bid consistent with these prices (displayed on Figure 5) presents only the lower bound of the intended bid by this low-value bidder [49]. The statistical tests below account for this censoring.
In all panels of these figures, the modal bid equals the bidder's value. Overbidding by the low-value bidder, however, is pronounced in Figure 5. About one-half of all low-value bids exceed 700 (51 percent in the ascending-bid auction and 47 percent in the second-price sealed-bid auction). Conditional on overbidding, the figure suggests that more aggressive bids such as 750 and 790 are more common in the sealed-bid auction. Figure 6 indicates that underbidding is more common than overbidding for the high-value bidder in the sealed-bid auction.
Figure 7 summarizes the bid combinations for the complete information sealed bid auctions in the treatment in which pairs of bidders are randomly re-assigned each period. The modal bid pair is on the value-revealing strategy equilibrium (700, 800), but other pairs are common. Most of the pairs lie to the right of the line drawn on the surface of this diagram. This line indicates where the low-value bid equals the high-value bid. Therefore, the high-value bidder nearly always wins the auction even though many bids deviate from the standard preference, dominant strategy equilibrium.
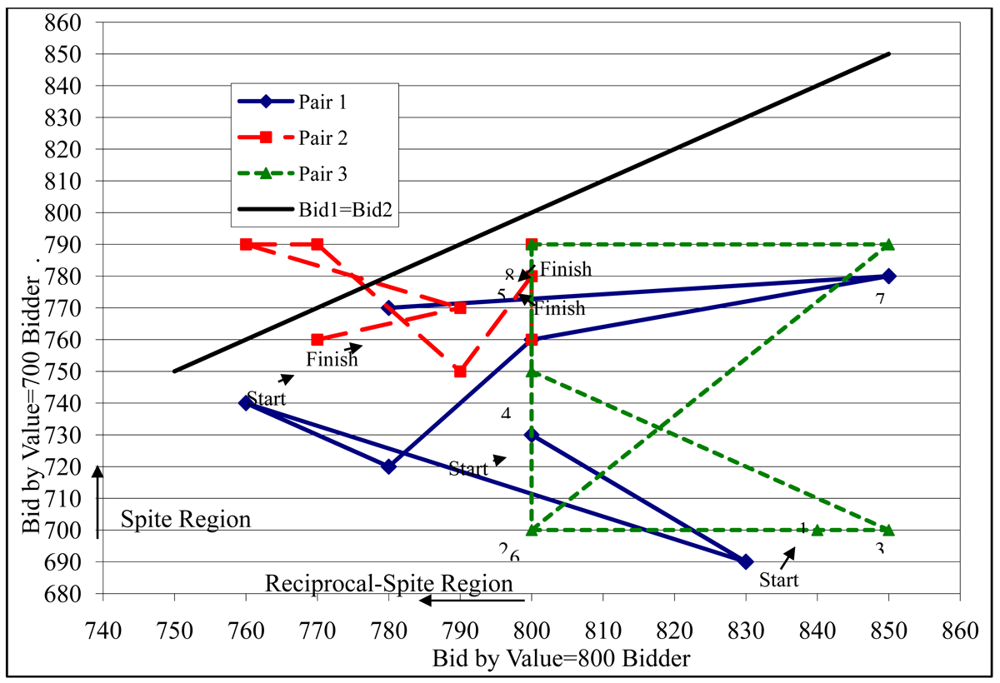
Figure 8 presents the time series path of bids for three example fixed pairs of bidders in this complete information sealed bid environment. Because of these fixed pairings, subjects could react directly to each other's bids in the previous periods. Some pairs (not shown on this figure) often bid repeatedly equal to their value, but many other pairs frequently changed their bids across rounds as illustrated by the three pairs in Figure 8. Typically, bid pairs remain below the Bid1 = Bid2 line that distinguishes the efficient and inefficient allocations. Pairs were also quite heterogeneous. For example, Pair 2 exhibited substantial underbidding by the high-value bidder (even leading to two cases where the low-value bidder won), whereas Pair 3 did not exhibit any such underbidding.
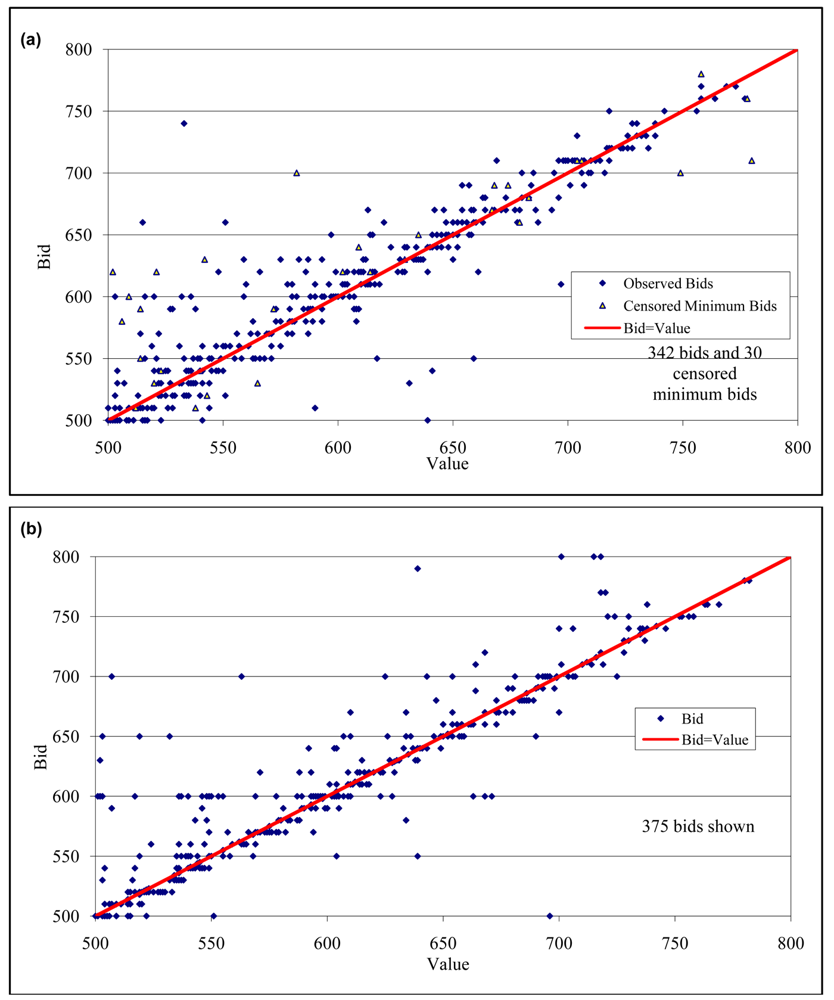
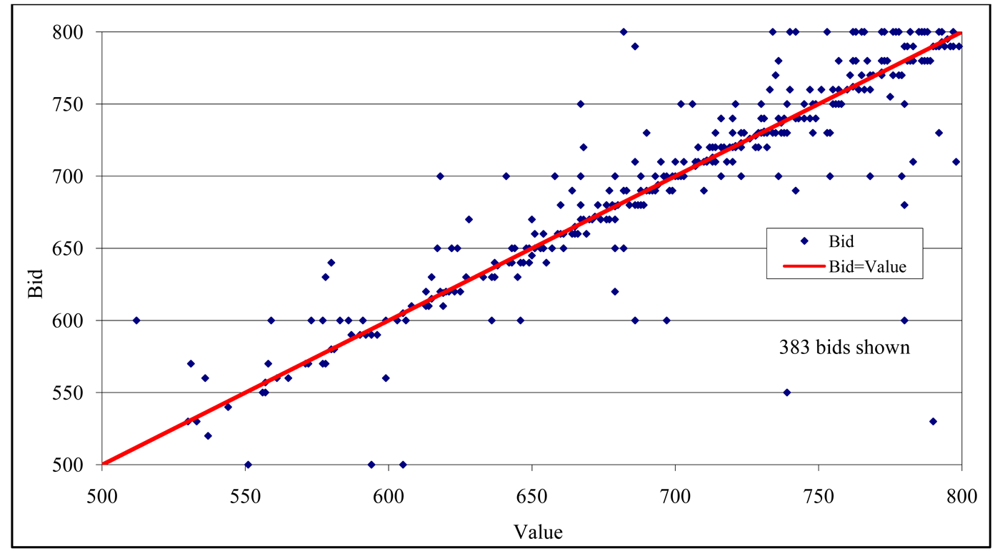
Figures 9 and 10 summarize the bids for the incomplete information environment. Recall that values are drawn from U[500,800]. The figures display bids separately for the buyer with the highest and the lowest value draws, although subjects only observed their own value draw and therefore did not know their ranking. For reference the figures indicate a solid line where bid = value. Again, we do not include the ascending-bid auction bids for the highest value bidder, since this bidder nearly always won the auction and so his bid is typically not observed.
Careful inspection of the figures should remind the reader that bids were constrained to 10-yen intervals, while value draws could correspond to any integer yen amount. Therefore, by design the bidders will typically not be able to bid exactly equal to their drawn value. Overbidding and underbidding appear about equally common on the figures, and on average bids are within one percent of value.
4.2. Hypothesis Testing: Complete Information Environment
This section reports tests of the hypotheses generated by the complete information reciprocity model presented in Section 2.1.
Hypothesis H1
In the complete information environment, (a) low-value bidders overbid relative to their values, and (b) overbidding is more common for low-value bidders than for high-value bidders.
Figure 5 above illustrates widespread overbidding by the low-value bidders. This indicates support for H1. To document the extent of this overbidding, we determined how frequently individuals bid above their value when they had the low value draw in the complete information environment, across both auction institutions. Thirty-nine of the 84 subjects (46 percent) submitted bids greater than their values in at least one-half of these cases. In other words, nearly half of the subjects submitted bids that exceeded their value at least half of the time when they knew that they had the lower value draw. By contrast, only eight out of 84 subjects (10 percent) submitted bids that were less than their values in at least half of these opportunities.
Table 1 reports results from several random-effects regression models to formally test part (b) of Hypothesis H1. These models include a dummy variable to indicate when the bid is submitted by the lower value bidder, and they also control for a time trend (using a standard form 1/period) and for the fixed versus random matching of bidding pairs. The estimates only use the sealed bid auction data, since as already noted the ascending price bids for the high-value bidder are heavily censored because this bidder typically wins.
The regression shown in column 1 determines whether bids relative to values are different between the low-value and the high-value bidders. The difference (Bid – Value) is actually lower for the low-value bidder, but this is mainly because of a small number of “throw-away” and overtly collusive bids, which were more common in the periods with fixed pairs of bidders. Although such bids were relatively rare, they add substantial variance and are a major reason that the regression coefficient estimate does not approach statistical significance. By contrast, the random effect probit model in column 2 is more robust to such outliers, and it indicates that the likelihood of overbidding is much higher for low-value bidders. Low-value bidders overbid 47 percent of the time, whereas high-value bidders overbid only 20 percent of the time. This difference is highly significant and is consistent with Hypothesis H1.
The theoretical model's predictions are based on agents who have spiteful preferences, which suggests that empirical results might be sharper when the analysis is focused more narrowly on those types of subjects. Therefore, columns 3 and 4 present estimates for the subset of subjects who bid above their value at least half the time when they had the low value draw. These 39 subjects represent roughly half the sample and their bids most clearly reveal spiteful preferences. Conclusions drawn for this spiteful subset of bidders are similar to those drawn for the entire sample.
Hypothesis H2
In the complete information environment, (a) low-value bidders bid higher in the second-price sealed-bid auction than in the ascending-bid auction, and (b) overbids (especially large overbids) are more common in the second-price sealed-bid auction than in the ascending-bid auction.
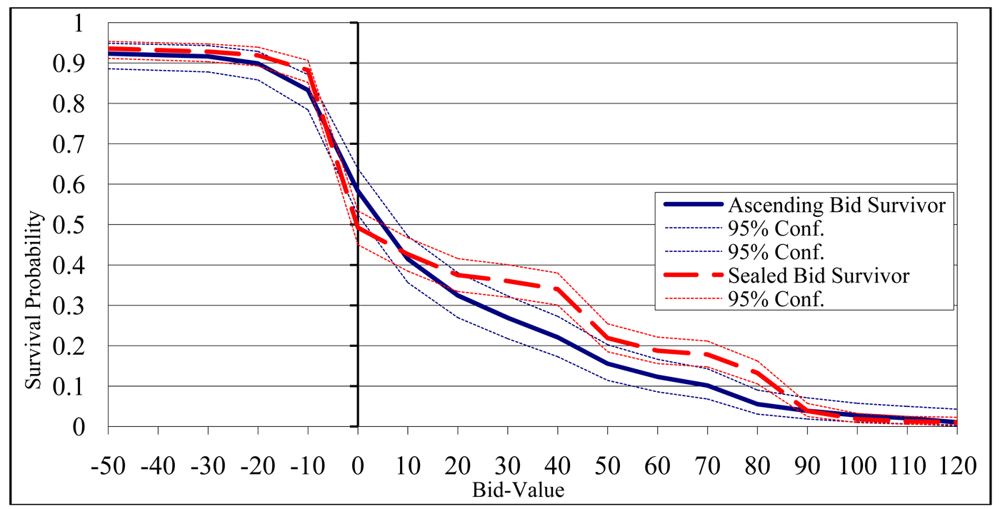
The figures and the summary statistics presented above provide some suggestive evidence in support of H2. For a formal statistical test, however, we must account for the censoring of the bids in the ascending-bid auction. Recall that for this institution we do not observe the bid of the winning bidder—only the price at which the other bidder drops out. This censoring occurs for 30 of the 305 (10 percent) of the low-value bidders' bids. We employ survival analysis to account for this censoring, where “failure” occurs when the rival bidder drops out. The approach we use accounts for differing censoring points since the rival bidder drops out at different prices in different periods.
Figure 11 presents a comparison of the Kaplan-Meier nonparametric estimate of the survival function S(x) = Prob (bid > x) for the two auction forms for the low-value bidders (e.g., see Cameron and Trivedi [50], Chapter 17). The median bid for the ascending-bid auction estimated using this method is 710, compared to 700 for the sealed bid auction. Overbidding (defined as any bid > 700) occurs with probability 0.58 in the ascending-bid auction, and with probability 0.49 in the sealed bid auction. The bid of 700, however, is the only place where the survivor function is higher for the ascending-bid auction. This is due to the higher mode of 700 in the sealed bid auction (cf Figure 5).
For all other bids < 800, the survivor function estimates imply that the sealed bid auction has a higher probability of observing bids exceeding all particular bid prices that are higher than 700. For example, if we define large overbid as a bid greater than or equal to 750, large overbidding occurs with probability 0.22 in the ascending-bid auction, and with probability 0.34 in the sealed bid auction. A log-rank test rejects the null hypothesis that these survivor functions are equal ( ; one-tailed p-value < 0.01). We therefore conclude that the data provide modest support Hypothesis H2, but only for the case of large overbids and not small overbids.
Since large overbids by low-value bidders are more common in the sealed-bid auction, a natural auxiliary hypothesis is that transaction prices are also higher in the sealed-bid auction:
Hypothesis H3
In the complete information environment, (a) transaction prices are higher in the second-price sealed-bid auction than in the ascending-bid auction, and (b) prices above 700 (especially greatly above 700) are more common in the second-price sealed-bid auction than in the ascending-bid auction.
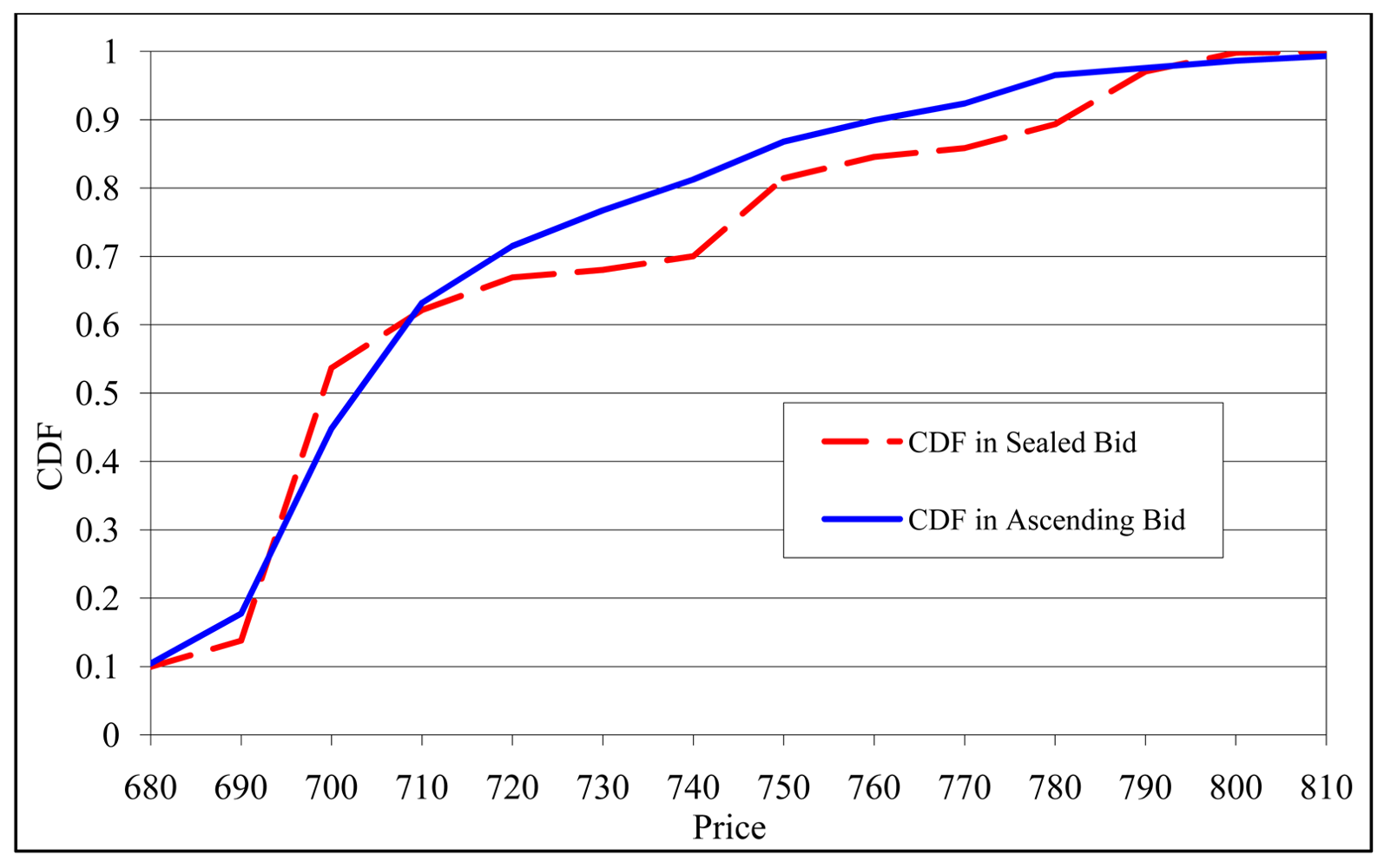
Figure 12 indicates that the cumulative distributions of transaction prices for the two auction institutions are ordered consistent with Hypothesis H3, since the sealed-bid CDF is lower than the ascending-bid CDF for the critical range of prices between 710 and 790. Table 2 indicates, however, that when considering all prices the data fail to reject the hypothesis that prices are equal across institutions (model 1), or that high prices are equally likely in either auction institution (model 2). Many of the prices are in the range of 690 to 710, which occur when the low-value bidder adopts a value-revealing strategy. Therefore, in order to focus on periods in which the low-value bidder exhibits some spiteful behavior, columns 3 and 4 report these same models after excluding the prices that are less than 711. Within this subset of data, which represents 35 percent of the price observations in columns 1 and 2, column 3 shows that transaction prices are significantly higher (by 11 yen) in the sealed-bid auction compared to the ascending-bid auction. Column 4 shows that the estimated likelihood that prices within this subsample exceed 740 increases from 25 percent in the ascending-bid auction to 54 percent in the sealed-bid auction. We therefore conclude that the data support the price differences indicated by Hypothesis H3 only when excluding lower prices that arise from value-revealing bid strategies.
4.3. Hypothesis Testing: Incomplete Information Environment
Section 2.2 established that even with spiteful preferences, in the incomplete information (unknown values) environment a unique symmetric equilibrium strategy exists where each bidder bids at her own value. Figures 9 and 10 indicate that significant dispersion of bids occurs both above and below value in the incomplete information data, partly due to the restriction that bids must be in 10-yen increments. Nevertheless, the data do not reject the null hypothesis that a linear bid function fit on the incomplete information sealed bid data has an intercept of 0 and a slope of 1 ( ; p-value = 0.60), consistent with the equilibrium model and much of the experimental literature on second price and ascending bid auctions with incomplete information. To test the model, however, we need to determine whether bids shift between the complete and incomplete information environments as predicted by spiteful preferences.
Hypothesis H4
(a) Low-value bidders bid higher and (b) high-value bidders bid lower in the complete information environment compared to the incomplete information environment.
Support for this hypothesis may be difficult to obtain since in the incomplete information environment subjects do not know when they have the low or high value draw. They may have reasonably confident beliefs when they have very low value draws near 500 or very high value draws near 800, but not when they have intermediate values in the range between 600 and 700.
Because bids are typically not observed for the higher value bidder in the ascending-bid auction, to test this hypothesis we consider only the sealed bid auction where all bids are observed. In order to make the two environments comparable, we normalize all bids by subtracting the associated value draw. We then regress this difference on a dummy variable for the complete information environment, using the same control variables as in the regressions reported above. To be consistent with Hypothesis H4, the dummy variable for the complete information environment should be positive for low-value bidders (H4a) and negative for high-value bidders (H4b). The results, shown in Table 3, indicate support for Hypothesis H4a but not for H4b, and the support is not strong because it only holds when restricting the analysis to the subsample of frequently overbidding subjects. Estimates are rather imprecise, in part because of a small number of low “throw-away” or collusive bids in the complete information environment noted earlier.
Another implication of the equilibrium result that bids should equal values in the incomplete information environment is that there should not be significant differences between bidding behavior for low and high value bidders.
Hypothesis H5
In the incomplete information environment, overbidding is not more common for low-value bidders than for high-value bidders.
This hypothesis is the counterpart of Hypothesis H1 (b), where for the complete information environment the hypothesis was that overbidding is more common for low-value bidders than for high-value bidders. Recall that Table 1 presented models of bid deviations and overbidding that partially supported Hypothesis H1 (b). The likelihood of overbidding is much higher for low-value bidders in the complete information environment, but the deviation between bid and value was not significantly different between low- and high-value bidders. Table 4 reports the identical models for the incomplete information environment, but this time the research hypothesis (H5) corresponds to the statistical null hypothesis that the dummy variable for the lower value is not significantly different from zero [51]. Consistent with Hypothesis H5, we find no evidence that bidding behavior is different for the low- and high-value bidders.
The final hypothesis is the incomplete information counterpart to Hypothesis H2. Recall that with complete information, overbids by the low-value bidder are predicted to be larger in the second-price compared to ascending-bid auction. By contrast, with incomplete information there should be no systematic difference between the bids across auction institutions.
Hypothesis H6
In the incomplete information environment, (a) lower value bidders do not bid higher in the second-price sealed-bid auction than in the ascending-bid auction, and (b) overbids (especially large overbids) are not more common in the second-price sealed-bid auction than in the ascending-bid auction.
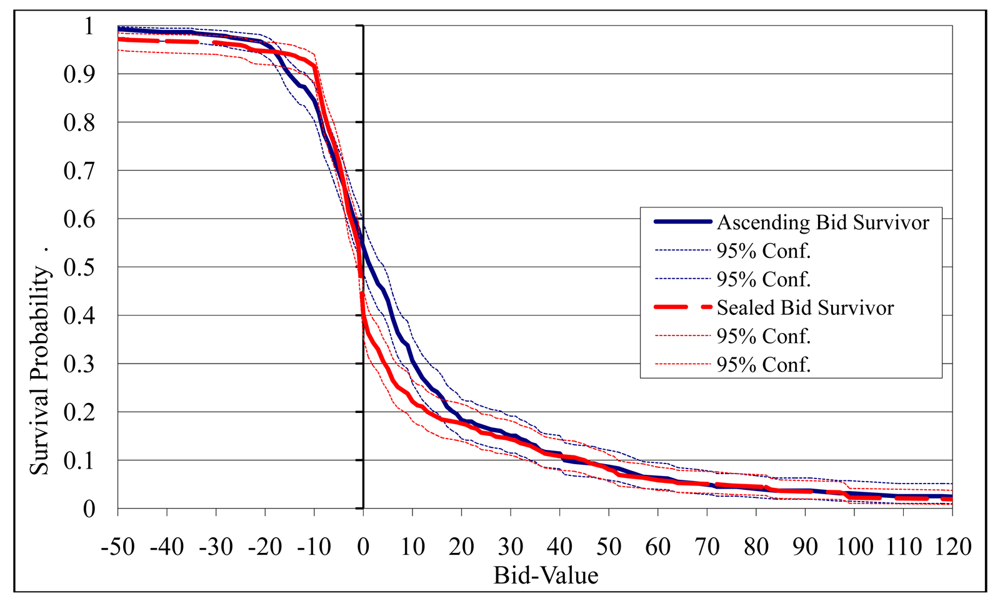
We test Hypothesis H6 in exactly the same way that we tested Hypothesis H2. To account for the bid censoring in the ascending-bid auction, we again employ survival analysis. In the incomplete information environment, this censoring occurs for 30 of the 372 (8 percent) of the low-value bidders' bids. Figure 13 presents a comparison of the Kaplan-Meier nonparametric estimate of the survival function for the two auction forms for the low-value bidders. The median bid for the ascending-bid auction estimated using this method is one yen above value, compared to one yen below value for the sealed bid auction. Overbidding (defined as any bid > value) occurs with probability 0.54 in the ascending-bid auction, and with probability 0.40 in the sealed bid auction. That is, similar to results in the experimental literature with incomplete information about rival values, bids are above and below value with approximately equal frequency. (Recall that bids exactly on values are not common in our environment due to the restriction that bids had to be in 10-yen increments.) There is virtually no evidence that the frequency of large overbids is different for the two auction institutions, and the survivor functions are essentially identical for all bids that are 20 or more yen greater than value. Moreover, a log-rank test fails to reject the null hypothesis that these survivor functions are equal ( ; p-value = 0.15). We therefore conclude that the data support Hypothesis H6: Overbidding by low value bidders in the incomplete information environment is not different in the sealed-bid and ascending-bid auctions.
5. Conclusions
We have investigated bidding behavior in both complete and incomplete information environments for two-person second price sealed-bid auctions and ascending-bid auctions for a single indivisible object with independent private values. Our intention-based bidding model features individuals who are reciprocally spiteful. A lower value bidder may be spiteful in the sense that he receives a positive psychological payoff when he loses if he reduces the winners' payoff. A high-value bidder who faces a spiteful bidder's over-bidding would reciprocate by underbidding to increase the likelihood that the spiteful bidder wins and incurs a negative monetary payoff. The possibility of this underbidding causes such spiteful bidders to refrain from bold overbidding. Our theoretical analysis in the complete information environment indicates that the equilibrium bidding strategy differs from the Nash equilibrium strategy set generated without spite and reciprocity, in the following three respects. First, the equilibrium strategy set is much smaller and does not contain any inefficient outcomes. Second, although a strategy of “bidding at one's value” is no longer part of an equilibrium strategy profile, the equivalent outcome in which the lower value bidder bids at her own value and loses is one of the equilibrium outcomes. Third, the threat of reciprocal underbidding is more important in ascending-bid auctions than second price sealed-bid auctions, since a rising calling price directly reveals the spiteful intention of a low-value bidder. This leads to a lower equilibrium spiteful over-bidding in ascending-bid auctions, which implies an even smaller equilibrium set with lower price upper bound.
As summarized in Table 5, our experimental results provide qualified support for the model's theoretical predictions. In the complete information setting, nearly half of the bids are consistent with spiteful overbidding. Bidders with lower private values are more prone to overbid in both auction formats, and large overbids and high prices are more common in the second price auctions than in the ascending-bid auctions. However, such systematic overbidding disappears when bidders' private values are unknown in the incomplete information setting. This is also consistent with the model, which predicts value-revealing bidding behavior as the unique symmetric Nash equilibrium, although this is not a dominant strategy equilibrium. Overall, results tend to be more consistent with the spite model that features reciprocity than the conventional or the spite-without-reciprocity models.
Subjects' decision-making seems to be different when they do or do not know each other's values. When they have complete information about all bidders' values, this allows them to evaluate their relative payoffs. A low-value bidder in our environment who bids 750, for example, knows that this bid will likely reduce the winning bidder's payoff by half relative to the payoff if all bids equal values. A bidder with the higher value can also perceive the spiteful intentions of her opponent's bid in the complete information environment. It is this spiteful intention that induces underbidding by the higher value bidder. This is the driving force behind our theoretical result that bidders make more timid overbids in the ascending-bid auction, because the rising calling price directly reveals the lower value bidder's spiteful intention. This can be interpreted as an additional evidence of negative reciprocity at work, but here in the context of an auction, consistent with negative reciprocity observed in the context of ultimatum and related games (e.g., see Charness and Rabin [28]).


| Model | All Bidders | Frequent Over-Bidders | ||
|---|---|---|---|---|
| 1 (Random Effects GLS) | 2 (Random Effects Probit) | 3 (Random Effects GLS) | 4 (Random Effects Probit) | |
| Dependent Variable | Bid − Value | = 1 if Bid > Value | Bid − Value | = 1 if Bid > Value |
| Dummy Variable = 1 if | −35.03 | 1.30** | −6.12 | 1.54** |
| Lower Value | (47.56) | (0.12) | (38.10) | (0.15) |
| Dummy Variable = 1 for | 5.40 | 0.22* | 20.72 | 0.08 |
| Fixed Pairings | (5.95) | (0.11) | (26.49) | (0.13) |
| 1/period | 94.99 | −0.11 | 155.03 | −0.26 |
| (85.23) | (0.19) | (170.91) | (0.23) | |
| Intercept | −21.17 | −1.61** | −28.47 | −0.45* |
| (27.18) | (0.22) | (46.29) | (0.20) | |
| Observations | 1150 | 1150 | 542 | 542 |
| Number of Bidders | 84 | 84 | 39 | 39 |
| R2 or Log-likelihood | 0.01 | −470.0 | 0.01 | −273.5 |
Notes: Standard errors (in parentheses) are based on a subjects random effects model and for the GLS regressions in columns 1 and 3 are calculated to be robust to unmodeled correlation of choices within clusters defined by sessions.*denotes significantly different from zero at the five-percent level, and**denotes significantly different from zero at the one-percent level.
| Model | All Prices | Excluding Prices < 711 | ||
|---|---|---|---|---|
| 1 (Random Effects GLS) | 2 (Random Effects Probit) | 3 (Random Effects GLS) | 4 (Random Effects Probit) | |
| Dependent Variable | Price | = 1 if Price > 740 | Price | = 1 if Price > 740 |
| Dummy Variable = 1 if | −16.73 | 0.04 | 11.36** | 0.77** |
| Sealed-Bid Auction | (12.51) | (0.12) | (3.07) | (0.16) |
| Dummy Variable = 1 | -28.73** | −0.05 | −4.73 | −0.17 |
| for Fixed Pairings | (10.87) | (0.10) | (2.91) | (0.15) |
| 1/period | 27.14 | −0.02 | −3.98 | −0.20 |
| (19.21) | (0.17) | (4.92) | (0.25) | |
| Intercept | 697.19** | −0.66** | 754.09** | 0.22 |
| (18.18) | (0.21) | (3.59) | (0.18) | |
| Observations | 887 | 887 | 312 | 312 |
| Number of Sessions | 7 | 7 | 7 | 7 |
| R2 or Log-likelihood | 0.01 | −465.6 | 0.05 | −178.7 |
Notes: Standard errors (in parentheses) are based on session random effects models.*denotes significantly different from zero at the five-percent level, and**denotes significantly different from zero at the one-percent level.
| Model | All Bidders | Frequent Over-Bidders | ||
|---|---|---|---|---|
| 1 (Lower Value Bidders) | 2 (Higher Value Bidders) | 3 (Lower Value Bidders) | 4 (Higher Value Bidders) | |
| Dependent Variable | Bid − Value | Bid − Value | Bid − Value | Bid − Value |
| Dummy Variable = 1 if | −43.03 | 6.34 | 24.86* | 27.86 |
| Complete Info. | (40.96) | (14.48) | (12.07) | (29.76) |
| Environment | ||||
| Dummy Variable = 1 for | −20.28 | 21.53 | −27.16 | 51.78 |
| Fixed Pairings | (17.24) | (12.32) | (18.27) | (42.97) |
| 1/period | 20.57 | 88.07 | 20.61 | 203.74 |
| (18.21) | (82.36) | (23.37) | (218.76) | |
| Intercept | 27.66 | −34.26 | 15.41** | −90.53 |
| (20.02) | (36.82) | (4.40) | (101.01) | |
| Observations | 957 | 956 | 424 | 391 |
| Number of Bidders | 84 | 84 | 39 | 39 |
| R2 | 0.00 | 0.01 | 0. 02 | 0.02 |
Notes: Standard errors (in parentheses) are based on a subjects random effects model and are calculated to be robust to unmodeled correlation of choices within clusters defined by sessions.*denotes significantly different from zero at the five-percent level,**denotes significantly different from zero at the one-percent level.
| Model | All Bidders | Frequent Over-Bidders | ||
|---|---|---|---|---|
| 1 (Random Effects GLS) | 2 (Random Effects Probit) | 3 (Random Effects GLS) | 4 (Random Effects Probit) | |
| Dependent Variable | Bid − Value | = 1 if Bid > Value | Bid − Value | = 1 if Bid > Value |
| Dummy Variable = 1 if | −4.30 | −0.05 | −13.69 | −0.10 |
| Lower Value | (6.70) | (0.13) | (7.25) | (0.20) |
| Dummy Variable = 1 for | −3.58 | 0.86** | −15.11 | 1.11** |
| Fixed Pairings | (5.40) | (0.13) | (13.10) | (0.20) |
| 1/period | −2.30 | −0.76** | 11.07 | −0.43 |
| (5.22) | (0.23) | (10.44) | (0.35) | |
| Intercept | 3.16 | −0.85** | 17.28* | 0.05 |
| (3.36) | (0.30) | (6.99) | (0.35) | |
| Observations | 763 | 763 | 273 | 273 |
| Number of Bidders | 48 | 48 | 17 | 17 |
| R2 or Log-likelihood | 0.00 | −325.8 | 0.02 | −136.2 |
Notes: Standard errors (in parentheses) are based on a subjects random effects model and for the GLS regressions in columns 1 and 3 are calculated to be robust to unmodeled correlation of choices within clusters defined by sessions.*denotes significantly different from zero at the five-percent level, and**denotes significantly different from zero at the one-percent level.
| Complete Information | Incomplete Information | |||||||
|---|---|---|---|---|---|---|---|---|
| Theoretical Prediction | Consistent with Hypothesis: | Theoretical Prediction | Consistent with Hypothesis: | |||||
| H1 | H2 | H3 | H4 | H5 | H6 | |||
| Conventional Model | S = A, b(v) = v | No | No | No | S = A, b(v) = v | No | Yes | Yes |
| Spite without Reciprocity | S = A, b(v) ≠ v | Yes | No | No | S = A, b(v) > v | No | Yes | Yes |
| Spite with Reciprocity | S = A, b(v) = v | Yes | Yes (for large overbids) | Yes (for prices > 710 | S = A, b(v) = v | Yes (for spiteful low value bidders) | Yes | Yes |
S: Bidding in a second price auctionA: Bidding in an ascending-bid auctionb(·): bid strategy
Acknowledgments
Financial support was provided by Grant-in-Aide for Scientific Research by Japanese Education Ministry #14330003 and #19330041. We are grateful for valuable comments provided by Masaki Aoyagi, Takuma Wakayama, conference audiences at the European Regional Meeting of the Economic Science Association, the Asian-Pacific Regional Meeting of the Economic Science Association, the Annual Conference of Experimental Economics in Japan, and seminar audiences at Osaka University, Tokyo University, and Kobe University. We acknowledge research assistance by H. Fujii, K. Suzuki, K. Kondo, H. Ohki, R. Tanaka, N. Mizuno, and H. Ando. An earlier version of this paper circulated under the title “Spite and Counter-Spite in Auctions.”
Appendix A: Known Values Case (Complete Information)
A-1. Property of β̂i and Proof of Lemma 1
To identify buyer i's threshold bid β̂i ∈ B, it is convenient to consider for a moment the larger bid strategy set B̅ = [0, b̅] ⊂ ℜ. Consider the following difference between the winning payoff and losing payoff of buyer i:
Specifying bi = bj = x and in , we define φi: B̅ → ℜ, i ∈ {1,2} by
A solution for φi (x) = 0 denoted by βi ∈ B̅ is the threshold tie bid, in the sense that buyer i strictly prefers to win when bj < βi, strictly prefers to lose when bj > βi, and weakly prefers to win by placing at least a tie bid when bj = βi. This is because buyer i's losing payoff is increasing in her own bid, so that the tie bid βi equates her winning payoff with her maximum losing payoff. Let us first prove the next lemma which characterizes βi, i ∈ {1,2}.
Lemma A1
(i) There exists a unique solution βi ∈ B̅ for each i ∈ {1,2}; (ii) β1 ∈ (v2, v1) and β2 = v2.
Proof of Lemma A1
Consider the case of buyer 2 first. The solution β2 to φ2(x) = 0 of (A2) is clearly unique and β2 = v2. Next, consider the case of buyer 1. It is easy to check that φ1(x) > 0 for all x ∈ [0, v2] and φ1(x) < 0 for all x ∈ [v1, b̅]. For all x ∈ (v2, v1), the function φ1(x) is continuous and differentiable with respect to x, and we have dφ1(x) / dx = −1 + 2γ1(v2 − x) / D < 0. Therefore, the solution β1 ∈ B̅ to φ1 (x) = 0 is unique and lies between v2 and v1.
For a given solution βi ∈ B̅, i ∈ {1,2}, we find its nearest number β̂i ∈ B such that βi ∈ [β̂i, β̂i + ε). Then, Lemma 1 immediately follows from Lemma A1.
A-2. Best Response Correspondences in the Second Price Auction
Let us state the best response correspondence for each buyer, which we repeatedly use in the proof of Proposition 1 below. The best response correspondence of buyer 2 for a given buyer 1's bid can be given by
Buyer 1's best response correspondence for a given buyer 2's bid can be stated as
A-3. The Equilibrium Set in the Second Price Auction
Proof of Proposition 1
Suppose that a bid profile . From (A3), (A4), and (A4′), it is easy to check that and .
Conversely, suppose that and . Let us first check the case where β1 = β̂1. Suppose that in the third line of (A4). Buyer 1's best response to is . Since b1 ∈ {β̂1, ⋯, b̅ − ε}, buyer 2's best response is b2 = b1 − ε by condition (A3), and therefore no equilibrium exists with . Consider or in the first line of (A4). Suppose the former case. Buyer 1's best response is . The first and the second lines of (A3) show that . Therefore, no equilibrium exists with . Suppose that . Buyer 1's best response is so that b1 ∈ {v2 + ε, ⋯, b̅}. From the third line of (A3), buyer 2's best response to b1 is b2 =b1 − ε whose range is consistent with . Therefore is an equilibrium. Suppose that . Recalling that β̂1 ∈ {v2, ⋯, v1 − ε}, we find that b1 = β̂1 + ε is the only best response of buyer 1 such that , from (A3) and (A4). Consequently, for is the only equilibrium bid profile.
As for the case where β1 ≠ β̂1 so that β1 ∈ (β̂1, β̂1 + ε), a similar analysis can be carried out based on (A3) and (A4′), and this leads to the same conclusion.
A-4. Property of β̂i,r and Proof of Lemma 2
We follow the same steps we used in Section A-1. First, consider the difference between buyer i's winning and losing payoff at a decision point r in the ascending-bid auction as below:
Specifying bi,r = bj,r = xr and in , we define ϕi: B̅r × B̅ → ℜ, i ∈ {1,2} by
Lemma A2
For r ∈ [0, v1), there exists a unique r̅ ∈ (v2, v1) such that r̅ = β1,r̅. For r ∈ [v1, b̅], there exists a unique r = v1 such that β1,v1 = v1.
There exists a unique solution β1,r ∈ (v2, v1) for all r ∈ [0, r̅].
For all r ∈ [0, v2], β1,r = β1,0 = β1. For all r ∈ (v2, r̅], β1,r is strictly decreasing in r.
There is no solution to ϕ1(x, r) = 0 for all r ∈ (r̅, b̅], except r = v1.
Proof of Lemma A2
(i) We can identify r̅ = β1,r̅ as a solution xr to ϕ1(xr, r)∣r=xr = 0. Consider r ∈ [v1, b̅]. It is immediate from the first line of (A5) that r̅ = v1 and it is unique. Consider next r ∈ [0, v1). From the second line of (A5), r̅ is a solution to
Note that ϕ1(xr, xr) is continuous in xr. Since ϕ1(v2, v2) = v1 − v2 > 0 and ϕ1(v1, v1) = −γ1((v2 − v1)2/ε) < 0, by the mean value theorem, a solution xr = r̅ exists and satisfies r̅ ∈ (v2, v1). Also the derivative of ϕ1 (xr, xr) with respect to xr ∈ (v2, v1) is given by
(ii) and (iii) βi,r ∈ B̅r is the solution to ϕ1(xr, r) = 0 for given r. Consider either r ∈ [0, v2] or r ∈ (v2, v1) and examine the second line of (A5);
Consider first r ∈ [0, v2]. Then, (A8) coincides with (A1). Therefore there exists unique β1,r = β1,0 = β1 for all r by Lemma A1. Next consider r ∈ (v2, v1). Let us solve (A8) momentarily for xr ∈ B̅ instead of xr ∈ B̅r, and denote the solution by β̅1,r. For given r, ϕ1 (xr, r) > 0 for all xr ≤ v2, and ϕ1(xr, r) < 0 for all xr ≥ v1. Since ϕ1(xr, r) is a continuous quadratic function of xr, by the mean value theorem there exists unique solution β̅1,r ∈ (v2, v1) for each r ∈ (v2, v1). To examine whether β̅1,,r ≥ r, let us apply the implicit function theorem to ϕ1(β̅1,r, r) = 0, since ϕ1(xr, r) is continuous and differentiable with respect to both arguments. Then, we obtain
(iv) From the first line of (A5), there is no solution to ϕ1 (xr, r) = 0 for r ∈ (v1, b̅]. Since we have just observed that there is no solution for r ∈ (r̅, v1) in the proof of (iii), this establishes the result.
The second step is to find a number β̂1,r ∈ Br such that β̂1,r ∈ [β̂1,r, β̂1,r + ε) for each relevant r ∈ B. In the main text, we call this number β̂1,r ∈ Br the threshold bid for buyer 1 at decision point r. As we have already observed that β̂2,r = v2, β̂2,r = v2 for r ∈ {0, ⋯,v2}, and no buyer 2's exists otherwise. This proves the part of Lemma 2(ii) regarding β̂2,r. Lemma A2′ below immediately follows from Lemma A2, which facilitates the proof of the rest of Lemma 2.
Lemma A2′
There exists r̂ ∈{v2, ⋯, v1 − ε} such that r̂ = min{r ∈ B∣ r = β̂1,r}.
There exists a unique threshold bid β̂1,r ∈ {max{v2, r}, ⋯,v1 − ε} for each r ∈ {0, ∈, ⋯, r̂}.
For all r, r′ ∈ {0, ε, ⋯, v2}, β̂1,r = β̂1,r′, whereas for all r ∈ {v2 + ε, ⋯, r̂}, β̂1,r is non-increasing in r.
There is no threshold bid for buyer 1 for all r ∈ {r̂ + ε, ⋯, b̅}, except r = v1.
A-5. The Best Response Correspondences in an Ascending-bid Auction
The best response correspondence of buyer 2 for a given buyer 1's bid at decision point r ∈ {0, ⋯, v2 − ε} can be stated as
Buyer 1's best response correspondence for a given buyer 2's bid at decision point r ∈ {0, ⋯, r̂} can be stated as
For r ∈ {r̂+,ε, ⋯, v1− ε },
A-6. Proof of Lemma 3
An interim equilibrium set Er is called null if Er = {(r, r)}. If Er−ε is not null and there is only one active buyer, then the auction terminates at r − ε and buyers will never reach the decision point r and beyond, by the rule of ascending-bid auction which prohibits reentry. Thus, proving Lemma 3 is equivalent to proving the following Lemma 3′.
Lemma 3′
r = r̂ + ε is the minimum r at which Er is null, where r̂ = β̂1,r̂.
Proof of Lemma 3′
Consider the case r = r̂ + ε. Note that r̂ ∈ {v2, ⋯, v1 − ε} from Lemma A2′. Suppose that b1,r = r. From the first line of (A10′) or (A10″), buyer 2's best response is b2,r = r. From the second line of (A11″), buyer 1's best response is also b1,r = r, so that (b1,r, b2,r) = (r, r) is interim equilibrium at r. Next suppose that b1,r = r + ε = r̂ + 2ε. From the second line of (A10″) or (A10‴), buyer 2's best response is b2,r =b1,r −ε=r̂+ε=r when r̂ + ε ≤ ε as well as when r̂ + ε = v1. By (A11″), (b1,r = r + ε) ∉ BR1,r(b2 = r). Consequently at r = r̂ + ε, the set Er is a singleton with (b1,,r, b2,r) = (r, r), so that Eris null.
Consider the case r = r̂ and β1,r̂ = β̂1,r̂. Suppose that b1,r = r. From the first line of (A10′) and (A10″), buyer 2's best response is b2,r = r. From the second line of (A11), (b1,r = r) ∈ BR1,r(b2,r = r). Suppose that b1,r = r + ε. Buyer 2's best response is b2,r = b1,r − ε = r from the second line of (A10″) or (A10″). Then (b1,r = r + ε) ∈ BR1,r(b2,r = r) from the second line of (A11). Suppose that b1,r ≥ r + 2ε. Buyer 2's best response is b2,r = b1,r − ε = r + ε. Since b2,r > β̂1,r, from the third line of (A11), {b1,,r ∣ b1,,r ≥ r + 2ε} ⊄ BR1,,r (b2,r =r + ε). It follows that Er̂ = {(r̂ + ε, r), (r̂, r̂)}, which is not null.
Consider the case r = r̂ and β1,r̂ ∈ (β̂1,r̂, β̂1,r̂ + ε). Suppose that b1,r = r. From the first line of (A10′) or (A10″), buyer 2's best response is b2,r = r. From the first line of (A11′), (b1,r = r) ∉ BR1,r(b2,r = r). Suppose that b1,r = r + ε. Buyer 2's best response is b2,r = b1,r − ε = r from the second line of (A10′) or (A10″). Then (b1,r = r + ε) ∈ BR1,r(b2,r = r) from the first line of (A11′). Suppose that b1,r ≥ r + 2ε. Buyer 2's best response is b2,r = b1,r − ε = r + ε. Since b2,r > β̂1,r, from the second line of (A11′), {b1,r∣b1,r ≥ r + 2ε} ⊄ BR1,r(b2,r = r + ε). Therefore Er̂ = {(r̂ + ε, r̂)}, which is not null.
To sum up, Er̂+ε = {(r̂ + ε, r + ε)}, and either Er̂ = {(r̂ + ε, r̂), (r̂, r̂)} or Er̂ = {(r̂ + ε, r̂)}. Hence, r = r̂ is the maximum r whose interim equilibrium set is not null. Buyers will never reach the decision point r ≥ r̂ + ε by the rule of ascending-bid auction.
A-7. The Interim Equilibrium in an Ascending-bid Auction
Proof of Proposition 2
Since bidding at r ≥ r̂ + ε will never be realized by Lemma 3, the equilibrium analysis should be focused on the case r ∈ {0, ε, ⋯, r̂}.
(ii) The part of Proof of Lemma 3′ dealing with the case r = r̂ = β̂1,r provides the proof.
(i) Suppose that . Since β̂1,r ∈ {v2, ⋯ v1 − ε}, it is clear from (A10), (A10′), (A10″), (A11), and (A11′) that and .
Conversely, suppose that and . Let us first check the case β1,r = β̂1,r. Suppose that in the third line of (A11). Buyer 1's best response is , and b1,r ∈ {β̂1,r, ⋯, b − ε}. Buyer 2's best response is by the third line of (A10), the second line of (A10′), or (A10″). Therefore there is no interim equilibrium with .
Suppose next that for r ∈ {0, ε, ⋯, v2 − ε} in the first line of (A11). Buyer 1's best response is . If b1,r ∈ {r + ε, ⋯, v2 − ε}, the first line of (A10) shows that buyer 2's best response is b2,r ≥ b1,r + ε. If b1,r = v2, buyer 2's best response is b2,r ≥ v2 from the second line of (A10). In neither case, b2,r is consistent with . If b1 ∈ {v2 + ε, ⋯, b̅}, buyer 2's best response is b2,r = b1,r − ε from the third line of (A10) so that b2,r ∈ {v2, ⋯, b̅ − ε} which is again not consistent with . Therefore, there is no interim equilibrium with when r ∈ {0, ε, ⋯, v2 − ε}.
To examine the remaining case of , in the first line of (A11), let us first consider r ∈ {0, ε, ⋯, v2}. Suppose that . Buyer 1's best response is from (A11) so that b1,r ∈ {v2 + ε, ⋯, b̅}. From the third line of (A10) or the second line of (A10′), buyer 2's best response is b2,r = b1,r − ε. Therefore by (A10), (A10′) and (A11), buyer 1's best response must be so that b1,r ∈ {v2 + ε, ⋯, β̂1,r} is consistent with . Suppose next that . Since β̂1,r ∈ {v2, ⋯, v1 − ε}, b1,r = β̂1,r + ε is the only best response of buyer 1 such that from the second line of (11) and (A10′) or the third line of (A10).
Second, consider the case r ∈ {v2 + ε, ⋯, r̂ − ε}. Suppose that . It is easy to check from (A10″) and the first line of (A11) that is buyer 1's only best response such that . Suppose that . From (A10″) and the second line of (A11), is buyer 1's only best response such that . Consequently, the bid profiles that satisfy and must be where .
The last case to examine is the case where β1,r ≠ β̂1,r so that β1,r ∈ (β̂1,r, β̂1,r + ε). Based on the conditions (A11′) instead of (A11) together with (A10) and (A10′), we can carry out similar analysis and derive the same conclusion.
A-8. The Equilibrium in an Ascending-Bid Auction
Proof of Proposition 3
Proposition 2 implies that no buyer stops the auction at any r ∈ {0, ⋯, v2 − ε}, so that Er\(Er ∩ Br) = ∅. Since all interim equilibrium bid profiles are the form of (b1,r, b2,r) = (b2,r + ε, b2,r), [Er\(Er ∩ Br)]∪[Er+ε\(Er+ε ∩ B r+ε)] = (Er ∪ Er+ε)\((Er ∪ Er+ε)∩Br+ε) for all r ∈ {v2, ⋯, r̂}. Since Er̂ ⊂ Er̂−ε ⋯ ⊂ Ev2 = ⋯ = E0 =E, . Then, it follows that . Therefore, a bid strategy profile is an equilibrium if and only if .
Appendix B: Unknown Values Case (Incomplete Information)
B-1. Buyer's Expected Utility
Consider symmetric buyers who employ the same bid strategy br: V̅ → B̅r. For given realization of v and z, the deterministic utility function of (4) when the buyer bids as if her value is x can be rewritten as
Let Δ be the set of cumulative probability distributions with support V̅. The buyer perceives her rival's value z as a random variable following the probability distribution G(z) ∈ Δ with density function g(z). Since we consider a strictly increasing bid function br (·), the buyer wins when z falls below x, and she loses otherwise. (Since we consider only continuous bid function and continuous value distribution, the probability of a tie is zero.) Also note that at decision point r, buyers are not allowed to bid below r, so that they update G(z) conditional on . Then, the buyer's expected utility EUz: V̅ × B̅ → ℜ at a decision point r is obtained by taking expectation of (B1) with respect to z, such that
The first term of (B2) represents the expected value of monetary winning payoff. The second term represents the buyer's expected psychological payoff when she loses. For r ∈ [0, max{v, z}), an increase in r raises the weight α(·, r) by decreasing its denominator. When the denominator becomes zero, the weight α(·, r) vanishes.
B-2. Unique Symmetric Equilibrium Bidding Function
Proof of Proposition 4
Consider a continuous and continuously differentiable bidding function br(·) that is strictly increasing and br (0) = 0. At every decision point r ∈ B̅, a buyer whose value is v ∈ V̅ chooses an optimal x ∈ V̅ which maximizes her expected payoff EUz(x, r) of (B2), when x = v. Since EUz(x, r) is continuous in x, take the first derivative with respect to x and evaluate it at v. Then, we obtain the following first order condition:
Note that the integral of (B3) corresponds to the case v < z. Then, the first order condition (B3) can be rewritten as
It is immediate that a bidding function v = br(v) for all v ∈ [r, v̅] ⊂ V̅ satisfies the condition (B4) for all r ∈ B̅. Therefore, the value-revealing bidding strategy v = br(v) for all v ∈ [r, v̅] ⊂ V̅ generates a symmetric interim equilibrium for all r ∈ B̅. Note that the case where r = 0 corresponds to the second price auction.
To prove uniqueness, suppose that v̂ > br(v̂) for some v̂ ∈ V̅. If this strategy br(·) constitutes a symmetric interim equilibrium, the condition (B4) must hold at x = v̂. Since γ > 0 and , the first term of the LHS of (B4) is positive and the second term is either positive or zero for all z ∈ [v̂, v̅], no matter what the shape of br(z) is for z ∈ V̅ other than v̂. Therefore, the bidding function that specifies v̂ > br(v̂) for some v̂ ∈ V̅ does not fulfill the condition (B4) and cannot generate a symmetric interim equilibrium at any r.
Next suppose that v̂ < br(v̂) for some v̂ ∈ V̅. The first term of the LHS of (B4) is negative. In order to satisfy the condition (B4), there must be some ẑ ∈ [v̂, v̅] such that ẑ > br(z̅) so that the second term of the LHS of (B4) becomes positive. If br(·) generates a symmetric interim equilibrium, the condition (B4) must hold for a buyer whose value is ẑ as well. We have already observed, however, that such a bidding function cannot generate a symmetric interim equilibrium at any r. Therefore, the bidding function that specifies br(v̂) > v̂ for some v̂ ∈ V̅ does not generate a symmetric interim equilibrium at any r. Consequently a value-revealing bidding strategy v = br(v) is a unique equilibrium strategy for the second price auction as well as the ascending-bid auction. Hence the highest possible decision point where the ascending-bid auction terminates is .
Appendix C: Experiment Instructions (Translation)
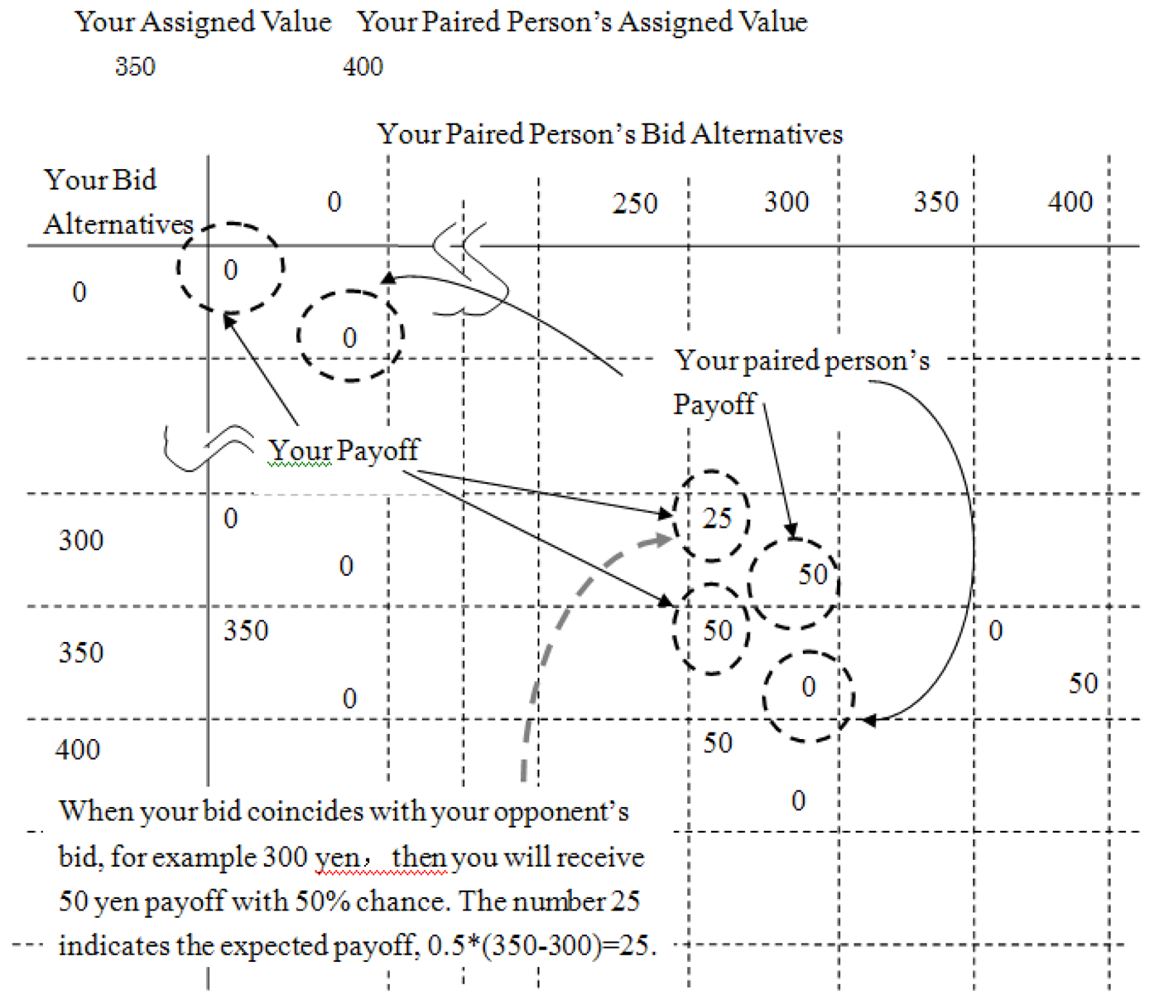
Thank you for participating in our experiment. This is a study on auctions. The Ministry of Science and Education has provided funds for our research. The instructions are simple. You are being paid 1,000 yen in cash as start-up money. All you have to do is to make a bid in each of the auction situations according to the rules described in this instruction. In each round of auctions, depending on the bid you make and the resolution of the uncertainty, you may receive or pay a specified amount of money as a result of transaction.
Your acts will be recorded and kept only in terms of purely anonymous data for the academic research on microeconomics.
Furthermore, and most importantly, this is not a project to see if you can make a “right” decision, or if you can come up with a “correct” answer.
Instructions
<1> What Are We Bidding for?
We will ask you to bid, not for a commodity as in a real auction market, but for a monetary prize. In other words, you are going to compete for the right to earn a monetary prize. In an exchange for the prize, a winner has to pay according to the rules of the auction.
At the beginning of each round of auction game, we will assign each of you a number. This represents a prize value to you. Once you win the auction, then you will receive the prize worth that value number, and you must pay the amount specified by the corresponding auction rules to obtain the prize. Your payoff is the difference between the prize and the amount of payment. If you do not win, you will not receive any prize and pay nothing, that is, your payoff is zero.
You know your prize value for sure once it is assigned to you. But you may or may not know the value assigned to the other participants in this experiment, depending on the experimental design.
<2> The Auction Rules
We will run two kinds of auctions. One is a sealed bid auction, called the second-price auction, and the other is an open bid auction, called the ascending-bid auction. The experiment starts with a session of sealed bid auctions, containing eight rounds of auctions each with fresh value assignment, and then proceeds to a session of ascending-bid auctions also containing eight rounds.
(1) The Second-Priced Sealed Bid Auction
Each of you is paired with another anonymous participant. Every auction round starts with the value assignment. You and the other participant receive a number each as your prize value, which we call “assigned value.” After receiving the assigned value, both of you are asked to make a bid. That is, you have to specify a number to submit to the experimenters. We collect those submitted bids, and identify a bidder who submitted the higher bid between the two of you, as a winner. The winner receives the right to obtain her assigned value. In exchange, the winner has to pay the amount equal to the lower bid in the pair, that is, the bid amount the non-winner submitted. Please note that the payment required by the winner is not her own bid.
You know that you are paired with someone, but you do not know who is paired with you. There are two treatments as to pairing. In one treatment, you are paired with a different person, randomly determined, in every round. We call this treatment, “Part 1.” In the other treatment, you are paired with a person randomly in a first round, and continue to bid against this same anonymous person in the rest of the rounds. We call this treatment “Part 2.” In Part 1, we start with the second price auction for eight rounds, and then proceed to “Part 2” for eight rounds. After that, we conduct the ascending-bid auction experiments under the treatment of Part 1 and then Part 2.
Upon being instructed to do so, the first thing you have to do is to double click the icon indicated by “Sealed Bid” on your windows screen. Then you will see the dialogue window shown below, popping up in your screen.
Make sure that you see the header “Sealed Bid” on the left of the dialogue window. Your ID number will be shown in a box in the first line of the dialogue window. Do not let the other participant know your ID number. This is very important to maintain the academic quality of our experiments. And please do not close this window by yourself. Once every necessary step is complete, the window will automatically close.
Next, the experimenter will send you a private “assigned value,” which will appear in the box of the dialogue window labeled “Value Assignment.” In the event you win, this is the prize you are entitled to earn by making the appropriate payment. Only after the assigned values are distributed, the face of the “send bid” button turns black and you can then type the amount you decide to bid in the box labeled “Your Bid.” The minimum bid unit is 10 yen. If you are sure about that amount, then click the “send bid” button to transmit that information to the experimenter. Your bid won't reach the experimenter unless you click the “send bid” button. After all bids are transmitted, the system identifies the bidder whose submitted bid is the higher in the pair as a winner, and lets her know that she is the winner. You will find the winner's ID number shown in the box labeled “Winner's ID” in the middle part of the dialogue window. The further right box under the header “the second highest bid” will show the amount that the winner has to pay, which is the lower bid in the pair. If you are the winner, the further left box under the header “payoff” will show the number that is your payoff obtained by subtracting the payment from your assigned value. On the other hand, if you are not the winner, the number in the box under the “payoff” is zero, since you do not get the prize and do not have to make any payment. For example, consider the case where your assigned value is 400 yen. Suppose that you bid 300 yen, and the other participant paired with you bids 350 yen. In this case, you are not the winner since your bid is not the highest, and your payoff is zero. Next, suppose that the other participant paired with you bids 200 yen instead. Your bid, 300 yen, is the highest bid and you become the winner. Then you win the prize of 400 yen but must pay 200 yen, which comes down to the payoff of 200 yen. If you win, If you do not win, If you and the other participant bid the same amount, then a winner will be randomly selected. In this case, you will be a winner with probability of 50%. In the previous example, suppose that two of you bid 300 yen. Then, you can obtain the prize of 400 yen and make the payment of 300 yen with probability of 50%, and obtain zero payoff otherwise. In the very bottom of the dialogue window, you find the “comments” box. Please type why and how you have come to a bid decision, when we, the experimenters, ask you to do so. Having finished typing your comments, click the “send comments” button. Your comments won't be sent to the experimenters unless you click the “send comments” button.
(2) The Ascending-Bid Auction
In the ascending-bid auction, we, the experimenters, raise a price gradually from a very low level. At the beginning of the ascending-bid auction, all of you are “active” in the sense that you are bidding at that price level. Unless you indicate that you wish to withdraw from bidding, you are considered being active and willing to pay that amount of indicated price in the event that you become the winner at this very moment. As long as two of you are active, we continue to raise the price. At the moment when one bidder withdraws from bidding, then the remaining bidder becomes the winner awarded with the prize, and she has to pay the last price level at which two bidders were active. After you double click the icon named “Ascending Bid” on your screen, you will see the following dialogue window.
Please make sure that your ID number is shown in the box located at the top of the dialogue window. DO NOT let the other participants know of your ID. Similar to the experiment of the second-price sealed bid auction, you will see your assigned value pop up in the corresponding box. If you become a winner, this is the amount you will get as a prize. Underneath that box, there is a box indicating the “current price”. Once the auction starts, the number shown in that box rises gradually from 0 yen. As the number increases, the price thermometer on the left of the dialogue window grows higher. The price increases by 10 yen. Let us consider the case where the number in the “current price” box is 100. Suppose that you are willing to pay 100 yen if you win at this moment, but you would not want to pay more than 100 yen. In this case, click the “Drop” button to indicate that you wish to withdraw from bidding when the number in the “current price” box gets up to 110. Your withdrawal bid level will be recorded as 100. Unless you click the “Drop” button, your wish to withdraw would not be transmitted to the experimenter. As long as the “current price” increases, the other participant paired with you is active. When one of the pair drops, the process of the ascending-bid auction stops. If the price stops increasing before you click the “Drop” button, this means that you win. Then, you will obtain the prize worth your assigned value, and your payment is 100 yen, which is one unit (= 10 yen) lower than the price level at which the process stops. The payment amount will be indicated in the “payment” box. The ID number of the winner will be shown in the “winner” box. Your payoff will be indicated under the large box in the middle under the header of “payoff.” If you win, your payoff is your prize minus the payment. If you do not win, your payoff is zero. Such information will be listed in that box in each round. Each new result enters at the top of the list. Let us review the above details by some examples. Suppose that your assigned value is 400 yen. Suppose that the number in the “current price” box increases and stops at 350 before you click the “drop” button. This means that you win, and your payment is one step earlier than the 350 level, which is 340 yen. Your payoff is 400 minus 340, which is 60 yen. Suppose that you click the “drop” button at 360. It means that you do not win, and your payoff is zero. When two of you simultaneously click the “drop” button, then a winner will be randomly selected, and the winner pays the price at the moment of withdrawal minus 10. At the bottom of the dialogue window, there is the “comments” box. Describe why and how you figure out the amount of price at which you choose to withdraw, when instructed to do so. To transmit your comments to the experimenter, click the “send” button.
<3> The Experiment Procedure
After you sit down in front of the computer terminal, each of you will be given ID number, which you continue to use during the full course of experiment. Do not show that number to any other participant. It is very important for the academic quality of this experiment that you keep your ID number completely private.
(1) Pairing
Having mentioned elsewhere, you are paired with another person among those participants in this room. You will never be told with whom you are paired. In Part 1, the person you paired with will be determined randomly every round of the auction, while in Part 2, your paired person will be determined randomly in the first round, and maintained the same anonymous person through out all rounds.
(2)Value Assignment
There are two ways in which your value is assigned in a round. In one case, which we call “treatment VA1,” your value is selected randomly from a predetermined set of values, which consists of 700 and 800, every round. Your computer screen informs you of your own value only, but if you receive 700, it automatically implies that your paired participant receives 800, and vice versa.
In the other case, which we call “treatment VA2,” your value is a purely random variable from a predetermined range of value of [500,800] with uniform distribution. In every round, a fresh value is drawn independently. Again, you are informed of your own value only, and never be informed of the realized value drawn for your paired person. But the same random procedure is applied to both of you and your paired person, independently.
In order to get familiar with the auction rules, the first four rounds are for your practice. The outcomes from the subsequent rounds are recorded for real prize and payment.
Please make sure that you fully understand the rules and procedure. You will be given a short quiz after all the instruction is completed.
(3) How to Use Payoff Table
Your payoff is a joint product of your own bid choice and a bid chosen by the other participant paired with you. The other participant's payoff is also a joint product. Though there are numerous combinations of your bid and the other participant's bid, in the treatment VA1, we provide you a payoff table that looks like the figure shown below. The table lists your payoffs and the other participant's payoffs under the various but limited number of bid combinations, because of the space limit.
The figure below shows the example of the payoff table with your assigned value being 350 yen and the other participant's being 400 yen. The further left column lists the possible bids you can choose, and the first row lists the bids available for your paired person. Though those possible bids are listed with 50 yen increments, you are free to bid in 10 yen increments in the auction.
There are two numbers shown in each cell. The number in the upper left of the cell is your payoff and the number in the lower right of the cell is the other participant's payoff.
For example, suppose that your bid is 350 yen and the other participant bids at 300 yen. Then, your bid is higher and you are the winner. You will be awarded 350 yen prize, your assigned value, and you have to pay 300 yen, the other participant's bid level, so that your net payoff is 50. The other participant who loses receives zero net payoff. Let us consider another case. Suppose that you bid 350 yen and the other participant bids 400 yen. Since her bid is higher, she is the winner and gets 400 yen prize and pays 350 yen equal to your bid. Her net payoff is 50, subtracting 350 from 400, which is shown in the lower right of the cell in the row of your 350 bid and the column of the other participant's bid 400. Another important case is the event of tie. Suppose that you bid 300 yen and the other participant bids also 300 yen. Then the winner will be randomly selected. That is, you become the winner with 50% chance, receiving your value prize of 350 yen and paying 300 yen. Your net payoff is 50 yen in when you win, and your expected payoff is 25 yen, which is shown in the upper left of the corresponding cell. Since the other participant's assigned value is 400 yen, her expected payoff is 50 = 0.5*(400 – 300), which is shown in the lower right of the corresponding cell.
<4> The Summary of the Course of the Experiments
There are two parts regarding pairing; In Part 1 you are paired with a new randomly selected person among other participants every round. In Part 2 you are paired with a randomly selected person in the first round and maintain the same person in the rest of the rounds.
There are two treatments regarding value assignment. In treatment VA1, you are assigned either 700 or 800 yen randomly, and in treatment VA2, you are assigned with a random number drawn from the range between 500 and 800 yen according to the uniform distribution. Each draw is independent.
There are two types of auctions; one is the second-price sealed bid auction and the other is the ascending-bid auction, and the sealed bid auction precedes the ascending bid auction.
As a total, there are 2 × 2 × 2 variations in our experimental treatments. We will run on average 8 rounds for each treatment. At the beginning of the first sealed-bid auction experiment, there are four rounds set as the practice session. All payoffs generated during the practice session will not be counted. After completing the practice rounds, then we move on to the first set of 8 rounds of auction and start recording the realized payoffs.
Your payoffs will be all recorded. At the end of the experimental session, we will pay you the cumulative amount in cash, on the spot.
<5> Now, We Are Ready to Start
Please read this instruction carefully. It is very important that you understand these instructions. Should you have any questions, please feel free to ask us.
Once we start explaining the instructions, you are not allowed to talk to any other participants. You can only talk to us, the experimenters, if necessary. You are not allowed to look at the other participants' PC screens. This no talking and no peeking rule is very important for the validity of our experiments. Not conforming to this rule would jeopardize the quality of our experiments.
References and Notes
- Attiyeh, G.; Franciosi, R.; Isaac, R.M. Experiments with the pivotal process for providing public goods. Publ. Choice 2000, 102, 95–114. [Google Scholar]
- Kawagoe, T.; Mori, T. Can the pivotal mechanism induce truth-telling? An experimental study. Publ. Choice 2001, 108, 331–354. [Google Scholar]
- Cason, T.N.; Saijo, T.; Sjöström, T.; Yamato, T. Secure implementation experiments: Do strategy-proof mechanisms really work? Game. Econ. Behav. 2006, 57, 206–235. [Google Scholar]
- Kagel, J.H.; Levin, D. Independent private value auctions: bidder behavior in first- second- and third-price auctions with varying number of bidders. Econ. J. 1993, 103, 868–879. [Google Scholar]
- Harstad, R.M. Dominant strategy adoption and bidders' experience with pricing rules. Exp. Econ. 2000, 3, 261–280. [Google Scholar]
- Coppinger, V.; Smith, V.; Titus, J. Incentives and behavior in English, Dutch, and Sealed-Bid Auctions. Econ. Inq. 1980, 18, 1–22. [Google Scholar]
- Cox, J.; Roberson, B.; Smith, V. Theory and behavior of single object auctions. In Research in Experimental Economics; Smith, V., Ed.; JAI Press: Greenwich, CT, USA, 1982. [Google Scholar]
- Kagel, J.H.; Harstad, R.M.; Levin, D. Information impact and allocation rules in auctions with affiliated private values: A laboratory study. Econometrica 1987, 55, 1275–1304. [Google Scholar]
- Chew, S.H.; Nishimura, N. Revenue Non-Equivalence between the English and the Second-Price Auctions: Experimental Evidence. J. Econ. Behav. Organ. 2003, 51, 443–458. [Google Scholar]
- The “Japanese” version of English auction is the type of ascending-bid auction we employed in our theoretical and experimental analyses, where all the bidders are active from the start by pushing their buttons as default and they leave the auction by releasing their buttons. Thus, they are not allowed to leave the auction and reenter at the later stage. It is well known that the value-revealing bidding strategy generates the unique dominant strategy equilibrium and there is no room for any asymmetric equilibrium such as jump-bidding strategy (see Milgrom and Weber [11] for example.)
- Milgrom, P.; Weber, R. A Theory of Auctions and Competitive Bidding. Econometrica 1982, 50, 1089–1122. [Google Scholar]
- Saijo, T.; Nakamura, H. The “spite” dilemma in voluntary contribution mechanism experiments. J. Confl. Resolut. 1995, 39, 535–560. [Google Scholar]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Segal, U.; Sobel, J. Tit for tat: Foundations of preferences for reciprocity in strategic settings. J. Econ. Theor. 2007, 136, 197–216. [Google Scholar]
- Dufwenberg, M.; Kirchsteiger, G. A theory of sequential reciprocity. Game. Econ. Behav. 2004, 47, 268–298. [Google Scholar]
- Falk, A.; Fischbacher, U. A theory of reciprocity. Game. Econ. Behav. 2006, 54, 293–315. [Google Scholar]
- Morgan, J.; Steiglitz, K.; Reis, G. The spite motive and equilibrium behavior in auctions. Contrib. Econ. Anal. Pol. 2003, 2, 5:1–5:27. [Google Scholar]
- Cooper, D.; Fang, H. Understanding overbidding in second price auctions: An experimental study. Econ. J. 2008, 118, 1572–1595. [Google Scholar]
- Andreoni, J.; Che, Y.-K.; Kim, J. Asymmetric information about rivals' types in standard auctions: An experiment. Game. Econ. Behav. 2007, 59, 240–259. [Google Scholar]
- Herrmann, B.; Orzen, H. The Appearance of Homo Rivalis: Social Preferences and the Nature of Rent Seeking; CeDEx Discussion Paper 2008, No.2008–10; University of Nottingham: Nottingham, UK, 2008. [Google Scholar]
- Arora, A.; Greenwald, A.; Kannan, K.; Krishnan, R. Effects of information-revelation policies under market-structure uncertainty. Manag. Sci. 2007, 53, 1234–1248. [Google Scholar]
- Cason, T.N.; Kannan, K.; Siebert, R. An experimental study of information revelation policies in sequential auctions. Manag. Sci. 2011, 57, 667–688. [Google Scholar]
- Edelman, B.; Ostrovsky, M.; Schwarz, M. Internet advertising and the generalized second-price auction: Selling billions of dollars worth of keywords. Am. Econ. Rev. 2007, 97, 242–259. [Google Scholar]
- As highlighted in Cason et al. [3], subjects fail to choose dominant strategies when other, non-dominant strategy Nash equilibria exist. This led Saijo et al. [25] to introduce secure implementation, where the goal is achieved by both dominant and Nash equilibria.
- Saijo, T.; Sjostrom, T.; Yamato, T. Secure implementation. Theor. Econ. 2007, 2, 203–229. [Google Scholar]
- Their original paper deals only with the incomplete information environment, which we extend here to the complete information setting.
- Their model has the simplest form among various reciprocity models proposed, yet general enough to include such models as Rabin [13] and Charness and Rabin [28]. They provide axiomatic foundation for reciprocity models and obtain utility representation theorem which prescribes utility function of the form (3) except that σi is player i 's mixed strategy and is player i 's belief about player j 's mixed strategy. Also the constant term Rj = 0 in the Segal and Sobel's model, whereas Rj ≠ 0 in other reciprocity models. Like other reciprocity models, they consider the framework of the psychological game developed by Geanakoplos, Pearce, and Stacchetti [29] in which beliefs play an important role. Segal and Sobel [14] showed that the concept of Nash equilibrium directly applicable in their framework in the sense that each player i considers her best response for a given belief , and in equilibrium the belief must coincide with the actual strategy choice, i.e., As long as we restrict our attentions to the analysis of equilibrium behavior, not off-equilibrium, we can avoid discussions of beliefs. Thus, we conduct our analysis based on a degenerate form of (3) treating beliefs implicitly, although we include an analysis that incorporates beliefs in our working paper Nishimura et al. [30]. For more detail discussions of beliefs, see Sobel [31].
- Charness, G.; Rabin, M. Understanding social preferences with simple tests. Q. J. Econ. 2002, 117, 817–869. [Google Scholar]
- Geanakoplos, J.; Pearce, D.; Stacchetti, E. Psychological games and sequential rationality. Game. Econ. Behav. 1989, 1, 60–79. [Google Scholar]
- Nishimura, N.; Cason, T.; Saijo, T.; Ikeda, Y. Spite and Counter-Spite in Auctions; Working paper; Shinshu University: Matsumoto, Nagano, Japan; Purdue University: West Lafayette, IN, USA, 2007. [Google Scholar]
- Sobel, J. Interdependent preferences and reciprocity. J. Econ. Lit. 2005, 43, 392–436. [Google Scholar]
- We set reference losing payoff to be zero for both buyers. The reciprocity model prescribes utility as a sum of own monetary payoff and psychological payoff. Note that buyer i's psychological payoff in the event of winning is zero and omitted in (3), since both her rival's payoff and reference losing payoff in that event are zero.
- To be precise, the negative weight means spite motivation.
- It is common in reciprocity models to normalize the deviation from some reference by the payoff range defined by the maximum and the minimum payoff available under the relevant consideration. Here, we add ε to the denominator to be consistent with the case of ascending-bid auction, without loss of generality. Such need arises due to the requirement of a discrete bid strategy space.
- In order to identify β̂1 ∈ B, we first solve for a real number x ∈ [0, b̅] that satisfies , i.e.,equating buyer 1's winning and losing payoff when b1 = b2 = x. We then find the nearest β̂1 ∈ B satisfying x ∈ [β̂1,β̂1 + ε). It is easy to check that β̂1 exists and β̂1 ∈ {v2, ⋯, v1 − ε}. For more detail, see Appendix A-1.
- Based on Lemma 1, we can derive the best response correspondences for both buyers. See Appendix A-2.
- The position of buyer's threshold bids depend on Ri, i ∈ {1, 2}. The conclusions of our qualitative analyses summarized at the end of subsection 2.1A, 2.1B, and 2.2, however, are unaffected by the size of the reference payoffs.
- This is not the only case where allowing for the possibility of reciprocity leads to eliminating some of Nash equilibria generated by the standard model. The well-known example is an ultimatum game which has multiple Nash equilibria under the standard model. Allowing reciprocity eliminates the proposer's strategy of choosing the most self-advantageous offer expecting the receiver to accept it that is sub-game perfect Nash equilibrium under the standard model, but keeps other Nash equilibria that would have failed the sub-game perfect refinement.
- A change in the weight as r increases can lead to a different bid decision. As shown in Proposition 2 below and related discussion to follow, each equilibrium bid decision at the every decision point reached in the ascending-bid auction is also equilibrium in the previous decision point (not vice versa), and all the way back to the very start of auction. In this sense our model maintains consistency. The related issue can be found in the context of sequential decision making through partial resolution of risk particularly via non-expected utility preferences. If we want to maintain the dynamic consistency in preferences, it is known that preferences must satisfy consequentialism (Hammond [40]). It seems, however, inappropriate to impose consequentialism on preferences especially when we deal with players' intentions explicitly.
- Hammond, P. Consequentialist foundations of expected utility. Theor. Decis. 1988, 25, 25–78. [Google Scholar]
- In the same manner as described in [35], β̂1,r is derived from the solution xr ∈ [r, b̅] to , i.e., equating buyer 1's winning and losing payoff when b1,r = b2,r = xr.Then, find the smallest number β̂1,r ∈ Br satisfying xr ∈ [β̂1,r,β̂1,r + ε). It can be shown that β̂1,r ∈ {max{v2, r}, ⋯, v1 − ε). For more details, see Appendix A-4.
- Though we omit the argument regarding beliefs in our analysis, it may be worthwhile to point out the following; First, it is clear from Definition 3 that every equilibrium bidding strategy profile belongs to interim equilibrium Er for all . Second, since Er̂ has the lowest upper bound, there would not arise any need to revise a belief that is consistent with equilibrium bid on the equilibrium path. With these two properties, our Definition 3 is consistent with the definition of Sequential Reciprocity Equilibrium by Dufwenberg and Kirschteiger [15].
- The psychological dynamics are different in nature from the comparison of Nash equilibrium versus subgame perfect Nash equilibrium. The subgame perfect equilibrium set in the conventional, self-interested preferences ascending-bid auction is equivalent to the Nash equilibrium set in the second price auction without its inefficient elements. However, with the spite motivation the maximum equilibrium price in the ascending bid auction is r̂. Thus, the ascending-bid auction price predicted for buyers of spite-with-reciprocity is bounded by the maximum price predicted in the conventional model.
- The corresponding tie bid xr defined in [41] is 748.3 for r = 720, 746.3 for r = 730, and 744.2 for r = 740. It follows that r̂ = 740
- It is well known that the symmetric equilibrium bidding strategy must be strictly increasing in the buyer type (value in this model) in the auction where the highest bidder wins; for example, see Milgrom [46].
- Milgrom, P. Putting Auction Theory to Work; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Kagel, J. Auctions: A survey of experimental research. In The Handbook of Experimental Economics; Kagel, J., Roth, A., Eds.; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- These figures pool the data from the treatments with fixed groups and randomly-reformed groups of bidders. The subsequent analysis controls for different matching rules in the parametric regression models.
- The censoring problem is much greater for the high-value bidder, since in the ascending-bid auction this bidder wins in 278 of the relevant 309 auctions. Therefore, we do not report a bid distribution for the high-value bidder for this auction institution, nor do we use such bids in any of the statistical tests that follow.
- Cameron, C.; Trivedi, P. Microeconometrics: Methods and Applications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- As in Table 1, we only employ the sealed bid auction data in these regressions because the high-value bidders' bids are rarely observed in the ascending price auction.
- JEL Classifications: C72, D44
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nishimura, N.; Cason, T.N.; Saijo, T.; Ikeda, Y. Spite and Reciprocity in Auctions. Games 2011, 2, 365-411. https://doi.org/10.3390/g2030365
Nishimura N, Cason TN, Saijo T, Ikeda Y. Spite and Reciprocity in Auctions. Games. 2011; 2(3):365-411. https://doi.org/10.3390/g2030365
Chicago/Turabian StyleNishimura, Naoko, Timothy N. Cason, Tatsuyoshi Saijo, and Yoshikazu Ikeda. 2011. "Spite and Reciprocity in Auctions" Games 2, no. 3: 365-411. https://doi.org/10.3390/g2030365