Speech Is Silver, Silence Is Golden
Abstract
:1. Introduction
2. The Game and the Experiment


| Session | Treatment | Treatment | Treatment |
|---|---|---|---|
| (# subjects) | (subsession code) | (subsession code) | (subsession code) |
| 3(18) | No comm. (SS31) | c = 0 (SS32) | c = 5 (SS33) |
| 4(24) | c = 0 (SS41) | c = 3 (SS42) | No communication (SS43) |
| 5(20) | c = 3 (SS51) | c = 0 (SS52) | No communication (SS53) |
3. Results

| Message time in seconds | Communication structure in percent | |||||
|---|---|---|---|---|---|---|
| SS | Cost | Mean | Std. Dev | No | One-way | Two-way |
| 32 | 0 | 5 | 5 | 0 | 1 | 99 |
| 33 | 5 | 42 | 35 | 4 | 57 | 39 |
| 41 | 0 | 2 | 3 | 0 | 0 | 100 |
| 42 | 3 | 37 | 31 | 4 | 56 | 40 |
| 51 | 3 | 34 | 26 | 1 | 52 | 47 |
| 52 | 0 | 7 | 7 | 0 | 2 | 98 |
| Subsession | SS31 | SS32 | SS33 | SS41 | SS42 | SS43 | SS51 | SS52 | SS53 |
|---|---|---|---|---|---|---|---|---|---|
| Cost | NC | 0 | 5 | 0 | 3 | NC | 3 | 0 | NC |
| Profit | 11.4 | 23.4 | 18.4 | 23.6 | 19.5 | 13.2 | 20 | 21.5 | 12.3 |

4. Conclusions
- 1Free-riding often refers to public goods situations where it is optimal to not provide the public good. In this paper we use the term in the sense of not taking a costly action (i.e., to communicate) that is beneficial for others while taking advantage of others’ sacrificing actions.
- 2They use a simultaneous one-shot communication device in each period whereas our setup is more akin to a dynamic communication device. This design difference makes is harder for them to directly study the intention to free-ride on the communication cost.
- 3We use data from an experiment described and motivated in detail in Andersson and Holm [8]. That paper is focussed on the resulting equilibria, welfare effects and the type of communication with a specific emphasis on market entry situations. It does not discuss the general phenomenon of free-riding in the communication stage.
- 4Let the probabilities of choosing strategies N, X, Y, B for a player be given by (pN, pX, pY,1- pN- pX-pY). Then the symmetric mixed Nash equilibria are given by ((1/4- a,a,a,3/4 - a),(1/4 - a,a,a,3/4 - a)) for each 0 ≤ a ≤ 1/4. More importantly, all of these equilibria give rise to the same payoff of 12 for both players. In Andersson and Holm [8] we investigate both a symmetric game and an asymmetric game. To avoid the complications with tacit coordination in the asymmetric game we concentrate on the symmetric variant where the only way to coordinate is through communication.
- 6The difference in communication cost (c = 3 and c = 5) was motivated by the desire to study effects of variation in communication cost in Andersson and Holm [8]. We will not stress this treatment difference in the present paper since there were no substantial differences in free-riding between these treatments.
- 7Instructions are available in Appendix A.
- 8Clearly, with c > 0, the game allows for many equilibria, but these do not necessarily imply free-riding. For instance, in the following equilibrium profile both players bear the same communication cost: I.) The Row player sends the initial message that they should play (X,Y) and then plays X if he gets a confirmation from the Column player that she will play Y. If Row does not get this confirmation, he plays a mixed strategy consistent with Nash-equilibrium. II) The Column player initiates communication, but if she receives the suggestion to play “(X,Y)” she sends a confirming message and acts according to the message. If she does not get this message, she will play a mixed Nash-equilibrium. Still, even if this profile shows that some equilibrium behaviour excludes free-riding in communication, there may be an incentive to free-ride since many probably consider the confirmation message to be redundant.
- 9This game differs slightly from the typical Chicken and Hawk Dove games, where it is normally assumed that it is somewhat better to communicate when the other player also does so, compared to communicate when the other player does not.
- 10With subsequent subsessions it is justified to worry about potential order effects. However, there is no clear evidence of order effects for the sessions analyzed in this paper. The reader is referred to section 5.4 in Andersson and Holm [8], where this issue is thoroughly discussed.
- 11It should be noted that the original design consisted of several other sessions and that the original experiment was not primarily designed to study free-riding of communication.
- 13When comparing c = 3 and c = 5 a Wilcoxon-Mann-Whitney test shows a weak difference between SS33 and SS42 (n = 21, p = 0.0632) but not between SS33 and SS51 (n = 19, p = 0.2828) when only considering period 1 choices. For choices at period 10 there is no difference (p = 0.1764 and p = 0.6823 respectively). When it comes to the difference in proportions of one-way communication between c = 3 and c = 5 in period 1 a proportions test reveals no difference (p = 0.2320 and p = 0.4302 for the above comparisons). For period 10 the corresponding proportions test p-values are (p = 0.6426 and p = 0.1719).
- 14Since it is also efficient that only one subject sends a message when it is costly one can argue that this is “coordination” on the efficient outcome rather than free-riding. However, this coordination also implies voluntary or involuntary free-riding since it is essential that at least one take the communication cost. Thus, even if this indication not only involves free-riding, we argue that there is an element of it to motivate us using the concept.
- 15As noted by Crawford [11], reassurance may have a strong effect on coordination success.
- 16For a more elaborate account of the welfare effects of communication, see Andersson and Holm [8].
- 17Of course one should always be careful when extrapolating results to the policy domain. The effect of costly communication has been shown in the different context of infinitely repeated Bertrand games, to facilitate collusion (Andersson and Wengström [12]).
- 18c was set to 0,3 or 5
Acknowledgments
Appendix
A. Experimental instructions
B. General Information
C. Strategic Situation
- Stay out
- Only enter market x
- Only enter market y
- Enter both markets
| The co-player: | stay out | enters x | enters y | enters both |
| Your strategy: | ||||
| stay out | 12 (12) | 12 (24) | 12 (24) | 12 (36) |
| enter x: | 24 (12) | 8 (8) | 24 (24) | 8 (20) |
| enter y: | 24 (12) | 24 (24) | 8 (8) | 8 (20) |
| enter both: | 36 (12) | 20 (8) | 20 (8) | 4 (4) |
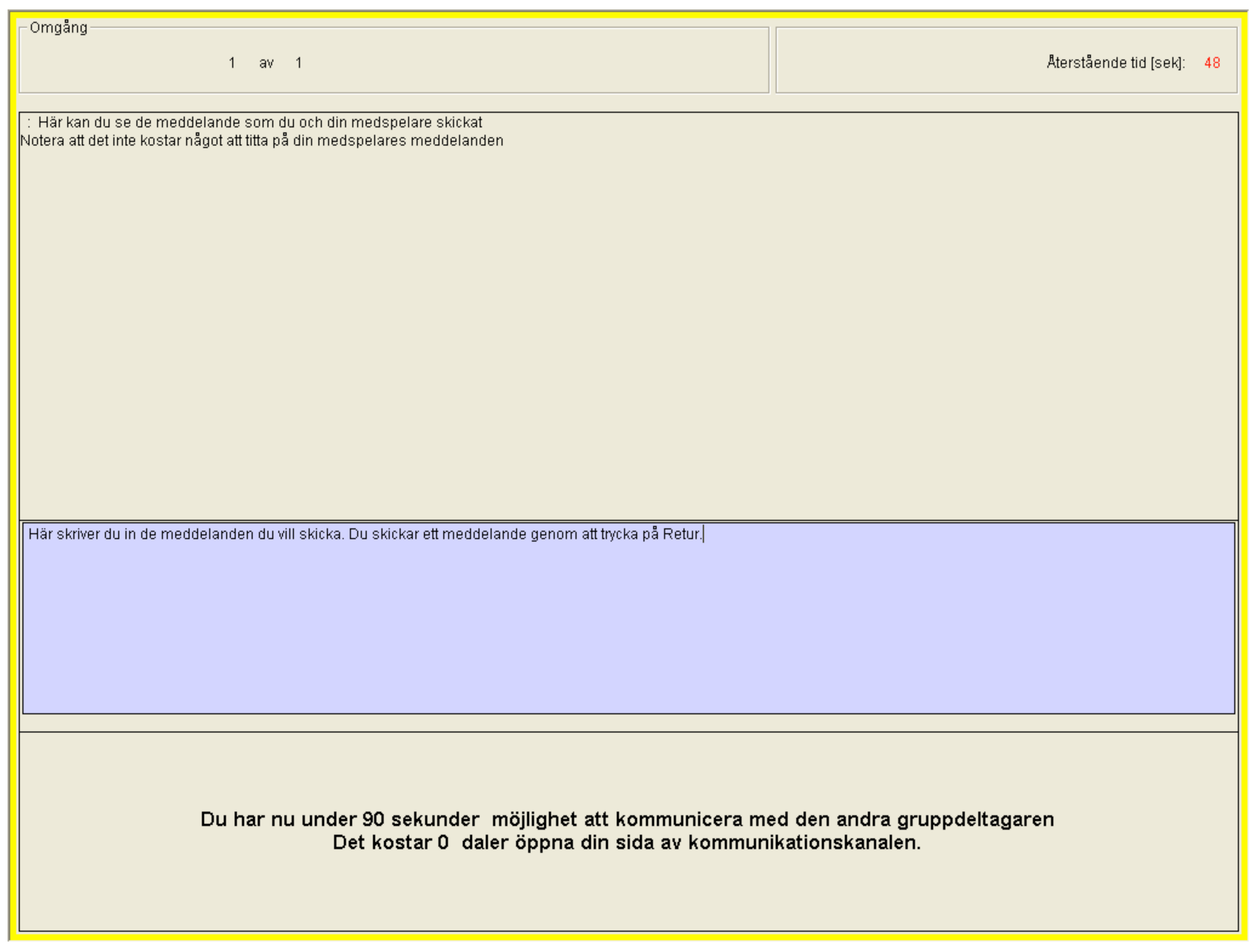
- Top box: Here you are able to see the messages that you and your co-player have sent. Note that it does not cost anything to read your co-player’s messages.
- Middle box: You can write the messages you want to send here. You send the message by pressing Enter.
- Bottom box: You have the opportunity to communicate with the other participant for 90 s. It costs 0 daler to open your side of the communication channel.
Conflicts of Interest
References
- Cooper, R.; Dejong, D.; Forsythe, R.; Ross, T. Communication in the battle of the sexes game: Some experimental results. Rand J. Econ. 1989, 20, 568–587. [Google Scholar] [CrossRef]
- Cooper, R.; Dejong, D.; Forsythe, R.; Ross, T. Communication in coordination games. Q. J. Econ. 1992, 107, 739–771. [Google Scholar] [CrossRef]
- Blume, A.; Ortmann, A. The effects of costless pre-play communication: Experimental evidence from games with Pareto-ranked equilibria. J. Econ. Theory 2007, 132, 274–290. [Google Scholar] [CrossRef]
- Devetag, G.; Ortmann, A. When and why? A critical survey on coordination failure in the laboratory. Exp. Econ. 2007, 10, 331–344. [Google Scholar] [CrossRef]
- Kriss, P.H.; Blume, A.; Weber, R. Organizational Coordination with Decentralized Costly Communication; Carnegie Mellon University: Pittsburgh, PA, USA, 2012; unpublished. [Google Scholar]
- Isaac, R.M.; Walker, J.M.; Thomas, S. Divergent evidence on free-riding: an experimental examination of different explanations. Public Choice 1984, 43, 113–149. [Google Scholar] [CrossRef]
- Isaac, R.M.; Walker, J.M. Communication and free-riding behavior: The voluntary contribution mechanism. Econ. Inq. 1988, 26, 585–608. [Google Scholar] [CrossRef]
- Andersson, O.; Holm, H.J. Endogenous communication and tacit coordination in market entry games — an explorative experimental study. Int. J. Ind. Organ. 2010, 28, 477–495. [Google Scholar] [CrossRef]
- Roth, A.; Murnighan, K.; Schoumaker, F. The deadline effect in bargaining: Some experimental evidence. Am. Econ. Rev. 1988, 78, 806–823. [Google Scholar]
- Roth, A. Bargaining experiments. In The Handbook of Experimental Economics; Kagel, J., Roth, A., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; pp. 253–348. [Google Scholar]
- Crawford, V. A survey of experiments on communication via cheap talk. J. Econ. Theory 1998, 78, 286–298. [Google Scholar] [CrossRef]
- Andersson, O.; Wengström, E. Do Antitrust Laws Facilitate Collusion? Experimental Evidence of Costly Communication in Duopolies. Scand. J. Econ. 2007, 109, 321–339. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Andersson, O.; Holm, H.J. Speech Is Silver, Silence Is Golden. Games 2013, 4, 497-507. https://doi.org/10.3390/g4030497
Andersson O, Holm HJ. Speech Is Silver, Silence Is Golden. Games. 2013; 4(3):497-507. https://doi.org/10.3390/g4030497
Chicago/Turabian StyleAndersson, Ola, and Hakan J. Holm. 2013. "Speech Is Silver, Silence Is Golden" Games 4, no. 3: 497-507. https://doi.org/10.3390/g4030497
APA StyleAndersson, O., & Holm, H. J. (2013). Speech Is Silver, Silence Is Golden. Games, 4(3), 497-507. https://doi.org/10.3390/g4030497




