Space Debris Removal: A Game Theoretic Analysis
Abstract
:1. Introduction
2. Related Work
3. Space Debris Simulation Model
3.1. Collision Model
3.2. Breakup Model
3.3. Repeating Launch Sequence
3.4. Validation
4. Game Methodology
5. Simulation Results and Projections
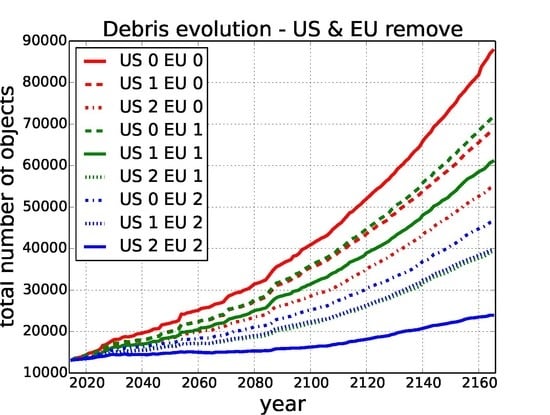
5.1. Debris Evolution
5.2. Risk Evolution
6. Game Theoretic Analysis
6.1. Two-Player Game
6.2. Strategic Substitutes and Existence of Pure Equilibrium
- •
- , [ selects a best response for i]
- •
- whenever . [ does not increase in ]
6.3. Evolutionary Dynamics
6.4. Three-Player Game
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- NORAD Two-Line Element Sets Current Data. Available online: https://celestrak.com/NORAD/elements/ (accessed on 1 February 2016).
- Carrico, T.; Carrico, J.; Policastri, L.; Loucks, M. Investigating orbital debris events using numerical methods with full force model orbit propagation. Adv. Astronaut. Sci. 2008, 130, 407–426. [Google Scholar]
- NASA Orbital Debris Program Office. Chinese Anti-Satellite Test Creates Most Severe Orbital Debris Cloud in History. In NASA Orbital Debris Quarterly News; NASA Orbital Debris Program Office: Houston, TX, USA, 2007. [Google Scholar]
- NASA Orbital Debris Program Office. Satellite Collision Leaves Significant Debris Clouds. In NASA Orbital Debris Quarterly News; NASA Orbital Debris Program Office: Houston, TX, USA, 2009. [Google Scholar]
- NASA Orbital Debris Program Office. International Space Station Again Dodges Debris. In NASA Orbital Debris Quarterly News; NASA Orbital Debris Program Office: Houston, TX, USA, 2011. [Google Scholar]
- Tahvonen, O. Carbon dioxide abatement as a differential game. Eur. J. Polit. Econ. 1994, 10, 685–705. [Google Scholar] [CrossRef]
- Kessler, D.J.; Cour-Palais, B.G. Collision frequency of artificial satellites: The creation of a Debris belt. J. Geophys. Res. 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
- Kessler, D.J.; Johnson, N.L.; Liou, J.C.; Matney, M. The Kessler syndrome: Implications to future space operations. In Proceedings of the American Astronautical Society—Guidance Control Conference, Breckenridge, CO, USA, 6–10 February 2010.
- Liou, J.C.; Johnson, N.L. A sensitivity study of the effectiveness of active debris removal in LEO. Acta Astronaut. 2009, 64, 236–243. [Google Scholar] [CrossRef]
- Liou, J.C.; Johnson, N.L.; Hill, N. Controlling the growth of future LEO debris populations with active debris removal. Acta Astronaut. 2010, 66, 648–653. [Google Scholar] [CrossRef]
- Liou, J.C. An active debris removal parametric study for LEO environment remediation. Adv. Space Res. 2011, 47, 1865–1876. [Google Scholar] [CrossRef]
- Harstad, B. Climate contracts: A game of emissions, investments, negotiations, and renegotiations. Rev. Econ. Stud. 2012, 79, 1527–1557. [Google Scholar] [CrossRef]
- Levhari, D.; Mirman, L.J. The great fish war: An example using a dynamic Cournot-Nash solution. Bell J. Econ. 1980, 11, 322–334. [Google Scholar] [CrossRef]
- Hardin, G. The tragedy of the commons. Science 1968, 162, 1243–1248. [Google Scholar] [CrossRef] [PubMed]
- Walsh, W.; Das, R.; Tesauro, G.; Kephart, J. Analyzing complex strategic interactions in multi-agent systems. In Proceedings of the AAAI-02 Workshop on Game-Theoretic and Decision-Theoretic Agents, Edmonton, AB, Canada, 28 July–1 August 2002.
- Wellman, M.P. Methods for empirical game-theoretic analysis. In Proceedings of the Twenty-First National Conference on Artificial Intelligence and the Eighteenth Innovative Applications of Artificial Intelligence Conference, Boston, MA, USA, 16–20 July 2006; AAAI Press: Menlo Park, CA, USA; MIT Press: Cambridge, MA, USA; London, UK, 2006; Volume 21, pp. 1552–1555. [Google Scholar]
- Jordan, P.R.; Vorobeychik, Y.; Wellman, M.P. Searching for approximate equilibria in empirical games. In Proceedings of the 7th International Joint Conference on Autonomous Agents and Multiagent Systems, Estoril, Portugal, 12–16 May 2008; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2008; Volume 2, pp. 1063–1070. [Google Scholar]
- Wellman, M.P.; Jordan, P.R.; Kiekintveld, C.; Miller, J.; Reeves, D.M. Empirical game-theoretic analysis of the TAC market games. In Proceedings of the AAMAS-06 Workshop on Game-Theoretic and Decision-Theoretic Agents, Hakodate, Japan, 8–10 May 2006.
- Phelps, S.; Parsons, S.; McBurney, P. An evolutionary game-theoretic comparison of two double-auction market designs. In Agent-Mediated Electronic Commerce VI. Theories for and Engineering of Distributed Mechanisms and Systems; Lecture Notes in Computer Science; Faratin, P., Rodríguez-Aguilar, J.A., Eds.; Springer: Berlin Germany; Heidelberg, Germany, 2005; Volume 3435, pp. 101–114. [Google Scholar]
- Ponsen, M.; Tuyls, K.; Kaisers, M.; Ramon, J. An evolutionary game-theoretic analysis of poker strategies. Entertain. Comput. 2009, 1, 39–45. [Google Scholar] [CrossRef]
- Hennes, D.; Claes, D.; Tuyls, K. Evolutionary advantage of reciprocity in collision avoidance. In Proceedings of the AAMAS 2013 Workshop on Autonomous Robots and Multirobot Systems (ARMS 2013), Saint Paul, MN, USA, 6–10 May 2013.
- Wellman, M.P.; Prakash, A. Empirical game-theoretic analysis of an adaptive cyber-defense scenario (preliminary report). In Proceedings of Conference on Decision and Game Theory for Security, 6–7 November 2014; pp. 43–58.
- Hennes, D.; Jong, S.D.; Tuyls, K.; Gal, Y.K. Metastrategies in large-scale bargaining settings. ACM Trans. Intell. Syst. Technol. (TIST) 2015, 7, 10. [Google Scholar] [CrossRef]
- Izzo, D. Pygmo and Pykep: Open Source Tools for Massively Parallel Optimization in Astrodynamics (The Case of Interplanetary Trajectory Optimization); Technical Report; Advanced Concept Team—European Space Research and Technology Centre (ESTEC): Noordwijk, The Netherlands, 2012. [Google Scholar]
- Liou, J.C.; Kessler, D.; Matney, M.; Stansbery, G. A new approach to evaluate collision probabilities among asteroids, comets, and Kuiper Belt objects. In Proceedings of the Lunar and Planetary Science Conference, League City, TX, USA, 17–21 March 2003; Volume 34, p. 1828.
- Vallado, D.A.; Crawford, P.; Hujsak, R.; Kelso, T. Revisiting spacetrack report #3. AIAA 2006, 6753, 2006. [Google Scholar]
- Johnson, N.L.; Krisko, P.H.; Liou, J.C.; Anz-Meador, P.D. Nasa’s new breakup model of EVOLVE 4.0. Adv. Space Res. 2001, 28, 1377–1384. [Google Scholar] [CrossRef]
- Klinkrad, H. Space Debris. In Encyclopedia of Aerospace Engineering; The American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010. [Google Scholar]
- Gibbons, R. A Primer in Game Theory; Financial Times Prentice Hall, Pearson Education: Harlow, Essex, UK, 1992. [Google Scholar]
- Nash, J. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Novshek, W. On the existence of Cournot equilibrium. Rev. Econ. Stud. 1985, 52, 85–98. [Google Scholar] [CrossRef]
- Rodrigo Bamón, J.F. Existence of Cournot equilibrium in large markets. Econometrica 1985, 53, 587–597. [Google Scholar]
- Dubey, P.; Haimanko, O.; Zapechelnyuk, A. Strategic complements and substitutes, and potential games. Games Econ. Behav. 2006, 54, 77–94. [Google Scholar] [CrossRef]
- Kukushkin, N.S. Best response dynamics in finite games with additive aggregation. Games Econ. Behav. 2004, 48, 94–110. [Google Scholar] [CrossRef]
- Kukushkin, N.S. A fixed-point theorem for decreasing mappings. Econ. Lett. 1994, 46, 23–26. [Google Scholar] [CrossRef]
- Kukushkin, N.S. Strategic supplements in games with polylinear interactions. Available online: http://www.eco.uc3m.es/temp/StrSuppl.pdf (accessed on 6 April 2016).
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Bloembergen, D.; Tuyls, K.; Hennes, D.; Kaisers, M. Evolutionary dynamics of multi-agent learning: A survey. J. Artif. Intell. Res. 2015, 53, 659–697. [Google Scholar]











| Strategy | Payoff Function |
|---|---|
| Remove 2 | |
| Remove 1 | |
| Remove 0 |
| EU 2 | EU 1 | EU 0 | |
|---|---|---|---|
| U.S. 2 | |||
| U.S. 1 | |||
| U.S. 0 | |||
| U.S. 2 | |||
| U.S. 1 | |||
| U.S. 0 |
| EU 2 | EU 1 | EU 0 | |
|---|---|---|---|
| U.S. 2 | |||
| U.S. 1 | |||
| U.S. 0 |
| EU 1 | EU 0 | ||
|---|---|---|---|
| CN 1 | U.S. 1 | ||
| U.S. 0 | |||
| CN 0 | U.S. 1 | ||
| U.S. 0 | |||
| CN 1 | U.S. 1 | ||
| U.S. 0 | |||
| CN 0 | U.S. 1 | ||
| U.S. 0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klima, R.; Bloembergen, D.; Savani, R.; Tuyls, K.; Hennes, D.; Izzo, D. Space Debris Removal: A Game Theoretic Analysis. Games 2016, 7, 20. https://doi.org/10.3390/g7030020
Klima R, Bloembergen D, Savani R, Tuyls K, Hennes D, Izzo D. Space Debris Removal: A Game Theoretic Analysis. Games. 2016; 7(3):20. https://doi.org/10.3390/g7030020
Chicago/Turabian StyleKlima, Richard, Daan Bloembergen, Rahul Savani, Karl Tuyls, Daniel Hennes, and Dario Izzo. 2016. "Space Debris Removal: A Game Theoretic Analysis" Games 7, no. 3: 20. https://doi.org/10.3390/g7030020
APA StyleKlima, R., Bloembergen, D., Savani, R., Tuyls, K., Hennes, D., & Izzo, D. (2016). Space Debris Removal: A Game Theoretic Analysis. Games, 7(3), 20. https://doi.org/10.3390/g7030020