Anticipated Communication in the Ultimatum Game
Abstract
:1. Introduction
2. Method
2.1. Experimental Design
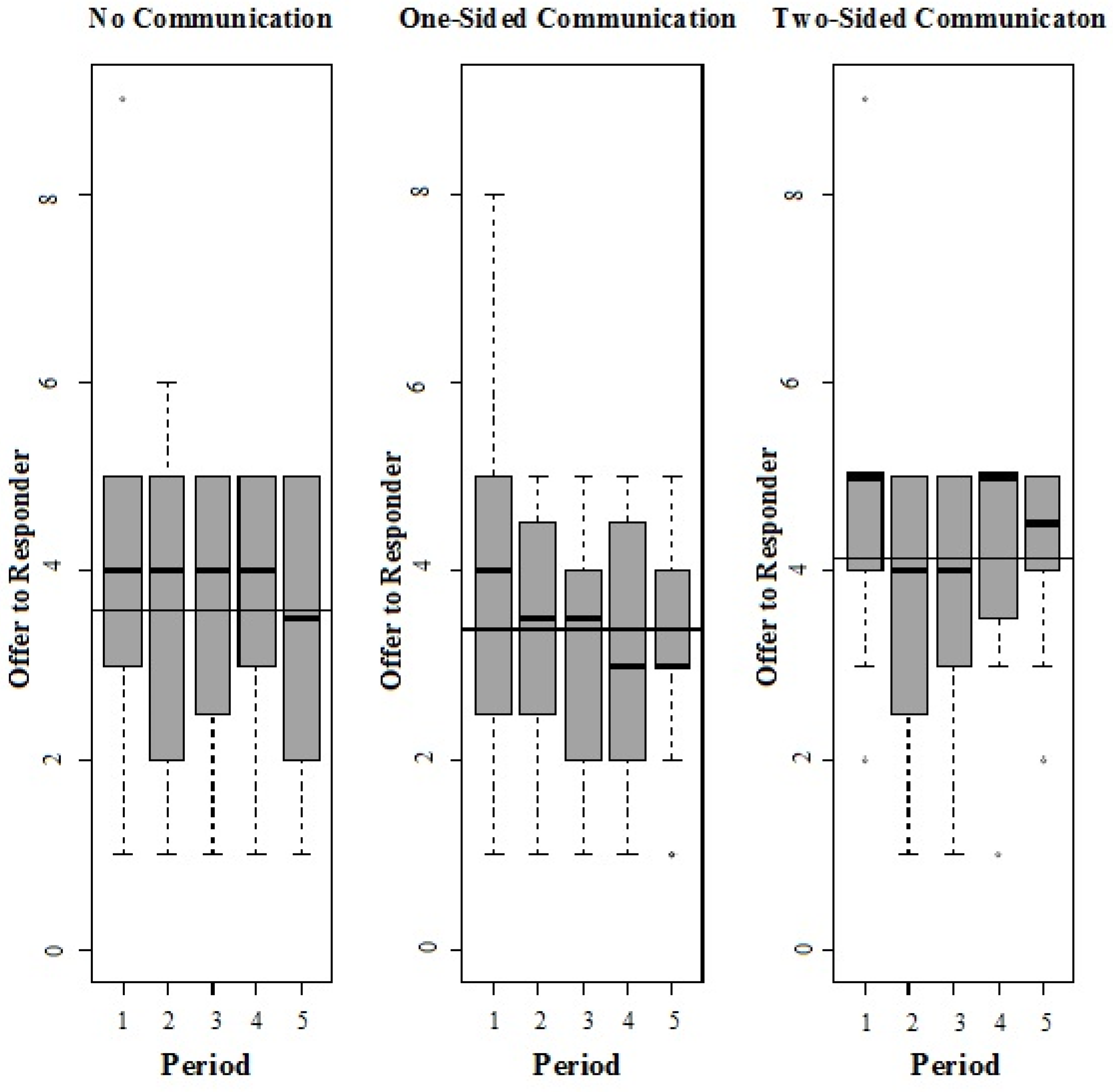
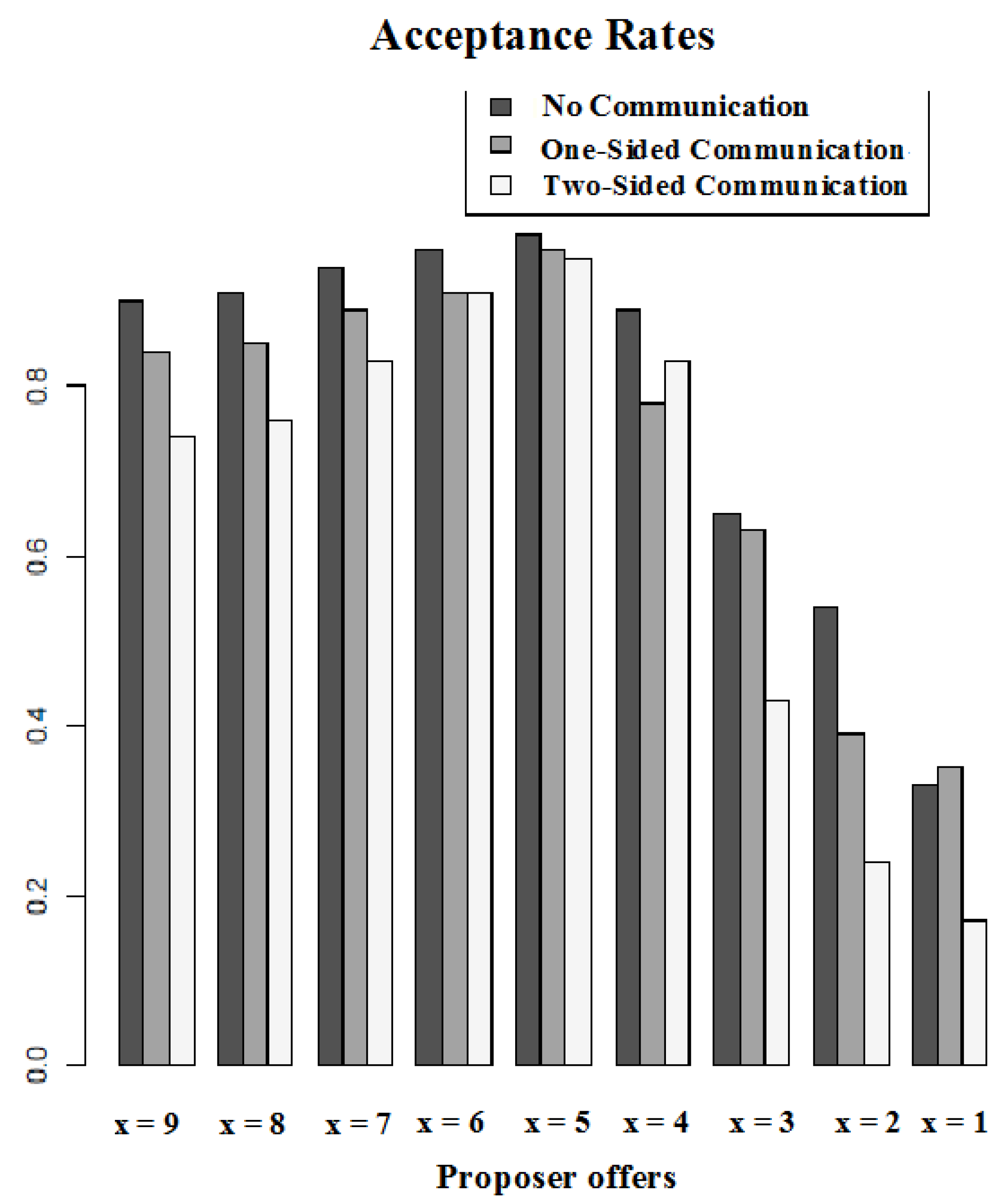
- No Communication: Standard condition where participants are anonymous and are not allowed to communicate, with a three minute time-gap during the communication phase.
- One-Sided Communication: X has the option to anonymously and unilaterally communicate in writing with Y during the communication phase.
- Two-Sided Communication: Both X and Y have the option to anonymously communicate with each other in writing during the communication phase.
2.2. Behavioral Predictions
2.3. Participants and Procedures
3. Results
3.1. Descriptive Statistics
3.2. Regression Analyses
3.2.1. Analysis of Proposer Behavior
3.2.2. Analysis of Responder Behavior
3.3. Analysis of the Informational Content of Messages
3.3.1. Game-Related Classification
3.3.2. Persuasion, Apology, Information or Other Classification
3.3.3. Fairness Classification
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Instructions (Translation from Italian)
Decision Tasks
[A message
{Messages
Earnings
Appendix B. Comparisons of Individual Average Offers
| p-Value | |||
|---|---|---|---|
| No Communication | One-Sided Communication | Two-Sided Communication | |
| Period 1 vs. Period 2 | 0.8783 | 0.5782 | 0.0564 |
| Period 1 vs. Period 3 | 0.9443 | 0.4612 | 0.1116 |
| Period 1 vs. Period 4 | 0.9777 | 0.5150 | 0.4453 |
| Period 1 vs. Period 5 | 0.4535 | 0.4614 | 0.4901 |
| Period 2 vs. Period 3 | 0.7675 | 0.7924 | 0.6698 |
| Period 2 vs. Period 4 | 0.7575 | 0.8679 | 0.2148 |
| Period 2 vs. Period 5 | 0.4189 | 0.9113 | 0.1494 |
| Period 3 vs. Period 4 | 0.9888 | 0.9008 | 0.3879 |
| Period 3 vs. Period 5 | 0.5571 | 0.8351 | 0.2696 |
| Period 4 vs. Period 5 | 0.5204 | 0.9004 | 0.8818 |
| p-Value | ||||||
|---|---|---|---|---|---|---|
| Period 1 | Period 2 | Period 3 | Period 4 | Period 5 | Overall | |
| No Communication vs. One-Sided Communication | 0.8449 | 0.4203 | 0.4045 | 0.4040 | 0.9557 | 0.1970 |
| No Communication vs. Two-Sided Communication | 0.0388 | 0.8992 | 0.6286 | 0.1911 | 0.0248 | 0.0101 |
| One-Sided Communication vs. Two-Sided Communication | 0.0325 | 0.4437 | 0.1320 | 0.0246 | 0.0053 | 0.0000 |
Appendix C. Panel Regressions
| Offer∼ | 1() | |||||
|---|---|---|---|---|---|---|
| (1) | (2) | (1) | (2) | (1) | (2) | |
| (Intercept) | 3.935 | 3.775 | −0.519 | −0.476 | 0.381 | 0.332 |
| (0.327) | (0.234) | (0.352) | (0.262) | (0.239) | (0.239) | |
| One-Sided communication | −0.360 | −0.210 | −0.249 | −0.417 | −0.083 | −0.260 |
| (0.439) | (0.188) | (0.478) | (0.206) | (0.439) | (0.188) | |
| Two-Sided communication | 0.220 | 0.550 | 0.431 | 0.443 | 0.071 | 0.434 |
| (0.439) | (0.188) | (0.448) | (0.192) | (0.450) | (0.192) | |
| Period | −0.115 | −0.062 | 0.012 | −0.002 | −0.039 | −0.023 |
| (0.094) | (0.054) | (0.097) | (0.057) | (0.094) | (0.055) | |
| One-Sided communication*Period | 0.050 | −0.056 | −0.059 | |||
| (0.132) | (0.145) | (0.133) | ||||
| Two-Sided communication*Period | 0.110 | 0.004 | 0.123 | |||
| (0.132) | (0.136) | (0.138) | ||||
| W- | 1.74 | 16.42 | 2.09 | 17.30 | 0.12 | 13.01 |
| 1056.73 | 1053.43 | 360.53 | 356.74 | 385.65 | 383.45 | |
| No. of observations | 300 | 300 | 300 | 300 | 300 | 300 |
| Reject ∼ | Coeff (Std. Err.) | ||
|---|---|---|---|
| (1) | (2) | (3) | |
| (Intercept) | −3.348 (0.824) | −3.240 (0.496) | −3.810 (0.565) |
| One-Sided communication | 0.593 (0.682) | 0.264 (0.423) | 0.408 (0.545) |
| Two-Sided communication | 1.027 (1.194) | 1.012 (0.443) | 0.945 (0.307) |
| x_LOW | 1.116 (0.973) | 1.193 (0.362) | 1.483 (0.531) |
| x_HIGH | 3.087 (1.020) | 2.887 (0.517) | 3.583 (0.576) |
| −0.325 (0.224) | −0.312 (0.216) | −0.098 (0.044) | |
| One-Sided communication*Period | 0.061 (0.120) | 0.049 (0.107) | |
| Two-Sided communication*Period | −0.013 (0.100) | −0.023 (0.100) | |
| x_LOW*Period | 0.117 (0.192) | 0.115 (0.190) | |
| x_HIGH*Period | 0.262 (0.235) | 0.257 (0.233) | |
| One-Sided communication*x_LOW | −0.076 (1.137) | ||
| Two-Sided communication*x_LOW | 0.226 (1.164) | ||
| One-Sided communication*x_HIGH | −0.474 (0.923) | ||
| Two-Sided communication*x_HIGH | −0.144 (1.149) | ||
| W- | 0.34 | 7.20 | 19.53 |
| W- | 38.33 | 45.18 | 331.50 |
| Log-likelihood | −1216.37 | −1217.60 | −1220.10 |
| 2462.74 | 2457.19 | 2454.21 | |
| No. of observations | 2700 | 2700 | 2700 |
Appendix D. Categorization Procedure
I decided to offer you 6, leaving me with 4. You didn’t split half half? No, I chose a~little bit less for myself.’’
"HELLO, it’s hot outside today... isn’t it?"
"NO MESSAGE"
input str244 message "I decided to offer you 6, leaving me with 4. You didn’t split half half? No, I chose a~little bit less for myself." "HELLO, it’s hot outside today... isn’t it?" "NO MESSAGE" end
gen indicator1 = regexm(" " + message + " ", "[,\. ](ultimatum|offer|accept|reject|
payoff|euro|currency|earn)[,\. ]")
gen indicator2 = regexm(" " + message + " ", "[^A-Z] (ultimatum|offer|accept|reject|
payoff|euro|currency|earn)[^A-Z]")
egen game_content = rowmax(indicator*) list message game_content

References
- Xiao, E.; Houser, D. Avoiding the sharp tongue: Anticipated written messages promote fair economic exchange. J. Econ. Psychol. 2009, 30, 393–404. [Google Scholar] [CrossRef]
- Ellingsen, T.; Johannesson, M. Anticipated verbal feedback induces altrusitic behavior. Evol. Hum. Behav. 2007, 29, 100–105. [Google Scholar] [CrossRef]
- Brook, R.; Servátka, M. The anticipatory effect of nonverbal communication. Econ. Lett. 2016, 144, 45–48. [Google Scholar]
- Charness, G.; Gneezy, U. What’s in a name? Anonymity and social distance in dictator and ultimatum games. J. Econ. Behav. Organ. 2008, 68, 29–35. [Google Scholar] [CrossRef]
- Xiao, E.; Houser, D. Emotion expression in human punishment behavior. Proc. Natl. Acad. Sci. USA 2005, 102, 7398–7401. [Google Scholar] [CrossRef] [PubMed]
- Andersson, O.; Galizzi, M.M.; Hoppe, T.; Kranz, S.; van der Wiel, K.; Wengström, E. Persuasion in experimental ultimatum games. Econ. Lett. 2010, 108, 16–18. [Google Scholar] [CrossRef]
- Gneezy, U. Deception: The role of consequences. Am. Econ. Rev. 2005, 95, 384–394. [Google Scholar] [CrossRef]
- Selten, R. Die Strategiemethode zur Erforschung des eingeschränkt rationalen Verhaltens im Rahmen eines Oligopolexperimentes. In Beitraäge zur Experimentellen Wirtschaftsforschung; Sauermann, H., Ed.; Mohr Siebeck: Tübingen, Germany, 1967; pp. 136–168. [Google Scholar]
- Oosterbeek, H.; Sloof, R.; Van De Kuilen, G. Cultural differences in ultimatum game experiments: Evidence from a meta-analysis. Exp. Econ. 2004, 7, 171–188. [Google Scholar] [CrossRef]
- Brandts, J.; Charness, G. The strategy versus the direct-response method: A first survey of experimental comparisons. Exp. Econ. 2011, 14, 375–398. [Google Scholar] [CrossRef]
- Roth, A. Bargaining experiments. In The Handbook of Experimental Economics; Kagel, J., Roth, A.E., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; pp. 253–348. [Google Scholar]
- Zultan, R. Strategic and Social Pre-Play Communication in the Ultimatum Game. J. Econ. Psychol. 2012, 33, 425–434. [Google Scholar] [CrossRef]
- Battigalli, P.; Charness, G.; Dufwenberg, M. Deception: The role of guilt. J. Econ. Behav. Organ. 2013, 93, 227–232. [Google Scholar] [CrossRef]
- Battigalli, P.; Dufwenberg, M. Guilt in games. Am. Econ. Rev. 2007, 97, 170–176. [Google Scholar] [CrossRef]
- Andreoni, J.; Rao, J.M. The power of asking: How communication affects selfishness, empathy, and altruism. J. Public Econ. 2011, 95, 513–520. [Google Scholar]
- Houser, D.; Xiao, E. Classification of natural language messages using a coordination game. Exp. Econ. 2011, 14, 1–14. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
| 1. | By viewing the ultimatum game simply as the dictator game with the recipient having the option to veto the allocation, then one may attribute any behavioral differences between the games to the existence of this veto option in the ultimatum game. |
| 2. | Empirically, Brandts and Charness [10] conclude that both the strategy- and the direct response-method yield similar results in general, consistent with what game theory predicts. |
| 3. | Refer to the instructions in the Appendix A for details. |
| 4. | The random effects linear and probit models are estimated using the maximum likelihood estimation method. |
| 5. | A feasible estimation approach with monotonic strategy-vectors is to define a minimum acceptance threshold for a responder, i.e., the minimum amount that the responder is willing to accept, and then analyze how it changes across treatments (see, for example, Zultan [12]). |
| 6. | GLLAMM refers to the Stata program to fit generalized linear latent and mixed models. |
| 7. | As a disclaimer, we acknowledge that equal is not necessarily fair. However, for most participants in the ultimatum game, there is a high positive correlation between the two concepts. |
| 8. | In particular, for Andreoni and Rao [15], one sided communication results in lower contributions compared to no communication and all other communication conditions. |
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| ☐ | ☐ | ☐ | ☐ | ☐ | ☐ | ☐ | ☐ | ☐ |
| No Communication | One-Sided Communication | Two-Sided Communication | |
|---|---|---|---|
| Period 1 | |||
| Mean offer | 3.85 (1.755) | 3.65 (1.785) | 4.65 (1.309) |
| Acceptance Rates | 76% | 72% | 59% |
| Period 2 | |||
| Mean offer | 3.65 1.631 | 3.35 (1.387) | 3.65 (1.424) |
| Acceptance Rates | 79% | 72% | 62% |
| Period 3 | |||
| Mean offer | 3.55 (1.572) | 3.25 (1.333) | 3.85 (1.309) |
| Acceptance Rates | 79% | 73% | 68% |
| Period 4 | |||
| Mean offer | 3.60 (1.501) | 3.30 (1.342) | 4.20 (1.221) |
| Acceptance Rates | 79% | 73% | 69% |
| Period 5 | |||
| Mean offer | 3.30 (1.525) | 3.35 (1.226) | 4.35 (0.813) |
| Acceptance Rates | 82% | 76% | 67% |
| Overall | |||
| Mean offer | 3.59 (1.577) | 3.38 (1.405) | 4.14 (1.239) |
| Acceptance Rates | 79% | 73% | 65% |
| Offer∼ | |||
|---|---|---|---|
| All Periods | |||
| (Intercept) | 3.775 (0.234) | −0.476 (0.262) | 0.332 (0.239) |
| One-sided communication | −0.210 (0.188) | −0.417 (0.206) | −0.260 (0.188) |
| Two-Sided communication | 0.550 (0.188) | 0.443 (0.192) | 0.434 (0.192) |
| Period | −0.062 (0.054) | −0.002 (0.057) | −0.023 (0.055) |
| First Period | |||
| (Intercept) | 3.850 (0.355) | −0.674 (0.305) | 0.253 (0.284) |
| One-sided communication | −0.200 (0.503) | 0.000 (0.431) | −0.000 (0.401) |
| Two-Sided communication | 0.800 (0.503) | 0.800 (0.415) | 0.783 (0.445) |
| Last Period | |||
| (Intercept) | 3.300 (0.267) | −0.610 (0.354) | −0.000 (0.280) |
| One-Sided communication | 0.050 (0.358) | −0.382 (0.472) | −0.126 (0.397) |
| Two-Sided communication | 1.050 (0.358) | 0.608 (0.441) | 1.281 (0.474) |
| W- | 16.42 | 17.30 | 13.01 |
| W- | 3.96 | 3.72 | 3.10 |
| W- | 7.80 | 4.22 | 8.80 |
| No. of observations | 300 | 300 | 300 |
| No. of observations | 60 | 60 | 60 |
| Reject ∼ | Coeff (Std. Err.) | ||
|---|---|---|---|
| All Periods | First Period | Last Period | |
| (Intercept) | −3.810 (0.565) | −3.575 (0.578) | −4.936 (0.951) |
| One-Sided communication | 0.408 (0.545) | 0.231 (0.397) | 0.479 (0.632) |
| Two-Sided communication | 0.945 (0.307) | 1.011 (0.401) | 1.047 (0.397) |
| x_LOW | 1.483 (0.531) | 1.472 (0.527) | 2.047 (0.977) |
| x_HIGH | 3.583 (0.576) | 3.118 (0.555) | 4.212 (0.977) |
| −0.098 (0.044) | |||
| W- | 19.53 | 8.68 | 4.18 |
| W- | 331.50 | 47.63 | 65.16 |
| Log-likelihood | −1220.10 | −270.28 | −238.14 |
| No. of observations | 2700 | 540 | 540 |
| Communication Treatment | ||
|---|---|---|
| One-Sided Communication | Two-Sided Communication | |
| Persuasion | 23 (51%) | 33 (35%) |
| Information | 20 (44%) | 49 (52%) |
| Apology | 0 (0%) | 0 (0%) |
| Other | 2 (4%) | 12 (13%) |
| Total | 45 (100%) | 94 (100%) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capizzani, M.; Mittone, L.; Musau, A.; Vaccaro, A. Anticipated Communication in the Ultimatum Game. Games 2017, 8, 29. https://doi.org/10.3390/g8030029
Capizzani M, Mittone L, Musau A, Vaccaro A. Anticipated Communication in the Ultimatum Game. Games. 2017; 8(3):29. https://doi.org/10.3390/g8030029
Chicago/Turabian StyleCapizzani, Mario, Luigi Mittone, Andrew Musau, and Antonino Vaccaro. 2017. "Anticipated Communication in the Ultimatum Game" Games 8, no. 3: 29. https://doi.org/10.3390/g8030029




