1. Introduction
Few humans are motivated solely by their private gains. Most have more complex motivations, usually including some moral considerations, a concern for fairness or an element of altruism or even spite or envy towards others. There can even be a concern for the well-being of one’s peer group, community, country or even humankind. By contrast, for a long time, almost all of economics was based on the premise of narrow self-interest, by and large following the lead of Adam Smith’s
Inquiry into the Nature and Causes of the Wealth of Nations (1776) [
1]. However, Adam Smith himself also thought humans in fact have more complex and often social concerns and motives, a theme developed in his
Theory of Moral Sentiments (1759) [
2].
1 Philosophers still argue about how to reconcile the themes of these two books in the mind of one and the same author. Did Adam Smith change his mind between the first and second book? Or was his position in his second book to demonstrate that well-functioning markets would result in beneficial results for society at large even if all individuals were to act only upon their own narrow self interest?
In view of the overwhelming experimental evidence that only a minority of people behave in accordance with predictions based on pure material self-interest, it appears relevant to ask whether and how alternative preferences affect outcomes in standard economic interactions. It is commonly believed that if an element of altruism or morality were added to economic agents’ self-interest, then outcomes would improve for all. Presumably, people would not cheat when trading with each other, and they would work hard even when not monitored or remunerated by way of bonus schemes. They would contribute to public goods, respect and defend the interests of others, and might even be willing to risk their lives to save the lives of others.
While this has certainly proved to be right in some interactions,
2 the belief is not generally valid. For example, Lindbeck and Weibull (1988) [
10] demonstrate that altruism can diminish welfare among strategically interacting individuals engaged in intertemporal decision-making. The reason is that if interacting individuals are aware of each others’ altruism, then even altruists will to some extent exploit each others’ altruism, resulting in misallocation of resources. One prime example is under-saving for one’s old age, with the rational expectation that others will help if need be. In this example, everyone would benefit from commitment not to help each other, as this could induce intertemporally optimal saving.
Likewise, Bernheim and Stark (1988) [
11] show that altruism may be harmful to long-run cooperation. There, the reason is that in repeated games between altruists, punishments from defection may be less harsh if the punisher is altruistic—just like a loving parent who cannot credibly threaten misbehavior by a child with even a mild punishment. Specifically, in repeated interactions, the mere repetition of a static Nash equilibrium in the stage game has better welfare properties between altruists than between purely self-interested individuals, thus diminishing the punishment from defecting from cooperation. However, altruism also diminishes the temptation to defect in the first place, since defecting harms the other party. Bernheim and Stark (1988) [
11] show that the net effect of altruism may be to diminish the potential for cooperation in the sense that it diminishes the range of discount factors that enables cooperation as a subgame-perfect equilibrium outcome.
The aim of the present study is to examine strategic interactions between altruists, as well as between moralists, more closely, in order to shed light on the complex and non-trivial effects of altruism and morality on equilibrium behavior and the associated material welfare. By ‘altruism’, we mean here that an individual cares not only about own material welfare but also about the material welfare of others, in line with Becker (1974 [
12], 1976 [
5]) , Andreoni (1988) [
13], Bernheim and Stark (1988) [
11], and Lindbeck and Weibull (1988) [
10]. As for ‘morality’, we rely on recent results in the literature on preference evolution, results which show that a certain class of preferences, called
Homo moralis preferences, stands out as being particularly favored by natural selection (Alger and Weibull, 2013 [
14], 2016 [
15]). A holder of such preferences maximizes a weighted sum of own material payoff evaluated at the true strategy profile and own material payoff evaluated at hypothetical strategy profiles in which some or all of the other player’s strategies have been replaced by the individual’s own strategy
3.
We examine the effects of altruism and such morality for behavior and outcomes in static and repeated interactions. Some of the results may appear surprising and counterintuitive. We also show similarities and differences between altruism and morality, the main difference between these two motivations being due to the fact that while the first is purely consequentialistic, the second is partly deontological. In other words, the first motivation is only concerned with resulting material allocations, the second places some weight on “duty” or the moral value of acts, a concern about what is “the right thing to do” in the situation at hand.
Our study complements other theoretical analyses of the effects of pro-social preferences and/or moral values on the qualitative nature of equilibrium outcomes in a variety of strategic interactions. In economics, see Arrow (1973) [
22], Becker (1974) [
12], Andreoni (1988 [
13], 1990 [
23]), Bernheim (1994) [
24], Levine (1998) [
25], Fehr and Schmidt (1999) [
26], Akerlof and Kranton (2000) [
27], Bénabou and Tirole (2006) [
28], Alger and Renault (2007) [
29], Ellingsen and Johannesson (2008) [
30], Englmaier and Wambach (2010) [
31], Dufwenberg et al. (2011) [
32], and Sarkisian (2017) [
33]. For related models of social norms, see Young (1993) [
34], Kandori, Mailath, and Rob (1993) [
35], Sethi and Somanathan (1996) [
36], Bicchieri (1997) [
37], Lindbeck, Nyberg, and Weibull (1999) [
38], Huck, Kübler, and Weibull (2012) [
39], and Myerson and Weibull (2015) [
40].
4Our study also complements a large literature on theoretical analyses of the evolution of behaviors in populations. For recent contributions, see Lehmann and Rousset (2012) [
42], Van Cleve and Akçay (2014) [
43], Allen and Tarnita (2014) [
44], Ohtsuki (2014) [
45], Peña, Nöldeke, and Lehmann (2015) [
46], and Berger and Grüne (2016) [
47]. For surveys of related work on agent-based simulation models, see Szabó and Borsos (2016) [
48] and Perc et al. (2017) [
49].
In the next section, we define the three classes of preferences that we study and review some known results. We then turn to studying repeated interactions (
Section 3), and coordination games (
Section 4), and finally conclude.
2. Definitions and Preliminaries
We consider n-player normal-form games (for any ) in which each player has the same set X of (pure or mixed) strategies, and is the material payoff to strategy when used against strategy profile for the other players. By ‘material payoff’, we mean the tangible consequences of playing the game, defined in terms of the individual’s monetary gains (or losses), or, more generally, his or her indirect consumption utility from these gains (or losses). We assume to be aggregative in the sense that is invariant under permutation of the components of . The strategy set X is taken to be a non-empty, compact and convex set in some normed vector space.
We say that an individual is purely self-interested, or a
Homo oeconomicus if he only cares about his own material payoff, so that his utility is
An individual is an
altruist if he cares about his own material payoff and also attaches a weight, his or her
degree of altruism , to the material payoffs to others, so that his utility is:
Finally, an individual is a
Homo moralis if he cares about his own material payoff and also attaches a weight to what his material payoff would be should others use the same strategy as him. Formally, the utility to a
Homo moralis with degree of morality
is
where
is a random
-vector such that with probability
exactly
of the
components of
are replaced by
, while the remaining components of
keep their original values (for each
m, there are
ways to replace
m of the
components of
). For instance, writing
and
for the strategies of
i’s two opponents when
:
We observe that a Homo oeconomicus can be viewed as an altruist with degree of altruism , and as a Homo moralis with degree of morality .
Our purpose is to compare equilibria of interactions in which all individuals are altruists with interactions in which all individuals are moralists. We are interested both in the equilibrium behaviors as well as in the material welfare properties of these equilibria. We will use
to refer to the
n-player game between altruists with common degree of altruism
, with payoff functions defined in (
1), and
to refer to the
n-player game between
Homo moralis with common degree of morality
, with payoff functions defined in (
2).
2.1. Necessary First-Order Conditions
Consider a simple public goods game, with
where
is
i’s contribution to the public good. Assume further that
. It turns out that in this interaction equilibria in
coincide with those in
when
.
More generally, for interactions in which the strategy set
X is an interval and
is continuously differentiable, any interior symmetric Nash equilibrium strategy
in game
, for any
, satisfies the first-order condition
(By permutation invariance of
, all partial derivatives with respect to other players’ strategies are identical). Moreover, (
5) is also necessary for an interior strategy
to be a symmetric Nash equilibrium strategy in the same interaction between moralists,
for
(Alger and Weibull, 2016). Higher-order conditions may differ, however, so that the set of symmetric equilibria do not necessarily coincide.
5 Nevertheless, in the above public good example, they do.
Figure 1 shows the unique symmetric Nash-equilibrium contribution in the public goods game between moralists,
, as a function of community size
n, for different degrees of morality, with higher curves for higher degrees of morality. This is also the unique symmetric Nash-equilibrium contribution in the public goods game between altruists,
, when the degree of altruism is the same as the degree of morality,
. Hence, the behavioral effects of morality and altruism are here indistinguishable.
2.2. Two-by-Two Games
We now briefly consider symmetric two-by-two games, with
denoting the material payoff accruing to a player using pure strategy
against pure strategy
. For mixed strategies, let
denote the players’ probabilities for using pure strategy 1. The expected material payoff from using mixed strategy
x against mixed strategy
y is bilinear:
In such an interaction, an altruist’s utility function is still bilinear:
while a
Homo moralis has a utility function with quadratic terms:
Depending on whether the sum of the diagonal elements of the payoff matrix,
, exceeds, equals, or falls short of the sum of the off-diagonal elements,
, the utility of
Homo moralis is either strictly convex, linear, or strictly concave in his own mixed strategy,
x. Hence, the set of symmetric equilibria of
typically differs from that of
even when
.
6As an illustration, consider a prisoner’s dilemma with the first pure strategy representing “cooperate”, that is, payoffs
. Using the standard notation
,
,
and
, it is easy to verify that “cooperation”, that is, the strategy pair
, is a Nash equilibrium in
if and only if
where
and that it is a Nash equilibrium in
if and only if
, where
We note that
In other words, it takes less altruism to turn cooperation into an equilibrium than it takes morality when the payoff loss
inflicted upon an opponent by defecting—which an altruist cares about—exceeds the difference between the own payoff gain
T from defecting unilaterally and from defecting together,
P, a payoff difference a moralist cares about. The reverse is true when
.
We next turn to exploring uncharted territories, by studying repeated interactions (
Section 3) and coordination (
Section 4).
3. Repetition
We analyze infinite repetition of two distinct classes of interaction: prisoners’ dilemmas and sharing games, respectively.
3.1. Repeated Prisoners’ Dilemmas
Consider an infinitely repeated prisoner’s dilemma with payoffs as above and with a common discount factor
. We will provide necessary and sufficient conditions for grim trigger (that is, cooperate until someone defects, otherwise defect forever), if used by both players, to constitute a subgame-perfect equilibrium that sustains perpetual cooperation.
7 We do this first for a pair of equally altruistic players, then for a pair of equally moral players, and finally compare the ability to sustain cooperation of altruists with that of moralists.
If played by two equally altruistic individuals with degree of altruism
, the stage-game utilities to the row player are the following (see (
6)):
Grim trigger, if used by both players, constitutes a subgame perfect equilibrium that sustains perpetual cooperation if
and
The first inequality makes one-shot deviations from cooperation unprofitable. The left-hand side is the per-period payoff obtained if both players always cooperate. If one player defects, he gets the “temptation utility”
once, and then the punishment payoff
forever thereafter. Inequality (
10) compares the present value of continued cooperation with the present value from a one-shot deviation. The second inequality, (
11), makes a one-shot deviation from non-cooperation (play of
) unprofitable; this inequality is necessary for the threat to play
D following defection to be credible. For further use below, we note that (
10) can be written more succinctly as a condition on
, or the players’ patience, namely as,
, where
Furthermore, denote by
the threshold value for
defined by (
11).
In sum, a pair of equally altruistic players can sustain perpetual cooperation either if altruism is strong enough,
(see (
9)), in which case
is a Nash equilibrium of the stage game and hence needs no threat of punishment to be sustained, or if players are selfish enough to credibly punish defection,
, and players are patient enough to prefer the long-term benefits from cooperation than the immediate reward from defection,
. In the intermediate case, that is, when
, cooperation is not sustainable for any discount factor
.
For example, suppose that and . If and , then and . In this case, cooperation is sustainable for any discount factor if , and for any sufficiently high discount factor () if . By contrast, if and , and . In this case, cooperation is sustainable for any discount factor if altruism is strong () and for any sufficiently high discount factor () if altruism is weak (), but cooperation is not sustainable at all for intermediate degrees of altruism ().
Turning now to moralists, the stage-game utilities to a row player with degree of morality
are given in (
7), so we now have
Comparison with the utility matrix for altruists reveals that while an altruist who defects internalizes the pain inflicted on the opponent, and is thus sensitive to the value
S, a moralist who defects internalizes the consequence of his action should both choose to defect simultaneously, and is thus sensitive to the value
P. Following the same logic as above, grim trigger sustains perpetual cooperation between two equally moral individuals as a subgame perfect equilibrium outcome if
, where
and
, where
In sum, a pair of equally moral players can sustain perpetual cooperation either if
(see (
8)), in which case
is an equilibrium of the stage game and the threat to punish by playing
D is not necessary to sustain cooperation in the repeated interaction, or if
and
.
We now turn to comparing a pair of selfish players to a pair of altruists or a pair of moralists. For selfish players, grim trigger constitutes a subgame perfect equilibrium that sustains perpetual cooperation if
, where
Since for any values of T, R, and P, and since for any and , we conclude the following. First, conditional on the threat to punish defectors being credible (i.e., and , respectively), altruists and moralists are better at sustaining cooperation than selfish individuals. Second, selfish individuals are better at sustaining cooperation than altruists (resp. moralists) if the latter cannot credibly threaten to punish defectors (i.e., resp. ).
Finally, comparing a pair of equally altruistic players with degree of altruism to a pair of equally moral players with degree of morality , does one pair face a more stringent challenge to sustain cooperation than the other? To answer this question, we distinguish three cases, depending on whether exceeds, falls short of, or equals .
Suppose first that
. Observe first that this implies
(where
was defined in (
9) and
in (
8)). In other words,
is an equilibrium of the stage game between altruists whenever it is an equilibrium of the stage game between moralists. Moreover, whenever
is not an equilibrium of the stage game, altruists and moralists are equally capable of credibly threatening to play
D following a defection, so that both altruists and moralists can sustain cooperation if sufficiently patient. However, it is easy to verify that
implies
: thus, if
, grim trigger constitutes a subgame perfect equilibrium that sustains perpetual cooperation for the altruists but not for the moralists.
Second, suppose that . Observe first that this implies : this means that if , then is an equilibrium of the stage game between moralists but not of the stage game between altruists. Since implies , and , the conclusion is as follows. When , there exist values of for which altruists are not able to sustain cooperation for any discount factor , whereas a pair of moralists with any degree of morality can sustain perpetual cooperation; namely, for any if , and for all if .
Finally, suppose that . Then, it is straightforward to verify that the opposite conclusion obtains, namely that there exist degrees of morality for which moralists are not able to sustain cooperation for any , whereas a pair of altruists with arbitrary degree of altruism can sustain perpetual cooperation (for any if , and for all if ).
3.2. Repeated Sharing
The observation that it may be harder for altruists than for egoists to sustain cooperation in an infinitely repeated game was pointed out by Bernheim and Stark (1988 [
11], Section II.B). We first recapitulate their model. We then carry through the same analysis for
Homo moralis, and finally compare the two. The stage-game is the same as used by Bernheim and Stark, and represents sharing of consumption goods.
3.2.1. Altruism
The stage game is a two-player simultaneous-move game in which each player’s strategy set is
for some small
, where a player’s strategy is the amount of his consumption good that he keeps. If player 1 chooses
and player 2 chooses
, payoffs are
for player 1, and
for player 2, where
.
8 A necessary first-order condition for an interior Nash equilbrium is thus
and likewise for player 2. Bernheim and Stark consider the symmetric case when
, in which case the first-order condition is their Equation (
16).
9 They use this to identify the following unique symmetric Nash equilibrium of the stage game
:
They compare this with the unique symmetric Pareto optimum,
, the solution of
The utility evaluated at the stage-game equilibrium is
and the utility evaluated at the Pareto-optimal strategy pair is
.
Bernheim and Stark consider an infinitely repeated play of this stage game, with discount factor
. They note that perpetual play of “cooperation”,
, is sustained in subgame perfect equilibrium by the threat of (perpetual) reversion to
iff
, where
where
is the maximal utility from a one-shot deviation from cooperation, that is,
Solving this maximization problem, we find that a player who would optimally deviate from cooperation would play
Noting that, for
,
and
, we observe that pure altruists do not benefit from deviation. Hence, pure altruists can sustain cooperation irrespective of
.
10Bernheim and Stark proceed by considering a numerical example,
and
, and find that the lowest discount factor
then needed to sustain cooperation is strictly
increasing with
. In other words, altruism makes cooperation harder. We proceed in parallel with them by setting
,
and
. Then,
,
and
for all
above approximately 0.05.
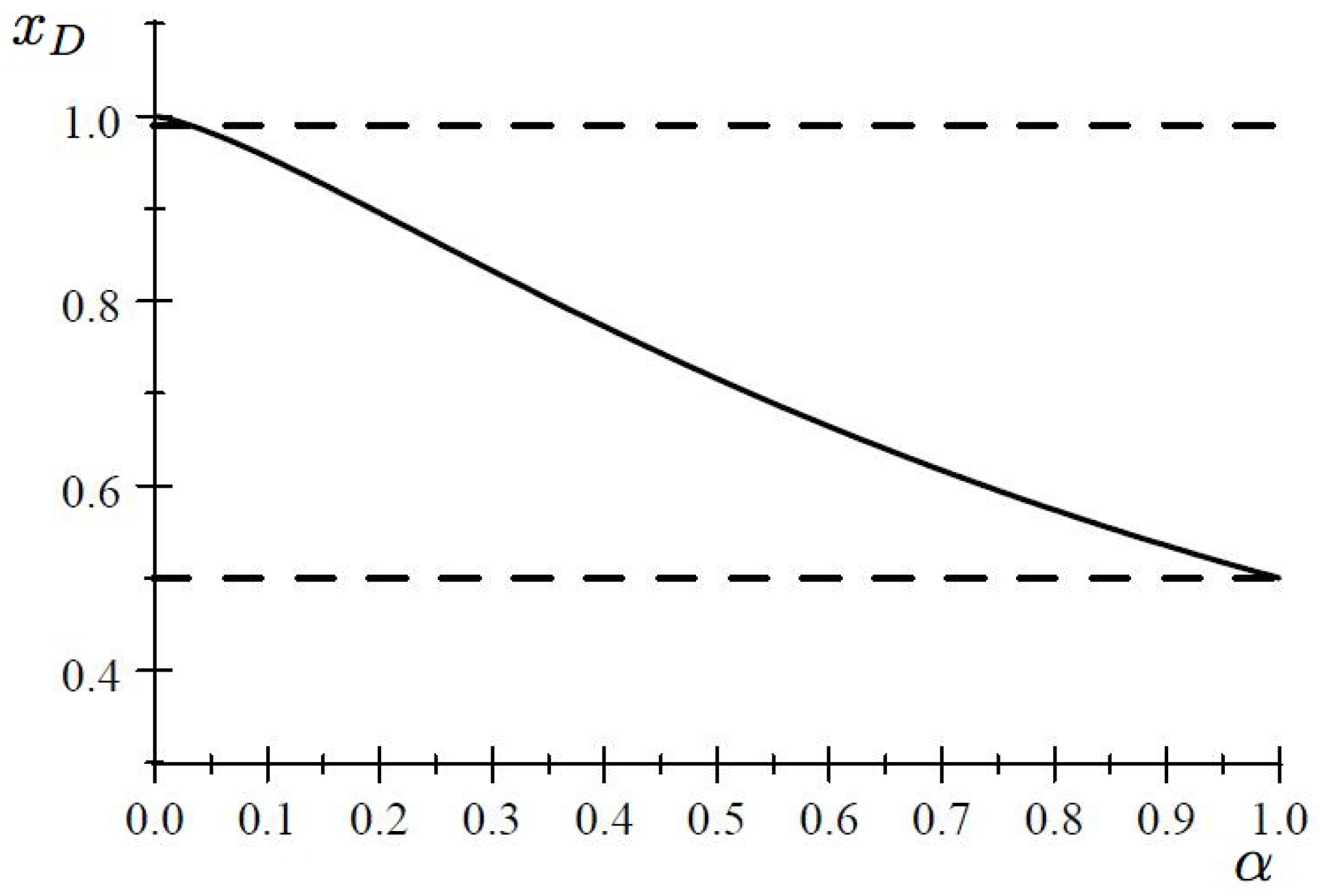
Figure 2 shows that indeed
for such values of
.
For such
,
Hence,
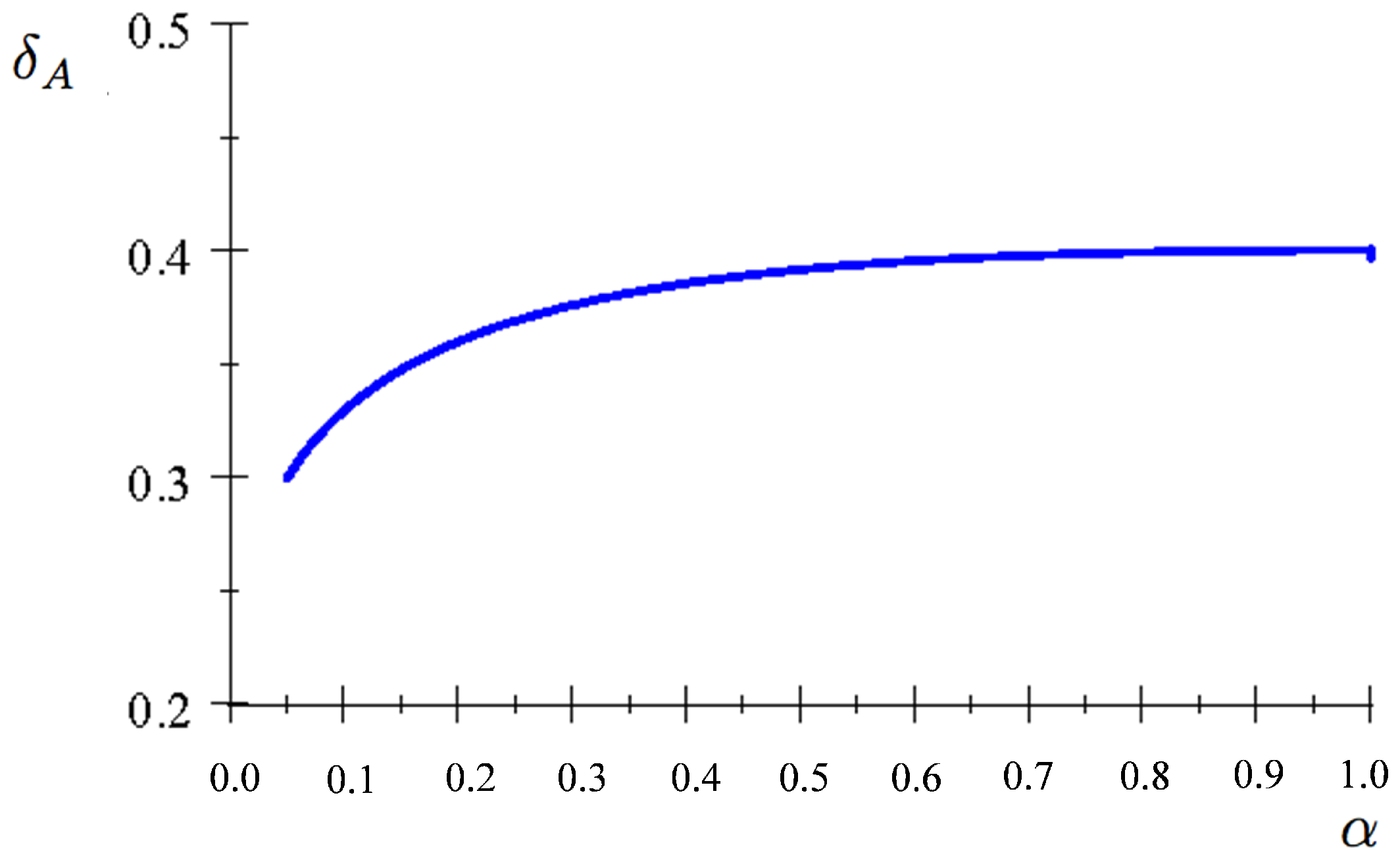
Figure 3 shows
as a function of
when
, for
. In particular, as
, both the nominator and denominator in the definition tend to zero. By l’Hopital’s rule,
as
.
These numerical results agree with those reported in Table 1 in Bernheim and Stark (1988) [
11], when keeping in mind that our altruism parameter
is a transformation of theirs (see footnote 9 above). In this numerical example, a pair of
Homo oeconomicus (
), can sustain cooperation only if
. Altruism thus here has an economically significant negative impact on the ability to sustain cooperation, since even a small degree of altruism, such as
, raises the discount factor needed for cooperation by 40%.
3.2.2. Morality
The stage-game is again a two-player simultaneous-move game in which each player’s strategy set is
for some small
. If player 1 chooses
and player 2 chooses
, payoffs are
for player 1, and
for player 2, where
. A necessary first-order condition for an interior Nash equilibrium is thus
for player 1, and likewise for player 2. Suppose that
. Then, the unique symmetric equilibrium strategy is
Comparing a pair of altruists with a common degree of altruism to a pair of moralists with common degree of morality , we note that .
Henceforth, assume that the first term is the smallest, that is,
. Then, the utility evaluated at the Nash equilibrium strategy is
The unique symmetric Pareto-optimal strategy is still , and the utility evaluated at this strategy is .
Consider an infinitely repeated play of this stage game, with discount factor
. Perpetual “cooperation”, play of
, is sustained in subgame perfect equilibrium by the threat of (perpetual) reversion to
if and only if
, where
and
is the maximal utility from a one-shot deviation from cooperation, that is,
Solving this maximization problem, we find that a player who would optimally deviate from cooperation would play
, where
is the unique solution to the fixed-point equation
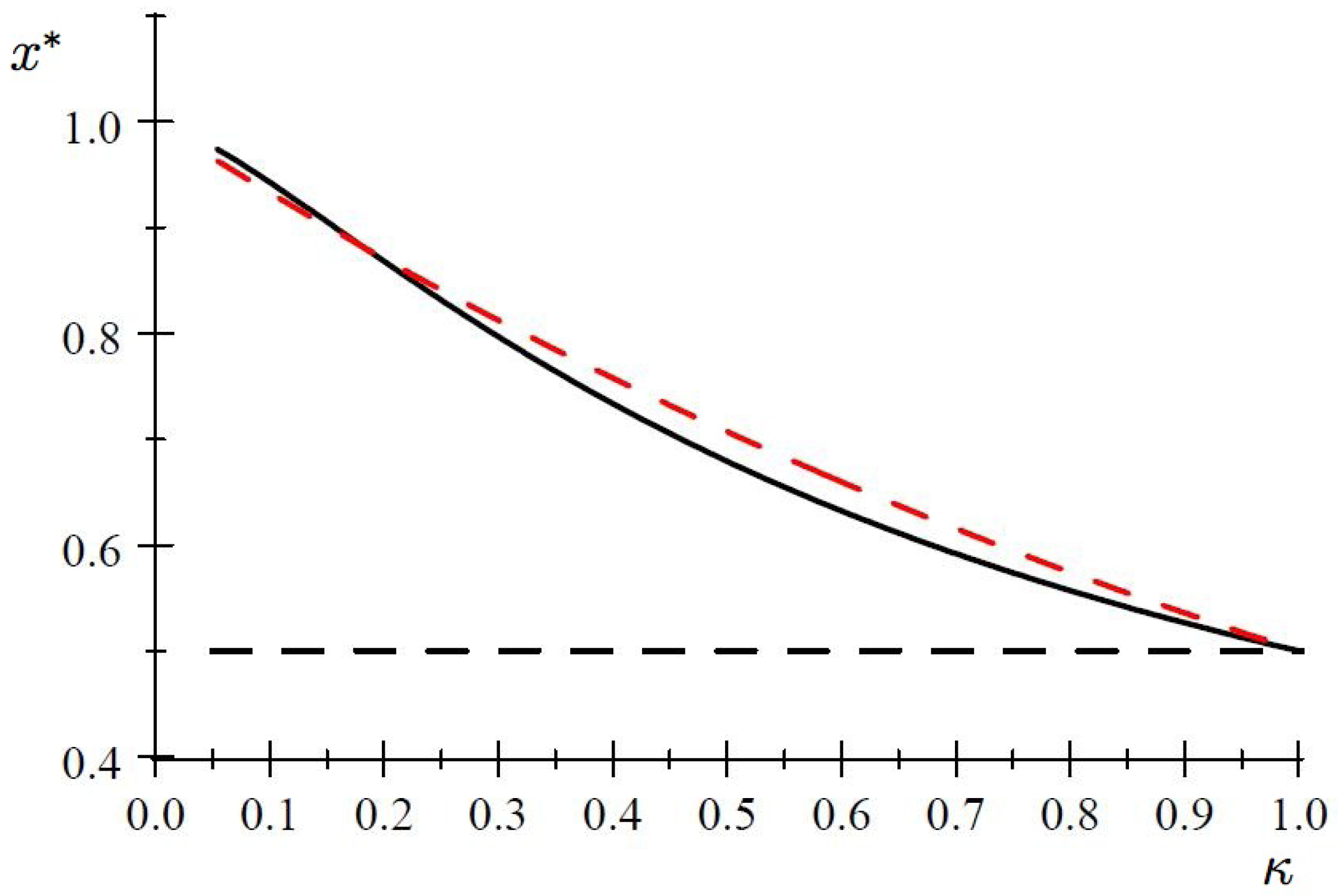
Figure 4 plots the solution as a function of
, for
(and for
).
We proceed by considering the numerical example that we studied under altruism. Let thus
and
, and assume that
(which guarantees an interior solution, both for
and
). We use the approximation
, indicated by the dashed curve in
Figure 4. This gives the approximation
The condition (
17) for sustainable cooperation can thus be written as
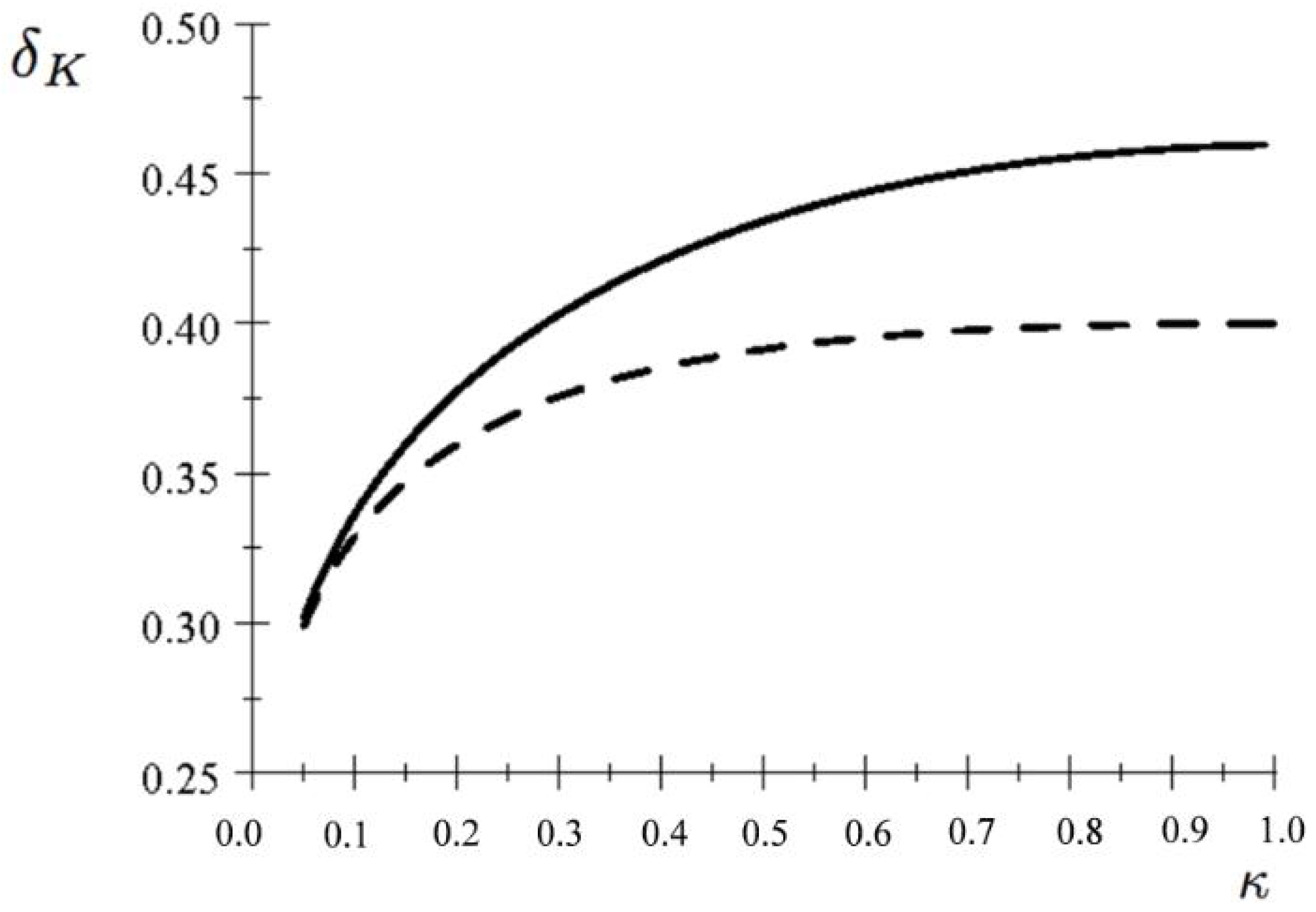
Figure 5 shows the right-hand side as a function of
(for
) when
. The dashed curve is drawn for altruists with
. We see that, for
, cooperation is somewhat harder to sustain between moralists than between altruists with
. In summary, in this numerical example, cooperation is easiest to maintain between purely self-interested individual than between altruists, and easier to sustain between altruists than between moralists.
Does this qualitative result partly depend on the numerical approximation? Does it hold for all
? In order to investigate these issues, assume that
, and note that
if and only if
, an inequality that can be written as
This inequality clearly holds strictly at
, and by continuity also for all
that are small enough. For
, (
18) holds with equality, since then it boils down to
which clearly holds by equality. See
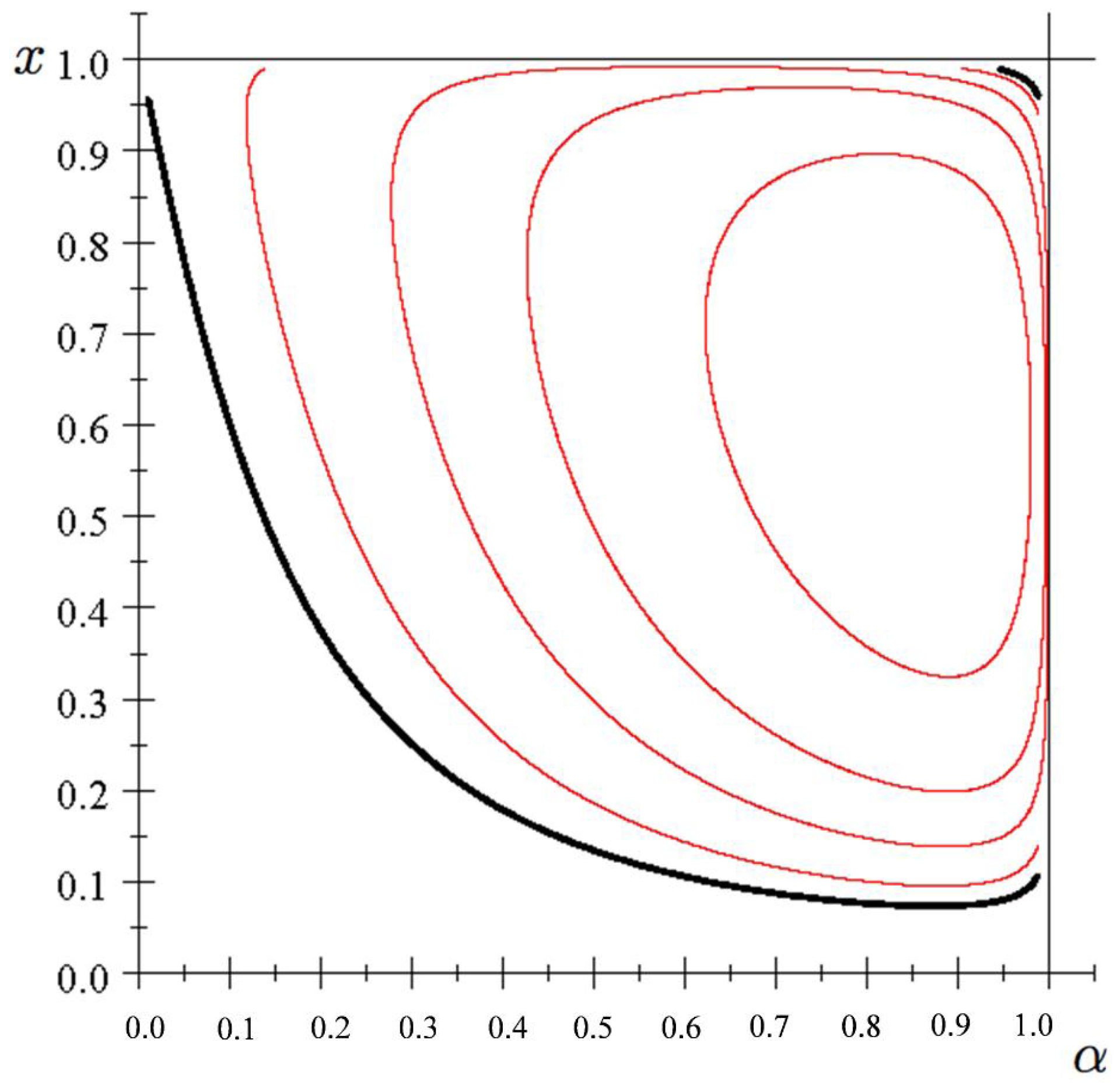
Figure 6, which shows isoquants for the difference between the right-hand and left-hand sides in (
18). The thick curve is the zero isoquant (where the inequality is an equality) and the thin curves positive isoquants (where the inequality is slack). The diagram suggests that for every
there exists an
such that (
18) holds strictly. Hence, the difference between altruism and morality is not due to the approximation of
.
3.3. Preference Representations
Both in the repeated prisoners’ dilemma and in the repeated sharing game, we represented the players’ (selfish, altruistic, moral) utility functions over behavior strategies in the repeated game as the normalized present values of their per-period (selfish, altruistic, moral) utilities as defined over their actions in the stage game. Is this consistent with defining their utility functions directly in the repeated game; the game they actually play?
Consider the infinitely repeated play of any symmetric two-player game in material payoffs with common strategy set
X and material payoff function
, and with common discount factor
. In terms of normalized present values, the material payoff function of a player using behavior strategy
in the repeated game, when the opponent uses behavior strategy
, is then
where
is the player’s own action in period
t and
the action of the opponent. The function
is thus a selfish players’ utility function in the repeated game.
First, consider altruistic players. By definition, the utility function, in the repeated game, of such a player with degree of altruism
is
Hence, the utility function coincides with the normalized present value representation that we used in our analysis of the prisoners’ dilemma and sharing game.
Secondly, for a
Homo moralis player with degree of morality
, the utility function in the repeated game is, by definition,
so also the repeated-games utility function of a moralist coincides with the normalized present value representation that we used in the two games.
In sum, the additive separability over time, inherent in the very definition of payoff functions in repeated games, makes the difference between “stage-game preferences” and “repeated-games preferences” immaterial, both in the case of altruism and in the case of morality.
4. Coordination
Suppose there are n players who simultaneously choose between two actions, A and B. Write for the choice of individual i, where means that i chooses A, and that instead B is chosen. Let the material payoff to an individual from choosing A when others choose action A be . Likewise, let the individual’s material payoff from choosing B when others choose B be , where . Examples abound. Think of A and B as two distinct “norms”, with A being the socially efficient norm. We examine under which conditions the socially inefficient norm B can be sustained in equilibrium. We will also investigate if both norms can be simultaneously and partly sustained in heterogenous populations, in the sense that some individuals take action A while others take action B.
Writing
for the strategy profile of
i’s opponents and
for the payoff function of a purely self-interested player
, we have
The utility function of an altruistic player
i with degree of altruism
is
Evidently the efficient norm A, that is all playing A, can always be sustained as a Nash equilibrium for arbitrarily altruistic players. In addition, the inefficient norm B is a Nash equilibrium. For if all others choose B, then so will any player i, no matter how altruistic. We will now see that this last conclusion does not hold for moralists.
Consider
Homo moralis players, where player
i has degree of morality
. Such a player’s utility function is
where
is a random vector in
such that with probability
exactly
of the
components of
are replaced by
, while the remaining components of
keep their original values. Thanks to the linearity of the material payoff function (
19), the utility function
can be written as
The efficient norm
A can clearly be sustained as a Nash equilibrium, since when all the others are playing
A, individual
i gets utility
from taking action
A and
from taking action
B. By contrast, the inefficient norm cannot be sustained for all degrees of morality. To see this, first suppose all individuals have the same degree of morality
. If all the others are playing
B, any individual gets utility
from also playing
B and would get utility
from deviating to
A. Hence, the inefficient norm can be sustained in Nash equilibrium if and only if
.
This result shows that morality can have a qualitatively different effect than altruism upon behavior in interactions with strategic complementarities. In the present case of a simple coordination game, morality eliminates the inefficient equilibrium if and only if the common degree of morality exceeds . By contrast, the inefficient equilibrium is still an equilibrium under any degree of altruism. No matter how much the parties care for each other, they always want to use the same strategy, even if this results in a socially inefficient outcome. Moralists are partly deontologically motivated and evaluate own acts not only in terms of their expected consequences, given others’ action, but also in terms of what ought to be done.
We finally examine heterogeneous populations. First, suppose that the coordination game defined above is played by
individuals, among which all but one are purely self-interested and the remaining individual is a
Homo moralis with degree of morality
. Under complete information, such a game has a Nash equilibrium in which all the self-interested play
B while the unique
Homo moralis plays
A. In this equilibrium, the moral player exerts a negative externality on the others—which causes partial mis-coordination. Had the moralist instead been an altruist, he would also play
B if the others do, and would thus be behaviorally indistinguishable from the purely self-interested individuals. More generally, altruists as well as self-interested individuals do not care about “the right thing to do” should others do likewise. They only care about the consequences for own and—if altruistic—others’ material payoffs, from their unilateral choice of action. By contrast, moralists also care about what would happen if, hypothetically, others would act like them. In coordination games, this may cause a bandwagon effect reminiscent of that shown in Granovetter’s (1978) [
51] threshold model of collective action, a topic to which we now turn.
Like Granovetter, we analyze a population in which each individual faces a binary choice and takes a certain action, say
A, if and only if sufficiently many do likewise. More precisely, each individual has a population threshold for taking action
A. Our model of coordination can be recast in these terms. Indeed, for each individual
, defined by his personal degree of morality
, one can readily determine the minimum number of other individuals who must take action
A before he is willing to do so. Consider any player
i’s choice. If he expects
others to take action
A, then his utility from taking action
B is
while, from taking action
A, it is
Hence, individual
i will take action
A if and only if
or
In other words, whenever individual
i expects the population share
of others taking action
A to exceed (respectively, fall short of) his or her
threshold , where
he/she takes action
A (respectively
B). We note that the threshold of an individual is strictly decreasing in the individual’s degree of morality. Moreover, individuals with high enough degrees of morality have negative thresholds and will thus take action
A even alone. The threshold of an individual with zero degree of morality, that is,
Homo oeconomicus, is
.
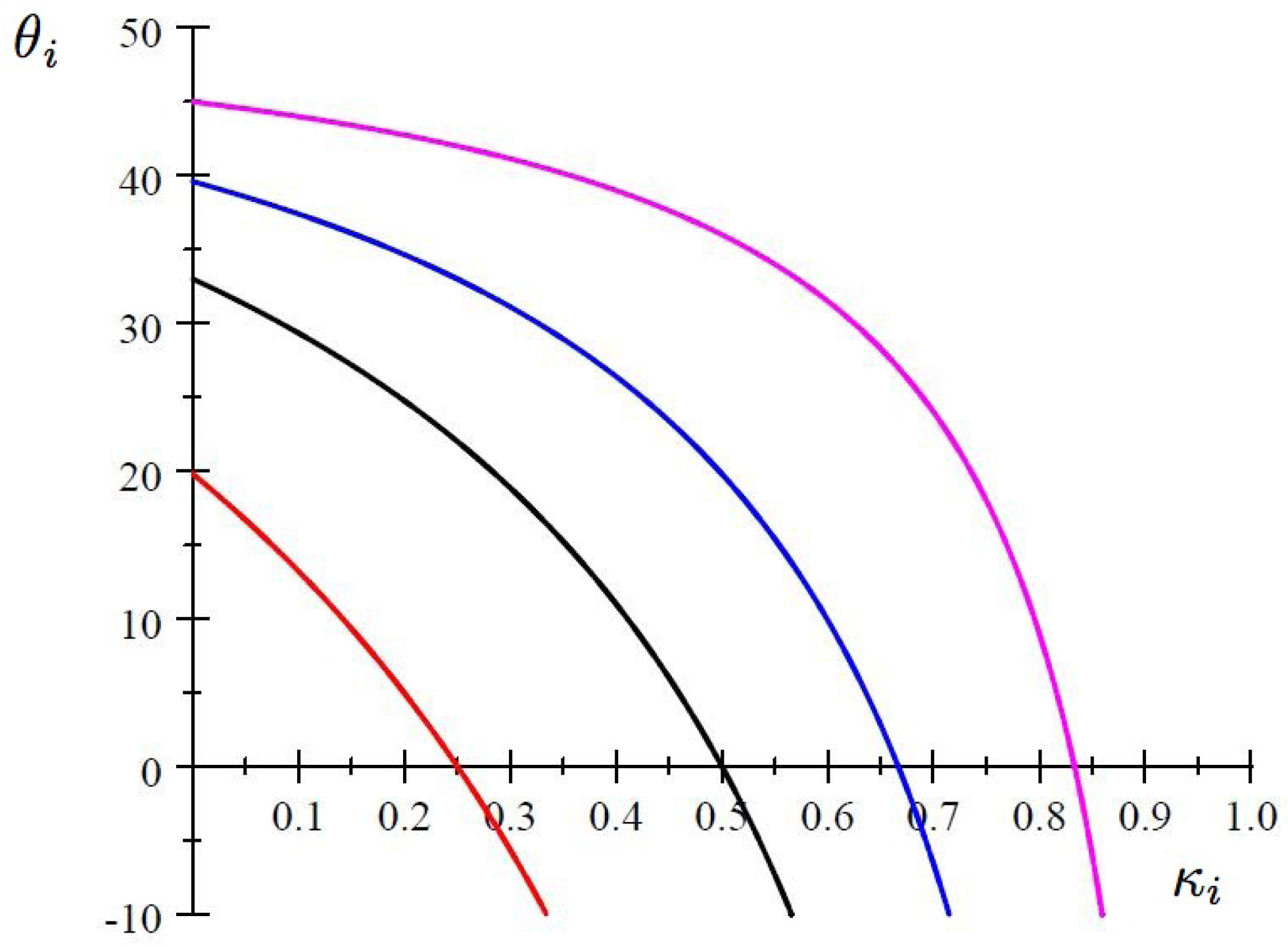
Figure 7 below shows the threshold as a function of
for different values of
, and with population shares (in percentages) on the vertical axis. Starting from the bottom, the curves are drawn for
,
,
, and
. The bottom curve, the one for
, shows that an individual with degree of morality
is willing to switch from
B to
A even if nobody else switches, an individual with degree of morality
is willing to make this switch if 14% of the others also switch, etc. This curve also reveals that as long as there is at least 20% who are sufficiently moral, and thus willing to switch even if nobody else does, or only a small number have switched, then a bandwagon effect among myopic individuals will eventually lead the whole population to switch, step by step, even if as many as 80% of the individuals are driven by pure self-interest.
Let
F be any continuous cumulative distribution function (CDF) on
such that for every
,
is the population share of individuals with thresholds not above
. Then,
is a continuous representation of the cumulative threshold distribution in the population, with
and
for all
. By Bolzano’s intermediate-value theorem,
for at least one
.
11 Let
be the non-empty and compact set of such fixed points.
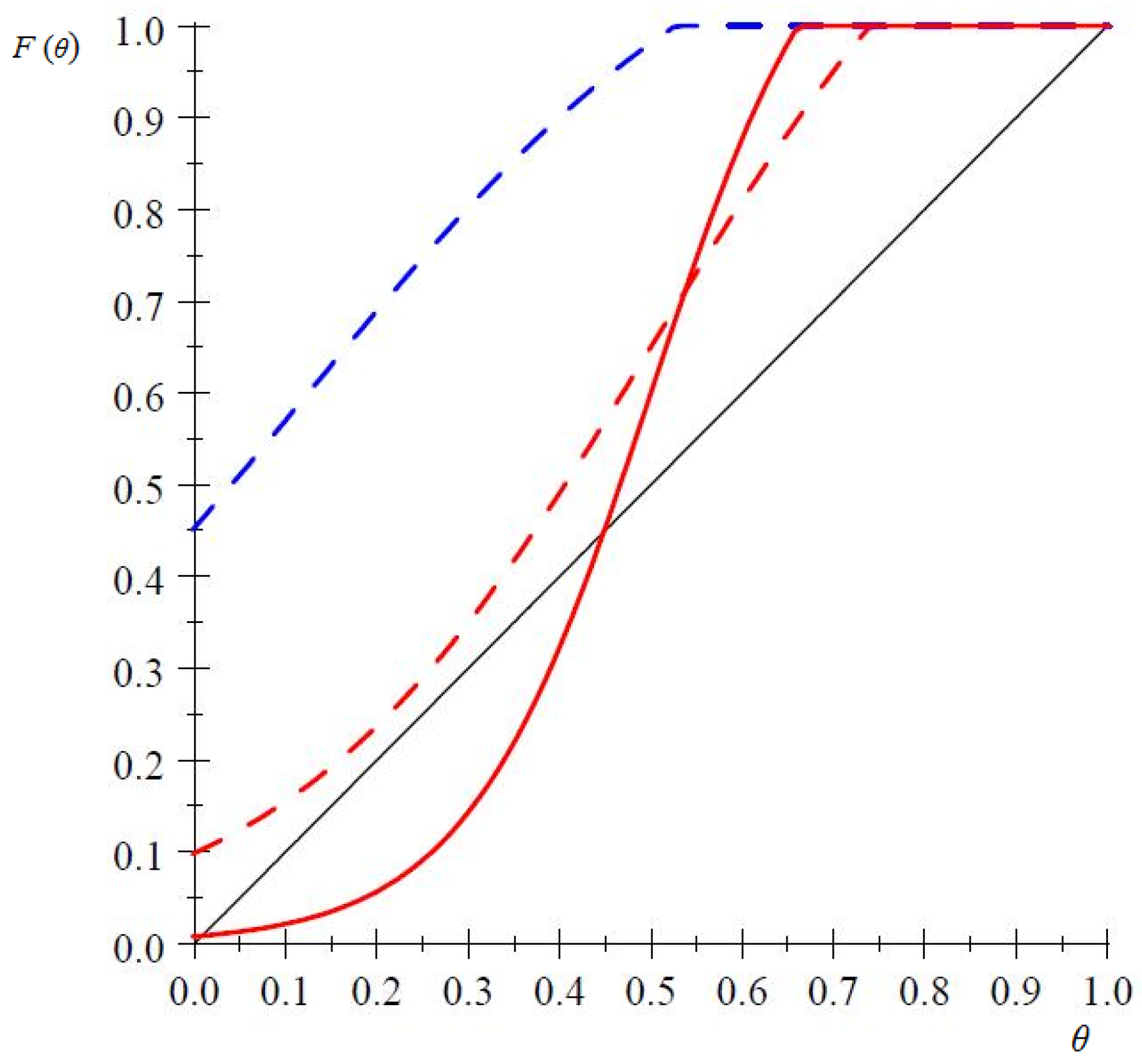
Figure 8 below shows three different CDFs. The two dashed curves represent relatively heterogenous populations, and those curves have one intersection with the diagonal, and hence the unique fixed point then is
. The solid curve represents a relatively homogeneous population and this distribution function has three intersections with the diagonal, and thus three fixed points; one close to zero, another near 0.45, and the third one being
. All fixed points are Nash equilibria in a continuum population, and are approximate Nash equilibria in finite but large populations. In the diagram, all fixed points except the one near 0.45 have index +1. Those equilibria are stable in plausible population dynamics, while the fixed point near 0.45 has index
and is dynamically unstable.
12 Figure 8 can be used for discussion of dynamic scenarios. Suppose that initially all individuals were to take action
B. All those with non-positive thresholds
(that is, with relatively high morality) would immediately switch to
A. If others see this, then the most moral among them (that is, those with lowest threshold) will follow suit. Depending on population size and its morality distribution, this process may go on until the population shares taking action
A reaches or surpasses
, at which point all remaining individuals will switch to
A. This is what may happen in a relatively heterogeneous population with morality distribution such that there is only one fixed point, which then necessarily is
. By contrast, in a relatively homogenous population with smallest fixed point
, once the adjustment process reaches the point where the population share taking action
A is
, the process will either halt or switch back and forth close to
. Hence, the population may get stuck there. Had it instead started somewhere above the middle fixed point, it could lead the population gradually towards norm
A and finally jump to that norm.
A discrete-time version of this process is as follows. Consider a situation in which initially only strategy
B exists, so that initially everybody plays
B. Suddenly, strategy
A appears, the interpretation being that it is discovered or invented. For each threshold number of individuals
, where
, let
be the number of individuals who have that threshold. If
, then nobody ever switches to
A. However, if
, the number of individuals
who have switched from
B to
A at time
, where
t denotes the number of time periods after strategy
A was discovered, we have
, and
for all
. The process stops before everybody has switched if there exists some
t such that
, i.e., if
Otherwise, it goes on until the whole population has switched to the efficient norm. In this process,
Homo moralis act as leaders because they are willing to lead by example. By contrast, altruists as well as self-interested individuals do not care about the right thing to do, should others follow their lead. They care about own material payoff, as well as that of others for altruists, given what the others do. Hence, the cascading effect obtained with moral individuals does not obtain in groups of altruists or self-interested people. We illustrate with two examples, both in which
.
Table 1 shows two distributions of the thresholds. In the first example, a total of 21 individuals switch, and this takes four periods. In the second example, all individuals have switched after six periods, in spite of a slower start. Indeed, in the first example, we have
,
,
,
, but since the remaining individuals require at least 22 people to have switched before them, they do not switch. In the second example, the process starts with just one individual switching,
, but then
,
,
,
,
.
5. Conclusions
Altruism and morality are considered virtues in almost all societies and religions worldwide. We do not question this here. Instead, we ask whether altruism and morality help improve the material welfare properties of equilibria in strategic interactions. Our analysis reveals a complex picture; sometimes, altruism and morality have beneficial effects, sometimes altruism is better than morality, sometimes the reverse is true, sometimes they are equivalent, and sometimes self-interest is best! The commonly held presumption that altruism and morality always lead to better outcomes is thus not generally valid. Our analysis unveiled two non-trivial and potentially important phenomena that we believe are robust and general. However, before attacking these two phenonema, we showed that in canonical and one-shot public-goods games with arbitrary many participants, altruism and morality are behaviorally undistinguishable and lead to unambiguously increase material welfare in equilibrium. We also showed that altruism and morality induce different behaviors and outcomes in simple games. With these observations as a back-drop, we turned to the above-mentioned two phenomena.
The first phenomenon is that it may be more difficult to sustain long-run cooperation in infinitely repeated interactions between altruists and moralists than between egoists. More specifically, we showed this for infinitely repeated prisoners’ dilemmas and infinitely repteated sharing games, in both cases focussing on repeated-games strategies based on the threat of perpetual play of the stage-game Nash equilibrium. While altruists and moralists are less tempted to deviate from cooperation and less prone to punish each other—an altruist internalizes the pain inflicted upon the opponent and a moralist internalizes what would happen if both were to deviate simultaneously—the stage-game Nash equilibrium between altruists and between moralists results in higher material payoffs than between self-interested players. This renders the punishment following a deviation less painful, both for the deviator and for the punisher. In the stage-games considered here, the latter effect is always strong enough to outweigh the former, so that both altruism and morality
worsen the prospects for long-run social efficiency. More extensive analyses are called for in order to investigate whether this result obtains for other stage-games and punishment strategies (see, e.g., Mailath and Samuelson, 2006, [
53]).
The second phenomenon is that morality, but not altruism, can eliminate socially inefficient equilibria in coordination games. More precisely, while Homo moralis preferences have the potential to eliminate socially inefficient equilibria, neither self-interest nor altruism can. The reason is that while a Homo moralis is partly driven by the “right thing” to do (in terms of the material payoffs if others were to follow his behavior), a self-interested or altruistic individual is solely driven by what others actually do, and hence has no incentive to unilaterally deviate from an inefficient equilibrium. We also showed that when coordination games are played in heterogeneous populations, individuals with a high degree of morality, even if acting myopically, may initiate population cascades away from inefficient equilibria towards a more efficient social “norm”. In such cascades, the most morally motivated take the lead and are followed by less morally motivated individuals and may finally be followed even by purely self-interested individuals (when sufficiently many others have switched).
Advances in behavioral economics provide economists with richer and more realistic views of human motivation. Sound policy recommendations need to be based on such more realistic views. Otherwise, the recommendations are bound to fail, and may even be counter-productive. Our results show how altruism and morality may affect behavior and welfare in a few, but arguably canonical, strategic interactions. Clearly, much more theoretical and empirical work is needed for a fuller understanding to be reached, and we hope that this paper can serve as an inspiration.