1. Foreword
The physics of strongly-correlated electron systems is characterized by a complex phenomenology that includes multiple competing phases, divergent responses, and anomalous metallic states [
1]. In these materials the interplay between correlated electrons and phonons further enhances the complexity both in terms of the appearance of new phases and of amplification of materials responses. Mixed-stack charge-transfer (ms-CT) crystals offer an interesting opportunity to study strongly correlated electrons coupled to molecular vibrations and lattice modes. In these crystals, planar
π-conjugated molecules with strong electron donor (D) and acceptor (A) character alternatively form face-to-face stacks. Electrons are delocalized along the stack, leading to fractional charge: ... D
+ρA
−ρD
+ρA
−ρD
+ρA
−ρ ... The most impressive demonstration of strong correlations in these systems is offered by the so-called neutral-ionic phase transition (NIT) [
2], a transition from a valence insulator (
) to a Mott insulator (
), that can be induced by temperature [
3], pressure [
4], or even light [
5,
6,
7,
8,
9]. Both continuous and discontinuous NITs are known, and a precise control of chemical pressure drives the transition to very low temperatures, in the regime of quantum phase transitions [
10,
11,
12].
NIT is always accompanied by lattice dimerization [
2], eventually leading to ferroelectric behavior [
13]. Large dielectric anomalies at NIT are due to the electronic charge fluxes induced by the dimerization mode [
14,
15]. Other evidence of the intimate entanglement of correlated electrons and phonons is found in several anomalies in infrared (IR) and Raman (R) spectra [
2], and in an intense diffuse X-ray scattering signal [
16].
Competing electronic ground states on a deformable lattice can result in the simultaneous stability of different phases. Multistability is a rare phenomenon in molecular materials that requires the precise balance between strong and competing interactions [
17,
18]. Multistability in the close proximity of the discontinuous pressure-induced NIT of TTF-CA has been experimentally observed [
19] and extensively discussed in Ref. [
20]. Light absorption in multistable systems can populate metastable states, that may be hidden to conventional investigation tools [
21], in the so-called photoinduced NIT (PINIT) [
5,
6,
7,
8,
9]. The possibility to switch a neutral crystal into an ionic ferroelectric metastable state by light absorption is intriguing both from a fundamental perspective and in view of innovative applications.
Ground state properties, including not just charge distribution and lattice structure [
20,
22], but also other specific and experimentally accessible quantities, like vibrational spectra [
23], diffuse X-ray scattering data [
16], the dielectric anomaly [
14,
15], have been satisfactorily described in recent years based on a modified Hubbard model accounting for the inequivalence of lattice sites, and introducing the coupling to a molecular vibration, modulating on-site energies, and to a lattice mode, modulating hopping integrals. The same model, extended to describe the first electronic excited state, captures the basic physics driving the early time dynamics following impulsive excitation at the PINIT [
24].
This feature article has several objectives. One is to collect NIT results from papers over many years, and to present in a single, coherent picture our best current modeling of ms-CT stacks. We hope that this article will be a useful entry to newcomers to the field. The NIT literature is covered in depth in the companion articles of this issue. Specifically, the contribution from Masino et al. [
25] discusses the vibrational spectroscopy and experimental characterization of NIT in ms-CT crystals. There is considerable interest nowadays in strongly correlated electronic systems, in low-dimensional systems, in frustrated interactions and quantum phases, in nonlinear responses and in electron-vibration coupling. The physics of NIT systems such as ms-CT crystals overlaps these topics and illustrates them.
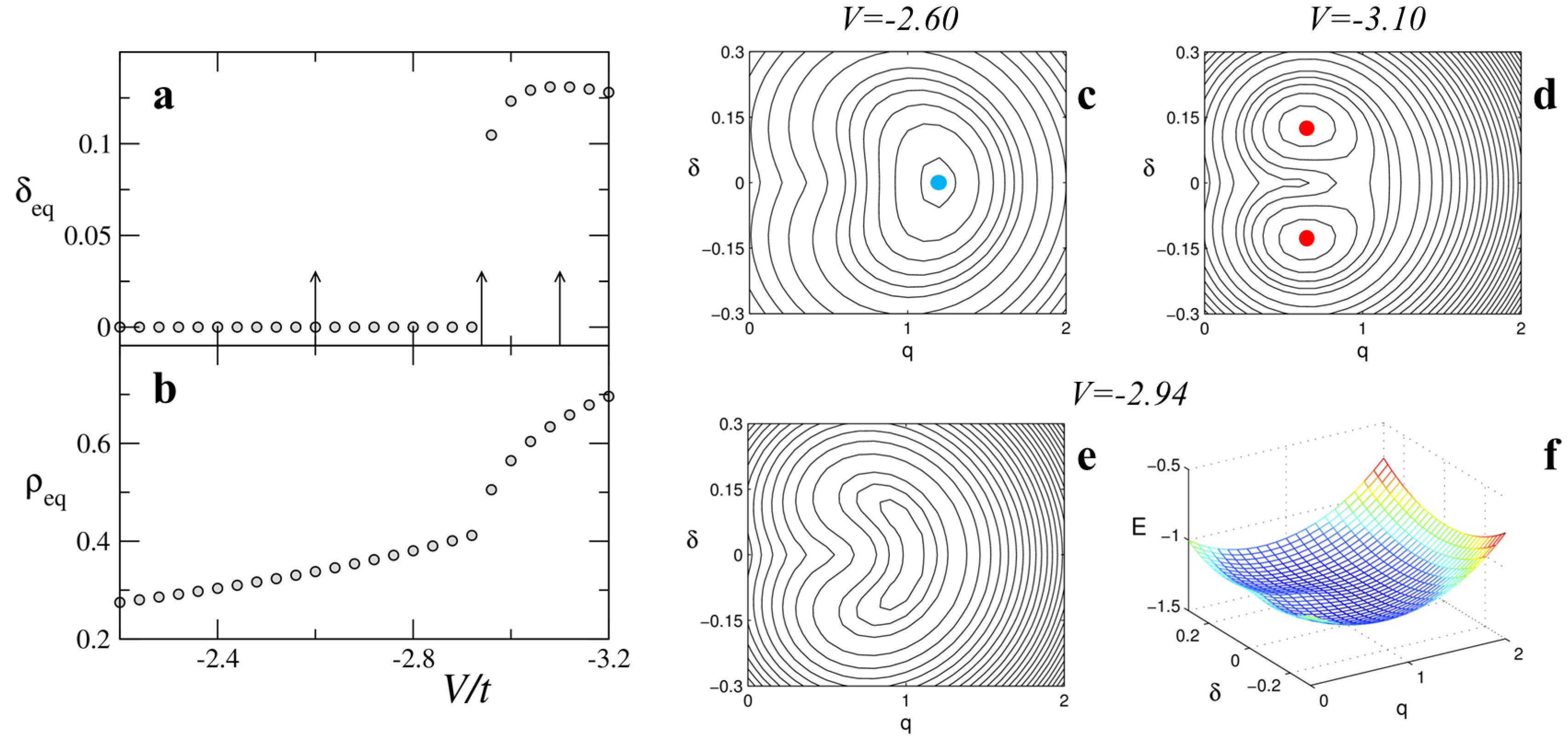
4. Vibrational Spectra at the Continuous NIT of DMTTF-CA
Correlated and mobile electrons in soft lattices manifest in large anharmonicity and electronic charge flows driven by vibrational motion in ms-CT crystals undergoing NIT. It is, therefore, not surprising that the interpretation of vibrational spectra is rather complex but also that it offers detailed information about the entanglement of electronic and vibrational degrees of freedom. The theoretical modeling of vibrational spectra can follow different approaches. In the most common harmonic approximation, vibrational spectra are calculated from the electronic properties at the PES equilibrium positions. The harmonic frequency is indeed related to the PES curvature, while IR and Raman intensities are proportional to the square of the first derivatives with respect to relevant coordinates of the polarization and polarizability, respectively. While results based on the harmonic approximation provided key insight on the vibrational properties at NIT (e.g., the softening of the Peierls mode and its huge IR intensity [
14,
15]), the strongly anharmonic PESs in
Figure 5 and
Figure 6 suggest relaxing the harmonic approximation. In the following, we will rely on a time-correlation function (TCF) approach that makes use of the anharmonic PESs, the explicit dependence of
and
on vibrational coordinates (see
Figure 3 and
Figure 4), and finite temperature [
23].
To this aim, we exploit the fluctuation-dissipation theorem of linear response theory to express optical spectra in terms of the Fourier transform of relevant time-correlation functions (TCFs). For IR absorption spectroscopy the imaginary (dissipative) part of the dielectric constant of the material is obtained from the Fourier transform of the TCF of the dielectric polarization
[
65]:
where ℏ is the reduced Planck constant,
is the Boltzmann constant,
is the vacuum permittivity,
V is the volume. Similarly, the TCF of the polarizability
is related to the intensity of the non-resonant Raman scattering [
65]:
While Equations (
13) and (
14) are exact, resulting from a quantum mechanical treatment of the interaction between light and matter in the weak coupling regime, approximations are introduced in the calculation of TCFs. We adopt a semiclassical approach to TCFs, with the vibrational motion governed by classical equations of motion in the quantum mechanical potential obtained from the model Hamiltonian. The two effective vibrational coordinates
q and
, defined in
Section 2.4 and
Section 2.5, are considered and polarization and polarizability are evaluated along many classical trajectories to compute the respective correlation functions [
23]. Since our electronic model is strictly 1D, the components of the electronic polarization and polarizability that are probed correspond to those along the stack axis
(see
Section 2.6). Equation (
13) therefore targets the IR absorption for incident light polarized along
, while Raman spectra calculated via Equation (
14) correspond to those with both incident and scattered light along the same direction. Raman spectra in the molecular vibrations region are usually taken with incident and scattered light polarized perpendicular to the stack axis, probing instead the molecular polarizability. To simulate these spectra we approximate the molecular polarizability by a linear expansion on
q.
We explicitly focus on the vibrational spectra across the continuous NIT of DMTTF-CA. To allow for a direct comparison with experimental spectra, the unperturbed harmonic frequencies of the Peierls and molecular modes are set to
and
, respectively, with coupling constants
and
. The small value of
is due to the fact here we focus on a specific mode, namely the one responsible for the band observed at about 1450
in the room temperature Raman spectra of DMTTF-CA [
66]. The contribution from other modes to the charge instability can be accounted for by increasing the strength of electrostatic interactions. The continuous NIT of DMTTF-CA is induced by increasing the electrostatic interaction
V according to an empirical
relationship derived by reproducing the evolution of vibrational spectra in the molecular vibrations region (see inset of
Figure 7 and discussion below). Other details of the calculation can be found in the original paper [
23].
Figure 7 shows the calculated IR (polarized parallel to the stack axis) and Raman (perpendicular polarization) spectra in the spectral region of molecular vibrations. The Raman spectra (black lines) are characterized by the softening of approximately 100 cm
−1 of the totally symmetric molecular vibration band upon approaching NIT at
K. In the N phase (see
,
K), the IR spectra (red lines) are characterized by the presence of the combination bands
. Combination bands of appreciable intensity naturally result from the strong anharmonicity of the PES, which in turn arises from the coupling between vibrations and delocalized electron (see
Section 3). Upon approaching the transition (see
,
K) combination bands broaden and, because of the softening of the Peierls mode, their spacing from the central Raman band at
cm
−1 is reduced. We observe that the hot band (
) is generally broader and more intense than the cold band (
). For
the PES is locally flat, and while the harmonic frequency of the Peierls mode vanishes, our finite temperature simulation (
K) yields
cm
−1, measured as half the difference of the position of the two bands. The PESs for
present the double minima characteristic of dimerized system, causing the progressive disappearance of the side bands and the observation of the intramolecular mode at
cm
−1 in both IR and Raman spectra. For instance, for
and
K the IR spectrum shows the coexistence of the peak of the molecular mode, signaling stack dimerization, with combination bands, that are instead characteristic of regular stacks. This results from our ensemble average of classical dynamics that includes both trajectories crossing the barrier separating the two minima at finite
δ and trajectories that are instead trapped in one of the two potential wells.
The comparison of calculations in
Figure 7 with experimental spectra of DMTTF-CA [
23,
66] in the region of molecular vibrations is very good. While this result holds for any reasonable parameterization of a continuous NIT, a truly quantitative agreement on the softening of the Raman active molecular vibration as well as the evolution of the related IR combination bands upon approaching NIT is obtained by fine tuning the
V as shown in the inset of
Figure 7). In effect,
is optimized for Raman and IR spectra at temperature
T.
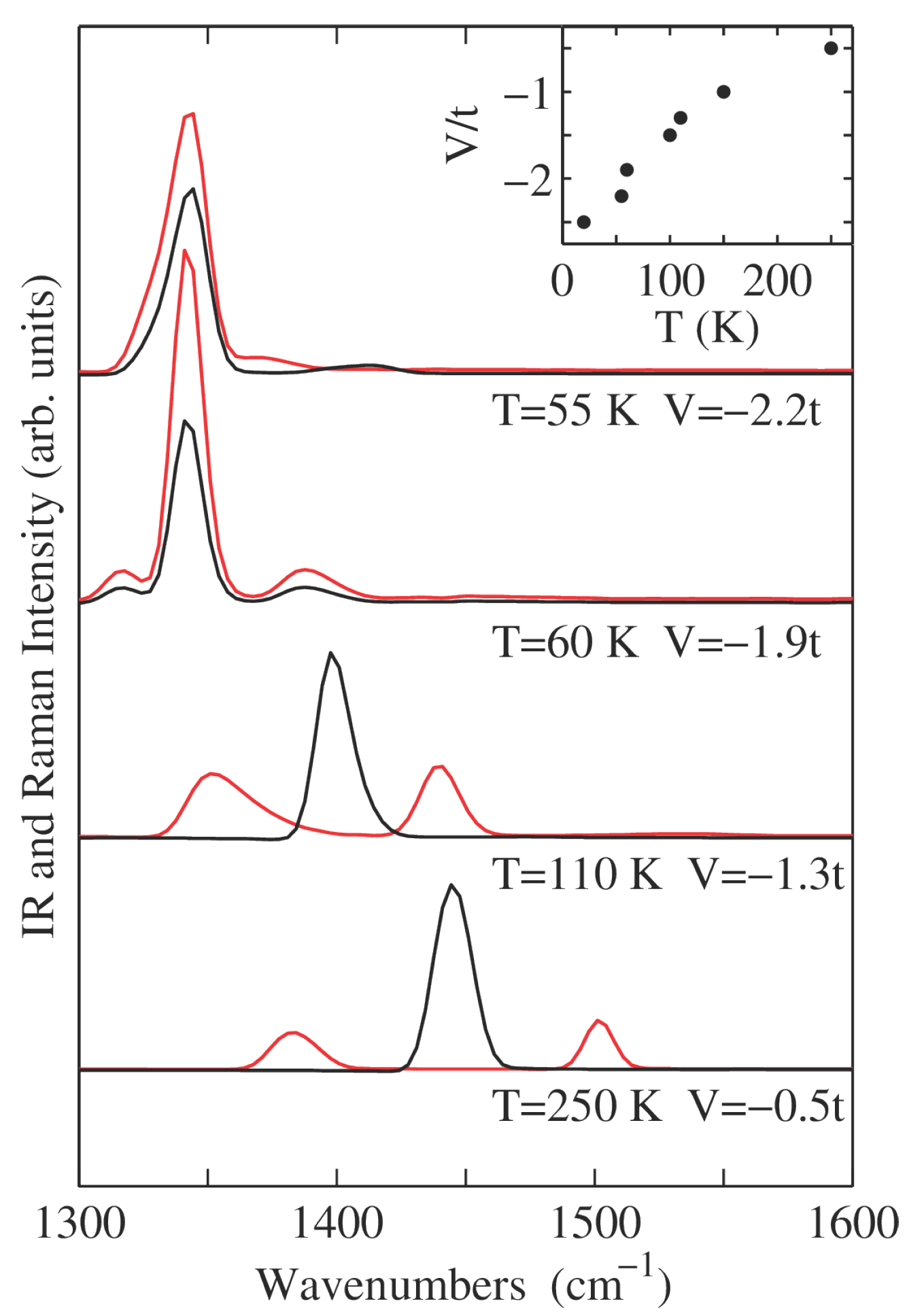
We now turn our attention to the region of lattice phonons. Panel a of
Figure 8 shows the IR spectra, largely dominated by the absorption band of the Peierls mode. The Peierls mode softens upon approaching NIT from about 60 cm
−1 (
,
K) to 40 cm
−1 (
,
K). This softening is consistent with the half difference between combination bands in
Figure 7. The intensity of the Peierls mode grows upon approaching NIT as can be better appreciated by the integrated intensity in the 0–100 cm
−1 interval shown in
Figure 8b. The spectral weight grows by approximately a factor 4 upon approaching the transition at
K (dashed line) and decreases in the I phase.
These results were recently experimentally confirmed for TTF-CA [
67]. Although the model is optimized to describe the continuous transition of DMTTF-CA, it is interesting to note that the relative increase of the intensity of the Peierls mode is consistent with the measurements on TTF-CA, where the 0–100 cm
−1 spectral weight grows from 600 ω
−1cm
−2 at 300 K to 2000 ω
−1cm
−2 at the transition temperature of 81 K (approximate values, from Figure 7 of Ref. [
67]).
The growing intensity of the Peierls mode at NIT can be understood from a joint inspection the PES and of the
surface (i.e., the dependence of
on the vibrational coordinates
q and
δ) and their evolution as a function of
V. In fact, while the PES governs the classical dynamics of the systems, the IR absorption intensity depends on the amplitude of fluctuations of the
correlation function, according to Equation (
13). Panel c of
Figure 8 superimposes the
surface (color map) and the PES (isolines) for a N system (
). We notice that the
surface closely resembles
in
Figure 3a, as expected considering that
q enters Hamiltonian (
10) as an additive term to Γ. Since DMTTF-CA does not undergo a true NIT (
ρ is always smaller than 0.5 [
66]) it is equivalent to consider
or
(see
Section 2.6)). For this system with a largely N ground state, the single minimum of the PES (cross) lies in the region where the
surface is smooth. In this case thermal vibrational motion cannot induce large
fluctuations and the IR intensity remains modest. As the system approaches NIT, the PES minimum shifts towards the region of large
variations along
δ, and thermal lattice fluctuations induce larger and larger electronic charge flows along the stack that maximize at the dimerization transition. Large IR intensities still persist in a dimerized system such as that in
Figure 8d (
). In this case the PES presents two shallow minima separated by a small energy barrier that can be overcome at
K, causing large
variations. Further decrease of
V and/or
T traps the system in one of the two minima, suppressing the IR intensity. The anharmonic simulation provided here confirms the results of the harmonic calculation [
14,
15]. Indeed the harmonic approximation catches the main physics of the phenomenon, simply relating the IR intensity to the squared
δ derivative of the polarization at equilibrium
.
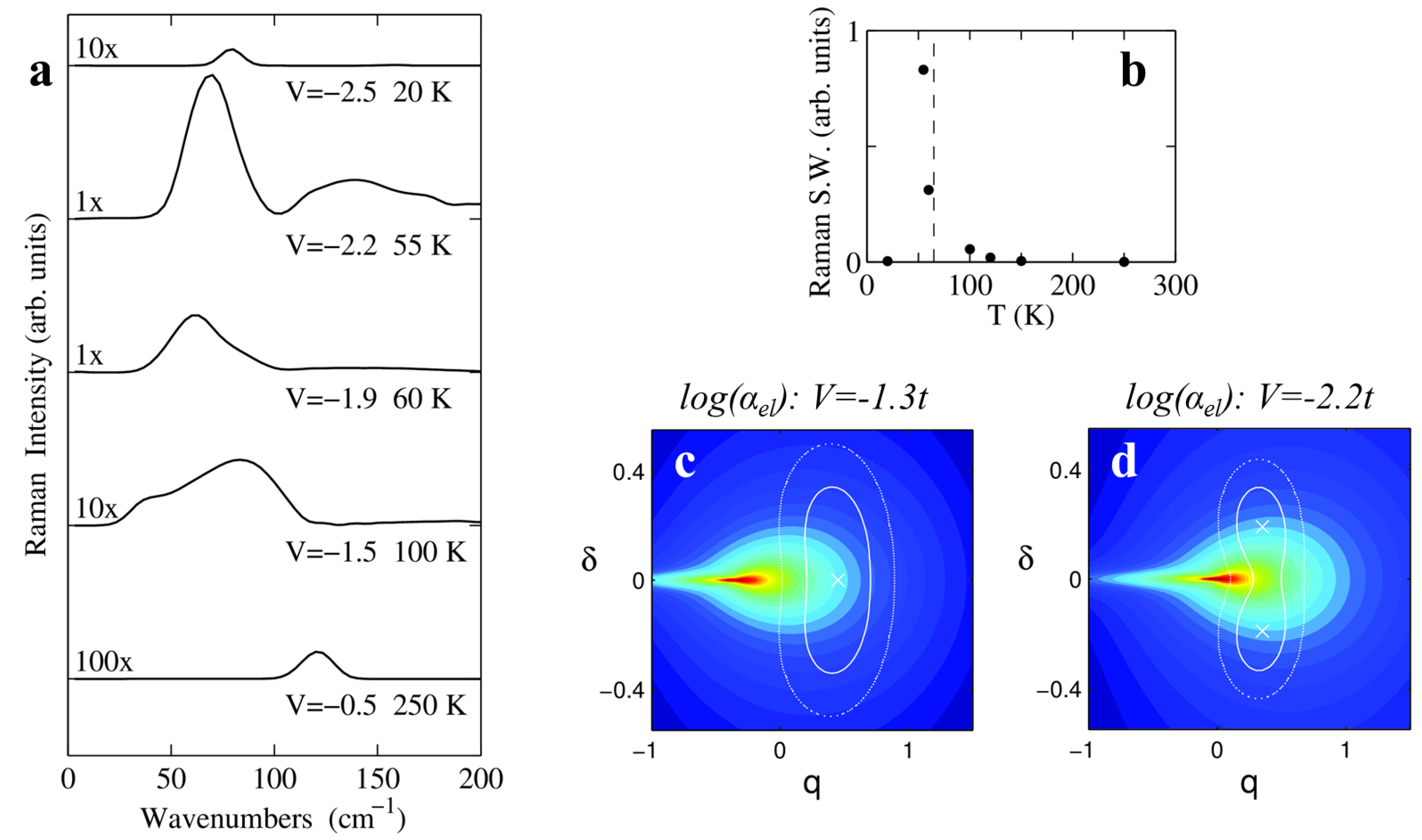
IR spectra in the lattice phonon region can be understood to a first approximation, in the harmonic limit. However, in the same spectral region Raman spectra are largely dominated by anharmonicity effects. Panel a in
Figure 9 shows Raman spectra calculated for light polarized along the stack axis, hence probing the polarizability due to delocalized electrons. In the high-
T N phase, the Peierls mode is silent in Raman spectra by symmetry, hence in the harmonic approximation no signal is expected in the region of lattice phonons. At
K (
, black line) the spectrum is characterized by the presence of a single band around 120
. The comparison with IR spectra in the region of lattice phonons (see
Figure 8a) and of molecular vibrations (see
Figure 7) allows identifying the Raman band as the overtone of the Peierls mode
. The overtone band is symmetry-allowed in the regular stack and its presence is a manifestation of the PES anharmonicity. This band softens upon approaching NIT and acquires an asymmetric shape that can be also ascribed to the anharmonicity of the potential. Most importantly, the intensity of the Raman peak greatly increases approaching the transition and maximizes at
K (blue line), where the appearance of the higher overtone
is predicted by the calculations. As can be seen by the integrated intensity plot in
Figure 9b, the maximum Raman signal occurs just below
K. In the dimerized phase at
K, the Peierls mode is directly observable both in Raman and IR (not shown) spectra at
cm
−1 [
23].
These theoretical results are confirmed by the experimental observation of a broad and intense Raman signal appearing below 100 cm
−1 in proximity of the
T-induced transition of DMTTF-CA [
23] and of the similar compound DMTTF-QBr
2Cl
2 [
68]. More interestingly, simulations provide a key to understand the anomalous Raman signal that is generated by
vibrations and electronic polarization at finite dimerization (see
Figure 4).
Figure 9c,d show the
surface (log-scale color map) with PES isolines superimposed. As the system evolves from a N regular phase (
Figure 9c,
) towards the transition, the PES minimum approaches the singularity of
and the system dynamics explores more and more regions that greatly contribute to the correlation function in Equation (
14). In the just-dimerized phase at
(
Figure 9d), the PES minima are located just across the singularity that is however accessible by thermal fluctuations at
K, conferring huge Raman signal to the overtones of the Peierls mode.
More generally, this careful theoretical analysis sheds light on the entanglement of charge and vibrational degrees of freedom that confers a strongly anharmonic character to systems close to the NIT. The effect is twofold: on one hand there is the so-called
mechanical anharmonicity, i.e., the PES dependence on vibrational coordinate largely deviates from quadratic behavior, leading to the appearence of combinations and overtone bands in vibrational spectra. On the other hand, the dependence of the electronic polarization and polarizability is strikingly different from lowest-order approximations. This
electrical anharmonicity is responsible for the large intensity of anharmonic features that are prominent in the vibrational spectra of ms-CT crystals [
23,
66,
69]. Finally, the observation of an anomalous Raman scattering in the lattice phonon region at NIT [
23] provided an indirect experimental evidence for the divergent electronic polarizability of the regular lattice.
5. Multistability and Photoinduced NIT
Multistability is the characteristic feature of discontinuous phase transitions, opening the way to metastable states, coexisting phases and photoinduced phase transitions. The energy of metastable domains depends on the domain length and on the boundaries, as discussed in [
20]. The
T-induced NIT of TTF-CA occurs at too low temperature to allow for the population of metastable domains, but the pressure-induced NIT at room temperature shows a sizable population of metastable domains, leading to coexisting N and I features in vibrational spectra as shown in Figure 20 of Masino et al. [
25]. While the thermal population of metastable domains is an interesting feature, the possibility to populate metastable states via photoexcitation in the so-called photoinduced NIT is even more interesting.
Light induced transitions have been observed in TTF-CA crystals at temperature close to the discontinuous NIT. Starting from the I phase a TTF-CA crystal is driven by light absorption to a metastable state similar to the N high-temperature phase [
5,
6]; and vice versa for a N crystal to a I-like state [
8]. Due to the long lifetime of metastable states, usually in the range of nanoseconds, this process is referred to as a photoinduced NIT (PINIT). PINIT has been demonstrated in TTF-CA through spectroscopic measurements (time resolved pump-probe experiments) [
5,
6,
8] . Moreover, in time resolved X-ray experiments it was possible to observe the PINIT through the evolution of specific Bragg reflections after photo excitation [
9], confirming the bulk nature of the observed phenomenon.
Theoretical modeling of PINIT is fairly recent and requires the addition of a pump pulse to systems of correlated electrons coupled to soft lattice and molecules. The Peierls-Holstein-Hubbard model for photoinduced transitions reviewed by Yonemitsu [
70,
71] is broadly similar to the full Hamiltonian in Equation (
10) with linear coupling to harmonic molecular and lattice modes. The model is applied to TTF-CA as well as to charge ordering transitions and Mott insulator to metal transitions in BEDT-TTF
2 salts that correspond to 3/4 filled 2D Hubbard models of D = TTF. Yonemitsu keeps the full Hubbard basis, explicitly treats the pump pulse of finite duration using the vector potential, and finds the time evolution of lattice and molecular vibrations in finite systems during and following an excitation pulse. We start instead with an impulsive, delta-function pulse at
and follow the time evolution of the system on anharmonic PES derived from other TTF-CA spectra. Accordingly, we explicitly and quite naturally address phenomena that results from the large anharmonicity of PES close to NIT and specifically the large coupling between the dimerization and the molecular-vibration motions, as discussed below.
In spectroscopic pump-probe experiments the crystal reflectivity in the visible region is measured after photoexcitation, to give information on the molecular properties [
6,
8]. This experiment will be discussed in the following. A threshold effect on the incident light intensity was observed for the PINIT along with a large non-linearity. Through a single photon absorption, multiple ionized DA pairs are created; the reported numbers vary from ten [
72] to a few hundred [
6] pairs. This behavior is very atypical, since, according to the standard exciton theory, transitions involving CT between more then one DA pair would be forbidden [
73,
74,
75].
PINIT in TTF-CA occurs in two steps. In the first few picoseconds (ps) after photoexcitation the CT mechanism is triggered and the first ionized chains are created; then from ∼10 ps to the first nanosecond (ns) the ionized chains reorganize and long-range ferroelectric order is created. This comparatively slow dynamics can be conveniently followed by time-resolved X-rays experiments [
9]. Optical pump-probe experiments, instead, offer a very detailed description of the early time dynamics of the system (0–10 ps) that we aim at modelling.
In particular we address very interesting experiments by Okamoto et al. [
72,
76], where the variation of reflectivity (
) of TTF-CA is measured in the visible region following an ultrafast (15 fs) laser pump pulse. The data were collected at different temperatures, different excitation photon density and at different probe wavelength. The pump beam is polarized parallel to the stacking axis
of TTF-CA with an energy interval of
eV that matches the broad CT band seen in the polarized absorption spectra of TTF-CA. The probe beam is polarized perpendicularly to
with an energy of 2.2 eV in the region of localized electronic excitations that are sensitive to the ionicity of the crystal.
spectra collected at different time delays between the pump and the probe are compared with the difference between spectra collected at 4 K (I phase) and at 90 K (N phase): the strong similarity between the shape of the pump-probe and the steady state spectra suggests that an I-like state is generated by the pump signal. Accordingly, the
variations were interpreted [
72,
76] as ionicity variations.
Since the pump photon irradiation density per DA pair was measured during the experiment, Okamoto et al. [
72,
76] estimated the number of ionized pairs created by a single photon absorption as
from the
jump at
. A detailed analysis of the temporal evolution of
shows an oscillatory component with frequencies related to molecular or lattice vibrations. In particular the
component was interpreted as related to the Peierls dimerization mode. Additionally, a wavelet analysis was performed on the oscillating signal to study the temporal evolution of the frequency components: some of them showed a significant shift in time. For example, the ∼957 cm
− component, which was assigned to an e-mv coupled vibration of CA (
), oscillates in time at almost the same frequency as the Peierls mode. We will demonstrate that this interesting result is again a consequence of the strong anharmonicity of PES close to the phase transition.
To model PINIT we need not only the ground state PES (G-PES) that has been used to discuss vibrational spectra, but the excited state PES (E-PES) as well. We report results obtained for standard TTF-CA model parameters, as discussed in
Section 3.1, but relax the mean field approximation, and explicitly account for nearest neighbor interactions.
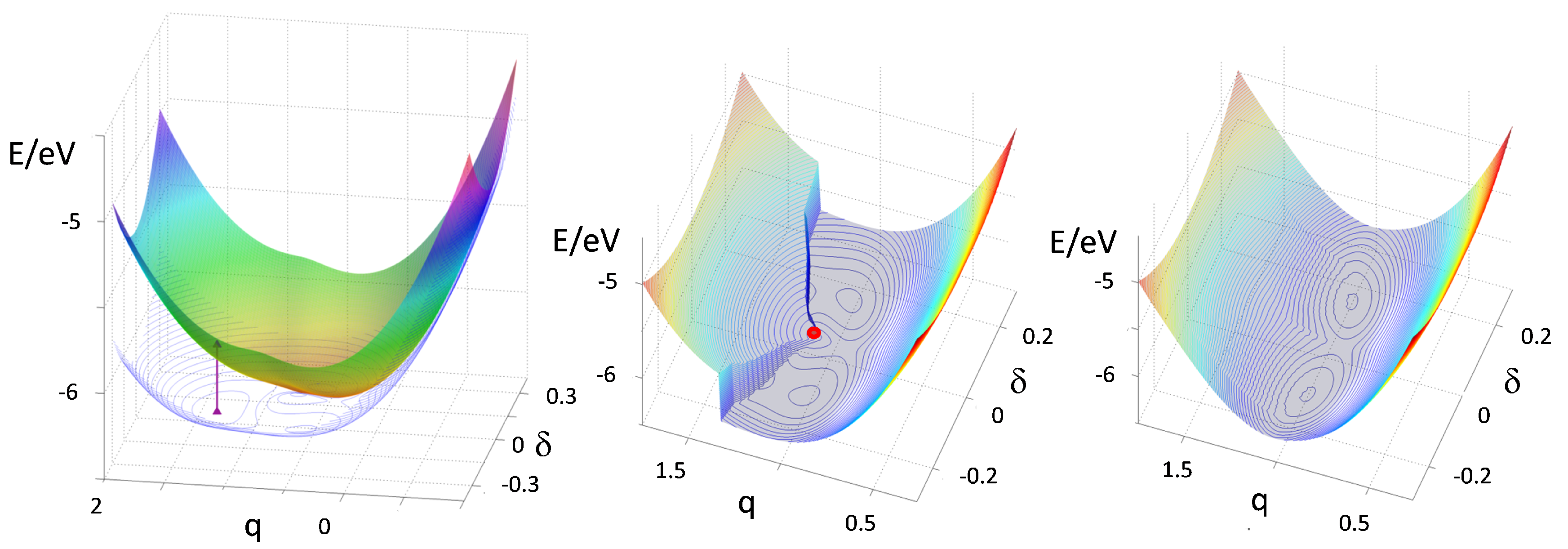
Figure 10, left panel, shows the adiabatic G-PES and E-PES calculated for
. The G-PES shows a stable neutral regular phase and two metastable dimerized minima at
. The two surfaces touch at a conical intersection, the red dot in the middle panel, that corresponds to the critical point
of the MHM discussed in
Section 2. The vertical arrow in the left panel marks the strong, optically allowed absorption polarized along the stack that initiates PINIT by generating a lattice-unrelaxed exciton of multielectron transfer character.
After a fs pump pulse, the photoexcited system evolves on the E-PES. The conical intersection makes it possible to tunnel towards one of the metastable minima. To model this complex dynamics we take advantage of the nature of the G-PES close to a discontinuous phase transition, where multistability indicates nearby surfaces. More specifically, the diabatic PES relevant to the neutral regular state and to the ionic dimerized state cross and generate the G-PES and E-PES when they are adiabatically mixed. Therefore, starting from the adiabatic PES for the ground and first excited state in
Figure 10 we construct the diabatic PES relevant to the ionic dimerized (metastable) state, as shown in
Figure 10, middle and left panels. This PES practically coincides with the E-PES in the region of the vertical excitation and with the G-PES in the dimerized metastable region. The middle panel shows the PES with minimum gap between E-PES and G-PES. The right panel is the diabatic PES obtained by smoothing out the gap. While the smoothing procedure is somewhat arbitrary, we emphasize that the dynamics is marginally affected by the details of the smoothing. In fact this critical region is only crossed once at the beginning of the photoexcited dynamics.
A detailed analysis of the early-time dynamics of the photoexcited system is reported in Ref. [
24]. Here in
Figure 11 we show the trajectory of the system after instantaneous excitation and the Fourier transforms of the
and
signals that show oscillating components at
55 and 945 cm
−1, respectively. The wavelet analysis of the same signal, shown as a color map on panel b in
Figure 11, clearly shows that the molecular vibration oscillates at a frequency that is not constant in time, but that in turn oscillates about a mean values (∼945 cm
−1) at a frequency that corresponds to that of the dimerization mode (∼55 cm
−1). In the equilibrium state, before photoexcitation, the system is in a neutral regular state. After vertical photoexcitation
q is wildly out of equilibrium and a very fast initial dynamics brings it towards the equilibrium position relevant to the photoexcited ionic states. This fast initial dynamics accounts for the observed initial rise of the reflectance variation. After the initial increase,
oscillates about the new equilibrium position with an amplitude that progressively decreases due to friction. Indeed, due to anharmonicity, the motion along the two coordinates is mixed and while
δ oscillates, different regions of the PES are explored, characterized by a different curvature along the
q coordinate, then explaining the modulation of the observed frequency for the
q mode by the
δ frequency, as shown in the inset of
Figure 11c, and in line with experimental observation.
Figure 11d shows the temporal evolution of the system ionicity, that closely resembles
. The variation of ionicity of the system is proportional to the number of D
+A
− pairs created upon photoexcitation, as shown on the right axis of
Figure 11d. Results in the figure tell us that upon vertical excitation (the dot located at
) almost 1.5 electrons are transferred from D to A sites, a result that calls for sizable correlation of the motion along the chain. However, ultrafast lattice relaxation, and more specifically the relaxation along the
q coordinate, further increases the number of transferred electrons, that oscillates with
q around an average value of about 4. This intriguing result is in line with the experimental observation that photoexcitation generates a domain (D
+A
−)
n with
within 20 fs.
Vertical excitation at 260 K, far from NIT for TTF-CA parameters, also generates ionic domains [
76]. In the simplest approximation, coherent oscillations of coupled molecular vibrations are again modeled by
q, but there are no
δ-oscillations since
δ = 0 is the minimum on both surfaces. Now the thermal population of the Peierls mode with
50 cm
−1 must be taken into account. We do so along the same lines discussed in the previous Section and in Ref. [
23]. We choose a symmetric
δ-distribution in
, the G-PES, follow the coherent dynamics after a vertical excitation, and weight the results of many runs by a Boltzmann factor in
. Coherent
δ-oscillations are generated with greatly reduced amplitude, as found experimentally [
76]. The most interesting feature is the doubled frequency
100 cm
−1 in the Fourier transform of
ρ that corresponds to
Figure 11e at 90 K. The frequency of the oscillations around
is doubled since
ρ is symmetric on
δ. For completeness, we note that the 90 K results near the NIT in
Figure 11 hardly change upon accounting for thermal population of the PES along
δ.
6. First Principles Model Parameters
The MHM provides a robust framework to understand the valence and structural instabilities in ms-CT crystals. Input parameters are required for MHM, as is typical in a semiempirical model. Parameters have traditionally been obtained and progressively refined for prototypical systems such as TTF-CA or DMTTF-CA on the basis of optical, vibrational and other experimental data. In this section we cover a recent alternative approach that instead relies on DFT electronic structure calculations [
61,
77]. This has the advantage that the crystal structure is the only experimental input needed, possibly at different temperature or pressure.
The most refined model for ms-CT crystals accounts for several interactions and hence several parameters enter
, Equation (
10). The parameter set includes those describing the electronic structure (
t,
z), the coupling to molecular and lattice vibrations (
and
), as well as intermolecular electrostatic interactions (
V,
or the derived
). Reliable estimates of these quantities can be obtained from atomistic calculations, with the notable exception of
.
As discussed in
Section 2, the MHM can be considered a 1D extension of the Mulliken dimer model, whose mean-field electronic properties are fully determined by
t and
. To fix these model parameters, we extract DA dimers from the experimental crystal structure of specific ms-CT crystals and run DFT calculations to map relevant states into the Mulliken two-state model. The mapping proceeds through the identification of two properties of choice that can be accessed by both approaches. In our case, we opt for quantities obtained from ground-state calculations in the singlet and in the triplet subspace, namely the ionicity
and the singlet-triplet gap
, leading to the following closed expressions:
The choice of ground-state properties is considered to be safer with respect to excited state calculations, which are known to be troublesome in CT systems within the framework of time-dependent DFT. Range-separated hybrid functionals, such as CAM-B3LYP or
ωB97XD provide reliable estimates for the sought quantities, in line with earlier empirical estimates [
61,
77]. The favorable comparison with experimental data for the ionicity
ρ in the crystal validates this choice
a posteriori.
In the adiabatic approximations underlying Hamiltonian (
10), the strength of the coupling to effective vibrational modes is measured by the relaxation energies
and
.
is defined as the energy gained upon intramolecular structural relaxation associated with the electron transfer from D to A and includes the contribution from several vibrational modes of the molecule, yet
q in Equation (
10) is an effective coordinate that accounts for their combined effect. It is, therefore, preferable to compute intramolecular reorganization through DFT calculations performed at the geometries optimized for isolated neutral and charged molecules as
, where
(
) is the hole (electron) relaxation energies for the D (A) defined in standard electron transfer theories.
On the other hand, a first principles estimate of
is computationally challenging as it would require the calculation of the energy for the formation of a bond-order charge density wave in the crystal (excluding dispersion and steric interactions that are modeled by an elastic term in the harmonic approximation, see Equation (
10)) along an effective dimerization coordinate that enforces rigid molecules. Given these practical difficulties, in this case a different approach with respect to that of
Section 3 has been proposed, and calculations are performed at the dimerization obtained from experimental crystal structure (
) and not at the optimal lattice geometry for a given
, or scanning the PES near equilibrium. This is straightforward in the case of regular stacks where
by definition. In dimerized systems, two independent DFT calculations are required for nonequivalent dimers in symmetry-broken stack, obtaining
.
The evaluation of long range intermolecular electrostatic interactions goes beyond the reach of first principles calculations, calling for multiscale approaches that can be parametrized
ab initio. Electrostatic models of atomistic resolution represent here an ideal compromise between accuracy and computational cost [
78]. In these approaches point atomic charges approximating the charge density of neutral or charged molecules and experimental atomic positions are employed to compute intermolecular interactions via direct electrostatic summations, possibly accounting also for the screening provided by molecular polarizabilities [
61]. Since
V is readily computed for a dimer and
for a crystal, we obtain the quantity
that enters the mean field approximation to (
10).
TTF-CA is by far the most studied ms-CT crystal and its crystal structure has been experimentally determined at temperatures ranging from 15 to 300 K, i.e., in a large interval around
K. In Ref. [
61] the parametrization described above has been performed for the different crystal structures, allowing the theoretical description of the NIT as a quantum phase transition where temperature only enters through the structural change. Apart from the dimerization occurring below
Tc, the most remarkable variation with
T of the parameters is the 45 meV increase of the Madelung energy shown in
Figure 12a. The effect of the increasing strength of electrostatic interactions on the MHM ground state energy and ionicity are shown in
Figure 12b,c, respectively. At room
T TTF-CA is largely neutral and its ground state is progressively destabilized by the increasing
due to the thermal contraction of the lattice. Upon decreasing temperature, the system enters a bistable region with coexisting N and I phases, the latter stabilized by the
increase. This bistability window is a characteristic of discontinuous transitions and relevant energies (free energies at finite
T) discriminate between the thermodynamically stable and the metastable phase (see also
Section 2.3 and
Section 3). The calculated evolution with temperature of the ionicity
, shown in
Figure 12c, favorably compares to experiment, although quantitative deviations are evident. In fact, TTF-CA turned out to be always too neutral or too ionic in the calculation, a flaw that can be attributed to the mean field treatment of electrostatics, which may suppress intermediate
states, or by finite temperature effects such as thermal population or disorder. Nevertheless, capturing the discontinuous NIT of TTF-CA in the correct temperature range and without introducing adjustable parameters is a remarkable result that validates the MHM parametrization through comparison with experiment. This result further confirms the nature of the NIT as a quantum phase transition driven by the increase of the Madelung energy with the lattice contraction.
In a more recent study [
77], some of us extended this approach to eleven ms-CT crystals, demonstrating the wide applicability of the first principles parametrization. With the only exception of just one among the 11 investigated systems, TMPD-TCNQ [
79] for which the method was inapplicable, in all other cases it has been possible to find good correlations between the experimental and the calculated ionicity
[
77]. Moreover, the different ms-CT crystals have been classified in terms of their bistable character and their propensity towards a discontinuous transition. The key parameter for the classification was identified as the ratio
(see
Section 2.3 and
Section 2.5), which returns a good correlation between parameters obtained from atomistic calculations for each system and their experimental behavior.
Theoretical calculations on specific experimental systems, explicitly accounting for the strong correlations characterizing ms-CT crystals, have been recently proven to be possible and reliable. The approach discussed here collapses the complexity of several systems into a few physically meaningful parameters, allowing to draw insightful connections between molecular chemistry, supramolecular organization in the solid state and the electronic properties of materials. All this can be then rationalized within the framework of the universal picture of NIT in ms-CT crystals provided by the MHM accounting for electron-phonon coupling.
7. Summary
The general situation discussed here with respect to modeling NIT is typical of the evolution of understanding of condensed phase systems. The initial focus on ionicity was soon expanded to the structural instability to dimerization and the -dependence of molecular vibration frequencies. Mixed stack CT crystals are a subgroup of the larger family of quasi-1D CT crystals that also include segregated stacks. The optical, magnetic, electrical, vibrational and structural properties of crystals with quasi-1D stacks have posed interesting experimental and theoretical challenges for decades. The present consensus is in terms of correlated electrons in extended Hubbard-like models, coupled to the Peierls phonon and molecular vibrations, and 2 or 3D considerations as suggested by experiment. We have not gone beyond 1D modeling of a single stack, but ferroelectricity in ms-CT crystals clearly requires that all stacks dimerize in the same sense.
The microscopic NIT model presented here is minimally required to account for the electronic properties of ms-CT stacks. The model has one lattice mode (
), one molecular mode (
q) and usually a mean field approximation for Coulomb interactions. The experimental situation is far more nuanced and complex. The IR and Raman spectra of TTF-CA or of DMTTF-CA presented in the companion work by Masino et al. [
25] require additional lattice phonons and more sophisticated vibrational analysis. Depending on one’s perspective, more quantitative treatment either underlines the approximate nature of the microscopic model or merely the need to introduce additional parameters. Although we have taken as few parameters as possible, there is a handful:
t and
, the basic parameters of the modified Hubbard model in the reduced basis,
measuring the strength of electrostatic intermolecular interactions in the ionic lattice,
V the electrostatic interaction between adjacent D
+ and A
− sites and
and
, the strength of the coupling of electrons to molecular and lattice modes, respectively. The model may be minimal but it is not simple and a consistent set of parameters is based on many experiments. While
,
V, and perhaps
are in the eV scale and can be evaluated with a reasonable accuracy, NIT inherently features competition (differences) between large energies. The state of the system depends sensitively on energies (
t,
and
) that are an order of magnitude smaller, and still quite challenging to evaluate reliably to 10% accuracy. Nevertheless, progress with parameter evaluation is an important aspect of modeling organic solids in general that makes credible small additional adjustments for comparison with experiment.
The MHM focuses on the HOMO of D and LUMO of A in extended correlated-electron stacks. The optical CT excitation around 1 eV is polarized along the stack and is the lowest electronic excitation, but not by much; excitations polarized in the molecular plane may start around 1.5 eV. Modern treatments of systems with a few D or A moieties sometimes distinguish among electronic excitations but often do not. A more general approach to the electronic structure of an extended stack and eventually to many stacks may well be possible and even required in the future.
The NIT model that we have discussed is spectroscopic in nature. The ground state energy
is a PES with a lattice and molecular coordinate, both strongly coupled to correlated electrons. The PES has a single minimum on the neutral side, two minima on the ionic side, and metastable states for very special parameter values in systems with discontinuous NIT. The PES accounts semi-quantitatively for vibrational spectra discussed in
Section 4 and by Masino et al. [
25]. The emergence of highly anharmonic surfaces from a purely harmonic lattice and molecular vibration is an interesting consequence of coupling to correlated electrons that are delocalized along the stack. As emphasized throughout, the model provides a unified treatment of continuous and discontinuous NIT with small changes of parameters. That is our principal result. We have invoked the excited-state PES to model the early dynamics of photoinduced NIT in TTF-CA, which speaks to the model’s robustness.