Dynamics of a Polymer Network Modeled by a Fractal Cactus
Abstract
:1. Introduction
2. Generalized Gaussian Structures
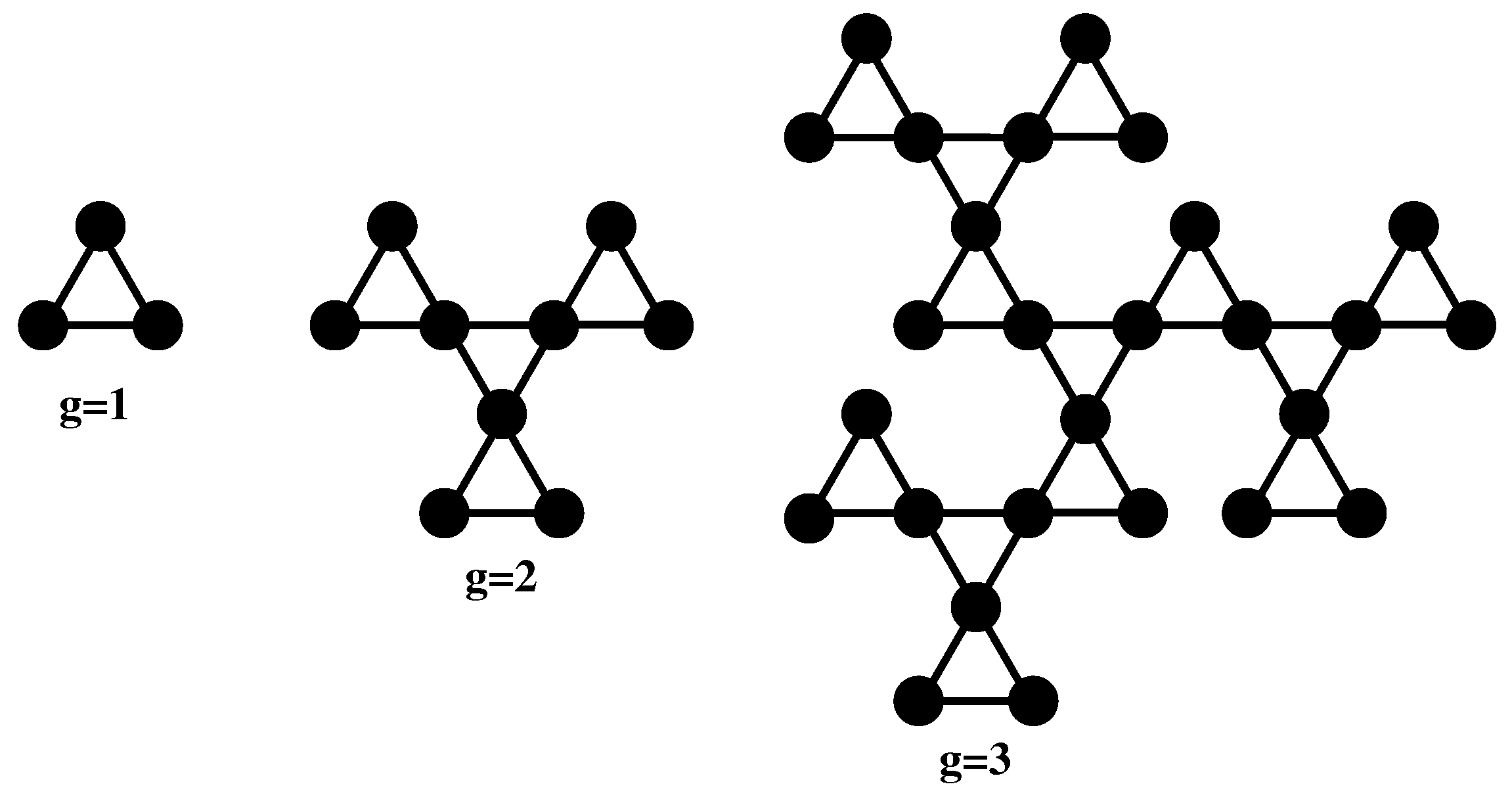
3. The Fractal Cactus Network and the Eigenvalue Spectrum
4. Relaxation Patterns
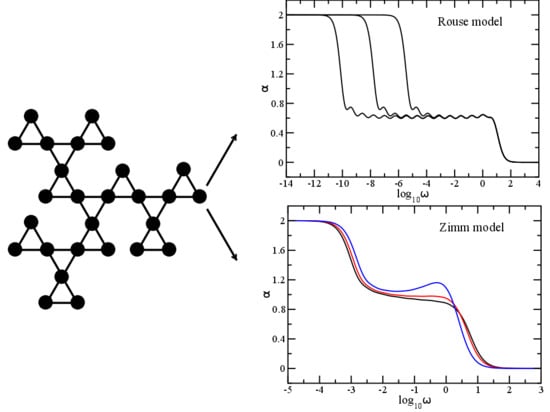
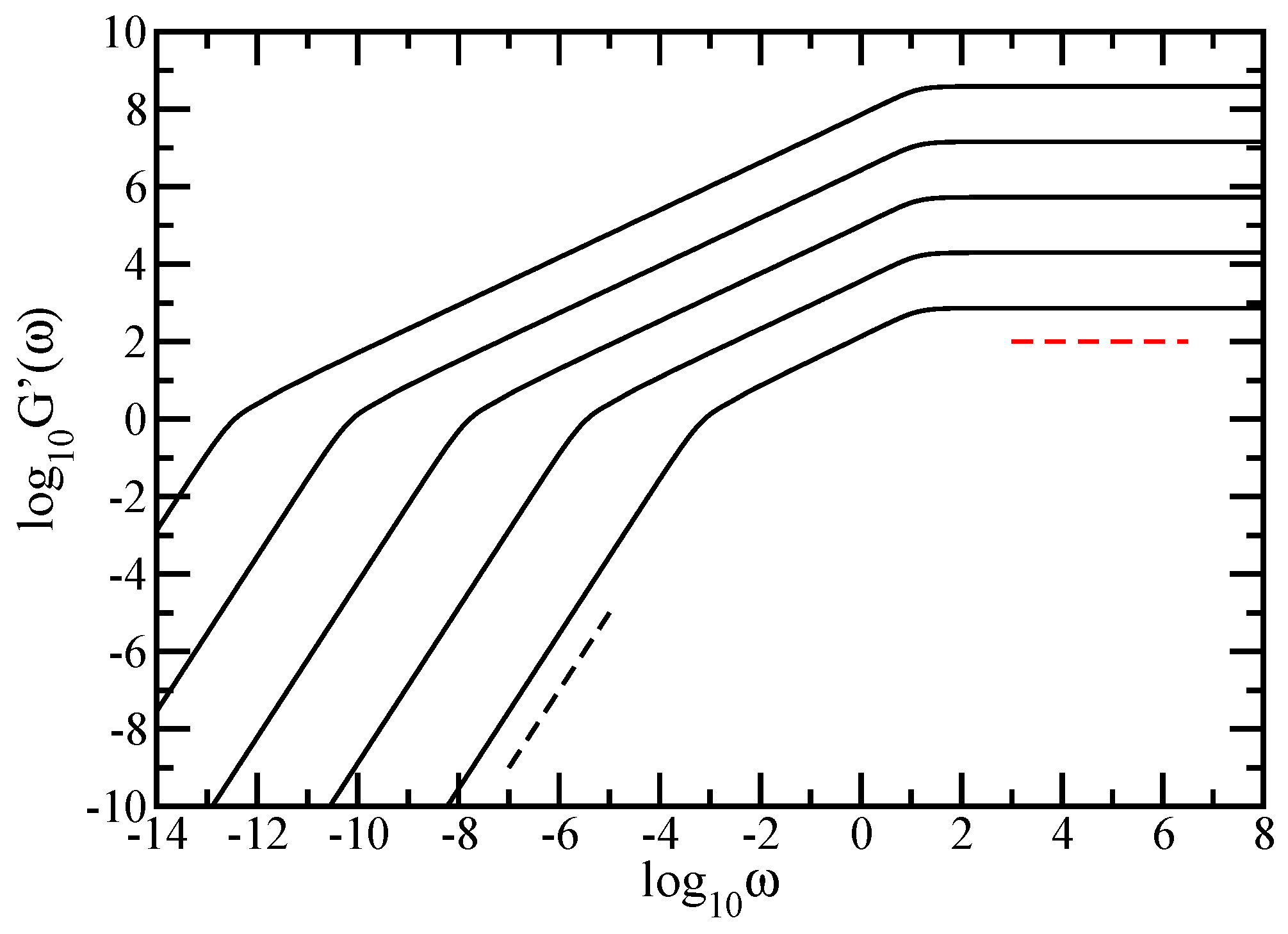
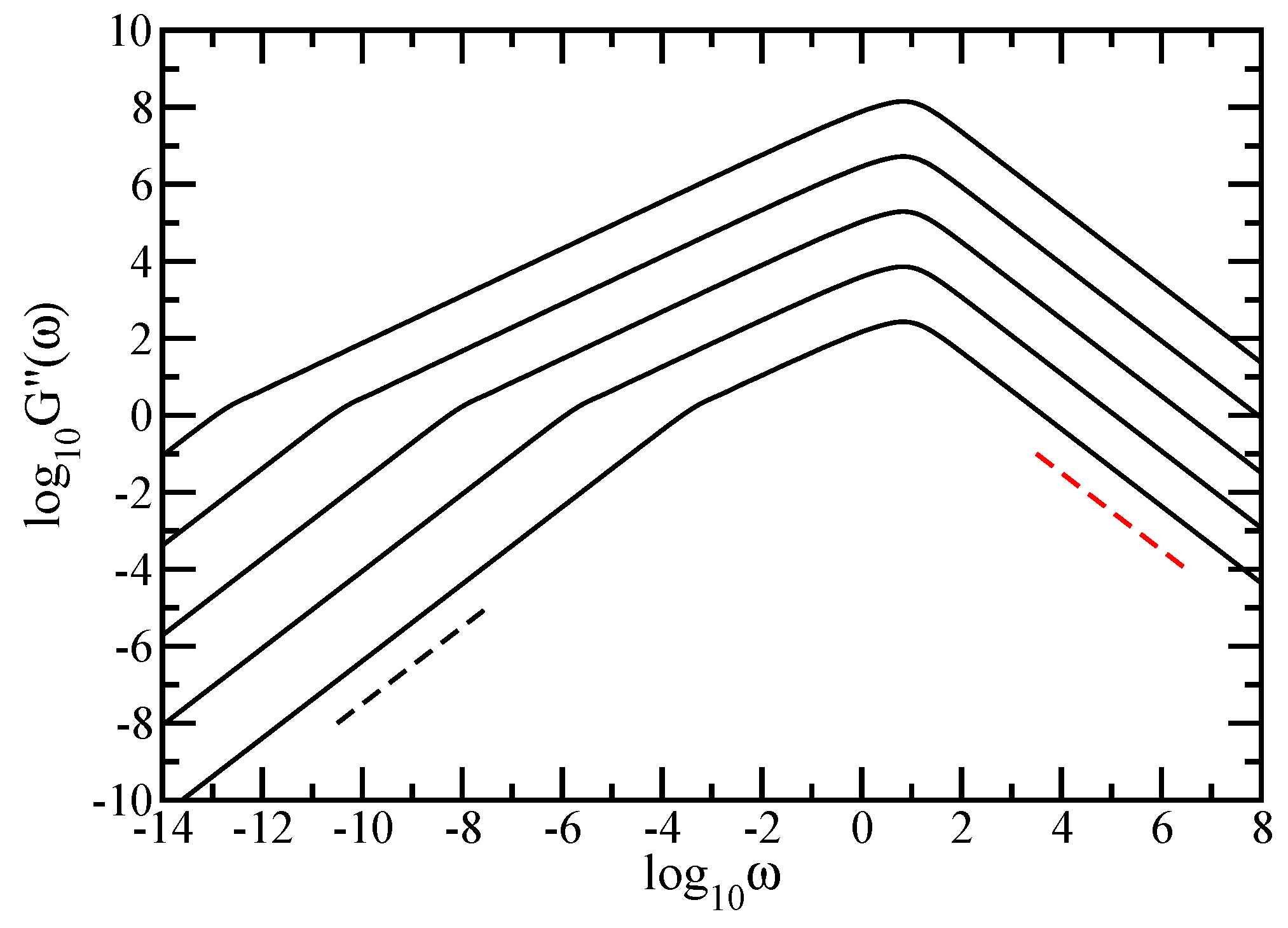
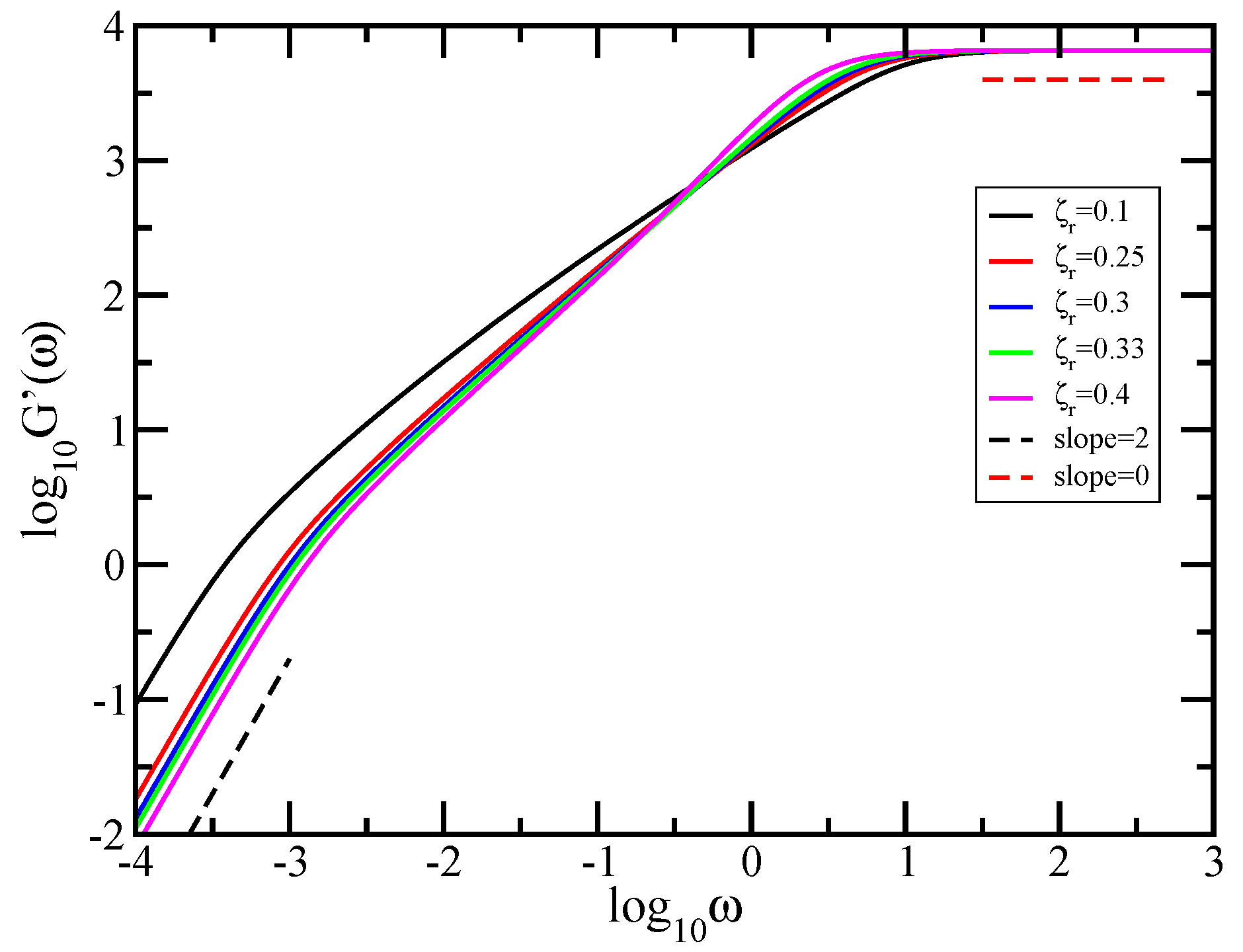
4.1. Results Obtained in the Rouse Approach
4.2. Comparison with Experimental Results from the Literature
4.3. Results Obtained in the Zimm Approach
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| g | generation of the fractal cactus |
| HI | hydrodynamic interaction |
| hydrodynamic interaction strength (or parameter) | |
| GGS | generalized Gaussian structures |
Appendix A. Decimation Procedure


References
- Rouse, P.E. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Zimm, B.H. Dynamics of Polymer Molecules in Dilute Solution: Viscoelasticity, Flow Birefringence and Dielectric Loss. J. Chem. Phys. 1956, 24, 269–278. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymers Physics; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Roovers, J. Star and Hyperbranched Polymers; Mishra, M.K., Kobayashi, S., Eds.; Marcel Dekker: New York, NY, USA, 1999. [Google Scholar]
- Gurtovenko, A.A.; Blumen, A. Generalized Gaussian Structures: Models for Polymer Systems with Complex Topologies. Adv. Polym. Sci. 2005, 182, 171–282. [Google Scholar]
- Fréchet, J.M.J.; Tomalia, D.A. Dendrimers and Other Dendritic Polymers; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Burchard, W. Solution Properties of Branched Macromolecules. Adv. Polym. Sci. 1999, 143, 113–194. [Google Scholar]
- Bosman, A.W.; Janssen, H.M.; Meijer, E.W. About dendrimers: Structure, physical properties, and applications. Chem. Rev. 1999, 99, 1665–1688. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Chen, Z.Y. Rouse Dynamics of a Dendrimer Model in the θ Condition. Macromolecules 1997, 30, 5104–5117. [Google Scholar] [CrossRef]
- Grimm, J.; Dolgushev, M. Dynamics of internally functionalized dendrimers. Phys. Chem. Chem. Phys. 2016, 18, 19050–19061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boris, D.; Rubinstein, M. A Self-Consistent Mean Field Model of a Starburst Dendrimer: Dense Core vs. Dense Shell. Macromolecules 1996, 29, 7251–7260. [Google Scholar] [CrossRef]
- Klos, J.S.; Sommer, J.-U. Simulations of Neutral and Charged Dendrimers in Solvents of Varying Quality. Macromolecules 2013, 46, 3107–3117. [Google Scholar] [CrossRef]
- Gurtovenko, A.A.; Markelov, D.A.; Gotlib, Y.Y.; Blumen, A. Dynamics of dendrimer-based polymer networks. J. Chem. Phys. 2003, 119, 7579–7590. [Google Scholar] [CrossRef]
- Voit, B.I.; Lederer, A. Hyperbranched and Highly Branched Polymer Architectures—Synthetic Strategies and Major Characterization Aspects. Chem. Rev. 2009, 109, 5924–5973. [Google Scholar] [CrossRef] [PubMed]
- Burchard, W. Angular Dependence of Scattered Light from Hyperbranched Structures in a Good Solvent. A Fractal Approach. Macromolecules 2004, 37, 3841–3849. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, B.; Zhang, H.; Zhou, S.; Guan, J.; Wang, Z. Determining global mean-first-passage time of random walks on Vicsek fractals using eigenvalues of Laplacian matrices. Phys. Rev. E 2010, 81, 031118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blumen, A.; von Ferber, C.; Jurjiu, A.; Koslowski, T. Generalized Vicsek Fractals: Regular Hyperbranched Polymers. Macromolecules 2004, 37, 638–650. [Google Scholar] [CrossRef]
- Volta, A.; Galiceanu, M.; Jurjiu, A. Relaxation dynamics of perturbed regular hyperbranched fractals. J. Phys. A Math. Theor. 2010, 43, 105205. [Google Scholar] [CrossRef]
- Jurjiu, A.; Dockhorn, R.; Mironova, O.; Sommer, J.-U. Two universality classes for random hyperbranched polymers. Soft Matter 2014, 10, 4935–4946. [Google Scholar] [CrossRef] [PubMed]
- Koslowski, T.; Jurjiu, A.; Blumen, A. Models of irregular hyperbranched polymers: Topological disorder and mechanical response. Macromol. Theory Simul. 2006, 15, 538–545. [Google Scholar] [CrossRef]
- Blumen, A.; Jurjiu, A.; Koslowski, T.; von Ferber, C. Dynamics of Vicsek fractals, models for hyperbranched polymers. Phys. Rev. E 2003, 67, 061103. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Zhang, Z.Z. Controlling the efficiency of trapping in treelike fractals. J. Chem. Phys. 2013, 139, 024106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jurjiu, A.; Biter, T.L.; Turcu, F. Relaxation dynamics of a multihierarchical polymer network. J. Chem. Phys. 2017, 146, 034902. [Google Scholar] [CrossRef] [PubMed]
- Galiceanu, M.; Oliveira, E.S.; Dolgushev, M. Relaxation dynamics of small-world degree-distributed treelike polymer networks. Phys. A 2016, 462, 376–385. [Google Scholar] [CrossRef]
- Jurjiu, A.; Galiceanu, M.; Farcasanu, A.; Chiriac, L.; Turcu, F. Relaxation dynamics of Sierpinski hexagon fractal polymer: Exact analytical results in the Rouse-type approach and numerical results in the Zimm-type approach. J. Chem. Phys. 2016, 145, 214901. [Google Scholar] [CrossRef] [PubMed]
- Jurjiu, A.; Biter, T.L.; Turcu, F. Dynamics of a Polymer Network Based on Dual Sierpinski Gasket and Dendrimer: A Theoretical Approach. Polymers 2017, 9, 245. [Google Scholar] [CrossRef]
- Jurjiu, A.; Maia, D.G.; Galiceanu, M. Relaxation dynamics of generalized scale-free polymer networks. Sci. Rep. 2018, 8, 3731. [Google Scholar] [CrossRef] [PubMed]
- Jurjiu, A.; Turcu, F.; Galiceanu, M. Dynamics of a Complex Multilayer Polymer Network: Mechanical Relaxation and Energy Transfer. Polymers 2018, 10, 164. [Google Scholar] [CrossRef]
- Liu, H.; Dolgushev, M.; Qi, Y.; Zhang, Z. Laplacian spectra of a class of small-world networks and their applications. Sci. Rep. 2015, 5, 9024. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galiceanu, M.; de Carvalho, L.T.; Mulken, O.; Dolgushev, M. Dynamics of Dual Scale-Free Polymer Networks. Polymers 2017, 9, 577. [Google Scholar] [CrossRef]
- Percec, V.; Ahn, C.-H.; Ungar, G.; Yeardley, D.J.P.; Möller, M.; Sheiko, S.S. Controlling polymer shape through the self-assembly of dendritic side-groups. Nature 1998, 391, 161–164. [Google Scholar] [CrossRef]
- Chang, J.; Zhao, Q.; Kang, L.; Li, H.; Xie, M.; Liao, X. Multiresponsive Supramolecular Gel Based on Pillararene-Containing Polymers. Macromolecules 2016, 49, 2814–2820. [Google Scholar] [CrossRef]
- Haghpanah, B.; Oftadeh, R.; Papadopoulos, J.; Vaziri, A. Self-similar hierarchical honeycombs. Proc. R. Soc. A 2013, 469, 20130022. [Google Scholar] [CrossRef]
- Newkome, G.R.; Wang, P.; Moorefield, C.N.; Cho, T.J.; Mohapatra, P.P.; Li, S.; Hwang, S.-H.; Lukoyanova, O.; Echegoyen, L.; Judith, A.; et al. Nanoassembly of a Fractal Polymer: A Molecular “Sierpinski Hexagonal Gasket”. Science 2006, 312, 1782–1785. [Google Scholar] [CrossRef] [PubMed]
- Shang, J.; Wang, Y.; Chen, M.; Dai, J.; Zhou, X.; Kuttner, J.; Hilt, G.; Shao, X.; Gottfried, J.M.; Wu, K. Assembling molecular Sierpinski triangle fractals. Nat. Chem. 2015, 7, 389–393. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zhang, X.; Li, N.; Wang, Y.; Yang, J.; Gu, G.; Zhang, Y.; Hou, S.; Peng, L.; Wu, K.; et al. Construction of Sierpinski Triangles up to the Fifth Order. J. Am. Chem. Soc. 2017, 139, 13749–13753. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Newkome, G.R. Terpyridine-based metallosupramolecular constructs: Tailored monomers to precise 2D-motifs and 3D-metallocages. Chem. Soc. Rev. 2018, 47, 3991–4016. [Google Scholar] [CrossRef] [PubMed]
- De Meijere, A.; Kozhushkov, S.I. The Chemistry of Highly Strained Oligospirocyclopropane Systems. Chem. Rev. 2000, 100, 93–142. [Google Scholar] [CrossRef] [PubMed]
- Jurjiu, A.; Koslowski, T.; Blumen, A. Dynamics of deterministic fractal polymer networks: Hydrodynamic interactions and the absence of scaling. J. Chem. Phys. 2003, 118, 2398–2404. [Google Scholar] [CrossRef]
- Yu, B. Analysis of flow in fractal porous media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
- Fan, J.A.; Yeo, W.-H.; Su, Y.; Hattori, Y.; Lee, W.; Jung, S.-Y.; Zhang, Y.; Liu, Z.; Cheng, H.; Falgout, L.; et al. Fractal design concepts for stretchable electronics. Nat. Commun. 2014, 5, 3266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubal, D.P.; Ayyad, O.; Ruiz, V.; Gomez-Romero, P. Hybrid energy storage: The merging of battery and supercapacitor chemistries. Chem. Soc. Rev. 2015, 44, 1777–1790. [Google Scholar] [CrossRef] [PubMed]
- Xie, N.; Shao, W.; Feng, L.; Lv, L.; Zhen, L. Fractal Analysis of Disordered Conductor-Insulator Composites with Different Conductor Backbone Structures near Percolation Threshold. J. Phys. Chem. C 2012, 116, 19517–19525. [Google Scholar] [CrossRef]
- Vicsek, T. Fractal Growth Phenomena; World Scientific: Singapore, 1989. [Google Scholar]
- Kouvaris, N.E.; Hata, S.; Diaz-Guilera, A. Pattern formation in multiplex networks. Sci. Rep. 2015, 5, 10840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- King, R.D.; Brown, B.; Hwang, M.; Jeon, T.; George, A.T. Alzheimer’s Disease Neuroimaging Initiative. Fractal dimension analysis of the cortical ribbon in mild Alzheimer’s disease. Neuroimage 2010, 53, 471–479. [Google Scholar] [CrossRef] [PubMed]
- Chiti, F.; Webster, P.; Taddei, N.; Clark, A.; Stefani, M.; Ramponi, G.; Dobson, C.M. Designing conditions for in vitro formation of amyloid protofilaments and fibrils. Proc. Natl. Acad. Sci. USA 1999, 96, 3590–3594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cross, S.S.; McDonagh, A.J.G.; Stephenson, T.J. Fractal and integer-dimensional analysis of pigmented skin lesions. Am. J. Dermatol. 1995, 17, 374–378. [Google Scholar] [CrossRef]
- Claridge, E.; Hall, P.N.; Keefe, M.; Allen, J.P. Shape analysis for classification of malignant melanoma. J. Biomed. Eng. 1992, 14, 229–234. [Google Scholar] [CrossRef]
- Tracqui, P. Biophysical model of tumor growth. Rep. Prog. Phys. 2009, 72, 1–30. [Google Scholar] [CrossRef]
- Galiceanu, M.; Blumen, A. Spectra of Husimi cacti: Exact results and applications. J. Chem. Phys. 2007, 127, 134904. [Google Scholar] [CrossRef] [PubMed]
- Galiceanu, M.; Jurjiu, A. Relaxation dynamics of multilayer triangular Husimi cacti. J. Chem. Phys. 2016, 145, 104901. [Google Scholar] [CrossRef] [PubMed]
- Loh, Y.L.; Yao, D.-X.; Carlson, E.W. Dimers on the triangular Kagome lattice. Phys. Rev. B 2008, 78, 224410. [Google Scholar] [CrossRef]
- Sommer, J.-U.; Blumen, A. On the statistics of generalized Gaussian structures: Collapse and random external fields. J. Phys. A 1995, 28, 6669–6674. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Bixon, M.; Zwanzig, R. Optimized Rouse–Zimm theory for stiff polymers. J. Chem. Phys. 1978, 68, 1896–1902. [Google Scholar] [CrossRef]
- Perico, A. Segmental relaxation in macromolecules. Acc. Chem. Res. 1989, 22, 336–342. [Google Scholar] [CrossRef]
- Toshchevikov, V.; Blumen, A.; Gotlib, Y.Y. Dynamics of Polymer Networks with Strong Differences in the Viscous Characteristics of their Crosslinks and Strands. Macromol. Theory Simul. 2007, 16, 359–377. [Google Scholar] [CrossRef]
- Schiessel, H. Unfold dynamics of generalized Gaussian structures. Phys. Rev. E 1998, 57, 5775–5781. [Google Scholar] [CrossRef]
- Ferla, R.L. Conformations and dynamics of dendrimers and cascade macromolecules. J. Chem. Phys. 1997, 106, 688–700. [Google Scholar] [CrossRef]
- Haggarty, S.J.; Clemons, P.A.; Schreiber, S.L. Chemical Genomic Profiling of Biological Networks Using Graph Theory and Combinations of Small Molecule Perturbations. J. Am. Chem. Soc. 2003, 125, 10543–10545. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.J. Low-Dimensional Manifolds in Reaction-Diffusion Equations. 1. Fundamental Aspects. J. Phys. Chem. A 2006, 110, 5235–5256. [Google Scholar] [CrossRef] [PubMed]
- Agliari, E.; Tavani, F. The exact Laplacian spectrum for the Dyson hierarchical network. Sci. Rep. 2017, 7, 39962. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agliari, E.; Barra, A.; Galluzzi, A.; Guerra, F.; Tantari, D.; Tavani, F. Retrieval Capabilities of Hierarchical Networks: From Dyson to Hopfield. Phys. Rev. Lett. 2015, 114, 028103. [Google Scholar] [CrossRef] [PubMed]
- Heilbronner, E.; Beck, H. Das HMO-Modell und Seine Anwendung; Chemie: Weinheim, Germany, 1968. [Google Scholar]
- Markelov, D.; Dolgushev, M.; Lähderanta, E. NMR Relaxation in Dendrimers. In Annual Reports on NMR Spectroscopy; Graham, A.W., Ed.; Academic Press: Oxford, UK, 2017; Volume 91, pp. 1–66. [Google Scholar]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Kirkwood, J.G.; Riseman, J. The Intrinsic Viscosities and Diffusion Constants of Flexible Macromolecules in Solution. J. Chem. Phys. 1948, 16, 565–573. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; AIP Press: New York, NY, USA, 1994. [Google Scholar]
- Rotne, J.; Prager, S. Variational Treatment of Hydrodynamic Interaction in Polymers. J. Chem. Phys. 1969, 50, 4831–4837. [Google Scholar]
- Biswas, P.; Kant, R.; Blumen, A. Stretch dynamics of flexible dendritic polymers in solution. J. Chem. Phys. 2001, 114, 2430–2441. [Google Scholar] [CrossRef]
- Perkins, T.; Smith, D.; Larson, R.; Chu, S. Stretching of a single tethered polymer in a uniform flow. Science 1995, 268, 83–87. [Google Scholar] [CrossRef] [PubMed]
- Hatfield, J.W.; Quake, S.R. Dynamic Properties of an Extended Polymer in Solution. Phys. Rev. Lett. 1999, 82, 3548–3551. [Google Scholar] [CrossRef] [Green Version]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: Hoboken, NY, USA, 1980. [Google Scholar]
- Vilgis, T.A. Polymeric fractals and the unique treatment of polymers. J. Phys. 1988, 49, 1481–1483. [Google Scholar] [CrossRef]
- Cates, M.E. Brownian dynamics of self-similar macromolecules. J. Phys. 1985, 46, 1059–1077. [Google Scholar] [CrossRef]
- Sowinska, M.; Urbanczyk-Lipkowska, Z. Advances in the chemistry of dendrimers. New J. Chem. 2014, 38, 2168–2203. [Google Scholar] [CrossRef]
- Yu, J.M.; Blacher, S.; Brouers, F.; Jérôme, R. Triblock Copolymer Based Thermoreversible Gels. 4. Effect of the Midblock and Characterization of the Sol-Gel Transition. Macromolecules 1997, 30, 4619–4625. [Google Scholar] [CrossRef]
- Lewis, C.L.; Stewart, K.; Anthamatten, M. The Influence of Hydrogen Bonding Side-Groups on Viscoelastic Behavior of Linear and Network Polymers. Macromolecules 2014, 47, 729–740. [Google Scholar] [CrossRef]
- Yan, T.; Schröter, K.; Herbst, F.; Binder, W.H.; Thurn-Albrecht, T. Nanostructure and Rheology of Hydrogen-Bonding Telechelic Polymers in the Melt: From Micellar Liquids and Solids to Supramolecular Gels. Macromolecules 2014, 47, 2122–2130. [Google Scholar] [CrossRef]
- Tang, S.; Wang, M.; Olsen, B.D. Anomalous Self-Diffusion and Sticky Rouse Dynamics in Associative Protein Hydrogels. J. Am. Chem. Soc. 2015, 137, 3946–3957. [Google Scholar] [CrossRef] [PubMed]
- Narita, T.; Indei, T. Microrheological Study of Physical Gelation in Living Polymeric Networks. Macromolecules 2016, 49, 4634–4646. [Google Scholar] [CrossRef]
- Haro-Pérez, C.; García-Castillo, A.; Arauz-Lara, J.L. Confinement-induced fluid-gel transition in polymeric solutions. Langmuir 2009, 25, 8911–8914. [Google Scholar] [CrossRef] [PubMed]
- Markelov, D.A.; Furstenberg, F.; Dolgushev, M. NMR relaxation in semiflexible Vicsek fractals. Polymer 2018, 144, 65–71. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef] [Green Version]
- Mülken, O.; Dolgushev, M.; Galiceanu, M. Complex Quantum Networks: From Universal Breakdown to Optimal Transport. Phys. Rev. E 2016, 93, 022304. [Google Scholar] [CrossRef] [PubMed]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurjiu, A.; Galiceanu, M. Dynamics of a Polymer Network Modeled by a Fractal Cactus. Polymers 2018, 10, 787. https://doi.org/10.3390/polym10070787
Jurjiu A, Galiceanu M. Dynamics of a Polymer Network Modeled by a Fractal Cactus. Polymers. 2018; 10(7):787. https://doi.org/10.3390/polym10070787
Chicago/Turabian StyleJurjiu, Aurel, and Mircea Galiceanu. 2018. "Dynamics of a Polymer Network Modeled by a Fractal Cactus" Polymers 10, no. 7: 787. https://doi.org/10.3390/polym10070787