A Real-Time Adaptive Control System for Border Irrigation
Abstract
:1. Introduction
2. Materials and Methods
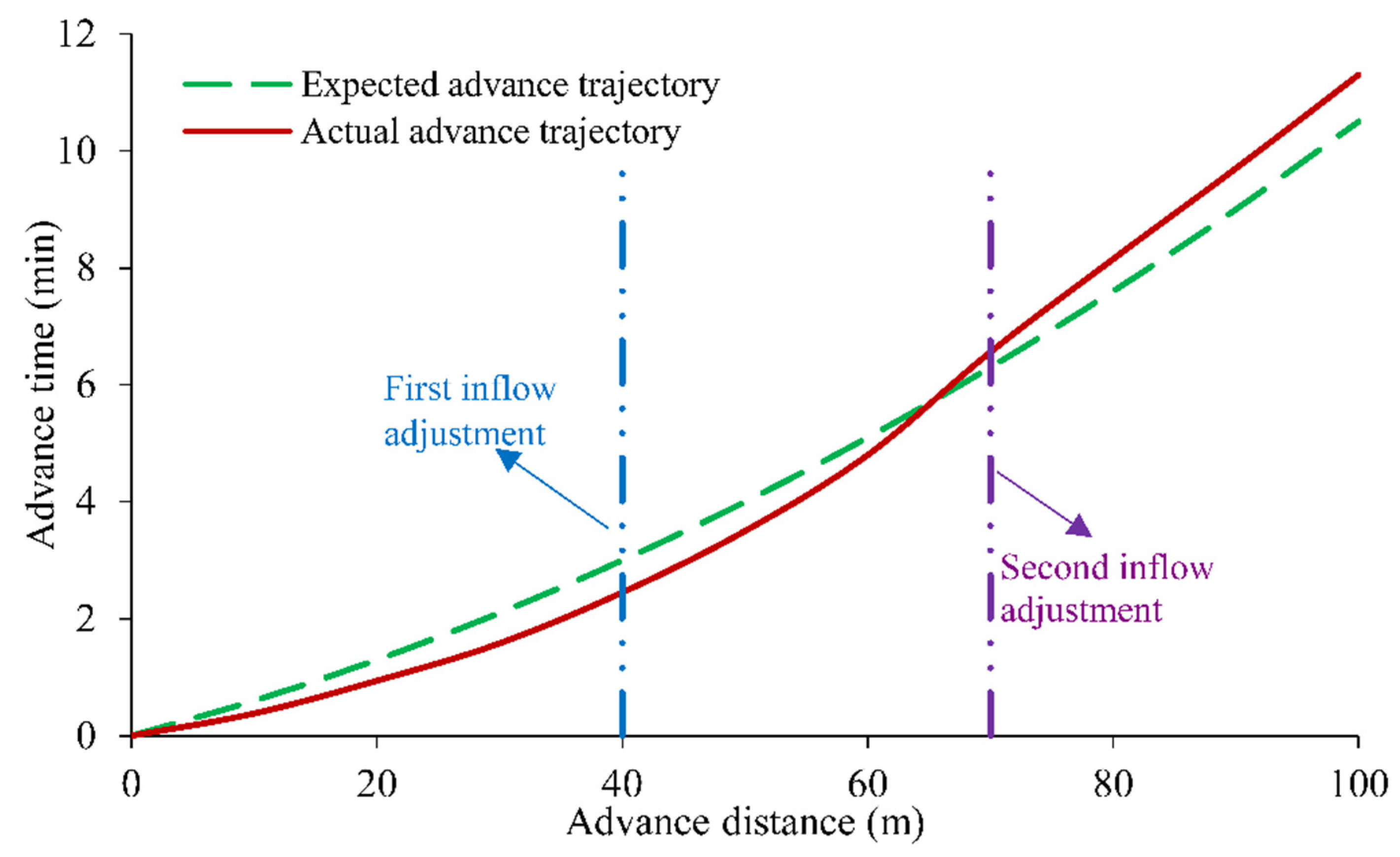
2.1. Description of Real-Time Adaptive Control Irrigation
2.2. Field Experiment and Data Measurement
2.3. Assessment of Irrigation Performance
2.4. Statistical Test
3. Results and Discussion
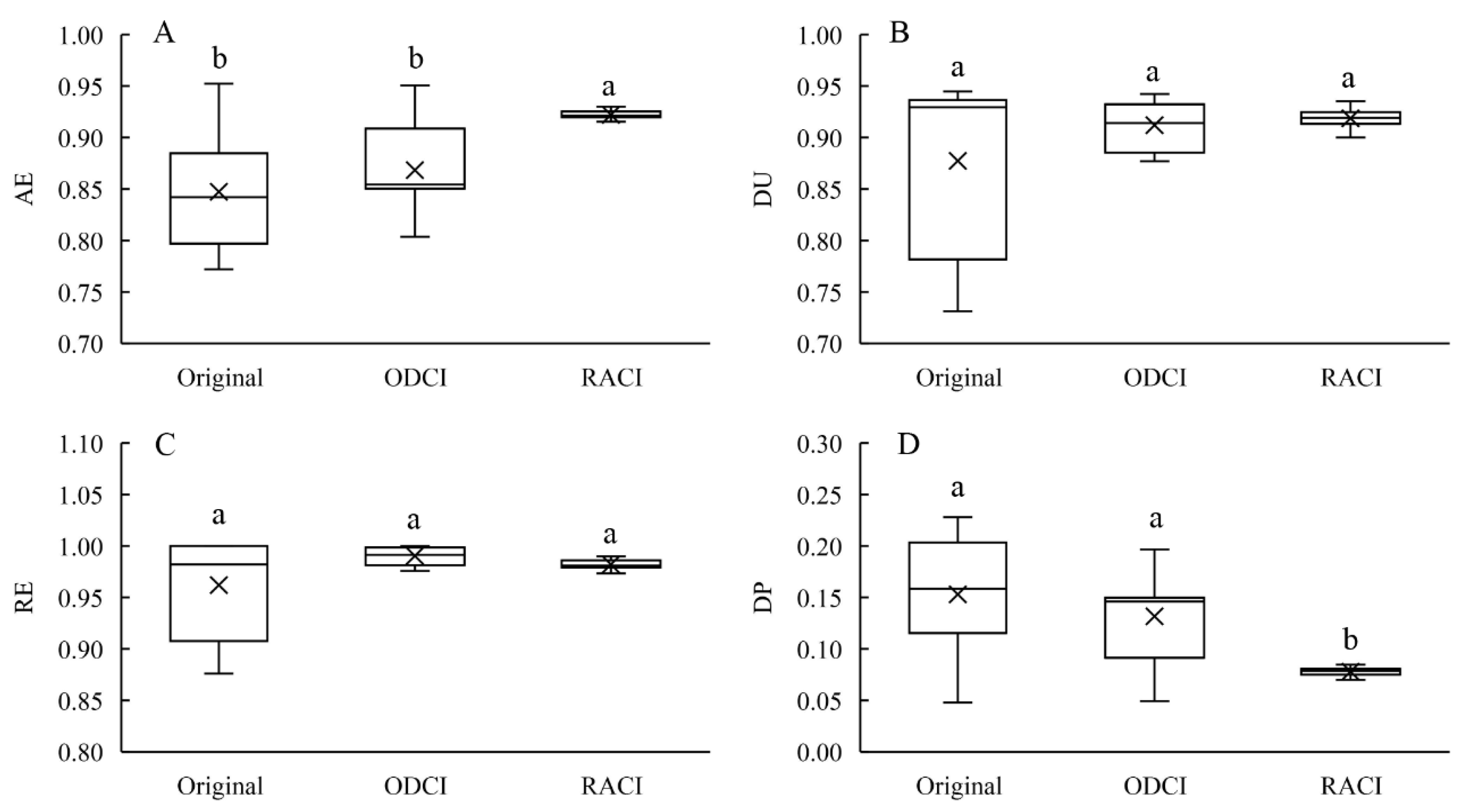
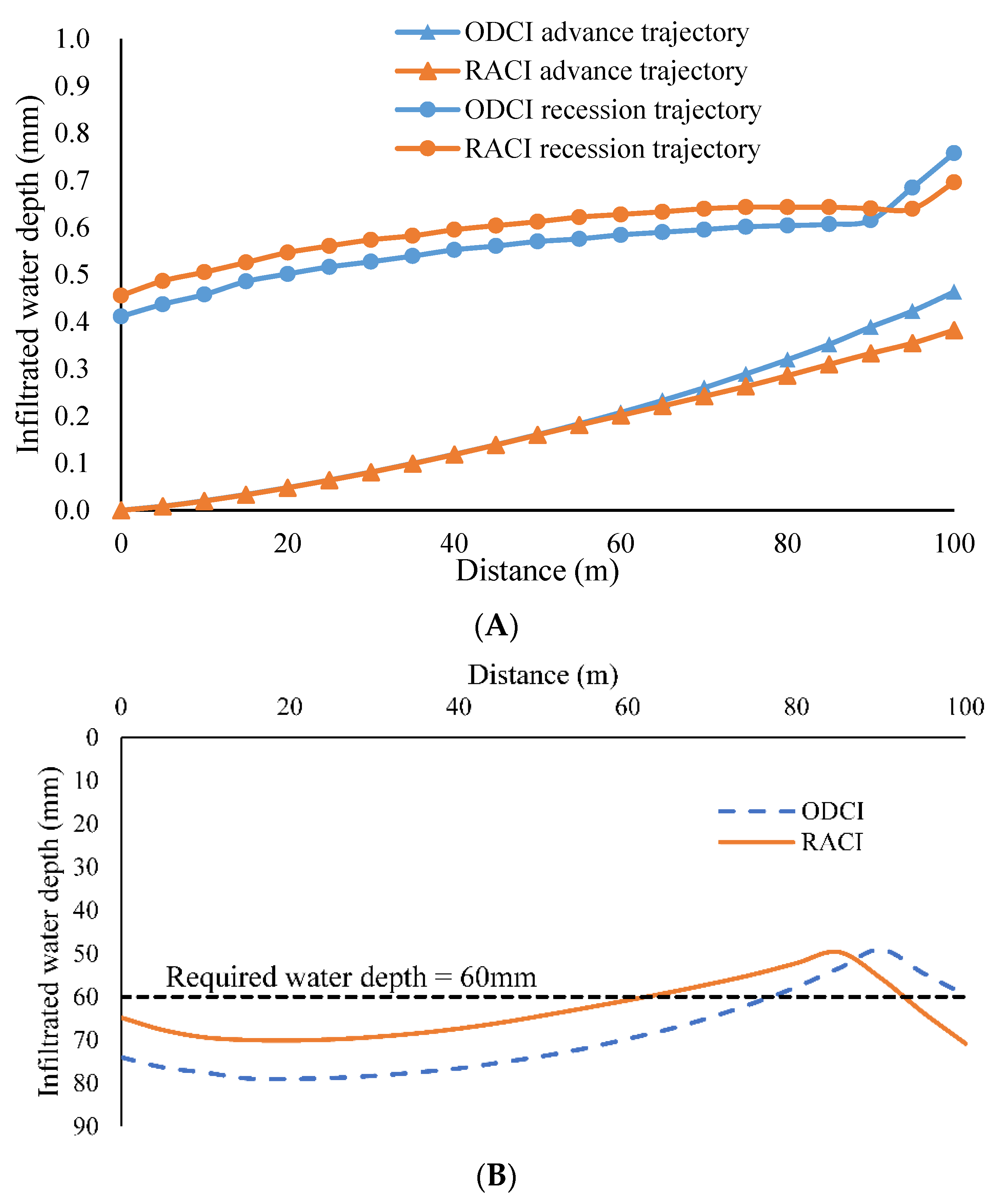
3.1. Assessment of Real-Time Adaptive Control Irrigation by Simulation
3.1.1. Analysis of Irrigation Performance
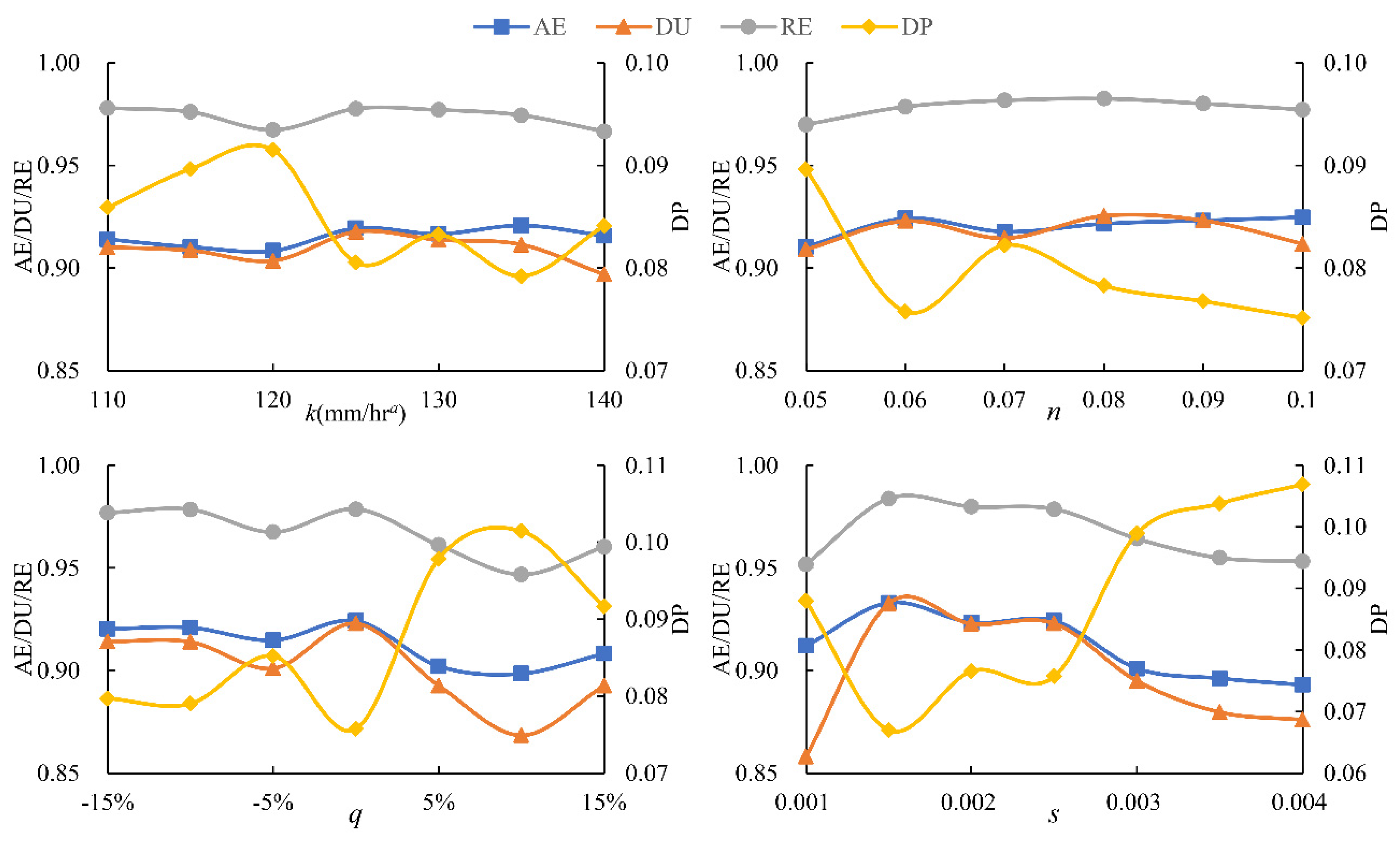
3.1.2. Sensitivity Analysis
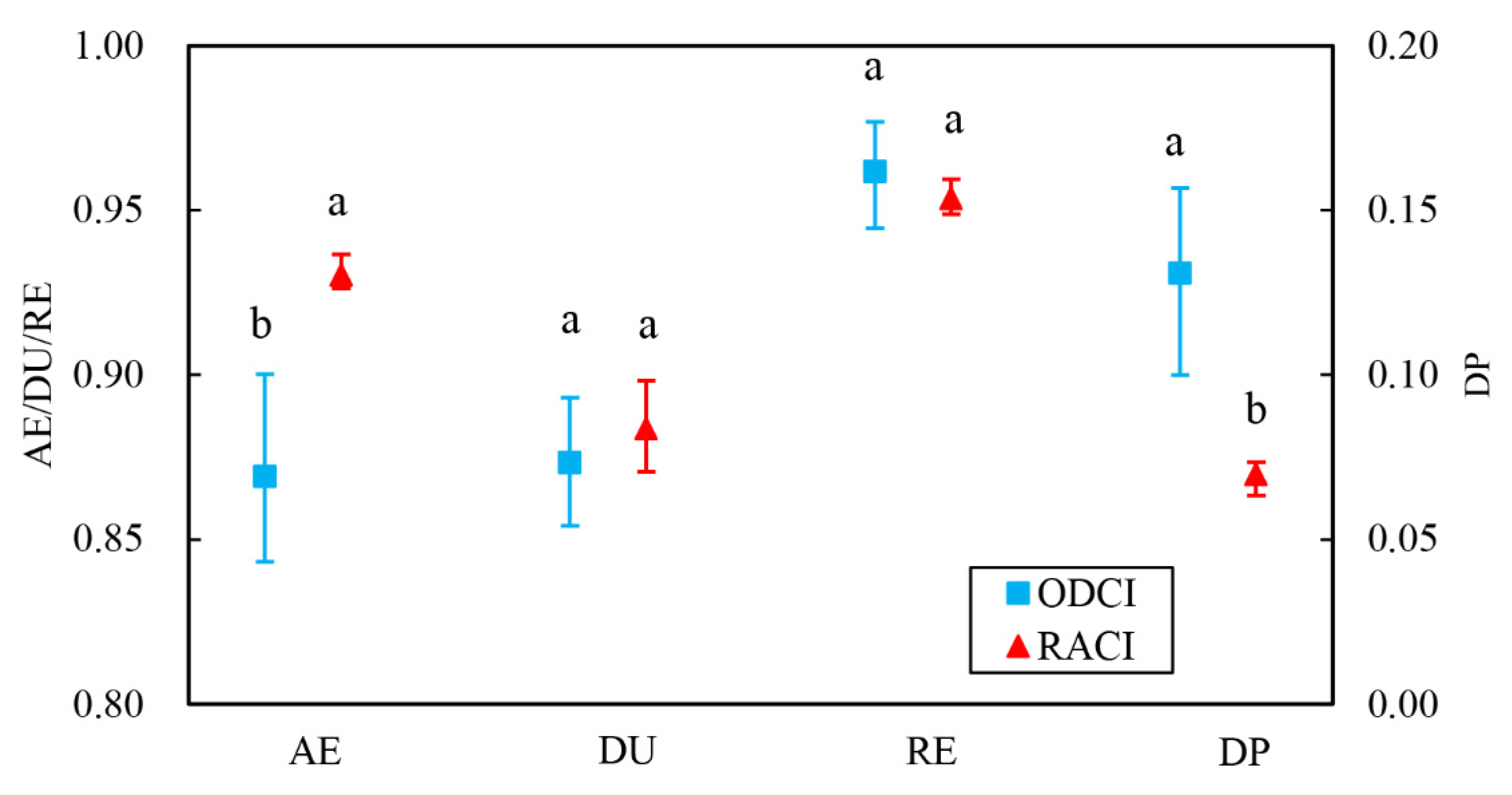
3.2. Experimental Verification
3.3. Comparison of RACI with Traditional Real-Time Control Irrigation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- China Statistics Press. China Statistical Yearbook; China Statistics Press: Beijing, China, 2021.
- Kang, S.; Hao, X.; Du, T.; Tong, L.; Su, X.; Lu, H.; Li, X.; Huo, Z.; Li, S.; Ding, R. Improving agricultural water productivity to ensure food security in China under changing environment: From research to practice. Agric. Water Manag. 2017, 179, 5–17. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Jia, B.Y.; Wu, S.Q.; Dai, J.Y.; Tang, D.S. Comprehensive Forecast of Urban Water-Energy Demand Based on a Neural Network Model. Water 2018, 10, 385. [Google Scholar] [CrossRef] [Green Version]
- Gu, Z.; Qi, Z.M.; Burghate, R.; Yuan, S.Q.; Jiao, X.Y.; Xu, J.Z. Irrigation Scheduling Approaches and Applications: A Review. J. Irrig. Drain. Eng. 2020, 146, 04020007. [Google Scholar] [CrossRef]
- Yang, Y.; Watanabe, M.; Zhang, X.; Zhang, J.; Wang, Q.; Hayashi, S. Optimizing irrigation management for wheat to reduce groundwater depletion in the piedmont region of the Taihang Mountains in the North China Plain. Agric. Water Manag. 2006, 82, 25–44. [Google Scholar] [CrossRef]
- Lv, L.; Yao, Y.; Zhang, L.; Dong, Z.; Jia, X.; Liang, S.; Ji, J. Winter wheat grain yield and its components in the North China Plain: Irrigation management, cultivation, and climate. Chil. J. Agric. Res. 2013, 73, 233–242. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Chen, X.; Vitousek, P.M. Chinese agriculture: An experiment for the world. Nature 2013, 497, 33–35. [Google Scholar] [CrossRef]
- Abioye, E.A.; Abidin, M.S.Z.; Mahmud, M.S.A.; Buyamin, S.; Ishak, M.H.I.; Abd Rahman, M.K.I.; Otuoze, A.O.; Onotu, P.; Ramli, M.S.A. A review on monitoring and advanced control strategies for precision irrigation. Comput. Electron. Agric. 2020, 173, 22. [Google Scholar] [CrossRef]
- Xu, J.; Cai, H.; Saddique, Q.; Wang, X.; Li, L.; Ma, C.; Lu, Y. Evaluation and optimization of border irrigation in different irrigation seasons based on temporal variation of infiltration and roughness. Agric. Water Manag. 2019, 214, 64–77. [Google Scholar] [CrossRef]
- Nie, W.B.; Li, Y.B.; Zhang, F.; Ma, X.Y. Optimal discharge for closed-end border irrigation under soil infiltration variability. Agric. Water Manag. 2019, 221, 58–65. [Google Scholar] [CrossRef]
- Mazarei, R.; Mohammadi, A.S.; Ebrahimian, H.; Naseri, A. Temporal variability of infiltration and roughness coefficients and furrow irrigation performance under different inflow rates. Agric. Water Manag. 2021, 245, 106465. [Google Scholar] [CrossRef]
- Gonzalez, C.R.; Cervera, L.; Moretfernandez, D. Basin irrigation design with longitudinal slope. Agric. Water Manag. 2011, 98, 1516–1522. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.J.; Gillies, M.H. Head ditch hydraulics and the variability of inflows to irrigation furrows. Irrig. Drain. 2010, 59, 442–452. [Google Scholar] [CrossRef] [Green Version]
- Bai, M.; Li, Y.; Tu, S.; Liu, Q. Analysis on cutoff time optimization of border irrigation to improve irrigated water quality. Trans. Chin. Soc. Agric. Eng. 2016, 32, 105–110. [Google Scholar]
- Chen, B.; Ouyang, Z.; Sun, Z.G.; Wu, L.F.; Li, F.D. Evaluation on the potential of improving border irrigation performance through border dimensions optimization: A case study on the irrigation districts along the lower Yellow River. Irrig. Sci. 2013, 31, 715–728. [Google Scholar] [CrossRef]
- Santos, F.L. Evaluation and adoption of irrigation technologies: Management-design curves for Furrow and Level Basin systems. Agric. Syst. 1996, 52, 317–329. [Google Scholar] [CrossRef]
- Gillies, M.; Smith, R.; Williamson, B.; Shanahan, M. Improving Performance of Bay Irrigation through Higher Flow Rates; Irrigation Australia Ltd.: Sydney, Australia, 2010; pp. 8–10. [Google Scholar]
- Smith, R.J.; Uddin, J.M.; Gillies, M.H.; Moller, P.; Clurey, K. Evaluating the performance of automated bay irrigation. Irrig. Sci. 2016, 34, 175–185. [Google Scholar] [CrossRef]
- Smith, R.J.; Uddin, M.J. Selection of flow rate and irrigation duration for high performance bay irrigation. Agric. Water Manag. 2020, 228, 11. [Google Scholar] [CrossRef]
- Morris, M.R.; Hussain, A.; Gillies, M.H.; O’Halloran, N.J. Inflow rate and border irrigation performance. Agric. Water Manag. 2015, 155, 76–86. [Google Scholar] [CrossRef]
- Salahou, M.K.; Jiao, X.; Lü, H. Border irrigation performance with distance-based cut-off. Agric. Water Manag. 2018, 201, 27–37. [Google Scholar] [CrossRef]
- Latimer, E.; Reddell, D. Components for an advance rate feedback irrigation system (ARHS). Trans. ASAE 1990, 33, 1162–1170. [Google Scholar] [CrossRef]
- Khatri, K.L.; Smith, R. Toward a simple real-time control system for efficient management of furrow irrigation. Irrig. Drain. J. Int. Comm. Irrig. Drain. 2007, 56, 463–475. [Google Scholar] [CrossRef]
- Koech, R.K.; Smith, R.J.; Gillies, M.H. A real-time optimisation system for automation of furrow irrigation. Irrig. Sci. 2014, 32, 319–327. [Google Scholar] [CrossRef]
- Nie, W.B.; Feng, Z.J.; Li, Y.B.; Zhang, F.; Ma, X.Y. Determining a reasonable distance of collecting irrigation data for real-time management of furrow irrigation. Irrig. Drain. 2022, 1–17. [Google Scholar] [CrossRef]
- Masseroni, D.; Ricart, S.; de Cartagena, F.R.; Monserrat, J.; Goncalves, J.M.; de Lima, I.; Facchi, A.; Sali, G.; Gandolfi, C. Prospects for Improving Gravity-Fed Surface Irrigation Systems in Mediterranean European Contexts. Water 2017, 9, 20. [Google Scholar] [CrossRef] [Green Version]
- Koech, R.; Langat, P. Improving Irrigation Water Use Efficiency: A Review of Advances, Challenges and Opportunities in the Australian Context. Water 2018, 10, 1771. [Google Scholar] [CrossRef] [Green Version]
- Uddin, J.; Smith, R.J.; Gillies, M.H.; Moller, P.; Robson, D. Smart Automated Furrow Irrigation of Cotton. J. Irrig. Drain. Eng. 2018, 144, 10. [Google Scholar] [CrossRef] [Green Version]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T.S.; Schlegel, J. Modern analysis of surface irrigation systems with WinSRFR. Agric. Water Manag. 2009, 96, 1146–1154. [Google Scholar] [CrossRef]
- Liu, K.H.; Jiao, X.Y.; Guo, W.H.; An, Y.H.; Salahou, M.K. Improving border irrigation performance with predesigned varied-discharge. PLoS ONE 2020, 15, e0232751. [Google Scholar] [CrossRef]
- Li, Q.Q.; Dong, B.D.; Qiao, Y.Z.; Liu, M.Y.; Zhang, J.W. Root growth, available soil water, and water-use efficiency of winter wheat under different irrigation regimes applied at different growth stages in North China. Agric. Water Manag. 2010, 97, 1676–1682. [Google Scholar] [CrossRef]
- Zhang, D.; Li, R.Q.; Batchelor, W.D.; Ju, H.; Li, Y.M. Evaluation of limited irrigation strategies to improve water use efficiency and wheat yield in the North China Plain. PLoS ONE 2018, 13, e0189989. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Lin, X.; Gu, S.; Wang, D. Effects of supplemental irrigation with micro-sprinkling hoses on soil physical properties, water consumption and grain yield of winter wheat. Acta Agron. Sin. 2019, 45, 879–892. [Google Scholar] [CrossRef]
- Burt, C.M.; Clemmens, A.J.; Strelkoff, T.S.; Solomon, K.H.; Bliesner, R.D.; Hardy, L.A.; Howell, T.A.; Eisenhauer, D.E. Irrigation performance measures: Efficiency and uniformity. J. Irrig. Drain. Eng. 1997, 123, 423–442. [Google Scholar] [CrossRef] [Green Version]
- Koech, R.K.; Smith, R.J.; Gillies, M.H. Evaluating the performance of a real-time optimisation system for furrow irrigation. Agric. Water Manag. 2014, 142, 77–87. [Google Scholar] [CrossRef]
- Gillies, M.H.; Smith, R.J.; Raine, S.R. Evaluating whole field irrigation performance using statistical inference of inter-furrow infiltration variation. Biosys. Eng. 2011, 110, 134–143. [Google Scholar] [CrossRef] [Green Version]
- Shahidian, S.; Serralheiro, R.P.; Serrano, J.M. Practical issues in developing a smart surface irrigation system with real-time simulation of furrow advance. Irrig. Drain. 2013, 62, 25–36. [Google Scholar] [CrossRef] [Green Version]
- Khatri, K.L.; Memon, A.A.; Shaikh, Y.; Pathan, A.; Shah, S.A.; Pinjani, K.K.; Soomro, R.; Smith, R.; Almani, Z. Real-Time Modelling and Optimisation for Water and Energy Efficient Surface Irrigation. J. Water Resour. Prot. 2013, 5, 681–688. [Google Scholar] [CrossRef]
- Wu, C.; Xu, D.; Bai, M.; Li, Y.; Li, F. Real-time feedback control technology for precise furrow irrigation. J. Drain. Irrig. Mach. Eng. 2020, 38, 536–540. [Google Scholar]
| Border | Average Slope s | Kostiakov Infiltration Parameters | Roughness Coefficient n | |
|---|---|---|---|---|
| k (mm hr−α) | a | |||
| S1 | 0.0022 | 104.607 | 0.68 | 0.095 |
| S2 | 0.0023 | 134.966 | 0.68 | 0.060 |
| S3 | 0.0023 | 130.123 | 0.68 | 0.065 |
| S4 | 0.0024 | 130.067 | 0.68 | 0.065 |
| S5 | 0.0025 | 122.236 | 0.68 | 0.060 |
| S6 | 0.0022 | 111.160 | 0.68 | 0.060 |
| S7 | 0.0014 | 122.771 | 0.68 | 0.060 |
| S8 | 0.0024 | 119.340 | 0.68 | 0.075 |
| S9 | 0.0017 | 110.402 | 0.68 | 0.060 |
| Border | Treatment | Initial Inflow Rate (L s−1 m−1) | Expected Advance Time of Observation Points (min) | Condition for Cutoff | ||||
|---|---|---|---|---|---|---|---|---|
| 40 m | 50 m | 60 m | 65 m | 70 m | ||||
| A1–A3 | ODCI | 4 | — | — | — | — | — | Inflow advances to 80 m |
| B1–B3 | RACI | 4 | 21.56 | 29.13 | 36.70 | 40.37 | 44.02 | Irrigation water amount reaches 36.76 m3 |
| Border | Original Irrigation Scheme | ODCI Scheme | RACI Scheme | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Inflow Rate (L s−1 m−1) | Cutoff-Distance Ratio | Inflow Rate (L s−1 m−1) | Cutoff-Distance Ratio | Initial Inflow Rate (L s−1 m−1) | First Adjustment | Second Adjustment | Cutoff Time (min) | |||
| Advance of Adjustment (m) | Inflow Rate after Adjustment (L s−1 m−1) | Advance of Adjustment (m) | Inflow Rate after Adjustment (L s−1 m−1) | |||||||
| S1 | 4.87 | 0.80 | 5.5 | 0.85 | 5.5 | 40 | 7 | — | — | 16.86 |
| S2 | 4.82 | 0.80 | 5.5 | 0.85 | 5.5 | 40 | 7 | — | — | 16.62 |
| S3 | 4.84 | 0.80 | 5.5 | 0.85 | 5.5 | 40 | 7 | — | — | 16.68 |
| S4 | 5.00 | 0.85 | 5.5 | 0.85 | 5.5 | 40 | 7 | — | — | 16.62 |
| S5 | 4.93 | 0.85 | 5.5 | 0.85 | 5.5 | — | — | — | — | 19.19 |
| S6 | 4.98 | 0.85 | 5.5 | 0.85 | 5.5 | 40 | 3 | 60 | 7 | 19.50 |
| S7 | 5.06 | 0.90 | 5.5 | 0.85 | 5.5 | 40 | 7 | — | — | 16.68 |
| S8 | 5.13 | 0.90 | 5.5 | 0.85 | 5.5 | 40 | 7 | — | — | 16.68 |
| S9 | 4.90 | 0.90 | 5.5 | 0.85 | 5.5 | 40 | 7 | 70 | 3 | 20.04 |
| Border Number | Treatment | Initial Inflow Rate (L s−1 m−1) | First Change | Second Change | Cutoff-Distance Ratio | Cutoff Time (min) | Irrigation Water Amount (m3) | ||
|---|---|---|---|---|---|---|---|---|---|
| Advance of Inflow Rate Change (m) | Inflow Rate after Change (L s−1 m−1) | Advance of Inflow Rate Change (m) | Inflow Rate after Change (L s−1 m−1) | ||||||
| A1 | ODCI | 3.94 | — | — | — | — | 0.8 | 57.96 | 41.11 |
| A2 | 4.01 | — | — | — | — | 0.8 | 54.06 | 39.02 | |
| A3 | 3.93 | — | — | — | — | 0.8 | 55.56 | 39.30 | |
| B1 | RACI | 3.18 | 40 | 5.58 | 65 | 3.05 | — | 52.20 | 36.80 |
| B2 | 3.31 | 40 | 6.07 | 60 | 3.13 | — | 52.32 | 36.87 | |
| B3 | 3.86 | 40 | 5.89 | 50 | 3.48 | — | 51.96 | 36.82 | |
| Comparison | RACI | Traditional Real-Time Control Irrigation | |
|---|---|---|---|
| Measurement | Before irrigation | Slope, infiltration parameters, and roughness coefficient of one border | Slope and roughness coefficient of every border |
| During irrigation | Inflow rate and advance time | Inflow rate and advance time | |
| Calculation | Expected advance trajectory and expected amount of irrigation water of one border before irrigation | Soil infiltration properties of every border in real-time during irrigation | |
| Adjustment basis | Simply compare the actual and expected advance time | Real-time simulate the irrigation process of every border and determine the optimal inflow rate or cutoff time | |
| Equipment requirements | Sensors of advance time, equipment for measuring and adjusting flow (accuracy of ±10% is acceptable), simple computing equipment (such as a microcontroller) | Sensors of advance time, equipment for accurately measuring and adjusting flow (some systems do not need to adjust inflow rate), equipment capable of performing complex calculations in a short time (such as computer) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Jiao, X.; Li, J.; Gu, Z.; Guo, W. A Real-Time Adaptive Control System for Border Irrigation. Agronomy 2022, 12, 2995. https://doi.org/10.3390/agronomy12122995
Liu K, Jiao X, Li J, Gu Z, Guo W. A Real-Time Adaptive Control System for Border Irrigation. Agronomy. 2022; 12(12):2995. https://doi.org/10.3390/agronomy12122995
Chicago/Turabian StyleLiu, Kaihua, Xiyun Jiao, Jiang Li, Zhe Gu, and Weihua Guo. 2022. "A Real-Time Adaptive Control System for Border Irrigation" Agronomy 12, no. 12: 2995. https://doi.org/10.3390/agronomy12122995






