Sunflower Seed Suction Stability Regulation and Seeding Performance Experiments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structure and Working Principle of the Seed-Metering Device
2.2. Design and Parameter Analysis of Key Components
2.2.1. Triaxial Dimension Measurement and Outline Extraction of Seeds
2.2.2. Key Parameter Design of Seed-Metering Plate
2.2.3. Design of the Adjusting Device
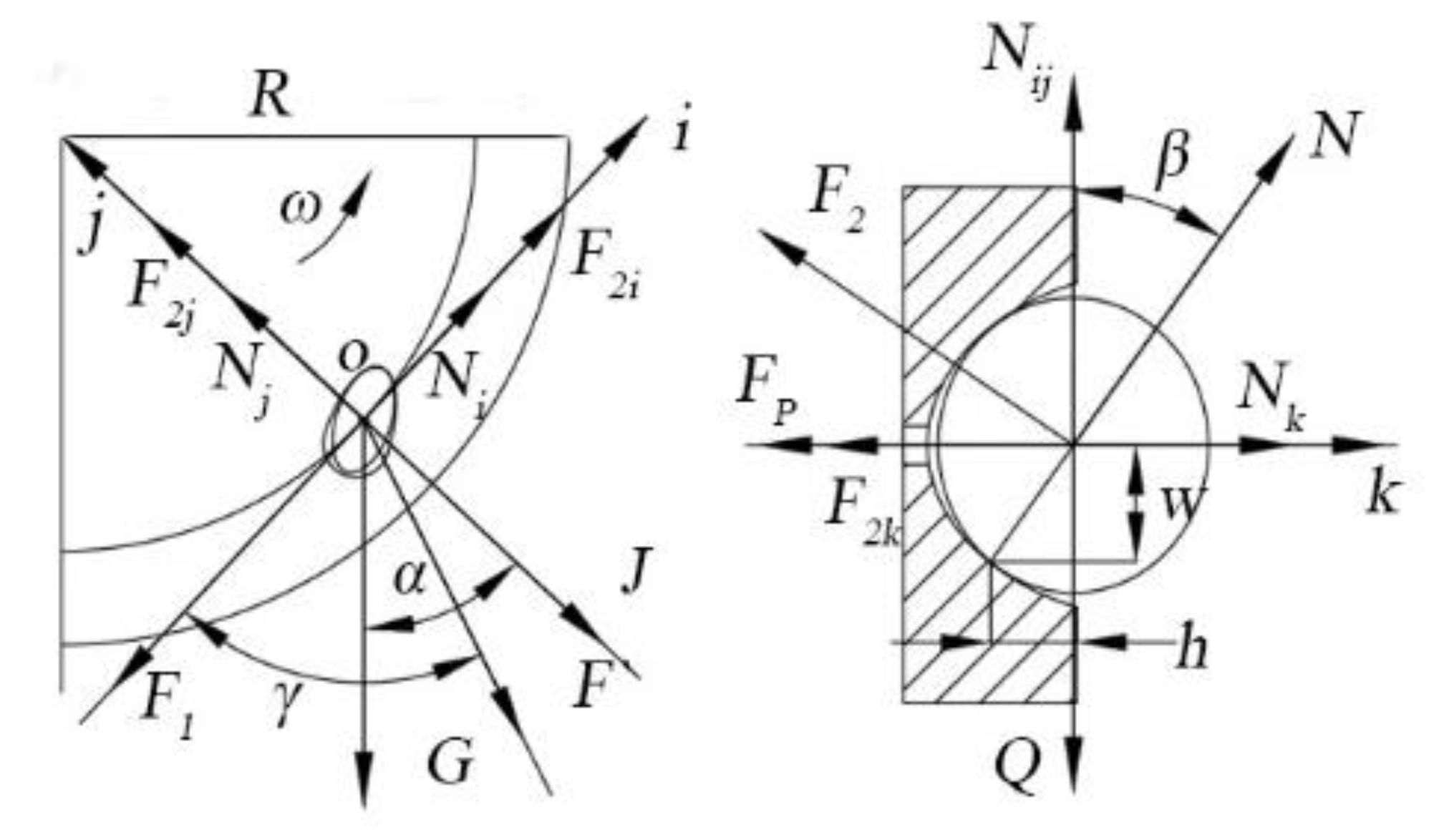
2.3. Analysis of the Principle of Suction and Movement of Sunflower Seeds
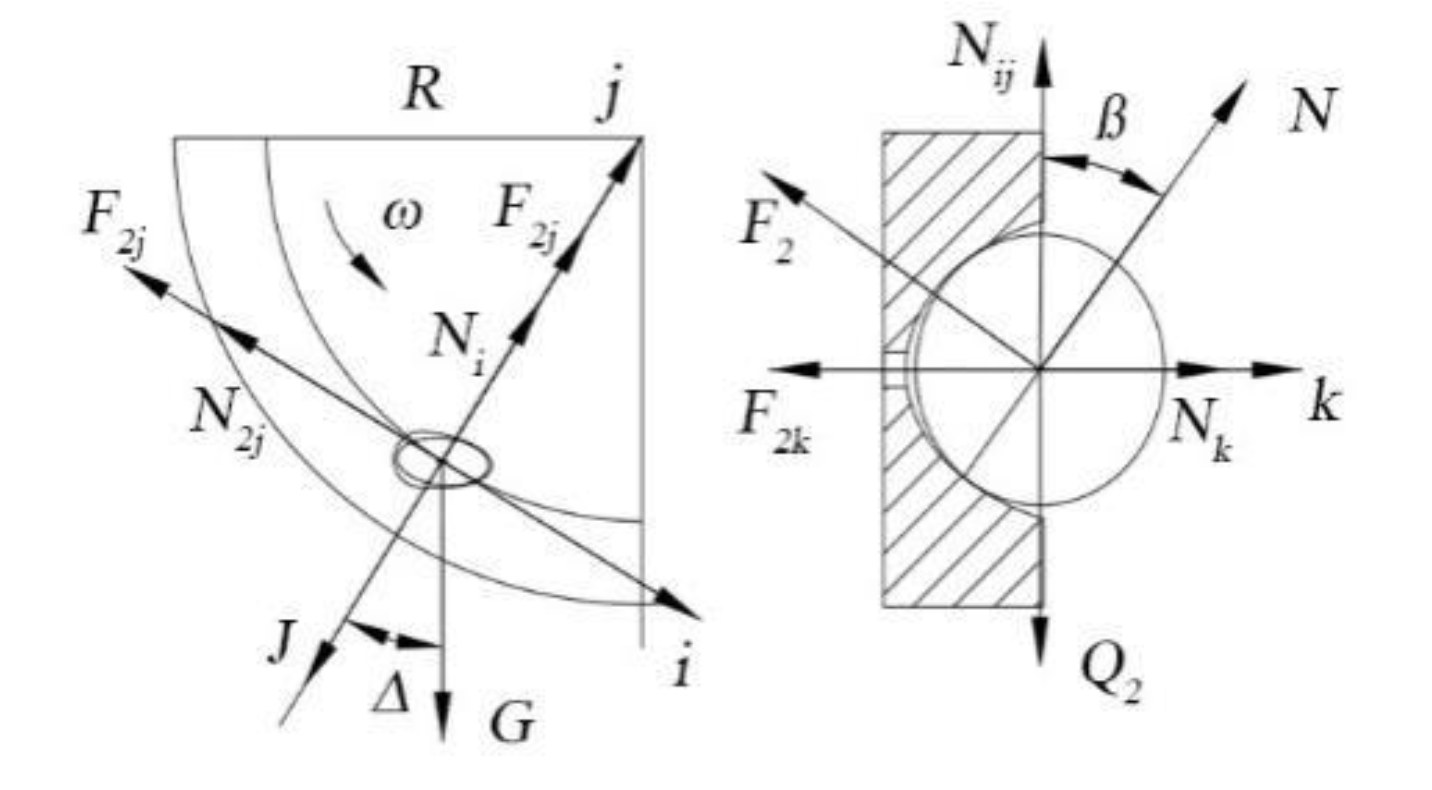
2.3.1. Analysis of the Forces on the Seeds during Suction
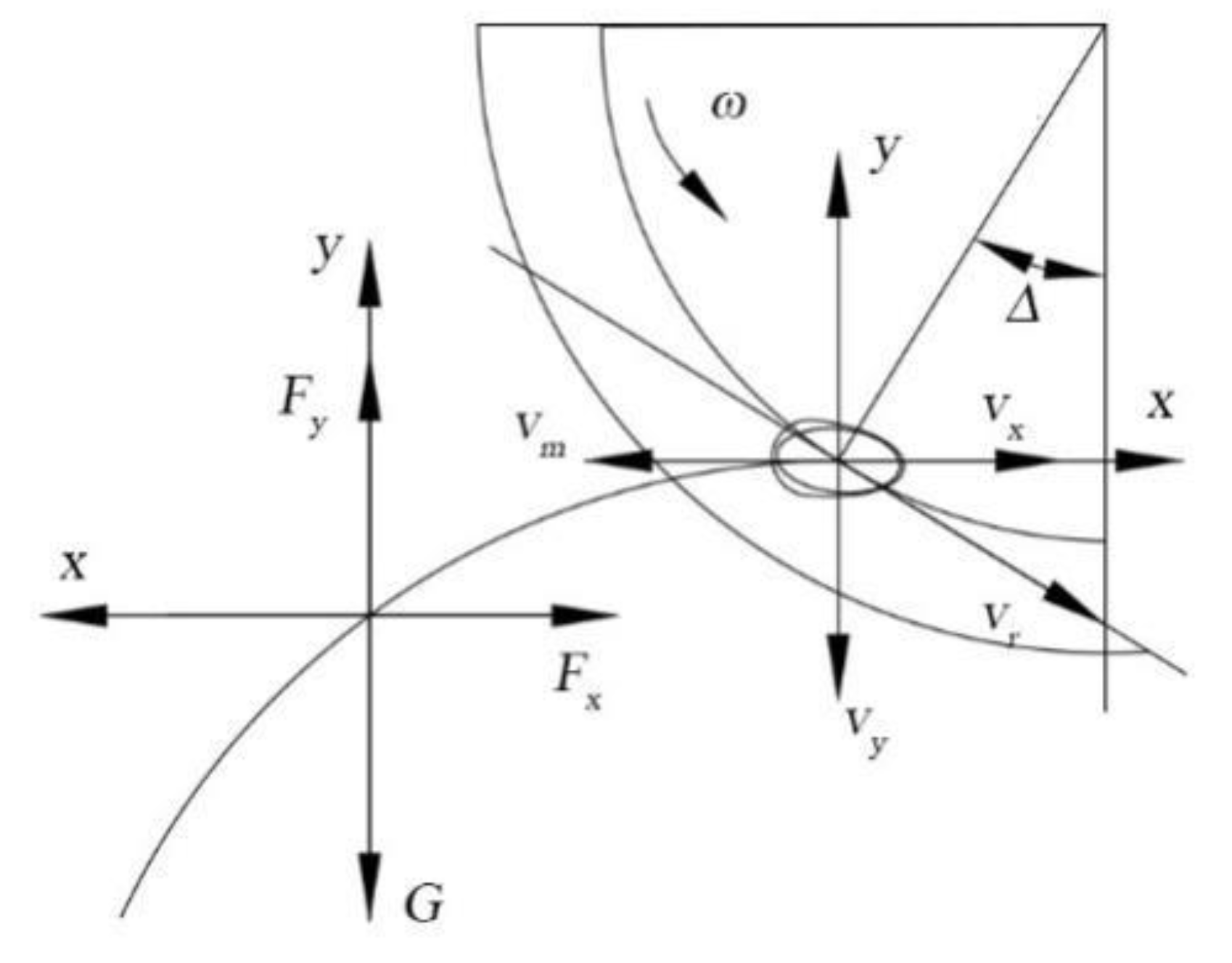
2.3.2. Analysis of the Force and Movement of the Seeds during Seeding
2.4. Seeding Performance Test
2.4.1. Test Equipment and Materials
2.4.2. Test Methods and Evaluation Indicators
2.4.3. Calculation Methods of Evaluation Indicators
3. Results and Discussion
3.1. Test Results
3.2. Mathematical Regression Modeling and Significance Testing
3.2.1. Qualified Index Regression Model
3.2.2. Multiple Index Regression Model
3.2.3. Miss Index Regression Model
3.3. Impact of Factors on Evaluation Indicators
3.3.1. Effect of Factors on the Qualified Index
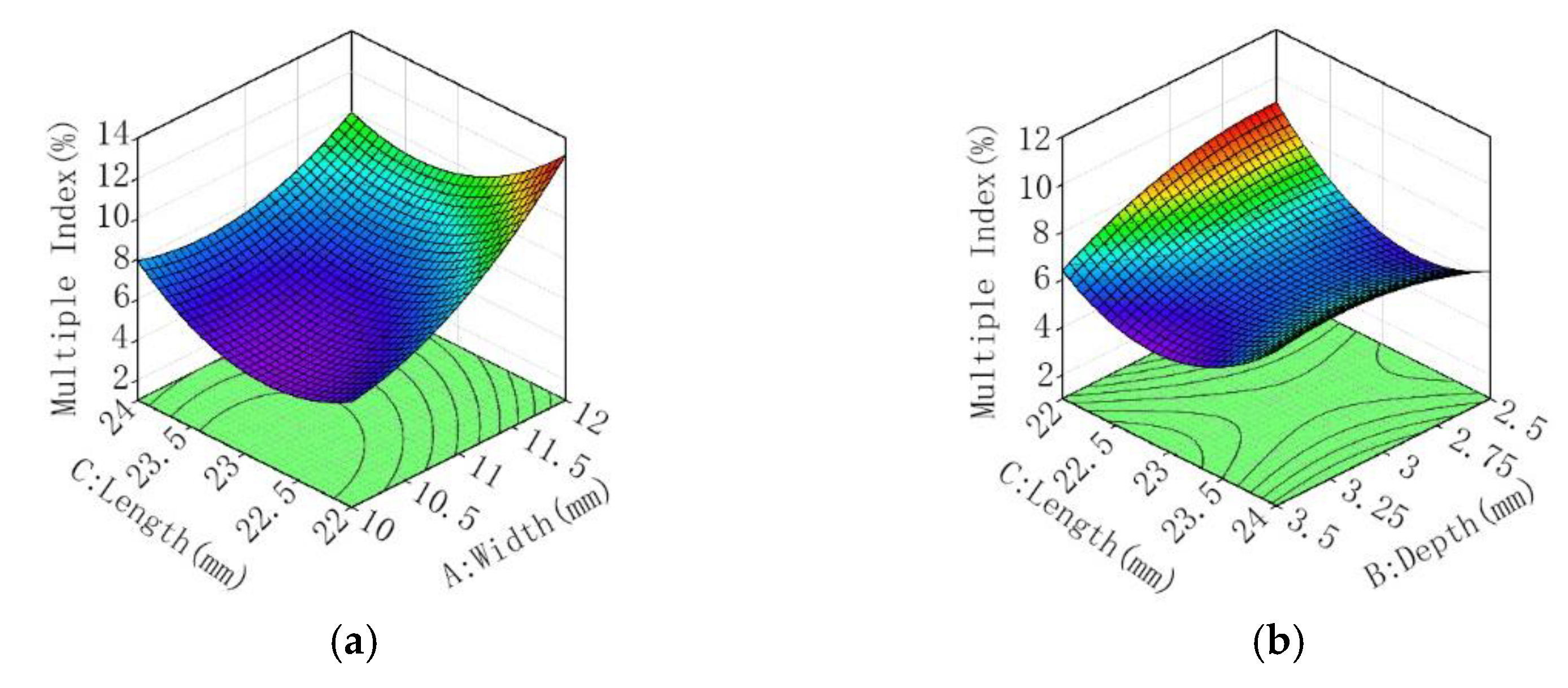
3.3.2. Effect of Factors on the Multiple Index
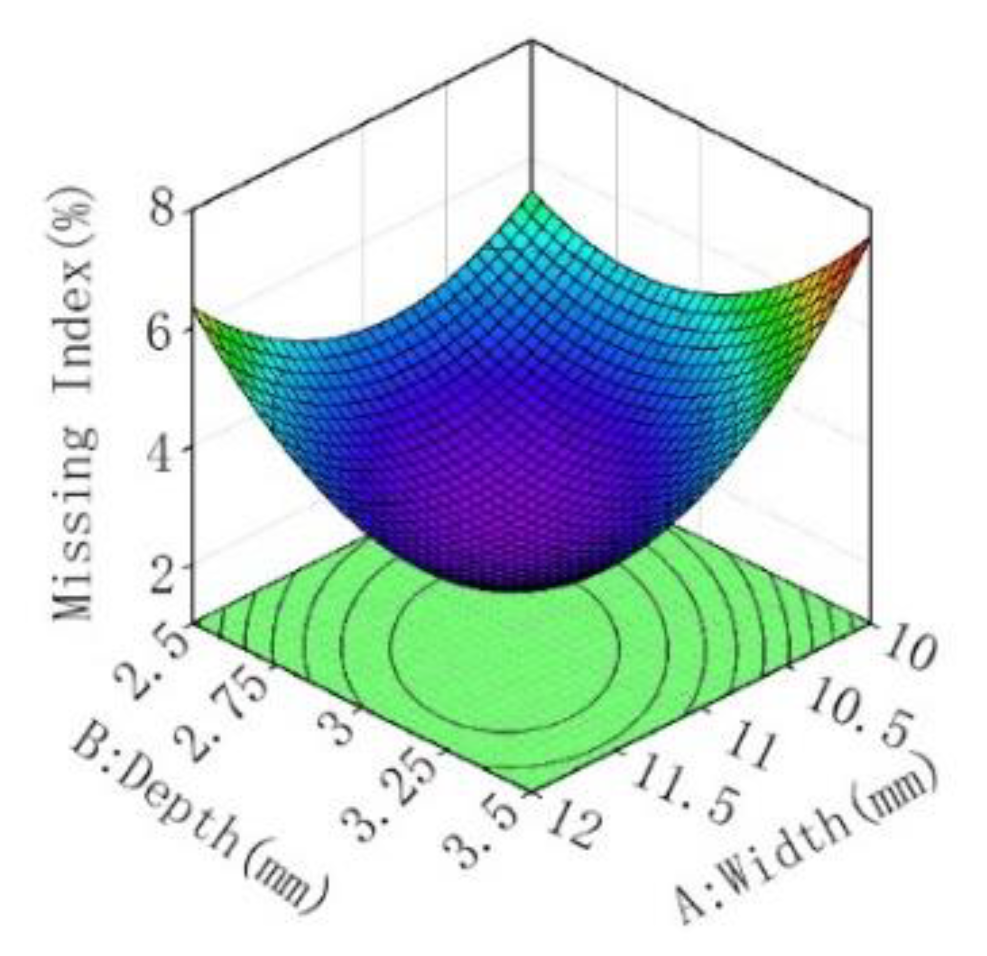
3.3.3. Effect of Factors on the Miss Index
3.4. Optimal Parameter Combinations and Validation Tests
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- United States Government Printing Office. United States Department of Agriculture Agricultural Statistics 1938–2018; United States Government Printing Office: Washingot, DC, USA, 2018.
- Zang, Y.; Zhang, L. The causes of Trade changes of Sunflower products in China—An empirical Analysis based on CMS Model. World Agric. 2020, 7, 53–60+84. [Google Scholar] [CrossRef]
- Li, Y. Investigation on present situation and Forecast of Development Prospect of Sunflower Industry. Agric. Dev. Equip. 2020, 41+44. [Google Scholar]
- Fei, L.; Zhen, L.; Dapeng, L.; Tao, Z. Design optimization and performance test of magnetic pickup finger seed metering device. INMATEH-Agric. Eng. 2021, 63, 137–144. [Google Scholar] [CrossRef]
- Leng, J. Experimental Study on the Performance of Precision Sorghum Seed Platter. Master’s Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2021. [Google Scholar]
- Chen, W.; Zhang, B.; Jiang, L.; Qiu, T.; Wang, L.; Yang, S. Research status and development trend of seed-metering device in China. Am. J. Agric. Res. 2020, 5, 98. [Google Scholar]
- Liao, Q.; Long, X.; Liao, Y.; Ding, Y. Research Progress of Precision Seeding for Rapeseed. Trans. Chin. Soc. Agric. Mach. 2017, 48, 1–16. [Google Scholar] [CrossRef]
- Shang, S.; Wu, X.; Yang, R. Research Status and Prospect of Plot sowing Equipment and Technology. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–20. [Google Scholar]
- Yang, L.; Yan, B.; Zhang, X.; Zhang, T.; Wang, Y.; Cui, T. Research Progress on Precision Planting Technology of Maize. Trans. Chin. Soc. Agric. Mach. 2016, 47, 38–48. [Google Scholar]
- Lai, Q.; Yu, Q.; Su, W.; Sun, K. Design and Experiment of Air-suction Ultra-narrow-rowDevice for Precise Panax notoginseng Seed Metering. Trans. Chin. Soc. Agric. Mach. 2019, 50, 102–112. [Google Scholar]
- Shi, S.; Zhou, J.; Liu, H.; Zhou, H. Design and Experiment of Pneumatic Precision Seed-metering Device with Guided Assistant Seed-filling. Trans. Chin. Soc. Agric. Mach. 2019, 50, 61–70. [Google Scholar]
- LI, Y.; Yang, L.; Zhang, X.; Cui, T.; Ding, L.; Wei, Y. Design and Experiment of Pneumatic Precision Seed-metering Device with Single Seed-metering Plate for Double-row. Trans. Chin. Soc. Agric. Mach. 2019, 50, 61–73. [Google Scholar] [CrossRef]
- Yi, S.; Chen, T.; Li, Y.; Tao, G.; Mao, X. Design and Test of Millet Hill-drop Seed-metering Device withCombination of Positive-negative Pressure and Hole Wheel. Trans. Chin. Soc. Agric. Mach. 2021, 52, 83–94. [Google Scholar] [CrossRef]
- Onal, I.; Degirjviencioglu, A.; Yazgi, A. An evaluation of seed spacing accuracy of a vacuum type precision metering unit based on theoretical considerations and experiments. Turk. J. Agric. For. 2012, 36, 133–144. [Google Scholar]
- Molin, J.P.; Bashford, L.L.; Bargen, K.V.; Leviticus, L.I. Design and evaluation of a punch planter for no-till systems. Trans. ASAE 1998, 41, 307. [Google Scholar] [CrossRef]
- Yazgi, A.; Degirmencioglu, A. Measurement of seed spacing uniformity performance of a precision metering unit as function of the number of holes on vacuum plate. Measurement 2014, 56, 128–135. [Google Scholar] [CrossRef]
- Ahmad, F.; Adeel, M.a.; Qiu, B.; Ma, J. Sowing uniformity of bed-type pneumatic maize planter at various seedbed preparation levels and machine travel speeds. Int. J. Agric. Biol. Eng. 2021, 14, 165–171. [Google Scholar] [CrossRef]
- Han, D.; Zhang, D.; Jing, H.; Yang, L.; Cui, T.; Ding, Y.; Wang, Z.; Wang, Y.; Zhang, T. DEM-CFD coupling simulation and optimization of an inside-filling air-blowing maize precision seed-metering device. Comput. Electron. Agric. 2018, 150, 426–438. [Google Scholar] [CrossRef]
- Junhong, L.; Qinghui, L.; Hui, Z.; Zhaoguo, Z.; Jinwen, Z.; Tiantian, W. Suction force on high-sphericity seeds in an air-suction seed-metering device. Biosyst. Eng. 2021, 211, 125–140. [Google Scholar]
- Wang, Z.; Zhang, X.; Huang, S.; Chen, W.; Li, J. Rice Seeds Feeding Process in Cell Wheel Based on High-speed Photography Technology. Trans. Chin. Soc. Agric. Mach. 2009, 40, 56–61. [Google Scholar]
- Gong, Z.; Chen, J.; Li, Y.; LI, J. Seed Force in Airflow Field of Vacuum Tray Precision Seeder Device during Suction Process of Seeds. Trans. Chin. Soc. Agric. Mach. 2014, 45, 92–97+117. [Google Scholar] [CrossRef]
- Li, F.; Chen, J.; Liu, F.; Liu, Y.; Zhang, T.; Zhao, M. Influence of seed adsorption posture on seeding performance based on high speed camera technology. J. China Agric. Univ. 2018, 23, 128–136. [Google Scholar] [CrossRef]
- Li, F.; Zhao, M.; Liu, F.; Liu, Y.; Zhang, T. Analysis on the Working Process and the Move ment of Seeds of Air Suction Metering Equipment. J. Agric. Mech. Res. 2018, 40, 150–154. [Google Scholar] [CrossRef]
- Ding, L.; Yang, L.; Zhang, X.; Cui, T.; Zhang, K.; Zhong, X. Effect of Seed Adsorption Posture of Corn Air-suction Metering Device on Seed Feeding Performance. Trans. Chin. Soc. Agric. Mach. 2021, 52, 40–50. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Q.; Zhang, Y.; Wang, W.; Yang, Y.; Zhang, L. Design and Experiment of Inclined Parabolic Cell Wheel in Seed Feeding Device for Wheat. Trans. Chin. Soc. Agric. Mach. 2018, 49, 116–124. [Google Scholar] [CrossRef]
- He, R.; Wang, J.; Xu, G.; He, X.; Duan, Q.; Ding, Q. Design and Experiment of Wheat Precisc Seed Metering Apparatuswith Positive and Negative Pressure with the Function of Limiting Seed Filling Posture. Trans. Chin. Soc. Agric. Mach. 2022, 53, 39–49+167. [Google Scholar]
- Lin, P.; Liao, Q.; Wang, L.; Wang, B.; Liu, H. Seed suction performance and experiment of sesame precision hole seeding metering device. J. Huazhong Agric. Univ. 2021, 40, 195–206. [Google Scholar] [CrossRef]
- Li, Z.; Yang, W.; Zhang, T.; Wang, W.; Zhang, S.; Wei, L. Design and suction performance test of sucking-seed plate combined with groove-tooth structure on high speed precision metering device of rapeseed. Trans. Chin. Soc. Agric. Eng. 2019, 35, 12–22. [Google Scholar] [CrossRef]
- Cao, X.; Ma, X.; LI, H. Design and experiments of pneumatic roller type precision seed-metering device for rapeseed plug seedlings. Trans. Chin. Soc. Agric. Eng. 2021, 37, 51–60. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, F.; Zhao, M.; Liu, Y.; Li, F.; Chen, C.; Zhang, Y. Movement law of maize population in seed room of seed metering device based on discrete element method. Trans. Chin. Soc. Agric. Eng. 2016, 32, 27–35. [Google Scholar] [CrossRef]
- Myer Kutz Associates, Inc. Handbook of Farm, Dairy and Food Machinery; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Hanqing, L.; Chunjiang, Z.; Bingxin, Y.; Lin, L.; Zhijun, M. Design and Verification of the Variable Capacity Roller-Wheel Precision Rice Direct Seed-Metering Device. Agronomy 2022, 12, 1798. [Google Scholar]
- Haoyi, W.; Xinping, S.; Hua, L.; Jieyi, F.; Xiaoping, Z.; Youzhi, X.; Yongjian, W.; Huaqing, L.; Zhimin, L. Design and Parameter Optimization of a Finger Clip Plate Garlic Seed-Metering Device Based on EDEM. Agronomy 2022, 12, 1543. [Google Scholar]
- Jian, X.; Junwei, H.; Weibin, W.; Chongyang, H.; Xiaoming, W.; Ting, T.; Shunli, S. Key Structure Design and Experiment of Air-Suction Vegetable Seed-Metering Device. Agronomy 2022, 12, 675. [Google Scholar]


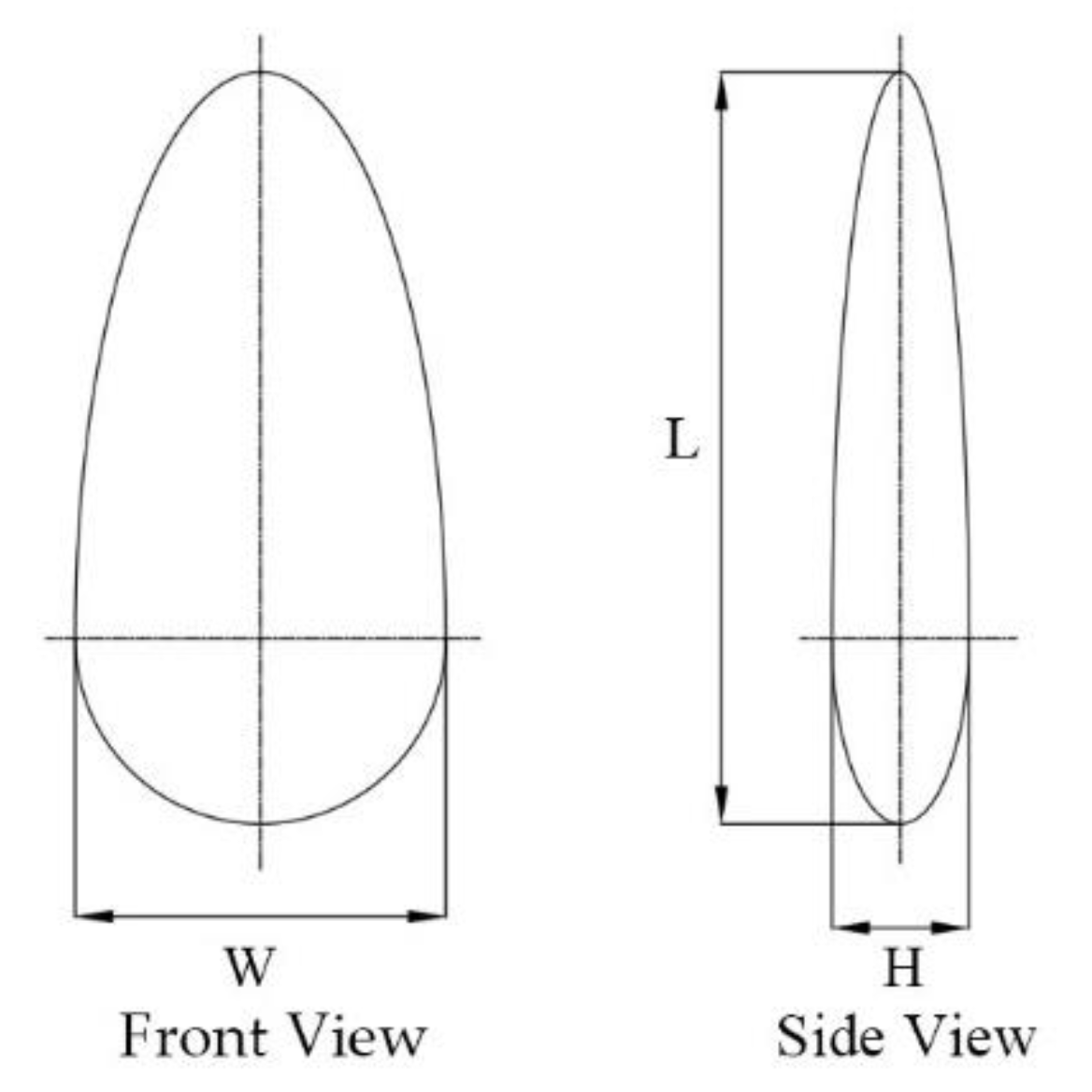

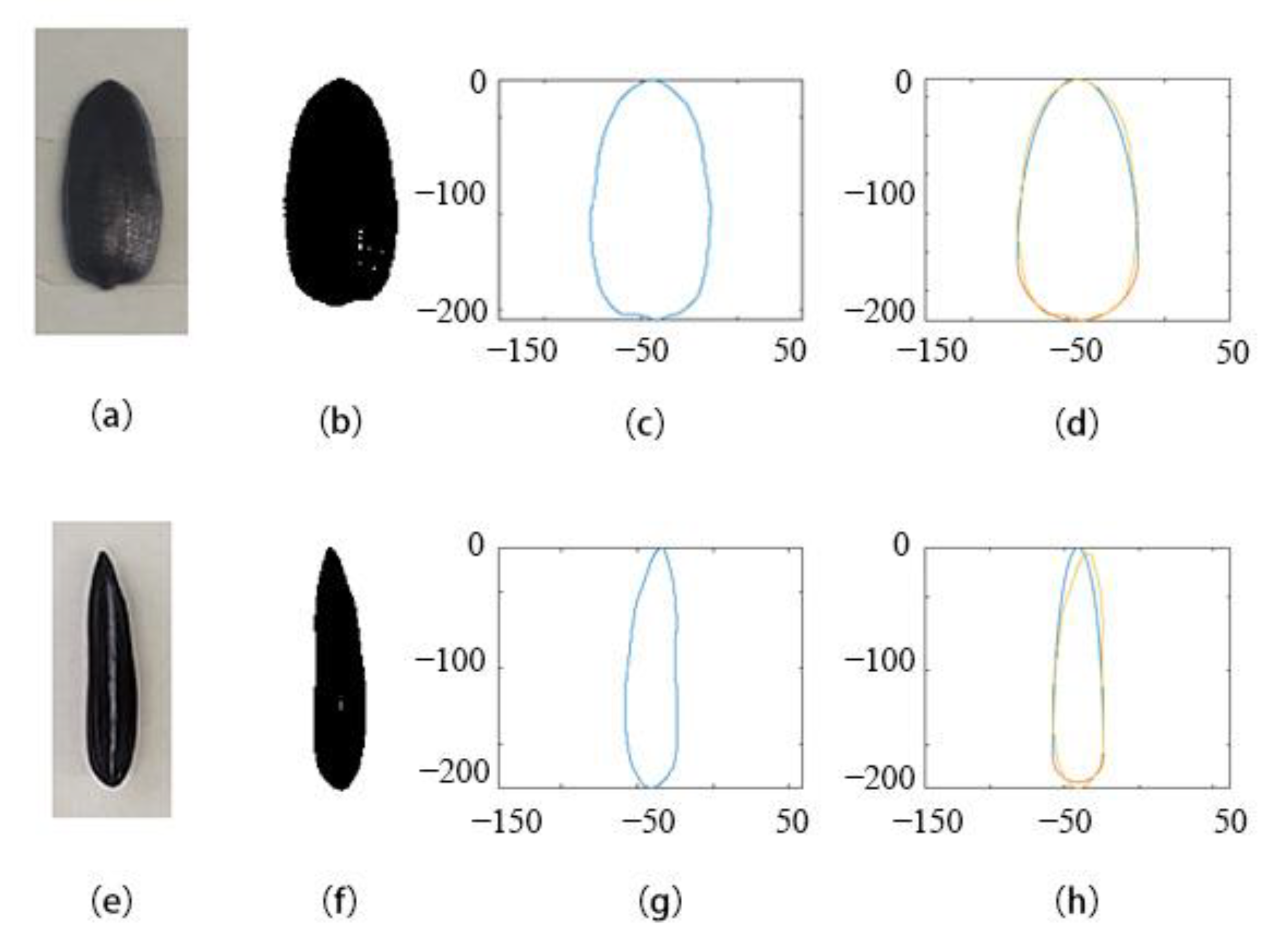

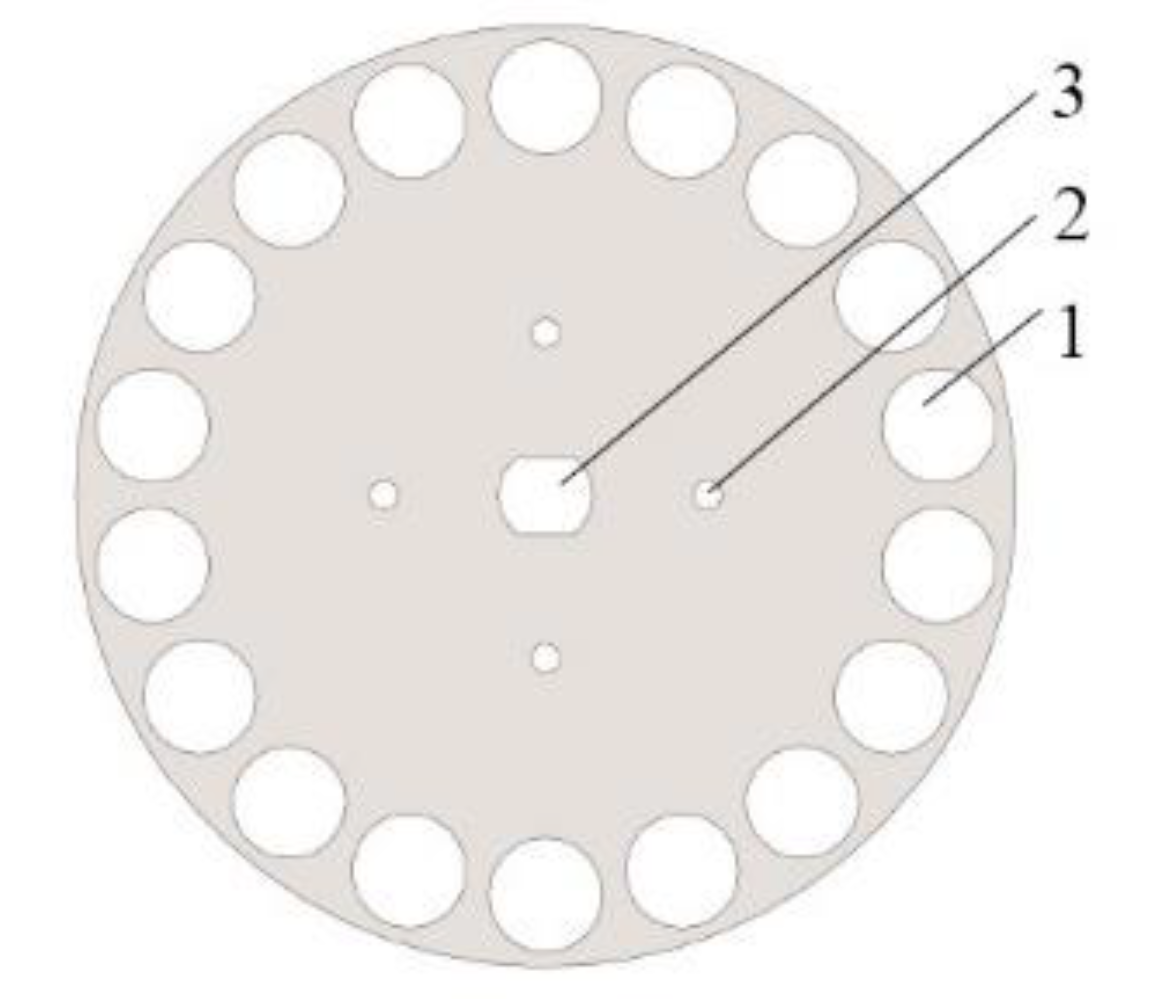
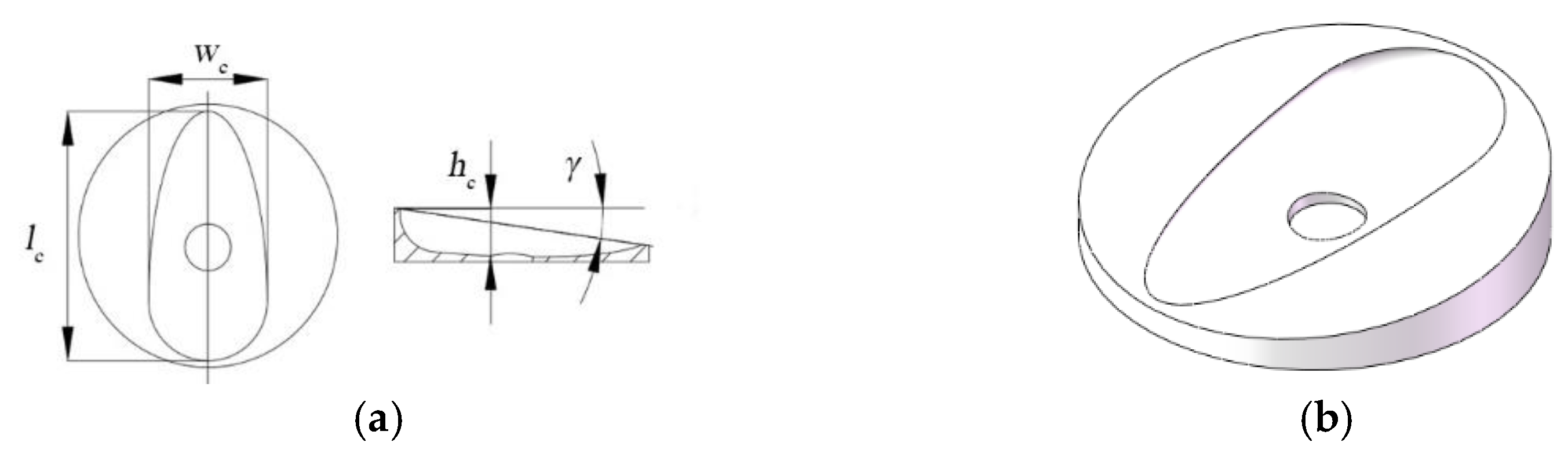



| Arguments | Length (mm) | Width (mm) | Thickness (mm) |
|---|---|---|---|
| Maximum | 20.04 | 9.61 | 5.92 |
| Average value | 16.93 | 7.56 | 4.23 |
| Minimum | 13.32 | 5.42 | 2.56 |
| Coefficient of variation | 7.6% | 10.1% | 15.6% |
| Level Code | Factors | ||
|---|---|---|---|
| Groove Width A/(mm) | Groove Depth B/(mm) | Groove Length C/(mm) | |
| 1 | 10 | 2.5 | 22 |
| 0 | 11 | 3 | 23 |
| −1 | 12 | 3.5 | 24 |
| Test Serial Number | Factors | Evaluation Indicators | ||||
|---|---|---|---|---|---|---|
| A | B | C | Qualified Index Y1 (%) | Multiple Index Y2 (%) | Miss Index Y3 (%) | |
| 1 | 1 | 0 | 1 | 86.38 | 10.82 | 2.80 |
| 2 | 1 | 1 | 0 | 86.92 | 8.30 | 4.78 |
| 3 | 1 | −1 | 0 | 84.16 | 9.38 | 6.46 |
| 4 | 1 | 0 | −1 | 82.43 | 13.55 | 4.02 |
| 5 | −1 | 0 | −1 | 89.94 | 5.40 | 4.66 |
| 6 | 0 | −1 | −1 | 86.34 | 9.15 | 4.51 |
| 7 | 0 | 1 | −1 | 89.61 | 6.60 | 3.79 |
| 8 | −1 | −1 | 0 | 90.35 | 4.58 | 5.07 |
| 9 | −1 | 1 | 0 | 88.42 | 4.19 | 7.39 |
| 10 | 0 | 0 | 0 | 90.35 | 6.55 | 3.10 |
| 11 | 0 | 0 | 0 | 91.44 | 5.48 | 3.08 |
| 12 | 0 | 0 | 0 | 90.74 | 5.85 | 3.41 |
| 13 | 0 | 1 | 1 | 88.27 | 7.28 | 4.45 |
| 14 | −1 | 0 | 1 | 87.06 | 7.50 | 5.44 |
| 15 | 0 | −1 | 1 | 89.79 | 6.13 | 4.08 |
| Evaluation Indicators | Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|---|
| Qualified Index | Model | 92.19 | 9 | 10.24 | 58.05 | 0.0002 | ** |
| A | 31.52 | 1 | 31.52 | 178.63 | <0.0001 | ** | |
| B | 0.832 | 1 | 0.832 | 4.72 | 0.082 | ||
| C | 1.26 | 1 | 1.26 | 7.16 | 0.044 | * | |
| AB | 5.5 | 1 | 5.5 | 31.16 | 0.0025 | ** | |
| AC | 11.66 | 1 | 11.66 | 66.09 | 0.0005 | ** | |
| BC | 5.74 | 1 | 5.74 | 32.51 | 0.0023 | ** | |
| A2 | 27.23 | 1 | 27.23 | 154.28 | <0.0001 | ** | |
| B2 | 1.63 | 1 | 1.63 | 9.26 | 0.0286 | * | |
| C2 | 10.36 | 1 | 10.36 | 58.73 | 0.0006 | ** | |
| Residual | 0.8823 | 5 | 0.1765 | ||||
| Lock of fit | 0.2722 | 3 | 0.0907 | 0.2975 | 0.8286 | ||
| Pure Error | 0.6101 | 2 | 0.305 | ||||
| Cor Total | 93.07 | 14 |
| Evaluation Indicators | Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|---|
| Multiple Index | Model | 86.88 | 9 | 9.65 | 27.18 | 0.001 | ** |
| A | 51.92 | 1 | 51.92 | 146.17 | <0.0001 | ** | |
| B | 1.03 | 1 | 1.03 | 2.9 | 0.1494 | ||
| C | 1.1 | 1 | 1.1 | 3.1 | 0.1384 | ||
| AB | 0.119 | 1 | 0.119 | 0.3351 | 0.5878 | ||
| AC | 5.83 | 1 | 5.83 | 16.42 | 0.0098 | ** | |
| BC | 3.42 | 1 | 3.42 | 9.64 | 0.0267 | * | |
| A2 | 6.63 | 1 | 6.63 | 18.67 | 0.0076 | ** | |
| B2 | 1.75 | 1 | 1.75 | 4.91 | 0.0775 | ||
| C2 | 15.03 | 1 | 15.03 | 42.31 | 0.0013 | ** | |
| Residual | 1.78 | 5 | 0.3552 | ||||
| Lock of fit | 1.19 | 3 | 0.3951 | 1.34 | 0.4547 | ||
| Pure Error | 0.5906 | 2 | 0.2953 | ||||
| Cor Total | 88.65 | 14 |
| Evaluation Indicators | Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|---|
| Miss index | Model | 21.68 | 9 | 2.41 | 15.49 | 0.0038 | ** |
| A | 2.53 | 1 | 2.53 | 16.28 | 0.01 | * | |
| B | 0.0105 | 1 | 0.0105 | 0.0676 | 0.8052 | ||
| C | 0.0055 | 1 | 0.0055 | 0.0354 | 0.8581 | ||
| AB | 4 | 1 | 4 | 25.72 | 0.0039 | ** | |
| AC | 1 | 1 | 1 | 6.43 | 0.0522 | ||
| BC | 0.297 | 1 | 0.297 | 1.91 | 0.2255 | ||
| A2 | 6.99 | 1 | 6.99 | 44.92 | 0.0011 | ** | |
| B2 | 6.76 | 1 | 6.76 | 43.46 | 0.0012 | ** | |
| C2 | 0.4321 | 1 | 0.4321 | 2.78 | 0.1564 | ||
| Residual | 0.7775 | 5 | 0.1555 | ||||
| Lock of fit | 0.7091 | 3 | 0.2364 | 6.9 | 0.1291 | ||
| Pure Error | 0.0685 | 2 | 0.0342 | ||||
| Cor Total | 22.46 | 14 |
| Number | Qualified Index | Multiple Index | Miss Index |
|---|---|---|---|
| 1 | 90.04 | 6.21 | 3.75 |
| 2 | 93.16 | 4.76 | 2.08 |
| 3 | 91.68 | 5.92 | 2.40 |
| Average value | 91.63 | 5.63 | 2.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Zhang, T.; Liu, F.; Li, N.; Li, J. Sunflower Seed Suction Stability Regulation and Seeding Performance Experiments. Agronomy 2023, 13, 54. https://doi.org/10.3390/agronomy13010054
Zhao X, Zhang T, Liu F, Li N, Li J. Sunflower Seed Suction Stability Regulation and Seeding Performance Experiments. Agronomy. 2023; 13(1):54. https://doi.org/10.3390/agronomy13010054
Chicago/Turabian StyleZhao, Xuan, Tao Zhang, Fei Liu, Na Li, and Junru Li. 2023. "Sunflower Seed Suction Stability Regulation and Seeding Performance Experiments" Agronomy 13, no. 1: 54. https://doi.org/10.3390/agronomy13010054






