The Spatial Distribution and Prediction of Soil Heavy Metals Based on Measured Samples and Multi-Spectral Images in Tai Lake of China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Collection and Chemical Analysis
2.2. Image Data Source and Processing
2.3. Model and Method
2.3.1. Selection of Modeling Factors
2.3.2. Model Method
2.3.3. Spatial Interpolation Method
2.3.4. Model Evaluation Method
3. Results and Discussion
3.1. Analysis of Heavy Metal Characteristics
3.2. Determine the Factors of Modeling
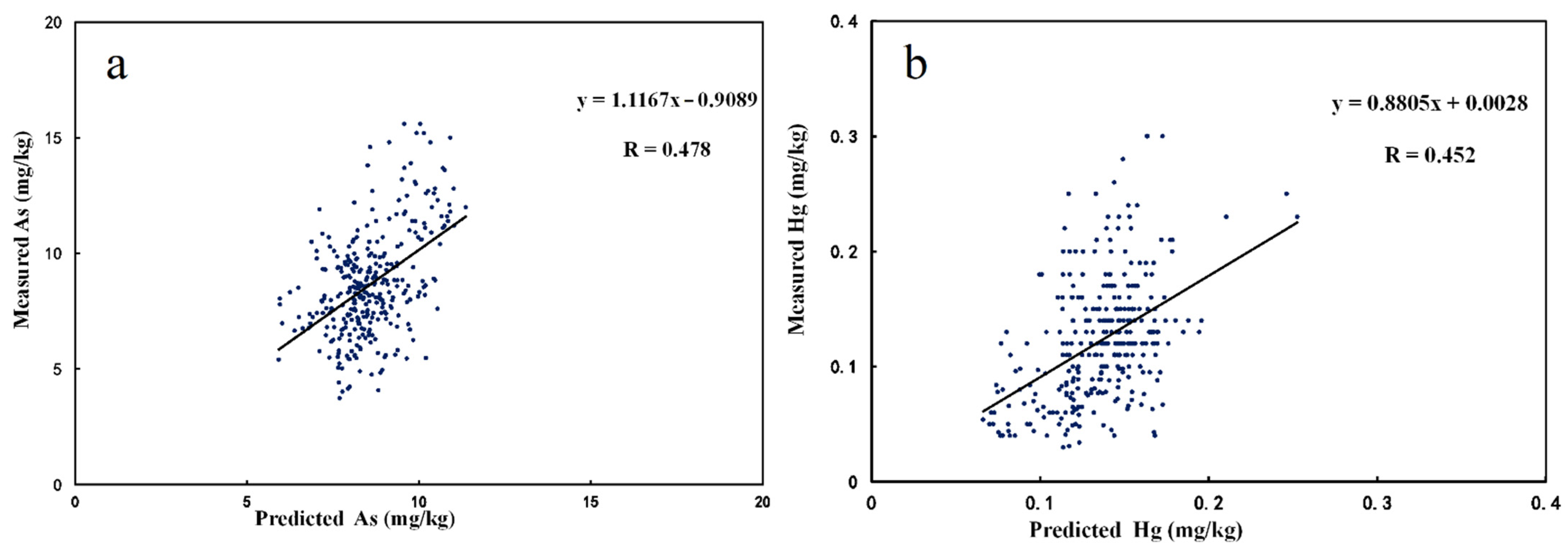
3.3. Model Accuracy Evaluation
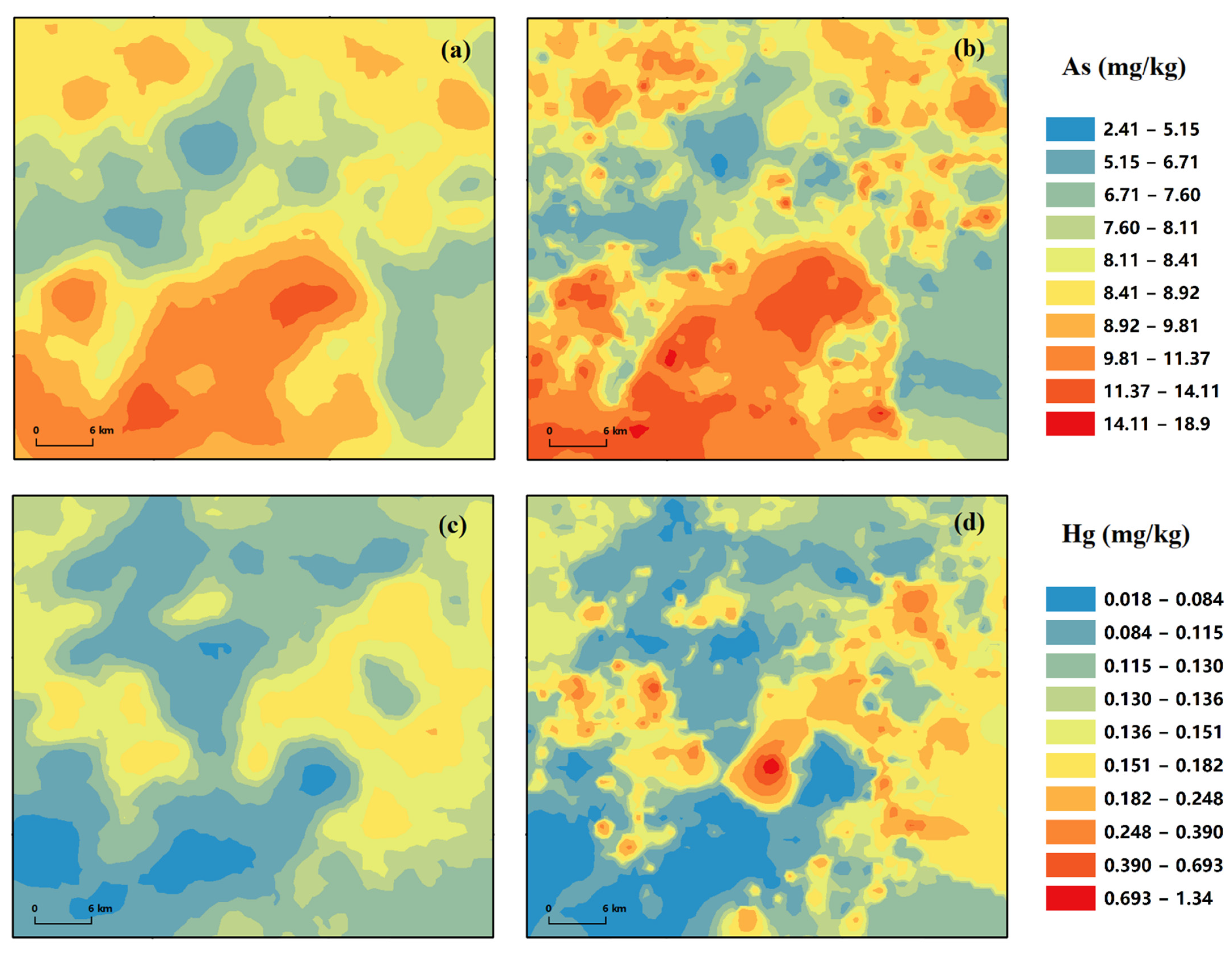
3.4. Spatial Distribution of Heavy Metal Content
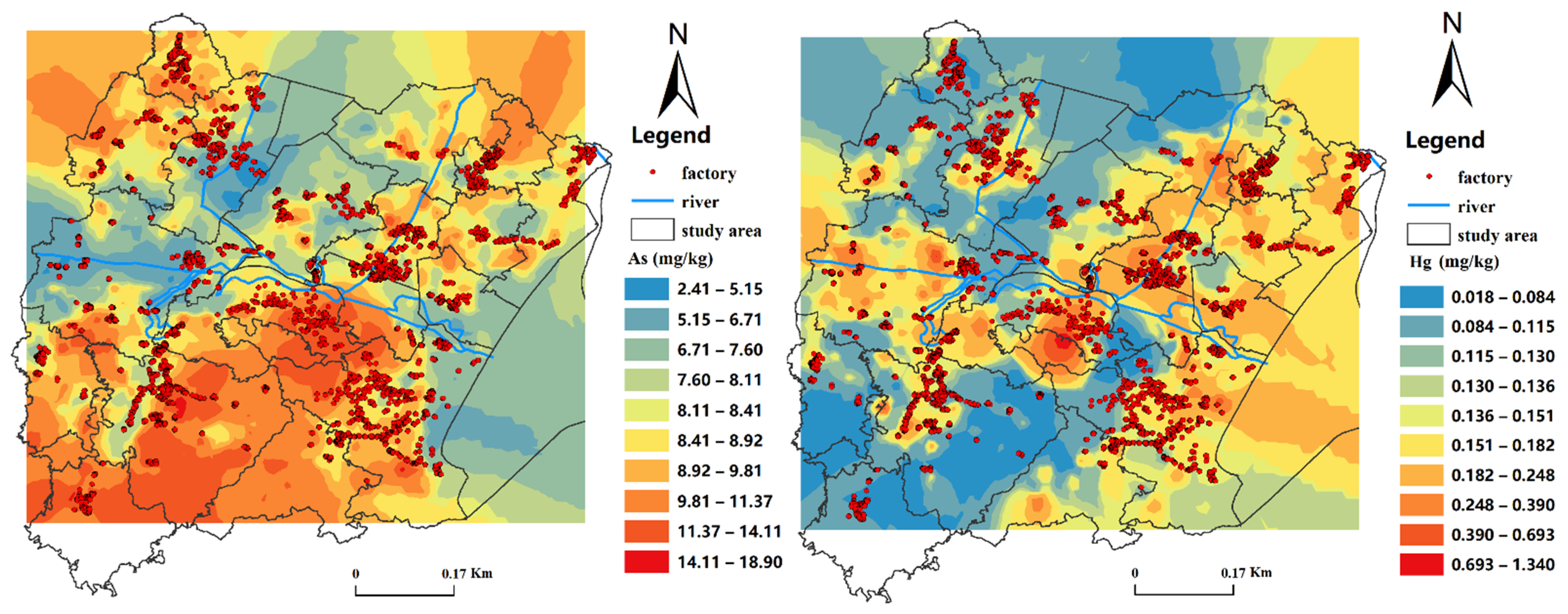
3.5. Relationship between Heavy Metal Agglomerations and Factory Distribution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, X.; Zhao, Y.; Zhao, X.; Wang, Y.; Deng, W. Sources of heavy metal pollution in agricultural soils of a rapidly industrializing area in the Yangtze Delta of China. Ecotoxicol. Environ. 2014, 108, 161–167. [Google Scholar] [CrossRef]
- Yang, Q.; Li, Z.; Lu, X.; Duan, Q.; Huang, L.; Bi, J. A review of soil heavy metal pollution from industrial and agricultural re-gions in China: Pollution and risk assessment. Sci. Total Env. 2018, 642, 690–700. [Google Scholar] [CrossRef] [PubMed]
- Castelli, M.; Rossi, B.; Corsetti, F.; Mantovani, A.; Spera, G.; Lubrano, C.; Silvestroni, L.; Patriarca, M.; Chiodo, F.; Menditto, A. Levels of cadmium and lead in blood: An application of validated methods in a group of patients with endocrine/metabolic disorders from the Rome area. Microchem. J. 2005, 79, 349–355. [Google Scholar] [CrossRef]
- Jiang, H.-H.; Cai, L.-M.; Wen, H.-H.; Hu, G.-C.; Chen, L.-G.; Luo, J. An integrated approach to quantifying ecological and human health risks from different sources of soil heavy metals. Sci. Total Environ. 2020, 701, 134466. [Google Scholar] [CrossRef]
- Durowoju, O.S.; Ekosse, G.-I.E.; Odiyo, J.O. Occurrence and Health-Risk Assessment of Trace Metals in Geothermal Springs within Soutpansberg, Limpopo Province, South Africa. Int. J. Environ. Res. Public Health 2020, 17, 4438. [Google Scholar] [CrossRef]
- Briffa, J.; Sinagra, E.; Blundell, R. Heavy metal pollution in the environment and their toxicological effects on humans. Heliyon 2020, 6, e04691. [Google Scholar] [CrossRef]
- Kemper, T.; Sommer, S. Estimate of Heavy Metal Contamination in Soils after a Mining Accident Using Reflectance Spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef]
- Ge, Y.; Thomasson, J.A.; Sui, R. Remote Sensing of Soil Properties in Precision Agriculture: A Review. Front. Earth Sci. 2006, 5, 229–238. [Google Scholar] [CrossRef]
- Simoniello, T.; Lanfredi, M.; Liberti, M.; Coppola, R.; Macchiato, M. Estimation of vegetation cover resilience from satellite time series. Hydrol. Earth Syst. Sci. 2008, 12, 1053–1064. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Gao, J.; Zha, Y. Hyperspectral sensing of heavy metals in soil and vegetation: Feasibility and challenges. ISPRS J. Photogramm. Remote Sens. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Hou, L.; Li, X.; Li, F. Hyperspectral-based Inversion of Heavy Metal Content in the Soil of Coal Mining Areas. J. Environ. Qual. 2019, 48, 57–63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luce, M.S.; Ziadi, N.; Gagnon, B.; Karam, A. Visible near infrared reflectance spectroscopy prediction of soil heavy metal concentrations in paper mill biosolid- and liming by-product-amended agricultural soils. Geoderma 2017, 288, 23–36. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Chen, J.; Ji, J.; Tian, Q.; Wu, X. Feasibility of Reflectance Spectroscopy for the Assessment of Soil Mercury Contamination. Environ. Sci. Technol. 2005, 39, 873–878. [Google Scholar] [CrossRef]
- Yan, R.; Fang, Z.; Singh, A.; Jun, P.; Sheng, Q.; He, S. Estimation of As and Cu Contamination in Agricultural Soils Around a Mining Area by Reflectance Spectroscopy: A Case Study. Pedosphere 2009, 19, 719–726. [Google Scholar]
- Pyo, J.; Hong, S.; Kwon, Y.; Kim, M.; Cho, K. Estimation of heavy metals using deep neural network with visible and infrared spectroscopy of soil. Sci. Total Environ. 2020, 741, 140162. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Liu, Z.; Hu, Y.; Shi, Z.; Pan, Y.; Wang, L.; Wang, G. Integrating a Hybrid Back Propagation Neural Network and Particle Swarm Optimization for Estimating Soil Heavy Metal Contents Using Hyperspectral Data. Sustainability 2019, 11, 419. [Google Scholar] [CrossRef] [Green Version]
- Choe, E.; Kim, K.-W.; Bang, S.; Yoon, I.-H.; Lee, K.-Y. Qualitative analysis and mapping of heavy metals in an abandoned Au–Ag mine area using NIR spectroscopy. Environ. Earth Sci. 2009, 58, 477–482. [Google Scholar] [CrossRef]
- Shi, J.; Wang, H.; Xu, J.; Wu, J.; Liu, X.; Zhu, H.; Yu, C. Spatial distribution of heavy metals in soils: A case study of Chang-xing, China. Environ. Geol. 2007, 52, 1–10. [Google Scholar] [CrossRef]
- Rogozan, G.C.; Micle, V.; Sur, I.M. Maps of Heavy Metals in CLUJ Country Soils Developed using the research-kringing method. Env. Eng. Manag. J. 2016, 15, 1035–1039. [Google Scholar] [CrossRef]
- Sur, I.M.; Micle, V.; Avram, S.; Marin, Ş.; Oros, V. Bioleaching of some Heavy Metals from Polluted soils. Env. Eng. Manag. J. 2012, 11, 1389–1393. [Google Scholar] [CrossRef]
- Mouazen, A.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Hou, Y.X.; Zhao, H.F.; Zhang, Z.; Wu, K.N. A novel method for predicting cadmium concentration in rice grain using genetic algorithm and back-propagation neural network based on soil properties. Environ. Sci. Pollut. Res. 2018, 25, 35682–35692. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, Y.-M.; Zhou, W.; Liu, Z.-H.; Pan, Y.-C.; Shi, Z.; Wang, L.; Wang, G.-X. Estimation Methods for Soil Mercury Content Using Hyperspectral Remote Sensing. Sustainability 2018, 10, 2474. [Google Scholar] [CrossRef] [Green Version]
- D’Emilio, M.; Macchiato, M.; Ragosta, M.; Simoniello, T. A method for the integration of satellite vegetation activities observtions and magnetic susceptibility measurements for monitoring heavy metals in soil. J. Hazard. Mater. 2012, 242, 118–126. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, J.; Zhao, N. Band selection method for retrieving soil lead content with hyperspectral remote sensing data. Remote Sens. 2010, 7831, 78311. [Google Scholar] [CrossRef]
- Zhou, Z.H. Neural Network and Its Application; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geo-Statistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Hodam, S.; Sarkar, S.; Marak, A.G.R.; Bandyopadhyay, A.; Bhadra, A. Spatial Interpolation of Reference Evapotranspiration in India: Comparison of IDW and Kriging Methods. J. Inst. Eng. Ser. A 2017, 98, 511–524. [Google Scholar] [CrossRef]
- Zhou, H.; Deng, Z.; Xia, Y.; Fu, M. A new sampling method in particle filter based on Pearson correlation coefficient. Neurocomputing 2016, 216, 208–215. [Google Scholar] [CrossRef]
- Mee, C. Soil Environmental Quality Risk Control Standard for Soil Contamination of Development Land. GB 15618-2018. 22 June 2018. Available online: https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/trhj/201807/t20180703_446027.shtml (accessed on 7 November 2021).

| Element | Cd | Hg | As | Pb | Cu | Zn |
|---|---|---|---|---|---|---|
| Maximum | 3.450 | 1.340 | 18.900 | 146.000 | 593.000 | 582.000 |
| Minimum | 0.028 | 0.018 | 2.410 | 21.100 | 14.400 | 37.500 |
| Mean | 0.216 | 0.132 | 8.625 | 28.003 | 29.348 | 72.574 |
| Standard deviation | 0.177 | 0.081 | 2.249 | 9.629 | 21.800 | 27.803 |
| Coefficient of variation (%) | 81.9 | 61.3 | 26.0 | 32.1 | 74.2 | 38.3 |
| Background value | 0.13 | 0.29 | 10 | 26.2 | 22.3 | 62.6 |
| Chinese soil criteria | 0.3 | 0.5 | 40 | 80 | 150 | 200 |
| Cd | Hg | As | Pb | Cu | Zn | |
|---|---|---|---|---|---|---|
| B1 | 0.045 | 0.212 ** | −0.370 ** | −0.071 | 0.089 | 0.013 |
| B2 | 0.040 | 0.248 ** | −0.385 ** | −0.071 | 0.033 | 0.013 |
| B3 | 0.034 | 0.222 ** | −0.401 ** | −0.085 | 0.013 | 0.014 |
| B4 | 0.046 | 0.228 ** | −0.321 ** | −0.030 | 0.035 | 0.029 |
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B8A | |
|---|---|---|---|---|---|---|---|---|---|
| As | −0.370 ** | −0.385 ** | −0.401 ** | −0.321 ** | −0.245 ** | −0.067 | −0.035 | −0.02 | −0.003 |
| Hg | 0.212 ** | 0.248 ** | 0.222 ** | 0.228 ** | 0.156 ** | 0.057 | 0.053 | 0.057 | 0.055 |
| LnB1 | LnB2 | LnB3 | LnB4 | NDVI | |||||
| As | −0.397 ** | −0.430 ** | −0.431 ** | −0.342 ** | −0.127 ** | ||||
| Hg | 0.222 ** | 0.254 ** | 0.231 ** | 0.234 ** | 0.128 ** | ||||
| Modeling Factors | Modeling Set | Verification Set | |||
|---|---|---|---|---|---|
| R | RMSE | R | RMSE | ||
| As | B1–B4 | 0.431 | 1.976 | 0.502 | 2.045 |
| B1–B4 & NDVI | 0.432 | 1.976 | 0.498 | 2.048 | |
| LnB1–LnB4 | 0.460 | 1.945 | 0.524 | 2.009 | |
| LnB1–LnB4 & NDVI | 0.462 | 1.943 | 0.526 | 2.007 | |
| B1–B4 & LnB1–LnB4 | 0.446 | 1.961 | 0.536 | 1.999 | |
| Hg | B1–B4 | 0.257 | 0.062 | 0.155 | 0.105 |
| B1–B4 & NDVI | 0.263 | 0.062 | 0.149 | 0.125 | |
| LnB1–LnB4 | 0.259 | 0.062 | 0.155 | 0.191 | |
| LnB1–LnB4 & NDVI | 0.268 | 0.066 | 0.161 | 0.105 | |
| B1–B4 &LnB1–LnB4 | 0.260 | 0.062 | 0.152 | 0.105 | |
| Modeling Factors | Modeling Set | Verification Set | |||
|---|---|---|---|---|---|
| R | RMSE | R | RMSE | ||
| As | B1–B4 | 0.530 | 1.860 | 0.507 | 2.048 |
| B1–B4 & NDVI | 0.513 | 1.865 | 0.532 | 1.999 | |
| LnB1–LnB4 | 0.519 | 1.874 | 0.467 | 2.097 | |
| LnB1–LnB4 & NDVI | 0.482 | 1.870 | 0.499 | 2.054 | |
| B1–B4 & LnB1–LnB4 | 0.497 | 1.909 | 0.525 | 2.006 | |
| Hg | B1–B4 | 0.273 | 0.062 | 0.149 | 0.105 |
| B1–B4 & NDVI | 0.318 | 0.062 | 0.177 | 0.105 | |
| LnB1–LnB4 | 0.263 | 0.061 | 0.163 | 0.105 | |
| LnB1–LnB4 & NDVI | 0.269 | 0.062 | 0.156 | 0.288 | |
| B1–B4 & LnB1–LnB4 | 0.292 | 0.061 | 0.186 | 0.105 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Liu, P.; Qiao, B.; Wu, K. The Spatial Distribution and Prediction of Soil Heavy Metals Based on Measured Samples and Multi-Spectral Images in Tai Lake of China. Land 2021, 10, 1227. https://doi.org/10.3390/land10111227
Zhao H, Liu P, Qiao B, Wu K. The Spatial Distribution and Prediction of Soil Heavy Metals Based on Measured Samples and Multi-Spectral Images in Tai Lake of China. Land. 2021; 10(11):1227. https://doi.org/10.3390/land10111227
Chicago/Turabian StyleZhao, Huihui, Peijia Liu, Baojin Qiao, and Kening Wu. 2021. "The Spatial Distribution and Prediction of Soil Heavy Metals Based on Measured Samples and Multi-Spectral Images in Tai Lake of China" Land 10, no. 11: 1227. https://doi.org/10.3390/land10111227








