Urban Growth Simulation Based on a Multi-Dimension Classification of Growth Types: Implications for China’s Territory Spatial Planning
Abstract
:1. Introduction
2. Literature Review
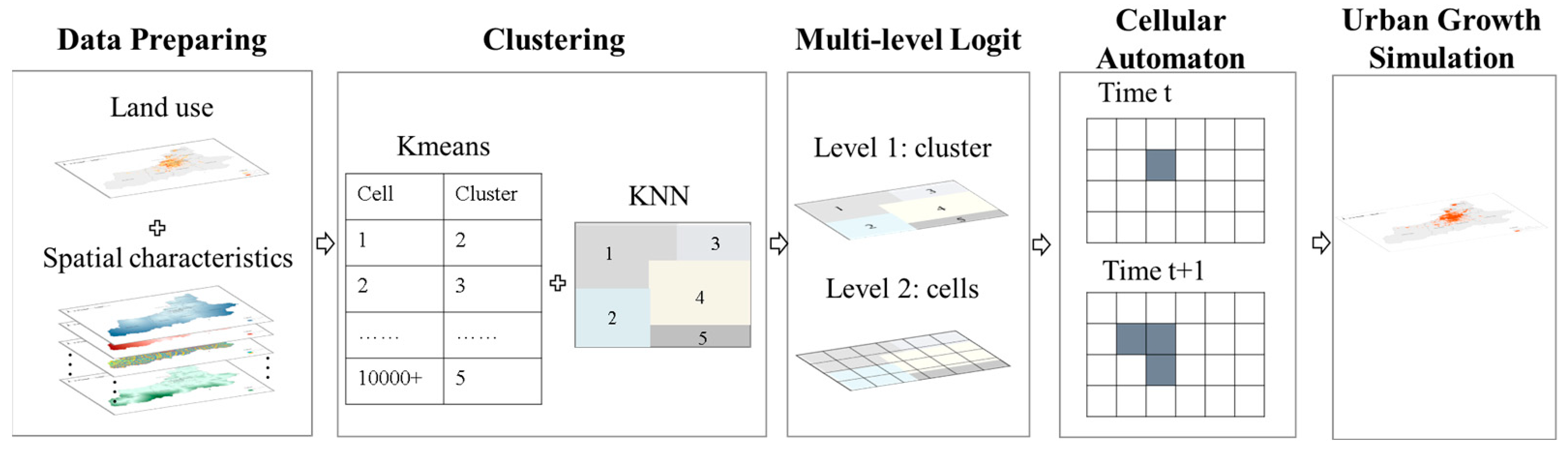
3. Method Design
3.1. Study Area
3.2. Data Source
4. Results
4.1. Classification Results
4.2. Multilevel Logit Model
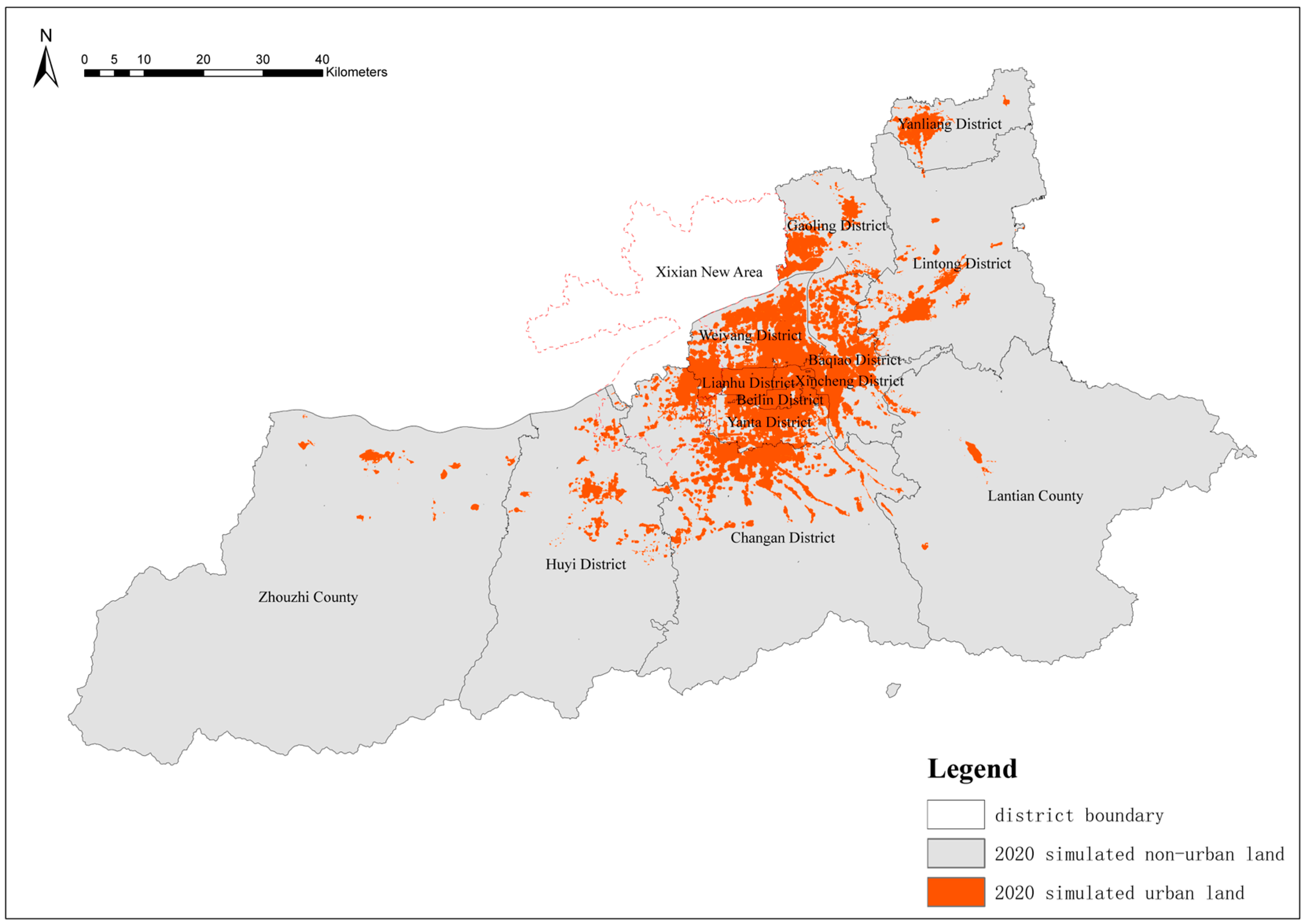
4.3. Urban Growth Simulation in Xi’an
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- United Nations. World Urbanization Prospects: The 2018 Revision; United Nations: New York, NY, USA, 2018. [Google Scholar]
- Seto Karen, C.; Güneralp, B.; Lucy, R.H. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Angel, S.; Parent, J.; Civco, D.L.; Blei, A.; Potere, D. The dimensions of global urban expansion: Estimates and projections for all countries, 2000–2050. Prog. Plan. 2011, 75, 53–107. [Google Scholar] [CrossRef]
- Aldalbahi, M.; Walker, G. Attitudes and policy implications of urban growth boundary and traffic congestion reduction in Riyadh, Saudi Arabia. In Proceedings of the International Conference Data Mining, Atlantic City, NJ, USA, 14–17 November 2015. [Google Scholar]
- McDonald, R.I.; Green, P.; Balk, D.; Fekete, B.M.; Revenga, C.; Todd, M.; Montgomery, M. Urban growth, climate change, and freshwater availability. Proc. Natl. Acad. Sci. USA 2011, 108, 6312–6317. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dinka, M.O.; Klik, A. Effect of land use–land cover change on the regimes of surface runoff—The case of Lake Basaka catchment (Ethiopia). Environ. Monit. Assess. 2019, 191, 278. [Google Scholar] [CrossRef] [PubMed]
- Guzha, A.C.; Rufino, M.; Okoth, S.; Jacobs, S.; Nóbrega, R. Impacts of land use and land cover change on surface runoff, discharge and low flows: Evidence from East Africa. J. Hydrol. Reg. Stud. 2018, 15, 49–67. [Google Scholar] [CrossRef]
- Ewing, R.; Lyons, T.; Siddiq, F.; Sabouri, S.; Kiani, F.; Hamidi, S.; Choi, D.-A.; Ameli, H. Growth Management Effectiveness: A Literature Review. J. Plan. Lit. 2022, 37, 08854122221077457. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, F. Regional and urban planning for growth in China. In International Encyclopedia of Geography: People, the Earth, Environment and Technology; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2020; pp. 1–8. [Google Scholar]
- American Planning Association. Growing Smart Guidebook. Chapter 6—Regional Planning; American Planning Association: Washington, DC, USA, 2002. [Google Scholar]
- Pacione, M. Urban Geography From Global to Local. In Urban Geography: A Global Perspective; Routledge: London, UK, 2009; pp. 1–15. [Google Scholar]
- Strano, E.; Viana, M.; da Fontoura Costa, L.; Cardillo, A.; Porta, S.; Latora, V. Urban Street Networks, a Comparative Analysis of Ten European Cities. Environ. Plan. B Plan. Des. 2013, 40, 1071–1086. [Google Scholar] [CrossRef] [Green Version]
- Dibble, J.; Prelorendjos, A.; Romice, O.; Zanella, M.; Strano, E.; Pagel, M.; Porta, S. On the origin of spaces: Morphometric foundations of urban form evolution. Environ. Plan. B Urban Anal. City Sci. 2017, 46, 707–730. [Google Scholar] [CrossRef] [Green Version]
- Salvati, L.; Carlucci, M. Land-use structure, urban growth, and periurban landscape: A multivariate classification of the European cities. Environ. Plan. B Plan. Des. 2015, 42, 801–829. [Google Scholar] [CrossRef]
- Nelson, A.C.; Moore, T. Assessing urban growth management: The case of Portland, Oregon, the USA’s largest urban growth boundary. Land Use Policy 1993, 10, 293–302. [Google Scholar] [CrossRef]
- Nelson, A.C.; Duncan, J.A.B. Growth Management Principles and Practices; Planners Press: Chicago, IL, USA, 1995. [Google Scholar]
- Tayyebi, A.; Pijanowski, B.C.; Tayyebi, A.H. An urban growth boundary model using neural networks, GIS and radial parameterization: An application to Tehran, Iran. Landsc. Urban Plan. 2011, 100, 35–44. [Google Scholar] [CrossRef]
- Mubarak, F.A. Urban growth boundary policy and residential suburbanization: Riyadh, Saudi Arabia. Habitat Int. 2004, 28, 567–591. [Google Scholar] [CrossRef]
- Ding, C.; Knaap, G.J.; Hopkins, L.D. Managing urban growth with urban growth boundaries: A theoretical analysis. J. Urban Econ. 1999, 46, 53–68. [Google Scholar] [CrossRef]
- Venkataraman, M. Analyzing Urban Growth Boundary Effects in the City of Bengaluru. ERN Urban Rural. Anal. Dev. Econ. (Top.) 2014, 49, 54–61. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, X.; Zhu, Y. A Study on Urban Growth Boundary Delimitation: The Case of Baoji, Weinan and Ankang Urban Master Plan. Open Cybern. Syst. J. 2015, 9, 1710–1715. [Google Scholar]
- Santé, I.; García, A.M.; Miranda, D.; Crecente, R. Cellular automata models for the simulation of real-world urban processes: A review and analysis. Landsc. Urban Plan. 2010, 96, 108–122. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Shi, X.; Zhang, X.; Chen, Y. Simulating land-use dynamics under planning policies by integrating artificial immune systems with cellular automata. Int. J. Geogr. Inf. Sci. 2010, 24, 783–802. [Google Scholar] [CrossRef]
- Cheng, J.; Masser, I. Understanding spatial and temporal processes of urban growth: Cellular automata modelling. Environ. Plan. B Plan. Des. 2004, 31, 167–194. [Google Scholar] [CrossRef]
- Yang, X.; Chen, R.; Zheng, X.Q. Simulating land use change by integrating ANN-CA model and landscape pattern indices. Geomat. Nat. Hazards Risk 2016, 7, 918–932. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Silva, E.A.; Clarke, K.C. Calibration of the SLEUTH urban growth model for Lisbon and Porto, Portugal. Comput. Environ. Urban Syst. 2002, 26, 525–552. [Google Scholar] [CrossRef]
- Osman, T.; Divigalpitiya, P.; Arima, T. Using the SLEUTH urban growth model to simulate the impacts of future policy scenarios on land use in the Giza Governorate, Greater Cairo Metropolitan region. Int. J. Urban Sci. 2016, 20, 407–426. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G.-O. Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 2002, 16, 323–343. [Google Scholar] [CrossRef]
- Liu, Y.; He, Q.; Tan, R.; Liu, Y.; Yin, C. Modeling different urban growth patterns based on the evolution of urban form: A case study from Huangpi, Central China. Appl. Geogr. 2016, 66, 109–118. [Google Scholar] [CrossRef]
- Müller, K.; Steinmeier, C.; Küchler, M. Urban growth along motorways in Switzerland. Landsc. Urban Plan. 2010, 98, 3–12. [Google Scholar] [CrossRef]
- He, Q.; Tan, R.; Gao, Y.; Zhang, M.; Xie, P.; Liu, Y. Modeling urban growth boundary based on the evaluation of the extension potential: A case study of Wuhan city in China. Habitat Int. 2018, 72, 57–65. [Google Scholar] [CrossRef]
- Wu, K.-Y.; Zhang, H. Land use dynamics, built-up land expansion patterns, and driving forces analysis of the fast-growing Hangzhou metropolitan area, eastern China (1978–2008). Appl. Geogr. 2012, 34, 137–145. [Google Scholar] [CrossRef]
- Sunde, M.G.; He, H.S.; Zhou, B.; Hubbart, J.A.; Spicci, A. Imperviousness Change Analysis Tool (I-CAT) for simulating pixel-level urban growth. Landsc. Urban Plan. 2014, 124, 104–108. [Google Scholar] [CrossRef]
- World Bank; Development Research Center of the State Council, The People’s Republic of China. China’s Urbanization and Land: A Framework for Reform; World Bank: Washington, DC, USA, 2014. [Google Scholar]
- Ke, X.; Qi, L.; Zeng, C. A partitioned and asynchronous cellular automata model for urban growth simulation. Int. J. Geogr. Inf. Sci. 2016, 30, 637–659. [Google Scholar] [CrossRef]
- Shu, B.; Bakker, M.M.; Zhang, H.; Li, Y.; Qin, W.; Carsjens, G.J. Modeling urban expansion by using variable weights logistic cellular automata: A case study of Nanjing, China. Int. J. Geogr. Inf. Sci. 2017, 31, 1314–1333. [Google Scholar] [CrossRef]
- Liang, X.; Liu, X.; Chen, G.; Leng, J.; Wen, Y.; Chen, G. Coupling fuzzy clustering and cellular automata based on local maxima of development potential to model urban emergence and expansion in economic development zones. Int. J. Geogr. Inf. Sci. 2020, 34, 1930–1952. [Google Scholar] [CrossRef]
- Sapena, M.; Fernández, L.Á.R. Identifying urban growth patterns through land-use/land-cover spatio-temporal metrics: Simulation and analysis. Int. J. Geogr. Inf. Sci. 2021, 35, 375–396. [Google Scholar] [CrossRef]
- Aithal, B.H.; Ramachandra, T.V. Visualization of Urban Growth Pattern in Chennai Using Geoinformatics and Spatial Metrics. J. Indian Soc. Remote Sens. 2016, 44, 617–633. [Google Scholar] [CrossRef]
- Sun, C.; Wu, Z.-F.; Lv, Z.-Q.; Yao, N.; Wei, J.-B. Quantifying different types of urban growth and the change dynamic in Guangzhou using multi-temporal remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 409–417. [Google Scholar] [CrossRef]
- Liu, X.; Ma, L.; Li, X.; Ai, B.; Li, S.; He, Z. Simulating urban growth by integrating landscape expansion index (LEI) and cellular automata. Int. J. Geogr. Inf. Sci. 2014, 28, 148–163. [Google Scholar] [CrossRef]
- Brueckner, J.K. Urban Sprawl: Diagnosis and Remedies. Int. Reg. Sci. Rev. 2000, 23, 160–171. [Google Scholar] [CrossRef]
- Seto, K.C.; Fragkias, M.; Güneralp, B.; Reilly, M.K. A meta-analysis of global urban land expansion. PLoS ONE 2011, 6, e23777. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Han, Y.; Pu, L.; Jiang, B.; Yuan, S.; Xu, Y. A Novel Model for Detecting Urban Fringe and Its Expanding Patterns: An Application in Harbin City, China. Land 2021, 10, 876. [Google Scholar] [CrossRef]
- Nong, Y.; Du, Q. Urban growth pattern modeling using logistic regression. Geo-Spat. Inf. Sci. 2011, 14, 62–67. [Google Scholar] [CrossRef]
- Dubovyk, O.; Sliuzas, R.; Flacke, J. Spatio-temporal modelling of informal settlement development in Sancaktepe district, Istanbul, Turkey. ISPRS J. Photogramm. Remote Sens. 2011, 66, 235–246. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z. Forty years of urban expansion in Beijing: What is the relative importance of physical, socioeconomic, and neighborhood factors? Appl. Geogr. 2013, 38, 1–10. [Google Scholar] [CrossRef]
- Tombolini, I.; Zambon, I.; Ippolito, A.; Grigoriadis, S.; Serra, P.; Salvati, L. Revisiting “Southern” Sprawl: Urban Growth, Socio-Spatial Structure and the Influence of Local Economic Contexts. Economies 2015, 3, 237–259. [Google Scholar] [CrossRef] [Green Version]
- Shu, B.; Zhang, H.; Li, Y.; Qu, Y.; Chen, L. Spatiotemporal variation analysis of driving forces of urban land spatial expansion using logistic regression: A case study of port towns in Taicang City, China. Habitat Int. 2014, 43, 181–190. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. Use of impervious surface in urban land-use classification. Remote Sens. Environ. 2006, 102, 146–160. [Google Scholar] [CrossRef]
- Dadhich, P.N.; Hanaoka, S. Spatio-temporal Urban Growth Modeling of Jaipur, India. J. Urban Technol. 2011, 18, 45–65. [Google Scholar] [CrossRef]
- Tian, G.; Jiang, J.; Yang, Z.; Zhang, Y. The urban growth, size distribution and spatio-temporal dynamic pattern of the Yangtze River Delta megalopolitan region, China. Ecol. Model. 2011, 222, 865–878. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Lu, G.; Liu, J.; Qin, C.-Z.; Zhou, C. Spatial prediction based on Third Law of Geography. Ann. GIS 2018, 24, 225–240. [Google Scholar] [CrossRef]
- Bárcena, J.F.; Camus, P.; García, A.; Álvarez, C. Selecting model scenarios of real hydrodynamic forcings on mesotidal and macrotidal estuaries influenced by river discharges using K-means clustering. Environ. Model. Softw. 2015, 68, 70–82. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Lin, Z.; Zhang, X.; Zhang, H. The delineation of urban growth boundaries in complex ecological environment areas by using cellular automata and a dual-environmental evaluation. J. Clean. Prod. 2020, 256, 120361. [Google Scholar] [CrossRef]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN Model-Based Approach in Classification. In On The Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Shu, B.; Zhu, S.; Qu, Y.; Zhang, H.; Li, X.; Carsjens, G.J. Modelling multi-regional urban growth with multilevel logistic cellular automata. Comput. Environ. Urban Syst. 2020, 80, 101457. [Google Scholar] [CrossRef]
- Balzter, H. Markov chain models for vegetation dynamics. Ecol. Model. 2000, 126, 139–154. [Google Scholar] [CrossRef]
- Zhou, L.; Dang, X.; Sun, Q.; Wang, S. Multi-scenario simulation of urban land change in Shanghai by random forest and CA-Markov model. Sustain. Cities Soc. 2020, 55, 102045. [Google Scholar] [CrossRef]
- Deng, X.; Bai, X. Sustainable urbanization in western China. Environ. Sci. Policy Sustain. Dev. 2014, 56, 12–24. [Google Scholar] [CrossRef]
- Fu, J.; Jiang, D.; Huang, Y. 1 km grid population dataset of China (2005, 2010). Acta Geogr. Sin. 2014, 69 (Suppl. S1), 41–44. [Google Scholar]
- Bai, X.; Chen, J.; Shi, P. Landscape Urbanization and Economic Growth in China: Positive Feedbacks and Sustainability Dilemmas. Environ. Sci. Technol. 2012, 46, 132–139. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Z.; Xu, X.; Kuang, W.; Zhou, W.; Zhang, S.; Li, R.; Yan, C.; Yu, D.; Wu, S.; et al. Spatial patterns and driving forces of land use change in China during the early 21st century. J. Geogr. Sci. 2010, 20, 483–494. [Google Scholar] [CrossRef]
- Wang, S.; Luo, X. The evolution of government behaviors and urban expansion in Shanghai. Land Use Policy 2022, 114, 105973. [Google Scholar]
- Huang, X.; Wang, H.; Xiao, F. Simulating urban growth affected by national and regional land use policies: Case study from Wuhan, China. Land Use Policy 2022, 112, 105850. [Google Scholar] [CrossRef]
- Bacău, S.; Domingo, D.; Palka, G.; Pellissier, L.; Kienast, F. Integrating strategic planning intentions into land-change simulations: Designing and assessing scenarios for Bucharest. Sustain. Cities Soc. 2022, 76, 103446. [Google Scholar] [CrossRef]
- Lin, J.; Liu, W. Demarcation of Urban Development Boundary. Beijing Plan. Rev. 2014, 6, 14–21. [Google Scholar]




| Type | Data | Units | Year | Data Source and Processing |
|---|---|---|---|---|
| Land use | Land-use cover | / | 2010,2020 | Data from GlobeLand30. 1 for urban area and 0 for non-urban area |
| Natural topography | Slope | Degree | 2020 | Data from digital elevation model provided by Geospatial Data Cloud (https://www.gscloud.cn/home) (accessed on 1 July 2022) |
| Aspect | / | 2020 | ||
| Transportation facilities proximity | Distance to train station | m | 2020 | Data from 1: 1,000,000 public version of basic geographic information data provided by National Catalogue Service for Geographic Information (https://www.webmap.cn) (accessed on 1 July 2022) Proximity was calculated by Euclidean distance in ARC GIS 10.7. |
| Distance to coach station | m | 2020 | ||
| Distance to airport | m | 2020 | ||
| Distance to subway station | m | 2020 | ||
| Distance to city road | m | 2020 | ||
| Distance to railroad | m | 2020 | ||
| Distance to highway | m | 2020 | ||
| Urban facilities proximity | Distance to colleges and universities | m | 2020 | Data from Gaode Open Platform (https://lbs.amap.com/) (accessed on 1 July 2022) Proximity was calculated by Euclidean distance in ARC GIS 10.7. |
| Distance to shopping centers | m | 2020 | ||
| Distance to companies | m | 2020 | ||
| Distance to hospitals | m | 2020 | ||
| Urban structure | Distance to local government agencies | m | 2020 | Data from Gaode Open Platform (https://lbs.amap.com/) (accessed on 1 July 2022) Proximity was calculated by Euclidean distance in ARC GIS 10.7. |
| Distance to center | m | 2020 | ||
| Economic factors | GDP per square kilometers | Yuan/km2 | 2010 | Data from China GDP spatial distribution km grid dataset [62]. |
| Restricted factors | Water resources | / | 2019 | Statistical Bulletin of Water Resources of Xi’an |
| Altitude | m | 2020 | Data from Digital Elevation Model provided by Geospatial Data Cloud (https://www.gscloud.cn/home) (accessed on 1 July 2022) | |
| Geological disasters | / | 2016 | National Geological Disaster Prevention and Control 13th Five-Year Plan | |
| Cultural relic protection units at provincial and national level | / | 2020 | Xi’an Historical and Cultural City Protection Plan (2019–2035) |
| Cluster | OT | DZ | NIS | SIS | EIS | WS | NS | WOS | EOS |
|---|---|---|---|---|---|---|---|---|---|
| Mean | Mean | Mean | Mean | Mean | Mean | Mean | Mean | Mean | |
| Land changed | 88.88% | 63.81% | 39.88% | 9.98% | 3.55% | 0.87% | 4.61% | 0.03% | 0.34% |
| Urban land in2010 | 86.55% | 48.44% | 56.91% | 17.96% | 12.09% | 3.28% | 11.93% | 0.55% | 1.67% |
| Urban land in2020| | 97.85% | 79.33% | 70.84% | 25.18% | 14.24% | 3.85% | 15.21% | 0.55% | 1.92% |
| Slope | 2.73 | 2.30 | 2.26 | 4.77 | 11.57 | 19.90 | 3.61 | 24.63 | 15.26 |
| Aspect | 184.28 | 187.15 | 176.46 | 181.38 | 186.48 | 178.56 | 174.97 | 175.24 | 182.40 |
| Distance to train station | 5319.51 | 8031.08 | 5530.86 | 15,705.85 | 9404.12 | 38,932.66 | 13,048.35 | 84,873.23 | 25,926.89 |
| Distance to airport | 27,504.24 | 29,604.12 | 18,865.97 | 36,544.54 | 47,386.43 | 52,152.24 | 32,497.70 | 82,795.05 | 67,345.78 |
| Distance to subway station | 769.90 | 1627.12 | 2640.03 | 7291.27 | 12,410.54 | 27,682.97 | 13,034.84 | 70,899.99 | 31,884.62 |
| Distance to city road | 750.77 | 1027.00 | 1581.17 | 1496.43 | 2816.20 | 5069.36 | 1191.93 | 7110.39 | 2756.58 |
| Distance to railroad | 3659.30 | 4519.74 | 1388.41 | 5479.90 | 4548.82 | 6949.57 | 6515.03 | 32,832.64 | 12,460.07 |
| Distance to highway | 2877.12 | 1364.51 | 1546.70 | 2764.84 | 6025.00 | 7146.71 | 2878.98 | 37,231.72 | 6051.43 |
| Distance to colleges and university | 774.66 | 1440.38 | 2110.46 | 4421.63 | 8065.32 | 9599.70 | 4599.22 | 29,290.74 | 14,530.31 |
| Distance to shopping center | 312.08 | 596.94 | 838.47 | 1502.10 | 3248.28 | 5073.79 | 1740.99 | 15,344.59 | 4823.38 |
| Distance to companies | 121.58 | 215.42 | 242.14 | 696.26 | 2028.99 | 2718.09 | 768.44 | 7938.00 | 3053.74 |
| Distance to hospitals | 690.36 | 1515.61 | 1692.65 | 3958.42 | 5792.40 | 11,617.91 | 2793.98 | 22,339.42 | 10,431.43 |
| Distance to local government agencies | 727.78 | 1963.91 | 2025.63 | 4269.77 | 9618.54 | 15,679.66 | 5169.62 | 31,663.20 | 27,395.15 |
| Distance to center | 20,022.64 | 16,849.66 | 28,103.68 | 13,810.31 | 36,005.25 | 23,043.75 | 51,379.60 | 66,180.72 | 63,614.50 |
| GDP per square kilometers | 157,019.10 | 77,716.75 | 32,388.96 | 6681.43 | 78,704.52 | 100,156.80 | 37,986.21 | 237,074.90 | 253,584.40 |
| Coefficient | Standard Error | 95% Confidence Interval | ||
|---|---|---|---|---|
| Fixed effects | ||||
| Slope | −0.62 *** | 0.07 | −0.76 | −0.48 |
| Aspect | 0.00 | 0.01 | −0.03 | 0.02 |
| Distance to train station | −2.41 *** | 0.08 | −2.57 | −2.24 |
| Distance to city road | 0.03 | 0.06 | −0.09 | 0.14 |
| Distance to railroad | 0.39 *** | 0.06 | 0.28 | 0.50 |
| Distance to companies | −19.69 *** | 0.30 | −20.28 | −19.10 |
| Distance to local government agencies | −2.34 *** | 0.08 | −2.49 | −2.18 |
| Distance to center | −1.09 *** | 0.05 | −1.19 | −1.00 |
| GDP per square kilometers | 1288.66 *** | 57.01 | 1176.93 | 1400.40 |
| constant | −9.60 *** | 0.88 | −11.33 | −7.88 |
| Random effects | Estimate | standard error | 95% confidence interval | |
| var(constant) | 3.94 | 1.91 | 1.52 | 10.19 |
| 2020 Land Use | 2020 CM-CA | 2010–2020 CM-CA | 2020–2030 CM-CA | |||
|---|---|---|---|---|---|---|
| Cluster | Non-Urban Area (km2) | Urban Area (km2) | Urban Area Percentage | Urban Area Percentage | Urban Growth Rate | Urban Growth Rate |
| OT | 345.42 | 15,657.39 | 97.84% | 86.22% | −0.0033 | −0.0004 |
| DZ | 990.63 | 3810.6 | 79.37% | 47.11% | −0.0132 | −0.0051 |
| NIS | 8397.45 | 20,377.44 | 70.82% | 70.35% | 0.1344 | 0.0681 |
| EIS | 95,548.77 | 15,870.42 | 14.24% | 16.86% | 0.0477 | 0.0505 |
| SIS | 49,361.22 | 16,629.84 | 25.20% | 25.60% | 0.0764 | 0.0718 |
| NS | 38,716.65 | 6943.59 | 15.21% | 16.35% | 0.0442 | 0.0493 |
| WS | 158,312.7 | 6348.06 | 3.86% | 3.69% | 0.0041 | 0.0057 |
| WOS | 302,944.7 | 1666.89 | 0.55% | 0.53% | −0.0002 | −0.0002 |
| EOS | 263,164.5 | 5161.5 | 1.92% | 1.97% | 0.0031 | 0.0031 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, S.; Xiao, Y.; Tang, L. Urban Growth Simulation Based on a Multi-Dimension Classification of Growth Types: Implications for China’s Territory Spatial Planning. Land 2022, 11, 2210. https://doi.org/10.3390/land11122210
Miao S, Xiao Y, Tang L. Urban Growth Simulation Based on a Multi-Dimension Classification of Growth Types: Implications for China’s Territory Spatial Planning. Land. 2022; 11(12):2210. https://doi.org/10.3390/land11122210
Chicago/Turabian StyleMiao, Siyu, Yang Xiao, and Ling Tang. 2022. "Urban Growth Simulation Based on a Multi-Dimension Classification of Growth Types: Implications for China’s Territory Spatial Planning" Land 11, no. 12: 2210. https://doi.org/10.3390/land11122210







