Addressing the Externalities from Genetically Modified Pollen Drift on a Heterogeneous Landscape
Abstract
:1. Introduction
2. Methods and Data
2.1. Landscape and Cross-Pollination Dynamics
2.2. Property Rights and the Regulatory Threshold for Cross-Pollination
2.3. Economic Objective
2.4. Modeling Approach
2.5. Data
2.5.1. Homogeneous and Unconstrained Landscape
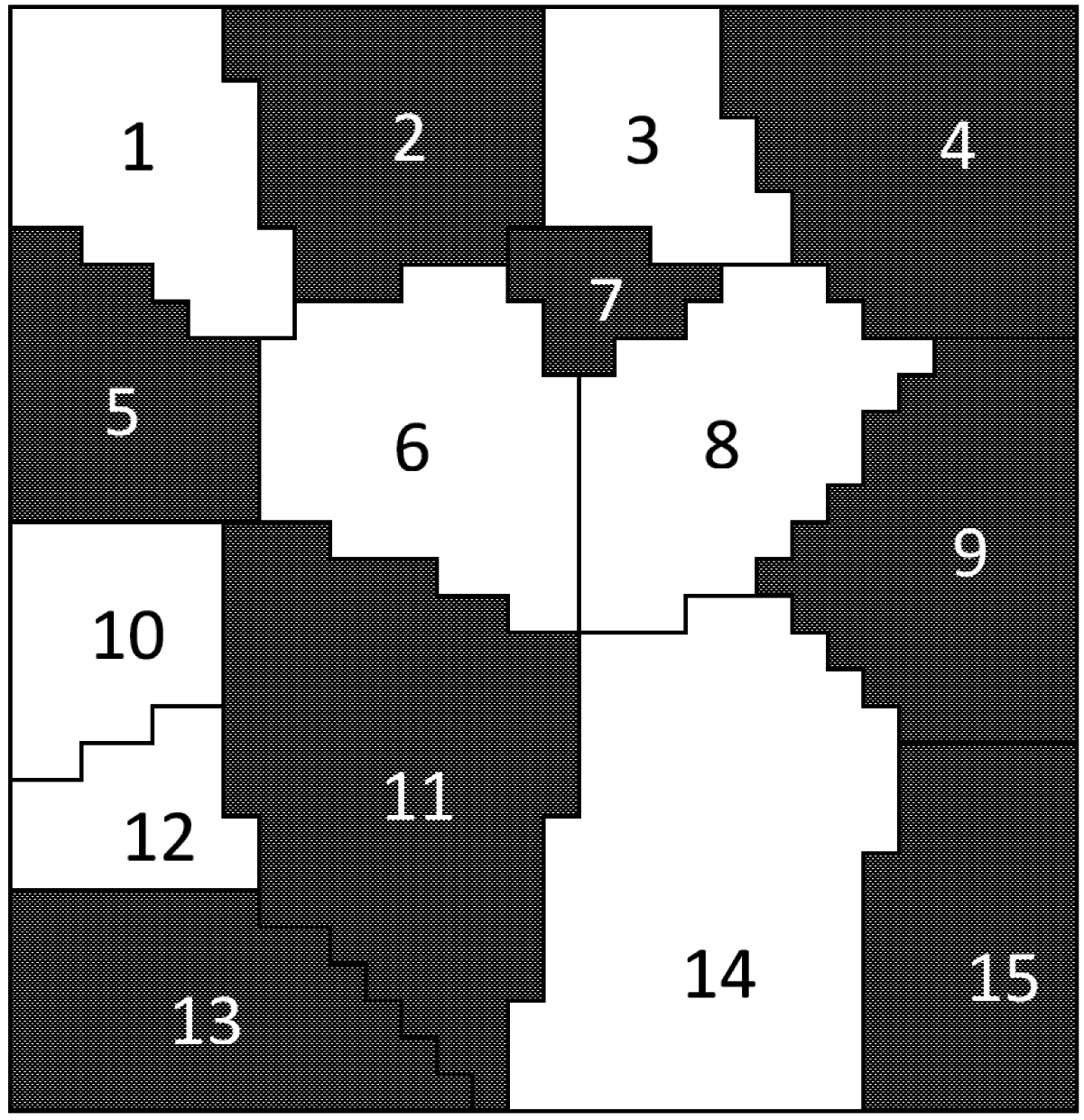
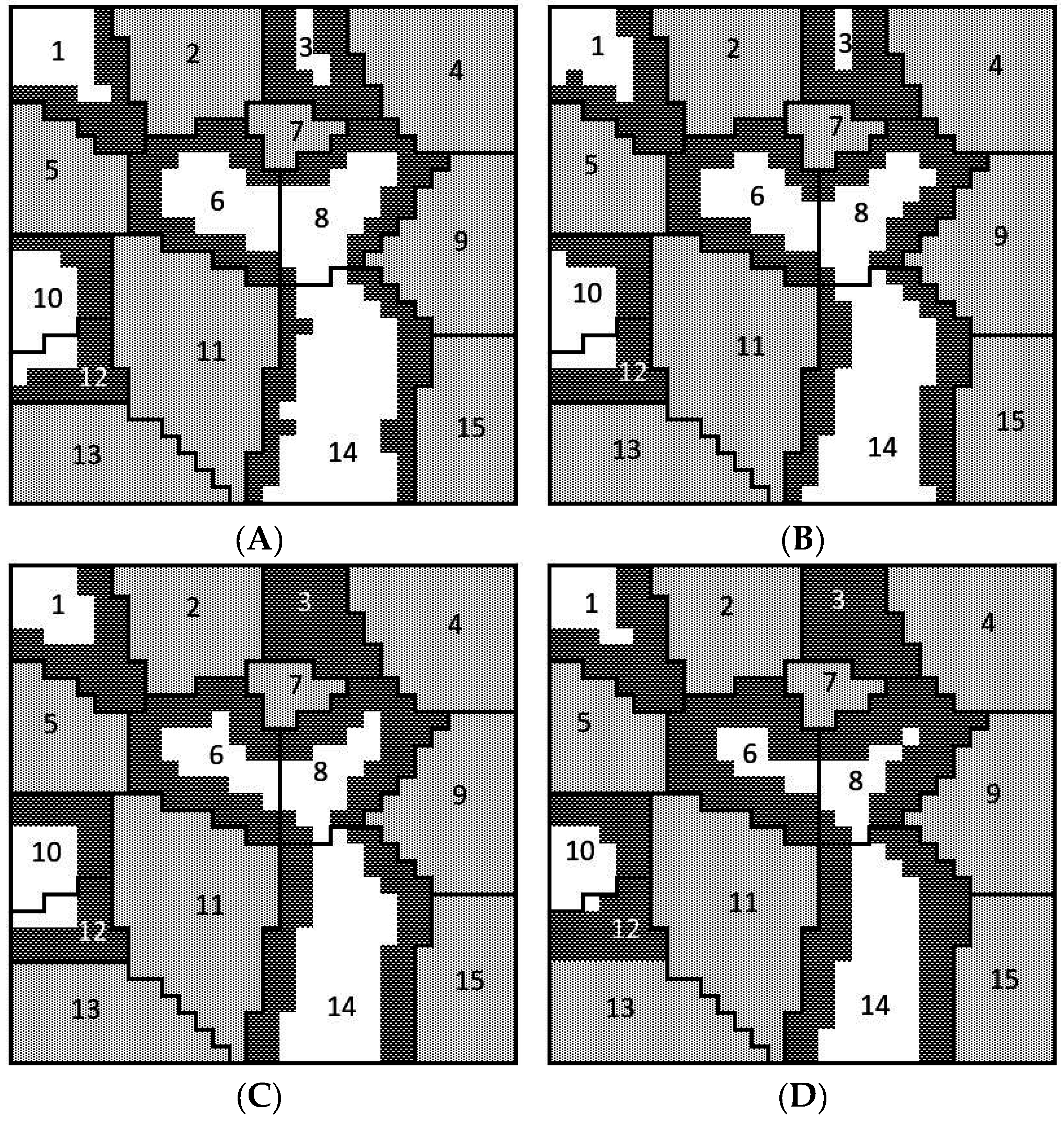
2.5.2. Heterogeneous and Constrained Landscape Analysis
3. Results and Discussion
3.1. The Homogeneous and Unconstrained Landscape
3.2. The Heterogeneous Landscape
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beckmann, V.; Soregaroli, C.; Wesseler, J. Coexistence rules and regulations in the European Union. Am. J. Agric. Econ. 2006, 88, 1193–1199. [Google Scholar] [CrossRef]
- Lusk, J.L.; Jamal, M.; Kurlander, L.; Roucan, M.; Taulman, L. A meta-analysis of genetically modified food valuation studies. J. Agric. Res. Econ. 2005, 30, 28–44. [Google Scholar]
- Costa-Font, M.; Gil, J.M.; Traill, W.B. Consumer acceptance, valuation of and attitudes towards genetically modified food: Review and implications for food policy. Food Policy 2008, 33, 99–111. [Google Scholar] [CrossRef]
- Fotopoulos, C.; Krystallis, A. Organic product avoidance: Reasons for rejection and potential buyers’ identification in a countrywide survey. Br. Food J. 2002, 104, 233–260. [Google Scholar] [CrossRef]
- Magnusson, M.K.; Arvola, A.; Hursti, U.K.; Åberg, L.; Sjödén, P. Choice of organic foods is related to perceived consequences for human health and to environmentally friendly behaviour. Appetite 2003, 40, 109–117. [Google Scholar] [CrossRef]
- Flood, C. Pollen drift and potential causes of action. J. Corp. Law 2002, 28, 473–497. [Google Scholar]
- Schenkelaars, P.; Wesseler, J. Farm-level GM Coexistence Policies in the EU: Context, Concepts, and Developments. EuroChoices 2016, 15, 5–11. [Google Scholar] [CrossRef]
- Beckmann, V.; Soregaroli, C.; Wesseler, J. Coexistence of genetically modified (GM) and non-modified (non GM) crops: Are the two main property rights regimes equivalent with respect to the coexistence value? In Genetically Modified Food and Global Welfare; Colin, C., Moschini, G., Sheldon, I., Eds.; Emerald Group Publishing: Bingley, UK, 2011; Volume 10, pp. 201–224. [Google Scholar]
- Consmüller, N.; Beckmann, V.; Petrick, M. An econometric analysis of regional adoption patterns of Bt maize in Germany. Agric. Econ. 2010, 41, 275–284. [Google Scholar] [CrossRef]
- Venus, T.; Punt, M.; Wesseler, J. Labelling genetically modified-free products—A case study of dairy companies in Germany. EuroChoices 2016, 15, 45–51. [Google Scholar]
- Quedas, F.M.; Ponte, J.; Trinidade, C.; Punt, M.; Wesseler, J. A question of segregation: ‘GM-free’ maize bread in Portugal. EuroChoices 2016, 15, 59–63. [Google Scholar] [CrossRef]
- Varacca, A.; Soregaroli, C. Identity preservation in international feed supply chains. EuroChoices 2016, 15, 38–43. [Google Scholar] [CrossRef]
- Wesseler, J. Biotechnologies and agrifood strategies: Opportunities, threads and economic implications. Bio-Based Appl. Econ. 2014, 3, 187–204. [Google Scholar]
- Skevas, T.; Fevereiro, P.; Wesseler, J. Coexistence regulations & agriculture production: A case study of five Bt maize producers in Portugal. Ecol. Econ. 2010, 69, 2402–2408. [Google Scholar]
- Groeneveld, R.; Wesseler, J.; Berentsen, P. Dominos in the dairy: An analysis of transgenic maize in Dutch dairy farming. Ecol. Econ. 2013, 86, 107–116. [Google Scholar] [CrossRef]
- Venus, T.; Punt, M; Dillen, K.; Wesseler, J. The costs of coexistence measures for genetically modified maize in Germany. J. Agric. Econ. 2016. [Google Scholar] [CrossRef]
- Demont, M.; Dillen, K.; Daems, W.; Sausse, C.; Tollens, E.; Mathijs, E. On the proportionality of EU spatial ex ante coexistence regulations. Food Policy 2009, 34, 508–518. [Google Scholar] [CrossRef]
- Beckmann, V.; Wesseler, J. Spatial dimension of externalities and the Coase theorem: Implications for co-existence of transgenic crops. In Regional Externalities; Heijman, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 223–242. [Google Scholar]
- Wesseler, J.; Beckmann, V.; Soregaroli, C. Coexistence of GM and non-GM supply chains in the EU: Policy framework and economic aspects. In Proceedings of the International Workshop on Socioeconomic Impacts of Genetically Modified Crops, Seville, Spain, 23–24 November 2011; pp. 75–79.
- Weekes, R.; Allnutt, T.; Boffey, C.; Morgan, S.; Bilton, M.; Daniels, R.; Henry, C. A study of crop-to-crop gene flow using farm scale sites of fodder maize (Zea mays L.) in the UK. Transgenic Res. 2007, 16, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Munro, A. The spatial impact of genetically modified crops. Ecol. Econ. 2008, 67, 658–666. [Google Scholar] [CrossRef] [Green Version]
- Ceddia, M.G.; Bartlett, M.; de Lucia, C.; Perrings, C. On the regulation of spatial externalities: Coexistence between GM and conventional crops in the EU and the ‘newcomer principle’. Aust. J. Agric. Resour. Econ. 2011, 55, 126–143. [Google Scholar] [CrossRef]
- Belcher, K.; Nolan, J.; Phillips, P.W. Genetically modified crops and agricultural landscapes: Spatial patterns of contamination. Ecol. Econ. 2005, 53, 387–401. [Google Scholar] [CrossRef]
- Perry, J.N. Sensitive dependencies and separation distances for genetically modified herbicide-tolerant crops. Proc. Biol. Soc. 2002, 269, 1173–1176. [Google Scholar] [CrossRef] [PubMed]
- Lavigne, C.; Klein, E.; Vallée, P.; Pierre, J.; Godelle, B.; Renard, M. A pollen-dispersal experiment with transgenic oilseed rape. Estimation of the average pollen dispersal of an individual plant within a field. Theor. Appl. Genet. 1998, 96, 886–896. [Google Scholar] [CrossRef]
- University of Arkansas Division of Agriculture Research and Extension. 2014 Crop Enterprise Budgets for Arkansas Field Crops Planted in 2014. December 2013. Available online: http://www.uaex.edu/farm-ranch/economics-marketing/docs/Budgets%202014_C.pdf (accessed on 9 August 2016).



| Parameter | Value |
|---|---|
| Cell side length (m) | 25 |
| Cell size (m2) | 625 |
| Dispersal parameter K | 455 |
| Dispersal parameter α | 0.125 |
| Threshold of cross-pollination (%) | 0.9 |
| Baseline economic parameters for GM, Non-GM, and Buffer | |
| Corn price ($/t) | 271.25 |
| Corn yield (t/ha) | 11 |
| Corn production costs ($/ha) | 1,498.78 |
| Profit ($/ha) | 1,484.97 |
| Parameter | Value |
|---|---|
| Number of cells s | 225 |
| Total surface t (ha) | 14 |
| Number of fields | 2 |
| Number of GM fields | 1 |
| Number of no-GM fields | 1 |
| Parameter | Value |
|---|---|
| Number of cells | 900 |
| Total surface (ha) | 56 |
| Number of fields | 15 |
| Number of GM fields | 8 |
| GM area (%) | 55% |
| Number of no-GM fields | 7 |
| No-GM area (%) | 45% |
| GM with Property Rights | ||||||||
| Profitability Non-GM | Thresholds of Cross-Pollination (%) | |||||||
| 5.00% | 2.00% | 1.50% | 1.00% | 0.90% | 0.50% | 0.2% | 0.10% | |
| 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| 5.0% | −1.9% | −3.3% | −3.8% | −4.6% | −4.8% | −5.7% | −6.5% | −7.6% |
| 10.0% | 0.2% | −1.3% | −1.8% | −2.7% | −2.9% | −3.8% | −4.7% | −5.8% |
| 15.0% | 2.2% | 0.6% | 0.1% | −0.8% | −1.0% | −2.0% | −2.9% | −4.1% |
| 20.0% | 4.3% | 2.6% | 2.1% | 1.2% | 1.0% | 0.0% | −1.0% | −2.2% |
| 25.0% | 6.3% | 4.6% | 4.0% | 3.0% | 2.8% | 1.8% | 0.7% | −0.5% |
| 30.0% | 8.4% | 6.6% | 6.0% | 5.0% | 4.8% | 3.7% | 2.6% | 1.3% |
| Non-GM with Property Rights | ||||||||
| Profitability GM | Thresholds of Cross-Pollination (%) | |||||||
| 5.00% | 2.00% | 1.50% | 1.00% | 0.90% | 0.50% | 0.25% | 0.10% | |
| 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| 5.0% | −1.3% | −2.2% | −2.7% | −3.3% | −3.4% | −4.4% | −5.3% | −6.2% |
| 10.0% | 1.2% | 0.2% | −0.4% | −1.0% | −1.1% | −2.2% | −3.2% | −4.3% |
| 15.0% | 3.5% | 2.5% | 1.9% | 1.2% | 1.1% | −0.1% | −1.1% | −2.3% |
| 20.0% | 5.9% | 4.8% | 4.1% | 3.4% | 3.3% | 2.0% | 0.9% | −0.4% |
| 25.0% | 8.3% | 7.1% | 6.4% | 5.6% | 5.5% | 4.1% | 2.9% | 1.6% |
| 30.0% | 10.7% | 9.4% | 8.7% | 7.8% | 7.7% | 6.2% | 4.9% | 3.5% |
| Non-GM Profitability | Threshold of Cross-Pollination | Field | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 8 | 10 | 12 | 14 | ||
| 10.0% | 5.00% | 0.7% | -- | -- | 1.6% | 1.8% | -- | 3.5% |
| 2.00% | -- | -- | -- | -- | 1.2% | -- | 1.7% | |
| 1.50% | -- | -- | -- | -- | -- | -- | 1.0% | |
| 1.00% | -- | -- | -- | -- | -- | -- | 1.0% | |
| 0.90% | -- | -- | -- | -- | -- | -- | -- | |
| 0.50% | -- | -- | -- | -- | -- | -- | -- | |
| 0.25% | -- | -- | -- | -- | -- | -- | -- | |
| 0.10% | -- | -- | -- | -- | -- | -- | -- | |
| 15.0% | 5.00% | 5.2% | -- | 3.6% | 6.2% | 6.4% | 0.4% | 8.2% |
| 2.00% | 1.0% | -- | 0.1% | 1.9% | 5.9% | -- | 6.3% | |
| 1.50% | 0.7% | -- | -- | 0.7% | 4.4% | -- | 5.6% | |
| 1.00% | 0.7% | -- | -- | 0.7% | 4.4% | -- | 5.6% | |
| 0.90% | -- | -- | -- | -- | 0.6% | -- | 3.2% | |
| 0.50% | -- | -- | -- | -- | -- | -- | 0.9% | |
| 0.25% | -- | -- | -- | -- | -- | -- | -- | |
| 0.10% | -- | -- | -- | -- | -- | -- | -- | |
| 20.0% | 5.00% | 9.8% | 1.1% | 8.1% | 10.9% | 11.0% | 4.8% | 12.9% |
| 2.00% | 5.4% | -- | 4.4% | 6.3% | 10.5% | -- | 10.9% | |
| 1.50% | 5.0% | -- | 2.8% | 5.1% | 9.0% | -- | 10.2% | |
| 1.00% | 5.0% | -- | 2.8% | 5.1% | 9.0% | -- | 10.2% | |
| 0.90% | 2.3% | -- | -- | 3.5% | 5.0% | -- | 7.6% | |
| 0.50% | -- | -- | -- | 0.5% | 3.0% | -- | 5.3% | |
| 0.25% | -- | -- | -- | -- | 2.5% | -- | 3.3% | |
| 0.10% | -- | -- | -- | -- | 1.0% | -- | 1.0% | |
| 25.0% | 5.00% | 14.4% | 5.3% | 12.6% | 15.5% | 15.7% | 9.1% | 17.6% |
| 2.00% | 9.8% | -- | 8.8% | 10.7% | 15.1% | 2.0% | 15.5% | |
| 1.50% | 9.4% | -- | 7.1% | 9.5% | 13.5% | -- | 14.8% | |
| 1.00% | 9.4% | -- | 7.1% | 9.5% | 13.5% | -- | 14.8% | |
| 0.90% | 6.6% | -- | 3.7% | 7.8% | 9.3% | -- | 12.1% | |
| 0.50% | 3.8% | -- | 2.1% | 4.7% | 7.3% | -- | 9.6% | |
| 0.25% | 2.0% | -- | -- | 1.2% | 6.7% | -- | 7.6% | |
| 0.10% | 0.3% | -- | -- | -- | 5.2% | -- | 5.2% | |
| 30.0% | 5.00% | 19.0% | 9.5% | 17.2% | 20.1% | 20.3% | 13.5% | 22.3% |
| 2.00% | 14.2% | 1.3% | 13.2% | 15.2% | 19.7% | 6.1% | 20.2% | |
| 1.50% | 13.8% | -- | 11.4% | 13.9% | 18.0% | 3.8% | 19.4% | |
| 1.00% | 13.8% | -- | 11.4% | 13.9% | 18.0% | 3.8% | 19.4% | |
| 0.90% | 10.9% | -- | 7.8% | 12.1% | 13.7% | 1.5% | 16.6% | |
| 0.50% | 7.9% | -- | 6.2% | 8.9% | 11.6% | 0.1% | 14.0% | |
| 0.25% | 6.1% | -- | 2.6% | 5.3% | 11.0% | 0.1% | 11.9% | |
| 0.10% | 4.3% | -- | -- | 1.5% | 9.4% | -- | 9.4% | |
| GM Profitability | Threshold of Cross-Pollination | Field | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 5 | 7 | 9 | 11 | 13 | 15 | ||
| 10.0% | 5.00% | -- | 6.1% | -- | -- | 4.7% | 0.7% | 5.8% | 4.2% |
| 2.00% | -- | 3.8% | -- | -- | 3.7% | -- | 5.8% | 3.7% | |
| 1.50% | -- | 3.4% | -- | -- | 1.6% | -- | 4.0% | 3.7% | |
| 1.00% | -- | 3.4% | -- | -- | 1.6% | -- | 4.0% | 3.7% | |
| 0.90% | -- | 3.0% | -- | -- | 0.1% | -- | 2.8% | 3.1% | |
| 0.50% | -- | 1.8% | -- | -- | 0.1% | -- | 1.6% | -- | |
| 0.25% | -- | -- | -- | -- | -- | -- | 1.6% | -- | |
| 0.10% | -- | -- | -- | -- | -- | -- | -- | -- | |
| 15.0% | 5.00% | 2.7% | 10.8% | 1.9% | -- | 9.3% | 4.9% | 10.4% | 8.7% |
| 2.00% | 0.7% | 8.2% | -- | -- | 8.2% | 2.5% | 10.4% | 8.2% | |
| 1.50% | -- | 7.9% | -- | -- | 6.0% | 1.3% | 8.5% | 8.2% | |
| 1.00% | -- | 7.9% | -- | -- | 6.0% | 1.3% | 8.5% | 8.2% | |
| 0.90% | -- | 7.4% | -- | -- | 4.2% | -- | 7.2% | 7.5% | |
| 0.50% | -- | 6.2% | -- | -- | 4.2% | -- | 5.9% | 3.7% | |
| 0.25% | -- | 4.1% | -- | -- | 2.5% | -- | 5.9% | 1.9% | |
| 0.10% | -- | 2.5% | -- | -- | -- | -- | 3.7% | 0.9% | |
| 20.0% | 5.00% | 6.8% | 15.5% | 5.9% | -- | 13.9% | 9.2% | 15.1% | 13.2% |
| 2.00% | 4.7% | 12.7% | 3.0% | -- | 12.7% | 6.5% | 15.1% | 12.7% | |
| 1.50% | 3.8% | 12.3% | 2.1% | -- | 10.3% | 5.2% | 13.0% | 12.7% | |
| 1.00% | 3.8% | 12.3% | 2.1% | -- | 10.3% | 5.2% | 13.0% | 12.7% | |
| 0.90% | 2.4% | 11.8% | 1.2% | -- | 8.4% | 2.4% | 11.6% | 12.0% | |
| 0.50% | -- | 10.5% | -- | -- | 8.4% | -- | 10.2% | 7.9% | |
| 0.25% | -- | 8.2% | -- | -- | 6.6% | -- | 10.2% | 5.9% | |
| 0.10% | -- | 6.5% | -- | -- | 3.0% | -- | 7.9% | 4.8% | |
| 25.0% | 5.00% | 10.8% | 20.2% | 9.9% | -- | 18.4% | 13.4% | 19.8% | 17.7% |
| 2.00% | 8.6% | 17.2% | 6.8% | -- | 17.2% | 10.6% | 19.8% | 17.2% | |
| 1.50% | 7.7% | 16.8% | 5.9% | -- | 14.6% | 9.2% | 17.5% | 17.2% | |
| 1.00% | 7.7% | 16.8% | 5.9% | -- | 14.6% | 9.2% | 17.5% | 17.2% | |
| 0.90% | 6.2% | 16.2% | 4.9% | -- | 12.6% | 6.1% | 16.1% | 16.4% | |
| 0.50% | 1.4% | 14.8% | -- | -- | 12.6% | 3.1% | 14.5% | 12.0% | |
| 0.25% | -- | 12.4% | -- | -- | 10.6% | 0.6% | 14.5% | 9.9% | |
| 0.10% | -- | 10.6% | -- | -- | 6.8% | -- | 12.0% | 8.7% | |
| 30.0% | 5.00% | 14.9% | 24.9% | 13.9% | -- | 23.0% | 17.6% | 24.4% | 22.2% |
| 2.00% | 12.5% | 21.7% | 10.6% | -- | 21.7% | 14.6% | 24.4% | 21.6% | |
| 1.50% | 11.5% | 21.2% | 9.6% | -- | 18.9% | 13.1% | 22.0% | 21.6% | |
| 1.00% | 11.5% | 21.2% | 9.6% | -- | 18.9% | 13.1% | 22.0% | 21.6% | |
| 0.90% | 9.9% | 20.6% | 8.6% | -- | 16.8% | 9.9% | 20.5% | 20.8% | |
| 0.50% | 4.8% | 19.1% | 2.8% | -- | 16.8% | 6.7% | 18.8% | 16.1% | |
| 0.25% | 2.4% | 16.6% | -- | -- | 14.7% | 4.0% | 18.8% | 13.9% | |
| 0.10% | -- | 14.6% | -- | -- | 10.5% | 1.2% | 16.2% | 12.7% | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mancini, M.C.; Kovacs, K.; Wailes, E.; Popp, J. Addressing the Externalities from Genetically Modified Pollen Drift on a Heterogeneous Landscape. Land 2016, 5, 33. https://doi.org/10.3390/land5040033
Mancini MC, Kovacs K, Wailes E, Popp J. Addressing the Externalities from Genetically Modified Pollen Drift on a Heterogeneous Landscape. Land. 2016; 5(4):33. https://doi.org/10.3390/land5040033
Chicago/Turabian StyleMancini, Mattia C., Kent Kovacs, Eric Wailes, and Jennie Popp. 2016. "Addressing the Externalities from Genetically Modified Pollen Drift on a Heterogeneous Landscape" Land 5, no. 4: 33. https://doi.org/10.3390/land5040033
APA StyleMancini, M. C., Kovacs, K., Wailes, E., & Popp, J. (2016). Addressing the Externalities from Genetically Modified Pollen Drift on a Heterogeneous Landscape. Land, 5(4), 33. https://doi.org/10.3390/land5040033





