The Geometrical Basis of Symmetry
Abstract
1. Introduction
2. Basic Concepts on the Transfer Matrix
3. Geometry of Transfer Matrices
4. Geometry of -Invariant Transfer Matrices
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Muga, J.G.; Palao, J.P.; Navarro, B.; Egusquiza, I.L. Complex absorbing potentials. Phys. Rep. 2004, 395, 357–426. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S.; Meisinger, P.N. -symmetric quantum mechanics. J. Math. Phys. 1999, 40, 2201–2229. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Complex extension of quantum mechanics. Phys. Rev. Lett. 2002, 89, 270401. [Google Scholar] [CrossRef] [PubMed]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Must a Hamiltonian be Hermitian? Am. J. Phys. 2003, 71, 1095–1102. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1018. [Google Scholar] [CrossRef]
- Bender, C.M.; Mannheim, P.D. symmetry and necessary and sufficient conditions for the reality of energy eigenvalues. Phys. Lett. A 2010, 374, 1616–1620. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Exact -symmetry is equivalent to Hermiticity. J. Phys. A 2003, 36, 7081. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermiticity and generalized - and -symmetries. J. Math. Phys. 2003, 44, 974–989. [Google Scholar] [CrossRef]
- Wang, Q.H.; Chia, S.Z.; Zhang, J.H. PT-symmetry as a generalization of Hermiticity. J. Phys. A 2010, 43, 295301. [Google Scholar] [CrossRef]
- Delabaere, E.; Pham, F. Eigenvalues of complex Hamiltonians with -symmetry. Phys. Lett. A 1998, 250, 25–28. [Google Scholar] [CrossRef]
- Klaiman, S.; Günther, U.; Moiseyev, N. Visualization of branch points in -symmetric waveguides. Phys. Rev. Lett. 2008, 101, 080402. [Google Scholar] [CrossRef] [PubMed]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation of -symmetry breaking in complex optical potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef] [PubMed]
- Levai, G. Spontaneous breakdown of symmetry in the complex Coulomb potential. Pramana 2009, 73, 329–335. [Google Scholar]
- Musslimani, Z.H.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N. Optical solitons in periodic potentials. Phys. Rev. Lett. 100, 030402. [Google Scholar]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Extension of -symmetric quantum mechanics to quantum field theory with cubic interaction. Phys. Rev. D 2004, 70, 025001. [Google Scholar] [CrossRef]
- Jones, H.F. Equivalent Hamiltonians for -symmetric versions of dual 2D field theories. J. Phys. A 2006, 39, 10123–10132. [Google Scholar] [CrossRef]
- Goldsheid, I.Y.; Khoruzhenko, B.A. Distribution of eigenvalues in non-Hermitian Anderson models. Phys. Rev. Lett. 1998, 80, 2897–2900. [Google Scholar] [CrossRef]
- Heinrichs, J. Eigenvalues in the non-Hermitian Anderson model. Phys. Rev. B 2001, 63, 165108. [Google Scholar] [CrossRef]
- Molinari, L.G. Non-Hermitian spectra and Anderson localization. J. Phys. A 2009, 42, 265204. [Google Scholar] [CrossRef]
- Bender, C.M.; Dunne, G.V.; Meisinger, P.N. Complex periodic potentials with real band spectra. Phys. Lett. A 1999, 252, 272–276. [Google Scholar] [CrossRef]
- Jones, H.F. The energy spectrum of complex periodic potentials of Kronig–Penney type. Phys. Lett. A 1999, 262, 242–264. [Google Scholar] [CrossRef]
- Znojil, M. -symmetric square well. Phys. Lett. A 2001, 285, 7–10. [Google Scholar] [CrossRef]
- Ahmed, Z. Energy band structure due to a complex, periodic, -invariant potential. Phys. Lett. A 2001, 286, 231–235. [Google Scholar] [CrossRef]
- Bagchia, B.; Quesne, C. sl(2, C) as a complex Lie algebra and the associated non-Hermitian Hamiltonians with real eigenvalues. Phys. Lett. A 2000, 273, 285–292. [Google Scholar] [CrossRef]
- Bender, C.M.; Klevansky, S.P. -symmetric representations of fermionic algebras. Phys. Rev. A 2011, 84, 024102. [Google Scholar] [CrossRef]
- Cherbal, O.; Trifonov, D.A. Extended - and -symmetric representations of fermionic algebras. Phys. Rev. A 2012, 85, 05212. [Google Scholar] [CrossRef]
- Rotter, I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A 2009, 42, 153001. [Google Scholar] [CrossRef]
- Ruter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Musslimani, Z.H. Beam dynamics in symmetric optical lattices. Phys. Rev. Lett. 2008, 100, 103904. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.C.; Christodoulides, D.N.; Fleischmann, R.; Kottos, T. optical lattices and universality in beam dynamics. Phys. Rev. A 2010, 82, 010103. [Google Scholar] [CrossRef]
- Longhi, S. Bloch oscillations in complex crystals with symmetry. Phys. Rev. Lett. 2009, 103, 123601. [Google Scholar] [CrossRef] [PubMed]
- Longhi, S. -symmetric laser absorber. Phys. Rev. A 2010, 82, 031801. [Google Scholar] [CrossRef]
- Chong, Y.D.; Ge, L.; Stone, A.D. -symmetry breaking and laser-absorber modes in optical scattering systems. Phys. Rev. Lett. 2011, 106, 093902. [Google Scholar] [CrossRef] [PubMed]
- Sukhorukov, A.A.; Xu, Z.; Kivshar, Y.S. Nonlinear suppression of time reversals in -symmetric optical couplers. Phys. Rev. A 2010, 82, 043818. [Google Scholar] [CrossRef]
- Ahmed, Z.; Bender, C.M.; Berry, M.V. Reflectionless potentials and symmetry. J. Phys. A 2005, 38, L627–L630. [Google Scholar] [CrossRef]
- Lin, Z.; Ramezani, H.; Eichelkraut, T.; Kottos, T.; Cao, H.; Christodoulides, D.N. Unidirectional invisibility dnduced by -symmetric periodic structures. Phys. Rev. Lett. 2011, 106, 213901. [Google Scholar] [CrossRef] [PubMed]
- Longhi, S. Invisibility in -symmetric complex crystals. J. Phys. A 2011, 44, 485302. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F.; Meister, B.K. Faster than Hermitian quantum mechanics. Phys. Rev. Lett. 2007, 98, 040403. [Google Scholar] [CrossRef] [PubMed]
- Bender, C.M.; Brody, D.C.; Caldeira, J.; Günther, U.; Meister, B.K.; Samsonov, B.F. -symmetric quantum state discrimination. Philos. Transact. A Math. Phys. Eng. Sci. 2013, 371, 20120160. [Google Scholar] [CrossRef] [PubMed]
- Ibáñez, S.; Martínez-Garaot, S.; Chen, X.; Torrontegui, E.; Muga, J.G. Shortcuts to adiabaticity for non-Hermitian systems. Phys. Rev. A 2011, 84, 023415. [Google Scholar] [CrossRef]
- Torosov, B.T.; Della Valle, G.; Longhi, S. Non-Hermitian shortcut to adiabaticity. Phys. Rev. A 2013, 87, 052502. [Google Scholar] [CrossRef]
- Lee, Y.C.; Hsieh, M.H.; Flammia, S.T.; Lee, R.K. Local symmetry violates the no-signaling principle. Phys. Rev. Lett. 2014, 112, 130404. [Google Scholar] [CrossRef] [PubMed]
- Weigert, S. The physical interpretation of -invariant systems. Czech J. Phys. 2004, 54, 1139–1142. [Google Scholar] [CrossRef]
- Jin, L.; Song, Z. A physical interpretation for the non-Hermitian Hamiltonian. J. Phys. A 2011, 44, 375304. [Google Scholar] [CrossRef]
- Sánchez-Soto, L.L.; Monzón, J.J.; Barriuso, A.G.; Cariñena, J. The transfer matrix: A geometrical perspective. Phys. Rep. 2012, 513, 191–227. [Google Scholar] [CrossRef]
- Needham, T. Visual Complex Analysis; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Anderson, J.W. Hyperbolic Geometry; Springer: New York, NY, USA, 1999. [Google Scholar]
- Ratcliffe, J.G. Foundations of Hyperbolic Manifolds; Springer: Berlin, Germany, 2006. [Google Scholar]
- O’Neill, B. Semi-Riemannian Geometry with Applications to Relativity; Academic Press: London, UK, 1983. [Google Scholar]
- Moschella, U. The de Sitter and anti-de Sitter sightseeing tour. In Proceedings of the 20th Seminaire Poincaré, Paris, France, 21 November 2005; pp. 1–12. [Google Scholar]
- Monzón, J.J.; Barriuso, A.G.; Montesinos-Amilibia, J.M.; Sánchez-Soto, L.L. Geometrical aspects of -invariant transfer matrices. Phys. Rev. A 2013, 87, 012111. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Spectral Singularities of Complex Scattering Potentials and Infinite Reflection and Transmission Coefficients at Real Energies. Phys. Rev. Lett. 2009, 102, 220402. [Google Scholar] [CrossRef] [PubMed]
- Cannata, F.; Dedonder, J.P.; Ventura, A. Scattering in -symmetric quantum mechanics. Ann. Phys. 2007, 322, 397–433. [Google Scholar] [CrossRef]
- Ahmed, Z. New features of scattering from a one-dimensional non-Hermitian (complex) potential. J. Phys. A 2012, 45, 032004. [Google Scholar] [CrossRef]
- Boonserm, P.; Visser, M. One dimensional scattering problems: A pedagogical presentation of the relationship between reflection and transmission amplitudes. Thai J. Math. 2010, 8, 83–97. [Google Scholar]
- Mostafazadeh, A.; Mehri-Dehnavi, H. Spectral singularities, biorthonormal systems and a two-parameter family of complex point interactions. J. Phys. A 2009, 42, 125303. [Google Scholar] [CrossRef]
- Ford, L.R. Automorphic Functions; AMS Chelsea Publishing: New York, NY, USA, 1972. [Google Scholar]
- Bolinder, E.F. Impedance and Power Transformations by the Isometric Circle Method and Non-Euclidean Hyperbolic Geometry; Technical Report; MIT: Cambridge, MA, USA, 1957. [Google Scholar]
- Rudolph, J.G.; Cheng, D.K. Isometric-circle interpretation of bilinear transformation and its application to VSWR minimization. Radio Sci. 1965, 69D, 1271–1283. [Google Scholar] [CrossRef]
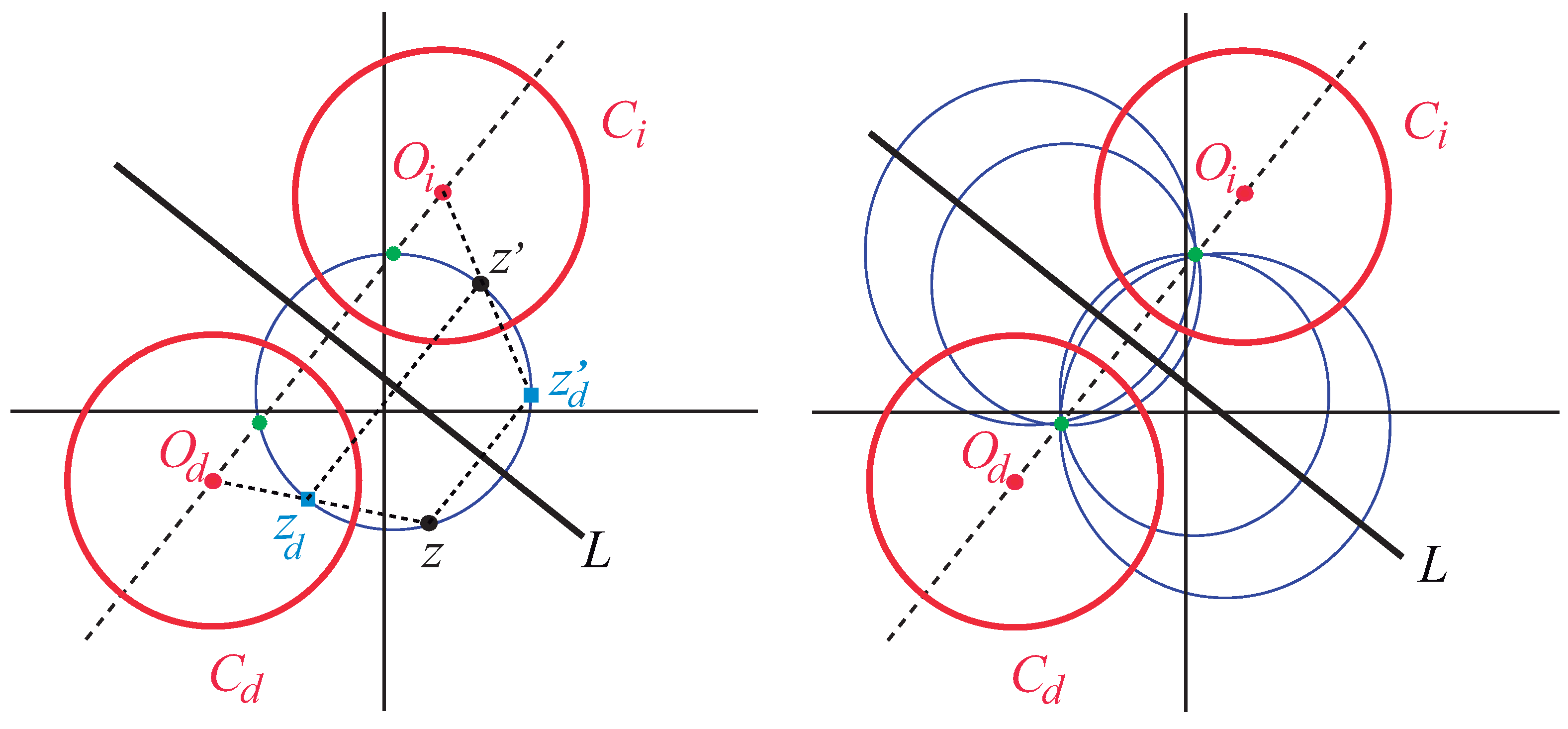
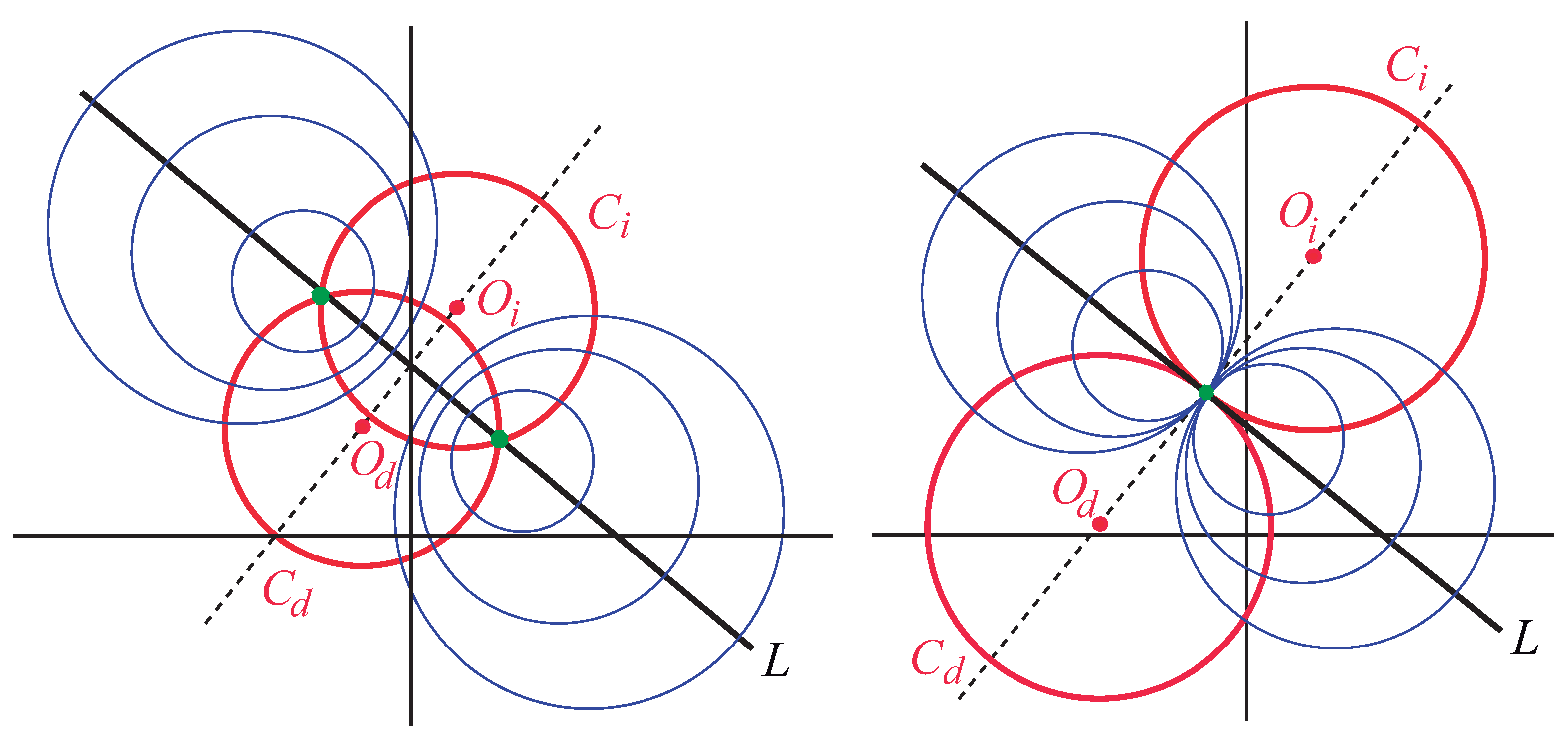

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Soto, L.L.; Monzón, J.J.
The Geometrical Basis of
. Symmetry 2018, 10, 494.
https://doi.org/10.3390/sym10100494
Sánchez-Soto LL, Monzón JJ.
The Geometrical Basis of
. Symmetry. 2018; 10(10):494.
https://doi.org/10.3390/sym10100494
Sánchez-Soto, Luis L., and Juan J. Monzón.
2018. "The Geometrical Basis of
" Symmetry 10, no. 10: 494.
https://doi.org/10.3390/sym10100494
Sánchez-Soto, L. L., & Monzón, J. J.
(2018). The Geometrical Basis of
. Symmetry, 10(10), 494.
https://doi.org/10.3390/sym10100494





