A Framework for Circular Multilevel Systems in the Frequency Domain

Abstract

In this paper, we will construct a new multilevel system in the Fourier domain using the harmonic wavelet. The main advantages of harmonic wavelet are that its frequency spectrum is confined exactly to an octave band, and its simple definition just as Haar wavelet. The constructed multilevel system has the circular shape, which forms a partition of the frequency domain by shifting and scaling the basic wavelet functions. To possess the circular shape, a new type of sampling grid, the circular-polar grid (CPG), is defined and also the corresponding modified Fourier transform. The CPG consists of equal space along rays, where different rays are equally angled. The main difference between the classic polar grid and CPG is the even sampling on polar coordinates. Another obvious difference is that the modified Fourier transform has a circular shape in the frequency domain while the polar transform has a square shape. The proposed sampling grid and the new defined Fourier transform constitute a completely Fourier transform system, more importantly, the harmonic wavelet based multilevel system defined on the proposed sampling grid is more suitable for the distribution of general images in the Fourier domain.

1. Introduction

Wavelet multiresolution representations are one of the effective techniques for analyzing signals and images. The wavelet multiresolution analysis (MRA) technology has been widely used in signal and image processing. It was first given by Mallat [1], and the authors study the difference of information between approximation of a signal at the resolution $2^{j+1}$ and $2^j$, by decomposing this signal on a wavelet basis of $L^2\left(R\right)$. The 2D general MRA technique possesses a square shape in the frequency domain [2,3,4]. To design the filter of circular-shape in the Fourier domain, the classical polar Fourier transformation is considered. However, the classical polar Fourier transform retains the same shape as in the space domain, so new approaches are investigated. One way is to redefine the sampling grid in the Fourier domain. In [5], the authors introduce a pseudo-polar Fourier transform that samples the Fourier transform on the pseudo-polar grid, also known as the concentric squares grid. We will give more details in Section 3. In addition, [6] samples on points that are equally spaced on an arbitrary arc of the unit circle, which brings about the Fractional Fourier transform; and, in [7], the sampling is on spirals of the form $A{W}^k$, with $A,W\in C$. Using this type of sampling, the authors develops a computation algorithm for numerically evaluating the $z-transform$. Our goal is to obtain the sampling grid in a circular shape; therefore, we hope to design a new type of sampling that ensures the sampling points concentrated in a circular region. Then, the sampling grid has a circular shape in the Fourier domain. Inspired by the pseudo-polar Fourier transform in [5], we will also redefine the Fourier transform on circular sampling grid.

In recent years, many kinds of directional wavelets filters have been designed, in order to further efficiently capture the details of signals. The most widely used directional multilevel system includes curvelets [8], contourlets [9] and shearlets [10,11]. What these wavelets have in common is that they have compact support multiscale structure in the space domain. In the Fourier domain, the support of a multilevel system constitutes a high redundant partition. To reduce the redundancy, we consider designing the multilevel system in the frequency domain directly. We also must ensure that the multilevel system constructs the basis of $L^2\left(R\right)$ in the space domain.

To design the multilevel system in the Fourier domain, wavelets with compact support in frequency are needed. According to the definition of the harmonic wavelet [12,13,14,15], it is suitable to construct a directional multilevel structure with harmonic wavelets whose Fourier transforms are compact and are constructed from simple functions like Haar wavelets [16] in the space domain. We will review the basic definition and property of harmonic wavelet in Section 2.

In this work, by defining the circular-shape Fourier transform (CFT), we will construct the circular-shape directional multilevel system (CMS) in the Fourier domain due to the compact support of harmonic wavelets [12,13,14,15,17]. The specific structure is totally different from the general Cartesian system. By introducing the CFT, we plan to give a parallel analogy with the general classical Descartes Fourier transform, and the corresponding circular-shape directional multilevel system is constructed naturally, which is suitable for the circular shape of images in the Fourier domain. More details will be given in Section 4.

This paper is organized as follows: Section 2 reviews the basic definition and property of harmonic wavelets. The design of CFT is given in Section 3. Then, in Section 4, the multilevel system in the frequency domain based harmonic wavelet is constructed. The quantitative test measures and test results are displayed in Section 5 and Section 6.

2. Preliminary

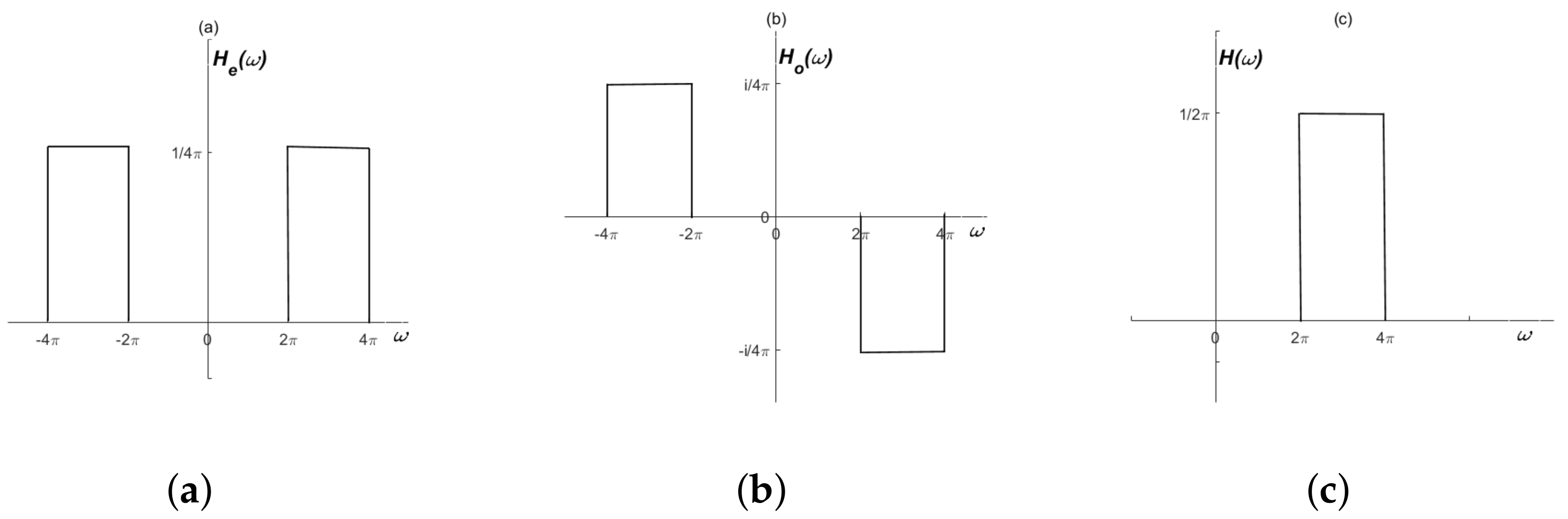
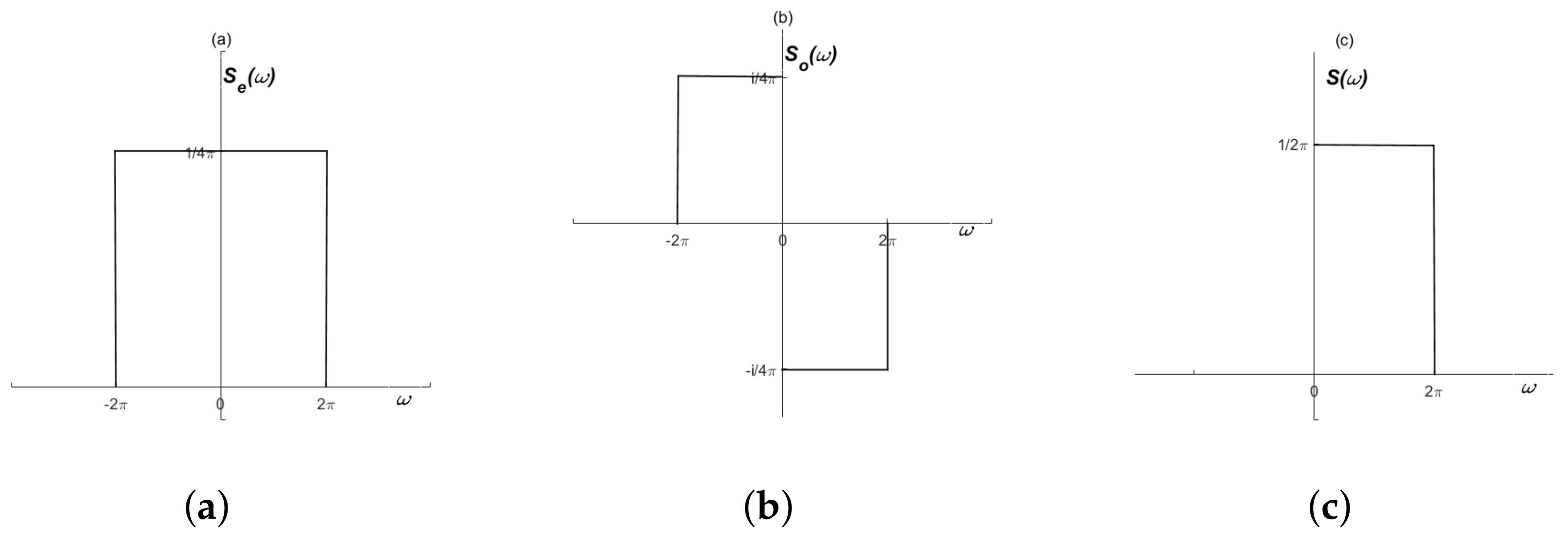
The Basic Definition

Harmonic wavelets are complex wavelets defined in the Fourier domain. It is consists of an even function $H_e\left(\omega \right)$ (see Figure 1a) as the real part and an odd function $H_o\left(\omega \right)$ (see Figure 1b) as the imaginary part, which are defined by

$$H_e\left(\omega \right)=\left\{\begin{array}{c}\begin{array}{c}1/4\pi ,\omega \in [-4\pi ,-2\pi )\cup [2\pi ,4\pi ),\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\end{array}\right.H_o\left(\omega \right)=\left\{\begin{array}{c}\begin{array}{c}i/4\pi ,\omega \in [-4\pi ,-2\pi ),\hfill \\ -i/4\pi ,\omega \in [2\pi ,4\pi ),\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\end{array}\right.$$

(1)

Combining $H_e$ and $H_o$, we get the harmonic function

$$H\left(\omega \right)=H_e\left(\omega \right)+i{H}_o\left(\omega \right).$$

(2)

From Label (1), we have

$$H\left(\omega \right)=\left\{\begin{array}{c}\begin{array}{c}1/2\pi ,\omega \in [2\pi ,4\pi ),\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\end{array}\right.$$

(3)

This is shown in Figure 1c.

The corresponding scaling function S is given in the same way, and the even and odd functions are defined as

$$S_e\left(\omega \right)=\left\{\begin{array}{c}\begin{array}{c}1/4\pi ,\omega \in [-2\pi ,2\pi ),\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\end{array}\right.S_o\left(\omega \right)=\left\{\begin{array}{c}\begin{array}{c}i/4\pi ,\omega \in [-2\pi ,0),\hfill \\ -i/4\pi ,\omega \in [0,2\pi ),\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\end{array}\right.$$

(4)

so that, from Label (4),

$$S\left(\omega \right)=S_e\left(\omega \right)+i{S}_o\left(\omega \right).$$

(5)

Therefore, we have

$$S\left(\omega \right)=\left\{\begin{array}{c}\begin{array}{c}1/2\pi ,\omega \in [0,2\pi ),\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\end{array}\right.$$

(6)

shown in Figure 2.

Then, the shifting and scaling of basic functions are denoted as $S_{j,\ell }\left(\omega \right)$ and $H_{j,\ell }\left(\omega \right)$, which are given as

$$\begin{array}{cc}\hfill S_{j,\ell }\left(\omega \right)& =1/2^{j}S(\omega /2^j-\ell ),\hfill \\ \hfill H_{j,\ell }\left(\omega \right)& =1/2^{j}H(\omega /2^j-\ell ),\hfill \end{array}$$

(7)

where $j\in Z$ is the scaling parameter, and $\ell \in R$ is the shifting parameter. According to Label (7), the harmonic wavelet system constructs a basis of $L^2\left(R\right)$ in the frequency domain; then, for $f\in L^2\left(R\right)$, we have

$$f\left(\omega \right)=\sum _{j=-\infty }^{+\infty }\sum _{\ell =-\infty }^{+\infty }{a}_{j,\ell }H(2^j\omega -\ell ),$$

(8)

$$f\left(\omega \right)=\sum _{\ell =-\infty }^{+\infty }{a}_{\ell }S(\omega -\ell )+\sum _{j=0}^{+\infty }\sum _{\ell =-\infty }^{+\infty }{a}_{j,\ell }H(2^j\omega -\ell ),$$

(9)

where

$$\begin{array}{c}\hfill a_{\ell }={\int }_{-\infty }^{+\infty }f\left(\omega \right)S(x-\ell )dx,a_{j,\ell }={\int }_{-\infty }^{+\infty }f\left(\omega \right)H(2^{j}x-\ell )dx.\end{array}$$

(10)

3. The Circular-Shape Fourier Transform (CFT)

This section describes the circular-shape Fourier transform (CFT). We begin with the sampling grid in the Fourier domain, including the Cartesian coordinates (see Figure 3a) for classical Fourier transform and the pseudo-polar grid in [5] (see Figure 3b). This grid samples points of equally spaced long rays but not equally angles. In order to have a circular structure, the sampling grid in concentric circles (see Figure 3c) is designed, which has equally arc and angle in each circle. This type of sampling is consistent with the distribution of images in the frequency domain.

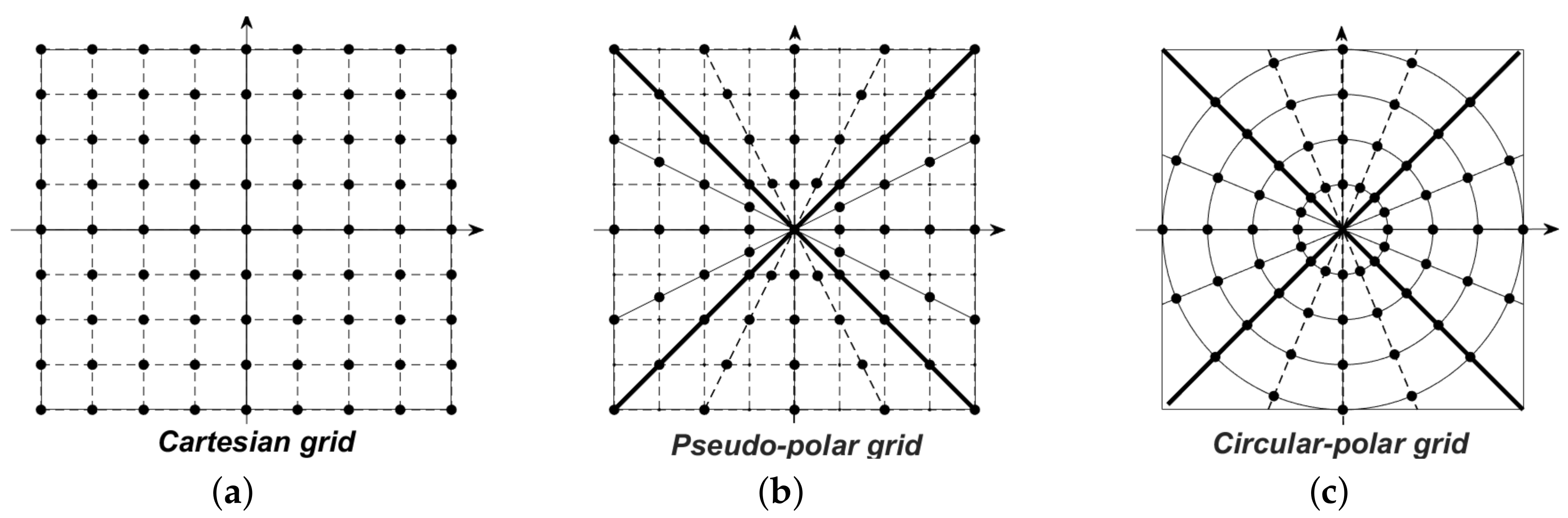
3.1. The Pseudo-Polar Grid

The pseudo-polar grid ${\Omega }_R$ is given as

$${\Omega }_R={\Omega }_R^1\cup {\Omega }_R^2,$$

(11)

where

$$\begin{array}{cc}\hfill {\Omega }_R^1=& \{(\frac{-4\ell k}{RN},\frac{2k}{R}):|\ell |\le N/2,|k|\le RN/2\},\hfill \\ \hfill {\Omega }_R^2=& \{(\frac{2k}{R},-\frac{4\ell k}{RN}):|\ell |\le N/2,|k|\le RN/2\},\hfill \end{array}$$

(12)

with $R=2$ the oversampling parameter. The nod of ${\Omega }_R^1$ is on the solid line in Figure 3b and the nod of ${\Omega }_R^2$ is on dotted line.

For an $N\times N$ image u, the general discrete Fourier transform $\widehat{u}$ is evaluated on the $N\times N$ Cartesian grid in the form

$$\widehat{u}({\omega }_x,{\omega }_y)=\sum _{x,y=-N/2}^{N/2-1}u(x,y)e^{-\frac{2\pi i}{N}(x{\omega }_x+y{\omega }_y)},$$

(13)

where $\{({\omega }_x,{\omega }_y):{\omega }_x,{\omega }_y=-N/2,\dots ,N/2.\}$, and

$$\sum _{x,y=-N/2}^{N/2-1}{\left|u(x,y)\right|}^2=\frac{1}{N^2}\sum _{{\omega }_x,{\omega }_y=-N/2}^{N/2-1}{\left|\widehat{u}({\omega }_x,{\omega }_y)\right|}^2.$$

(14)

Analogously, the pseudo-polar Fourier transform is the same as (13) (see [5]), but $\{({\omega }_x,{\omega }_y)\in {\Omega }_R.\}$. According to the Plancherel theorem, (14) can be modified by introducing the weighting function w

$$\sum _{x,y=-N/2}^{N/2-1}{\left|u(x,y)\right|}^2=\sum _{({\omega }_x,{\omega }_y)\in {\Omega }_R}^{N/2-1}w({\omega }_x,{\omega }_y){\left|\widehat{u}({\omega }_x,{\omega }_y)\right|}^2.$$

(15)

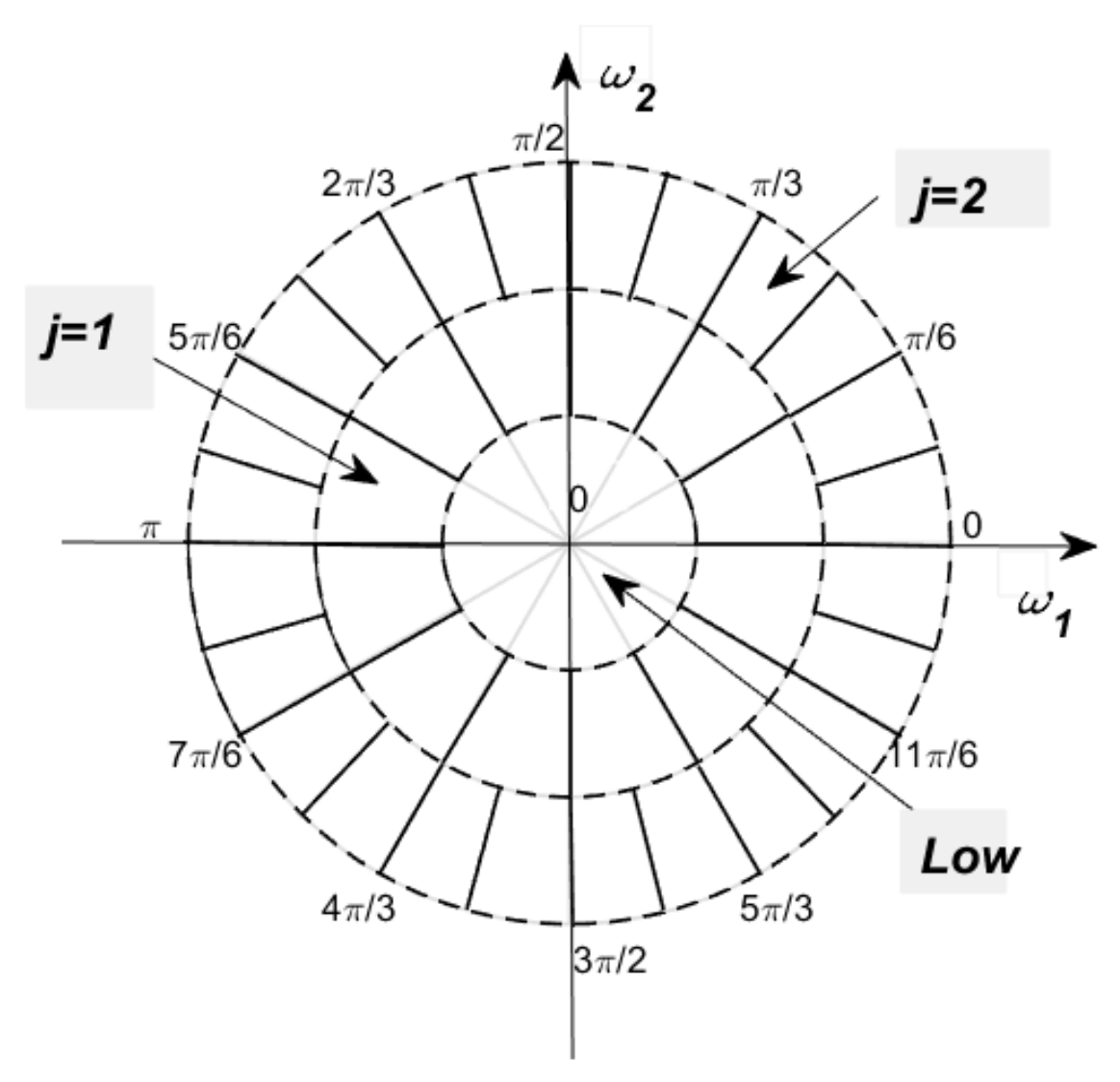
3.2. The Circular-Polar Grid (CPG)

In this section, the circular-polar grid (CPG) is designed (see Figure 3c), which is defined as

$$C_R=C_R^0\cup C_R^{♯};$$

(16)

where $C_R^0=\left\{(0,0)\right\}$ and $C_R^{♯}=C_R^1\cup C_R^2$

$$\begin{array}{cc}\hfill C_R^1=& \{(r\cos (\frac{\ell \pi }{m_0}),r\sin (\frac{\ell \pi }{m_0})):1\le |r|\le R,|\ell |\le \frac{m_0}{2}\},\hfill \\ \hfill C_R^2=& \{(r\sin (\frac{\ell \pi }{m_0}),r\cos (\frac{\ell \pi }{m_0})):1\le |r|\le R,|\ell |\le \frac{m_0}{2}\},\hfill \end{array}$$

(17)

where $m_0$ is the sampling number in each circle.

As can be seen from Figure 3c, the nod of $C_R^1$ is on a solid line and the nod on a dotted line belongs to $C_R^2$. In addition, r in (17) serves as the radius and ℓ serves as the parameter of angle. $m_0=16$ is the sampling number. In the CPG coordinates, the nod has the following characteristics, for

$$C_R^1({\omega }_x,{\omega }_y)=(r^1,{\theta }^1),C_R^2({\omega }_x,{\omega }_y)=(r^2,{\theta }^2),$$

(18)

where

$$\begin{array}{c}{r}^1=k_1,r^2=k_2,\hfill \\ {\theta }^1={\ell }_1\pi /m_0;{\theta }^2={\ell }_2\pi /m_0.\hfill \end{array}$$

(19)

$k_i=0,\dots R;$ $i=1,2$ and ${\ell }_i=-m_0/2,\dots m_0/2;$ $i=1,2$. For each fixed angle $\theta$, the samples of the CPG are equally spaced in the radial direction, and, for each fixed radius r, the grid possesses the same angle. Formally,

$$\begin{array}{c}\Delta r^1\triangleq (k_1+1)-k_1=1;\Delta r^2\triangleq (k_2+1)-k_2=1,\hfill \\ \Delta {\theta }^1\triangleq ({\ell }_1+1)\pi /m_0-{\ell }_1\pi /m_0=\pi /m_0,\hfill \\ \Delta {\theta }^2\triangleq ({\ell }_2+1)\pi /m_0-{\ell }_2\pi /m_0=\pi /m_0,\hfill \end{array}$$

(20)

where $r^1,r^2$ and ${\theta }^1,{\theta }^2$ are given by (19).

For an $N\times N$ image u, the CFT of $\widehat{u}$ on CPG holds

$$\sum _{x,y=-N/2}^{N/2-1}{\left|u(x,y)\right|}^2=\sum _{({\omega }_x,{\omega }_y)\in C_R}{w}_c({\omega }_x,{\omega }_y){\left|\widehat{u}({\omega }_x,{\omega }_y)\right|}^2,$$

(21)

and

$${\widehat{u}}_{C_R}({\omega }_x,{\omega }_y)=\sum _{x,y=-N/2}^{N/2-1}u(x,y)e^{-\frac{2\pi i}{R{m}_0+1}(x{\omega }_x+y{\omega }_y)}.$$

(22)

Using operator notation, we denote the refined $CFT$ of an image u as ${\mathcal{F}}_p$, where

$$\left({\mathcal{F}}_{p}u\right)(r,\ell )\triangleq {\widehat{u}}_{C_R}(r,\ell ),$$

(23)

with $r=-R,\dots ,R$, $\ell =-m_0/2,\dots ,m_0/2$. Now, our goal is to choose weight $w_c$, such that $w_c$ satisfies (21), and we have

$$\begin{array}{c}\sum _{({\omega }_x,{\omega }_y)\in C_R}{w}_c({\omega }_x,{\omega }_y){|\widehat{u}({\omega }_x,{\omega }_y)|}^2\hfill \\ =\sum _{({\omega }_x,{\omega }_y)\in C_R}{w}_c({\omega }_x,{\omega }_y)|\sum _{x,y=-N/2}^{N/2-1}u(x,y)E(x,y)|{}^2\hfill \\ =\sum _{({\omega }_x,{\omega }_y)\in C_R}{w}_c({\omega }_x,{\omega }_y)[\sum _{x,y=-N/2}^{N/2-1}\sum _{x^{\prime },y^{\prime }=-N/2}^{N/2-1}u(x,y)E(x,y)\overline{u(x^{\prime },y^{\prime })E(x^{\prime },y^{\prime })}]\hfill \\ =\sum _{({\omega }_x,{\omega }_y)\in C_R}{w}_c({\omega }_x,{\omega }_y)\sum _{x,y=-N/2}^{N/2-1}{|u(x,y)|}^2\hfill \\ +\sum _{(x,y)\ne (x^{\prime },y^{\prime })}u(x,y)\overline{u(x^{\prime },y^{\prime })}[\sum _{({\omega }_x,{\omega }_y)\in C_R}{w}_c({\omega }_x,{\omega }_y)E(x,y)\overline{E(x^{\prime },y^{\prime })}],\hfill \end{array}$$

(24)

where $E(x,y)\triangleq e^{-\frac{2\pi i}{R{m}_0}(x{\omega }_x+y{\omega }_y)}$. Compared with the left of equation (21), the weights $w_c$ holds

$$\sum _{({\omega }_x,{\omega }_y)\in C_R}{w}_c({\omega }_x,{\omega }_y)e^{-\frac{2\pi i}{Rm+1}(x{\omega }_x+y{\omega }_y)}=\delta (x,y);$$

(25)

with $-N/2\le x,y\le N/2-1$.

3.3. The Choice of Weights $w_c$

In the following, we present the basic condition of weights $w_c$, according to (25), which satisfies that

$$\begin{array}{cc}\hfill 0& =\sum _{({\omega }_x,{\omega }_y)\in C_R^{♯}}{w}_c({\omega }_x,{\omega }_y)[\cos (\frac{2\pi }{R{m}_0+1}x{\omega }_x)\cos (\frac{2\pi }{R{m}_0+1}y{\omega }_y)\hfill \\ & -\sin (\frac{2\pi }{R{m}_0+1}x{\omega }_x)\sin (\frac{2\pi }{R{m}_0+1}y{\omega }_y)];\hfill \\ \hfill 0& =\sum _{({\omega }_x,{\omega }_y)\in C_R^{♯}}{w}_c({\omega }_x,{\omega }_y)[\sin (\frac{2\pi }{R{m}_0+1}x{\omega }_x)\cos (\frac{2\pi }{R{m}_0+1}y{\omega }_y)\hfill \\ & +\cos (\frac{2\pi }{R{m}_0+1}x{\omega }_x)\sin (\frac{2\pi }{R{m}_0+1}y{\omega }_y)].\hfill \end{array}$$

(26)

According to the symmetry of the $CFT$, the weighting function $w_c$ is assumed to satisfy

$$\begin{array}{cc}\hfill w_c({\omega }_x,{\omega }_y)& =w_c({\omega }_y,{\omega }_x),({\omega }_x,{\omega }_y)\in C_R,\hfill \\ \hfill w_c({\omega }_x,{\omega }_y)& =w_c({\omega }_y,-{\omega }_x),({\omega }_x,{\omega }_y)\in C_R,\hfill \\ \hfill w_c({\omega }_x,{\omega }_y)& =w_c(-{\omega }_y,-{\omega }_x),({\omega }_x,{\omega }_y)\in C_R,\hfill \end{array}$$

(27)

where four equations of (27) describe the $({\omega }_y={\omega }_x)$-symmetry, $({\omega }_y=-{\omega }_x)$-symmetry and the $origin$-symmetry.

In addition,

$$\sum _{({\omega }_x,{\omega }_y)\in C_R}{w}_c({\omega }_x,{\omega }_y)=1.$$

(28)

To avoid high complexity, we choose the weight $w({\omega }_x,{\omega }_y)$ in the form:

$$w({\omega }_x,{\omega }_y)=\frac{w_0({\omega }_x,{\omega }_y)}{{\sum }_{{\omega }_x,{\omega }_y}{w}_0({\omega }_x,{\omega }_y)},$$

(29)

where

$$w_0({\omega }_x,{\omega }_y)=\frac{1}{m_{0}r},\{({\omega }_x,{\omega }_y):{\omega }_x^2+{\omega }_y^2=r^2\},$$

(30)

with $r\in [1,R]$, and $w(0,0)=1$.

4. The Construction of Multilevel System in Frequency Domain

In this section, we construct a new type multilevel system on $CPG$ in the frequency domain.

4.1. 2D Basic Harmonic Function

First, we define the 2D basic harmonic wavelet functions in the Fourier domain. For deriving convenience, the wavelet function $\mathit{H}$ and scaling function $\mathit{S}$ can be normalized in the form given by Definition 1 .

Definition 1.

The 2D harmonic basic functions are defined as

$$\begin{array}{cc}\hfill \mathit{H}(r,\theta )& :\triangleq H\left(2\pi \right|r\left|\cos \right(\left|\theta \right|\left)\right)S\left(2\pi \right|r\left|\sin \right(\left|\theta \right|\left)\right),\hfill \\ \hfill \mathit{S}(r,\theta )& :\triangleq S\left(2\pi \right|r\left|\cos \right(\left|\theta \right|\left)\right)S\left(2\pi \right|r\left|\sin \right(\left|\theta \right|\left)\right),\hfill \end{array}$$

(31)

with $r\in [-R,R]$, $\theta \in [0,\pi ]$.

Then, the support of $\mathit{H}(r,\theta )$ and $\mathit{S}(r,\theta )$ are investigated, according to (3) and (6),

$$H\left(2\pi \right|r\left|\cos \right(\left|\theta \right|\left)\right)\ne 0,S\left(2\pi \right|r\left|\sin \right(\left|\theta \right|\left)\right)\ne 0$$

(32)

hold simultaneously; therefore,

$$1\le \left|r\right|\cos \left(\right|\theta \left|\right)\le 2,0\le \left|r\right|\sin \left(\right|\theta \left|\right)\le 1.$$

(33)

Thus, the support of $\mathit{H}(r,\theta )$ is given as

$$\sqrt{2}\le \left|r\right|\le 2,\left|\theta \right|\le \pi /4.$$

(34)

Similarly,

$$\mathrm{supp}\mathit{S}(r,\theta )=\left\{\right(r,\theta ):0\le |r|\le 1,|\theta |\le \pi /4\}.$$

(35)

Next, the 2D scaling and shifting of $\mathit{H}(r,\theta )$ and $\mathit{S}(r,\theta )$ are defined.

Definition 2.

The 2D scaling and shifting of harmonic basic functions in the frequency domain are defined as

$$\begin{array}{c}{\mathit{H}}_{j,\ell }(r,\theta ):\triangleq H(2\pi 2^{-j}\left|r\right|\cos (2^j|\theta -\ell |\left)\right)S(2\pi 2^{-j}\left|r\right|\sin (2^j|\theta -\ell |\left)\right),\hfill \\ {\mathit{S}}_{j,\ell }(r,\theta ):\triangleq S(2\pi 2^{-j}\left|r\right|\cos (2^j|\theta -\ell |\left)\right)S(2\pi 2^{-j}\left|r\right|\sin (2^j|\theta -\ell |\left)\right),\hfill \\ {\mathit{H}}_{j,\ell }^{\ast }(r,\theta ):\triangleq H(2\pi 2^{-j}\left|r\right|\sin (2^j|\theta -\ell |\left)S\right(2\pi 2^{-j}\left|r\right|\cos (2^j|\theta -\ell |\left)\right),\hfill \\ {\mathit{S}}_{j,\ell }^{\ast }(r,\theta ):\triangleq S(2\pi 2^{-j}\left|r\right|\sin (2^j|\theta -\ell |-\frac{\pi }{2}\left)\right)S(2\pi 2^{-j}\left|r\right|\sin (2^j|\theta -\ell |\left)\right),\hfill \end{array}$$

(36)

with $j,\ell \in R$.

4.2. The Polar Harmonic Multilevel System in the Frequency Domain (PHMS) on CPG

In this section, we give the definition of the polar harmonic multilevel system (PHMS) defined on CPG.

Definition 3.

The 2D PHMS on CPG is defined as

$$PHMS:\triangleq {\mathit{H}}_{j,{\ell }_j}(r,\theta )\cup {\mathit{S}}_{j,{\ell }_j}(r,\theta )\cup {\mathit{H}}_{j,{\ell }_j}^{\ast }(r,\theta )\cup {\mathit{S}}_{j,{\ell }_j}^{\ast }(r,\theta ),$$

(37)

where ${\mathit{H}}_{j,\ell }$, ${\mathit{H}}_{j,\ell }^{\ast }$, ${\mathit{S}}_{j,\ell }$ and ${\mathit{S}}_{j,\ell }^{\ast }$ are given in (36). The level parameter $j\le \left[{\log }_{2}R\right]$, the shifting parameter is related to j, and we defined the ${\ell }_j=\ell 2^{-j}\frac{\pi }{4}$ with $\left|\ell \right|\le 2^j,\ell \in Z$.

From $\left|\ell \right|\le 2^j$, we have $2(2^{j+1}+1)$ subbands in each level j, in order to reduce the overlap, we choose $2\left(2^{j+1}\right)$ subbands; then, the PHMS constructs a partition of the Fourier domain. We displayed the PHMS structure in Figure 4.

For a signal or image u, the corresponding PHMS transform $\mathcal{P}\left(u\right)$ in the frequency domain can be defined as

$$\begin{array}{cc}\hfill \mathcal{P}\left(u\right)\triangleq <{\widehat{u}}_{C_R},PHMS>& =\sum _{j=0}^J\sum _{{\ell }_j=-\ell (2^{-j}\frac{\pi }{4})}^{\ell (2^{-j}\frac{\pi }{4})}\sum _{\ell =-2^j}^{2^j}({\mathit{H}}_{j,{\ell }_j}.\ast {\widehat{u}}_{C_R}+{\mathit{S}}_{j,{\ell }_j}.\ast {\widehat{u}}_{C_R}\hfill \\ & +{\mathit{H}}_{j,{\ell }_j}^{\ast }.\ast {\widehat{u}}_{C_R}+{\mathit{S}}_{j,{\ell }_j}^{\ast }.\ast {\widehat{u}}_{C_R}),\hfill \end{array}$$

(38)

with ${\ell }_j=\ell 2^{-j}\frac{\pi }{4}$, $\left|\ell \right|\le 2^j,\ell \in Z$, where ${\widehat{u}}_{C_R}$ is the $CPFT$ of u, defined in (22). In addition, ${}^{\prime }.{\ast }^{\prime }$ is the dot product, and the matrix $M_1.\ast M_2$ is defined as

$${(M_1.\ast M_2)}_{i,j}={\left(M_1\right)}_{i,j}{\left(M_2\right)}_{i,j}.$$

(39)

Theorem 1.

The discrete polar harmonic multilevel system PHMS defined on CPG forms a framelet of $L^2\left(R^2\right)$.

According to the framelet defined in [18], for the signal $\mathit{U}$ in (38),

$${\parallel \mathit{U}\parallel }^2\le {\parallel <\mathit{U},PHMS>\parallel }^2\le c{\parallel \mathit{U}\parallel }^2,$$

(40)

where $c<+\infty$ is the constant; therefore, PHMS forms a framelet of $L^2\left(R^2\right)$.

Then two denoising reconstruction tests of PHMS are shown in Figure 5.

5. Quantitative Test Measures

In the following, several performance measures are introduced to test the quality of the $PHMS$. The quality measure is the Monte Carlo estimate for the different operator norm by generating a sequence of five random images $u_i,i=1,\dots ,5$ on $CPG$ for $R=256,\ell =8$ with standard normally distributed entries.

• Isometry of $CFT$:

  (a)

  Closeness to tight: $M_{clo}={\max }_{i=1,\dots ,5}\frac{\parallel {\mathcal{F}}_p^{\ast }{\mathcal{F}}_p{u}_i-u_i{\parallel }_2}{\parallel u_i{\parallel }_2},$

  (b)

  Quality of preconditioning. $M_{qua}=\frac{{\lambda }_{\max }\left({\mathcal{F}}_p^{\ast }{\mathcal{F}}_p\right)}{{\lambda }_{\min }\left({\mathcal{F}}_p^{\ast }w{\mathcal{F}}_p\right)}.$

• Tight Frame Property: The operator norm $\parallel {\mathcal{P}}^{\ast }{\mathcal{P}-I\parallel }_{op}$, which is defined as $M_{tig}={\max }_{i=1,\dots ,5}\frac{\parallel {\mathcal{P}}^{\ast }\mathcal{P}{u}_i-u_i{\parallel }_2}{\parallel u_i{\parallel }_2}.$
• Robustness:

  (a)

  Thresholding: Let u be the regular sampling of a Gaussian function with mean 0 and variance 512 on ${\left[257\right]}^2$ generating an $512\times 512$ image. Two types of robustness are considered, for $k=1,2$, and $M_{p_k}=\frac{\parallel {\mathcal{P}}^{\ast }{T}_{p_k}{\mathcal{P}u-u\parallel }_2}{{\parallel u\parallel }_2}$.

  $T_{p_1}$:

  $T_{p_1}$ discards $100(1-2^{-p_1})$ percent of coefficient, with $p_1=[2:2:20]$.

  $T_{p_2}$:

  $T_{p_2}$ keeps the absolute value of coefficients bigger than $m/2^{p_2}$ with m is the maximal absolute value of all coefficients, where $p_2=[0.5:0.5:5]$.

  (b)

  Quantization: The quality measure is given as $M_p=\frac{\parallel {\mathcal{P}}^{\ast }{Q}_q{\mathcal{P}u-u\parallel }_2}{{\parallel u\parallel }_2},$ where $Q_q\left(c\right)=round(c/(m/2^q))·(m/2^q)$, and $q\in [5:-0.5:0.5]$.

6. Test Results

In this section, the test results of $PHMS$ on $CPG$ for quantitative measure in (1)–(3) are shown.

First the performance with respect to quantitative measures in $\left(1\right)$, $\left(2\right)$ are presented in

Table 1. Results of Labels (1)–(2).

${\mathit{M}}_{\mathit{clo}}$	${\mathit{M}}_{\mathit{qua}}$	${\mathit{M}}_{\mathit{tig}}$
0.00946092	1.9342627	0.1036731

.

From Table 1, the error of tightness $M_{tig}$ for the $PHMS$ transform is about 0.1, which confirms that the multilevel system is indeed not a tight frame. The main reason is the redundancy of the multilevel structure due to the radius in (36). The quantity $M_{clo}\approx 0.0095$ and $M_{qua}\approx 1.934$ suggests that the circular-polar Fourier transform provides good properties in terms of isometry, which allows us to employ the conjugate gradient method to compute the inverse of ${\mathcal{F}}_p$. The weight w should also be chosen carefully.

Second, the robustness measurements in $\left(3\right)$ displayed in

Table 2. Results of Label $\left(3\right)$.

${\mathit{M}}_{{\mathit{p}}_1}$	3.6 × 10${}^{-6}$	1.7 × 10${}^{-5}$	5.9 × 10${}^{-3}$	2.1 × 10${}^{-2}$	0.9 × 10${}^{-2}$
${\mathit{M}}_{{\mathit{p}}_{\mathbf{2}}}$	0.009	0.063	0.103	0.172	0.197
${\mathit{M}}_{\mathit{p}}$	0.051	0.065	0.083	0.126	0.143

:

Table 2 shows the robustness of $PHMS$. Even discarding $100(1-2^{-10})\approx 99.9\%$ of the coefficients, the image still can be recovered with error $M_{P_1}=0.9\times {10}^{-2}$. The second row suggests that just the coefficient greater than thresholding value $m(1-1/2^{0.001})\approx 0.1\%$ can give a good reconstruction with $M_{p_2}=0.009$. In the third row, the quantization of robustness $M_p$ is displayed.

7. Conclusions

In this work, we developed and implemented a polar harmonic multilevel system on the circular-polar grid based on the multiscale theory, and testified to the performance of the $PHMS$ in four different quantitative measures, which suggests that the $PHMS$ transform is suitable for the circular-shape Fourier transform. Another advantage of the $PHMS$ is that the circular low frequency region in the frequency domain is consistent with the image spectrum distribution, which can process the multilevel structure more effectively.