Spin-Orbital Momentum Decomposition and Helicity Exchange in a Set of Non-Null Knotted Electromagnetic Fields
Abstract
:1. Introduction
2. Duality and Helicity in Maxwell Theory in a Vacuum
- If the integral of is zero, both the magnetic and the electric helicities are constant during the evolution of the electromagnetic field.
- If the integral of is not zero, the helicities are not constant, but they satisfy:so there is an interchange of helicities between the magnetic and electric parts of the field [8].
- For every value of the integral of , the electromagnetic helicity h, defined as:is a conserved quantity.
3. Fourier Decomposition and Helicity Basis for the Electromagnetic Field in a Vacuum
4. Magnetic and Electric Helicities in the Helicity Basis
5. Magnetic and Electric Spin in the Helicity Basis
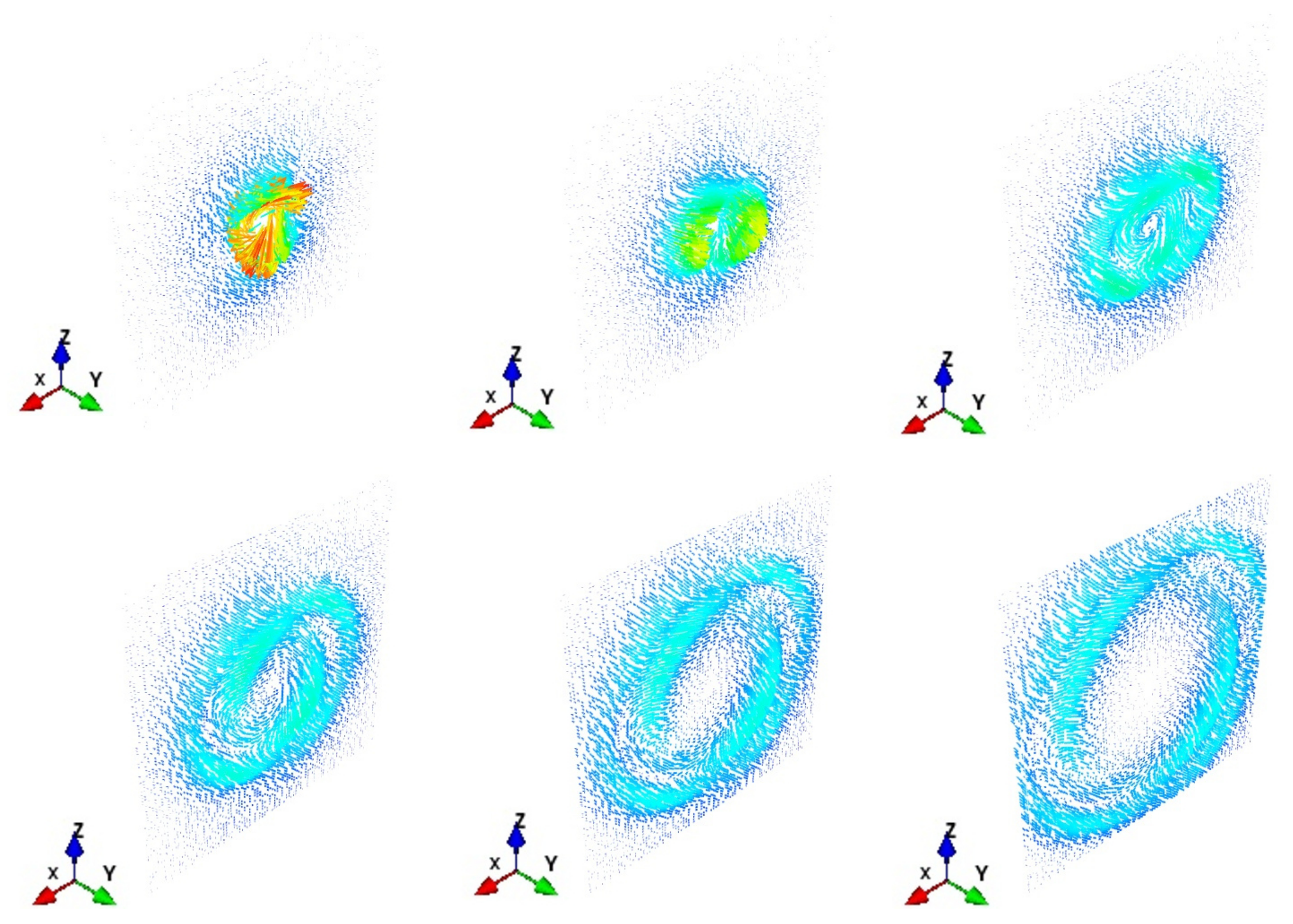
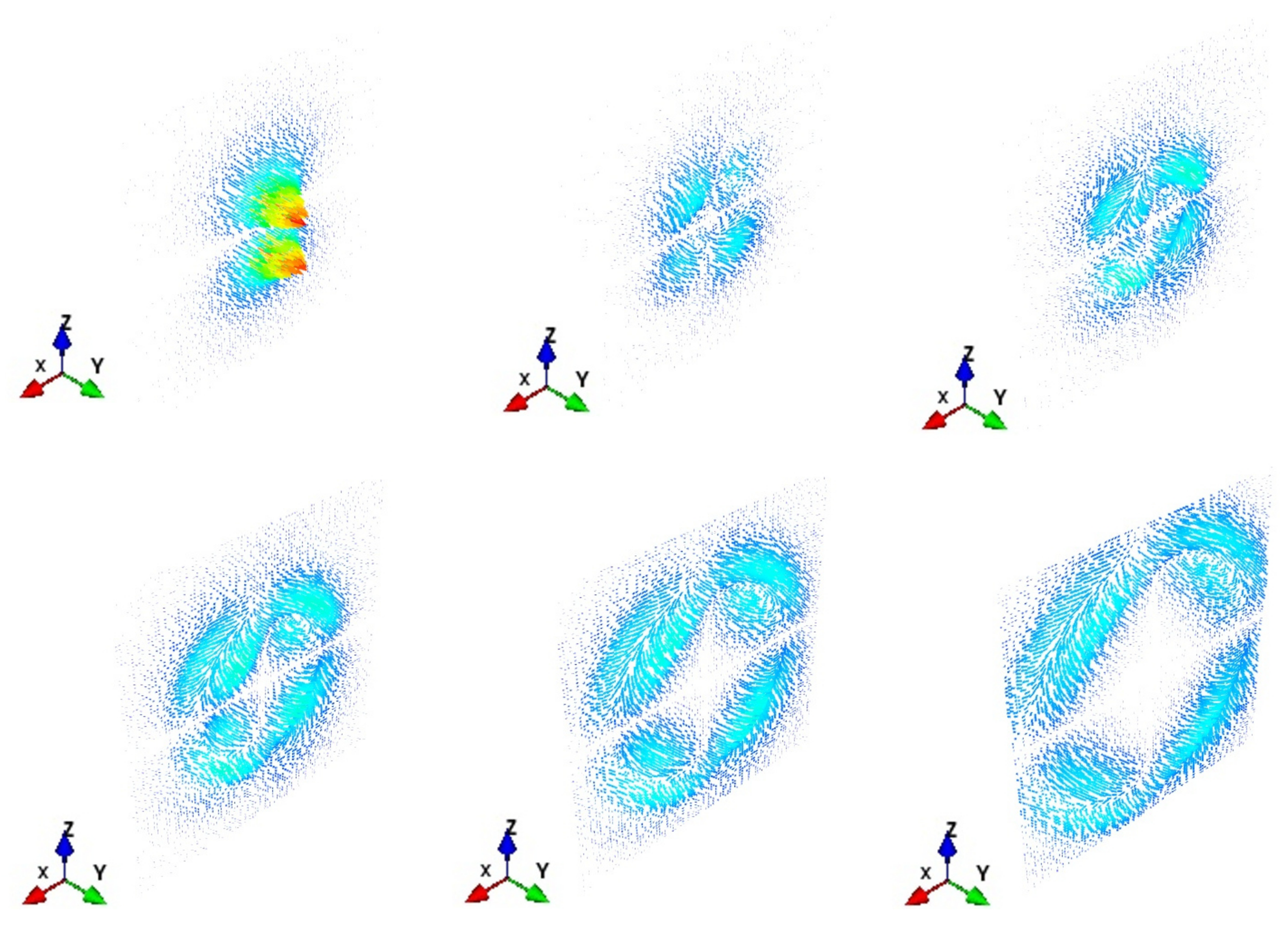
6. The Angular Momentum Decomposition for Non-Null Toroidal Electromagnetic Fields
7. Same Spin-Orbital Decomposition with Different Behavior in the Helicities
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Enk, S.J.; Nienhuis, G. Spin and orbital angular momentum of photons. Europhys. Lett. 1994, 25, 497–501. [Google Scholar] [CrossRef]
- Van Enk, S.J.; Nienhuis, G. Commutation rules and eigenvalues of spin and orbital angular momentum of radiation fields. J. Mod. Opt. 1994, 41, 963–977. [Google Scholar] [CrossRef]
- Allen, L.; Barnett, S.M.; Padgett, M.J. (Eds.) Optical Angular Momentum; Institute of Physics: Bristol, UK, 2003. [Google Scholar]
- Bliokh, K.Y.; Aiello, A.; Alonso, M. The Angular Momentum of Light; Andrews, D.L., Babiker, M., Eds.; Cambridge University Press: Hong Kong, China, 2012. [Google Scholar]
- Arrayás, M.; Trueba, J.L. A class of non-null toroidal electromagnetic fields and its relation to the model of electromagnetic knots. J. Phys. A Math. Theor. 2015, 48, 025203. [Google Scholar] [CrossRef]
- Afanasiev, G.N.; Stepanovsky, Y.P. The helicity of the free electromagnetic field and its physical meaning. Nuovo Cim. A 1996, 109, 271–279. [Google Scholar] [CrossRef]
- Trueba, J.L.; Rañada, A.F. The electromagnetic helicity. Eur. J. Phys. 1996, 17, 141–144. [Google Scholar] [CrossRef]
- Arrayás, M.; Trueba, J.L. Exchange of helicity in a knotted electromagnetic field. Ann. Phys. (Berl.) 2012, 524, 71–75. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bekshaev, A.Y.; Nori, F. Dual electromagnetism: Helicity, spin, momentum and angular momentum. New J. Phys. 2013, 15, 033026. [Google Scholar] [CrossRef]
- Berry, M.V. Optical currents. J. Opt. A Pure Appl. Opt. 2009, 11, 094001. [Google Scholar] [CrossRef]
- Ra nada, A.F. A topological theory of the electromagnetic field. Lett. Math. Phys. 1989, 18, 97–106. [Google Scholar] [CrossRef]
- Ra nada, A.F. Knotted solutions of the Maxwell equations in a vacuum. J. Phys. A Math. Gen. 1990, 23, L815–L820. [Google Scholar] [CrossRef]
- Ra nada, A.F. Topological electromagnetism. J. Phys. A Math. Gen. 1992, 25, 1621–1641. [Google Scholar] [CrossRef]
- Ra nada, A.F.; Trueba, J.L. Electromagnetic knots. Phys. Lett. A 1995, 202, 337–342. [Google Scholar] [CrossRef]
- Ra nada, A.F.; Trueba, J.L. Two properties of electromagnetic knots. Phys. Lett. A 1997, 232, 25–33. [Google Scholar] [CrossRef]
- Ra nada, A.F.; Trueba, J.L. A topological mechanism of discretization for the electric charge. Phys. Lett. B 1998, 422, 196–200. [Google Scholar] [CrossRef] [Green Version]
- Ra nada, A.F.; Trueba, J.L. Topological Electromagnetism with Hidden Nonlinearity. In Modern Nonlinear Optics III; Evans, M.W., Ed.; John Wiley & Sons: New York, NY, USA, 2001; pp. 197–253. [Google Scholar]
- Irvine, W.T.M.; Bouwmeester, D. Linked and knotted beams of light. Nat. Phys. 2008, 4, 716–720. [Google Scholar] [CrossRef]
- Besieris, I.M.; Shaarawi, A.M. Hopf-Rañada linked and knotted light beam solution viewed as a null electromagnetic field. Opt. Lett. 2009, 34, 3887–3889. [Google Scholar] [CrossRef] [PubMed]
- Arrayás, M.; Trueba, J.L. Motion of charged particles in a knotted electromagnetic field. J. Phys. A Math. Theor. 2010, 43, 235401. [Google Scholar] [CrossRef]
- Van Enk, S.J. The covariant description of electric and magnetic field lines of null fields: Application to Hopf-Rañada solutions. J. Phys. A Math. Theor. 2013, 46, 175204. [Google Scholar] [CrossRef]
- Kedia, H.; Bialynicki-Birula, I.; Peralta-Salas, D.; Irvine, W.T.M. Tying knots in light fields. Phys. Rev. Lett. 2013, 111, 150404. [Google Scholar] [CrossRef] [PubMed]
- Hoyos, C.; Sircar, N.; Sonnenschein, J. New knotted solutions of Maxwell’s equations. J. Phys. A Math. Theor. 2015, 48, 255204. [Google Scholar] [CrossRef]
- Kedia, H.; Foster, D.; Dennis, M.R.; Irvine, W.T.M. Weaving knotted vector fields with tunable helicity. Phys. Rev. Lett. 2016, 117, 274501. [Google Scholar] [CrossRef] [PubMed]
- Arrayás, M.; Bouwmeester, D.; Trueba, J.L. Knots in electromagnetism. Phys. Rep. 2017, 667, 1–61. [Google Scholar] [CrossRef]
- Arrayás, M.; Trueba, J.L. Collision of two hopfions. J. Phys. A Math. Theor. 2017, 50, 085203. [Google Scholar] [CrossRef]
- Kamchatnov, A.M. Topological solitons in magnetohydrodynamics. Zh. Eksp. Teor. Fiz. 1982, 82, 117–124. [Google Scholar]
- Semenov, V.S.; Korovinski, D.B.; Biernat, H.K. Euler potentials for the MHD Kamchatnov-Hopf soliton solution. Nonlinear Process. Geophys. 2002, 9, 347–354. [Google Scholar] [CrossRef]
- Thompson, A.; Swearngin, J.; Wickes, A.; Bouwmeester, D. Constructing a class of topological solitons in magnetohydrodynamics. Phys. Rev. E 2014, 89, 043104. [Google Scholar] [CrossRef] [PubMed]
- Smiet, C.B.; Candelaresi, S.; Thompson, A.; Swearngin, J.; Dalhuisen, J.W.; Bouwmeester, D. Self-organizing knotted magnetic structures in plasma. Phys. Rev. Lett. 2015, 115, 095001. [Google Scholar] [CrossRef] [PubMed]
- O’Holleran, K.; Dennis, M.R.; Padgett, M.J. Topology of light’s darkness. Phys. Rev. Lett. 2009, 102, 143902. [Google Scholar] [CrossRef] [PubMed]
- Dennis, M.R.; King, R.P.; Jack, B.; O’Holleran, K.; Padgett, M.J. Isolated optical vortex knots. Nat. Phys. 2010, 6, 118–121. [Google Scholar] [CrossRef]
- Romero, J.; Leach, J.; Jack, B.; Dennis, M.R.; Franke-Arnold, S.; Barnett, S.M.; Padgett, M.J. Entangled optical vortex links. Phys. Rev. Lett. 2011, 106, 100407. [Google Scholar] [CrossRef] [PubMed]
- Desyatnikov, A.S.; Buccoliero, D.; Dennis, M.R.; Kivshar, Y.S. Spontaneous knotting of self-trapped waves. Sci. Rep. 2012, 2, 771. [Google Scholar] [CrossRef] [PubMed]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on Structured Light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Faddeev, L.; Niemi, A.J. Stable knot-like structures in classical field theory. Nature 1997, 387, 58–61. [Google Scholar] [CrossRef]
- Hall, D.S.; Ray, M.W.; Tiurev, K.; Ruokokoski, E.; Gheorge, A.H.; Möttönen, M. Tying quantum knots. Nat. Phys. 2016, 12, 478–483. [Google Scholar] [CrossRef]
- Taylor, A.J.; Dennis, M.R. Vortex knots in tangled quantum eigenfunctions. Nat. Commun. 2016, 7, 12346. [Google Scholar] [CrossRef] [PubMed]
- Volovik, G.E.; Mineev, V.O. Particle-like solitons in superfluid He phases. Zh. Eksp. Teor. Fiz. 1977, 73, 767–773. [Google Scholar]
- Dzyloshinskii, I.; Ivanov, B. Localized topological solitons in a ferromagnet. Pis’ma Zh. Eksp. Teor. Fiz. 1979, 29, 592–595. [Google Scholar]
- Kawaguchi, Y.; Nitta, M.; Ueda, M. Knots in a spinor Bose-Einstein condensate. Phys. Rev. Lett. 2008, 100, 180403. [Google Scholar] [CrossRef] [PubMed]
- Kleckner, A.; Irvine, W.T.M. Creation and dynamics of knotted vortices. Nat. Phys. 2013, 9, 253–258. [Google Scholar] [CrossRef]
- Kleckner, A.; Irvine, W.T.M. Liquid crystals: Tangled loops and knots. Nat. Mat. 2014, 13, 229–231. [Google Scholar]
- Dalhuisen, J.W.; Bouwmeester, D. Twistors and electromagnetic knots. J. Phys. A Math. Theor. 2012, 45, 135201. [Google Scholar] [CrossRef]
- Thompson, A.; Swearngin, J.; Wickes, A.; Bouwmeester, D. Classification of electromagnetic and gravitational hopfions by algebraic type. J. Phys. A Math. Theor. 2015, 48, 205202. [Google Scholar] [CrossRef]
- Barnett, S.M. On the six components of optical angular momentum. J. Opt. 2011, 13, 064010. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Moffatt, H.K. The degree of knottedness of tangled vortex lines. J. Fluid Mech. 1969, 35, 117–129. [Google Scholar] [CrossRef]
- Berger, M.A.; Field, G.B. The topological properties of magnetic helicity. J. Fluid Mech. 1984, 147, 133–148. [Google Scholar] [CrossRef]
- Moffatt, H.K.; Ricca, R.L. Helicity and the Calugareanu Invariant. Proc. R. Soc. A 1992, 439, 411–429. [Google Scholar] [CrossRef]
- Berger, M.A. Introduction to magnetic helicity. Plasma Phys. Control. Fusion 1999, 41, B167–B175. [Google Scholar] [CrossRef]
- Dennis, M.R.; Hannay, J.H. Geometry of Calugareanu’s theorem. Proc. R. Soc. A 2005, 461, 3245–3254. [Google Scholar] [CrossRef]
- Ricca, R.L.; Nipoti, B. Gauss’ linking number revisited. J. Knot Theor. Ramif. 2011, 20, 1325–1343. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Alonso, M.A.; Ostrovskaya, E.A.; Aiello, A. Angular momenta and spin-orbit interaction of nonparaxial light in free space. Phys. Rev. A 2010, 82, 063825. [Google Scholar] [CrossRef]
- Barnett, S.M. Rotation of electromagnetic fields and the nature of optical angular momentum. J. Mod. Opt. 2010, 57, 1339–1343. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bialynicki-Birula, I.; Bialynicki-Birula, Z. Canonical separation of angular momentum of light into its orbital and spin parts. J. Opt. 2011, 13, 064014. [Google Scholar] [CrossRef]
- Ynduráin, F.J. Mecánica Cuántica; Alianza Editorial: Madrid, Spain, 1988. [Google Scholar]
- Bialynicki-Birula, I. Local and nonlocal observables in quantum optics. New J. Phys. 2014, 16, 113056. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arrayás, M.; Trueba, J.L. Spin-Orbital Momentum Decomposition and Helicity Exchange in a Set of Non-Null Knotted Electromagnetic Fields. Symmetry 2018, 10, 88. https://doi.org/10.3390/sym10040088
Arrayás M, Trueba JL. Spin-Orbital Momentum Decomposition and Helicity Exchange in a Set of Non-Null Knotted Electromagnetic Fields. Symmetry. 2018; 10(4):88. https://doi.org/10.3390/sym10040088
Chicago/Turabian StyleArrayás, Manuel, and José L. Trueba. 2018. "Spin-Orbital Momentum Decomposition and Helicity Exchange in a Set of Non-Null Knotted Electromagnetic Fields" Symmetry 10, no. 4: 88. https://doi.org/10.3390/sym10040088




