Multiple Slip Effects on Magnetohydrodynamic Axisymmetric Buoyant Nanofluid Flow above a Stretching Sheet with Radiation and Chemical Reaction
Abstract
:1. Introduction
2. Mathematical Formulation
3. Finite Element Method Solutions
3.1. Variational Formulations
3.2. Finite Element Formulations
4. Results and Discussion
5. Conclusions
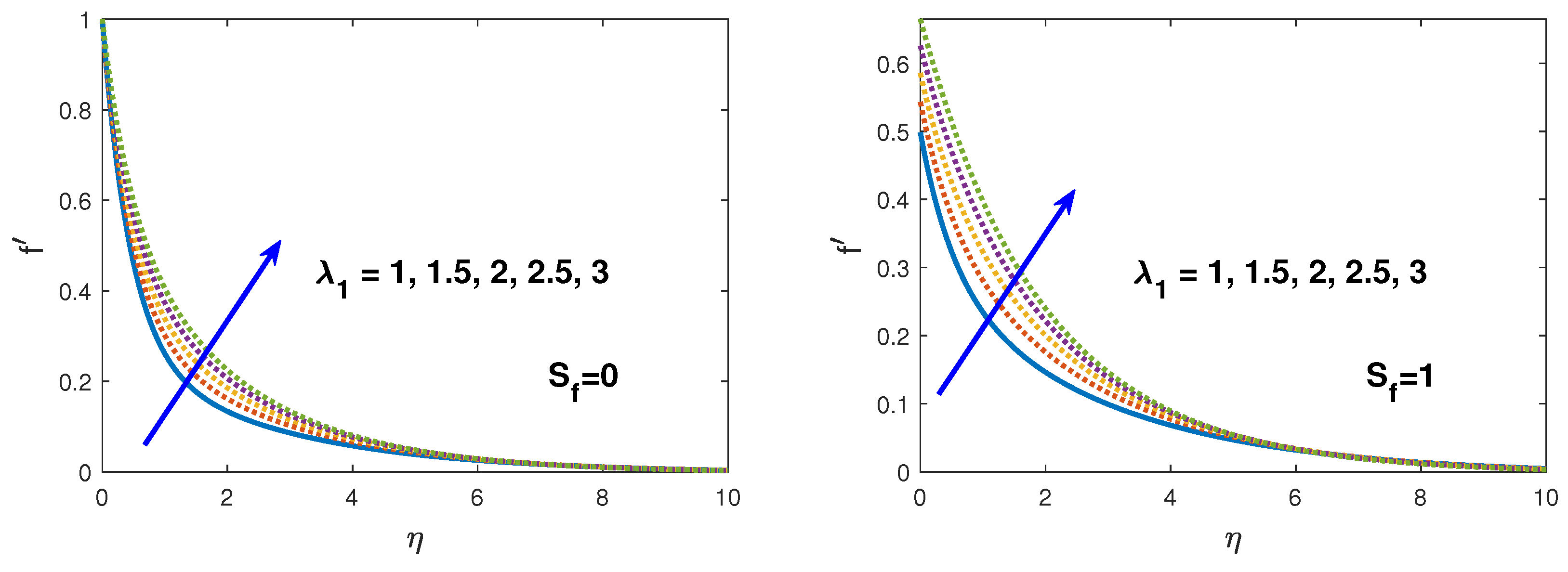
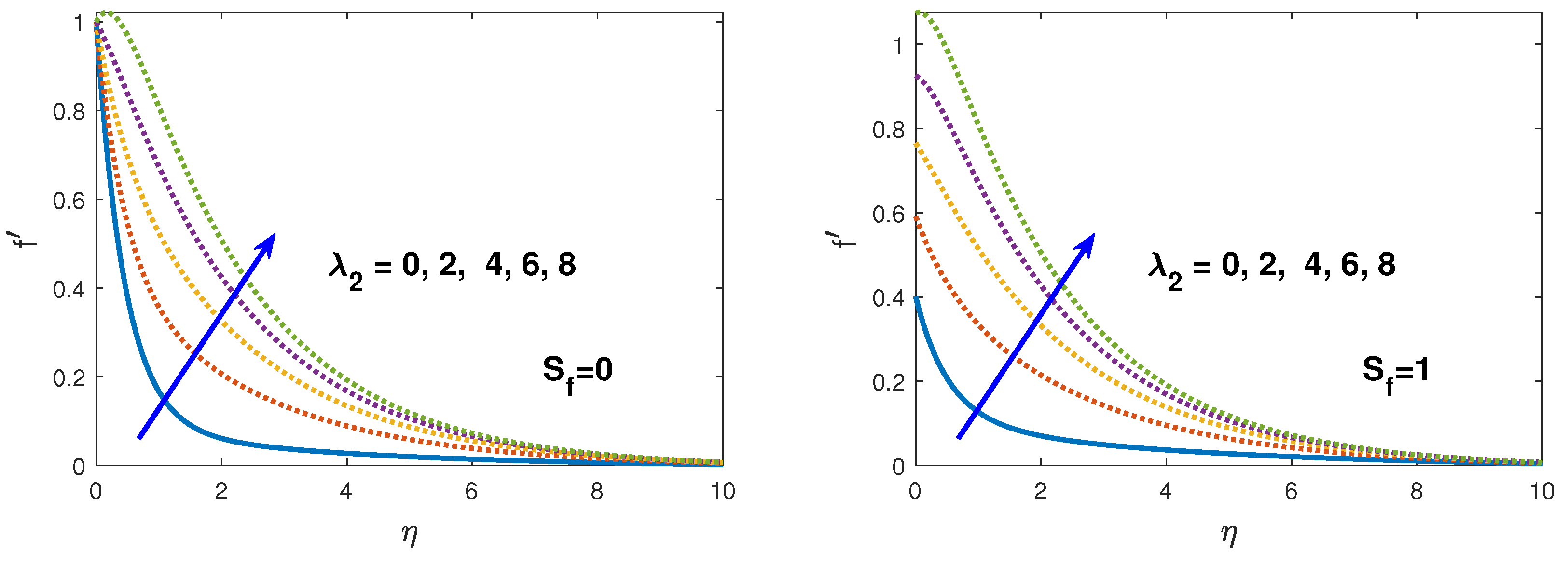
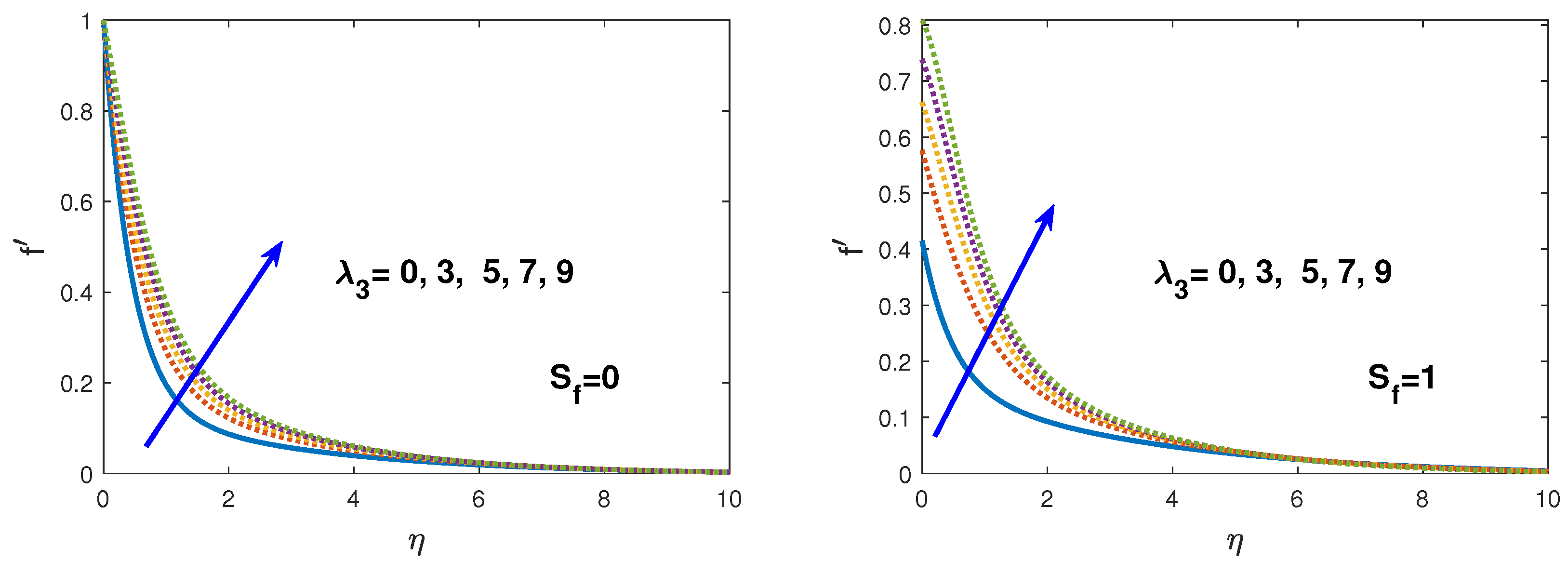
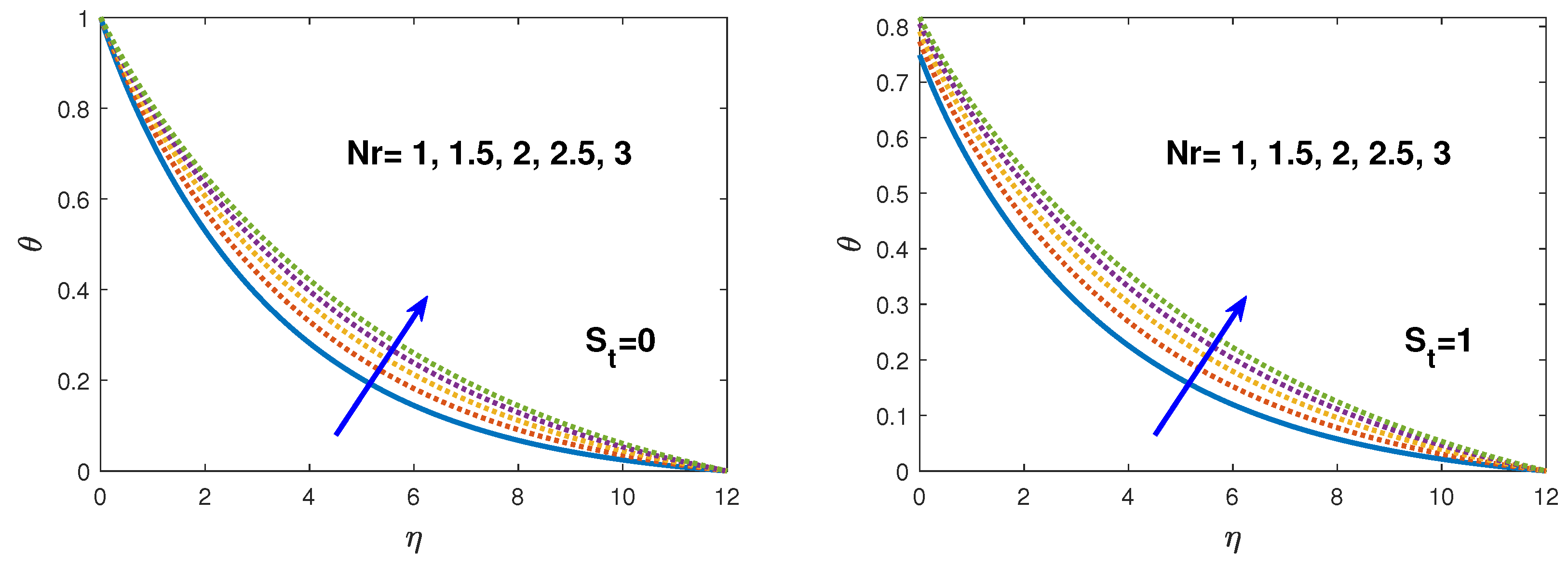
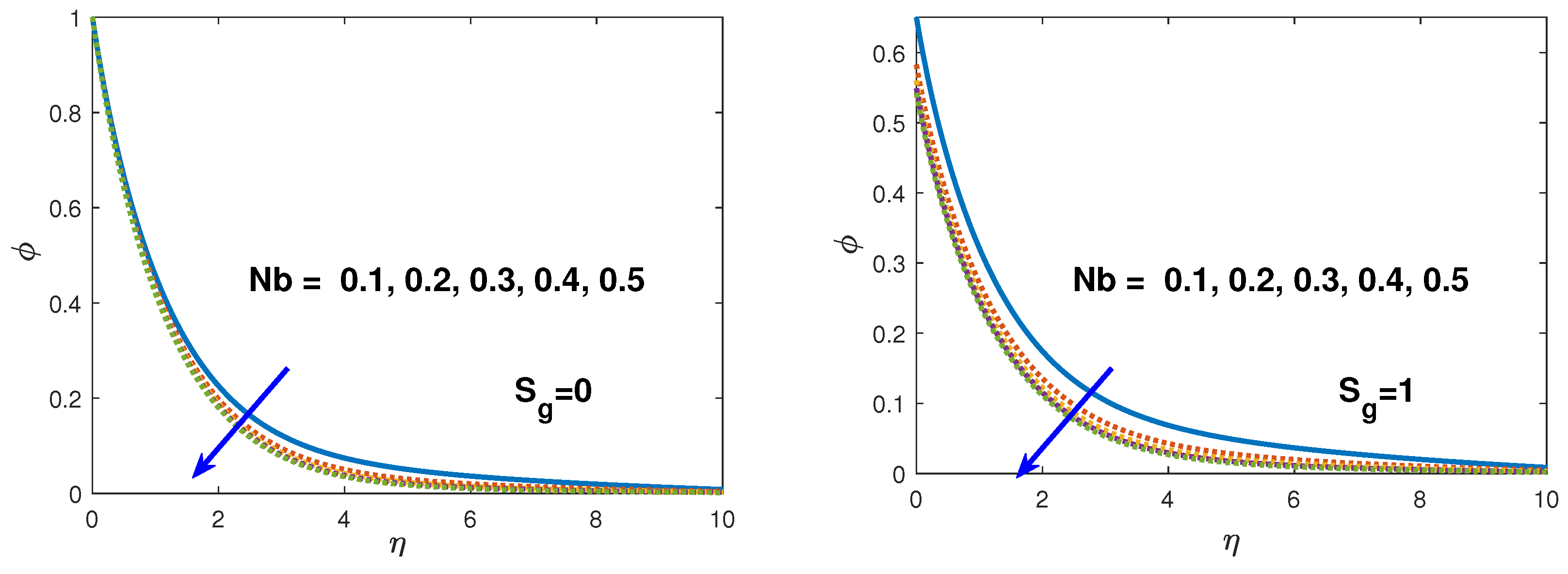
- In the existence of the hydrodynamic, thermal, solute and nano-fluid slip the velocity, temperature, solute concentration and nano-fluid volume fraction boundary layers increases.
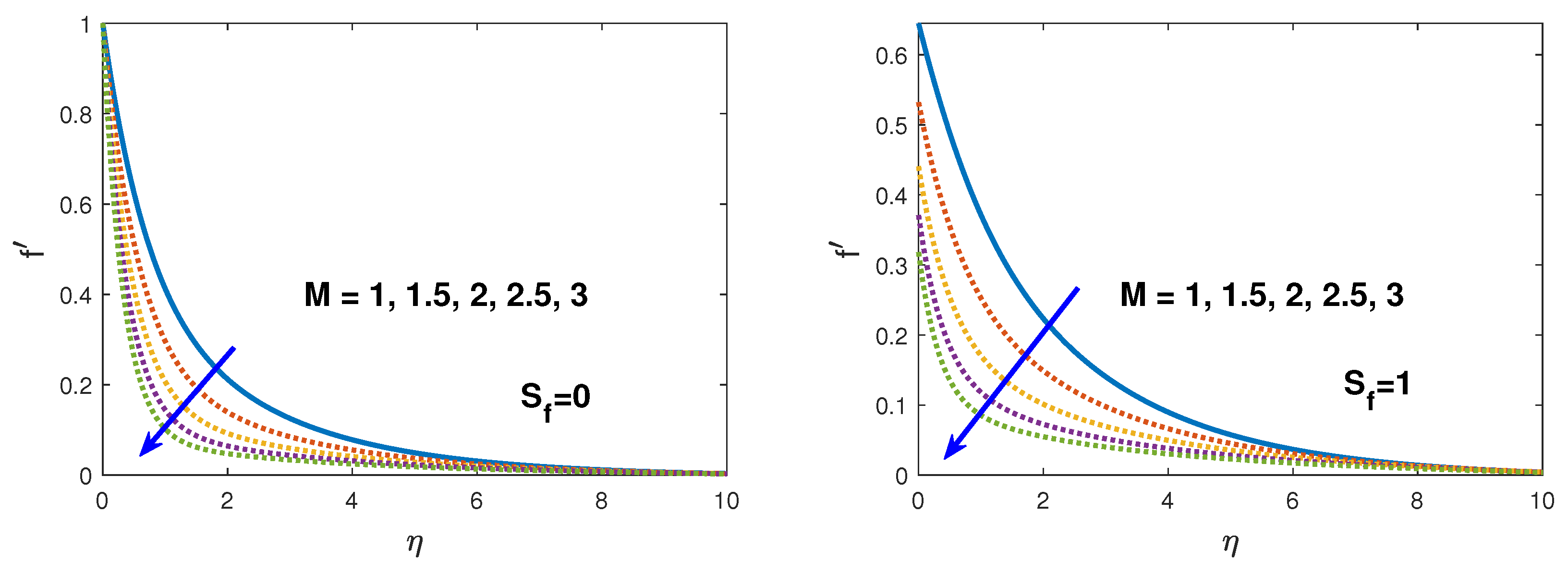
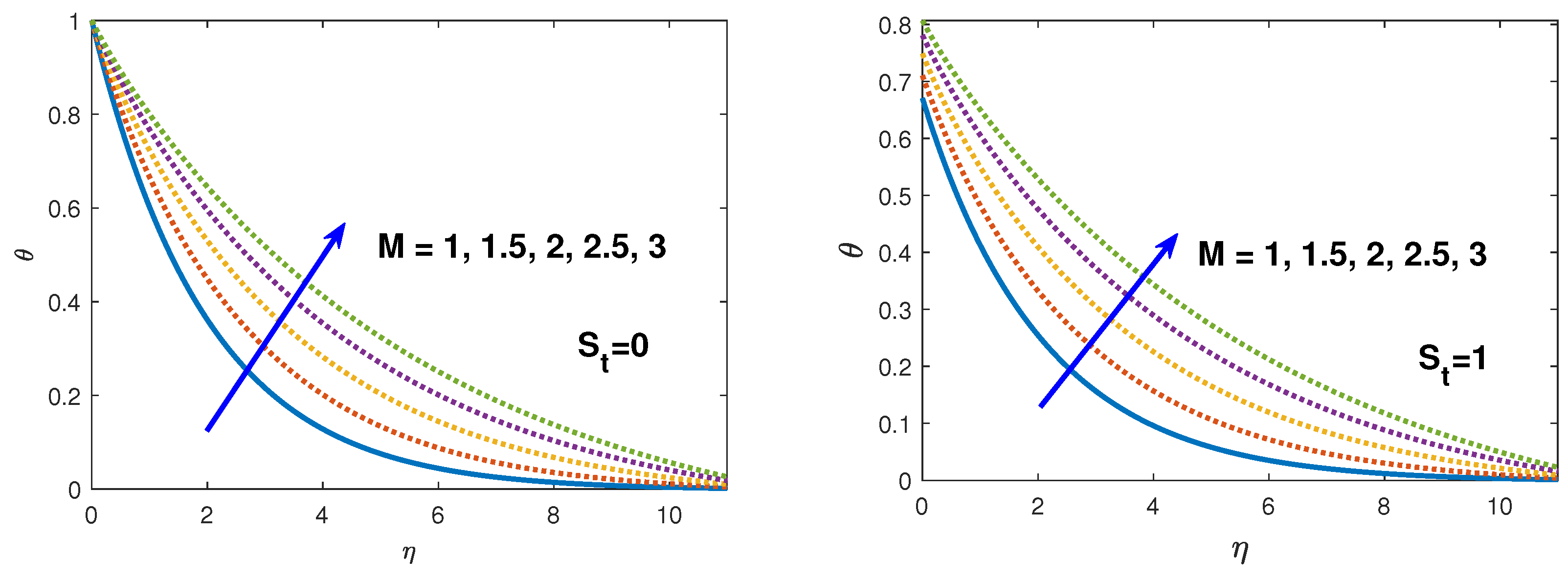
- The radial velocity profile decreases while temperature and solute concentration increases with the increase in magnetic field and slip conditions.
- The velocity profile increases with increasing buoyancy parameters ().
- After enhancement of magnetic and thermal radiation parameter the effect of thermal slip for temperature profile increased the boundary layer.
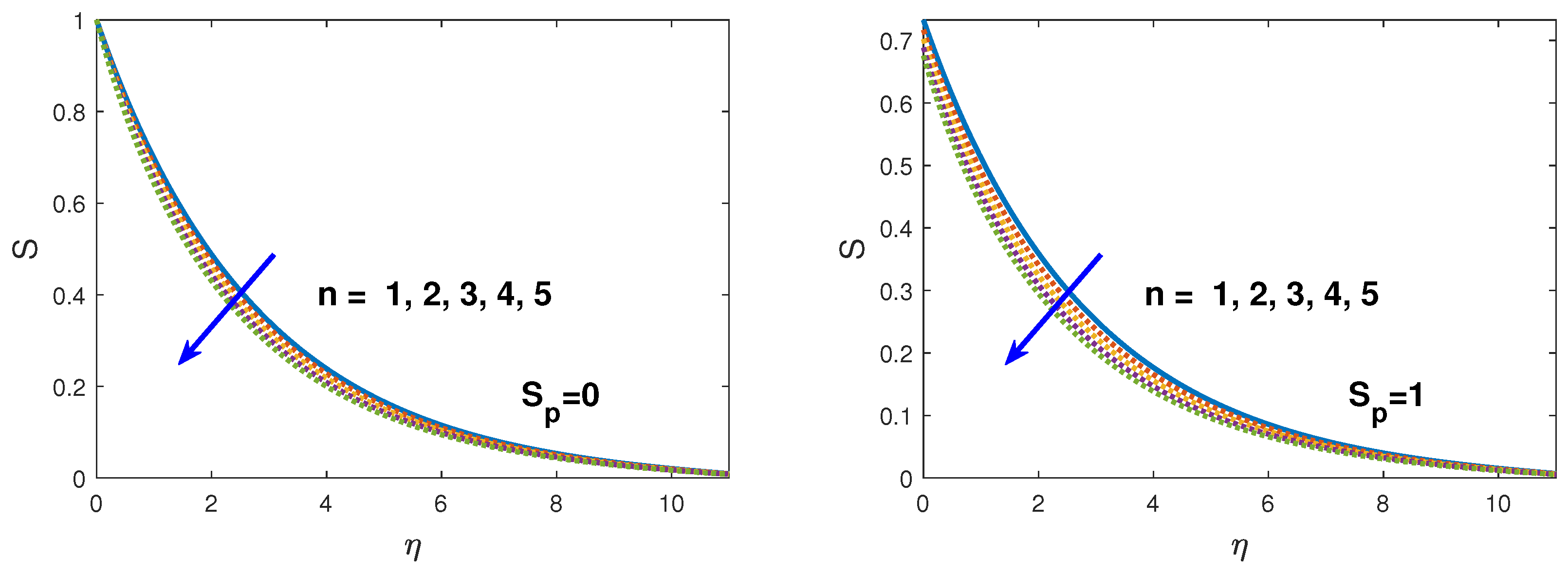
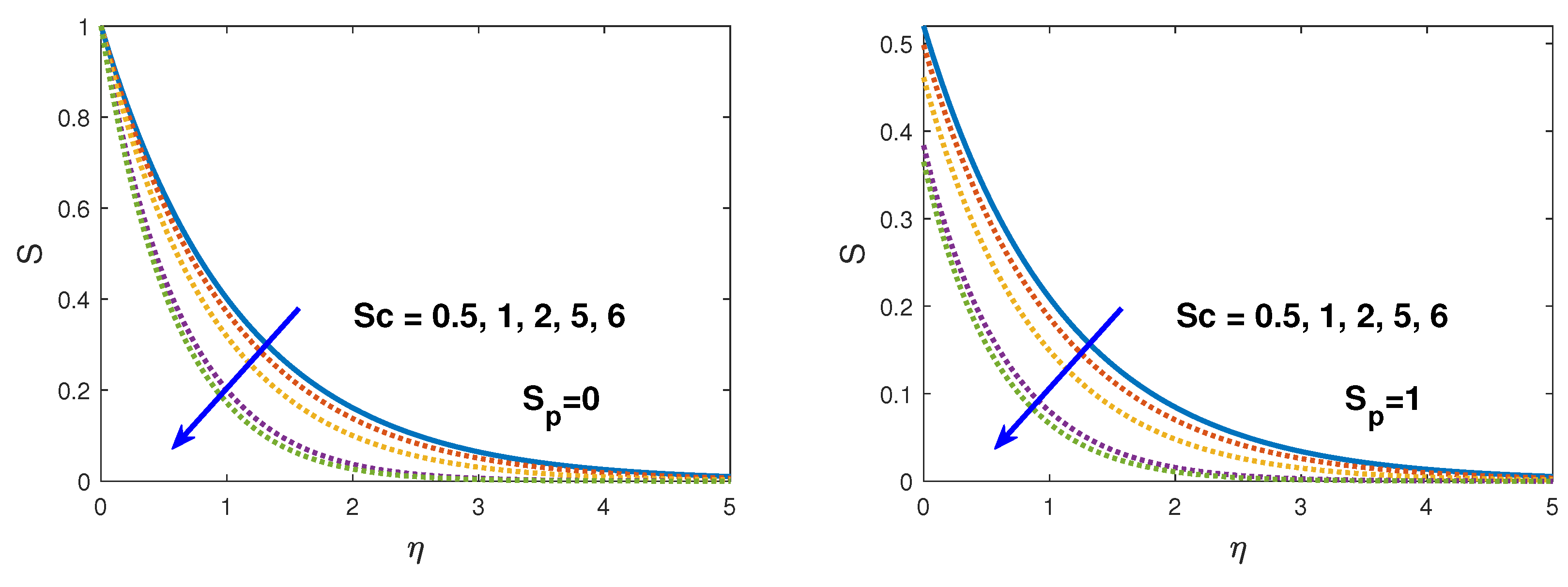
- Solute concentration decreases with an increase in the stretching parameter, solutal slip, Schmidt number and chemical reaction parameter.
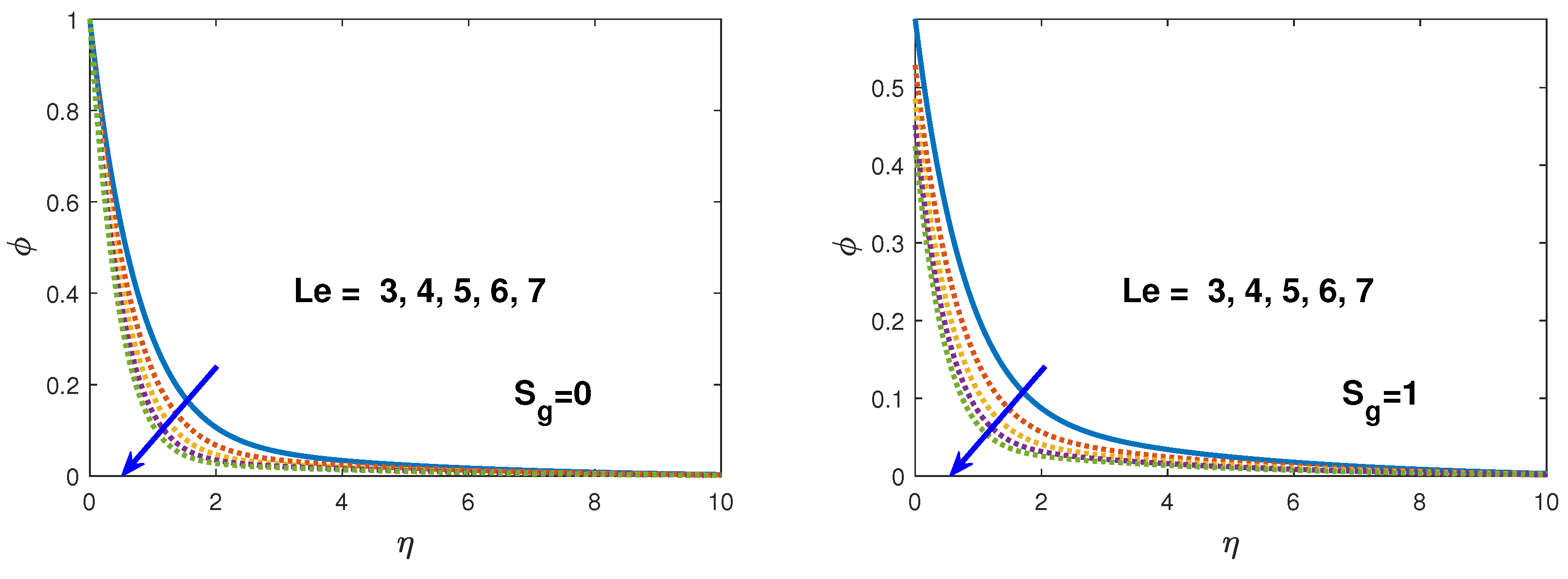
- The nano-fluid volume fraction profile retards with large values of Brownian motion parameter and Lewis number.
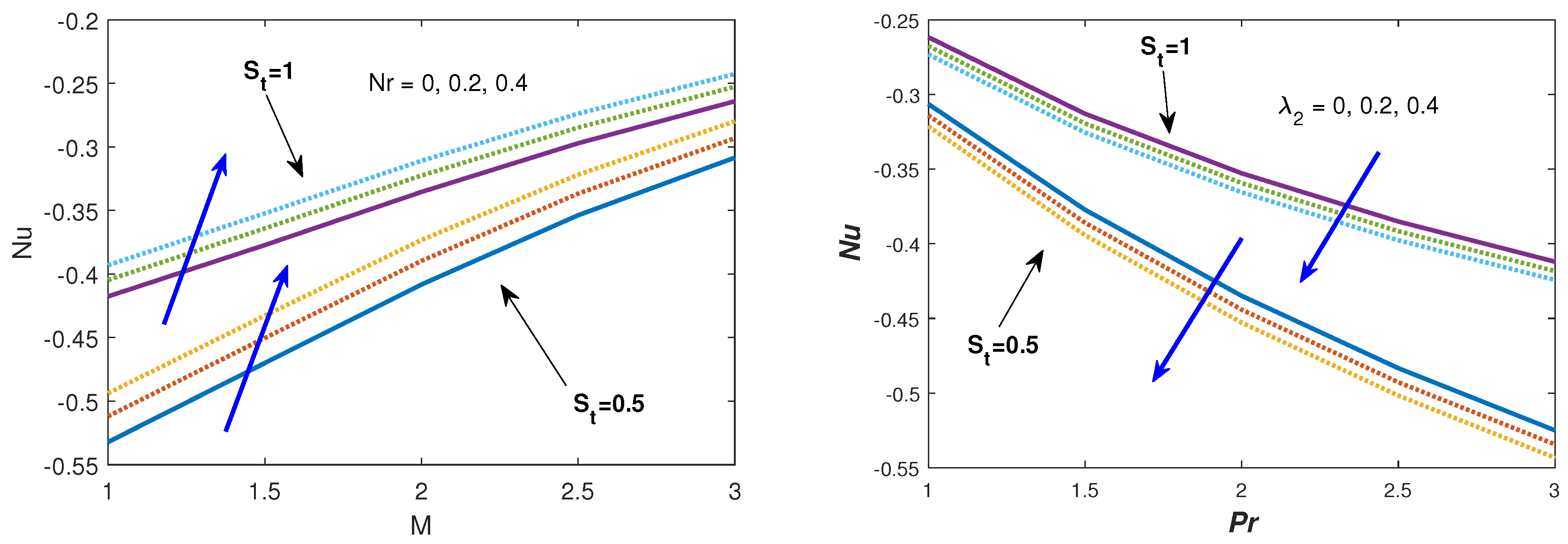
- Nusselt number increases in the presence of thermal slip with the increasing values of magnetic and thermal radiation parameters. Whereas, the effect is reversed for enhancing the values of solutal buoyancy parameter and Prandtl number.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| u,w | velocity components |
| B | magnetic field strength |
| uniform magnetic field strength | |
| Brownian parameter | |
| Schmidt number | |
| thermophoresis parameter | |
| Lewis number | |
| heat flux | |
| Brownian diffusion | |
| thermophoretic diffusion | |
| solute parameter | |
| chemical reaction | |
| constant temperature | |
| nanoparticle volume fraction | |
| ambient temperature | |
| ambient nanoparticle volume fraction | |
| M | magnetic parameter |
| Prandtl number | |
| thermal radiation | |
| a constant | |
| n | power-law exponent |
| hydrodynamic slip | |
| thermal slip | |
| solute slip | |
| nano-fluid slip | |
| temperature slip factor | |
| solutal concentration slip factor | |
| nanoparticle concentration slip factor | |
| mean absorbtion coefficient |
Greek Symbol
| ratio of nanoparticle heat capacity | |
| kinetic viscosity | |
| electric conductivity | |
| Stefan-Boltzmann constant | |
| thermal diffusivity | |
| viscosity of the fluid | |
| solute concentration | |
| chemical reaction | |
| ambient solute concentration | |
| Buoyancy parameters |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Lab.: Springfield, IL, USA, 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids. Chem. Eng. Sci. 2012, 84, 182–187. [Google Scholar] [CrossRef]
- Kandelousi, M.S. Nanofluid Heat and Mass Transfer in Engineering Problems; BoD-Books on Demand: Norderstedt, Germany, 2017. [Google Scholar]
- Sheikholeslami, M.; Shamlooei, M.; Moradi, R. Numerical simulation for heat transfer intensification of nanofluid in a porous curved enclosure considering shape effect of Fe3O4 nanoparticles. Chem. Eng. Process. Intensif. 2018, 124, 71–82. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S. Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. Int. J. Heat Mass Transf. 2017, 106, 1261–1269. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Sadoughi, M. Simulation of CuO-water nanofluid heat transfer enhancement in presence of melting surface. Int. J. Heat Mass Transf. 2018, 116, 909–919. [Google Scholar] [CrossRef]
- Ali Lund, L.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. The Cheng–Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid: A revised model. Int. J. Heat Mass Transf. 2013, 65, 682–685. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M. Numerical Analysis of Boundary Layer Flow Adjacent to a Thin Needle in Nanofluid with the Presence of Heat Source and Chemical Reaction. Symmetry 2019, 11, 543. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary-layer flow of nanofluids over a moving surface in a flowing fluid. Int. J. Therm. Sci. 2010, 49, 1663–1668. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nasiri, M.; Khezerloo, M.; Laraqi, N. Numerical investigation of magnetic field effect on mixed convection heat transfer of nanofluid in a channel with sinusoidal walls. J. Magn. Magn. Mater. 2016, 401, 159–168. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D. Numerical investigation for two phase modeling of nanofluid in a rotating system with permeable sheet. J. Mol. Liq. 2014, 194, 13–19. [Google Scholar] [CrossRef]
- Hatami, M.; Sheikholeslami, M.; Ganji, D. Nanofluid flow and heat transfer in an asymmetric porous channel with expanding or contracting wall. J. Mol. Liq. 2014, 195, 230–239. [Google Scholar] [CrossRef]
- Soundalgekar, V.; Gupta, S.; Aranake, R. Free convection effects on MHD Stokes problem for a vertical plate. Nucl. Eng. Des. 1979, 51, 403–407. [Google Scholar] [CrossRef]
- Elbashbeshy, E. Heat and mass transfer along a vertical plate with variable surface tension and concentration in the presence of the magnetic field. Int. J. Eng. Sci. 1997, 35, 515–522. [Google Scholar] [CrossRef]
- Jena, S.; Mishra, S.; Dash, G. Chemical reaction effect on MHD Jeffery fluid flow over a stretching sheet through porous media with heat generation/absorption. Int. J. Appl. Comput. Math. 2017, 3, 1225–1238. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Mann, A. On MHD radiative Jeffery nanofluid flow with convective heat and mass boundary conditions. Neural Comput. Appl. 2018, 30, 2739–2748. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD Flow and Heat Transfer over Vertical Stretching Sheet with Heat Sink or Source Effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Najib, N.; Bachok, N.; Arifin, N.M.; Ishak, A. Stagnation point flow and mass transfer with chemical reaction past a stretching/shrinking cylinder. Sci. Rep. 2014, 4, 4178. [Google Scholar] [CrossRef]
- Mishra, S.; Dash, G.; Pattnaik, P. Flow of heat and mass transfer on MHD free convection in a micropolar fluid with heat source. Alex. Eng. J. 2015, 54, 681–689. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A.; Pop, I. Boundary layer flow and heat transfer over a nonlinearly permeable stretching/shrinking sheet in a nanofluid. Sci. Rep. 2014, 4, 4404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmed, J.; Mahmood, T.; Iqbal, Z.; Shahzad, A.; Ali, R. Axisymmetric flow and heat transfer over an unsteady stretching sheet in power law fluid. J. Mol. Liq. 2016, 221, 386–393. [Google Scholar] [CrossRef]
- Shahzad, A.; Ahmed, J.; Khan, M. On heat transfer analysis of axisymmetric flow of viscous fluid over a nonlinear radially stretching sheet. Alex. Eng. J. 2016, 55, 2423–2429. [Google Scholar] [CrossRef] [Green Version]
- Khan, I.; Alqahtani, A.M. MHD Nanofluids in a Permeable Channel with Porosity. Symmetry 2019, 11, 378. [Google Scholar] [CrossRef]
- Makinde, O.D.; Mabood, F.; Ibrahim, M.S. Chemically reacting on MHD boundary-layer flow of nanofluids over a non-linear stretching sheet with heat source/sink and thermal radiation. Therm. Sci. 2018, 22, 495–506. [Google Scholar] [CrossRef]
- Mabood, F.; Shateyi, S. Multiple Slip Effects on MHD Unsteady Flow Heat and Mass Transfer Impinging on Permeable Stretching Sheet with Radiation. Model. Simul. Eng. 2019, 2019, 3052790. [Google Scholar] [CrossRef]
- Nayak, B.; Mishra, S.; Krishna, G.G. Chemical reaction effect of an axisymmetric flow over radially stretched sheet. Propuls. Power Res. 2019, 8, 79–84. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. FÜR Angew. Math. Und Phys. Zamp 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gireesha, B.; Ramesh, G.; Bagewadi, C. Heat transfer in MHD flow of a dusty fluid over a stretching sheet with viscous dissipation. J. Appl. Sci. Res. 2012, 3, 2392–2401. [Google Scholar]
- Jalil, M.; Asghar, S.; Yasmeen, S. An exact solution of MHD boundary layer flow of dusty fluid over a stretching surface. Math. Probl. Eng. 2017, 2017, 2307469. [Google Scholar] [CrossRef]
- Nawaz, M.; Hayat, T. Axisymmetric stagnation-point flow of nanofluid over a stretching surface. Adv. Appl. Math. Mech. 2014, 6, 220–232. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Analytical and numerical solutions for axisymmetric flow of nanofluid due to non-linearly stretching sheet. Int. J. Non-Linear Mech. 2015, 71, 22–29. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Alsaedi, A. Axisymmetric flow of a nanofluid over a radially stretching sheet with convective boundary conditions. Curr. Nanosci. 2012, 8, 328–334. [Google Scholar] [CrossRef]
- Pal, D. Heat and mass transfer in stagnation-point flow towards a stretching surface in the presence of buoyancy force and thermal radiation. Meccanica 2009, 44, 145–158. [Google Scholar] [CrossRef]
- Almakki, M.; Dey, S.; Mondal, S.; Sibanda, P. On Unsteady Three-Dimensional Axisymmetric MHD Nanofluid Flow with Entropy Generation and Thermo-Diffusion Effects. Entropy 2017, 19, 168. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.; Ismail, A.M. Multiple slips effects on MHD Casson fluid flow in porous media with radiation and chemical reaction. Can. J. Phys. 2015, 94, 26–34. [Google Scholar] [CrossRef]
- Gupta, D.; Kumar, L.; Bég, O.A.; Singh, B. Finite-element simulation of mixed convection flow of micropolar fluid over a shrinking sheet with thermal radiation. Proc. Inst. Mech. Eng. Part J. Process. Mech. Eng. 2014, 228, 61–72. [Google Scholar] [CrossRef]
- Gupta, D.; Kumar, L.; Bég, O.A.; Singh, B. Finite element analysis of MHD flow of micropolar fluid over a shrinking sheet with a convective surface boundary condition. J. Eng. Thermophys. 2018, 27, 202–220. [Google Scholar] [CrossRef]
- Madhu, M.; Kishan, N. Finite Element Analysis of MHD viscoelastic nanofluid flow over a stretching sheet with radiation. Procedia Eng. 2015, 127, 432–439. [Google Scholar] [CrossRef]
- Mabood, F.; Das, K. Melting heat transfer on hydromagnetic flow of a nanofluid over a stretching sheet with radiation and second-order slip. Eur. Phys. J. Plus 2016, 131, 3. [Google Scholar] [CrossRef]
- Ali, M.E. Heat transfer characteristics of a continuous stretching surface. Wärme-und Stoffübertragung 1994, 29, 227–234. [Google Scholar] [CrossRef]




| Number of Elements | |||||
|---|---|---|---|---|---|
| 40 | 0.5275 | 0.0670 | 0.3416 | 0.2898 | 0.0546 |
| 80 | 0.5305 | 0.0670 | 0.3409 | 0.2898 | 0.0546 |
| 120 | 0.5310 | 0.0670 | 0.3408 | 0.2898 | 0.0547 |
| 160 | 0.5312 | 0.0670 | 0.3407 | 0.2898 | 0.0547 |
| 200 | 0.5313 | 0.0670 | 0.3407 | 0.2898 | 0.0547 |
| 240 | 0.5313 | 0.0670 | 0.3407 | 0.2898 | 0.0547 |
| 280 | 0.5314 | 0.0670 | 0.3407 | 0.2898 | 0.0547 |
| 320 | 0.5314 | 0.0670 | 0.3407 | 0.2898 | 0.0547 |
| Crane [31] | FEM | Crane [31] | FEM | ||
|---|---|---|---|---|---|
| 0 | 1 | 1 | 7 | 0.0009 | 0.0009 |
| 1 | 0.3679 | 0.3679 | 8 | 0.0003 | 0.0003 |
| 2 | 0.1353 | 0.1353 | 9 | 0.0001 | 0.0001 |
| 3 | 0.0498 | 0.0498 | 10 | 0.0000 | 0.0000 |
| 4 | 0.0183 | 0.0183 | 11 | 0.0000 | 0.0000 |
| 5 | 0.0067 | 0.0067 | 12 | 0.0000 | 0.0000 |
| 6 | 0.0025 | 0.0025 | 13,14,15 | 0.0000 | 0.0000 |
| M | Gireesha et al. [32] | Mudassar et al. [33] Exact Solution (a) | FEM (Our Results) (b) | Error in % |
|---|---|---|---|---|
| 0.0 | 1.000 | 1.000000 | 1.0000080 | 0.00080 |
| 0.2 | 1.095 | 1.095445 | 1.0954458 | 0.00007 |
| 0.5 | 1.224 | 1.224745 | 1.2247446 | 0.00003 |
| 1.0 | 1.414 | 1.414214 | 1.4142132 | 0.00006 |
| 1.2 | 1.483 | 1.483240 | 1.4832393 | 0.00005 |
| 1.5 | 1.581 | 1.581139 | 1.5811384 | 0.00004 |
| 2.0 | 1.732 | 1.732051 | 1.7320504 | 0.00003 |
| M | Mabood and Das [43] | Fazle [29] | FEM (Present) | Ali [44] | Fazle [29] | FEM (Present) | |
|---|---|---|---|---|---|---|---|
| 0 | −1.000008 | −1.0000084 | −1.0000082 | - | - | - | - |
| 1 | 1.4142135 | 1.41421356 | 1.41421353 | - | - | - | - |
| 5 | 2.4494897 | 2.44948974 | 2.44948963 | 0.72 | 0.8058 | 0.8088 | 0.8088 |
| 10 | 3.3166247 | 3.31662479 | 3.31662463 | 1 | 0.9691 | 1.0000 | 1.0000 |
| 50 | 7.1414284 | 7.14142843 | 7.14142839 | 3 | 1.9144 | 1.9237 | 1.9237 |
| 100 | 10.049875 | 10.0498756 | 10.0498751 | 10 | 3.7006 | 3.7207 | 3.7207 |
| 500 | 22.383029 | 22.3830293 | 22.3830283 | - | - | - | - |
| 1000 | 31.638584 | 31.6385840 | 31.6385833 | - | - | - | - |
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | −0.51871906 | −0.39914438 | −0.33469636 | ||||||
| 1.5 | 0.1 | 0.773 | 1 | 0.4 | 0.4 | 0.4 | −0.70007439 | −0.34330234 | −0.32039573 |
| 2 | −0.86037797 | −0.29152259 | −0.30916534 | ||||||
| 0.1 | −0.86037797 | −0.29152259 | −0.30916534 | ||||||
| 2 | 0.5 | 0.773 | 1 | 0.4 | 0.4 | 0.4 | −0.87456687 | −0.27774645 | −0.53903314 |
| 1 | −0.88233600 | −0.27260197 | −0.67751871 | ||||||
| 2 | −0.86809394 | −0.46620439 | −0.30740431 | ||||||
| 2 | 0.1 | 3 | 1 | 0.4 | 0.4 | 0.4 | −0.87169999 | −0.55675321 | −0.30668459 |
| 4 | −0.87422111 | −0.62457605 | −0.30622757 | ||||||
| 2 | −0.85775278 | −0.23671739 | −0.30981895 | ||||||
| 2 | 0.1 | 0.773 | 3 | 0.4 | 0.4 | 0.4 | −0.85618413 | −0.20495708 | −0.31022032 |
| 4 | −0.85513340 | −0.18408657 | −0.31049339 | ||||||
| 0.5 | −0.84545297 | −0.29890014 | −0.31058477 | ||||||
| 1 | −0.77396002 | −0.32928379 | −0.31696545 | ||||||
| 1.5 | −0.70660726 | −0.35282310 | −0.32248200 | ||||||
| 0.5 | −0.84570667 | −0.29845530 | −0.31051308 | ||||||
| 0.7 | −0.81650214 | −0.31161198 | −0.31317081 | ||||||
| 0.9 | −0.78749387 | −0.32389598 | −0.31577681 | ||||||
| 0.4 | −0.86037797 | −0.29152259 | −0.30916534 | ||||||
| 0.8 | −0.82636008 | −0.30157756 | −0.31127720 | ||||||
| 1.2 | −0.79384196 | −0.31065228 | −0.31323236 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, S.A.; Nie, Y.; Ali, B. Multiple Slip Effects on Magnetohydrodynamic Axisymmetric Buoyant Nanofluid Flow above a Stretching Sheet with Radiation and Chemical Reaction. Symmetry 2019, 11, 1171. https://doi.org/10.3390/sym11091171
Khan SA, Nie Y, Ali B. Multiple Slip Effects on Magnetohydrodynamic Axisymmetric Buoyant Nanofluid Flow above a Stretching Sheet with Radiation and Chemical Reaction. Symmetry. 2019; 11(9):1171. https://doi.org/10.3390/sym11091171
Chicago/Turabian StyleKhan, Shahid Ali, Yufeng Nie, and Bagh Ali. 2019. "Multiple Slip Effects on Magnetohydrodynamic Axisymmetric Buoyant Nanofluid Flow above a Stretching Sheet with Radiation and Chemical Reaction" Symmetry 11, no. 9: 1171. https://doi.org/10.3390/sym11091171






