The Casimir Densities for a Sphere in the Milne Universe
Abstract
:1. Introduction
2. Geometry and the Scalar Field Modes
3. Region inside the Sphere
3.1. Normalized Mode Functions
3.2. Hadamard Function
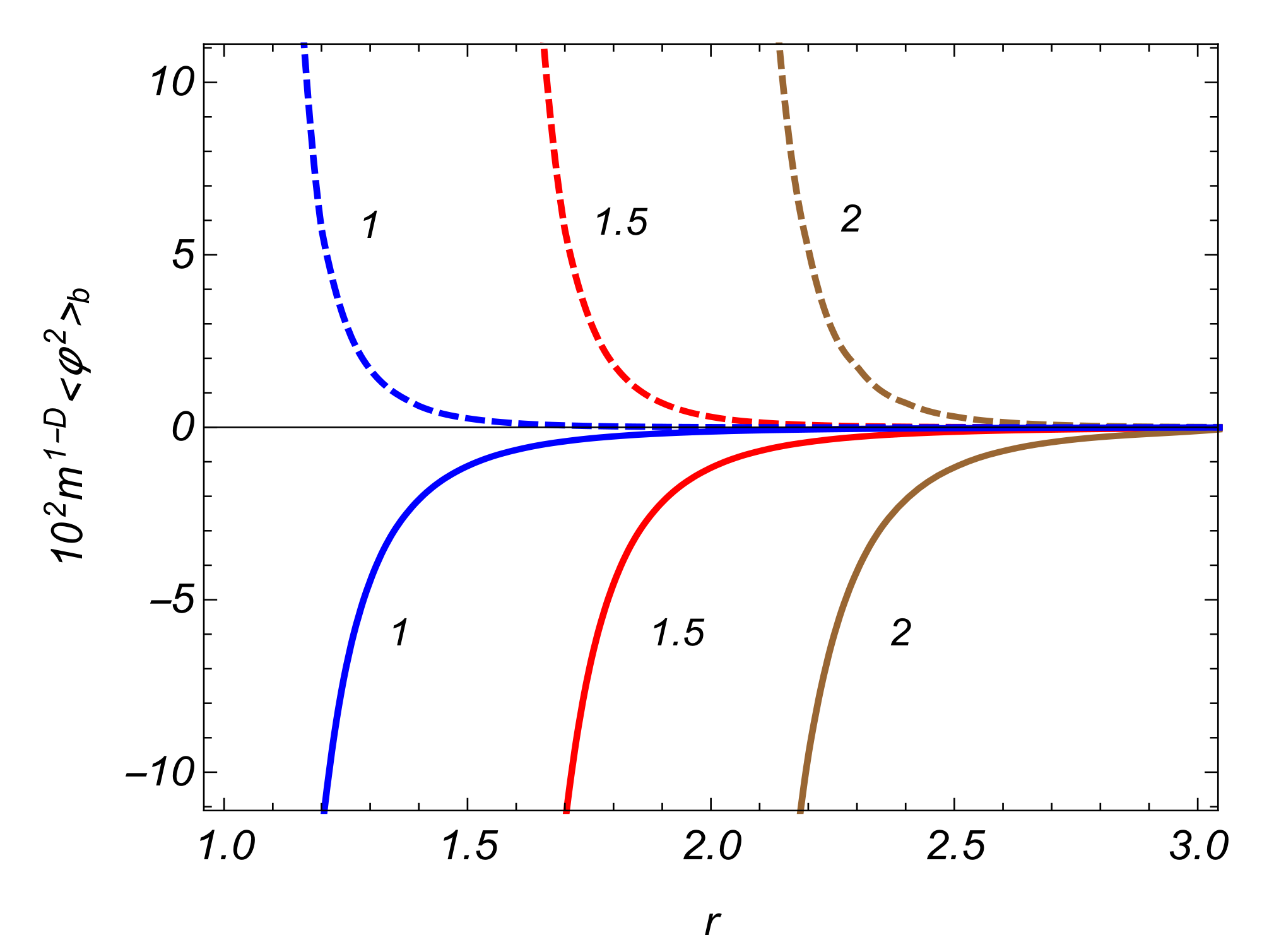
3.3. VEV of the Field Squared
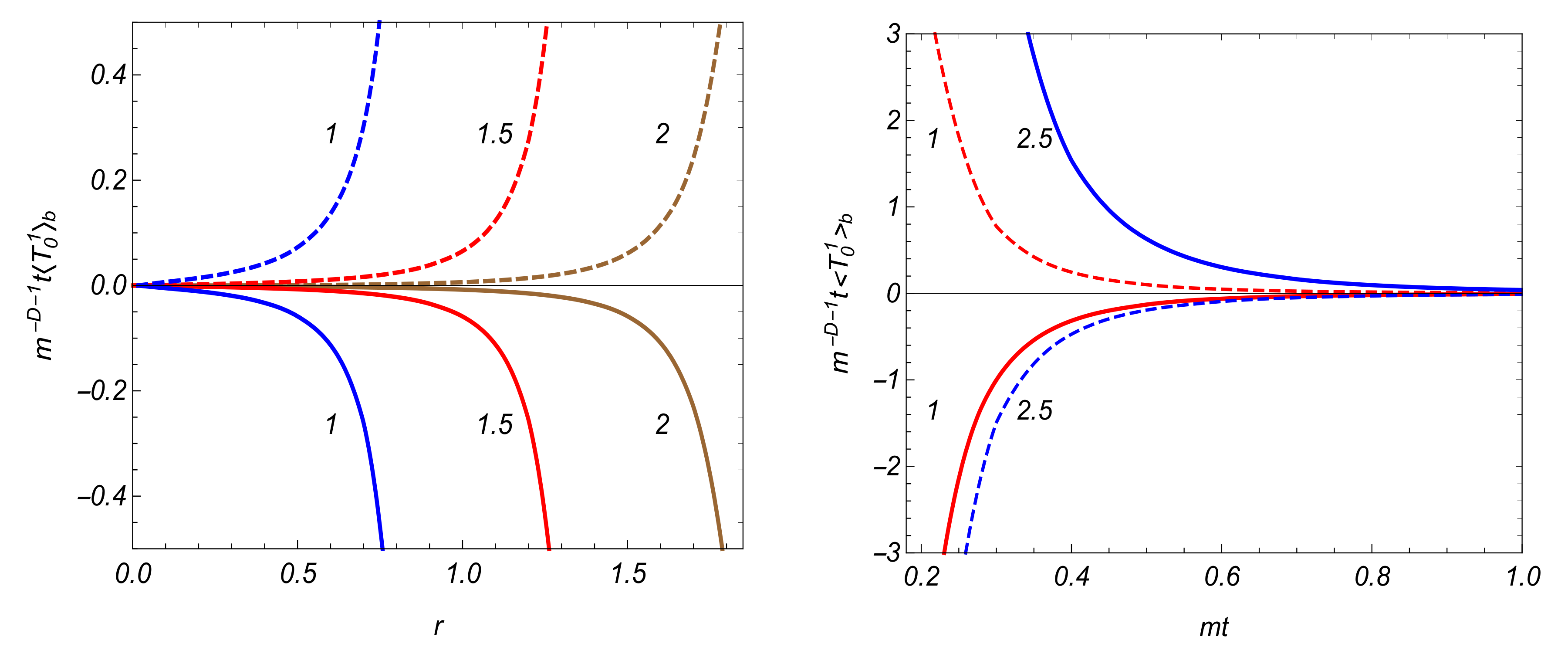
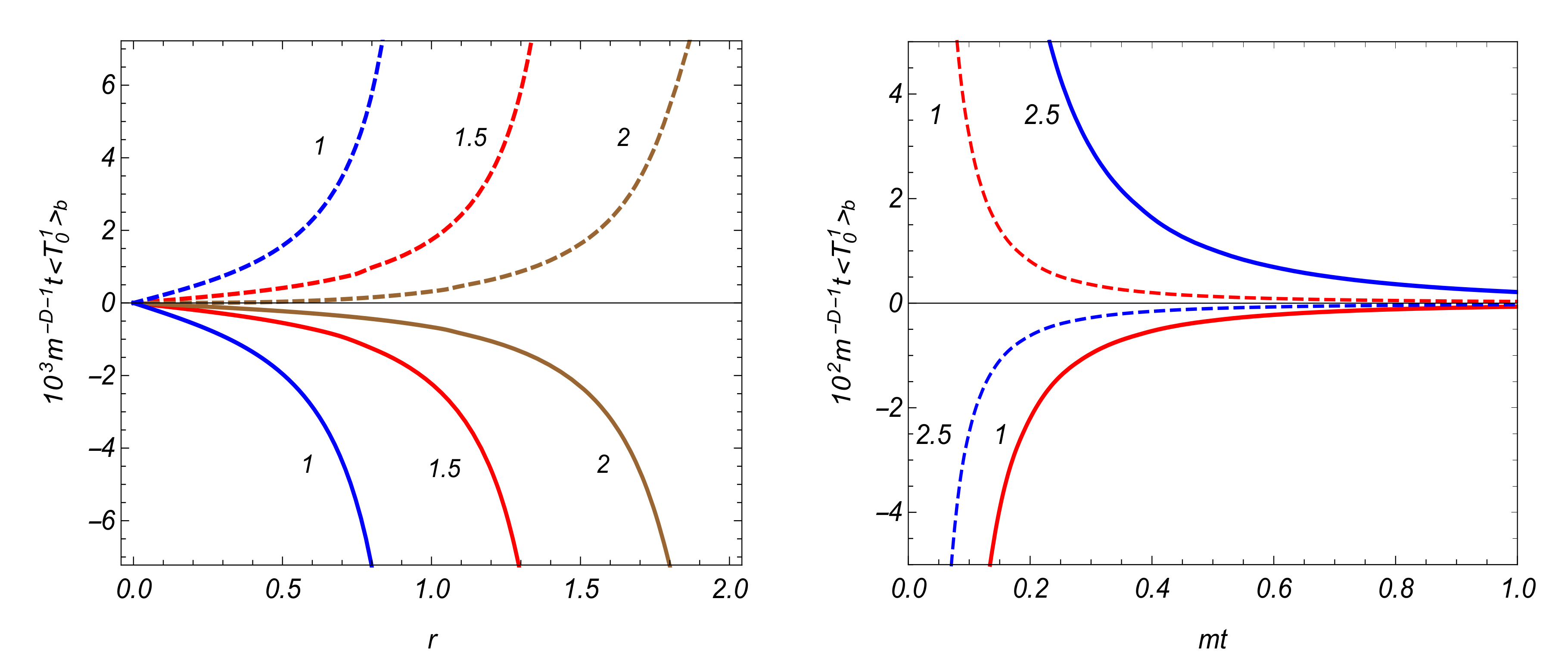
3.4. VEV of the Energy-Momentum Tensor
4. Exterior Region
4.1. Scalar Modes and the Hadamard Function
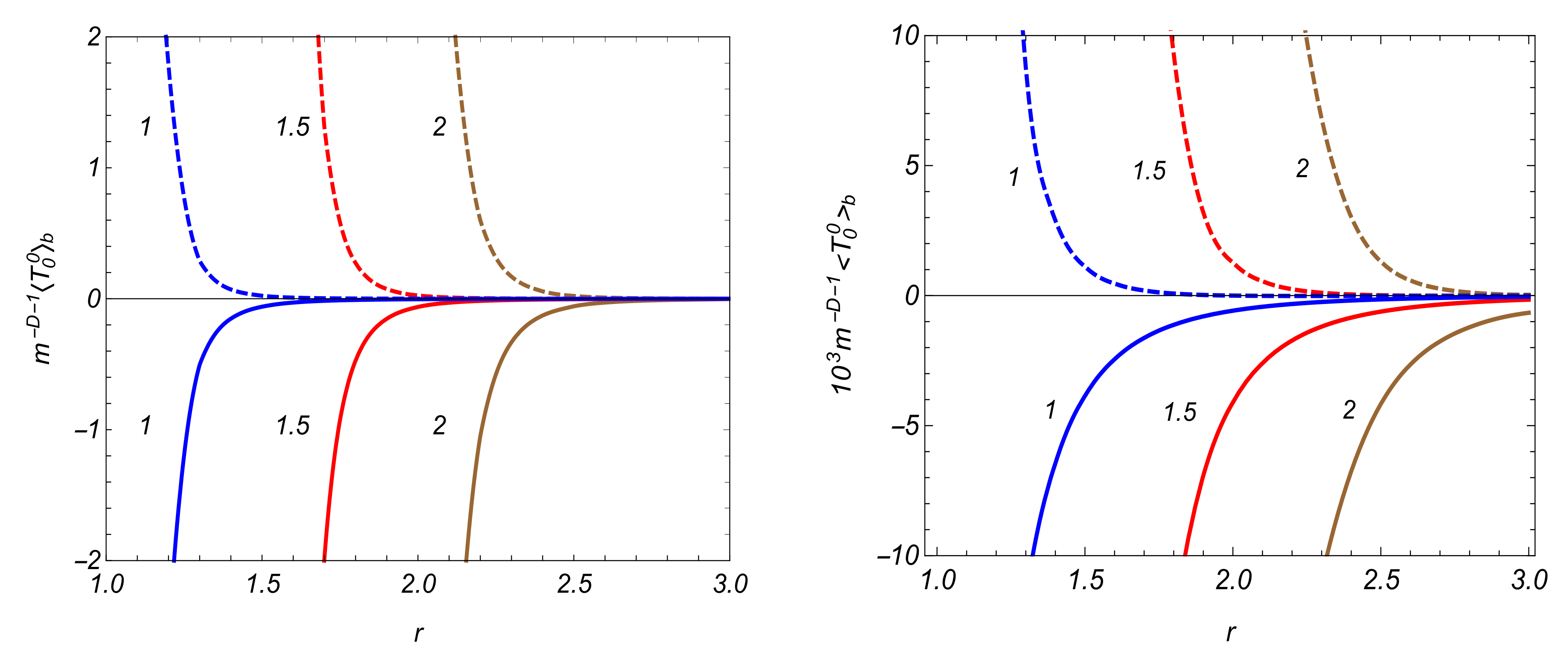
4.2. VEVs of the Field Squared and Energy-Momentum Tensor
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Summation Formula
References
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. Vacuum Quantum Effects in Strong Fields; Friedmann Laboratory Publishing: St. Petersburg, Russia, 1994. [Google Scholar]
- Fulling, S.A. Aspects of Quantum Field Theory in Curved Space-Time; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Parker, L.; Toms, D. Quantum Field Theory in Curved Spacetime: Quantized Fields and Gravity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Sommerfield, C.M. Quantization on spacetime hyperboloids. Ann. Phys. 1974, 84, 285–302. [Google Scholar] [CrossRef]
- Gromes, D.; Rothe, H.; Stech, B. Field quantization on the surface X2 = constant. Nucl. Phys. B 1974, 75, 313–332. [Google Scholar] [CrossRef]
- DiSessa, A. Quantization on hyperboloids and full space-time field expansion. J. Math. Phys. 1974, 15, 1892–1900. [Google Scholar] [CrossRef]
- Davies, P.C.W.; Fulling, S.A. Quantum vacuum energy in two dimensional space-times. Proc. R. Soc. Lond. A 1977, 354, 59–77. [Google Scholar]
- Bunch, T.S. Stress tensor of massless conformal quantum fields in hyperbolic universes. Phys. Rev. D 1978, 18, 1844. [Google Scholar] [CrossRef]
- Bunch, T.S.; Christensen, S.M.; Fulling, S.A. Massive quantum field theory in two-dimensional Robertson-Walker space-time. Phys. Rev. D 1978, 18, 4435. [Google Scholar] [CrossRef]
- Yamamoto, K.; Tanaka, T.; Sasaki, M. Particle spectrum created through bubble nucleation and quantum field theory in the Milne universe. Phys. Rev. D 1995, 51, 2968. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, T.; Sasaki, M. Quantized gravitational waves in the Milne universe. Phys. Rev. D 1997, 55, 6061. [Google Scholar] [CrossRef] [Green Version]
- Higuchi, A.; Iso, S.; Ueda, K.; Yamamoto, K. Entanglement of the vacuum between left, right, future, and past: The origin of entanglement-induced quantum radiation. Phys. Rev. D 2017, 96, 083531. [Google Scholar] [CrossRef] [Green Version]
- Fulling, S.A.; Parker, L.; Hu, B.L. Conformal energy-momentum tensor in curved spacetime: Adiabatic regularization and renormalization. Phys. Rev. D 1974, 10, 3905. [Google Scholar] [CrossRef]
- Chitre, D.M.; Hartle, J.B. Path-integral quantization and cosmological particle production: An example. Phys. Rev. D 1977, 16, 251. [Google Scholar] [CrossRef]
- Nariai, H. On a quantized scalar field in some Bianchi-type I universe. Prog. Theor. Phys. 1977, 58, 560–574. [Google Scholar] [CrossRef] [Green Version]
- Nariai, H. On a quantized scalar field in some Bianchi-type I universe. II: DeWitt’s two vacuum states connected causally. Prog. Theor. Phys. 1977, 58, 842–849. [Google Scholar] [CrossRef] [Green Version]
- Nariai, H.; Tomimatsu, A. On the creation of scalar particles in an isotropic universe. Prog. Theor. Phys. 1978, 59, 296–298. [Google Scholar] [CrossRef] [Green Version]
- Nariai, H. Canonical approach to the creation of scalar particles in the Chitre-Hartle model-universe. Prog. Theor. Phys. 1980, 63, 324–326. [Google Scholar] [CrossRef] [Green Version]
- Mensky, M.B.; Karmanov, O.Y. Application of the propagator method to pair production in the Robertson-Walker metric. Gen. Rel. Grav. 1980, 12, 267–277. [Google Scholar] [CrossRef]
- Azuma, T. The renormalized energy-momentum tensor in a Robertson-Walker universe. Prog. Theor. Phys. 1981, 66, 892–902. [Google Scholar] [CrossRef] [Green Version]
- Charach, C.; Parker, L. Uniqueness of the propagator in spacetime with cosmological singularity. Phys. Rev. D 1981, 24, 3023. [Google Scholar] [CrossRef]
- Charach, C. Feynman propagators and particle creation in linearly expanding Bianchi type-I universes. Phys. Rev. D 1982, 26, 3367. [Google Scholar] [CrossRef]
- Azuma, T.; Tomimatsu, A. Low-energy behavior of a quantized scalar field in the linearly expanding universe. Gen. Rel. Grav. 1982, 14, 629–636. [Google Scholar] [CrossRef]
- Calzetta, E.; Castagnino, M. Feynman propagator in a linearly expanding universe. Phys. Rev. D 1983, 28, 1298. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Kirillova, E.N.; Odintsov, S.D. The Green functions in curved spacetime. Class. Quantum Grav. 1987, 4, 711. [Google Scholar] [CrossRef]
- Winters-Hilt, S.; Redmount, I.H.; Parker, L. Physical distinction among alternative vacuum states in flat spacetime geometries. Phys. Rev. D 1999, 60, 124017. [Google Scholar] [CrossRef]
- Tolley, A.J.; Turok, N. Quantum fields in a big-crunch-big-bang spacetime. Phys. Rev. D 2002, 66, 106005. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A.; Petrosyan, T.A.; Abajyan, S.V.; Nersisyan, B.B. Scalar Casimir effect in a linearly expanding universe. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850177. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Romeo, A.; Bytsenko, A.A.; Zerbini, S. Zeta Regularization Techniques with Applications; World Scientific: Singapore, 1994. [Google Scholar]
- Mostepanenko, V.M.; Trunov, N.N. The Casimir Effect and Its Applications; Clarendon: Oxford, UK, 1997. [Google Scholar]
- Milton, K.A. The Casimir Effect: Physical Manifestation of Zero-Point Energy; World Scientific: Singapore, 2002. [Google Scholar]
- Parsegian, V.A. Van der Vaals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Dalvit, D.; Milonni, P.; Roberts, D.; da Rosa, F. (Eds.) Casimir Physics; Lecture Notes in Physics; Springer: Berlin, Germany, 2011; Volume 834. [Google Scholar]
- Casimir, H.B.G. Introductory remarks on quantum electrodynamics. Physica 1953, 19, 846–849. [Google Scholar] [CrossRef]
- Boyer, T.H. Quantum electromagnetic zero-point energy of a conducting spherical shell and the Casimir model for a charged particle. Phys. Rev. 1968, 174, 1764–1776. [Google Scholar] [CrossRef]
- Davies, B. Quantum electromagnetic zero-point energy of a conducting spherical shell. J. Math. Phys. 1972, 13, 1324–1329. [Google Scholar] [CrossRef]
- Balian, R.; Duplantier, B. Electromagnetic waves near perfect conductors. II. Casimir effect. Ann. Phys. 1978, 112, 165–208. [Google Scholar] [CrossRef]
- Milton, K.A.; DeRaad, L.L., Jr.; Schwinger, J. Casimir self-stress on a perfectly conducting spherical shell. Ann. Phys. 1978, 115, 388–403. [Google Scholar] [CrossRef]
- Teo, L.P. Casimir effect of the electromagnetic field in D-dimensional spherically symmetric cavities. Phys. Rev. D 2010, 82, 085009. [Google Scholar] [CrossRef] [Green Version]
- Leonhardt, U.; Simpson, W.M.R. Exact solution for the Casimir stress in a spherically symmetric medium. Phys. Rev. D 2011, 84, 081701(R). [Google Scholar] [CrossRef] [Green Version]
- Milton, K.A.; Saharian, A.A. Casimir densities for a spherical boundary in de Sitter spacetime. Phys. Rev. D 2012, 85, 064005. [Google Scholar] [CrossRef] [Green Version]
- Olaussen, K.; Ravndal, F. Electromagnetic vacuum fields in a spherical cavity. Nucl. Phys. B 1981, 192, 237–258. [Google Scholar] [CrossRef]
- Olaussen, K.; Ravndal, F. Chromomagnetic vacuum fields in a spherical bag. Phys. Lett. B 1981, 100, 497–499. [Google Scholar] [CrossRef]
- Brevik, I.; Kolbenstvedt, H. Electromagnetic Casimir densities in dielectric spherical media. Ann. Phys. 1983, 149, 237–253. [Google Scholar] [CrossRef]
- Brevik, I.; Kolbenstvedt, H. Casimir stress in spherical media when εμ = 1. Can. J. Phys. 1984, 62, 805–810. [Google Scholar] [CrossRef]
- Grigoryan, L.S.; Saharian, A.A. Casimir effect for a perfectly conducting spherical surface. Dokl. Akad. Nauk Arm. SSR 1986, 83, 28. (In Russian) [Google Scholar]
- Grigoryan, L.S.; Saharian, A.A. Photon vacuum in a spherical layer between perfectly conducting surfaces. Izv. Akad. Nauk. Arm. SSR Fiz. 1987, 22, 3, reprinted in J. Contemp. Phys. 1987, 22, 1. [Google Scholar]
- Saharian, A.A. The Generalized Abel–Plana Formula. Applications to Bessel Functions and Casimir Effect; Report No. ICTP/2007/082; Yerevan State University Publishing House: Yerevan, Armenia, 2008. [Google Scholar]
- Saharian, A.A. Scalar Casimir effect for D-dimensional spherically symmetric Robin boundaries. Phys. Rev. D 2001, 63, 125007. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A.; Setare, M.R. Casimir densities for a spherical shell in the global monopole background. Class. Quantum Grav. 2003, 20, 3765. [Google Scholar] [CrossRef]
- Saharian, A.A.; Setare, M.R. Casimir densities for two concentric spherical shells in the global monopole space-time. Int. J. Mod. Phys. A 2004, 19, 4301–4321. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A. Quantum vacuum effects in the gravitational field of a global monopole. Astrophysics 2004, 47, 260–272. [Google Scholar] [CrossRef]
- Saharian, A.A.; Bezerra de Mello, E.R. Spinor Casimir densities for a spherical shell in the global monopole spacetime. J. Phys. A Math. Gen. 2004, 37, 3543. [Google Scholar] [CrossRef] [Green Version]
- Bezerra de Mello, E.R.; Saharian, A.A. Spinor Casimir effect for concentric spherical shells in the global monopole spacetime. Class. Quantum Grav. 2006, 23, 4673. [Google Scholar] [CrossRef] [Green Version]
- Bezerra de Mello, E.R.; Saharian, A.A. Vacuum polarization by a global monopole with finite core. J. High Energy Phys. 2006, 10, 049. [Google Scholar] [CrossRef] [Green Version]
- Bezerra de Mello, E.R.; Saharian, A.A. Polarization of the fermionic vacuum by a global monopole with finite core. Phys. Rev. D 2007, 75, 065019. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A.; Setare, M.R. Casimir densities for a spherical brane in Rindler-like spacetimes. Nucl. Phys. B 2005, 724, 406–422. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A.; Setare, M.R. Surface Casimir densities on a spherical brane in Rindler-like spacetimes. Phys. Lett. B 2006, 637, 5–11. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A.; Setare, M.R. Casimir densities for two spherical branes in Rindler-like spacetimes. J. High Energy Phys. 2007, 02, 089. [Google Scholar] [CrossRef]
- Setare, M.R.; Mansouri, R. Casimir effect for a spherical shell in de Sitter space. Class. Quantum Grav. 2001, 18, 2331. [Google Scholar] [CrossRef] [Green Version]
- Setare, M.R. Casimir stress for concentric spheres in de Sitter space. Class. Quantum Grav. 2001, 18, 4823. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A. A summation formula over the zeros of the associated Legendre function with a physical application. J. Phys. A Math. Theor. 2008, 41, 415203. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A. A summation formula over the zeros of a combination of the associated Legendre functions with a physical application. J. Phys. A Math. Theor. 2009, 42, 465210. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Saharyan, N.A. Wightman function and the Casimir effect for a Robin sphere in a constant curvature space. Eur. Phys. J. C 2014, 74, 3047. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Saharian, A.A.; Yeranyan, A.H. Casimir densities from coexisting vacua. Phys. Rev. D 2014, 89, 105006. [Google Scholar] [CrossRef] [Green Version]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover: New York, NY, USA, 1972. [Google Scholar]
- Saharian, A.A. Energy-momentum tensor for a scalar field on manifolds with boundaries. Phys. Rev. D 2004, 69, 085005. [Google Scholar] [CrossRef] [Green Version]
- Maldacena, J.; Pimentel, G.L. Entanglement entropy in de Sitter space. J. High Energy Phys. 2013, 02, 038. [Google Scholar]
- Kanno, S.; Murugan, J.; Shocka, J.P.; Soda, J. Entanglement entropy of α-vacua in de Sitter space. J. High Energy Phys. 2014, 07, 072. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, S.; Panda, S. Entangled de Sitter from stringy axionic Bell pair I: An analysis using Bunch-Davies vacuum. Eur. Phys. J. C 2018, 78, 52. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S. Quantum entanglement in de Sitter space from stringy axion: An analysis using α vacua. Nucl. Phys. B 2019, 943, 114606. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S. Spectrum of cosmological correlation from vacuum fluctuation of stringy axion in entangled de Sitter space. Eur. Phys. J. C 2020, 80, 67. [Google Scholar] [CrossRef]
- Sasaki, M.; Tanaka, T.; Yamamoto, K. Euclidean vacuum mode functions for a scalar field on open de Sitter space. Phys. Rev. D 1995, 51, 2979. [Google Scholar] [CrossRef] [PubMed] [Green Version]

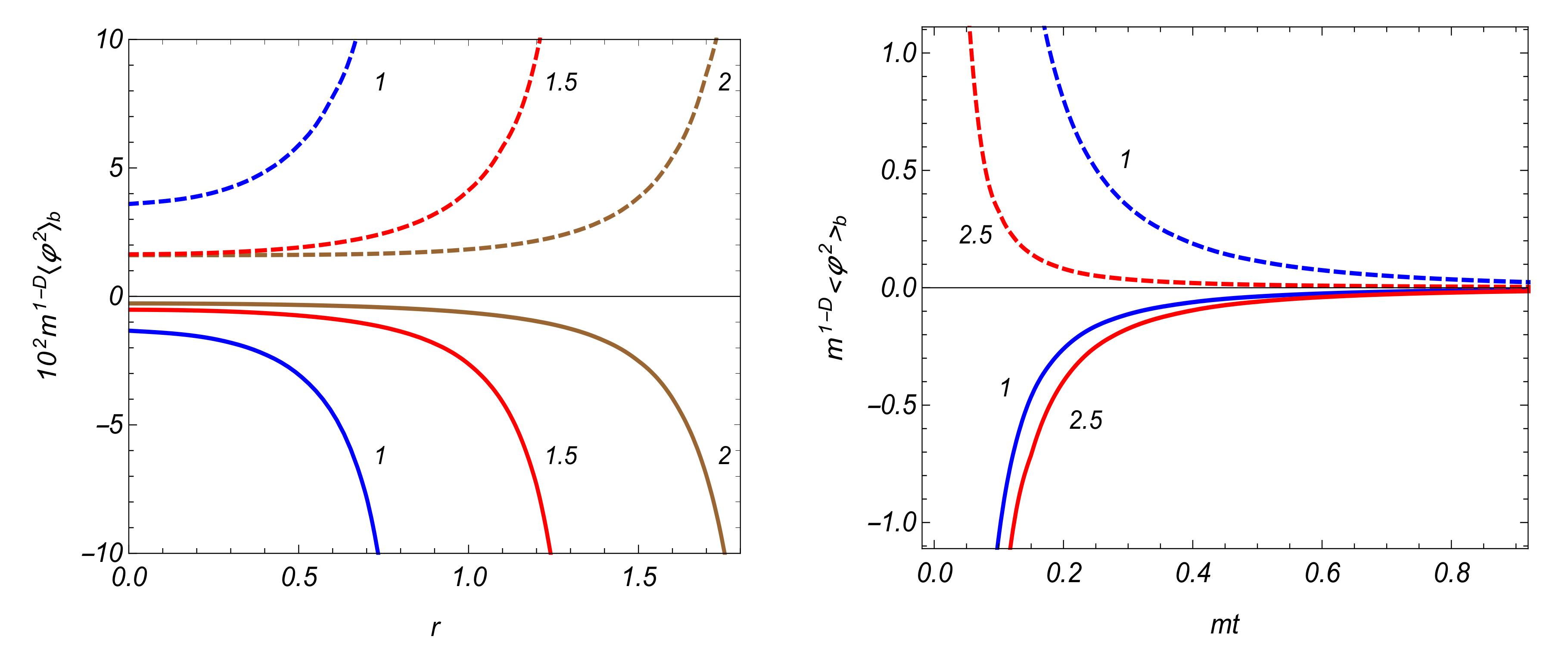

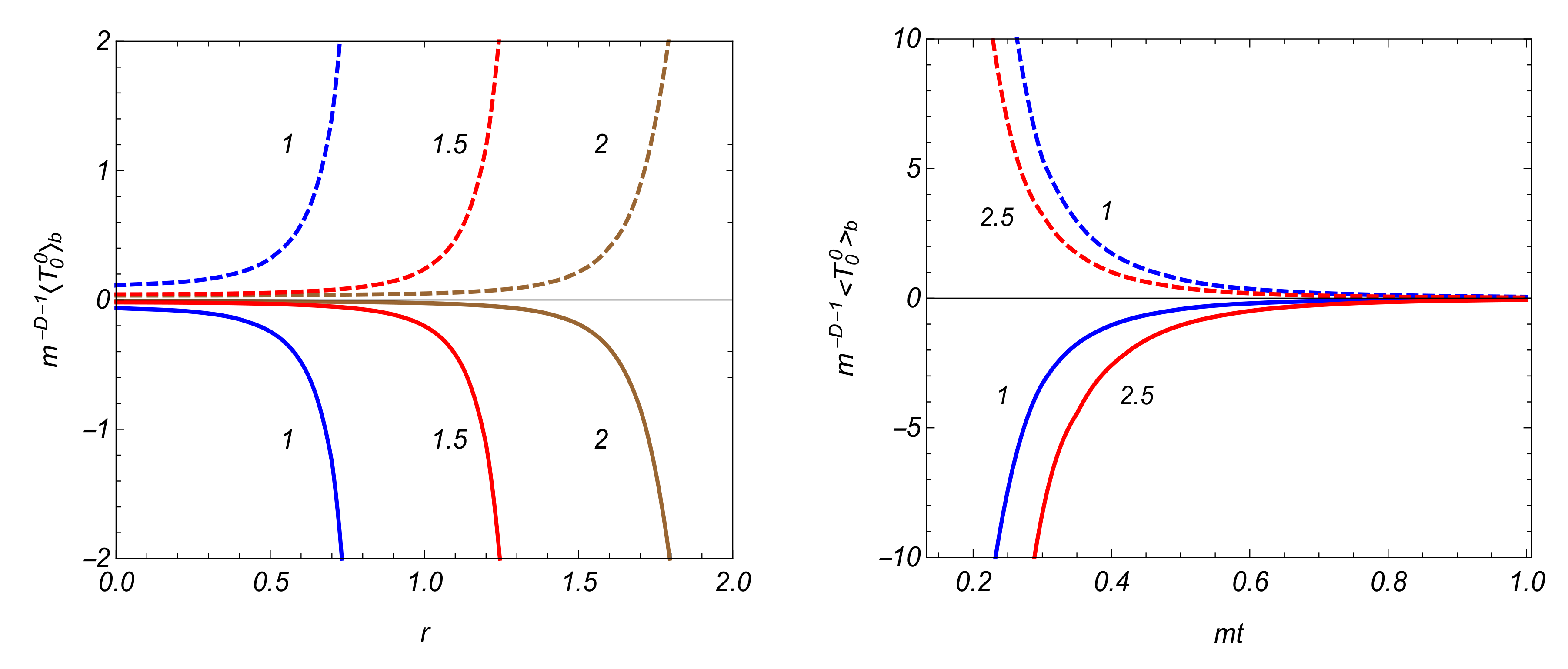
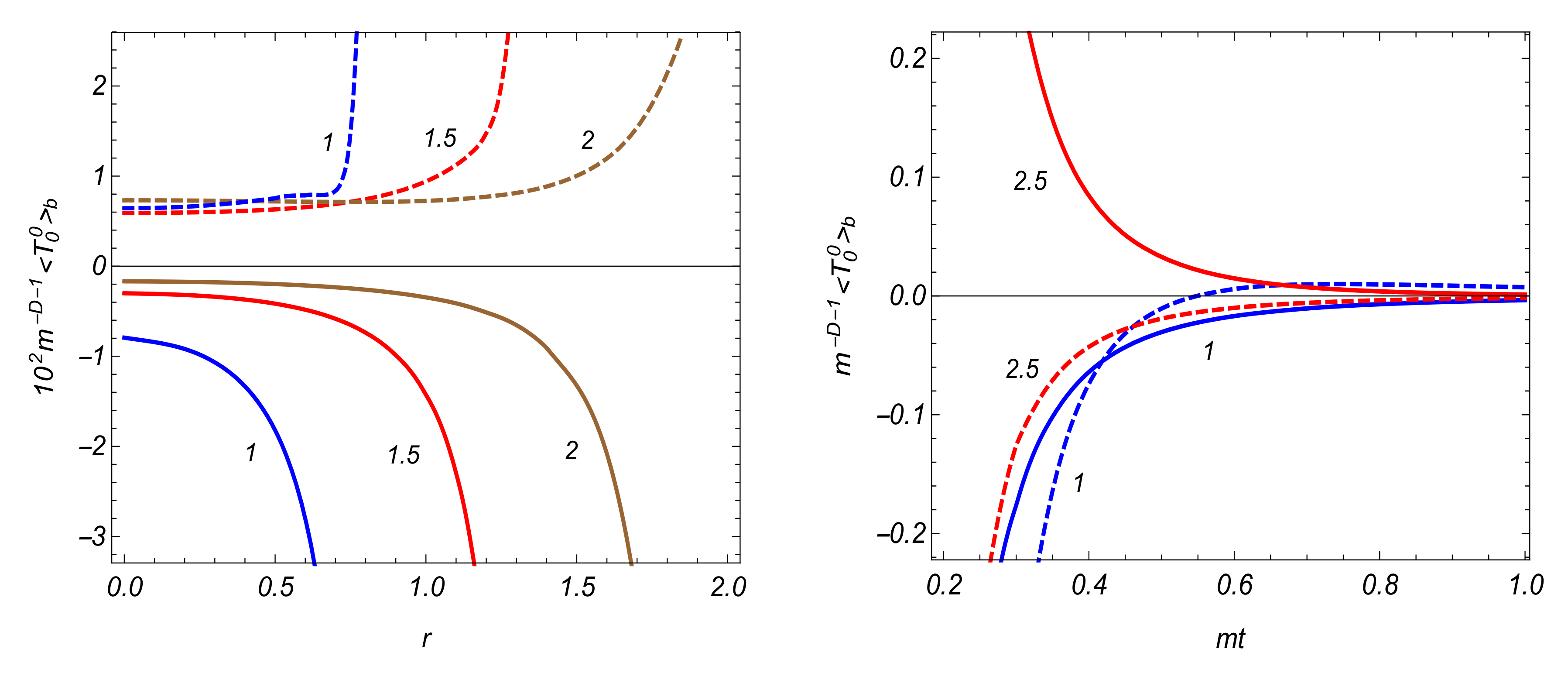
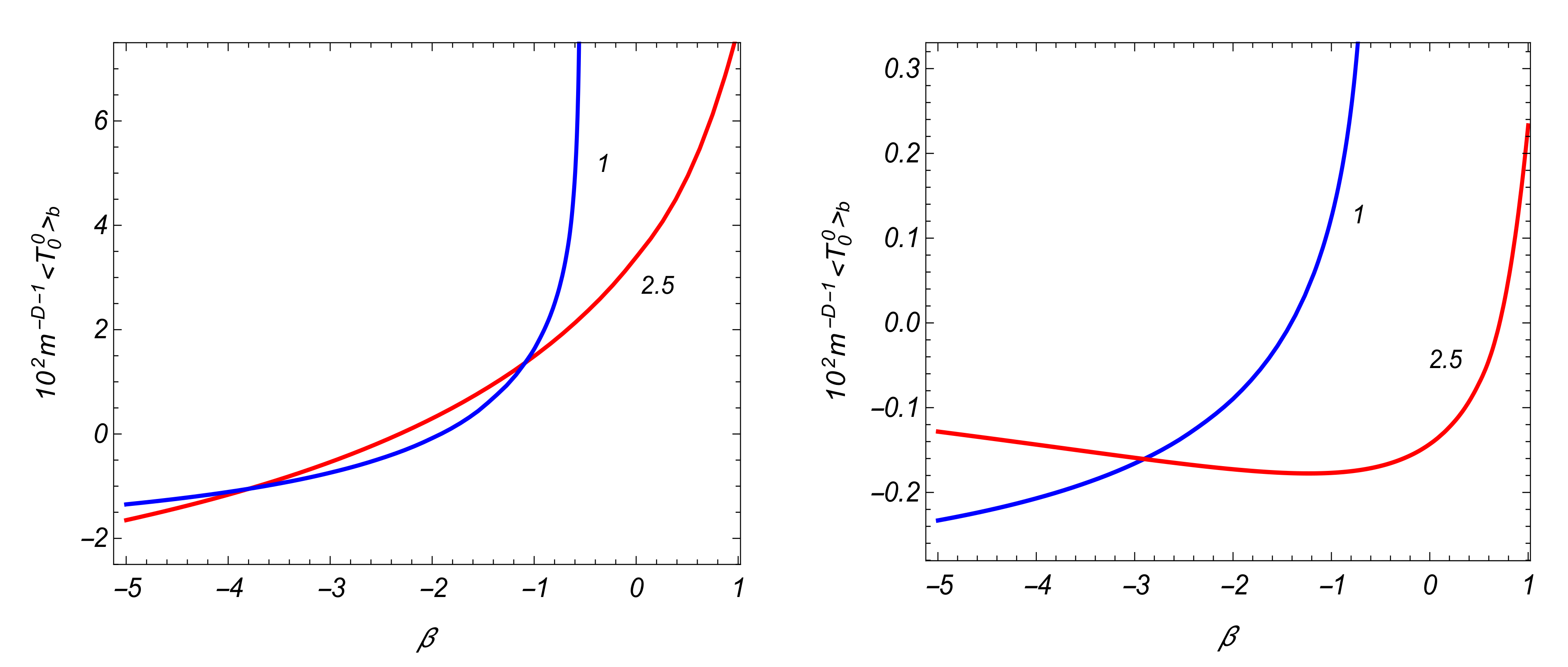


| 0.5 | 1 | 1.5 | 2 | 4 | 6 | 8 | 10 | |
|---|---|---|---|---|---|---|---|---|
| 0.164 | 0.313 | 0.438 | 0.537 | 0.751 | 0.833 | 0.875 | 0.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saharian, A.A.; Petrosyan, T.A. The Casimir Densities for a Sphere in the Milne Universe. Symmetry 2020, 12, 619. https://doi.org/10.3390/sym12040619
Saharian AA, Petrosyan TA. The Casimir Densities for a Sphere in the Milne Universe. Symmetry. 2020; 12(4):619. https://doi.org/10.3390/sym12040619
Chicago/Turabian StyleSaharian, Aram A., and Tigran A. Petrosyan. 2020. "The Casimir Densities for a Sphere in the Milne Universe" Symmetry 12, no. 4: 619. https://doi.org/10.3390/sym12040619





