Magneto-Optical Tools to Study Effects in Dirac and Weyl Semimetals
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Kerr Rotation as a Function of the Electric and Magnetic Fields
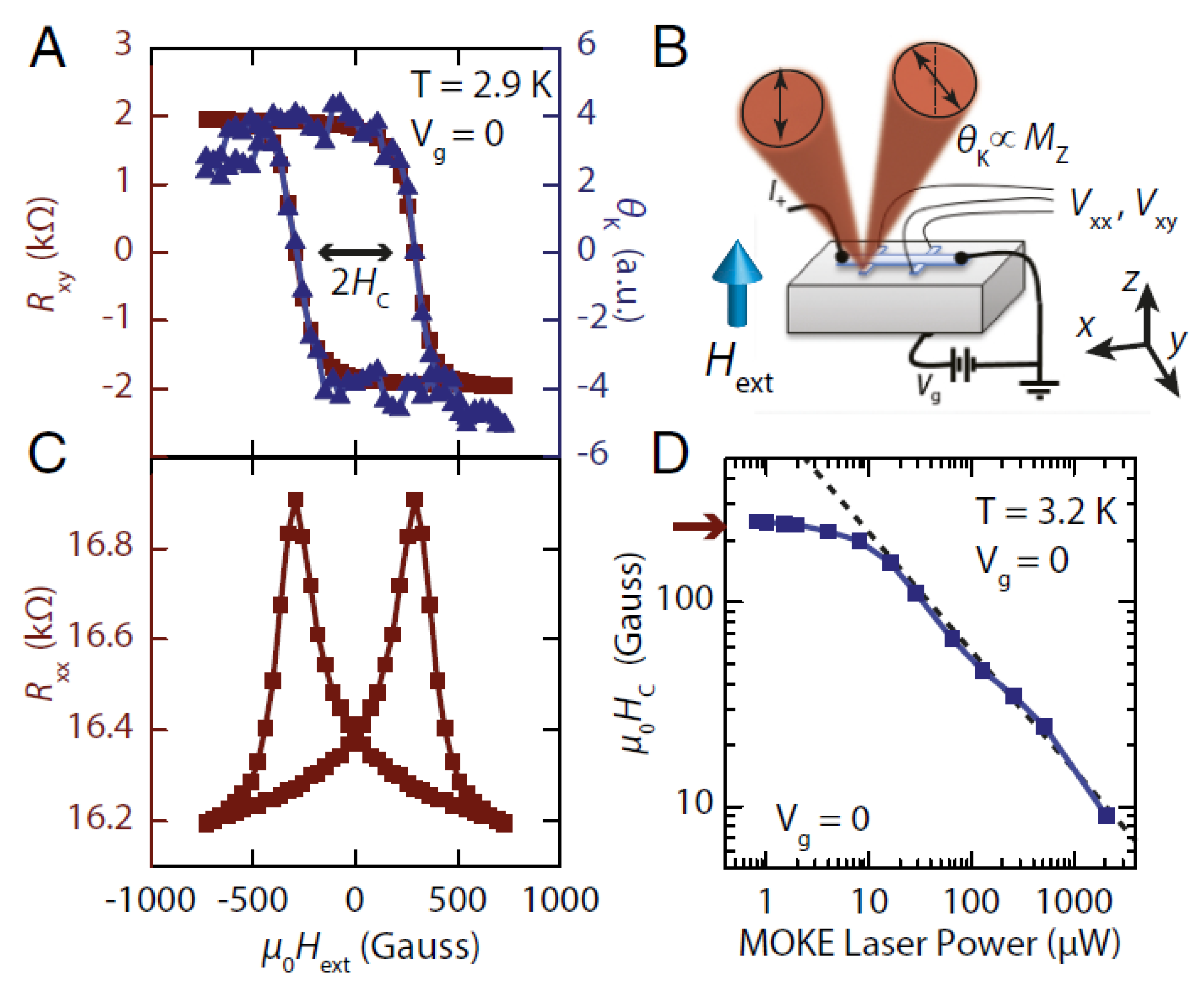
3.2. Magneto-Optical Kerr Signal Combined with Anomalous Hall Effect Measurements
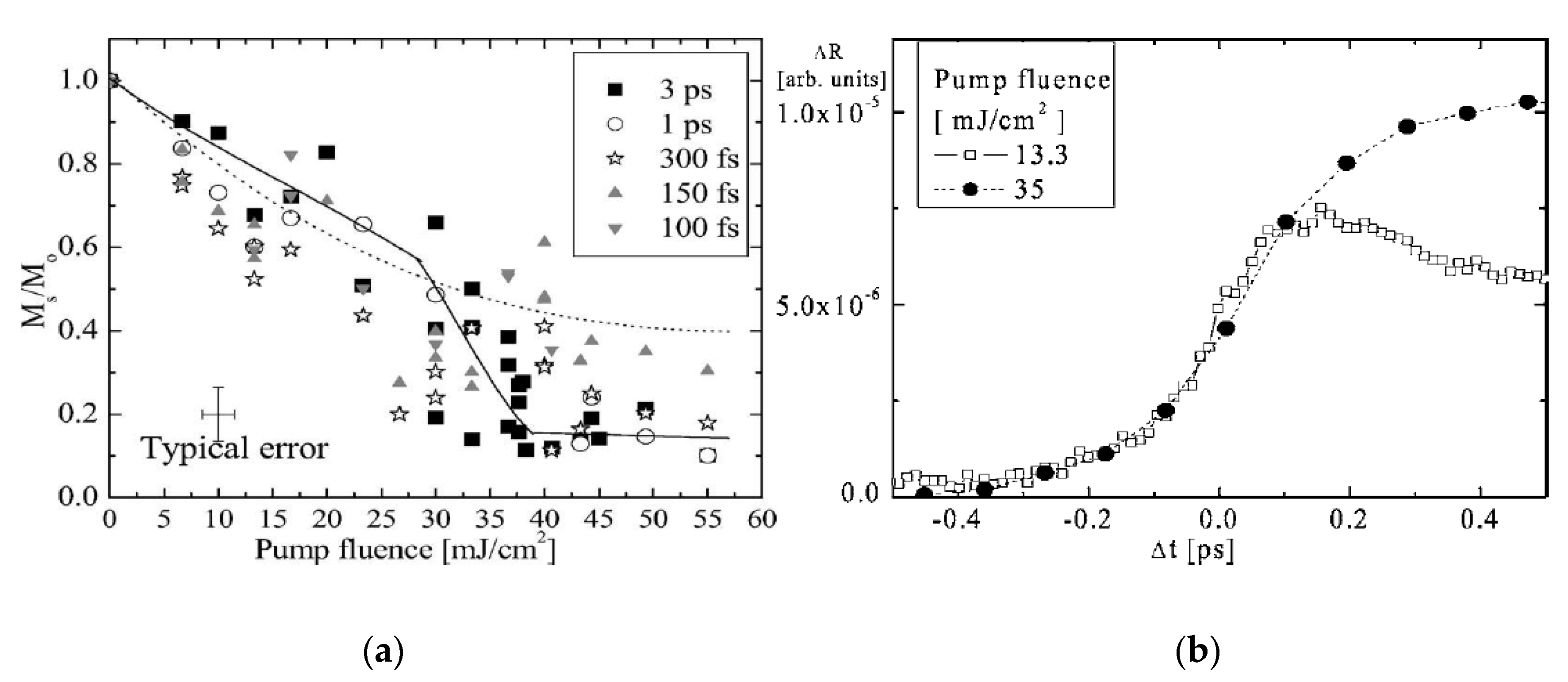
3.3. Magneto-Optical Kerr Signal as a Function of Pump Intensity
3.4. Magneto-Optical Kerr and Faraday Imaging
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef] [Green Version]
- Vafek, O.; Vishwanath, A. Dirac fermions in solids: From high-T c cuprates and graphene to topological insulators and Weyl semimetals. Annu. Rev. Condens. Matter Phys. 2014, 5, 83–112. [Google Scholar] [CrossRef] [Green Version]
- Jia, S.; Xu, S.-Y.; Hasan, M.Z. Weyl semimetals, Fermi arcs and chiral anomalies. Nat. Mater. 2016, 15, 1140–1144. [Google Scholar] [CrossRef] [Green Version]
- Yan, B.; Felser, C. Topological materials: Weyl semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337–354. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Xu, S.-Y.; Ni, N.; Mao, Z. Transport of topological semimetals. Annu. Rev. Mater. Res. 2019, 49, 207–252. [Google Scholar] [CrossRef] [Green Version]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 15001. [Google Scholar] [CrossRef] [Green Version]
- Bernevig, A.; Weng, H.; Fang, Z.; Dai, X. Recent progress in the study of topological semimetals. J. Phys. Soc. Jpn. 2018, 87, 41001. [Google Scholar] [CrossRef]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac semimetal in three dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Chen, X.-Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac semimetal and topological phase transitions in A 3 Bi (A = Na, K, Rb). Phys. Rev. B 2012, 85, 195320. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Weng, H.; Wu, Q.; Dai, X.; Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd 3 As 2. Phys. Rev. B 2013, 88, 125427. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.-Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.-C. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dirac, P.A.M. The quantum theory of the electron. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1928, 117, 610–624. [Google Scholar]
- Weyl, H. Elektron und gravitation. I. Z. Phys. 1929, 56, 330–352. [Google Scholar] [CrossRef]
- Burkov, A.A. Chiral anomaly and diffusive magnetotransport in Weyl metals. Phys. Rev. Lett. 2014, 113, 247203. [Google Scholar] [CrossRef]
- Ye, L.; Kang, M.; Liu, J.; Von Cube, F.; Wicker, C.R.; Suzuki, T.; Jozwiak, C.; Bostwick, A.; Rotenberg, E.; Bell, D.C. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 2018, 555, 638–642. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, Y.; Lou, R.; Liu, Z.; Li, M.; Huang, Y.; Shen, D.; Weng, H.; Wang, S.; Lei, H. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co 3 Sn 2 S 2 with magnetic Weyl fermions. Nat. Commun. 2018, 9, 1–8. [Google Scholar]
- Dulal, R.P.; Dahal, B.R.; Forbes, A.; Bhattarai, N.; Pegg, I.L.; Philip, J. Weak localization and small anomalous Hall conductivity in ferromagnetic Weyl semimetal Co 2 TiGe. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef]
- Puphal, P.; Pomjakushin, V.; Kanazawa, N.; Ukleev, V.; Gawryluk, D.J.; Ma, J.; Naamneh, M.; Plumb, N.C.; Keller, L.; Cubitt, R. Topological Magnetic Phase in the Candidate Weyl Semimetal CeAlGe. Phys. Rev. Lett. 2020, 124, 17202. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.-L. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bostwick, A.; Ohta, T.; Seyller, T.; Horn, K.; Rotenberg, E. Quasiparticle dynamics in graphene. Nat. Phys. 2007, 3, 36–40. [Google Scholar] [CrossRef]
- Sprinkle, M.; Siegel, D.; Hu, Y.; Hicks, J.; Tejeda, A.; Taleb-Ibrahimi, A.; Le Fèvre, P.; Bertran, F.; Vizzini, S.; Enriquez, H. First direct observation of a nearly ideal graphene band structure. Phys. Rev. Lett. 2009, 103, 226803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.L.; Analytis, J.G.; Chu, J.-H.; Liu, Z.K.; Mo, S.-K.; Qi, X.-L.; Zhang, H.J.; Lu, D.H.; Dai, X.; Fang, Z. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 2009, 325, 178–181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.-K.; Shen, Z.X.; Fang, Z.; Dai, X. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.K.; Jiang, J.; Zhou, B.; Wang, Z.J.; Zhang, Y.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Peng, H.; Dudin, P. A stable three-dimensional topological Dirac semimetal Cd 3 As 2. Nat. Mater. 2014, 13, 677–681. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Liu, E.; Shi, W.; Muechler, L.; Gayles, J.; Felser, C.; Sun, Y. Topological surface Fermi arcs in the magnetic Weyl semimetal Co 3 Sn 2 S 2. Phys. Rev. B 2018, 97, 235416. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.F.; Liang, A.J.; Liu, E.K.; Xu, Q.N.; Li, Y.W.; Chen, C.; Pei, D.; Shi, W.J.; Mo, S.K.; Dudin, P. Magnetic Weyl semimetal phase in a Kagomé crystal. Science 2019, 365, 1282–1285. [Google Scholar] [CrossRef] [Green Version]
- Crepaldi, A.; Autès, G.; Gatti, G.; Roth, S.; Sterzi, A.; Manzoni, G.; Zacchigna, M.; Cacho, C.; Chapman, R.T.; Springate, E.; et al. Enhanced ultrafast relaxation rate in the Weyl semimetal phase of MoTe2 measured by time- and angle-resolved photoelectron spectroscopy. Phys. Rev. B 2017, 96, 241408. [Google Scholar] [CrossRef] [Green Version]
- Fanciulli, M.; Schusser, J.; Lee, M.-I.; El Youbi, Z.; Heckmann, O.; Richter, M.C.; Cacho, C.; Spezzani, C.; Bresteau, D.; Hergott, J.-F.; et al. Spin, time, and angle resolved photoemission spectroscopy on WTe2. Phys. Rev. Res. 2020, 2, 13261. [Google Scholar] [CrossRef] [Green Version]
- Cattelan, M.; Fox, N.A. A perspective on the application of spatially resolved ARPES for 2D materials. Nanomaterials 2018, 8, 284. [Google Scholar] [CrossRef] [Green Version]
- Finizio, S.; Kronenberg, A.; Vafaee, M.; Foerster, M.; Litzius, K.; de Lucia, A.; Menteş, T.O.; Aballe, L.; Krüger, B.; Jourdan, M. Magnetic configurations in nanostructured Co2MnGa thin film elements. New J. Phys. 2015, 17, 83030. [Google Scholar] [CrossRef]
- Higo, T.; Man, H.; Gopman, D.B.; Wu, L.; Koretsune, T.; van’t Erve, O.M.J.; Kabanov, Y.P.; Rees, D.; Li, Y.; Suzuki, M.-T. Large magneto-optical Kerr effect and imaging of magnetic octupole domains in an antiferromagnetic metal. Nat. Photonics 2018, 12, 73. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, E.; Wang, W.; Liu, Y.; Chen, Z.-G.; Lu, S.; Liang, S.; Cao, J.; Yuan, X.; Tang, L. Room-temperature chiral charge pumping in Dirac semimetals. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef]
- Yeats, A.L.; Mintun, P.J.; Pan, Y.; Richardella, A.; Buckley, B.B.; Samarth, N.; Awschalom, D.D. Local optical control of ferromagnetism and chemical potential in a topological insulator. Proc. Natl. Acad. Sci. USA 2017, 114, 10379–10383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jadidi, M.; Kargarian, M.; Mittendorff, M.; Aytac, Y.; Shen, B.; König-Otto, J.; Winnerl, S.; Ni, N.; Murphy, T.E.; Drew, H.D. Optical Control of Chiral Charge Pumping in a Topologcial Weyl Semimetal. Bull. Am. Phys. Soc. 2019, 64, po4.00001. [Google Scholar]
- Koopmans, B.; Van Kampen, M.; Kohlhepp, J.T.; De Jonge, W.J.M. Ultrafast magneto-optics in nickel: Magnetism or optics? Phys. Rev. Lett. 2000, 85, 844. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.P.; Hübner, W.; Lefkidis, G.; Bai, Y.; George, T.F. Paradigm of the time-resolved magneto-optical Kerr effect for femtosecond magnetism. Nat. Phys. 2009, 5, 499–502. [Google Scholar] [CrossRef]
- Regensburger, H.; Vollmer, R.; Kirschner, J. Time-resolved magnetization-induced second-harmonic generation from the Ni (110) surface. Phys. Rev. B 2000, 61, 14716. [Google Scholar] [CrossRef] [Green Version]
- Kampfrath, T.; Ulbrich, R.G.; Leuenberger, F.; Münzenberg, M.; Sass, B.; Felsch, W. Ultrafast magneto-optical response of iron thin films. Phys. Rev. B 2002, 65, 104429. [Google Scholar] [CrossRef]
- Van Kampen, M.; Koopmans, B.; Kohlhepp, J.T.; De Jonge, W.J.M. Laser-induced precession in canted-spin ferromagnets. J. Magn. Magn. Mater. 2002, 240, 291–293. [Google Scholar] [CrossRef]
- Vodungbo, B.; Gautier, J.; Lambert, G.; Sardinha, A.B.; Lozano, M.; Sebban, S.; Ducousso, M.; Boutu, W.; Li, K.; Tudu, B. Laser-induced ultrafast demagnetization in the presence of a nanoscale magnetic domain network. Nat. Commun. 2012, 3, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Deb, M.; Molho, P.; Barbara, B.; Bigot, J.-Y. Controlling laser-induced magnetization reversal dynamics in a rare-earth iron garnet across the magnetization compensation point. Phys. Rev. B 2018, 97, 134419. [Google Scholar] [CrossRef]
- Schellekens, A.J.; De Vries, N.; Lucassen, J.; Koopmans, B. Exploring laser-induced interlayer spin transfer by an all-optical method. Phys. Rev. B 2014, 90, 104429. [Google Scholar] [CrossRef] [Green Version]
- Beaurepaire, E.; Merle, J.-C.; Daunois, A.; Bigot, J.-Y. Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 1996, 76, 4250. [Google Scholar] [CrossRef]
- Cheskis, D.; Porat, A.; Szapiro, L.; Potashnik, O.; Bar-Ad, S. Saturation of the ultrafast laser-induced demagnetization in nickel. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 72, 014437. [Google Scholar] [CrossRef]
- Elazar, M.; Sahaf, M.; Szapiro, L.; Cheskis, D.; Bar-Ad, S. Single-pulse magneto-optic microscopy: A new tool for studying optically induced magnetization reversals. Opt. Lett. 2008, 33, 2734–2736. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Zhang, C.; Zhang, Y.; Yan, Z.; Lyu, T.; Zhang, M.; Li, Z.; Song, C.; Zhao, M.; Leng, P.; et al. The discovery of dynamic chiral anomaly in a Weyl semimetal NbAs. Nat. Commun. 2020, 11, 1259. [Google Scholar] [CrossRef]
- Xu, S.-Y.; Belopolski, I.; Sanchez, D.S.; Neupane, M.; Chang, G.; Yaji, K.; Yuan, Z.; Zhang, C.; Kuroda, K.; Bian, G. Spin polarization and texture of the Fermi arcs in the Weyl fermion semimetal TaAs. Phys. Rev. Lett. 2016, 116, 96801. [Google Scholar] [CrossRef]
- Lv, B.Q.; Muff, S.; Qian, T.; Song, Z.D.; Nie, S.M.; Xu, N.; Richard, P.; Matt, C.E.; Plumb, N.C.; Zhao, L.X. Observation of Fermi-arc spin texture in TaAs. Phys. Rev. Lett. 2015, 115, 217601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vahaplar, K.; Kalashnikova, A.M.; Kimel, A.V.; Gerlach, S.; Hinzke, D.; Nowak, U.; Chantrell, R.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A. All-optical magnetization reversal by circularly polarized laser pulses: Experiment and multiscale modeling. Phys. Rev. B 2012, 85, 104402. [Google Scholar] [CrossRef]
- Bucciantini, L.; Roy, S.; Kitamura, S.; Oka, T. Emergent Weyl nodes and Fermi arcs in a Floquet Weyl semimetal. Phys. Rev. B 2017, 96, 41126. [Google Scholar] [CrossRef] [Green Version]
- Hübener, H.; Sentef, M.A.; De Giovannini, U.; Kemper, A.F.; Rubio, A. Creating stable Floquet–Weyl semimetals by laser-driving of 3D Dirac materials. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.; Xu, S.-Y.; Chan, C.-K.; Zhang, C.-L.; Chang, G.; Lin, Y.; Xie, W.; Palacios, T.; Lin, H.; Jia, S. Direct optical detection of Weyl fermion chirality in a topological semimetal. Nat. Phys. 2017, 13, 842–847. [Google Scholar] [CrossRef]
- Tancin, R.J.; Chang, Z.; Gu, M.; Radhakrishna, V.; Lucht, R.P.; Goldenstein, C.S. Ultrafast laser-absorption spectroscopy for single-shot, mid-infrared measurements of temperature, CO, and CH4 in flames. Opt. Lett. 2020, 45, 583–586. [Google Scholar] [CrossRef] [Green Version]
- Stamm, C.; Murer, C.; Berritta, M.; Feng, J.; Gabureac, M.; Oppeneer, P.M.; Gambardella, P. Magneto-optical detection of the spin Hall effect in Pt and W thin films. Phys. Rev. Lett. 2017, 119, 87203. [Google Scholar] [CrossRef] [PubMed]



© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheskis, D. Magneto-Optical Tools to Study Effects in Dirac and Weyl Semimetals. Symmetry 2020, 12, 1412. https://doi.org/10.3390/sym12091412
Cheskis D. Magneto-Optical Tools to Study Effects in Dirac and Weyl Semimetals. Symmetry. 2020; 12(9):1412. https://doi.org/10.3390/sym12091412
Chicago/Turabian StyleCheskis, Dima. 2020. "Magneto-Optical Tools to Study Effects in Dirac and Weyl Semimetals" Symmetry 12, no. 9: 1412. https://doi.org/10.3390/sym12091412




