Output Tracking Control for High-Order Nonlinear Systems with Time Delay via Output Feedback Design

Abstract

Design approach of an output feedback tracking controller is proposed for a class of high-order nonlinear systems with time delay. To deal with the time delays, an appropriate Lyapunov–Krasovskii the tracking analysis is ingeniously constructed, and an output feedback tracking controller is designed by using a homogeneous domination method. It is shown that the proposed output controller independent of time delay can make the tracking error be adjusted to be sufficiently small and render all the trajectory of the closed-loop system as bounded. An example is given to illustrate the effectiveness of the proposed method.

1. Introduction

In the field of nonlinear control, stabilization and output tracking problems are two of the most important and challenging problems. In this paper, we mainly focus on an output feedback practical tracking problem for a class of high-order time delay nonlinear systems of the form:

$$\begin{array}{l}{\dot{x}}_i(t)=x_{i+1}{(t)}^{p_i}+{\phi }_i(t, x(t), x(t-d), u(t)),i=1,\dots ,n-1,\\ {\dot{x}}_n(t)=u+{\phi }_n(t, x(t), x(t-d), u(t)),\\ y(t) =x_1(t)-y_r(t)\end{array}$$

(1)

where $x(t)={(x_1(t),\dots ,x_n(t))}^{\mathrm{T}}\in R^n$, $u(t)\in R$, and $y(t)\in R$ are states, input, and ouput of the system. Corresponding to this, $y_r(t)\in R$ is a given unmeasurable reference signal. The constant $d\ge 0$ is a given time delay parameter of the system, and the system initial condition is $x(\theta )={\phi }_0(\theta ),$ $\theta \in [0, d].$ The nonlinear function ${\phi }_i(\cdot )$ is a continuous function, and $p_i\in R_{odd}^{\ge 1}:=\{p/q\in [0, \infty ):p$ and $q$ are odd integers, $p\ge q$, $(i=1,\dots ,n-1)$.

The practical output tracking problem of a nonlinear system (1) has received a great deal of attention over the past years, and many important results have been achieved. The work [1] by Celikovsky and Huang studied the local output tracking problem. Because it is not suitable for a global case, in [2], the problem of global output tracking was considered. The work [3] investigated the adaptive practical output tracking problem. Later, in [4,5,6,7,8,9,10,11,12,13,14], the above works are extended to more general cases under some weak conditions.

It has been known that solving the above problem via output feedback design for high-order nonlinear systems is very challenging and difficult compared to the state feedback case. Because there is no general and effective method to design a non-linear observer, the theory of output feedback control design developed more slowly. Recently, some results were reported, for example, [6,7,8,9,10,11].

However, most of the above results do not consider the effect of time delay. It is well known that time delay phenomenon is ubiquitous and inevitable in nature, which is one of the main reasons for the instability of system performance. Therefore, the design of a controller for stabilization and output tracking problems of nonlinear systems with time delay has important significance in the field of control engineering. Thus, there is little coverage on this issue. In [15,16,17,18], we only solved the problem by state feedback control. Lyapunov–Krasovskii method is a powerful tool in stability analysis and controller design for time delay systems in [19,20,21,22,23,24,25,26]. Study for the output tracking control time delay problem developed more slowly than the stabilization case with time delay. For the output tracking time delay problems via output feedback, there are some new interesting works (see [27,28,29,30]). However, these results only investigate the case $p_i$ equal one for considered systems (1). For a high-order time delay nonlinear system (1), the output tracking problem becomes more complicated and difficult to solve. However, to the best of our knowledge, the global practical output problem of nonlinear systems with partial unmeasured states and time delay via output feedback have not yet been considered to date, which motivates this research.

This paper mainly studies the output tracking control problem for a class of high-order nonlinear systems with time delay by using the output feedback domination approach.

The main contributions of this work can be summarized as follows: (i) it should be noticed that the output feedback tracking control problem for high-order nonlinear systems has been mainly studied in [2,3,4,5,6,7,8,9,10,11]. However, by the introduction of time delay factors, the output feedback tracking control problem for the high-order nonlinear system is first studied in this paper by using a homogeneous domination method [31,32,33]; (ii) by comparison with the case $p_i=1$ in [27,28,29,30], how to construct an appropriate Lyapunov–Krasovskii functional for high-order nonlinear system (1) is a non-trivial work. A new Lyapunov–Krasovskii functional for solving the practical output tracking problem is constructed.

Works [34,35] investigated a finite-time output feedback stabilization problem for stochastic high-order nonlinear systems, and work [36] studied a global finite-time control problem for a class of switched nonlinear systems with different powers via output feedback. However, these results do not consider effect of time delay.

This paper addresses the output feedback tracking problem of a class of high-order nonlinear time delay systems. However, if a general nonlinear system or a nonlinear symmetric system can be transformed into the considered system in this article, then the method proposed in this article can also be used.

Throughout the paper, we adopt such notations: $R$ denotes the set of all real numbers, $R^{+}$ denotes the set of positive real numbers, and $R^i$ represents the i-dimensional Euclidean space. $\left|\right|x\left|\right|$ denotes the Euclidean norm of vector $x(t)$. For any vector $x(t)\in R^n$, denote ${\overline{x}}_i(t):={(x_1(t),\dots ,x_i(t))}^T\in R^i,$ $i=1,\dots ,n$.

2. Mathematical Preliminaries

Several lemmas are used throughout this paper. We first give the definition of homogeneous function related to the following two lemmas.

Definition 1 

([31]). For a set of coordinates $x=\left(x_1,\dots ,x_n\right)\in R^n$ and a n-tuple of positive real numbers $r=(r_1,\dots ,r_n)$.

(i)

The dilation ${\Delta }_s^r(x)$ is defined by ${\Delta }_s^r(x)=\left(s^{r_1}{x}_1,\cdots ,s^{r_n}{x}_n\right),$ $\forall s>0$, with $r_i$ being called as the weights of the coordinate. For simplicity, we define dilation weight$\Delta =(r_1,\dots ,r_n)$.

(ii)

A function $V:R^n\to R$ is said to be homogeneous of degree m ($m\in R$) if $V({\Delta }_s^m(x))=s^{m}V(x_1,\cdots ,x_n),$ $\forall s>0, \forall x\in R^n/\left\{0\right\}.$

(iii)

A vector field $f={(f_1,\dots ,f_n)}^T: R^n\to R^n$ is said to be homogeneous of degree k if the component $f_i$ is homogeneous of degree $k+r_i$ for each i, that is, $f_i(s^{r_1}{x}_1,\cdots ,s^{r_n}{x}_n)=s^{k+r_i}{f}_i(x_1,\cdots ,x_n),$ $\forall s>0$, $\forall x\in R^n/\left\{0\right\},$ $i=1,\dots ,n$.

(iv)

${\Vert x\Vert }_{\Delta ,p}={({{\displaystyle {\sum }_{i=1}^n\left|x_i\right|}}^{p/r_i})}^{1/p}, \forall x\in {ℝ}^n, p\ge 1$denote a homogeneous $p$-norm. For simplicity, write ${\Vert x\Vert }_{\Delta }$ for ${\Vert x\Vert }_{\Delta ,2}$.

Lemma 1 

([31]) . Denote $\Delta$ as dilation weight, and suppose $V_1(x)$ and $V_2(x)$ are homogeneous functions with degree $m_1$ and $m_2$, respectively. Then, $V_1(x)V_2(x)$ is still a homogeneous function with degree of $m_1+m_2$ with respect to the same dilation weight.

Lemma 2 

([31]) . Suppose $V:R^n\to R$ is a homogeneous function of degree $m$ with respect to the dilation weight $\Delta$. Then, the following statements hold:

(i)

$\partial V/\partial x_i$is homogeneous of degree$m-r_i$with$r_i$being the homogeneous weight of$x_i$.

(ii)

There is a constant$\overline{\sigma }>0$such that$V(x)\le \overline{\sigma }{\Vert x\Vert }_{\Delta }^m$. Moreover, if$V(x)$is positive definite, there is a constant$\underset{\_}{\sigma }>0$such that$\underset{\_}{\sigma }{\Vert x\Vert }_{\Delta }^m\le V(x)$.

Lemma 3 

([33]) . Let $x,y\in R$ and $p\ge 1$ be an integer. Then:

$${\left|x+y\right|}^p\le 2^{p-1}\left|x^p+y^p\right|, {\left(\left|x\right|+\left|y\right|\right)}^{1/p}\le {\left|x\right|}^{1/p}+{\left|y\right|}^{1/p}\le 2^{\left(p-1\right)/p}{\left(\left|x\right|+\left|y\right|\right)}^{1/p}$$

If $p$ is an odd positive integer, then,

$${\left|x-y\right|}^p\le 2^{p-1}\left|x^p-y^p\right|, \left|x^{1/p}-y^{1/p}\right|\le 2^{\left(p-1\right)/p}{\left|x-y\right|}^{1/p}.$$

Lemma 4 

([33]) . For any positive real numbers, c, d, and any real-valued function $\gamma (x,y)>0$ , the following holds

$${\left|x\right|}^c{\left|y\right|}^d\le \frac{c}{c+d}\gamma (x,y){\left|x\right|}^{c+d}+\frac{d}{c+d}{\gamma }^{-c/d}(x,y){\left|y\right|}^{c+d}$$

3. Problem Formulation and Key Assumptions

In this paper, our objective is to provide a solution to global practical output tracking of a system (1) via using the output feedback controller of the following form

$$\begin{array}{l}\dot{\zeta }=\alpha (\zeta , y), \zeta \in R^m\\ u(t)=g(\zeta ,y),\end{array}$$

(2)

such that, for any $\epsilon >0$ and every $x(0)\in R^n$, there exists a finite time $T(\epsilon , x(0))>0$ rendering the tracking error of the closed-loop system (1) and (2), thus it satisfies

$$\left|y(t)\right|=\left|x_1(t)-y_r(t)\right|<\epsilon ,\forall t\ge T>0$$

(3)

and all states of the closed-loop system (1) and (2) are well defined and globally bounded on $[0,\infty )$.

To make this possible, the following assumptions are imposed on system (1) and reference signal $y_r(t)$.

Assumption 1.

There exist positive constants$C_1, C_2$, and$\tau \ge 0$ such that:

$$\begin{array}{cc}\left|{\phi }_i(t,x(t),x(t-d),u(t))\right|\hfill & \le C_1({\left|x_1(t)\right|}^{(r_i+\tau )/r_1}+{\left|x_2(t)\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|x_i(t)\right|}^{(r_i+\tau )/r_i}\hfill \\ & +{\left|x_1(t-d)\right|}^{(r_i+\tau )/r_1}+{\left|x_2(t-d)\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|x_i(t-d)\right|}^{(r_i+\tau )/r_i})+C_2\hfill \end{array}$$

(4)

where $r_i (i=1,\dots ,n)$ are defined so as to satisfy:

$$r_1=1,\hspace{1em}{r}_i{p}_{i-1}=\tau +r_{i-1}$$

(5)

Remark 1.

Unlike the conditions in [6,7,8,9], Assumption 1 contains time delay terms. Further, when$p_i$equals one, the assumption becomes an important hypothesis in literature [27].

Assumption 2.

For the reference function$y_r(t)$and its derivative, there exists a constant$D>0$such that:

$$\max \left\{\left|y_r(t)\right|,\left|{\dot{y}}_r(t)\right|\right\}\le D, \forall t>0$$

Remark 2.

Assumption 2 indicates condition for the reference signal$y_r(t)$. It is a standard condition for solving the practical output tracking problem of nonlinear systems in [2,3,4,5,6,7,8,9,10,11,12,13,23,25,26].

Next, we construct an output feedback controller for system (1) under Assumptions 1 and 2. To achieve this goal, we first construct an output feedback controller for the nominal system of system (1) by setting ${\varphi }_i(t,x,u)=0, i=1,\dots ,n$, i.e., the following nominal system:

$${\dot{z}}_i(t)=z_{i+1}^{p_i}(t), i=1,\dots ,n-1,\hspace{1em}{\dot{z}}_n(t)=v(t),\hspace{1em}y(t)=z_1(t)$$

(6)

where $p_i\in {ℝ}_{\mathrm{odd}}^{\ge 1}$ for $i=1,\dots ,n-1$.

Our control objective is to find a controller of the form:

$$\begin{array}{l}\dot{\eta }=\alpha (\eta , y),\hspace{1em}\eta \in R^{n-1}\\ v(t)=g(\eta ,y),\end{array}$$

(7)

with continuous functions $\alpha :R^n\to R^{n-1}$ and $v:R^n\to R$ satisfying $\alpha (0, 0)=0,\hspace{1em}g(0,0)=0$ such that the closed-loop system (6) and (7) is globally asymptotically stable.

Using a similar approach as in [7,32], we construct an output feedback controller for system (6), which can be described in the following proposition.

Proposition 1 

([7,32]). For the system (6), suppose there exists an output controller based on observer.

$$v(\widehat{z})=-{\beta }_n{[{\widehat{z}}_n^{\mu /r_n}+{\beta }_{n-1}\{{\widehat{z}}_{n-1}^{\mu /r_{n-1}}+\cdots +{\beta }_2({\widehat{z}}_2^{\mu /r_2}+{\beta }_1{z}_1^{\mu /r_1})\dots \}]}^{\left(r_n+\tau \right)/\mu }$$

(8)

$$\begin{array}{ccc}{\dot{\eta }}_2=-L_1{\widehat{z}}_2^{p_1},\hfill & {\widehat{z}}_2={\left[{\eta }_2+L_1{z}_1\right]}^{r_2/r_1}& \\ {\dot{\eta }}_k=-L_{k-1}{\widehat{z}}_k^{p_{k-1}},\hfill & {\widehat{z}}_k={\left[{\eta }_k+L_{k-1}{\widehat{z}}_{k-1}\right]}^{r_k/r_{k-1}},& k=3,\dots ,n\end{array}$$

(9)

with a positive definite, $C^1$, and radially unbounded Lyapunov function,

$$\begin{array}{l}\hspace{1em}V=V_1+V_2,\\ \hspace{1em}{V}_1={\displaystyle \sum _{i=1}^n{{\displaystyle {\int }_{z_i^{*}}^{z_i}\left(s^{\mu /r_i}-z_i^{*\mu /r_i}\right)}}^{\left(2\mu -\tau -r_i\right)/\mu }ds},\\ \hspace{1em}{V}_2={\displaystyle \sum _{i=1}^n{\displaystyle {\int }_{{\left({\eta }_i+L_{i-1}{z}_{i-1}\right)}^{\left(2\mu -\tau -r_{i-1}\right)/r_{i-1}}}^{z_i^{\left(2\mu -\tau -r_{i-1}\right)/r_i}}\left(s^{r_{i-1}/\left(2\mu -\tau -r_{i-1}\right)}-\left({\eta }_i+L_{i-1}{z}_{i-1}\right)\right)}ds}\end{array}$$

(10)

such that:

$$\dot{V}\le -\frac{1}{4}{\displaystyle \sum _{j=1}^n{\xi }_j^2}-\frac{1}{4}{\displaystyle \sum _{j=2}^n{\zeta }_j^2}$$

(11)

where $\widehat{z}={[{\widehat{z}}_1,{\widehat{z}}_2,\dots ,{\widehat{z}}_n]}^T\in R^n$, ${\widehat{z}}_1=z_1=y$ and $r_i (i=2,\dots ,n+1)$ are defined by (5) and $L_i>0\hspace{1em}(i=1,\dots ,n-1)$ are the gains to be selected later, and:

$${\xi }_i=z_i^{\mu /r_i}-z_i^{\ast \mu /r_i}, z_i^{\ast }=-{\beta }_{i-1}^{r_i/\mu }{\xi }_{i-1}^{r_i/\mu },z_1^{\ast }=0, {\zeta }_i={\left(z_i^{p_{i-1}}-{\widehat{z}}_i^{p_{i-1}}\right)}^{\mu /p_i{r}_{i-1}},$$

$\mu \ge {\max }_{1\le i\le n}\left\{\tau +r_i\right\}$ and ${\beta }_i>0, i=1, \dots , n$ are constants. Then, the closed-loop system (6), (8), and (9) is globally asymptotically stable.

Since the proof of the proposition is exactly the same [11,33], it is omitted here.

Note that, from (10), it is easy to verify that $V>0$ and is radially unbounded with respect to:

$$Z:={\left[z_1,\dots ,z_n,{\eta }_2,\dots ,{\eta }_n\right]}^T$$

(12)

Denoting the dilation weight:

$$\Delta =\underset{\mathrm{for} z_1,\dots ,z_n}{\underbrace{[r_1,r_2,\dots ,r_n}},\underset{\mathrm{for}{\eta }_2,\dots ,{\eta }_n}{\underbrace{r_1,r_2,\dots ,r_{n-1}]}}$$

(13)

the closed-loop system (6) with the output controller (8) and (9) can be rewritten in a compact form as:

$$\dot{Z}=F(Z)={\left[z_2^{p_1},\dots ,z_n^{p_{n-1}},v\left(z_1,{\eta }_2,\dots ,{\eta }_n\right), f_{n+1},\dots ,f_{2n-1}\right]}^T$$

(14)

where $f_{n+1}:={\dot{\eta }}_2,f_{n+2}:={\dot{\eta }}_3,\dots ,f_{2n-1}:={\dot{\eta }}_n$.

By Definition 1, we can prove that $F(Z)$ is homogeneous of degree $\tau$ and $V(Z)$ is homogeneous of degree $2\mu -\tau$ with respect to dilation weight $\Delta$. By Lemma 4, the following holds:

$$\frac{\partial V(Z)}{\partial Z_i}\le {\gamma }_1{\Vert Z\Vert }_{\Delta }^{2\mu -\tau -r_i}, {\gamma }_1>0, \mathrm{for} i = 1, \dots , n$$

(15)

In addition, by Proposition 1, closed-loop system (8), (14) and (9) is globally asymptotically stable. Therefore, the following holds:

$$\dot{V}(Z)|{}_{(14)}=\frac{\partial V(Z)}{\partial Z}F(Z)\le -{\gamma }_2{\Vert Z\Vert }_{\Delta }^{2\mu }$$

(16)

where ${\gamma }_2>0$ is a constant and ${\Vert Z\Vert }_{\Delta }=\sqrt{{\displaystyle {\sum }_{i=1}^{2n-1}{\left|Z_i\right|}^{2/r_i}}}$.

4. Output Tracking Control via Output Feedback Design

In this section, we state and prove our result.

Theorem 1.

Consider system (1) under Assumptions 1 and 2. For any given delay constant d, the global practical output tracking problem stated above is solvable by an output feedback of the form (7), and a design method for such a control is explicitly given.

Proof. 

First, we define a change of coordinates:

$$z_1(t):=y(t),\hspace{1em}{M}^{{\kappa }_i}{z}_i(t):=x_i(t),\hspace{1em}i=2,\dots ,n,\hspace{1em}{M}^{{\kappa }_n+1}v(t):=u(t)$$

(17)

where ${\kappa }_1=0, {\kappa }_i=({\kappa }_{i-1}+1)/p_{i-1}$, $i=2,\dots ,n$ and constant gain $M\ge 1$ are determined later. Under (17), system (1) can be rewritten in variables $z_i$ as:

$$\begin{array}{l}{\dot{z}}_i(t)=M{z}_{i+1}^{p_i}(t)+{\psi }_i(t,z(t), z(t-d),v(t)),i=1,\dots ,n-1,\\ {\dot{z}}_n(t)=Mv(t)+{\psi }_n(t,z(t), z(t-d),v(t)), \hspace{1em}\\ y(t)=z_1(t)\end{array}$$

(18)

where:

$$\begin{array}{l}{\psi }_1(t,z(t), z(t-d),v(t)):={\phi }_1(t,x(t),x(t-d),u(t))-{\dot{y}}_r(t)\\ {\psi }_i(t,z(t), z(t-d),v(t)):=\frac{{\phi }_i(t,x(t),x(t-d),u(t))}{M^{{\kappa }_i}},\hspace{1em}i=2,\dots ,n.\end{array}$$

(19)

By Assumption 1, Lemma 3, and $M\ge 1$, it is not difficult to get the following to hold:

$$\begin{array}{c}\left|{\psi }_1(z_1(t), z_1(t-d))\right|\le C_1\left({\left|z_1(t)+y_r(t)\right|}^{(r_1+\tau )/r_1}+{\left|z_1(t-d)+y_r(t-d)\right|}^{(r_1+\tau )/r_1}\right)+C_2+\left|{\dot{y}}_r\right|\hfill \\ \left|{\psi }_i({\overline{z}}_i(t), z_1(t-d),\dots , z_i(t-d)\right|=\left|\frac{{\phi }_i({\overline{x}}_i(t), x_1(t-d),\dots , x_i(t-d))}{M^{{\kappa }_i}}\right| \hfill \\ \le \frac{C_1}{M^{{\kappa }_i}}([{\left|z_1(t)+y_r(t)\right|}^{(r_i+\tau )/r_1}+{\left|M^{{\kappa }_2}{z}_2(t)\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|M^{{\kappa }_i}{z}_i(t)\right|}^{(r_i+\tau )/r_i}]\hfill \\ +[{\left|z_1(t-d)+y_r(t-d)\right|}^{(r_i+\tau )/r_1}+{\left|M^{{\kappa }_2}{z}_2(t-d)\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|M^{{\kappa }_i}{z}_i(t-d)\right|}^{(r_i+\tau )/r_i}])+\frac{C_2}{M^{{\kappa }_i}}\hfill \\ \end{array}$$

Further, by Assumption 2, we can easily calculate:

$$\begin{array}{c}\left|{\psi }_1(z_1(t), z_1(t-d))\right|\le {\overline{C}}_1\left({\left|z_1(t)\right|}^{(r_1+\tau )/r_1}+{\left|z_1(t-d)\right|}^{(r_1+\tau )/r_1}\right)+{\overline{C}}_2\hfill \\ \left|{\psi }_i({\overline{z}}_i(t), z_1(t-d),\dots , z_i(t-d)\right|\hfill \\ \le {\overline{C}}_1{M}^{1-v_i}{\displaystyle \sum _{j=1}^i\left({\left|z_j(t)\right|}^{(r_i+\tau )/r_j}+{\left|z_j\left(t-d\right)\right|}^{(r_i+\tau )/r_j}\right)}+\frac{{\overline{C}}_2}{M^{{\kappa }_i}},\hspace{1em}i=2,\dots ,n\hfill \end{array}$$

(20)

where ${\overline{C}}_1>0, {\overline{C}}_2>0$ only dependent on constants $C_1, C_2, \tau , {\kappa }_i \mathrm{and} M$ and ${\nu }_i=\min \left\{1-{\kappa }_j(r_i+\tau )/r_j+{\kappa }_i, 2\le j\le i, 1\le i\le n\right\}>0$ are some constants.

By the definition of $r_j=\tau {\kappa }_j+1/(p_1\dots p_{j-1})$,

$$\begin{array}{c}{\kappa }_j\frac{r_{i+1}{p}_i}{r_j}-{\kappa }_i=\frac{\tau {\kappa }_j+{\kappa }_j/p_1\dots p_{i-1}-{\kappa }_i/p_1\dots p_{j-1}}{\tau {\kappa }_j+1/p_1\dots p_{j-1}}\le \frac{\tau {\kappa }_j}{\tau {\kappa }_j+1/p_1\dots p_{j-1}}<1,\\ j=2,\dots ,i,i=1,\dots ,n.\end{array}$$

(21)

Notice that the two systems (1) and (18) are equivalent to each other, and, hence, we can work on system (18) instead of system (1) whenever it is more convenient. Now, by Proposition 1, we can construct an output controller for system (18) in the form:

$$v(\widehat{z})=-{\beta }_n{[{\widehat{z}}_n^{\mu /r_n}+{\beta }_{n-1}\{{\widehat{z}}_{n-1}^{\mu /r_{n-1}}+\cdots +{\beta }_2({\widehat{z}}_2^{\mu /r_2}+{\beta }_1{z}_1^{\mu /r_1})\cdots \}]}^{\left(r_n+\tau \right)/\mu }$$

(22)

$$\begin{array}{ccc}{\dot{\eta }}_2=-M{L}_1{\widehat{z}}_2^{p_1},\hfill & {\widehat{z}}_2={\left({\eta }_2+L_1{z}_1\right)}^{r_2/r_1}& \\ {\dot{\eta }}_k=-M{L}_{k-1}{\widehat{z}}_k^{p_{k-1}},\hfill & {\widehat{z}}_k={\left({\eta }_k+L_{k-1}{\widehat{z}}_{k-1}\right)}^{r_k/r_{k-1}},& k=3,\dots ,n\end{array}$$

(23)

Using (12) and (14), the closed-loop system (18), (22), and (23) can be written in the following form:

$$\dot{Z}=MF\left(Z\right)+{\left[{\psi }_1(\cdot ), {\psi }_2(\cdot ), {\psi }_3(\cdot ) ,\dots ,{\psi }_n(\cdot ),0,\dots , 0\right]}^T$$

(24)

Hence, adopting the same Lyapunov function (10), i.e., $V(Z)$, the time derivative of $V(Z)$ along the trajectory of (24) satisfies:

$$\begin{array}{ccc}\hfill \dot{V}(Z)& =& M\frac{\partial V(Z)}{\partial Z}F(Z)\hfill \\ \hfill & & +\frac{\partial V(Z)}{\partial Z}{\left[{\psi }_1(\cdot ), {\psi }_2(\cdot ), {\psi }_3(\cdot ) ,\dots ,{\psi }_n(\cdot ),0,\dots , 0\right]}^T\hfill \\ \hfill & \le & -M\gamma {\Vert Z\Vert }_{\Delta }^{2\mu }+{\displaystyle \sum _{i=1}^n\frac{\partial V(Z)}{\partial Z_i}}{\psi }_i(\cdot ).\hfill \end{array}$$

(25)

Further, using (20), one obtains:

$$\begin{array}{cc}\hfill \dot{V}(Z) \le & -M\gamma {\Vert Z\Vert }_{\Delta }^{2\mu }\hfill \\ \hfill & +{\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{1-{\nu }_i}\left|\frac{\partial V(Z)}{\partial Z_i}\right|[\left({\left|z_1(t)\right|}^{(r_i+\tau )/r_1}+{\left|z_2(t)\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|z_i\right|}^{(r_i+\tau )/r_i}\right)}\hfill \end{array}$$

$$+\left({\left|z_1(t-d)\right|}^{(r_i+\tau )/r_1}+{\left|z_2(t-d)\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|z_i(t-d)\right|}^{(r_i+\tau )/r_i}\right)]+{\overline{C}}_2{\displaystyle \sum _{i=1}^n\frac{1}{M^{{\kappa }_i}}\left|\frac{\partial V(Z)}{\partial Z_i}\right|}.$$

(26)

Since, by Lemma 2 and (15), $\frac{\partial V(Z)}{\partial Z_i}$ is homogeneous of degree $2\mu -\tau -r_i$, the terms:

$$\left|\frac{\partial V(Z)}{\partial Z_i}\right|\left({\left|z_1\right|}^{(r_i+\tau )/r_1}+{\left|z_2\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|z_i\right|}^{(r_i+\tau )/r_i}\right)$$

and:

$$\left|\frac{\partial V(Z)}{\partial Z_i}\right|\left({\left|z_1(t-d)\right|}^{(r_i+\tau )/r_1}+{\left|z_2(t-d)\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|z_i(t-d)\right|}^{(r_i+\tau )/r_i}\right)$$

are homogeneous of degree $2\mu$, and, hence, it follows from Lemmas 1 and 2 that, for each $i=1,\dots ,n$, there exists constants ${\stackrel{⌢}{\lambda }}_i, {\stackrel{⌣}{\lambda }}_i>0$ such that:

$$\begin{array}{l}\left|\frac{\partial V(Z)}{\partial Z_i}\right|[\left({\left|z_1\right|}^{(r_i+\tau )/r_1}+{\left|z_2\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|z_i\right|}^{(r_i+\tau )/r_i}\right)\\ +\left({\left|z_1(t-d)\right|}^{(r_i+\tau )/r_1}+{\left|z_2(t-d)\right|}^{(r_i+\tau )/r_2}+\cdots +{\left|z_i(t-d)\right|}^{(r_i+\tau )/r_i}\right)]\\ \le {\stackrel{⌢}{\lambda }}_i{\Vert Z(t)\Vert }_{\Delta }^{2\mu }+{\stackrel{⌣}{\lambda }}_i{\Vert Z(t-d)\Vert }_{\Delta }^{2\mu }\end{array}$$

Furthermore, it follows from Lemmas 2 and 4 that there are positive constants $a_1,{\overline{a}}_2,{\tilde{a}}_2$ such that:

$$\begin{gathered} \begin{array}{cc}{\overline{C}}_2\left|\frac{\partial V(Z)}{\partial Z_1}\right|\hfill & \le a_1{\Vert Z\Vert }_{\Delta }^{2\mu -\tau -r_1}\hfill \\ \hfill & =a_1{\left(M^{1/2\mu }{\Vert Z\Vert }_{\Delta }\right)}^{2\mu -\tau -r_1}{\left(M^{-\left(2\mu -\tau -r_1\right)/\left(2\mu (\tau +r_1)\right)}\right)}^{\tau +r_1}\hfill \\ \hfill & \le \frac{\gamma }{2}M{\Vert Z\Vert }_{\Delta }^{2\mu }+{\overline{a}}_2{M}^{-\left(2\mu -\tau -r_1\right)/(\tau +r_1)},\hfill \end{array} \\ \begin{array}{cc}{\overline{C}}_2\left|\frac{\partial V(Z)}{\partial Z_i}\right|\hfill & \le a_1{M}^{{\kappa }_i}{\Vert Z\Vert }_{\Delta }^{2\mu -\tau -r_i}{\left(M^{-{\kappa }_i/(\tau +r_i)}\right)}^{\tau +r_i}\hfill \\ \hfill & \le M^{{\kappa }_i}{\Vert Z\Vert }_{\Delta }^{2\mu }+{\tilde{a}}_2{M}^{-2\mu {\kappa }_i/(\tau +r_i)},\hspace{1em}i=2,\dots ,n\hfill \end{array} \end{gathered}$$

(27)

Now, substituting (27) and the above into (26) leads to:

$$\begin{gathered} \begin{array}{cc}\hfill \dot{V}(Z) \le & -M\gamma {\Vert Z\Vert }_{\Delta }^{2\mu }\hfill \\ \hfill & +{\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{1-{\nu }_i}\left({\stackrel{⌢}{\lambda }}_i{\Vert Z(t)\Vert }_{\Delta }^{2\mu }+{\stackrel{⌣}{\lambda }}_i{\Vert Z(t-d)\Vert }_{\Delta }^{2\mu }\right)}+\frac{\gamma }{2}M{\Vert Z\Vert }_{\Delta }^{2\mu }+{\overline{a}}_2{M}^{-\left(2\mu -\tau -r_1\right)/(\tau +r_1)},\hfill \\ \hfill & +{\displaystyle \sum _{i=2}^n\frac{1}{M^{{\kappa }_i}}\left(M^{{\kappa }_i}{\Vert Z\Vert }_{\Delta }^{2\mu }+{\tilde{a}}_2{M}^{-2\mu {\kappa }_i/(\tau +r_i)}\right)}\hfill \end{array} \\ \begin{array}{ccc}\hfill \dot{V}(Z(t))& \le & -M\gamma {\Vert Z(t)\Vert }_{\Delta }^{2\mu }\hfill \\ \hfill & & +{\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{1-{\nu }_i}\left({\stackrel{⌢}{\lambda }}_i{\Vert Z(t)\Vert }_{\Delta }^{2\mu }+{\stackrel{⌣}{\lambda }}_i{\Vert Z(t-d)\Vert }_{\Delta }^{2\mu }\right)}+\frac{\gamma }{2}M{\Vert Z(t)\Vert }_{\Delta }^{2\mu }+{\overline{a}}_2{M}^{-\left(2\mu -\tau -r_1\right)/(\tau +r_1)}\hfill \\ \hfill & & +{\displaystyle \sum _{i=2}^n\left({\Vert Z(t)\Vert }_{\Delta }^{2\mu }+{\tilde{a}}_2{M}^{-2\mu {\kappa }_i/(\tau +r_i)-{\kappa }_i}\right)}\hfill \\ \hfill & =& -M\left[\left(\frac{\gamma }{2}-(n-1)M^{-1}-{\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{-{\nu }_i}{\stackrel{⌢}{\lambda }}_i}\right){\Vert Z(t)\Vert }_{\Delta }^{2\mu }-\left({\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{-{\nu }_i}{\stackrel{⌣}{\lambda }}_i}\right){\Vert Z(t-d)\Vert }_{\Delta }^{2\mu }\right]\hfill \\ \hfill & & +{\overline{a}}_2{M}^{-\left(2\mu -\tau -r_1\right)/(\tau +r_1)}+{\displaystyle \sum _{i=2}^n{\tilde{a}}_2{M}^{-(2\mu +\tau +r_i){\kappa }_i/(\tau +r_i)}}\hfill \end{array} \\ =-M\left[\left(\frac{\gamma }{2}-G_1(M)\right){\Vert Z(t)\Vert }_{\Delta }^{2\mu }-\left({\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{-{\nu }_i}{\stackrel{⌣}{\lambda }}_i}\right){\Vert Z(t-d)\Vert }_{\Delta }^{2\mu }\right]+a_2{G}_2(M) \end{gathered}$$

(28)

where:

$$\begin{array}{l}{G}_1(M)=(n-1)M^{-1}+{\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{-{\nu }_i}{\stackrel{⌢}{\lambda }}_i}\\ G_2(M)=a_2\left(M^{-\left(2\mu -\tau -r_1\right)/(\tau +r_1)}+{\displaystyle \sum _{i=2}^n{M}^{-(2\mu +\tau +r_i){\kappa }_i/(\tau +r_i)}}\right),a_2=\max \left({\overline{a}}_2,{\tilde{a}}_2\right)\end{array}$$

(29)

both of which are positive and monotonically decreasing to zero as $M$ increases indefinitely.

To deal with the time delays, we construct a Lyapunov–Krasovskii functional based on Lyapunov function (10):

$$U(Z(t))=V(Z(t))+W(Z(t)),W(Z(t))=\left({\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{1-{\nu }_i}{\stackrel{⌣}{\lambda }}_i}\right){\displaystyle {\int }_{t-d}^t{\Vert Z(s)\Vert }_{\Delta }^{2\mu }ds}$$

(30)

By (28) and (30), it yields:

$$\dot{U}(Z) \le -M\frac{\gamma }{2}{\Vert Z\Vert }_{\Delta }^{2\mu }+M\left(G_1(M)+{\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{-{\nu }_i}{\stackrel{⌣}{\lambda }}_i}\right){\Vert Z\Vert }_{\Delta }^{2\mu }+a_2{G}_2(M)$$

(31)

Now, let us define:

$$\Omega =\left\{M\ge 1| \frac{\gamma }{4}-G_1(M)-{\overline{C}}_1{\displaystyle \sum _{i=1}^n{M}^{-{\nu }_i}{\stackrel{⌣}{\lambda }}_i}>0\right\}$$

(32)

and take an arbitrary $M\in \Omega$. Then, the inequality (31) becomes:

$$\dot{U}(Z) \le -\frac{M\gamma }{4}{\Vert Z\Vert }_{\Delta }^{2\mu }+a_2{G}_2(M)$$

(33)

In (30), $V(Z)$ and $W(Z)$ are homogeneous of degree $2\mu -\tau$ and $2\mu$ with respect to $\Delta$, respectively. Hence, by Lemma 2, the following holds:

$${\lambda }_1{\Vert Z(t)\Vert }_{\Delta }^{2\mu -\tau }\le V(Z(t))\le {\lambda }_2{\Vert Z(t)\Vert }_{\Delta }^{2\mu -\tau }$$

(34)

and:

$${\varpi }_1{\Vert Z(t)\Vert }_{\Delta }^{2\mu }\le W(Z(t))\le {\varpi }_2{\Vert Z(t)\Vert }_{\Delta }^{2\mu }$$

(35)

where ${\lambda }_i>0,$${\varpi }_i>0, i=1,2$ are constants.

Moreover, by Lemma 4, we have:

$${\lambda }_2\frac{M}{M}{\Vert Z(t)\Vert }_{\Delta }^{2\mu -\tau }=M{\left({\left(\frac{{\lambda }_2}{M}\right)}^{1/\tau }\right)}^{\tau }{\Vert Z(t)\Vert }_{\Delta }^{2\mu -\tau }\le \frac{2\mu -\tau }{2\mu }M{\Vert Z(t)\Vert }_{\Delta }^{2\mu }+\frac{\tau M^{\left(\tau -2\mu \right)/\tau }}{2\mu }{\lambda }_2^{2\mu /\tau }$$

(36)

Then, we have:

$${\varpi }_1{\Vert Z(t)\Vert }_{\Delta }^{2\mu }\le U(Z(t))\le {\rho }_{2}M{\Vert Z(t)\Vert }_{\Delta }^{2\mu }+\frac{\tau }{2\mu M^{\left(2\mu -\tau \right)/\tau }}{\lambda }_2^{2\mu /\tau },$$

(37)

or:

$$\frac{{\varpi }_1\gamma }{4{\rho }_2}{\Vert Z(t)\Vert }_{\Delta }^{2\mu }\le \frac{\gamma }{4{\rho }_2}U(Z(t))\le M\frac{\gamma }{4}{\Vert Z(t)\Vert }_{\Delta }^{2\mu }+\frac{\gamma \tau }{8\mu {\rho }_2{M}^{\left(2\mu -\tau \right)/\tau }}{\lambda }_2^{2\mu /\tau },$$

(38)

where: ${\rho }_2=:\left({\varpi }_2+\frac{2\mu -\tau }{2\mu }\right)$.

Therefore, it follows from (33) and (38) that:

$$\begin{array}{cc}\hfill \dot{U}(Z(t)) & \le -\left(\frac{\gamma M}{4}{\Vert Z(t)\Vert }_{\Delta }^{2\mu }+\frac{\gamma \tau }{8\mu {\rho }_2{M}^{\left(2\mu -\tau \right)/\tau }}{\lambda }_2^{2\mu /\tau }\right) +\frac{\gamma \tau }{8\mu {\rho }_2{M}^{\left(2\mu -\tau \right)/\tau }}{\lambda }_2^{2\mu /\tau }+ a_2{G}_2(M)\hfill \\ \hfill & \le -\frac{\gamma }{4{\rho }_2}U(Z(t))+{\overline{G}}_2(M),\hfill \end{array}$$

(39)

where: ${\overline{G}}_2(M)=\frac{\gamma \tau }{8\mu {\rho }_2{M}^{\left(2\mu -\tau \right)/\tau }}{\lambda }_2^{2\mu /\tau }+ a_2{G}_2(M)$.

In the rest of the proof, we are shown similarly as in [7,29] that the state $Z(t)$ of closed-loop system (18), (22), and (23) is well-defined on $\left[0, +\infty \right)$ and is globally bounded. Since ${\overline{G}}_2(M)$ is positive and strictly monotonically decreasing to zero as $M\to \infty$, it is easily seen that, for any given $\epsilon >0$, one can choose a sufficiently large $M\in \Omega$ so as to satisfy:

$${\varpi }_1{}^{- \frac{1}{2\mu }}{\left(\frac{4{\rho }_2{\overline{G}}_2(M)}{\gamma }\right)}^{\frac{1}{2\mu }}<\epsilon$$

(40)

Next, introduce a subset by:

$$\Xi =\left\{Z\in {ℝ}^{2n-1} | U(Z)\ge \frac{8{\rho }_2{\overline{G}}_2(M)}{\gamma }\right\}\subset {ℝ}^{2n-1}$$

(41)

and let $Z(t)$ be the trajectory of (24) with an initial state $Z(0)$. Suppose $Z(t)\in \Xi$ for some $t\in [0,\infty )$. Then, using (38), it can be deduced that:

$$\dot{U}(Z(t)) \le -\frac{\gamma }{4{\rho }_2}U(Z(t))+{\overline{G}}_2(M)\le -{\overline{G}}_2(M)<0$$

(42)

This means that, if $Z(t)\in \Xi$, $U(Z(t))$ will decrease strictly with respect to $t$. Therefore, in a finite time $T$, $Z(t)$ must enter ${ℝ}^{2n-1}-\Xi$ and stay there forever. Hence, one can obtain the following relations:

$$\begin{array}{c}U(Z(t))-U(Z(0))={\displaystyle {\int }_0^t\dot{U}(Z(t))dt<0,\hspace{1em}t\in \left[0, T\right) }\\ U(Z(t)) <{\left(\frac{8{\rho }_2{G}_2(M)}{\gamma }\right)}^{\frac{2\mu -\tau }{2\mu }},\hspace{1em}t\in [T,\infty )\end{array}$$

(43)

which, together with (37), lead to:

$$\begin{gathered} \begin{array}{cc}\hfill \left|Z_i(t)\right|& \le {\Vert Z(t)\Vert }_{\Delta }^{r_i}\le {\left(\frac{1}{{\varpi }_1}U(Z(t))\right)}^{\frac{r_i}{2\mu }}\hfill \\ \hfill & \le {\varpi }_1{}^{- \frac{r_i}{2\mu }}U{(Z(0))}^{\frac{r_i}{2\mu }},\hspace{1em} t\in [0, T) \hfill \end{array} \\ \begin{array}{cc}\hfill \left|Z_i(t)\right|& \le {\Vert Z(t)\Vert }_{\Delta }^{r_i}\le {\left(\frac{1}{{\varpi }_1}U(Z(t))\right)}^{\frac{r_i}{2\mu }}\hfill \\ \hfill & \le {\varpi }_1{}^{- \frac{r_i}{2\mu }}{\left(\frac{8{\rho }_2{\overline{G}}_2(M)}{\gamma }\right)}^{\frac{r_i}{2\mu }}, \hspace{1em}t\in [T,+\infty )\hfill \end{array} \end{gathered}$$

(44)

For $i=1,\dots ,2n-1$. This implies that the trajectory $Z(t)$ of system (24) is well defined and globally bounded on $\left[0, +\infty \right)$.

Next, we prove that:

$$\left|y(t)\right| =\left|x_1(t)-y_r(t)\right| <\epsilon ,\hspace{1em}\forall t\ge T>0$$

(45)

This can be easily seen from (35), (40), and (43) as follows:

$$\begin{array}{cc}\hfill \left|y(t)\right|& =\left|x_1(t)-y_r(t)\right| =\left|z_1(t)\right|\le {\Vert Z(t)\Vert }_{\Delta }\hfill \\ \hfill & \le {\left(\frac{1}{{\varpi }_1}U(Z(t))\right)}^{\frac{1}{2\mu }}\le {\varpi }_1{}^{- \frac{1}{2\mu }}{\left(\frac{8{\rho }_2{\overline{G}}_2(M)}{\gamma }\right)}^{\frac{1}{2\mu }}<\epsilon \hfill \end{array}$$

(46)

Finally, since the choice of $M\in \Omega$ depends on $\epsilon >0$, the finite time $T>0$ depends on $\epsilon >0$. Further, it is obvious that $T>0$ is dependent on each trajectory of (24), or equivalently on each initial state $Z(0)$ of (24). Therefore, the finite time $T>0$ satisfying (46) is dependent on both $\epsilon >0$ and $Z\left(0\right)$, i.e., $T:=T(\epsilon ,x(0),\zeta (0))$. □

The process of control design shows that the lower triangular growth condition as required by Assumption 1 is not necessary for achieving the global practical output tracking of the system (1). In fact, we can extend Theorem 1 under the following assumption.

Assumption 3.

For$i=1,2,\dots ,n$, there are constants$C_1>0, C_2>0, M>1, 0<{\nu }_i\le 1,$and$\tau \ge 0$such that:

$$\left|\frac{{\phi }_i(\cdot )}{M^{{\kappa }_i}}\right|\le C_1{M}^{1-{\nu }_i}{\displaystyle \sum _{j=1}^n\left({\left|\frac{x_j(t)}{M^{{\kappa }_j}}\right|}^{(r_i+\tau )/r_j}+{\left|\frac{x_j\left(t-d_j(t)\right)}{M^{{\kappa }_j}}\right|}^{(r_i+\tau )/r_j}\right)}+\frac{C_2}{M^{{\kappa }_i}},$$

(47)

where${\kappa }_1=0, r_1=1,\hspace{1em}{\kappa }_{i+1}=\left({\kappa }_i+1\right)/p_i,$and$r_{i+1}{p}_i=r_i+\tau >0,\hspace{1em}i=1,\dots ,n$.

It can be easily concluded that Assumption 1 is a special case of Assumption 3. The following theorem is a more general result on the global practical tracking of non-triangular systems.

Theorem 2.

Under Assumptions 2 and 3, the problem of global practical tracking via output feedback controller of the form (22), (23) can be solved for system (1).

Proof .

The proof is very similar to that of Theorem 1 and hence is omitted here. □

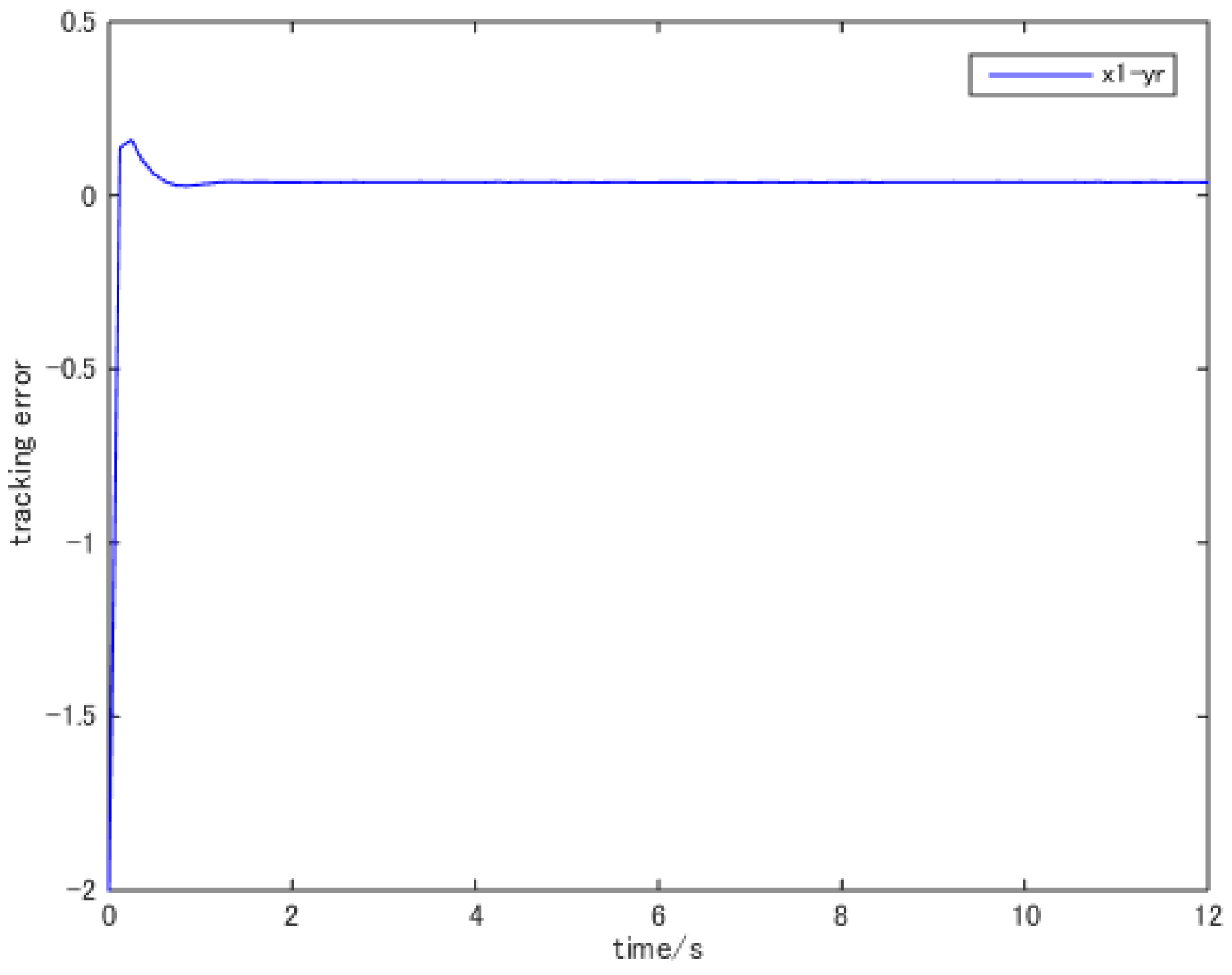
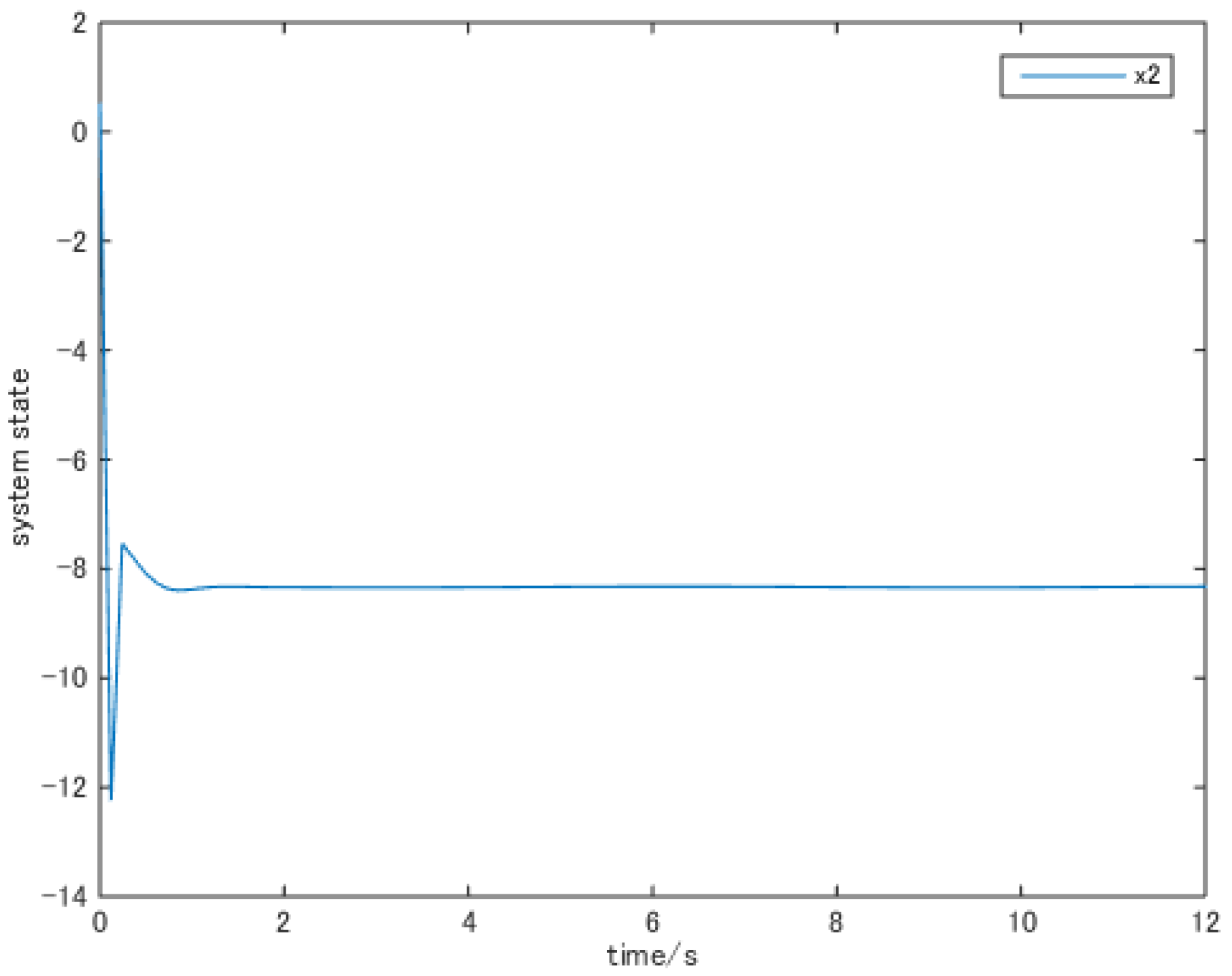
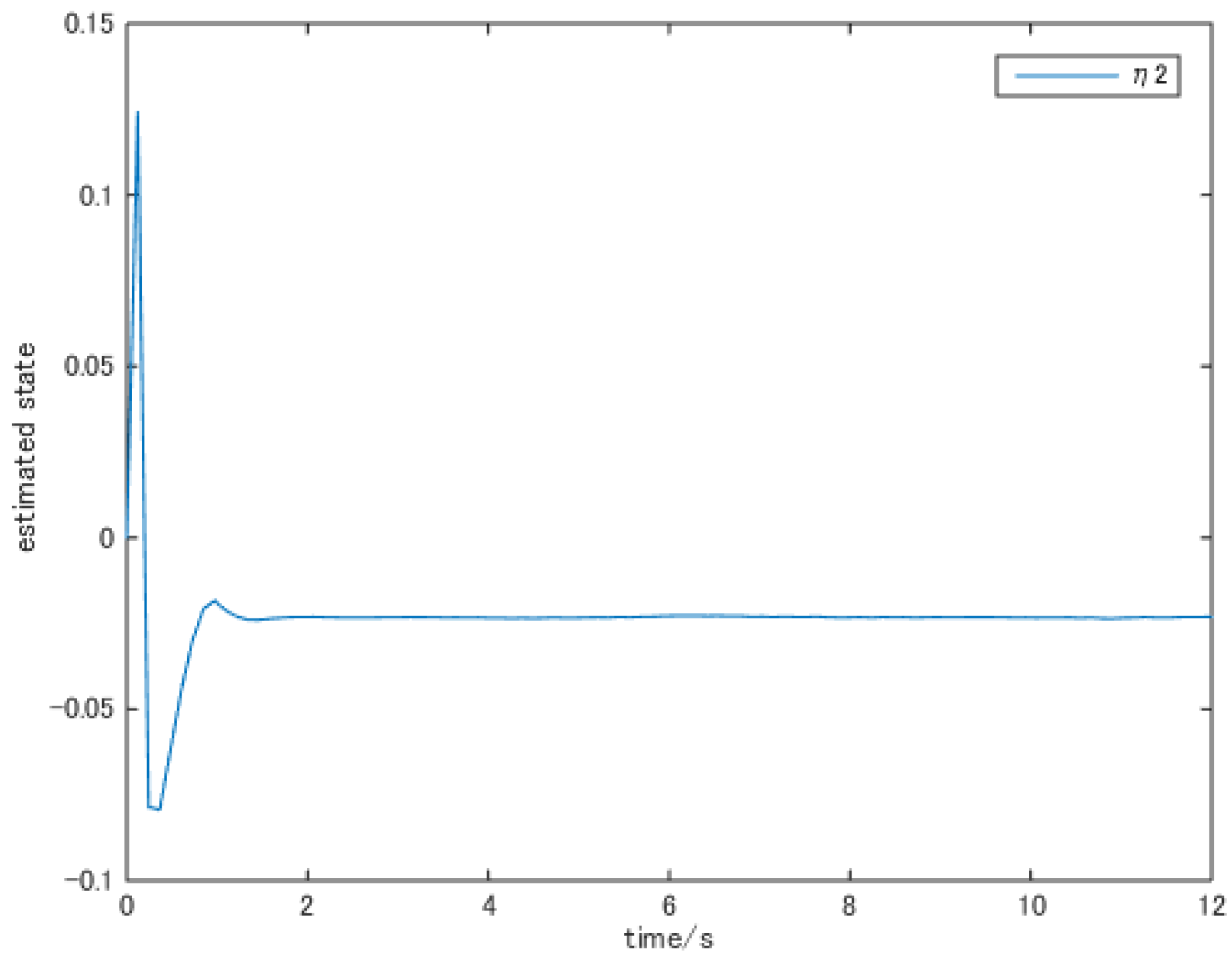
5. Example and Simulation

The above method is used for the following numerical example considering the inherently nonlinear time delay system:

$$\begin{array}{l}{\dot{x}}_1(t)=x_2^{5/3}(t)+0.25x_1^2(t)\sin (x_2(t))\\ {\dot{x}}_2(t)=u(t)+0.125x_2^{5/3}(t-0.2)\\ y(t)=x_1(t)-y_r(t)\end{array}$$

(48)

For $p_1=5/3, \tau =5/3, r_1=1, r_2=1$ and $\mu =5/3$, it is not difficult to prove that system (48) satisfies the conditions of Assumption 1. Therefore, following the design procedure above, the output controller can be constructed as:

$$\begin{array}{l}{\dot{\eta }}_2=-M^{3/5}\left({\eta }_2+L_1\left(x_1-y_r\right)\right)\\ u=-M^{8/5}{\beta }_2\left({\beta }_1{\left(x_1-y_r\right)}^{5/3}+{\left({\eta }_2+L_1\left(x_1-y_r\right)\right)}^{5/3}\right)\end{array}$$

(49)

choosing $L_1=0.6, {\beta }_1=1.1, {\beta }_2=2.1$ and $M=8$. In this simulation, the reference signal is chosen as $y_r(t)=\sin (t)$, and the initial condition is $x_1(0)=-2, x_2(0)=0.1$ and ${\eta }_2(0)=0$. From the following Figure 1, Figure 2, Figure 3 and Figure 4, the effectiveness of the design procedure is verified.

6. Conclusions

In this work, we addressed the practical output feedback tracking problem for a class of high-order nonlinear time delay systems which cannot be handled by existing approaches. The proposed output controller independent of time delay can make the tracking error arbitrarily capable of being adjusted to be sufficiently small and render all the trajectory of the closed-loop system as are bounded. Our future study is to extend the proposed method for more inherently nonlinear time-varying delay systems.