Stochastic Analysis of Train Running Safety on Bridge with Earthquake-Induced Irregularity under Aftershock
Abstract
:1. Introduction
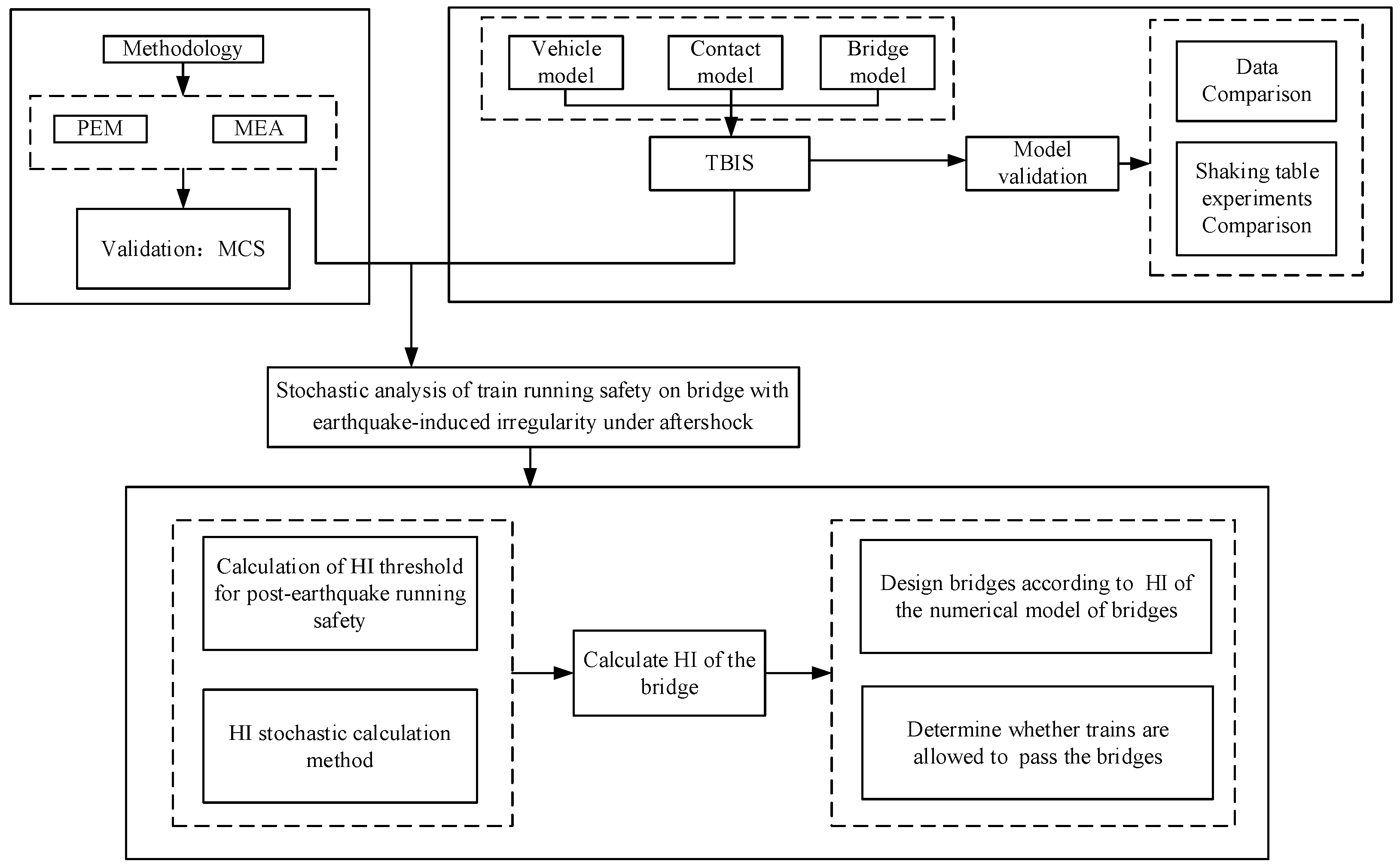
2. Methodology
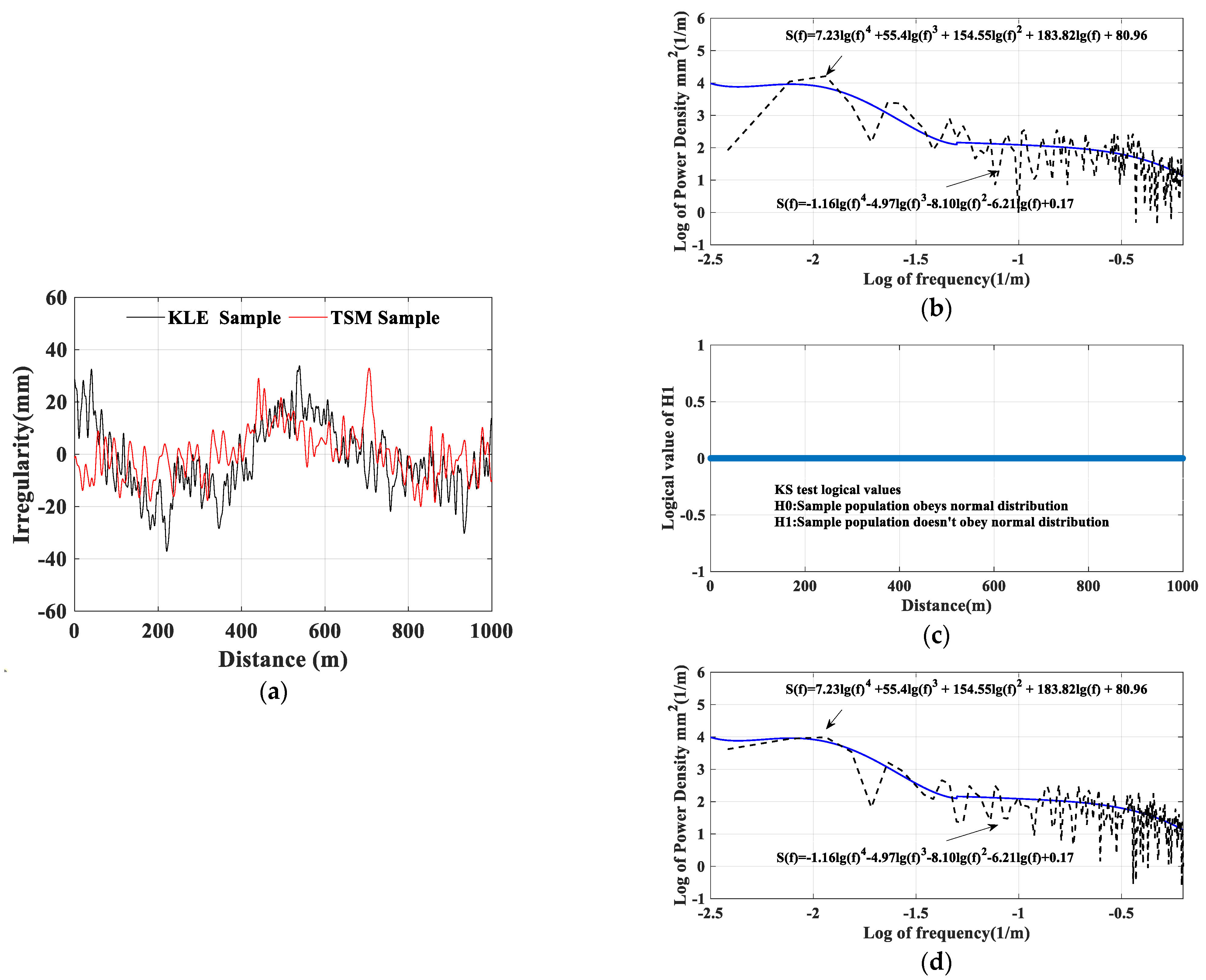
2.1. Earthquake-Induced Irregularity Generated by the Karhunen-Loeve Expansion (KLE) and the Trigonometric Series Method (TSM)
2.2. PEM for Stochastic Analysis
2.3. Moment Expansion Approximation (MEA) of the Probability Density Function (PDF)
3. Train–Bridge Interaction System (TBIS) Model
3.1. Finite Element Model
3.2. Wheel–Rail Contact Model
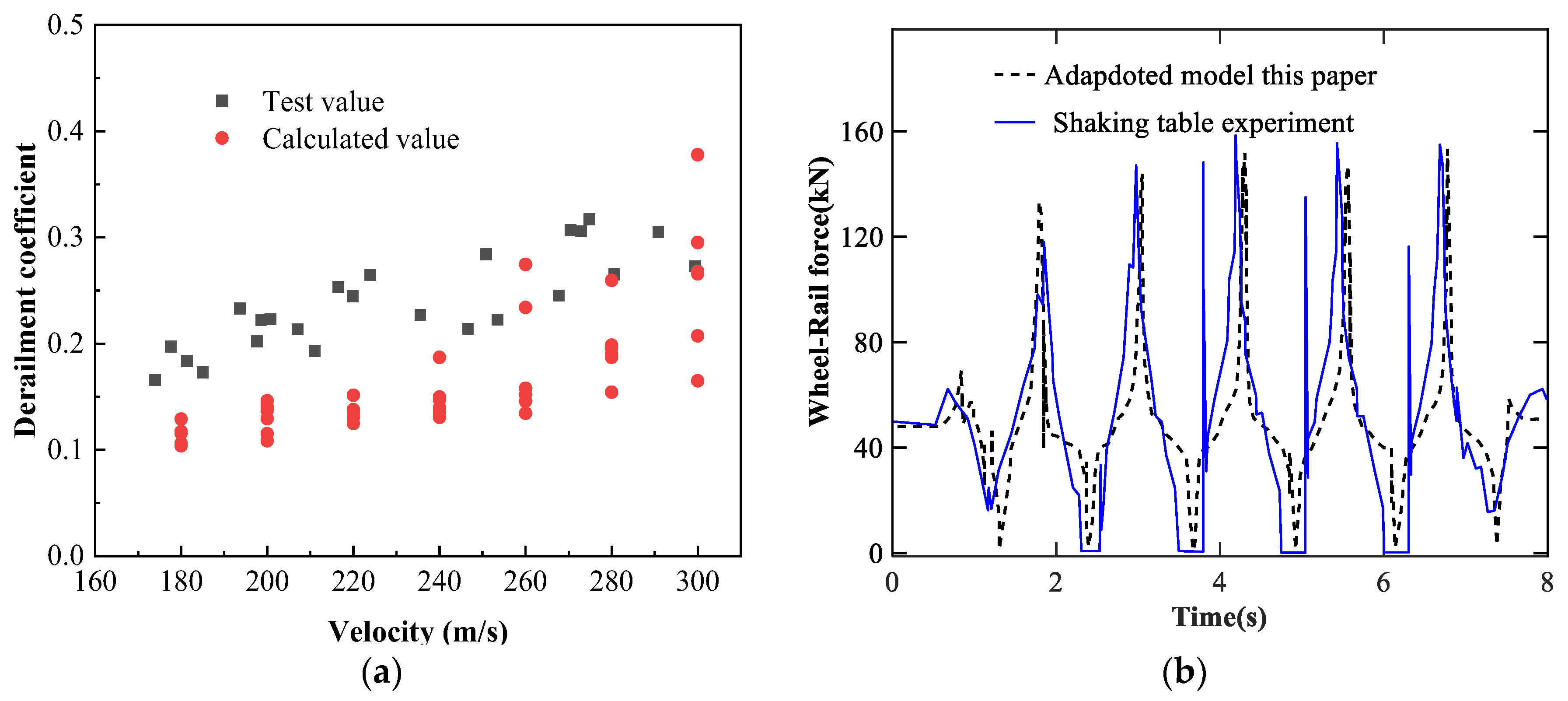
4. Numerical Analysis and Validation
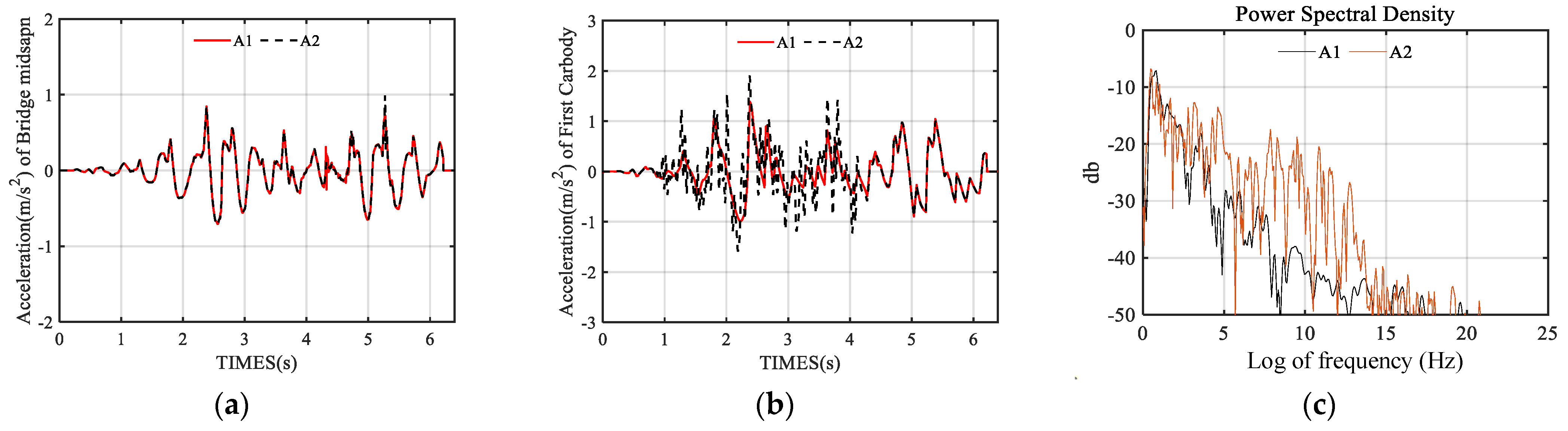
4.1. Response Analysis Based on Earthquake-Induced Irregularity
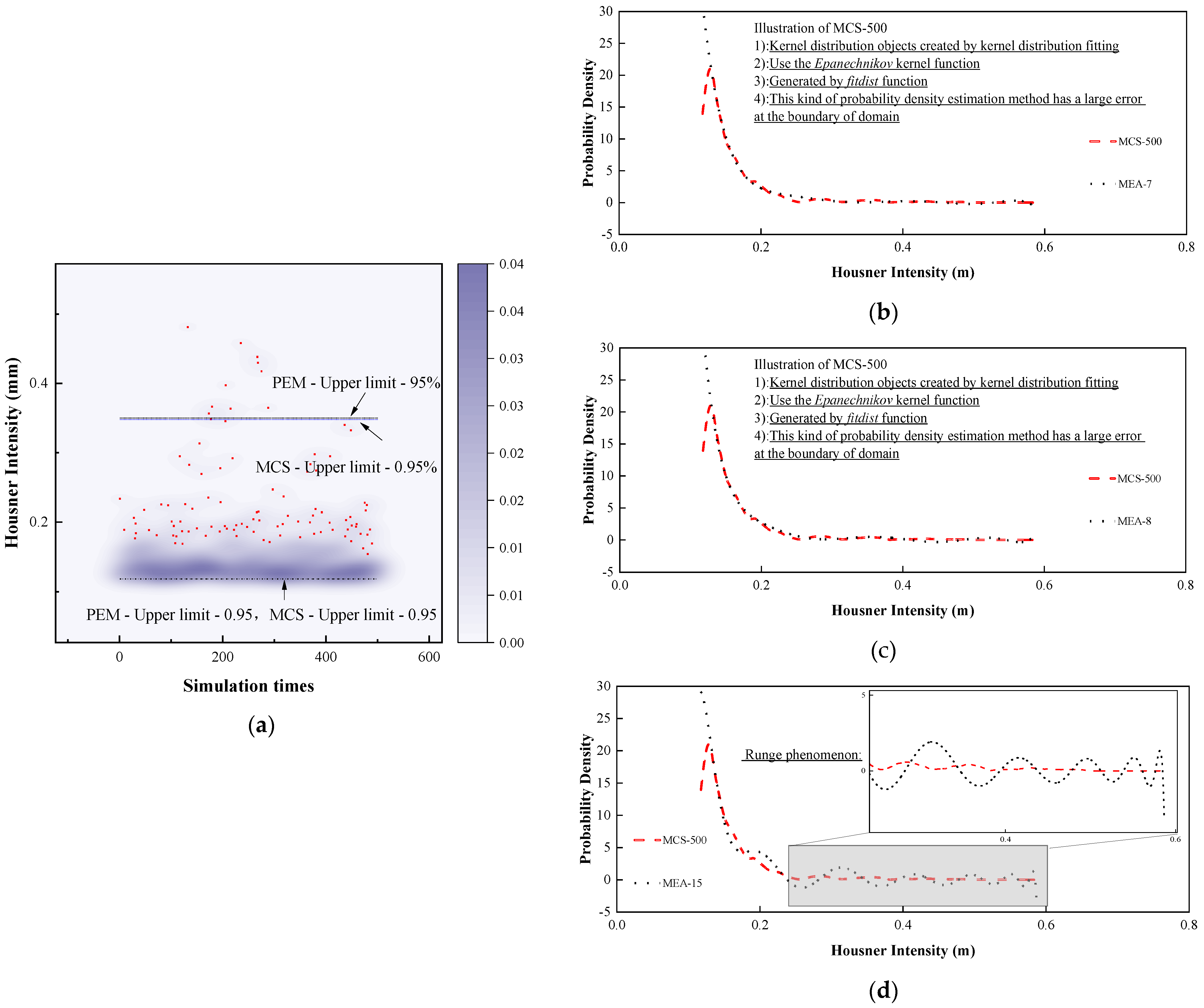
4.2. Comparison of the Point Estimate Method (PEM) with Monte Carlo Simulation (MCS)
4.3. Comparison of Moment Expansion Approximation (MEA) of the Probability Density Function (PDF) with MCS
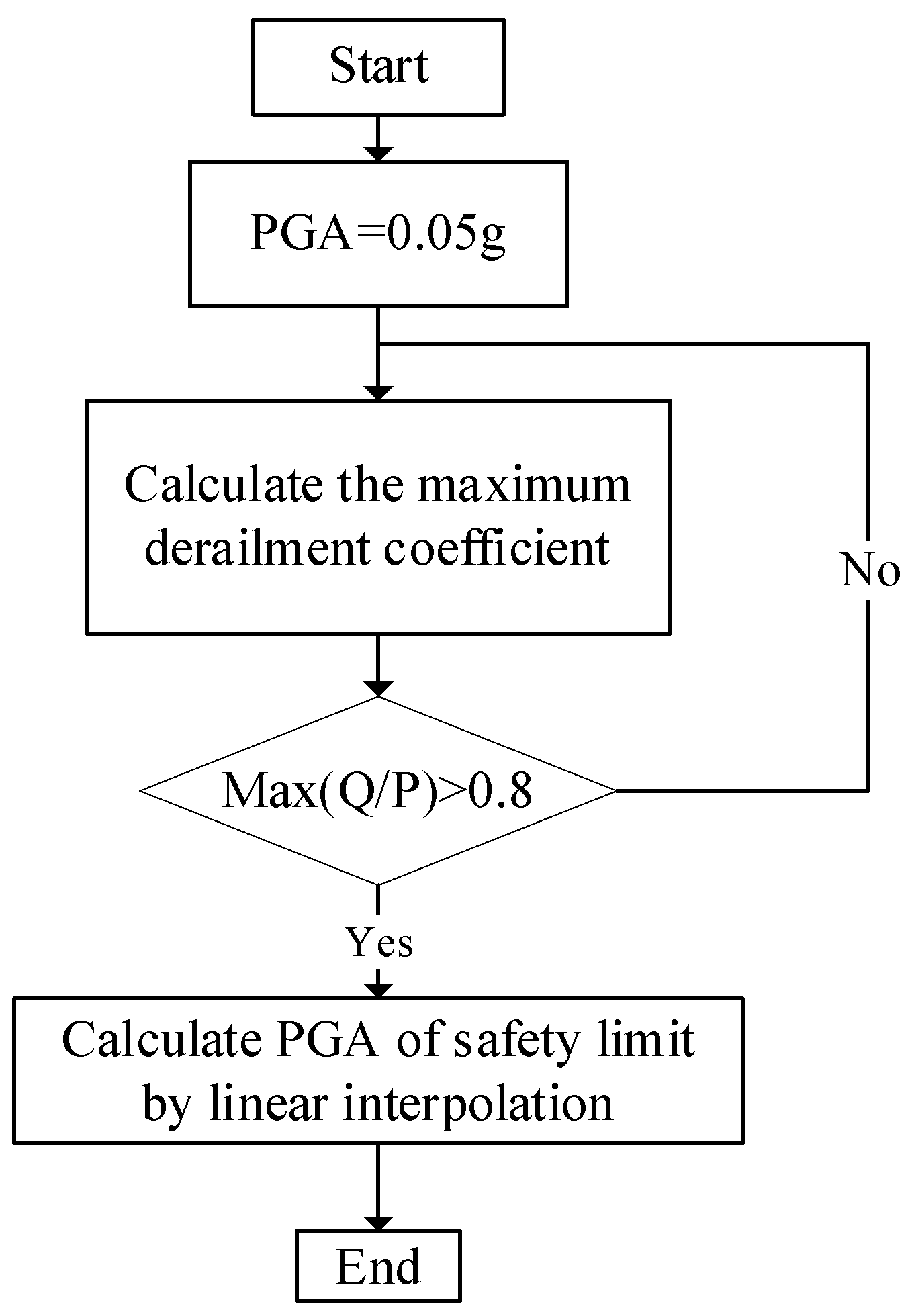
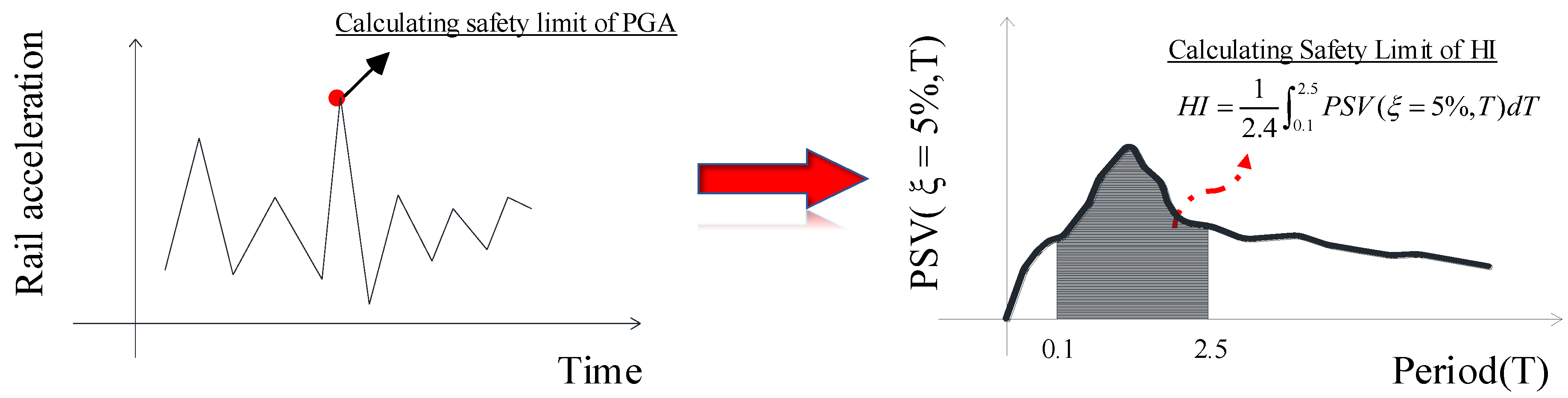
4.4. Safety Limit Determination
5. Results and Discussion
6. Conclusions
- Selected HI as running safety index, which has the minimum COV, and the HI limit value of bridge to guarantee the post-earthquake traffic safety has been stochastic calculated, weather the train can pass the train can be compared by the HI of this bridge and the HI limit value.
- The non-Gaussian response can be calculated by using the PEM and MEA, and the recommendations are to use 9 estimated points of PEM and 7–8 degrees polynomial of MEA, which already have very good accuracy, while too high order polynomials will create the Runge effect, affecting the accuracy of calculation.
- According to the proposed method in this paper, the HI can be calculated with full consideration of the randomness of aftershock intensity and structural parameters. By comparing the stochastic-calculated HI with the threshold value of the HI, the running safety post-earthquake can be well judged.
- After calculations, it is clear that the running safety performance of bridges after earthquakes measuring 0.1 g–0.15 g can be guaranteed because in this case, the rail deformation after the earthquake is very small; the existing TBIS has sufficient safety. For main shocks larger than 0.15 g, the possibility of the train passing the bridge after an earthquake is determined by the specific calculated value of HI.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mu, X. On disaster prevention and mitigation of urban Bridges based on lifeline engineering. In Proceedings of the Special for the Fourth National (International) Technical Summit Conference & the West Communication Scientific Technical Innovation Conference, Chongqing, China, 5 May 2009. [Google Scholar]
- Dai, S. Thoughts on earthquake rescue and communication of Qingjiang No. 7 bridge on Baocheng railway. In Proceedings of the Symposium on the Impact of Earthquake Disasters on Railways and Countermeasures, Chengdu, China, 27–28 August 2008. [Google Scholar]
- Kanga, X.; Jiang, L.; Bai, Y.; Caprani, C.C. Seismic damage evaluation of high-speed railway bridge components under different intensities of earthquake excitations. Eng. Struct. 2017, 152, 113–128. [Google Scholar] [CrossRef]
- Lai, Z.P.; Kang, X.; Jiang, L.Z.; Zhou, W.B.; Feng, Y.L.; Zhang, Y.T.; Yu, J.; Nie, L.X. Earthquake Influence on the Rail Irregularity on High-Speed Railway Bridge. Shock. Vib. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Jiang, L.Z.; Yu, J.; Zhou, W.B.; Yan, W.J.; Lai, Z.P.; Feng, Y.L. Applicability analysis of high-speed railway system under the action of near-fault ground motion. Soil Dyn. Earthq. Eng. 2020, 139, 106289. [Google Scholar] [CrossRef]
- Lai, Z.; Jiang, L.; Zhou, W.; Yu, J.; Zhang, Y.; Liu, X.; Zhou, W. Lateral girder displacement effect on the safety and comfortability of the high-speed rail train operation. Veh. Syst. Dyn. 2021, 60, 3215–3239. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Xiang, P.; Jiang, L.; Lai, Z. Safety and comfort assessment of a train passing over an earthquake-damaged bridge based on a probability model. Struct. Infrastruct. Eng. 2021, 17, 1–12. [Google Scholar] [CrossRef]
- Yu, J.; Jiang, L.; Zhou, W. Study of the Target Earthquake-Induced Track Irregularity Spectrum under Transverse Random Earthquakes. Int. J. Struct. Stab. Dyn. 2022, 22, 2250190. [Google Scholar] [CrossRef]
- Yu, J.; Jiang, L.; Zhou, W.; Liu, X.; Lai, Z. Seismic-Induced Geometric Irregularity of Rail Alignment under Transverse Random Earthquake. J. Earthq. Eng. 2022, 1–22. [Google Scholar] [CrossRef]
- Institute, R.T.R. Design Standards for Railway Structures and Commentary (Seismic Design); Maruzen: Tokyo, Japan, 2012. [Google Scholar]
- Luo, X. Study on methodology for running safety assessment of trains in seismic design of railway structures. Soil Dyn. Earthq. Eng. 2005, 25, 79–91. [Google Scholar] [CrossRef]
- Zhao, H.; Wei, B.; Jiang, L.; Xiang, P. Seismic running safety assessment for stochastic vibration of train–bridge coupled system. Arch. Civ. Mech. Eng. 2022, 22, 180. [Google Scholar] [CrossRef]
- Goda, K.; Taylor, C.A. Effects of aftershocks on peak ductility demand due to strong ground motion records from shallow crustal earthquakes. Earthq. Eng. Struct. Dyn. 2012, 41, 2311–2330. [Google Scholar] [CrossRef]
- Mao, J.F.; Yu, Z.W.; Xiao, Y.J.; Jin, C.; Bai, Y. Random dynamic analysis of a train-bridge coupled system involving random system parameters based on probability density evolution method. Probabilistic Eng. Mech. 2016, 46, 48–61. [Google Scholar] [CrossRef]
- Yu, Z.W.; Mao, J.F. A stochastic dynamic model of train-track-bridge coupled system based on probability density evolution method. Appl. Math. Model. 2018, 59, 205–232. [Google Scholar] [CrossRef]
- Jie, L.; Chen, J.B. Probability Density Evolution of Stochastic Structural Responses. J. Tongji Univ. 2003, 31, 1387–1391. [Google Scholar]
- Jiang, L.; Liu, X.; Zhou, T.; Xiang, P.; Chen, Y.; Feng, Y.; Lai, Z.; Cao, S.; Vanali, M. Application of KLE-PEM for Random Dynamic Analysis of Nonlinear Train-Track-Bridge System. Shock. Vib. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Z.; Peng, Y. Dimension reduction of Karhunen-Loeve expansion for simulation of stochastic processes. J. Sound Vib. 2017, 408, 168–189. [Google Scholar] [CrossRef]
- Jiang, L.Z.; Liu, X.; Xiang, P.; Zhou, W.B. Train-bridge system dynamics analysis with uncertain parameters based on new point estimate method. Eng. Struct. 2019, 199, 109454. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.Z.; Lai, Z.P.; Xiang, P.; Chen, Y.J. Sensitivity and dynamic analysis of train-bridge coupled system with multiple random factors. Eng. Struct. 2020, 221, 111083. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Xiang, P.; Lai, Z.; Zhang, Y.; Liu, L. A stochastic finite element method for dynamic analysis of bridge structures under moving loads. Struct. Eng. Mech. 2022, 82, 31–40. [Google Scholar] [CrossRef]
- Xu, L.; Zhai, W.M.; Gao, J.M. A probabilistic model for track random irregularities in vehicle/track coupled dynamics. Appl. Math. Model. 2017, 51, 145–158. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, Y.; Zhu, Z.; Li, Z.; Liu, H.; Yu, Z. Vehicle-track random vibrations considering spatial frequency coherence of track irregularitives. Veh. Syst. Dyn. 2021, 1–22. [Google Scholar] [CrossRef]
- Xiang, P.; Huang, W.; Jiang, L.; Lu, D.; Liu, X.; Zhang, Q. Investigations on the influence of prestressed concrete creep on train-track-bridge system. Constr. Build. Mater. 2021, 293, 123504. [Google Scholar] [CrossRef]
- Zeng, Z.-P.; Yu, Z.-W.; Zhao, Y.-G.; Xu, W.-T.; Chen, L.-K.; Lou, P. Numerical Simulation of Vertical Random Vibration of Train-Slab Track-Bridge Interaction System by PEM. Shock. Vib. 2014, 2014, 1–21. [Google Scholar] [CrossRef]
- Liu, X.; Xiang, P.; Jiang, L.Z.; Lai, Z.P.; Zhou, T.; Chen, Y.J. Stochastic Analysis of Train-Bridge System Using the Karhunen-Loeve Expansion and the Point Estimate Method. Int. J. Struct. Stab. Dyn. 2020, 20, 2050025. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D.; Burden, A.M. Numerical Analysis; Cengage Learning: Belmont, CA, USA, 2015. [Google Scholar]
- Wang, H.-P.; Chen, H.; Chen, C.; Zhang, H.-Y.; Jiang, H.; Song, T.; Feng, S.-Y. The Structural Performance of CFRP Composite Plates Assembled with Fiber Bragg Grating Sensors. Symmetry 2021, 13, 1631. [Google Scholar] [CrossRef]
- Wang, H.; Xiang, P.; Jiang, L. Optical Fiber Sensor Based In-Field Structural Performance Monitoring of Multilayered Asphalt Pavement. J. Lightwave Technol. 2018, 36, 3624–3632. [Google Scholar] [CrossRef]
- Lizhong, J.; Jian, Y.; Wangbao, Z. Study on geometrical irregularity of rail induced by transverse earthquake. Eng. Mech. 2022, 39, 13. [Google Scholar]
- Yu, J.; Jiang, L.Z.; Zhou, W.B.; Liu, X.; Nie, L.X.; Zhang, Y.T.; Feng, Y.L.; Cao, S.S. Running test on high-speed railway track-simply supported girder bridge systems under seismic action. Bull. Earthq. Eng. 2021, 19, 3779–3802. [Google Scholar] [CrossRef]
- Fan, W.L.; Wei, J.H.; Ang, A.H.S.; Li, Z.L. Adaptive estimation of statistical moments of the responses of random systems. Probabilistic Eng. Mech. 2016, 43, 50–67. [Google Scholar] [CrossRef]
- Castillo, E. Extreme Value Theory in Engineering; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zhao, Y.-G.; Ono, T. New point estimates for probability moments. J. Eng. Mech. 2000, 126, 433–436. [Google Scholar] [CrossRef]
- Changqing, L.; Junping, J.; Lizhong, J.; Yang, T. Theory and implementation of a two-step unconditionally stable explicit integration algorithm for vibration analysis of structures. Shock. Vib. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Zeng, Q.; Guo, X. Theory and Application of Vibration Analysis for Train Bridge Time-History System; China Railway Publishing: Beijing, China, 1999. [Google Scholar]
- Zhai, W.M.; Xia, H. Train-Track-Bridge Dynamic Interaction: Theory and Engineering Application; Science Press: Beijing, China, 2011. [Google Scholar]
- Nishimura, K.; Terumichi, Y.; Morimura, T.; Sogabe, K. Development of Vehicle Dynamics Simulation for Safety Analyses of Rail Vehicles on Excited Tracks. J. Comput. Nonlinear Dyn. 2009, 4, 011001.1–011001.9. [Google Scholar] [CrossRef]
- Zeng, Z.-P.; He, X.-F.; Zhao, Y.-G.; Yu, Z.-W.; Chen, L.-K.; Xu, W.-T.; Lou, P. Random vibration analysis of train-slab track-bridge coupling system under earthquakes. Struct. Eng. Mech. 2015, 54, 1017–1044. [Google Scholar] [CrossRef]
- Lin, J.L.; Zhang, W.S.; Li, J.J. Structural responses to arbitrarily coherent stationary random excitations. Comput. Struct. 1994, 50, 629–633. [Google Scholar] [CrossRef]
- Luo, X.; Miyamoto, T. Method for running safety assessment of railway vehicles against structural vibration displacement during earthquakes. Q. Rep. RTRI 2007, 48, 129–135. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.-Z.; Xiang, P.; Lai, Z.-P.; Feng, Y.-L.; Cao, S.-S. Dynamic response limit of high-speed railway bridge under earthquake considering running safety performance of train. J. Cent. South Univ. 2021, 28, 968–980. [Google Scholar] [CrossRef]
- Han, J.; Zhou, W. Correlation between ground motion intensity indices and sdof system responses with medium-to-long period based on the wenchuan earthquake data. Eng. Mech. 2011, 28, 185–196. [Google Scholar]

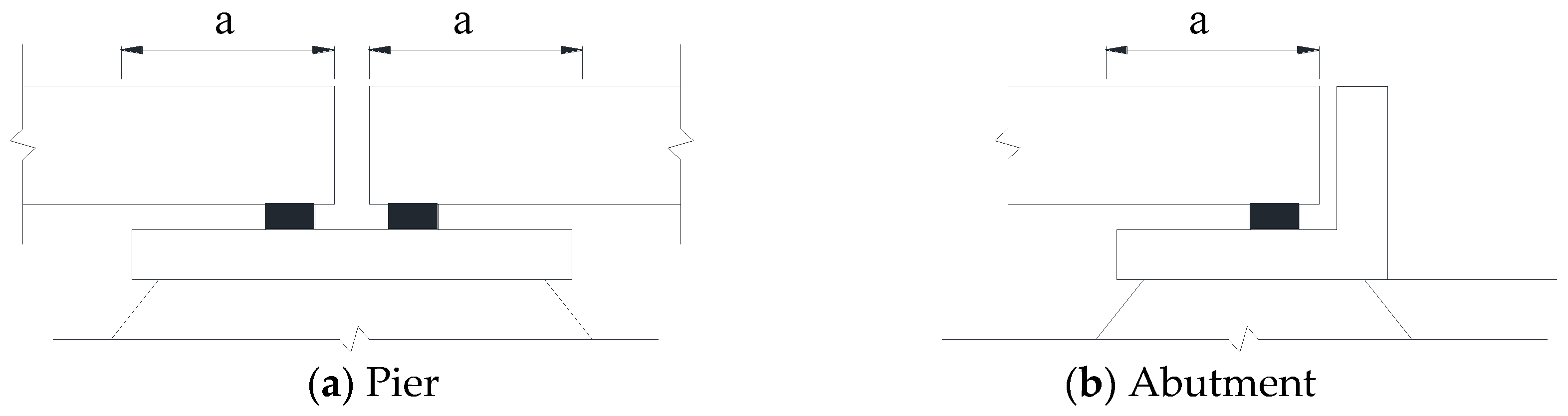



| Compression (m) | 0 | 0.02 | 0.03 | 0.035 |
|---|---|---|---|---|
| Force (N) | 0 | 0 | 2107 | 5596 |
| 0.9 | 0.8 | 0.7 | 0.6 | |||||
|---|---|---|---|---|---|---|---|---|
| Upper | Lower | Upper | Lower | Upper | Lower | Upper | Lower | |
| MEA | 0.3542 | 0.1184 | 0.2062 | 0.1210 | 0.1906 | 0.1228 | 0.1773 | 0.1246 |
| MCS | 0.3402 | 0.1182 | 0.2010 | 0.1203 | 0.1864 | 0.1218 | 0.1769 | 0.1233 |
| Variable | Symbol | Distribution | Mean Value | Std.D | Reference |
|---|---|---|---|---|---|
| Young’s modulus | Y.M | Gaussian | 34.51 GPa | 2.0706 GPa | [20] |
| Density | Den | Gaussian | [20] | ||
| Mass trains | Gaussian | 44 t | 2.2 t | [20] |
| Number | Name | COV |
|---|---|---|
| 1 | Sa-0.2 | 7.59539 |
| 2 | Sa-1.0 | 4.50385 |
| 3 | Sa-T1 | 3.87779 |
| 4 | Sv-T1 | 3.8068 |
| 5 | Sd-T1 | 3.78743 |
| 6 | PSA | 3.78743 |
| 7 | PSV | 3.5809 |
| 8 | PSD | 3.39373 |
| 9 | AI | 8.63451 |
| 10 | CAV | 3.41955 |
| 11 | VSI | 3.64544 |
| 12 | HI | 2.81931 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Xiang, P.; Zhao, H.; Yu, J.; Ye, B.; Yang, D. Stochastic Analysis of Train Running Safety on Bridge with Earthquake-Induced Irregularity under Aftershock. Symmetry 2022, 14, 1998. https://doi.org/10.3390/sym14101998
Tan J, Xiang P, Zhao H, Yu J, Ye B, Yang D. Stochastic Analysis of Train Running Safety on Bridge with Earthquake-Induced Irregularity under Aftershock. Symmetry. 2022; 14(10):1998. https://doi.org/10.3390/sym14101998
Chicago/Turabian StyleTan, Jincheng, Ping Xiang, Han Zhao, Jian Yu, Bailong Ye, and Delei Yang. 2022. "Stochastic Analysis of Train Running Safety on Bridge with Earthquake-Induced Irregularity under Aftershock" Symmetry 14, no. 10: 1998. https://doi.org/10.3390/sym14101998





