Thermal Conductivity Study of an Orthotropic Medium Containing a Cylindrical Cavity
Abstract
:1. Introduction
2. Basic Equations
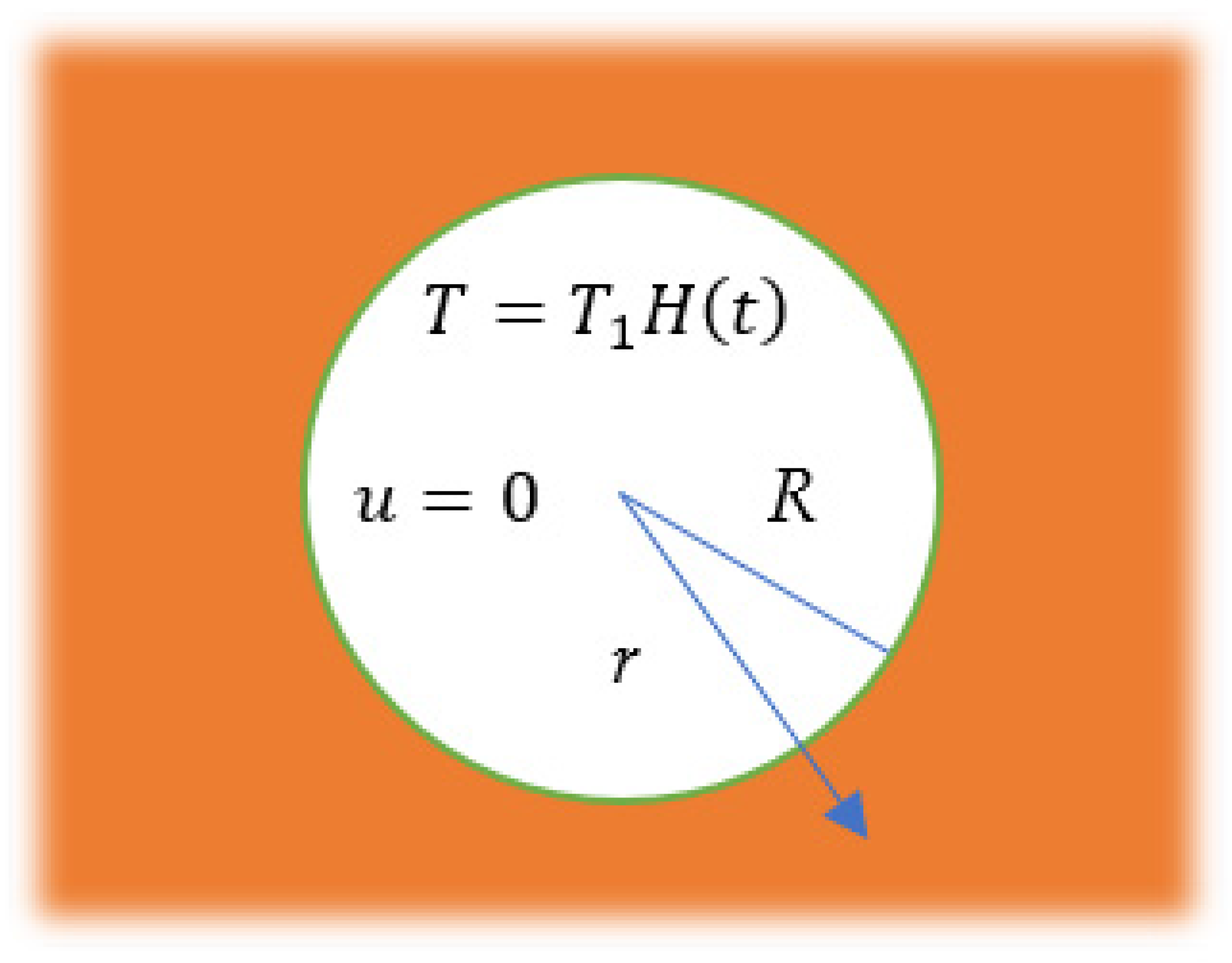
3. Application
4. Finite Element Technique
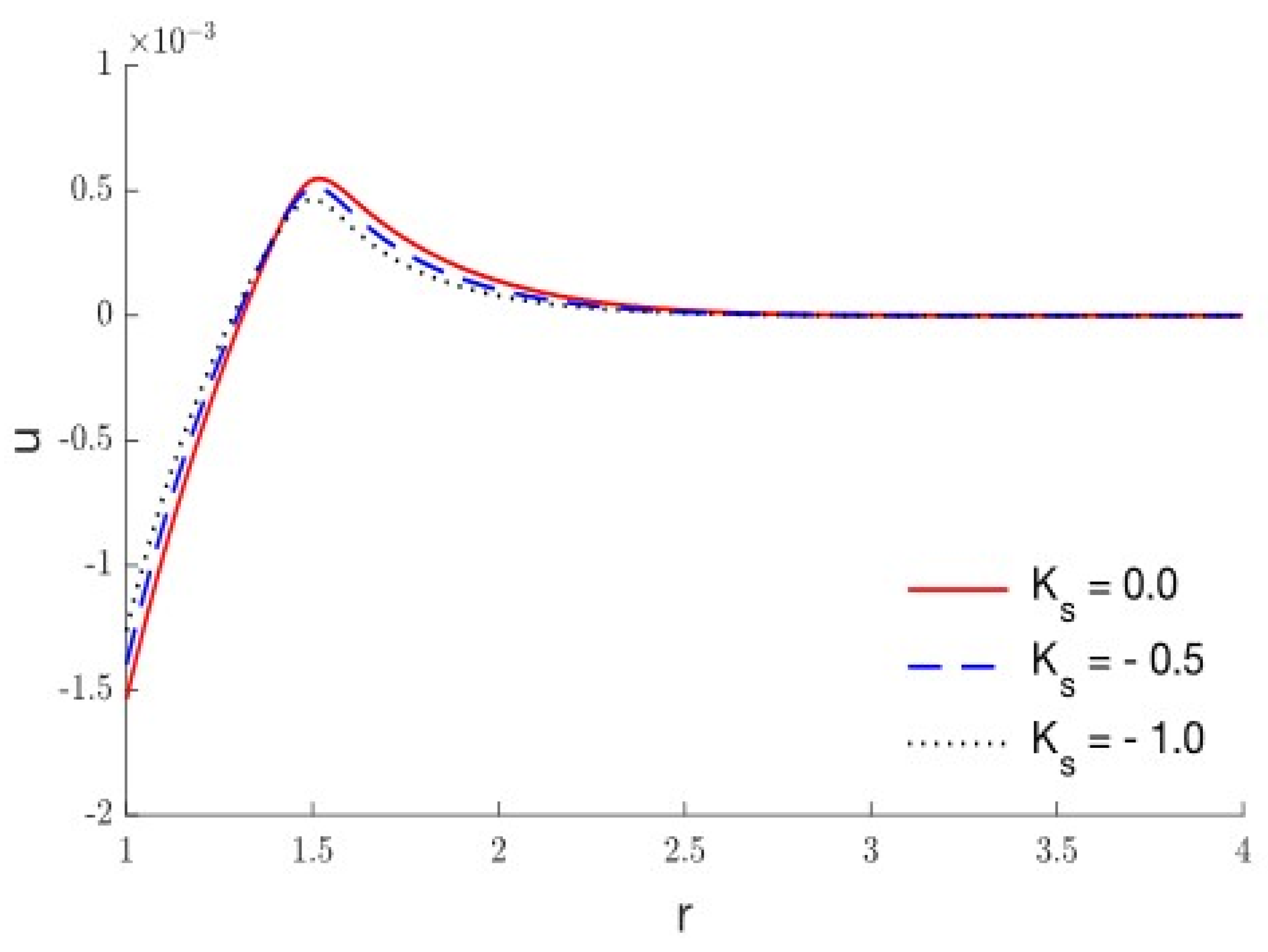
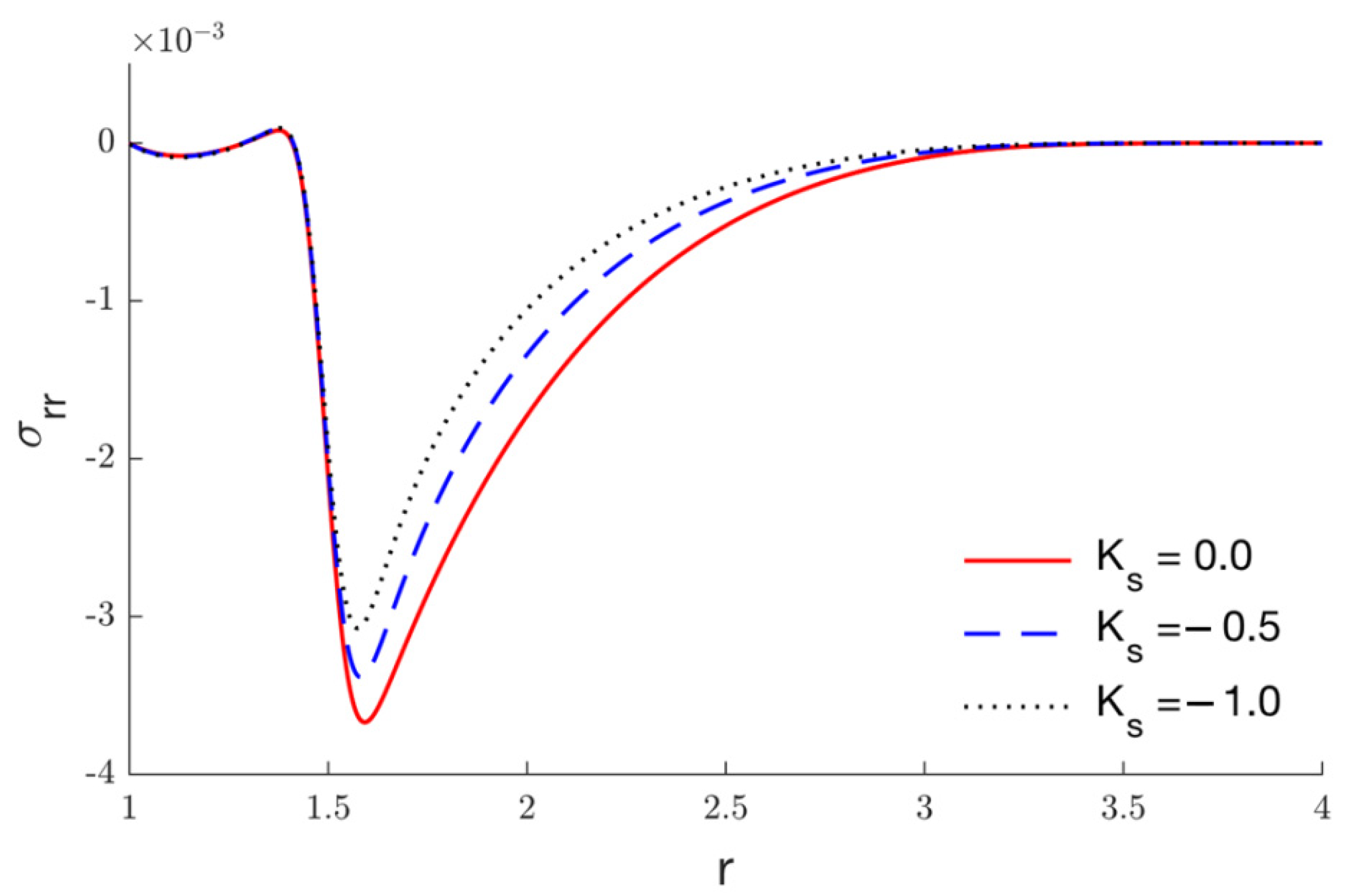
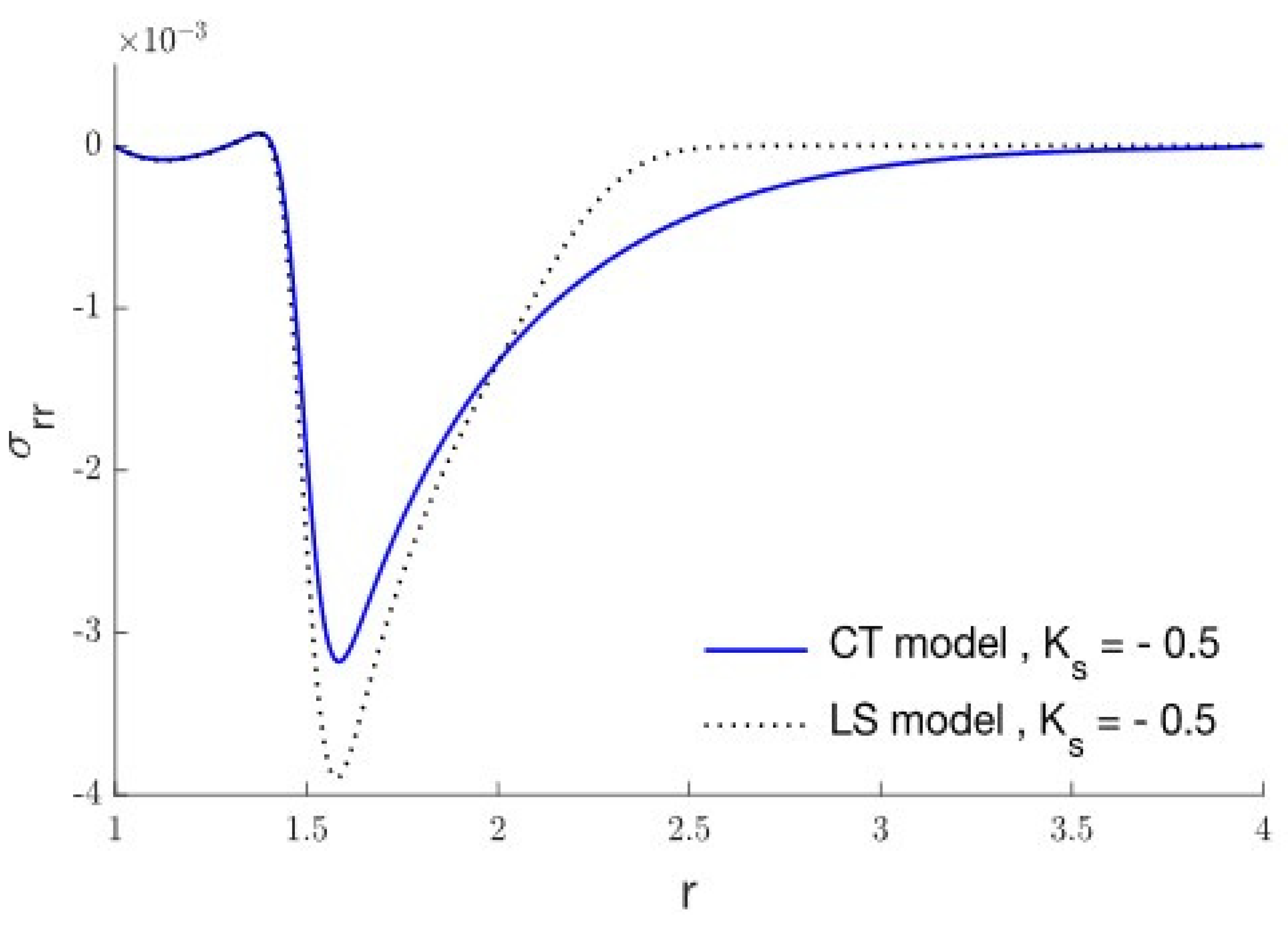
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biot, M.A. Thermoelasticity and Irreversible Thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Dhaliwal, R.S.; Sherief, H.H. Generalized thermoelasticity for anisotropic media. Q. Appl. Math. 1980, 38, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Singh, B. Wave propagation in a generalized thermoelastic material with voids. Appl. Math. Comput. 2007, 189, 698–709. [Google Scholar] [CrossRef]
- Alesemi, M. Plane waves in magneto-thermoelastic anisotropic medium based on (LS) theory under the effect of Coriolis and centrifugal forces. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; p. 012018. [Google Scholar]
- Marin, M.; Craciun, E.M.; Pop, N. Some Results in Green–Lindsay Thermoelasticity of Bodies with Dipolar Structure. Mathematics 2020, 8, 497. [Google Scholar] [CrossRef] [Green Version]
- Aboueregal, A.E.; Sedighi, H.M. The effect of variable properties and rotation in a visco-thermoelastic orthotropic annular cylinder under the Moore–Gibson–Thompson heat conduction model. Proc. Inst. Mech. Eng. Part L J. Mat. Des. Appl. 2021, 235, 1004–1020. [Google Scholar] [CrossRef]
- Biswas, S. Surface waves in porous nonlocal thermoelastic orthotropic medium. Acta Mech 2020, 231, 2741–2760. [Google Scholar] [CrossRef]
- Abd-Alla, A.M.; Abo-Dahab, S.M.; Bayones, F.S. Propagation of Rayleigh waves in magneto-thermo-elastic half-space of a homogeneous orthotropic material under the effect of rotation, initial stress and gravity field. JVC/J. Vib. Control 2013, 19, 1395–1420. [Google Scholar] [CrossRef]
- Abd-Alla, A.M.; Abo-Dahab, S.M.; Hammad, H.A.H. Propagation of Rayleigh waves in generalized magneto-thermoelastic orthotropic material under initial stress and gravity field. Appl. Math. Model. 2011, 35, 2981–3000. [Google Scholar] [CrossRef]
- Abd-Alla, A.M.; Abo-Dahab, S.M.; Hammad, H.A.; Mahmoud, S.R. On generalized magneto-thermoelastic rayleigh waves in a granular medium under the influence of a gravity field and initial stress. JVC/J. Vib. Control 2011, 17, 115–128. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B. Eigenfunction expansion method to analyze thermal shock behavior in magneto-thermoelastic orthotropic medium under three theories. J. Therm. Stresses 2018, 41, 366–382. [Google Scholar] [CrossRef]
- Demirdžić, I.; Horman, I.; Martinović, D. Finite volume analysis of stress and deformation in hygro-thermo-elastic orthotropic body. Comput. Methods Appl. Mech. Eng. 2000, 190, 1221–1232. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B.; Shaw, S. Rayleigh surface wave propagation in orthotropic thermoelastic solids under three-phase-lag model. J. Therm. Stresses 2017, 40, 403–419. [Google Scholar] [CrossRef]
- Ding, H.J.; Wang, H.M.; Chen, W.Q. A solution of a non-homogeneous orthotropic cylindrical shell for axisymmetric plane strain dynamic thermoelastic problems. J. Sound Vib. 2003, 263, 815–829. [Google Scholar] [CrossRef]
- Kaur, I.; Lata, P. Axisymmetric deformation in transversely isotropic magneto-thermoelastic solid with Green–Naghdi III due to inclined load. Int. J. Mech. Mater. Eng. 2020, 15, 3. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B. Eigenfunction expansion method to characterize Rayleigh wave propagation in orthotropic medium with phase lags. Waves Random Complex Media 2018, 29, 722–742. [Google Scholar] [CrossRef]
- Abbas, I.A.; Zenkour, A.M. The Effect of Rotation and Initial Stress on Thermal Shock Problem for a Fiber-Reinforced Anisotropic Half-Space Using Green-Naghdi Theory. J. Comput. Theor. Nanosci. 2014, 11, 331–338. [Google Scholar] [CrossRef]
- Kar, A.; Kanoria, M. Generalized thermoelastic functionally graded orthotropic hollow sphere under thermal shock with three-phase-lag effect. Eur. J. Mech.-A/Solids 2009, 28, 757–767. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abd-alla, A.-e.-n.N. Effects of thermal relaxations on thermoelastic interactions in an infinite orthotropic elastic medium with a cylindrical cavity. Arch Appl Mech 2007, 78, 283–293. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B.; Shaw, S. Thermal shock response in magneto-thermoelastic orthotropic medium with three-phase-lag model. J. Electromagn. Waves Appl. 2017, 31, 879–897. [Google Scholar] [CrossRef]
- Biswas, S. Rayleigh waves in porous nonlocal orthotropic thermoelastic layer lying over porous nonlocal orthotropic thermoelastic half space. Waves Random Complex Media 2021, 1–27. [Google Scholar] [CrossRef]
- Mondal, S.; Sur, A. Photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses. Waves Random Complex Media 2020, 31, 1835–1858. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I. Generalized thermoelastic interaction in a two-dimensional orthotropic material caused by a pulse heat flux. Waves Random Complex Media 2021, 1–18. [Google Scholar] [CrossRef]
- Alzahrani, F.; Hobiny, A.; Abbas, I.; Marin, M. An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry 2020, 12, 848. [Google Scholar] [CrossRef]
- Sharma, P.K.; Bajpai, A.; Kumar, R. Analysis of two temperature thermoelastic diffusion plate with variable thermal conductivity and diffusivity. Waves Random Complex Media 2021. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A.; Marin, M. Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. J. Taibah Univ. Sci. 2020, 14, 1369–1376. [Google Scholar] [CrossRef]
- Said, S.M. Eigenvalue approach on a problem of magneto-thermoelastic rotating medium with variable thermal conductivity: Comparisons of three theories. Waves Random Complex Media 2019, 31, 1322–1339. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A.; Alshehri, H.; Vlase, S.; Marin, M. Analysis of Thermoelastic Interaction in a Polymeric Orthotropic Medium Using the Finite Element Method. Polymers 2022, 14, 2112. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. Nonlinear transient thermal stress analysis of temperature-dependent hollow cylinders using a finite element model. Int. J. Struct. Stab. Dyn. 2014, 14, 1450025. [Google Scholar] [CrossRef]
- Abbas, I.A.; Kumar, R. 2D deformation in initially stressed thermoelastic half-space with voids. Steel Compos. Struct. 2016, 20, 1103–1117. [Google Scholar] [CrossRef]
- Kaur, H.; Lata, P. Effect of thermal conductivity on isotropic modified couple stress thermoelastic medium with two temperatures. Steel Compos. Struct. 2020, 34, 309–319. [Google Scholar] [CrossRef]
- Lata, P.; Kaur, I. Thermomechanical interactions in transversely isotropic magneto thermoelastic solid with two temperatures and without energy dissipation. Steel Compos. Struct. 2019, 32, 779–793. [Google Scholar] [CrossRef]
- Lata, P.; Kumar, R.; Sharma, N. Plane waves in an anisotropic thermoelastic. Steel Compos. Struct. 2016, 22, 567–587. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Alharbi, A.M.; Al-Autabi, A.A.M.K. Micropolar thermoelastic medium with voids under the effect of rotation concerned with 3phl model. Geomach. Eng. 2020, 21, 447–459. [Google Scholar] [CrossRef]
- Lata, P.; Singh, S. Deformation in a nonlocal magneto-thermoelastic solid with hall current due to normal force. Geomach. Eng. 2020, 22, 109–117. [Google Scholar] [CrossRef]
- Sarkar, N.; Mondal, S.; Othman, M.I.A. Effect of the laser pulse on transient waves in a non-local thermoelastic medium under Green-Naghdi theory. Struct. Eng. Mech. 2020, 74, 471–479. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abbas, I.A. LS model on thermal shock problem of generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Appl. Math. Model. 2011, 35, 3759–3768. [Google Scholar] [CrossRef]
- Alzahrani, F. The effects of variable thermal conductivity in semiconductor materials photogenerated by a focused thermal shock. Mathematics 2020, 8, 1230. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Mashat, D.S.; Allehaibi, A.M. Magneto-Thermoelastic Response in an Unbounded Medium Containing a Spherical Hole via Multi-Time-Derivative Thermoelasticity Theories. Materials 2022, 15, 2432. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abouelregal, A.E.; Marin, M. Generalized thermoelastic functionally graded on a thin slim strip non-gaussian laser beam. Symmetry 2020, 12, 1094. [Google Scholar] [CrossRef]
- Lata, P.; Singh, S. Stoneley wave propagation in nonlocal isotropic magneto-thermoelastic solid with multi-dual-phase lag heat transfer. Steel Compos. Struct. 2021, 38, 141–150. [Google Scholar] [CrossRef]
- Lata, P. Effect of energy dissipation on plane waves in sandwiched layered thermoelastic medium. Steel Compos. Struct. 2018, 27, 439–451. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Bary, A.A. Fractional magneto-Thermoelastic materials with phase-lag Green-Naghdi theories. Steel Compos. Struct. 2017, 24, 297–307. [Google Scholar] [CrossRef]
- Abd-Elaziz, E.M.; Othman, M.I.A. On a magneto-poro-thermoelastic medium under the influence of the Seebeck effect. Int. J. Numer. Anal. Methods Geomech. 2019, 44, 705–719. [Google Scholar] [CrossRef]
- Lata, P.; Kaur, I. Effect of time harmonic sources on transversely isotropic thermoelastic thin circular plate. Geomach. Eng. 2019, 19, 29–36. [Google Scholar] [CrossRef]
- Zhang, L.; Bhatti, M.M.; Michaelides, E.; Marin, M.; Ellahi, R. Hybrid nanofluid flow towards an elastic surface with tantalum and nickel nanoparticles, under the influence of an induced magnetic field. Eur. Phys. J. Spec. Top. 2022, 231, 521–533. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The size-dependent thermoelastic vibrations of nanobeams subjected to harmonic excitation and rectified sine wave heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The response of nanobeams with temperature-dependent properties using state-space method via modified couple stress theory. Symmetry 2020, 12, 1276. [Google Scholar] [CrossRef]
- Tiwari, R.; Kumar, R.; Kumar, A. Investigation of thermal excitation induced by laser pulses and thermal shock in the half space medium with variable thermal conductivity. Waves Random Complex Media 2022, 32, 2313–2331. [Google Scholar] [CrossRef]
- Tiwari, R.; Misra, J.C. Magneto-thermoelastic excitation induced by a thermal shock: A study under the purview of three phase lag theory. Waves Random Complex Media 2022, 32, 797–818. [Google Scholar] [CrossRef]
- Sherief, H.H.; Hamza, F.A. Modeling of variable thermal conductivity in a generalized thermoelastic infinitely long hollow cylinder. Meccanica 2016, 51, 551–558. [Google Scholar] [CrossRef]
- Marin, M.; Agarwal, R.P.; Mahmoud, S.R. Nonsimple material problems addressed by the Lagrange’s identity. Bound. Value Probl. 2013, 2013, 135. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, I.; Marin, M.; Hobiny, A.; Vlase, S. Thermal Conductivity Study of an Orthotropic Medium Containing a Cylindrical Cavity. Symmetry 2022, 14, 2387. https://doi.org/10.3390/sym14112387
Abbas I, Marin M, Hobiny A, Vlase S. Thermal Conductivity Study of an Orthotropic Medium Containing a Cylindrical Cavity. Symmetry. 2022; 14(11):2387. https://doi.org/10.3390/sym14112387
Chicago/Turabian StyleAbbas, Ibrahim, Marin Marin, Aatef Hobiny, and Sorin Vlase. 2022. "Thermal Conductivity Study of an Orthotropic Medium Containing a Cylindrical Cavity" Symmetry 14, no. 11: 2387. https://doi.org/10.3390/sym14112387






