Transient Controller Design Based on Reinforcement Learning for a Turbofan Engine with Actuator Dynamics
Abstract
:1. Introduction
2. System Uncertainties Analysis
3. Reinforcement Learning Algorithm
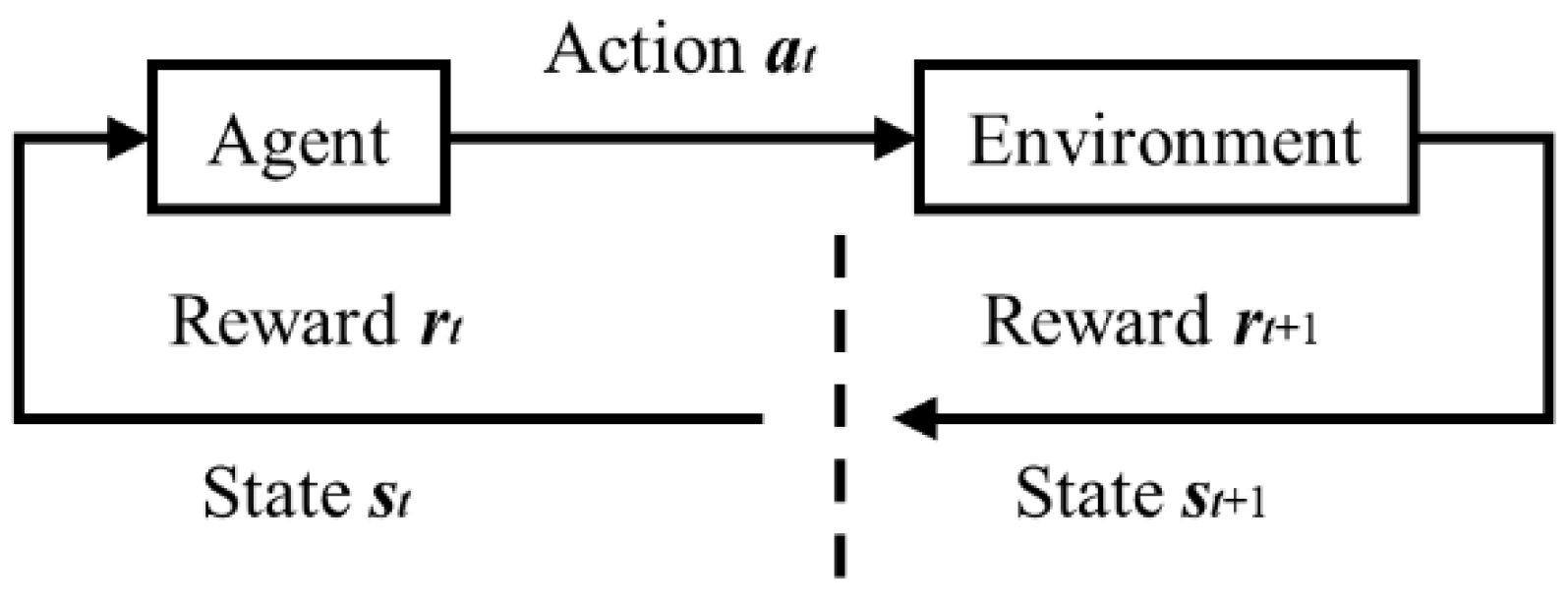
3.1. Preliminaries
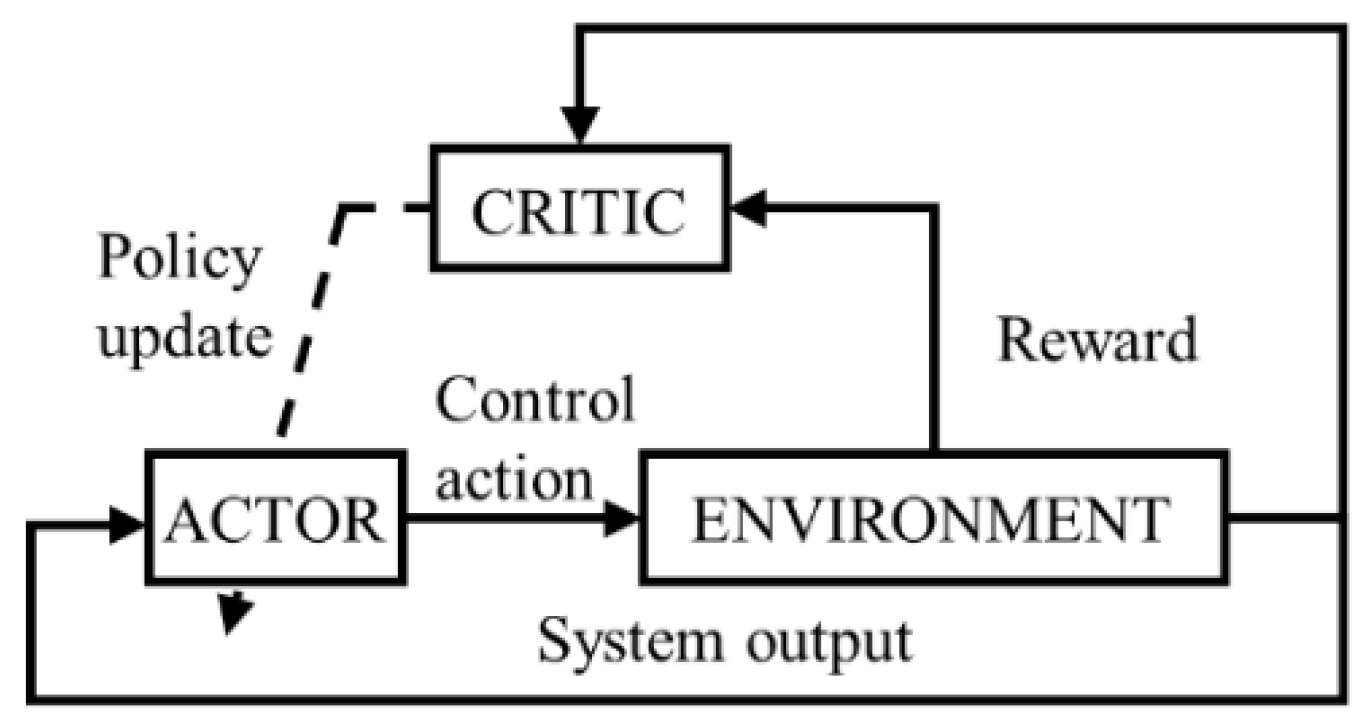
3.2. Framework of Reinforcement Learning
- (1)
- The actor network represents the optimal action policy. It is responsible for iteratively updating the network weights , choosing the current action ai based on the current state si, and obtaining the next state si+1 and the reward ri;
- (2)
- The critic network represents the Q-value obtained after taking action following the policy defined with the actor network at every state s. It is used to update the network weights and calculate the current ;
- (3)
- The target actor network is a copy of actor network . The weights of the target actor network are updated with the following soft update algorithm:where is the updating factor;
- (4)
- The target critic network is a copy of the critic network, and is used to calculate yi. Similarly, the weights are updated with the following soft update algorithm:where is the updating factor.
4. Reinforcement Learning Controller Design Procedure for Turbofan Engines
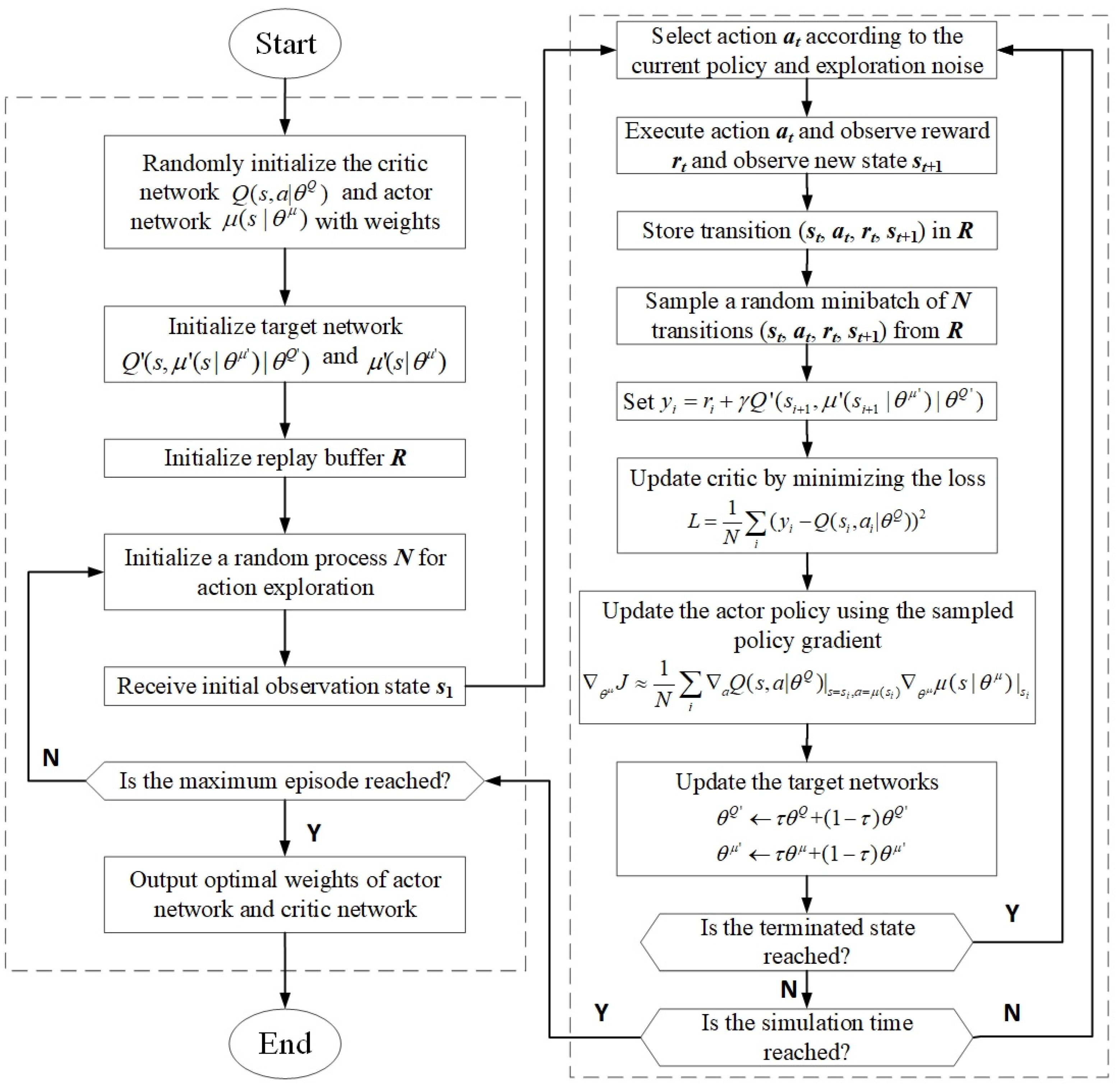
4.1. Framework Definition
4.2. DDPG Agent Creation
4.3. Reward Function
4.4. Problems and Solutions
4.5. Training Options
5. Simulation and Verification
5.1. Options Specification
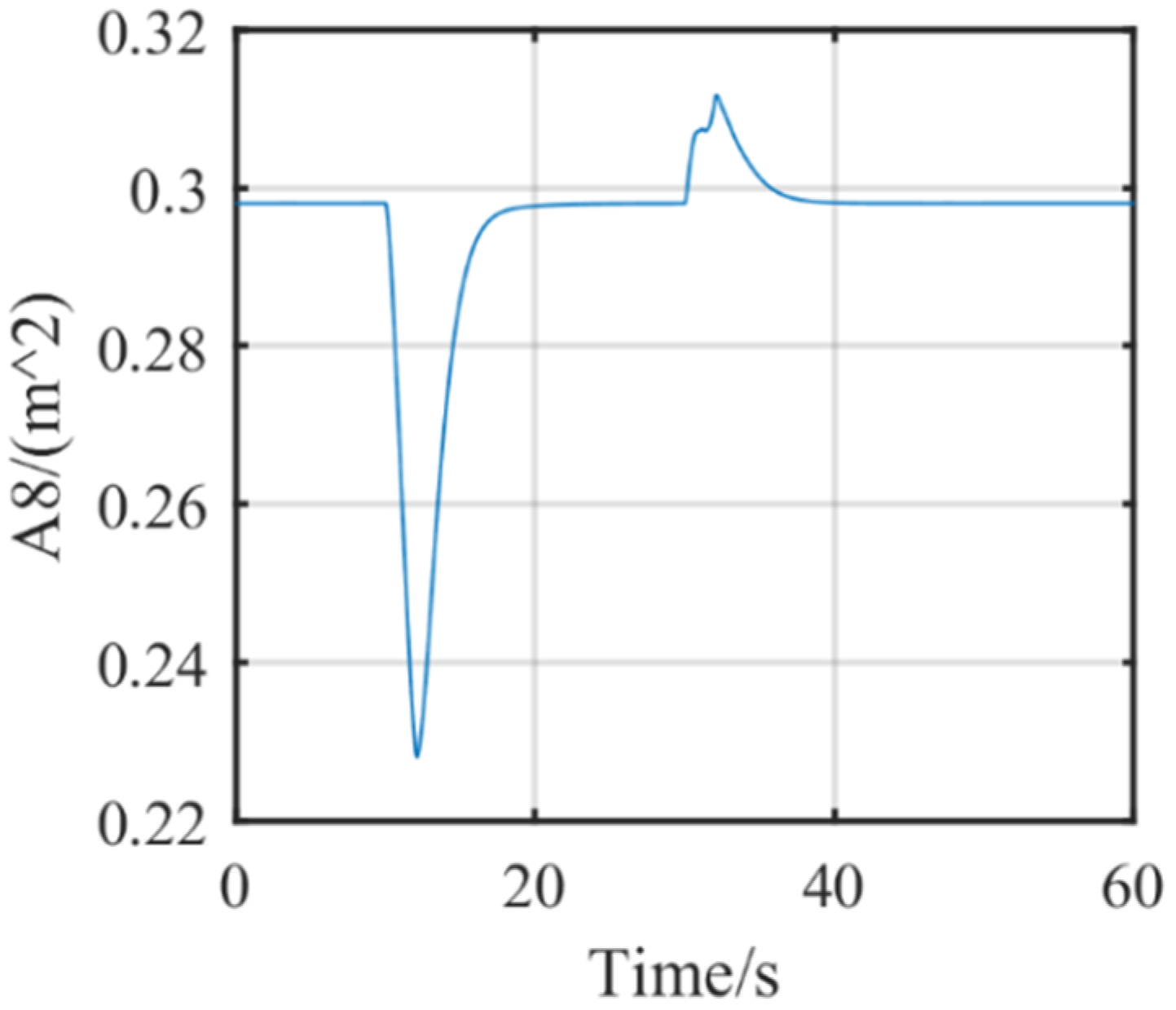
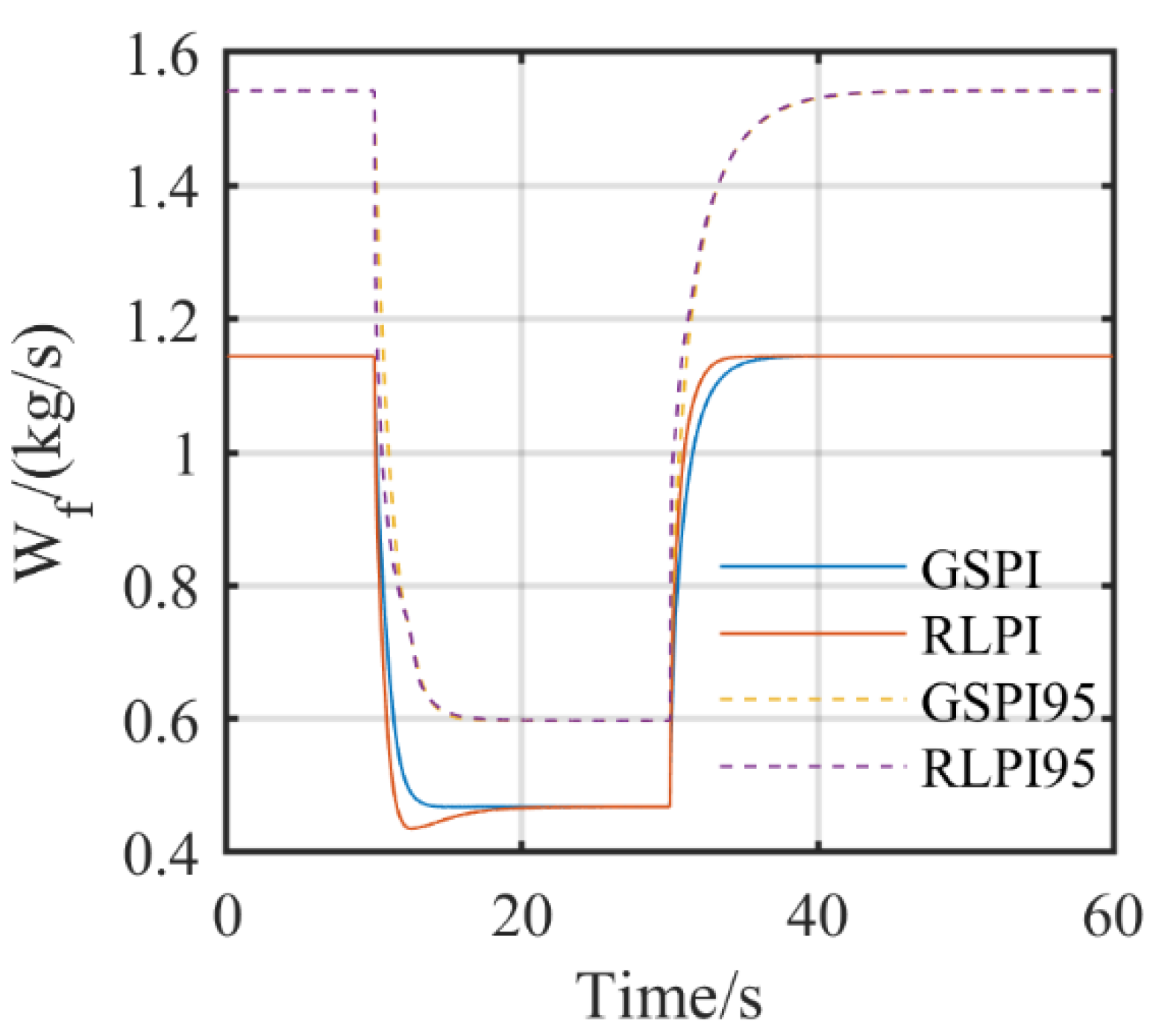
5.2. Simulation Results in Ideal Conditions and with Uncertainties
5.3. Simulation Results with Degradation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, M.; Wang, X.; Dan, Z.; Zhang, S.; Pei, X. Two freedom linear parameter varying μ synthesis control for flight environment testbed. Chin. J. Aeronaut. 2019, 32, 1204–1214. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, X.; Miao, K.; Pei, X.; Liu, J. Two Degree-of-freedom μ Synthesis Control for Turbofan Engine with Slow Actuator Dynamics and Uncertainties. J. Phys. Conf. Ser. 2021, 1828, 012144. [Google Scholar] [CrossRef]
- Gu, N.N.; Wang, X.; Lin, F.Q. Design of Disturbance Extended State Observer (D-ESO)-Based Constrained Full-State Model Predictive Controller for the Integrated Turbo-Shaft Engine/Rotor System. Energies 2019, 12, 4496. [Google Scholar] [CrossRef] [Green Version]
- Dan, Z.H.; Zhang, S.; Bai, K.Q.; Qian, Q.M.; Pei, X.T.; Wang, X. Air Intake Environment Simulation of Altitude Test Facility Control Based on Extended State Observer. J. Propuls. Technol. 2020; in press. [Google Scholar]
- Zhu, M.; Wang, X.; Pei, X.; Zhang, S.; Liu, J. Modified robust optimal adaptive control for flight environment simulation system with heat transfer uncertainty. Chin. J. Aeronaut. 2021, 34, 420. [Google Scholar] [CrossRef]
- Miao, K.Q.; Wang, X.; Zhu, M.Y. Full Flight Envelope Transient Main Control Loop Design Based on LMI Optimization. In Proceedings of the ASME Turbo Expo 2020, Virtual Online, 21–25 September 2020. [Google Scholar]
- Gu, B.B. Robust Fuzzy Control for Aeroengines; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2018. [Google Scholar]
- Amgad, M.; Shakirah, M.T.; Suliman, M.F.; Hitham, A. Deep-Learning Based Prognosis Approach for Remaining Useful Life Prediction of Turbofan Engine. Symmetry 2021, 13, 1861. [Google Scholar] [CrossRef]
- Zhang, X.H.; Liu, J.X.; Li, M.; Gen, J.; Song, Z.P. Fusion Control of Two Kinds of Control Schedules in Aeroengine Acceleration Process. J. Propuls. Technol. 2021; in press. [Google Scholar]
- Yin, X.; Shi, G.; Peng, S.; Zhang, Y.; Zhang, B.; Su, W. Health State Prediction of Aero-Engine Gas Path System Considering Multiple Working Conditions Based on Time Domain Analysis and Belief Rule Base. Symmetry 2022, 14, 26. [Google Scholar] [CrossRef]
- Frank, L.L.; Draguna, V.; Kyriakos, G.V. Reinforcement learning and feedback control. IEEE Control Syst. Mag. 2012, 32, 76–105. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2016, arXiv:1509.02971. [Google Scholar]
- Richard, S.S.; David, M.; Satinder, S.; Yishay, M. Policy Gradient Methods for Reinforcement Learning with Function Approximation. Adv. Neural Inf. Process. Syst. 2000, 12, 1057–1063. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic Policy Gradient Algorithms. In Proceedings of the International Conference on Machine Learning, Bejing, China, 22–24 June 2014; pp. 387–395. [Google Scholar]
- Giulia, C.; Shreyansh, D.; Roverto, C. Learning Transferable Policies for Autonomous Planetary Landing via Deep Reinforcement Learning. In Proceedings of the ASCEND, Las Vegas, NV, USA, 15–17 November 2021. [Google Scholar]
- Sun, D.; Gao, D.; Zheng, J.H.; Han, P. Reinforcement learning with demonstrations for UAV control. J. Beijing Univ. Aeronaut. Astronaut. 2021; in press. [Google Scholar]
- Kirk, H.; Steve, U. On Deep Reinforcement Learning for Spacecraft Guidance. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Hiroshi, K.; Seiji, T.; Eiji, S. Feedback Control of Karman Vortex Shedding from a Cylinder using Deep Reinforcement Learning. In Proceedings of the AIAA AVIATION Forum, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Hu, X. Design of Intelligent Controller for Variable Cycle Engine; Dalian University of Technology: Dalian, China, 2020. [Google Scholar]
- Li, Y.; Nie, L.C.; Mu, C.H.; Song, Z.P. Online Intelligent Optimization Algorithm for Adaptive Cycle Engine Performance. J. Propuls. Technol. 2021, 42, 1716–1724. [Google Scholar]
- Wang, F. Research on Prediction of Civil Aero-Engine Gas Path Health State And Modeling Method of Spare Engine Allocation; Harbin Institute of Technology: Harbin, China, 2020. [Google Scholar]
- Li, Z. Research on Life-Cycle Maintenance Strategy Optimization of Civil Aeroengine Fleet; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Richter, H. Advanced Control of Turbofan Engines; National Defense Industry Press: Beijing, China, 2013; p. 16. [Google Scholar]
- Miao, K.Q.; Wang, X.; Zhu, M.Y. Dynamic Main Close-loop Control Optimal Design Based on LMI Method. J. Beijing Univ. Aeronaut. Astronaut. 2021; in press. [Google Scholar]
- Zeyan, P.; Gang, L.; Xingmin, G.; Yong, H. Principle of Aviation Gas Turbine; National Defense Industry Press: Beijing, China, 2008; p. 111. [Google Scholar]






| Function | Description | Value |
|---|---|---|
| Critic Representation Options | Learn Rate | 0.001 |
| Gradient Threshold | 1 | |
| Actor Representation Option | Learn Rate | 0.0001 |
| Gradient Threshold | 1 | |
| DDPG Agent Options | Sample time | 0.01 |
| Target Smooth Factor | 0.003 | |
| Discount Factor | 1 | |
| Mini-Batch Size | 64 | |
| Experience Buffer Length | 1,000,000 | |
| Noise Options Variance | 0.3 | |
| Noise Options’ Variance Decay Rate | 0.00001 | |
| Training Options | Sample time | 0.01 |
| Maximum Episodes | 20,000 | |
| Maximum Steps per Episode | 1000 | |
| Score-Averaging Window Length | 2 | |
| Stop Training Value | 996 |
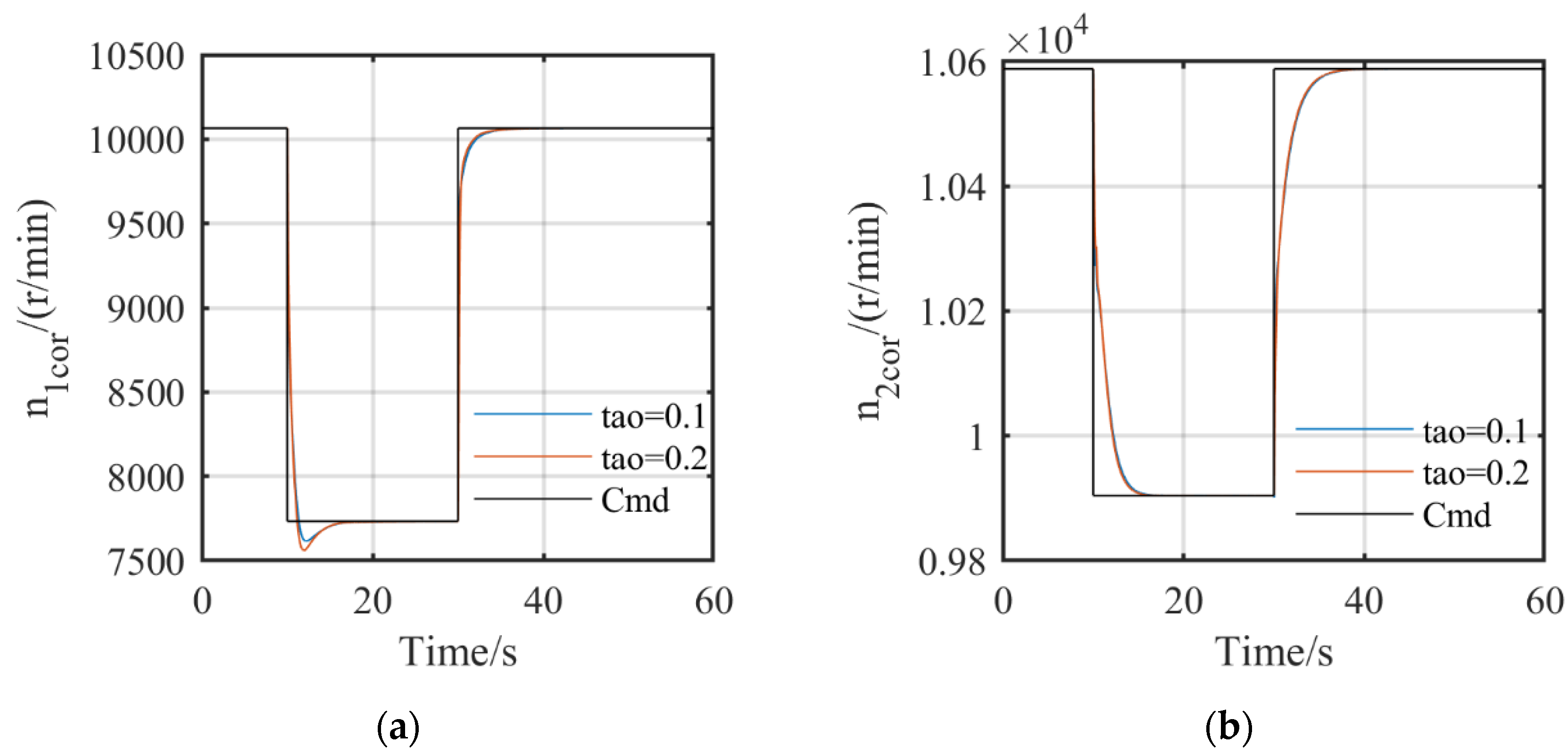
| τa | Speed | Ts/s | σ% | State |
|---|---|---|---|---|
| 0.1 | n1cor | 1.43 | 0 | Acceleration |
| 2.23 | 1.50 | Deceleration | ||
| n2cor | 3.84 | 0 | Acceleration | |
| 3.33 | 0 | Deceleration | ||
| 0.2 | n1cor | 1.18 | 0 | Acceleration |
| 2.90 | 2.23 | Deceleration | ||
| n2cor | 3.71 | 0 | Acceleration | |
| 3.15 | 0 | Deceleration |
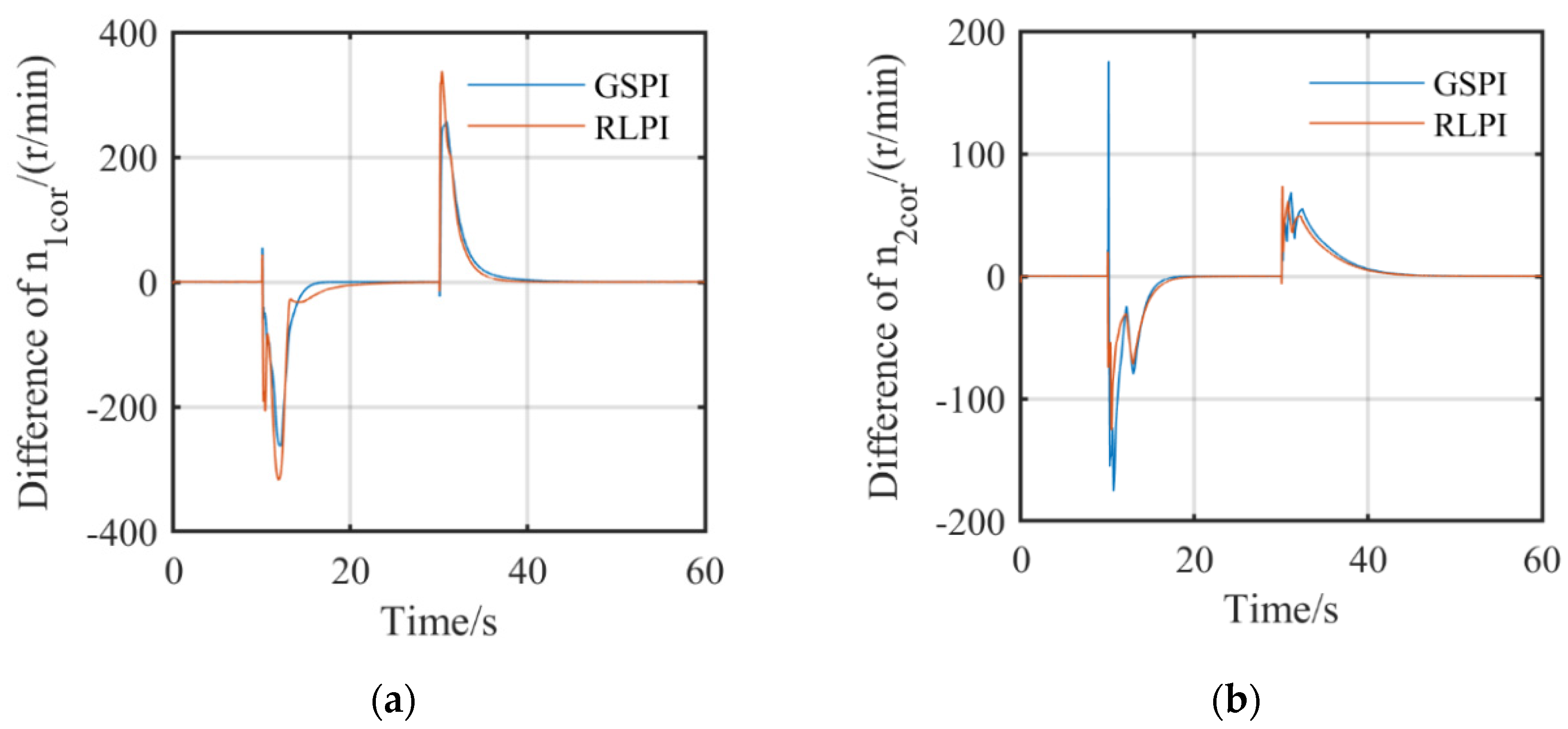
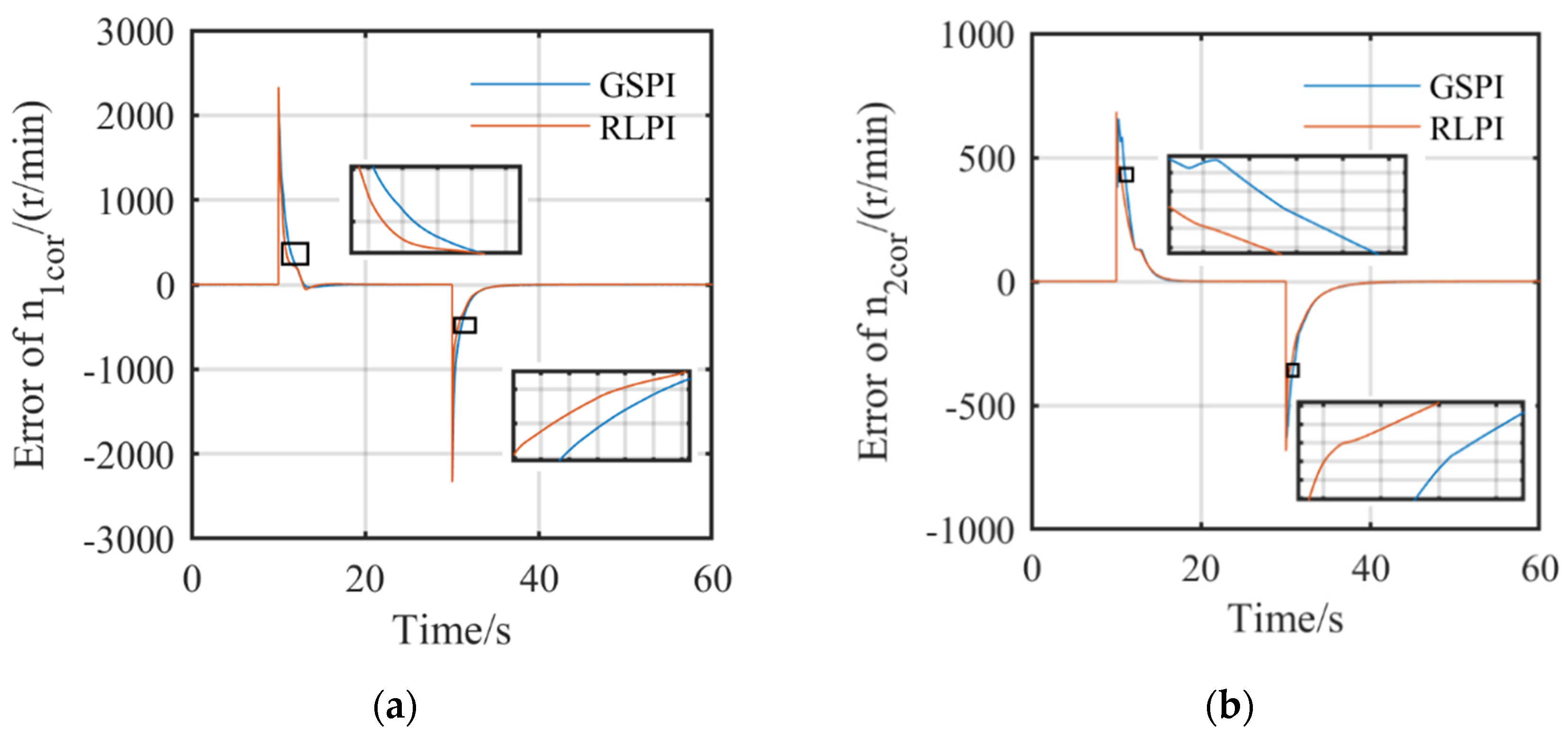
| Controller | Speed | Ts/s | σ% | State |
|---|---|---|---|---|
| GSPI | n1cor | 2.67 | 0 | Acceleration |
| 3.78 | 0.39 | Deceleration | ||
| n2cor | 5.31 | 0 | Acceleration | |
| 3.17 | 0 | Deceleration | ||
| RLPI | n1cor | 2.53 | 0 | Acceleration |
| 4.40 | 0.75 | Deceleration | ||
| n2cor | 5.27 | 0 | Acceleration | |
| 4.50 | 0 | Deceleration |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, K.; Wang, X.; Zhu, M.; Yang, S.; Pei, X.; Jiang, Z. Transient Controller Design Based on Reinforcement Learning for a Turbofan Engine with Actuator Dynamics. Symmetry 2022, 14, 684. https://doi.org/10.3390/sym14040684
Miao K, Wang X, Zhu M, Yang S, Pei X, Jiang Z. Transient Controller Design Based on Reinforcement Learning for a Turbofan Engine with Actuator Dynamics. Symmetry. 2022; 14(4):684. https://doi.org/10.3390/sym14040684
Chicago/Turabian StyleMiao, Keqiang, Xi Wang, Meiyin Zhu, Shubo Yang, Xitong Pei, and Zhen Jiang. 2022. "Transient Controller Design Based on Reinforcement Learning for a Turbofan Engine with Actuator Dynamics" Symmetry 14, no. 4: 684. https://doi.org/10.3390/sym14040684
APA StyleMiao, K., Wang, X., Zhu, M., Yang, S., Pei, X., & Jiang, Z. (2022). Transient Controller Design Based on Reinforcement Learning for a Turbofan Engine with Actuator Dynamics. Symmetry, 14(4), 684. https://doi.org/10.3390/sym14040684







