Analytical Investigation of Fractional-Order Korteweg–De-Vries-Type Equations under Atangana–Baleanu–Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid
Abstract
:1. Introduction
2. Preliminaries
3. Basic Concept of the Suggested Method
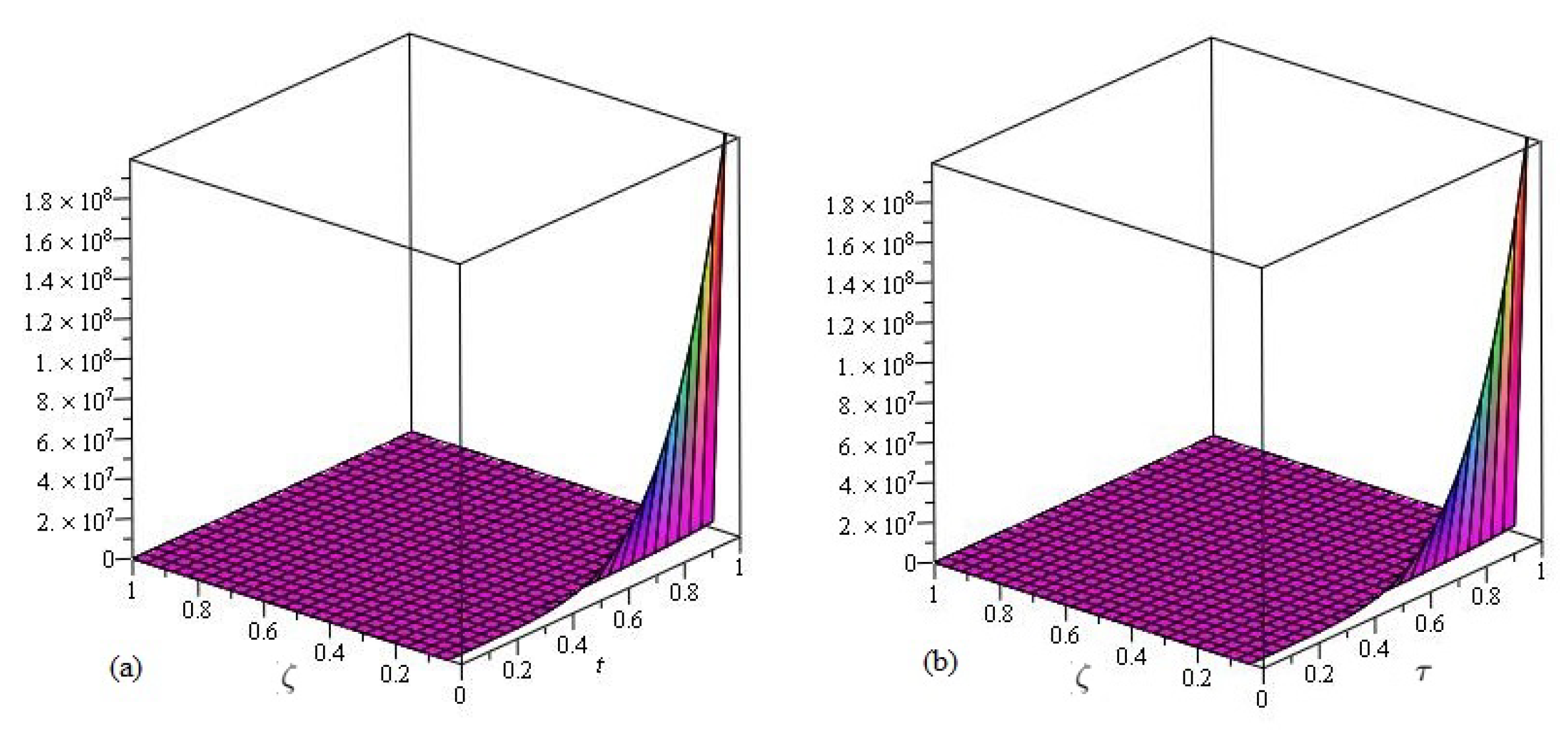
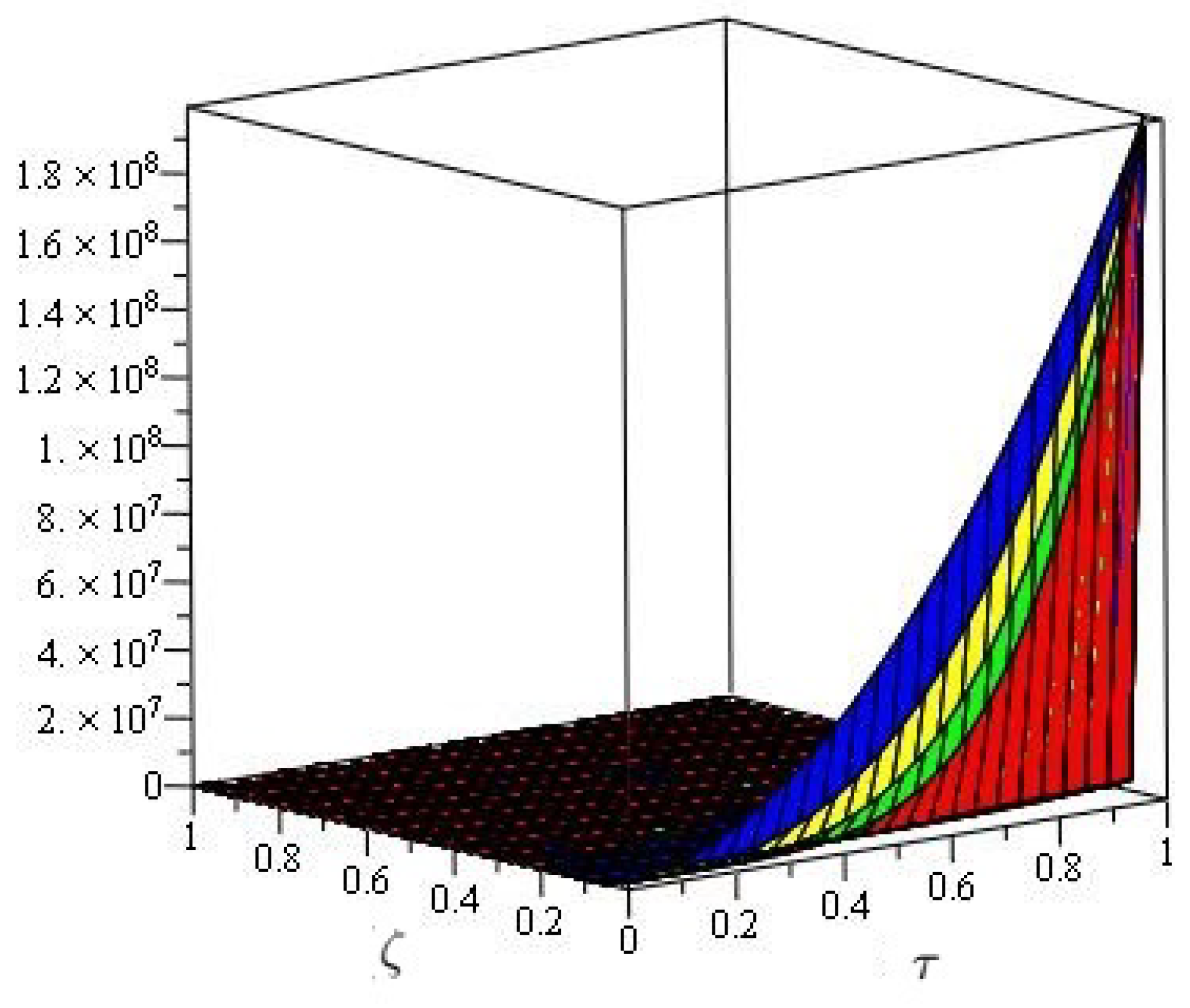
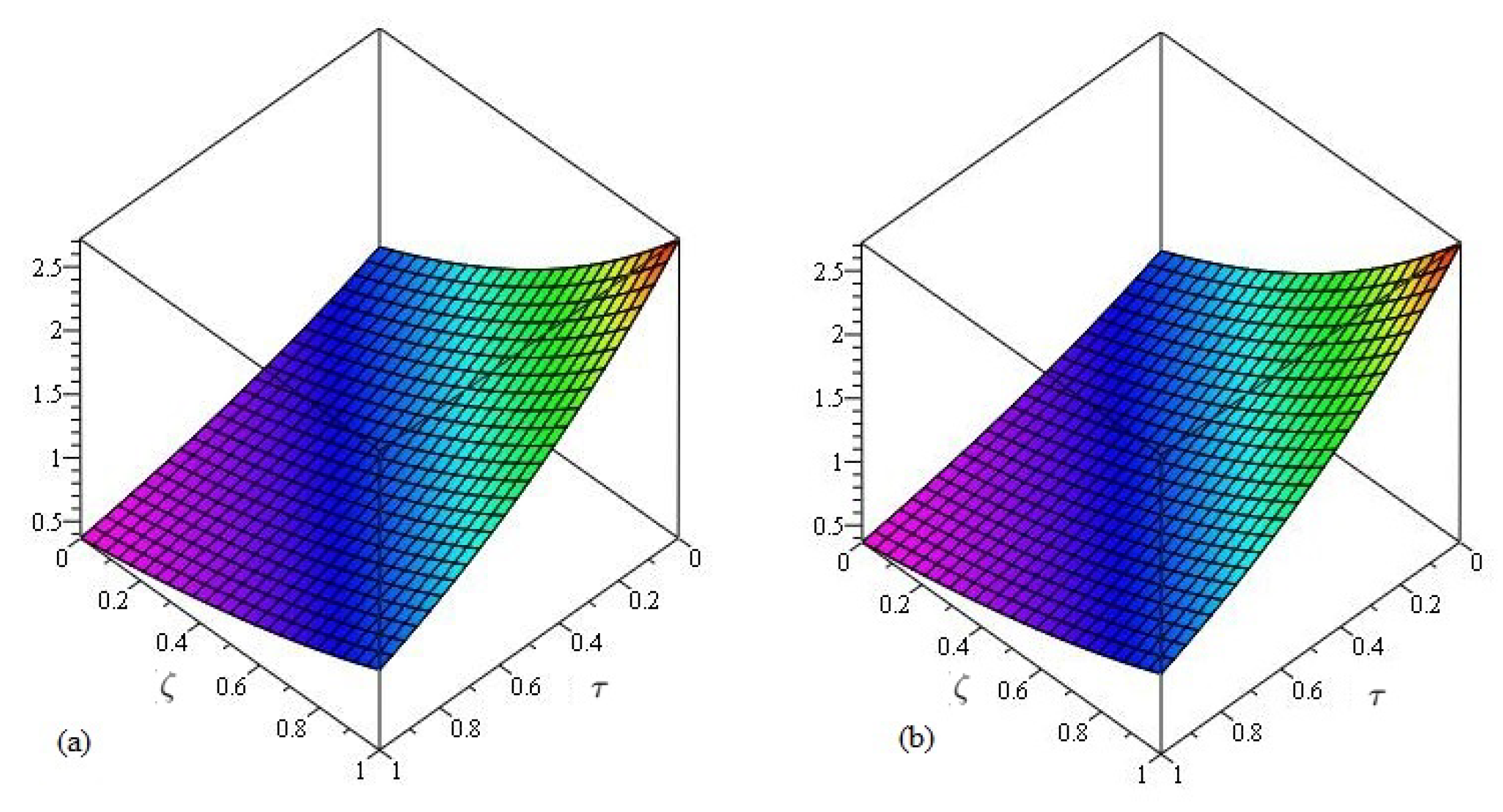
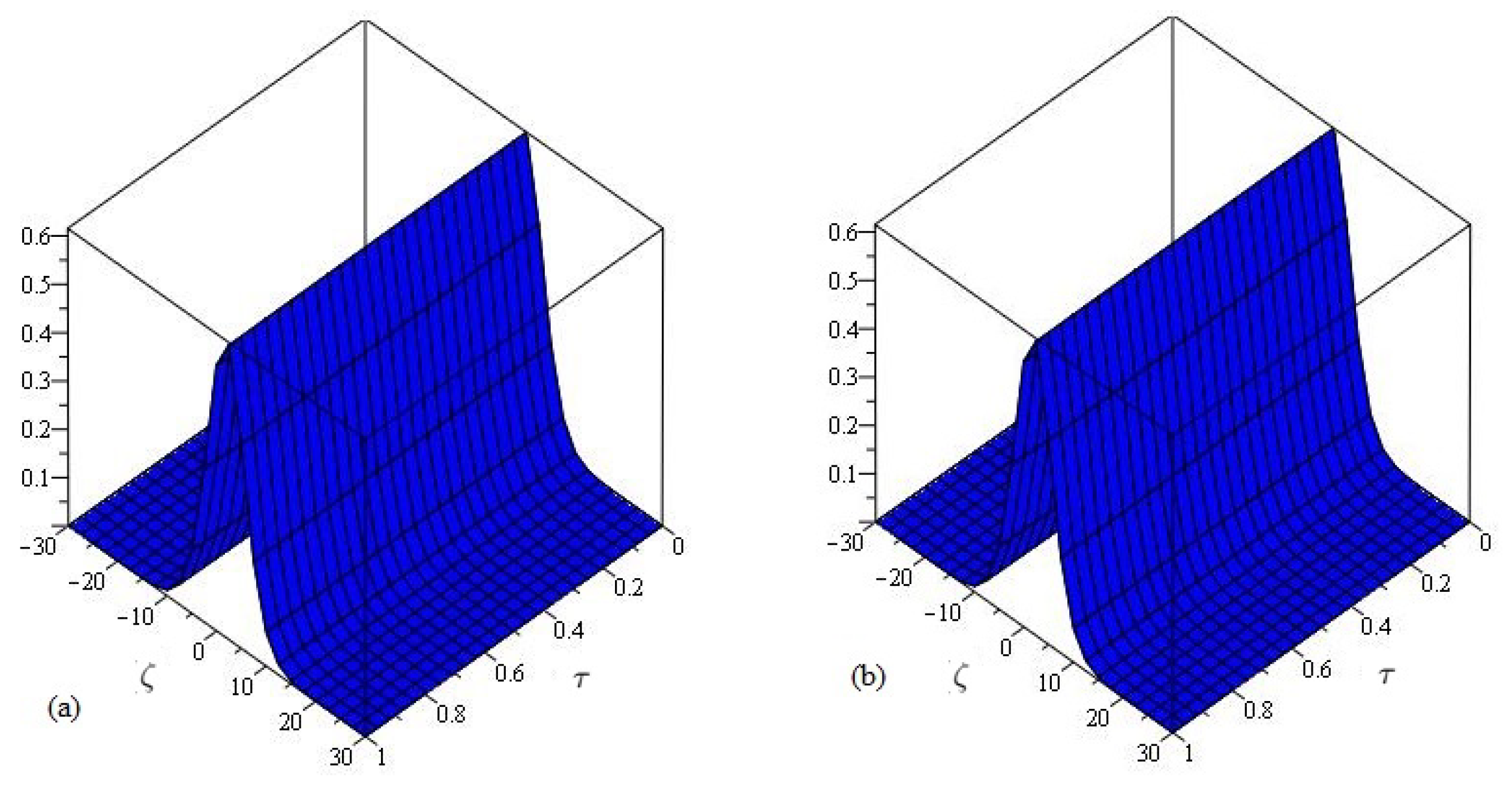
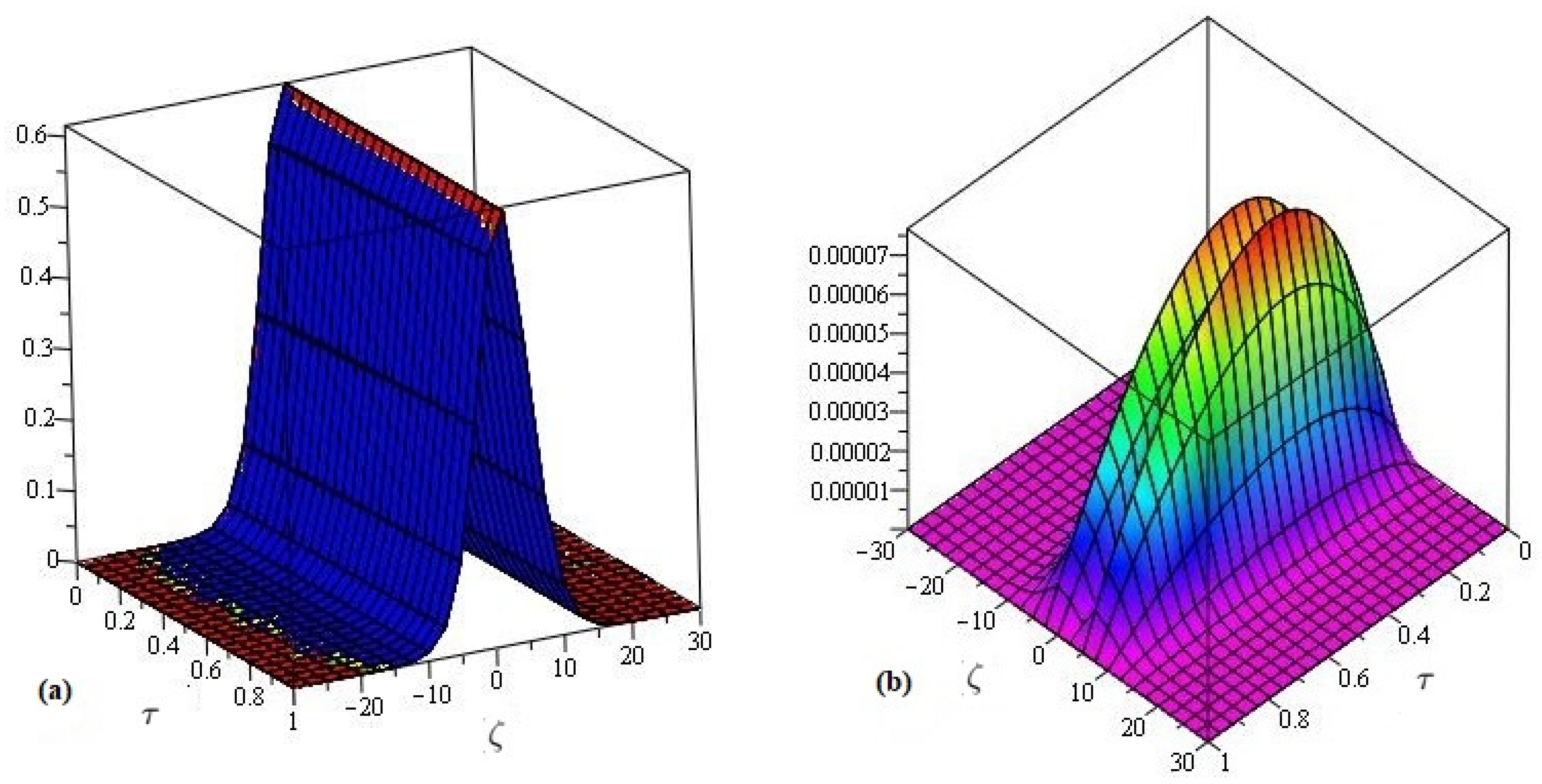
4. Numerical Implementations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baleanu, D.; Fernandez, A. On fractional operators and their classifications. Mathematics 2019, 7, 830. [Google Scholar] [CrossRef] [Green Version]
- Sunthrayuth, P.; Zidan, A.; Yao, S.; Shah, R.; Inc, M. The Comparative Study for Solving Fractional-Order Fornberg–Whitham Equation via ρ-Laplace Transform. Symmetry 2021, 13, 784. [Google Scholar] [CrossRef]
- Khader, M.M.; Saad, K.M. Numerical studies of the fractional Korteweg-de Vries, Korteweg-de Vries-Burgers and Burgers equations. Proc. Natl. Acad. Sci. India Sect. Phys. Sci. 2021, 91, 67–77. [Google Scholar] [CrossRef]
- Khader, M.M.; Saad, K.M.; Hammouch, Z.; Baleanu, D. A spectral collocation method for solving fractional KdV and KdV-Burgers equations with non-singular kernel derivatives. Appl. Numer. Math. 2021, 161, 137–146. [Google Scholar] [CrossRef]
- Saad, K.M.; AL-Shareef, E.H.; Alomari, A.K.; Baleanu, D.; Gomez-Aguilar, J.F. On exact solutions for time-fractional Korteweg-de Vries and Korteweg-de Vries-Burgers equations using homotopy analysis transform method. Chin. J. Phys. 2020, 63, 149–162. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.; Zidan, A.; Khan, A.; Hamed, Y.; Shah, R. Numerical Investigation of Fractional-Order Swift–Hohenberg Equations via a Novel Transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Alesemi, M.; Iqbal, N.; Abdo, M. Novel Investigation of Fractional-Order Cauchy-Reaction Diffusion Equation Involving Caputo-Fabrizio Operator. J. Funct. Spaces 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Khan, N.A.; Hameed, T.; Ahmed, S. Homotopy perturbation aided optimization procedure with applications to oscillatory fractional order nonlinear dynamical systems. Int. J. Model. Simul. Sci. Comput. 2019, 10, 1950026. [Google Scholar] [CrossRef]
- Alam, K.N.; Hameed, T.; Ayaz, M.; Abdul, R.O. The reaction dimerization: A resourceful slant applied on the fractional partial differential equation. Therm. Sci. 2019, 23 (Suppl. 6), 2095–2105. [Google Scholar]
- Khan, N.A.; Hameed, T.; Razzaq, O.A. Elegant scheme for one-way wave propagation in Kerr media. Eur. Phys. J. Plus 2020, 135, 1–33. [Google Scholar] [CrossRef]
- Naeem, M.; Zidan, A.; Nonlaopon, K.; Syam, M.; Al-Zhour, Z.; Shah, R. A New Analysis of Fractional-Order Equal-Width Equations via Novel Techniques. Symmetry 2021, 13, 886. [Google Scholar] [CrossRef]
- Agarwal, R.; Mofarreh, F.; Shah, R.; Luangboon, W.; Nonlaopon, K. An Analytical Technique, Based on Natural Transform to Solve Fractional-Order Parabolic Equations. Entropy 2021, 23, 1086. [Google Scholar] [CrossRef] [PubMed]
- Aljahdaly, N.; Agarwal, R.; Shah, R.; Botmart, T. Analysis of the Time Fractional-Order Coupled Burgers Equations with Non-Singular Kernel Operators. Mathematics 2021, 9, 2326. [Google Scholar] [CrossRef]
- Kazeminia, M.; Soleimani-Amiri, S.; Zahedi, S.A. Exact and numerical solutions for nonlinear higher order modified KdV equations by using variational iteration method. Adv. Stud. Theor. Phys. 2010, 4, 437–447. [Google Scholar]
- Shah, N.A.; El-Zahar, E.R.; Chung, J.D. Fractional Analysis of Coupled Burgers Equations within Yang Caputo-Fabrizio Operator. J. Funct. Spaces 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Goswami, A.; Singh, J.; Kumar, D. A reliable algorithm for KdV equations arising in warm plasma. Nonlin. Eng. 2016, 5, 7–16. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Kumar, S. A reliable algorithm for solving discontinued problems arising in nanotechnology. Sci. Iran. 2013, 20, 1059–1062. [Google Scholar]
- Wazwaz, A.-M. Partial Differential Equations and Solitary Waves Theory Higher Education; Springer: Beijing, China; Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Wazwaz, A.-M. (2+1)-Dimensional mKdV (N) equations by the mKdV recursion operator: Multiple soliton and multiple singular soliton solutions. Appl. Math. Comput. 2012, 219, 2535–2544. [Google Scholar] [CrossRef]
- LÃ, X.; Chen, S.-J. Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: One-lump-multi-stripe and one-lump-multi-soliton types. Nonlinear Dyn. 2021, 103, 947–977. [Google Scholar]
- El-Tantawy, S.A.; Salas Alvaro, H.; Alharthi, M.R. On the analytical and numerical solutions of the damped nonplanar Shamel Korteweg-de Vries Burgers equation for modeling nonlinear structures in strongly coupled dusty plasmas: Multistage homotopy perturbation method. Phys. Fluids 2021, 33, 043106. [Google Scholar] [CrossRef]
- Albalawi, W.; El-Tantawy, S.A.; Salas Alvaro, H. On the rogue wave solution in the framework of a Korteweg-de Vries equation. Results Phys. 2021, 30, 104847. [Google Scholar] [CrossRef]
- Almutlak, S.A.; El-Tantawy, S.A. On the approximate solutions of a damped nonplanar modified Korteweg-de Vries equation for studying dissipative cylindrical and spherical solitons in plasmas. Results Phys. 2021, 23, 104034. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Wazwaz, A.-M. Anatomy of modified Korteweg-de Vries equation for studying the modulated envelope structures in non-Maxwellian dusty plasmas: Freak waves and dark soliton collisions. Phys. Plasmas 2018, 25, 092105. [Google Scholar] [CrossRef]
- El-Tantawy, S.A. Rogue waves in electronegative space plasmas: The link between the family of the KdV equations and the nonlinear Schradinger equation. Astrophys. Space Sci. 2016, 361, 164–169. [Google Scholar] [CrossRef]
- Drazin, P.G.; Johnson, R.S. Solitons: An Introduction; Cambridge University Press: New York, NY, USA, 1989. [Google Scholar]
- Kakutani, T.; Ono, H. Weak non-linear hydromagnetic waves in a cold collision free plasma. J. Phys. Soc. Jpn. 1969, 26, 1305–1318. [Google Scholar] [CrossRef]
- Iqbal, N.; Akgul, A.; Shah, R.; Bariq, A.; Mossa Al-Sawalha, M.; Ali, A. On Solutions of Fractional-Order Gas Dynamics Equation by Effective Techniques. J. Funct. Spaces 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas Alvaro, H.; Alharthi, M.R. Novel analytical cnoidal and solitary wave solutions of the Extended Kawahara equation. Chaos Solitons Fractals 2021, 147, 110965. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas Alvaro, H.; Alharthi, M.R. On the dissipative extended Kawahara solitons and cnoidal waves in a collisional plasma: Novel analytical and numerical solutions. Phys. Fluids 2021, 33, 106101. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. New solitary wave solutions to the Kuramoto-Sivashinsky and the Kawahara equations. Appl. Math. Comput. 2006, 182, 1642–1650. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. Two-mode fifth-order KdV equations: Necessary conditions for multiple-soliton solutions to exist. Nonlinear Dyn. 2017, 87, 1685–1691. [Google Scholar] [CrossRef]
- Alesemi, M.; Iqbal, N.; Botmart, T. Novel Analysis of the Fractional-Order System of Non-Linear Partial Differential Equations with the Exponential-Decay Kernel. Mathematics 2022, 10, 615. [Google Scholar] [CrossRef]
- Goswami, A.; Singh, J.; Kumar, D. Numerical simulation of fifth order KdV equations occurring in magneto-acoustic waves. Ain Shams Eng. J. 2018, 9, 2265–2273. [Google Scholar] [CrossRef]
- Miansari, M.O.; Miansari, M.E.; Barari, A.; Ganji, D.D. Application of He’s Variational Iteration Method to nonlinear Helmholtz and fifth-order KdV equations. J. Appl. Math.-Stat. Inform. 2009, 5, 5–19. [Google Scholar]
- Abbasbandy, S.; Zakaria, F.S. Soliton solutions for the fifth-order KdV equation with the homotopy analysis method. Nonlinear Dyn. 2008, 51, 83–87. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Solitons and periodic solutions for the fifth-order KdV equation. Appl. Math. Lett. 2006, 19, 1162–1167. [Google Scholar] [CrossRef] [Green Version]
- Darvishi, M.T.; Khani, F. Numerical and explicit solutions of the fifth-order Korteweg-de Vries equations. Chaos Solitons Fractals 2009, 39, 2484–2490. [Google Scholar] [CrossRef]
- Hu, W.-P.; Deng, Z.-C. Multi-symplectic method for generalized fifth-order KdV equation. Chin. Phys. B 2008, 17, 3923. [Google Scholar]
- Zhang, S. Application of Exp-function method to a KdV equation with variable coefficients. Phys. Lett. A 2007, 365, 448–453. [Google Scholar] [CrossRef]
- Ozis, T.; Yildirim, A. Traveling wave solution of Korteweg-de Vries equation using He’s homotopy perturbation method. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 239–242. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for bifurcation of nonlinear problems. Int. J. Nonlinear Sci. Numer. Simul. 2005, 6, 207–208. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phys. Lett. A 2006, 350, 87–88. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Aljoufi, M.D.; Chung, J.D. An efficient approach for solution of fractional-order Helmholtz equations. Adv. Differ. Equ. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Mahgoub, M.; Sedeeg, A. A Comparative Study for Solving Nonlinear Fractional Heat -Like Equations via Elzaki Transform. Br. J. Math. Comput. Sci. 2016, 19, 1–12. [Google Scholar] [CrossRef]
- Chu, Y.M.; Shah, N.A.; Ahmad, H.; Chung, J.D.; Khaled, S.M. A comparative study of semi-analytical methods for solving fractional-order cauchy reaction-diffusion equation. Fractals 2021, 29, 2150143. [Google Scholar] [CrossRef]
- Singh, P.; Sharma, D. Comparative study of homotopy perturbation transformation with homotopy perturbation Elzaki transform method for solving nonlinear fractional PDE. Nonlinear Eng. 2019, 9, 60–71. [Google Scholar] [CrossRef]
- Aboodh, K.S. Application of new transform “Aboodh Transform” to partial differential equations. Glob. J. Pure Appl. Math. 2014, 10, 249–254. [Google Scholar]
- Aboodh, K.S. Solving fourth order parabolic PDE with variable coefficients using Aboodh transform homotopy perturbation method. Pure Appl. Math. J. 2015, 4, 219–224. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Baleanu, D.; Alqurashi, M.M. New aspects of ZZ transform to fractional operators with Mittag-Leffler kernel. Front. Phys. 2020, 8, 352. [Google Scholar] [CrossRef]
- Riabi, L.; Belghaba, K.; Cherif, M.H.; Ziane, D. Homotopy perturbation method combined with ZZ transform to solve some nonlinear fractional differential equations. Int. J. Anal. Appl. 2019, 17, 406–419. [Google Scholar]
- Zafar, Z.U.A. Application of ZZ transform method on some fractional differential equations. Int. J. Adv. Eng. Glob. Technol. 2016, 4, 1355–1363. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical Investigation of Fractional-Order Korteweg–De-Vries-Type Equations under Atangana–Baleanu–Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry 2022, 14, 739. https://doi.org/10.3390/sym14040739
Shah NA, Alyousef HA, El-Tantawy SA, Shah R, Chung JD. Analytical Investigation of Fractional-Order Korteweg–De-Vries-Type Equations under Atangana–Baleanu–Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry. 2022; 14(4):739. https://doi.org/10.3390/sym14040739
Chicago/Turabian StyleShah, Nehad Ali, Haifa A. Alyousef, Samir A. El-Tantawy, Rasool Shah, and Jae Dong Chung. 2022. "Analytical Investigation of Fractional-Order Korteweg–De-Vries-Type Equations under Atangana–Baleanu–Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid" Symmetry 14, no. 4: 739. https://doi.org/10.3390/sym14040739







