Investigation on the Formation and Evolution Mechanism of Flow-Resistance-Increasing Vortex of Aero-Engine Labyrinth Based on Entropy Generation Analysis
Abstract
:1. Introduction
2. The Formation Mechanism of the FRIV at the Tip of the Labyrinth Tooth
2.1. Definition of Flow-Resistance-Increasing Vortices
2.2. Theoretical of Entropy Generation
3. Simulation Model and Verification of Labyrinth
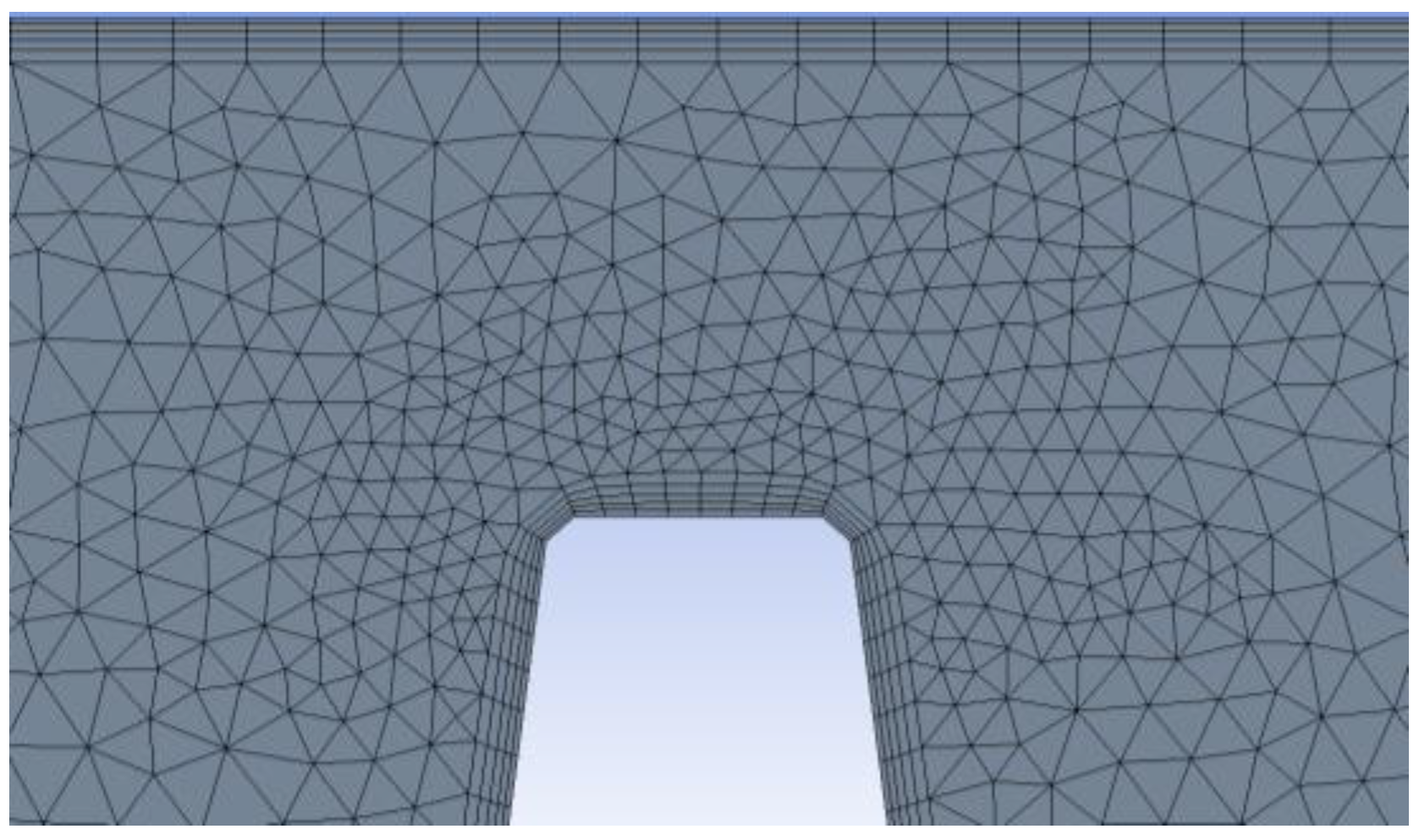
3.1. Numerical Approach and Computational Meshing
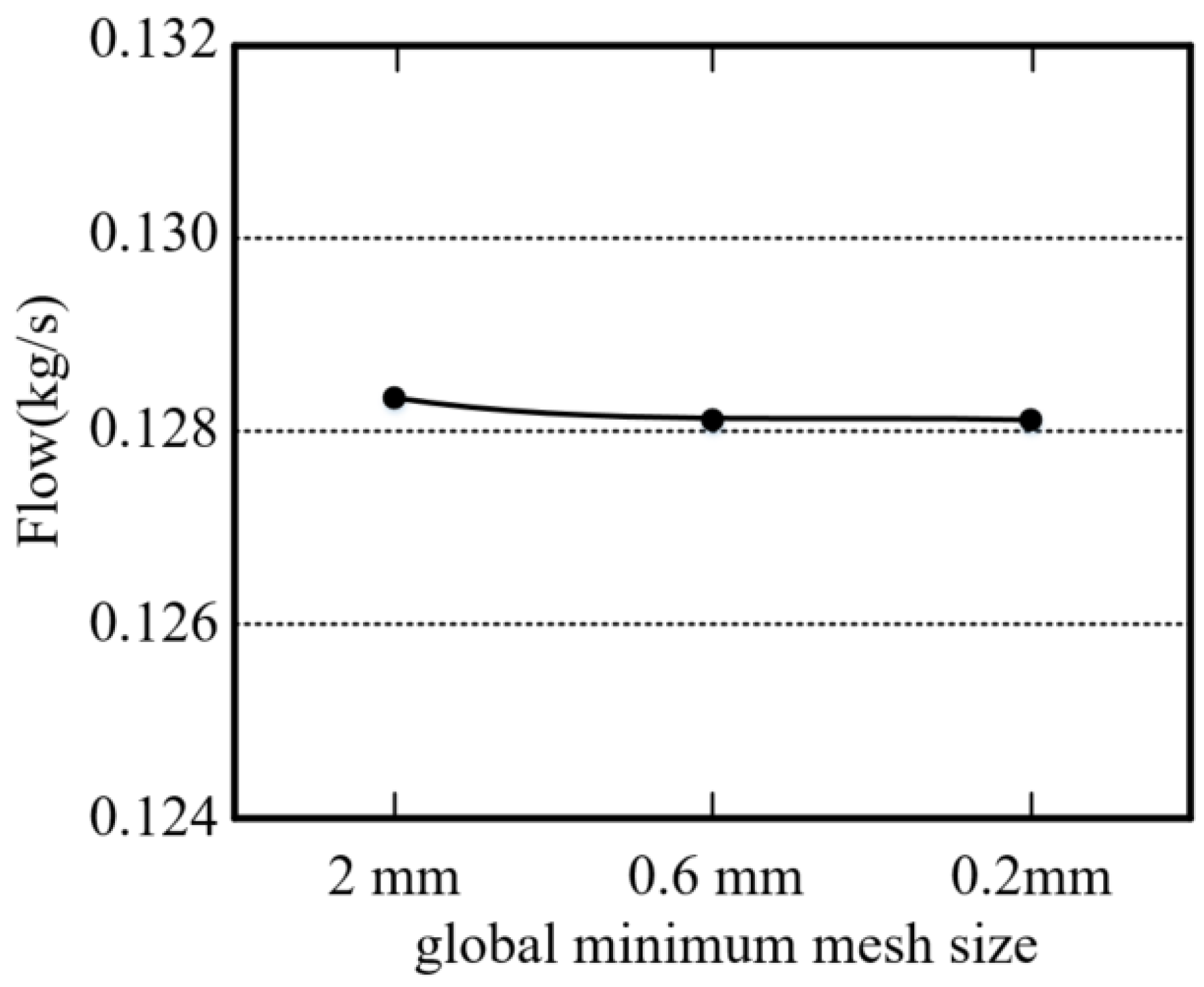
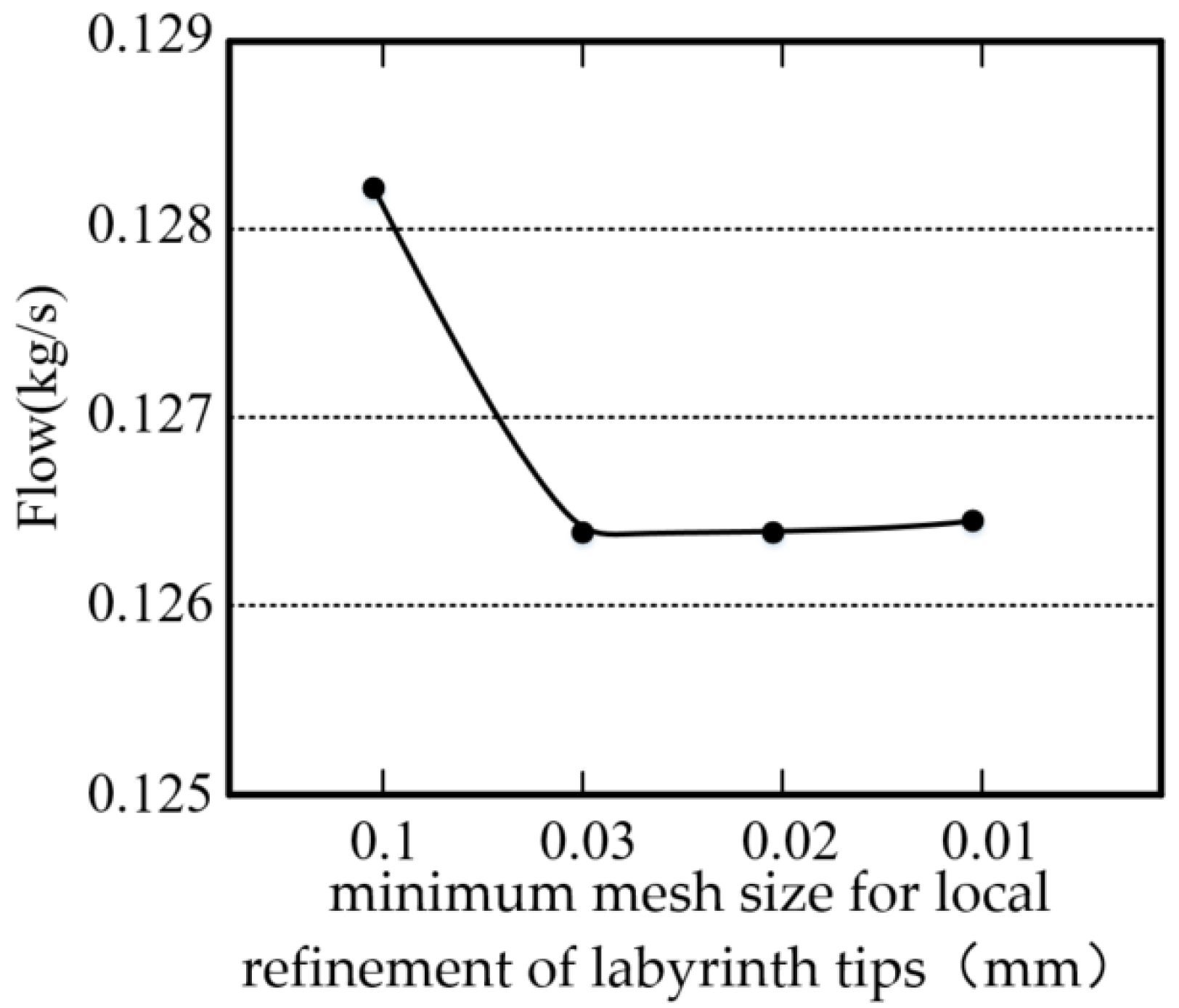
3.2. Boundary Conditions and Mesh Independent
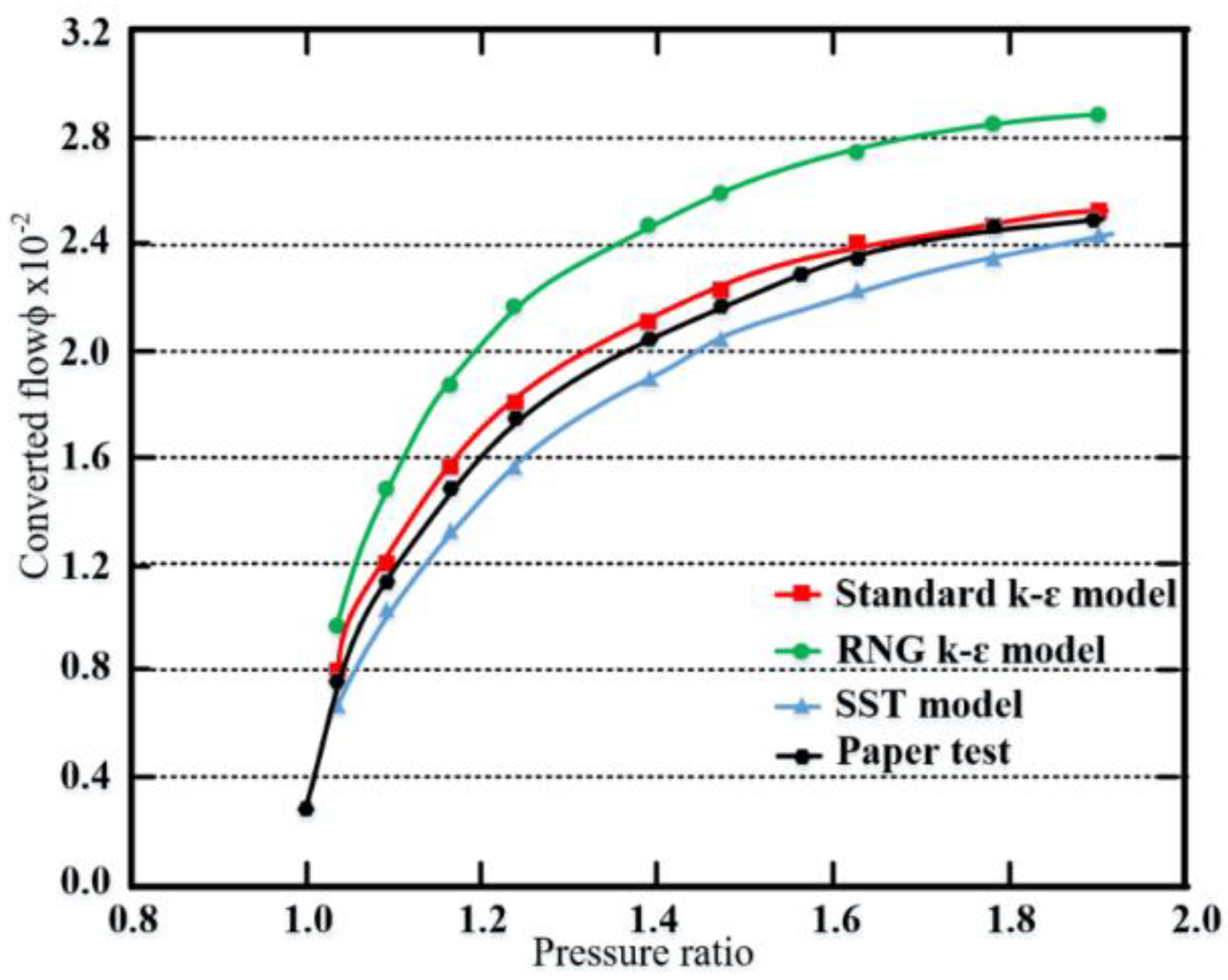
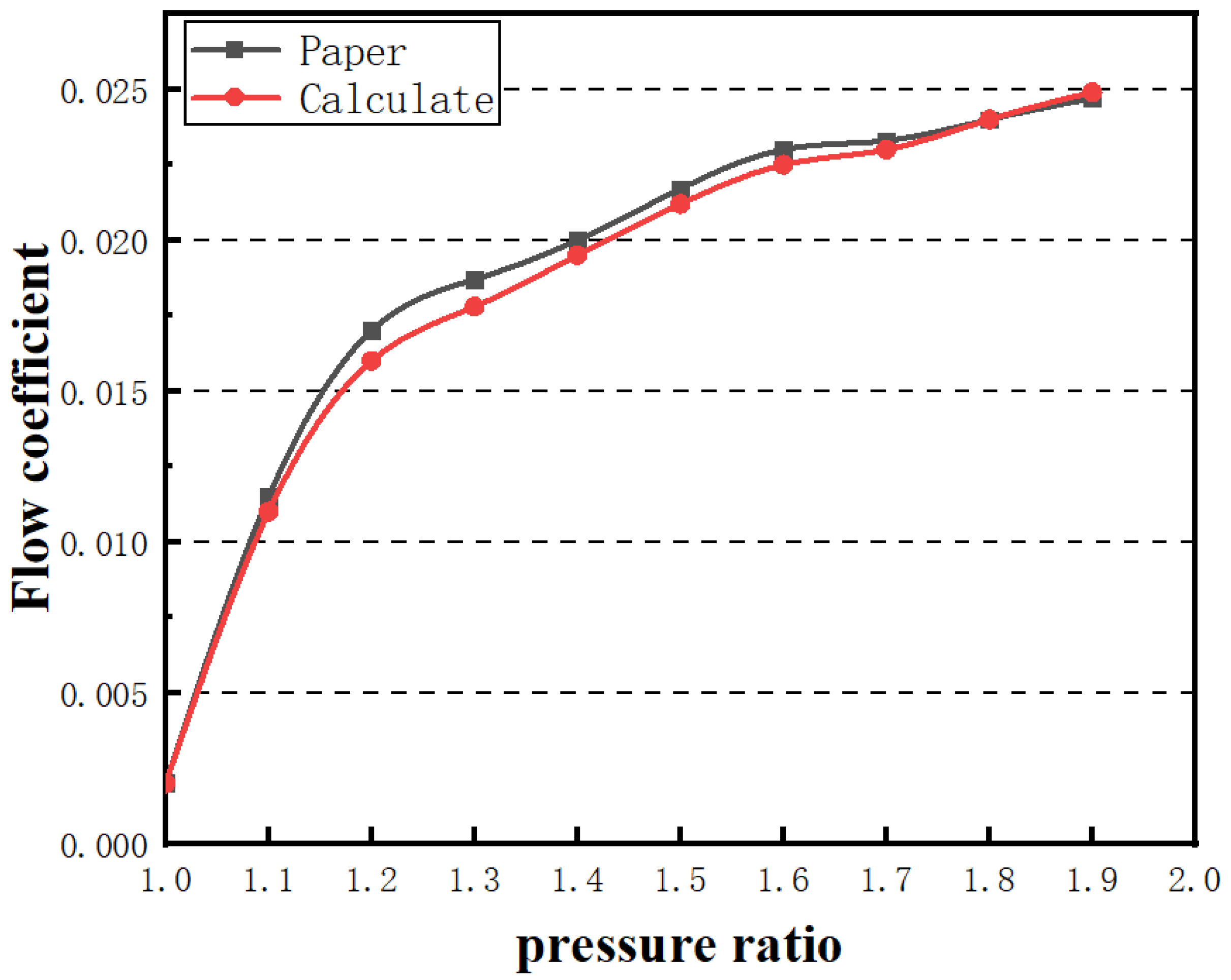
3.3. Model Checking
4. Results and Discussion
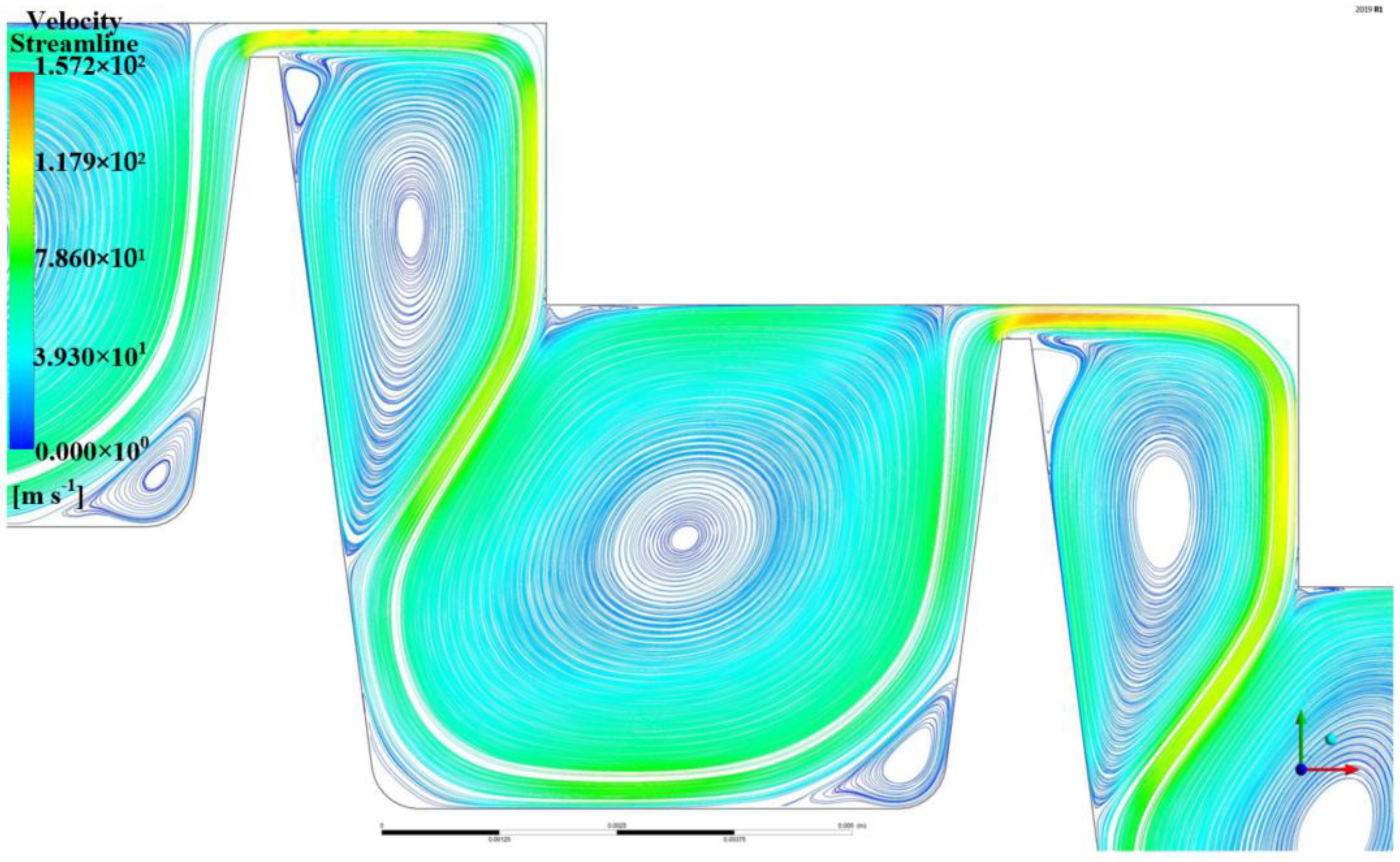
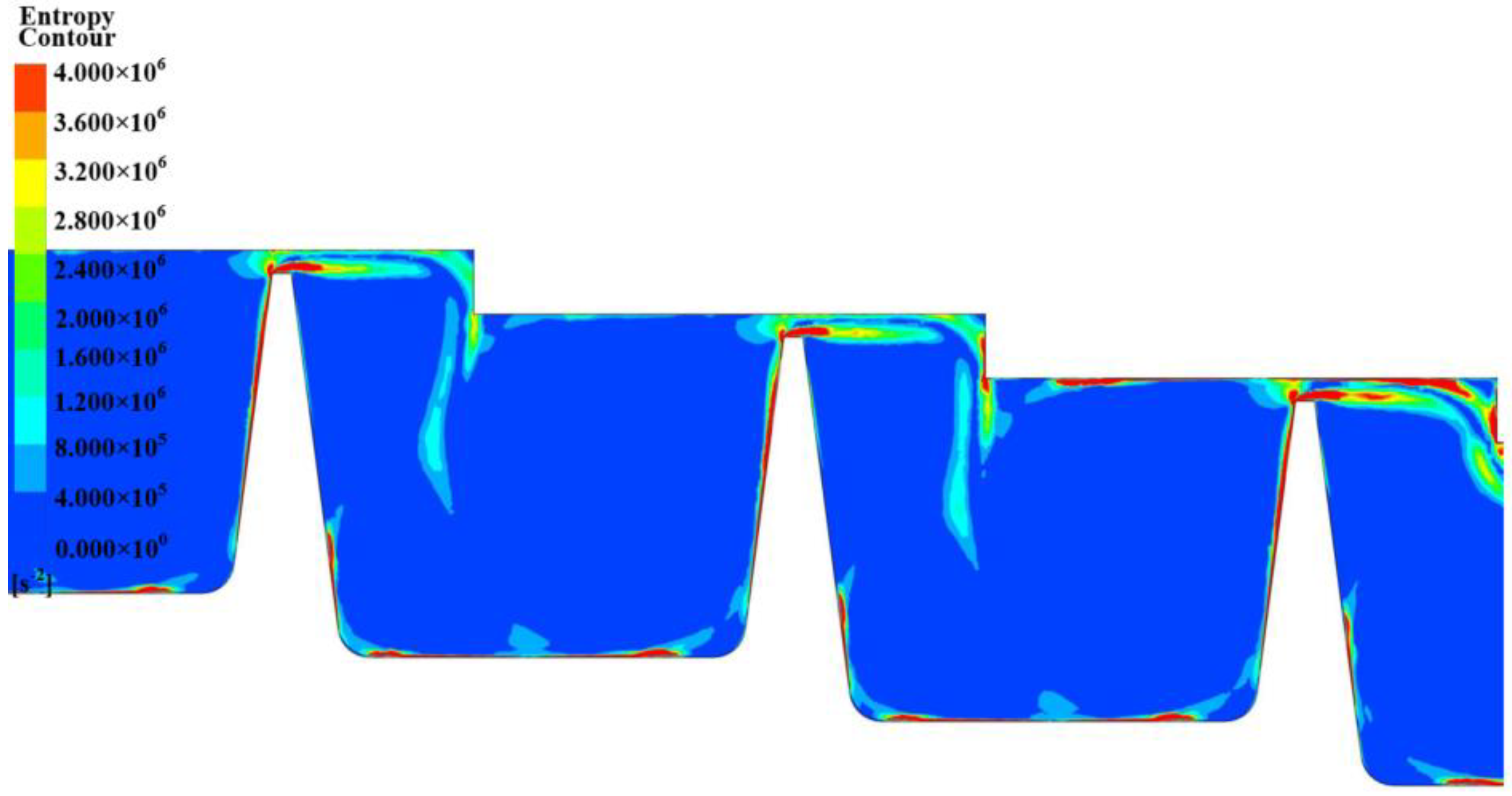
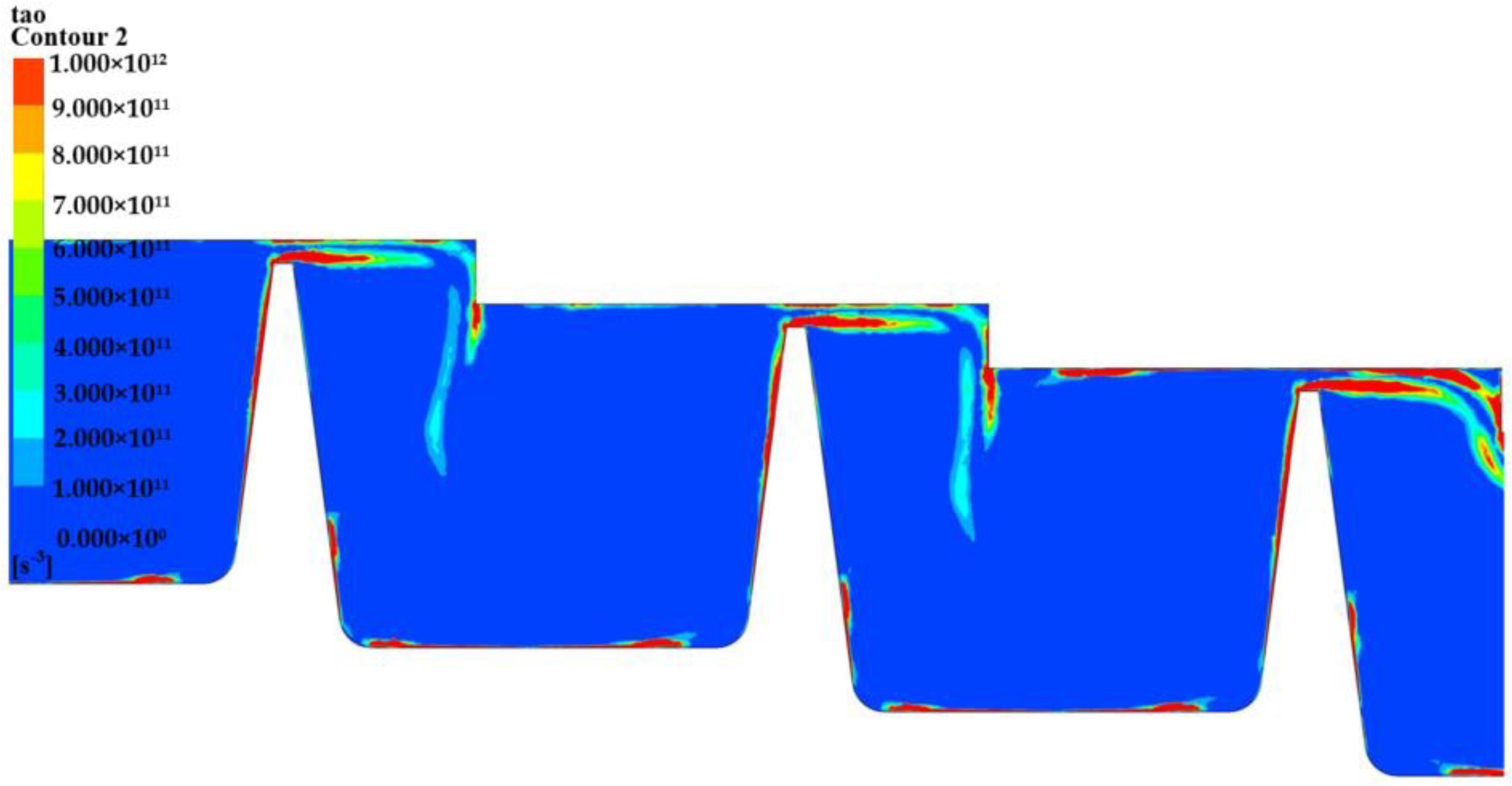
4.1. The Formation Mechanism of FRIV
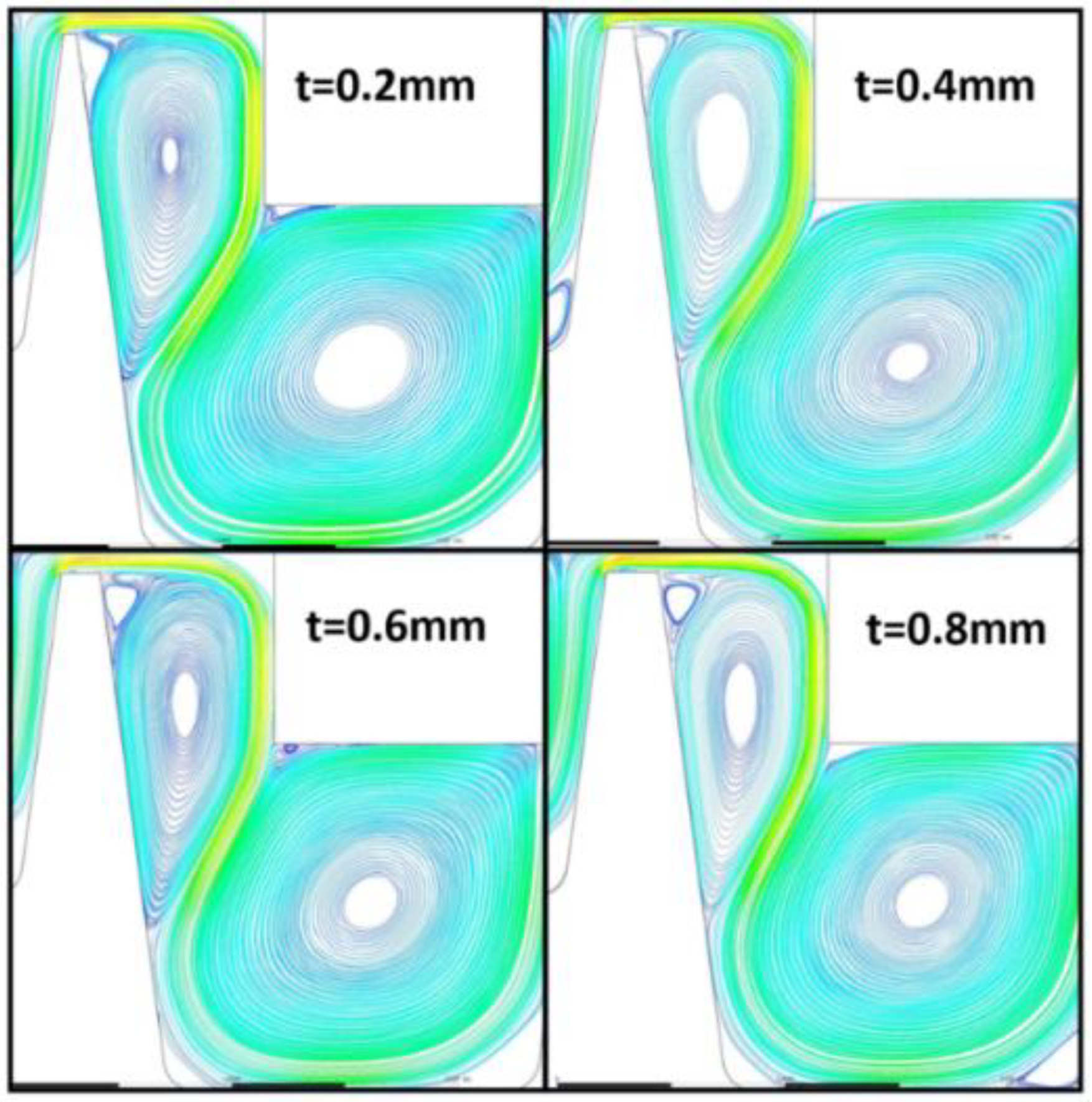
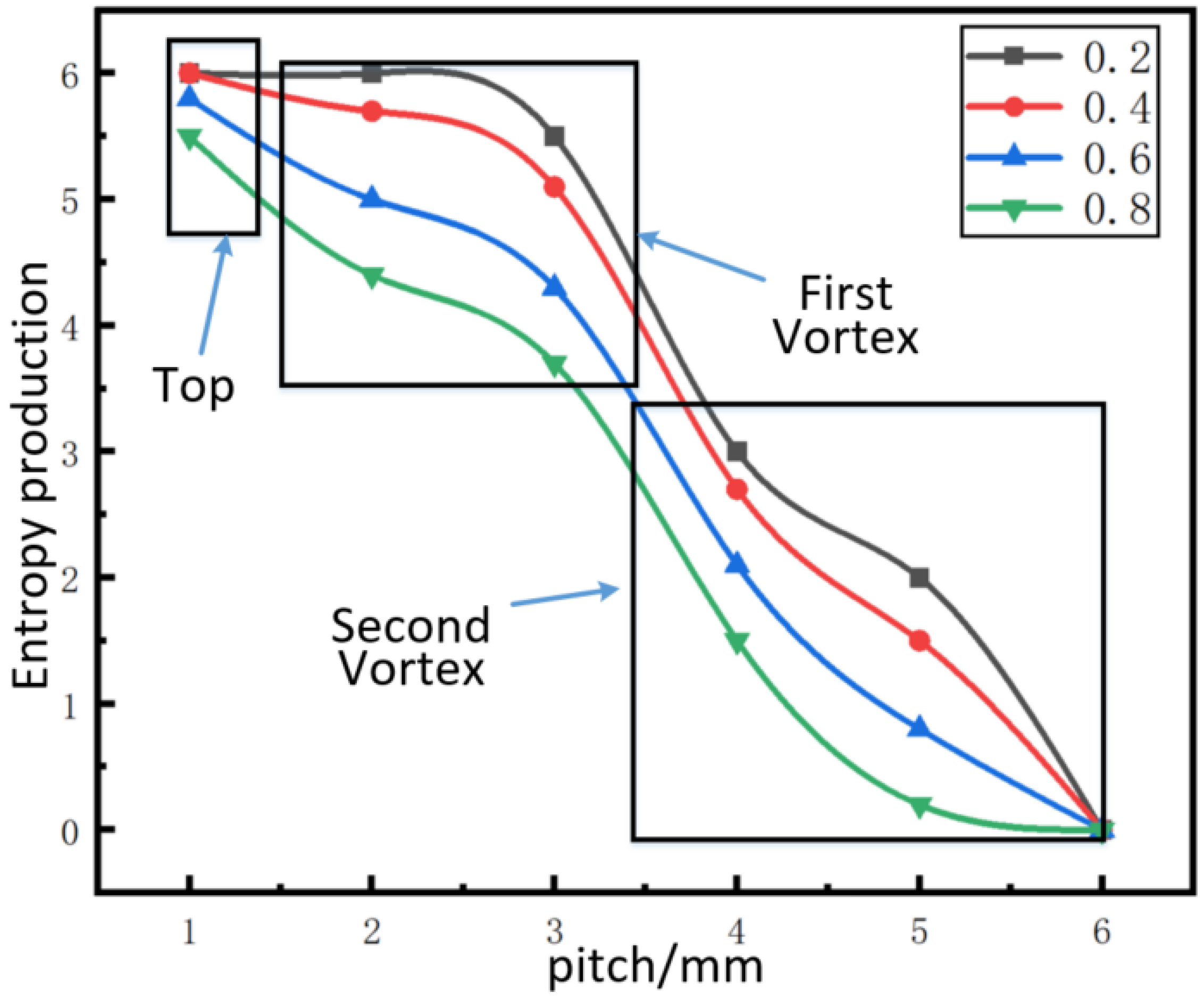
4.2. Influence of Labyrinth Tip width Variation on Entropy Generation
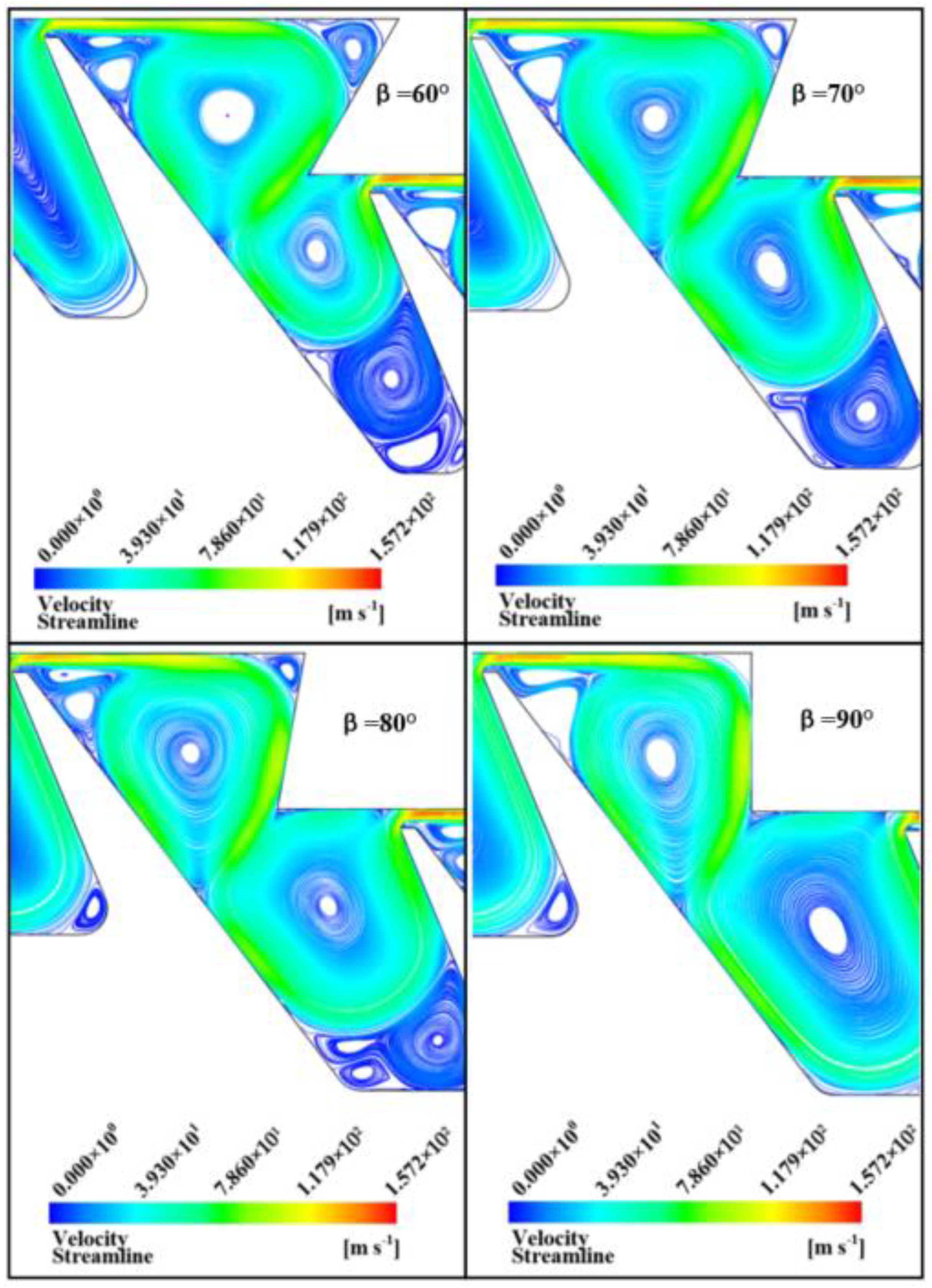
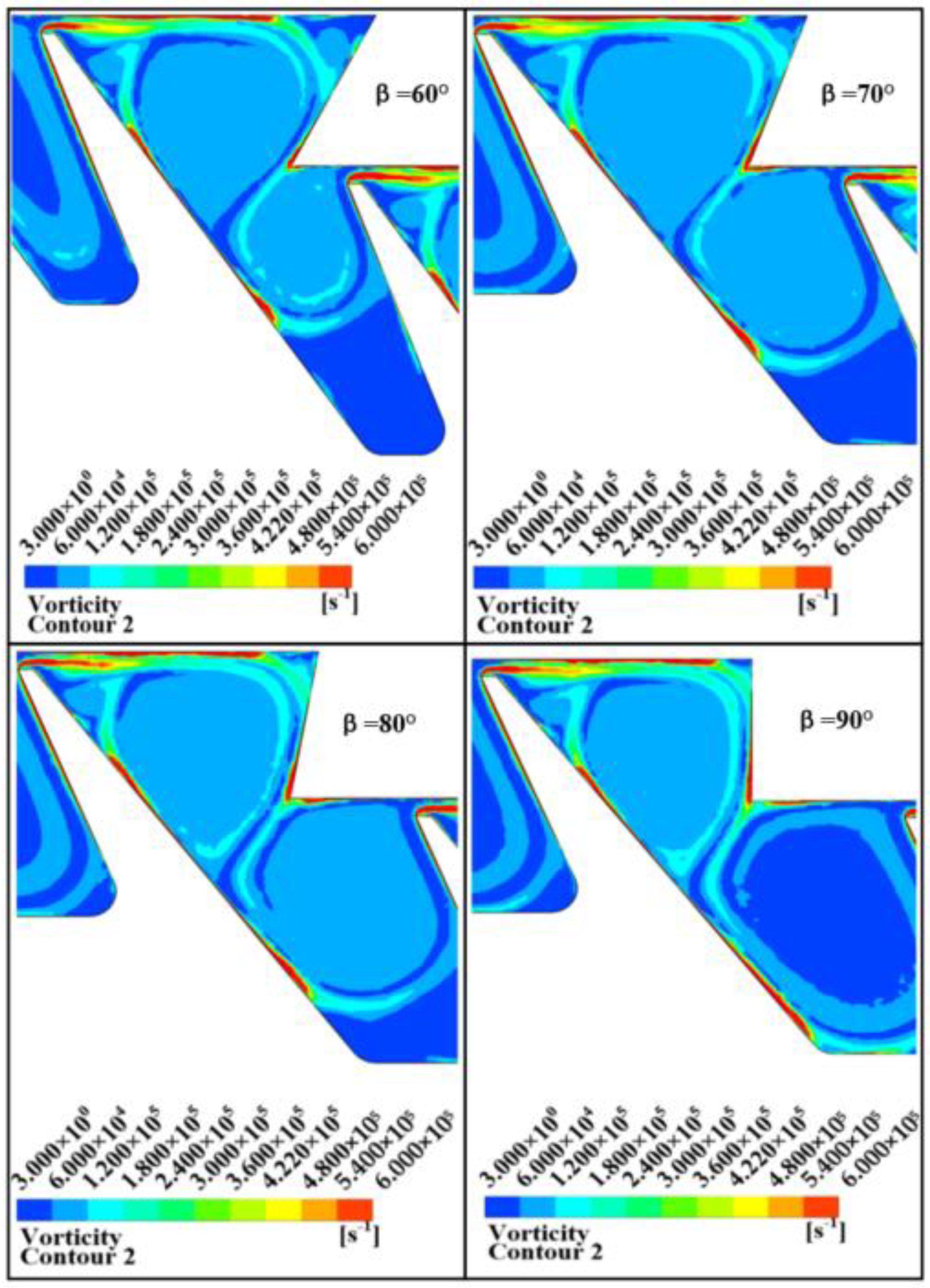
4.3. Influence of Labyrinth Inclination on Entropy Generation
4.4. Influence of Step Inclination Angle Change on Entropy Generation
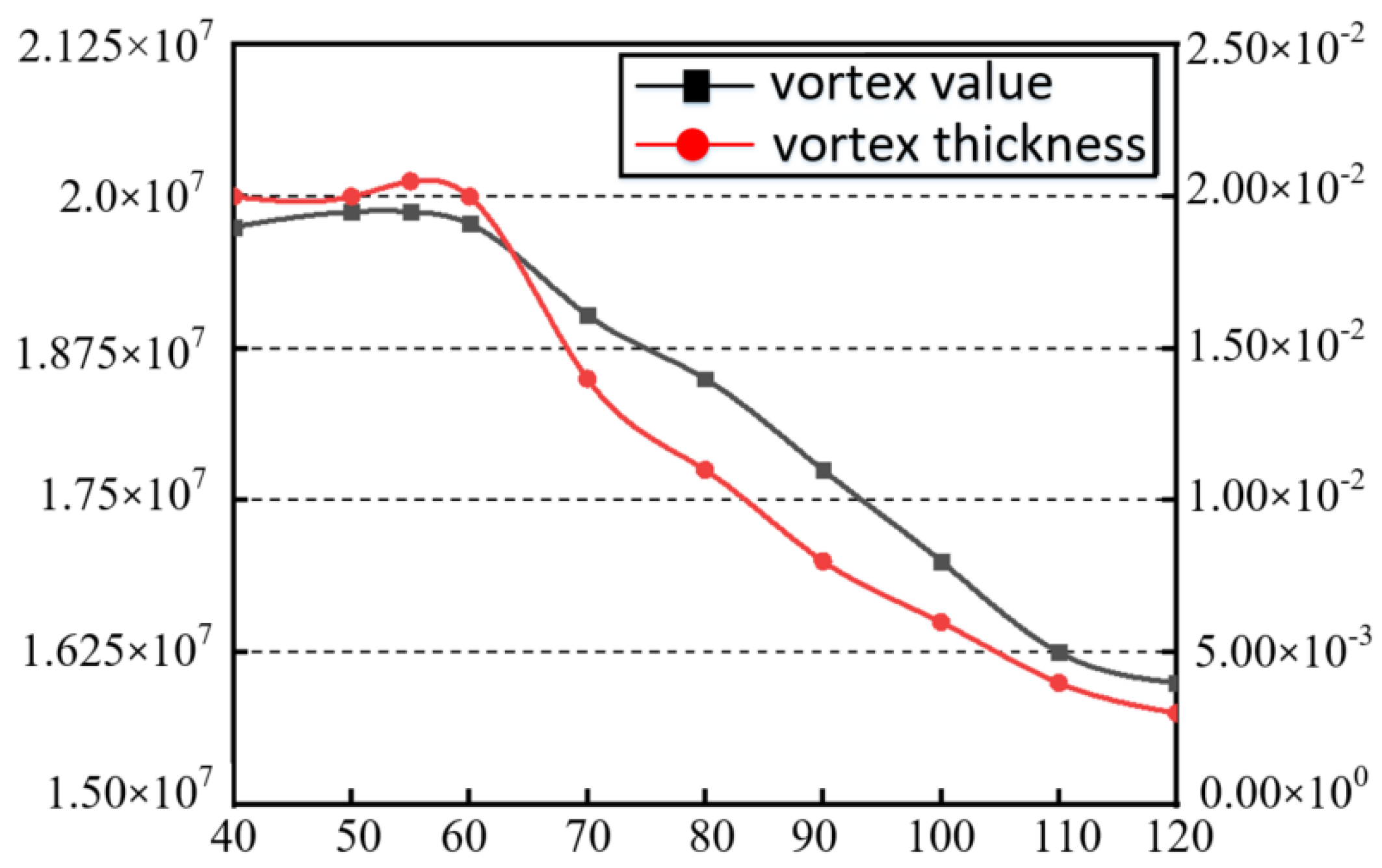
4.5. Influence of FRIV Strength on Leakage
5. Conclusions
- (1)
- The relative dissipative intensity distribution was the same as the vorticity distribution, and there was a region with a large correlation coefficient at the top of the tooth, where the vortex was stronger and the dissipation effect was stronger.
- (2)
- When the labyrinth width was small, the flow direction changed rapidly after the gas in the upper labyrinth cavity flowed into the labyrinth tip, which formed a FRIV at the labyrinth tip. With the increase of tooth width, the direction of fluid velocity was gradually reversed. In addition, the entropy generation and the resistance increase effect were weakened. When the labyrinth teeth were inclined forward, the FRIV on the top of the tooth increased significantly, and the entropy generation increased, almost occupying the entire labyrinth clearance. When the labyrinth teeth were inclined backward, the FRIV on the top of the tooth gradually weakened. As the inclination angle of the step decreased, the vortex at the inner step of the labyrinth squeezed toward the tooth tip and increased. In addition, the FRIV was enhanced, the entropy generation increased, and the sealing effect was strengthened.
- (3)
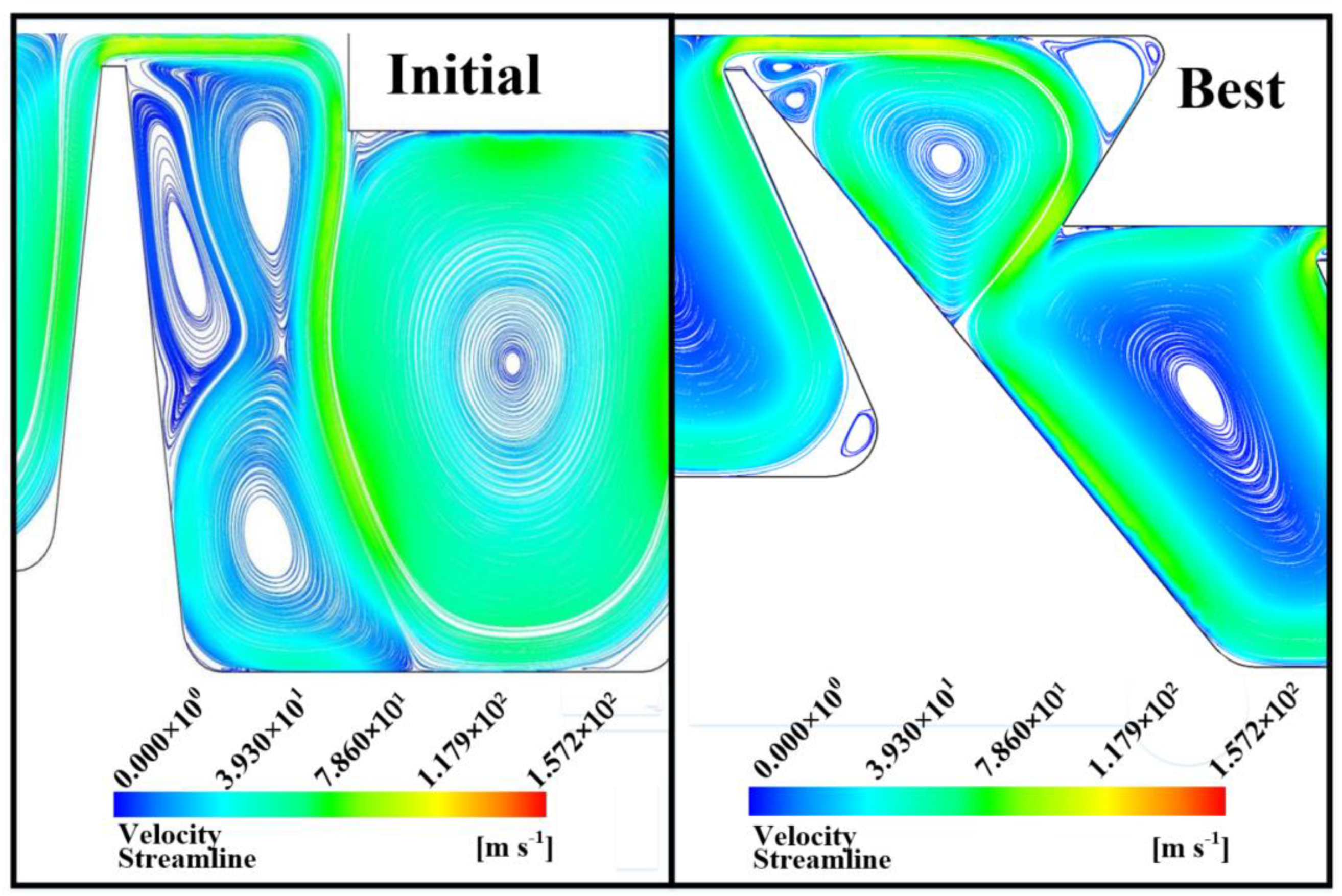
- By selecting reasonable labyrinth geometric parameters, the labyrinth tip velocity gradient and throttling effect can be enhanced, and the (ω∙∇)V and ω(∇∙V) terms in the vorticity transport equation can be increased, which can strengthen FRIV and reduce leakage. The results of this research show that the reasonable labyrinth parameters can reduce leakage by 22%. Therefore, the method of reducing leakage proposed in this paper is effective.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ludwig, L.P.; Johnson, R.L. Sealing Technology for Aircraft Gas Turbine Engines; AIAA: Reston, VA, USA, 2000. [Google Scholar]
- Guo, H.; Feng, Q. Experiment on flow characteristic in rotating labyrinth with consideration of clearance change. J. Aerosp. Power 2018, 33, 1779–1786. [Google Scholar]
- Hanzlik, H.J. Labyrinth Packing. US1831242A, 10 November 1931. [Google Scholar]
- Vermes, G.Z. A Fluid Mechanics Approach to the Labyrinth Seal Leakage Problem. J. Eng. Gas Turbines Power 1960, 83, 161. [Google Scholar] [CrossRef]
- Zimmermann, H.; Wolff, K.H. Air System Correlations: Part 1—Labyrinth Seals. In Proceedings of the Asme International Gas Turbine & Aeroengine Congress & Exhibition, Stockholm, Sweden, 2 June 1998. [Google Scholar]
- Nayak, K.C. Effect of Rotation on Leakage and Windage Heating in Labyrinth Seals With Honeycomb Lands. J. Eng. Gas Turbines Power 2020, 142, 081001. [Google Scholar] [CrossRef]
- Lee, S.I.; Kang, Y.J. Basic Research Trends on Labyrinth Seal of Gas Turbine. KSFM J. Fluid Mach. 2020, 23, 32–39. [Google Scholar] [CrossRef]
- Soemarwoto, B.I.; Kok, J.C. Performance Evaluation of Gas Turbine Labyrinth Seals Using Computational Fluid Dynamics. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; Volume 4. [Google Scholar]
- Rhode, D.L.; Demko, J.A. Prediction of Incompressible Flow in Labyrinth Seals. J. Fluids Eng. 1986, 108, 19–25. [Google Scholar] [CrossRef]
- Demko, J.A.; Morrison, G.L.; Rhode, D.L. The Prediction and Measurement of Incompressible Flow in a Labyrinth Seal. J. Eng. Gas Turbines Power 1989, 111, 189–195. [Google Scholar] [CrossRef]
- Stoff, H. Incompressible flow in a labyrinth seal. J. Fluid Mech. 2006, 100, 817–829. [Google Scholar] [CrossRef]
- Rhode, D.L.; Sobolik, S.R. Simulation of Subsonic Flow Through a Generic Labyrinth Seal. J. Eng. Gas Turbines Power 1985, 108, 429–437. [Google Scholar] [CrossRef]
- Rhode, D.L.; Hibbs, R.I. New model for flow over open cavities. I-Model development. J. Propuls. Power 1992, 8, 392–397. [Google Scholar] [CrossRef]
- Rhode, D.L.; Hibbs, R.I. New model for flow over open cavities. II-Assessment for seal leakage. J. Propuls. Power 1971, 8, 398–402. [Google Scholar] [CrossRef]
- Demko, J.A.; Morrison, G.L. Effect of shaft rotation on the incompressible flow in a labyrinth seal. J. Propuls. Power 1990, 6, 171–176. [Google Scholar] [CrossRef]
- Rapisarda, A.; Desando, A. Rounded Fin Edge and Step Position Effects on Discharge Coefficient in Rotating Labyrinth Seals. J. Turbomach. 2016, 138, 011005. [Google Scholar] [CrossRef]
- Scherer, T.; Waschka, W. Numerical Predictions of High-Speed Rotating Labyrinth Seal Performance: Influence of Rotation on Power Dissipation and Temperature Rise. In International Symposium on Heat Transfer in Turbomachinery; Begell House Inc.: Danbury, CT, USA, 1994. [Google Scholar]
- Nayak, K.; Ansari, A. The Effect of Rub-Grooves on Leakage and Windage Heating in Labyrinth Seals with Honeycomb Lands. In Proceedings of the Aiaa/Asme/Sae/Asee Joint Propulsion Conference & Exhibit, San Jose, CA, USA, 14–17 July 2013. [Google Scholar]
- Musthafa, K.C. The Effects of Tooth Tip Wear and its Axial Displacement in Rub-Grooves on Leakage and Windage Heating of Labyrinth Seals with Honeycomb Lands. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit (AIAA), Nashville, TN, USA, 8–11 July 2007. [Google Scholar]
- Kaliraj, K.R.; Yepuri, G.B. Parametric Studies on Gas Turbine Labyrinth Seal for the Secondary Air Flow Optimization at Static and Rotating Conditions. In Proceedings of the ASME 2019 Gas Turbine India Conference, Chennai, India, 5–6 December 2019. [Google Scholar]
- Desando, A.; Rapisarda, A. Numerical Analysis of Honeycomb Labyrinth Seals:Cell Geometry and Fin Tip Thickness Impact on the Discharge Coefficient. In Proceedings of the ASME Turbo Expo 2015, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Ganine, V.; Chew, J.W. Transient Aero-Thermo-Mechanical Multidimensional Analysis of a High Pressure Turbine Assembly Through a Square Cycle. J. Eng. Gas Turbines Power 2021, 143, 081008. [Google Scholar] [CrossRef]
- Childs, D.W. Turbomachinery Rotordynamics: Phenomena, Modeling, and Analysis. In Turbomachinery Rotordynamics Phenomena Modeling and Analysis; John Wiley and Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Wittig, S.L.; Dörr, K.L. Scaling Effects on Leakage Losses in Labyrinth Seals. J. Eng. Gas Turbines Power 1983, 105, 305–309. [Google Scholar] [CrossRef]
- Denecke, J.; Dullenkopf, K. Experimental Investigation of the Total Temperature Increase and Swirl Development in Rotating Labyrinth Seals. In Proceedings of the Asme Turbo Expo: Power for Land, Sea, & Air, Reno, NV, USA, 6–9 June 2005. [Google Scholar]
- Mcgreehan, W.F.; Ko, S.H. Power Dissipation in Smooth and Honeycomb Labyrinth Seals. In Proceedings of the ASME 1989 International Gas Turbine and Aeroengine Congress and Exposition, Toronto, ON, Canada, 4–8 June 1989. [Google Scholar]
- Willenborg, K.; Kim, S. Effects of Reynolds Number and Pressure Ratio on Leakage Loss and Heat Transfer in a Stepped Labyrinth Seal. J. Turbomach. 2001, 123, 815. [Google Scholar] [CrossRef]
- Stocker, H.L.; Cox, D.M. Aerodynamic Performance of Conventional and Advanced Design Labyrinth Seals with Solid-Smooth Abradable, and Honeycomb Lands; NASA: Washington, DC, USA, 1977; pp. 1–272.
- Rhode, D.L.; Adams, R.G. Rub-Groove Width and Depth Effects on Flow Predictions for StraightThrough Labyrinth Seals. J. Tribol. 2004, 126, 781–787. [Google Scholar] [CrossRef]
- Millward, J.A.; Edwards, M.F. Windage Heating of Air Passing Through Labyrinth Seals. J. Turbomach. 1996, 118, 414–419. [Google Scholar] [CrossRef]
- Waschka, W.; Wittig, S. Influence of High Rotational Speeds on the Heat Transfer and Discharge Coefficients in Labyrinth Seals. J. Turbomach. 1990, 114, 462–468. [Google Scholar] [CrossRef]
- Braun, E.; Dullenkopf, K. Optimization of Labyrinth Seal Performance Combining Experimental, Numerical and Data Mining Methods. In Proceedings of the Asme Turbo Expo: Turbine Technical Conference & Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Min, S.H.; Soo, I.L. Effect of clearance and Cavity Geometries on Leakage Performance of a Stepped Labyrinth Seal. Processes 2020, 8, 1496. [Google Scholar]
- Khan, N.S.; Shah, Q. Mechanical aspects of Maxwell nanofluid in dynamic system with irreversible analysis. ZAMM J. Appl. Math. Mech. 2021, 101, e202000212. [Google Scholar] [CrossRef]
- Ramzan, M.; Khan, N.S. Mechanical analysis of non-Newtonian nanofluid past a thin needle with dipole effect and entropic characteristics. Sci. Rep. 2021, 11, 19378. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Lifeng, H. Investigation on transient dynamics of rotor system in air turbine starterbased on magnetic reduction gear. J. Adv. Manuf. Sci. Technol. 2021, 1, 2021009. [Google Scholar] [CrossRef]
- Jiang, W.; Bin, W. A Novel Blade Tip Clearance Measurement Method Based on Event Capture Technique. Mech. Syst. Signal Process. 2020, 139, 106626. [Google Scholar]
- Weinberger, T.; Dullenkopf, K. Influence of Honeycomb Facings on the Temperature Distribution of Labyrinth Seals. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar]
- Shuiting, D.; Ziyao, W. Probabilistic failure risk assessment for aeroengine disks considering a transient process. Aerosp. Sci. Technol. 2018, 78, 696–707. [Google Scholar]
- Ding, S.; Che, W. Application of entropy equation in the judgement of flow direction in transient air system. J. Aerosp. Power 2017, 32, 2305–2313. [Google Scholar]
- Bertin, J.; Cummings, R. eBook Instant Access—for Aerodynamics for Engineers, International Edition; Pearson: London, UK, 2013. [Google Scholar]
- Allahverdyan, A.; Nieuwenhuizen, T. Steady adiabatic state: Its thermodynamics, entropy production, energy dissipation, and violation of Onsager relations. Phys. Rev. E 2000, 62, 845. [Google Scholar] [CrossRef]
- Denecke, J.; Frber, J. Dimensional Analysis and Scaling of Rotating Seals. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air. 2005, Reno, NV, USA, 6–9 June 2005. [Google Scholar]
- Dagan, A.; Arieli, R. Solutions of the vorticity transport equation at high Reynolds numbers. In Proceedings of the Thirteenth International Conference on Numerical Methods in Fluid Dynamics, Rome, Italy, 6–10 July 1992. [Google Scholar]
- Koh, Y.M. Vorticity and viscous dissipation in an incompressible flow. KSME J. 1994, 8, 35–42. [Google Scholar] [CrossRef]
- Barati, R. The numerical solution of the vorticity transport equation. In Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics, Paris, France, 7 July 1972. [Google Scholar]
- ANSYS Inc. ANSYS CFX 19.0; ANSYS Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Yu, Z.; Longtao, S. Numerical and Experimental Investigation on Dynamic performance of Bump Foil Journal Bearing Based on Journal Orbit. Chin. J. Aeronaut. 2021, 34, 586–600. [Google Scholar]
- ANSYS Inc. ANSYS CFX-Solver Modeling Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Prasad, B.V.S.S.; Manavalan, V.S. Computational and Experimental Investigations of Straight-Through Labyrinth Seals. In Proceedings of the Asme International Gas Turbine & Aeroengine Congress & Exhibition, Orlando, FL, USA, 2 June 1997. [Google Scholar]
- Yu, Z.; Tong, X. Digital-twin-driven geometric optimization of centrifugal impeller with free-form blades for five-axis flank milling. J. Manuf. Syst. 2021, 58, 22–35. [Google Scholar]
- Yu, Z.; Yue, S. Parametric Modeling Method for Integrated Design and Manufacturing of Radial Compressor Impeller. Int. J. Adv. Manuf. Technol. 2020, 10, 1178. [Google Scholar]








| Geometric Parameters | Symbol | Initial Value | Unit |
|---|---|---|---|
| Step height | H | 2 | mm |
| Teeth pitch | L | 7 | mm |
| Tooth height | h | 5 | mm |
| Tooth tip width | t | 0.3 | mm |
| Labyrinth inclination angle | α | 90 | degrees |
| Angle between face teeth | θ | 15 | degrees |
| Seal clearance | c | 0.36 | mm |
| Tooth to step distance | b | 2 | mm |
| Step inclined angle | β | 90 | degrees |
| Root rounding of steps | R1 | 0 | mm |
| Root rounding on pressure side | RL | 0.5 | mm |
| Fin tip fillet | RR | 0.5 | mm |
| Boundary Conditions | Value | Unit |
|---|---|---|
| Outlet pressure | 101,325 | Pa |
| Import and export pressure ratio | 1.5 | |
| Inlet temperature | 300 | K |
| Outlet temperature | 300 | K |
| Geometric Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Seal clearance | c | 0.36 | mm |
| Tooth height | h | 6 | mm |
| Teeth pitch | L | 6 | mm |
| Tooth tip width | t | 0.25 | mm |
| SE. NU. | Pressure Ratio | |||||||
|---|---|---|---|---|---|---|---|---|
| Test Results | Deviation | Deviation | Deviation | |||||
| 1 | 1.0357 | 0.7491 | 0.7813 | 4.29% | 0.9567 | 27.71% | 0.6659 | −11.11% |
| 2 | 1.0886 | 1.1621 | 1.2088 | 4.02% | 1.4731 | 26.77% | 1.0246 | −11.83% |
| 3 | 1.1598 | 1.5018 | 1.5467 | 2.99% | 1.8720 | 24.65% | 1.3265 | −11.67% |
| 4 | 1.2391 | 1.7480 | 1.7983 | 2.88% | 2.1557 | 23.32% | 1.5739 | −9.96% |
| 5 | 1.3878 | 2.0326 | 2.1025 | 3.44% | 2.4773 | 21.88% | 1.8981 | −6.62% |
| 6 | 1.4717 | 2.1616 | 2.2168 | 2.55% | 2.5940 | 20.00% | 2.0339 | −5.91% |
| 7 | 1.6290 | 2.3515 | 2.3816 | 1.28% | 2.7448 | 16.72% | 2.2314 | −5.11% |
| 8 | 1.7805 | 2.4116 | 2.4515 | 1.65% | 2.8365 | 17.62% | 2.3565 | −2.28% |
| 9 | 1.8974 | 2.4495 | 2.5106 | 2.50% | 2.8872 | 17.87% | 2.4371 | −0.50% |
| Geometrical Parameters | Symbol | Initial Value | Unit |
|---|---|---|---|
| Step height | H | 2 | mm |
| Tooth spacing | L | 7 | mm |
| Tooth height | h | 5 | mm |
| Tooth tip width | t | 0.2 | mm |
| Labyrinth inclination angle | α | 60 | degrees |
| Angle between face teeth | 15 | degrees | |
| Seal clearance | c | 0.36 | mm |
| Tooth to step distance | b | 2 | mm |
| Step inclined angle | β | 60 | degrees |
| Root rounding of steps | R1 | 0 | mm |
| Root rounding on pressure side | RL | 0.5 | mm |
| Fin tip fillet | RR | 0.5 | mm |
| Serial Number | Pressure Ratio | Best | Degree of Reduction | |
|---|---|---|---|---|
| 1 | 1.0357 | 0.7813 | 0.6124 | 21.6% |
| 2 | 1.0886 | 1.2088 | 0.9546 | 21.02% |
| 3 | 1.1598 | 1.5467 | 1.2565 | 18.76% |
| 4 | 1.2391 | 1.7983 | 1.5239 | 15.25% |
| 5 | 1.3878 | 2.1025 | 1.8981 | 12.09% |
| 6 | 1.4717 | 2.2168 | 2.0339 | 10.50% |
| 7 | 1.6290 | 2.3816 | 2.2314 | 8.4% |
| 8 | 1.7805 | 2.4515 | 2.3565 | 5.91% |
| 9 | 1.8974 | 2.5106 | 2.4371 | 4.91% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Ding, S.; Shao, L.; Zhao, S.; Qiu, T.; Zhou, Y.; Zhang, X.; Li, G. Investigation on the Formation and Evolution Mechanism of Flow-Resistance-Increasing Vortex of Aero-Engine Labyrinth Based on Entropy Generation Analysis. Symmetry 2022, 14, 881. https://doi.org/10.3390/sym14050881
Liu X, Ding S, Shao L, Zhao S, Qiu T, Zhou Y, Zhang X, Li G. Investigation on the Formation and Evolution Mechanism of Flow-Resistance-Increasing Vortex of Aero-Engine Labyrinth Based on Entropy Generation Analysis. Symmetry. 2022; 14(5):881. https://doi.org/10.3390/sym14050881
Chicago/Turabian StyleLiu, Xiaojing, Shuiting Ding, Longtao Shao, Shuai Zhao, Tian Qiu, Yu Zhou, Xiaozhe Zhang, and Guo Li. 2022. "Investigation on the Formation and Evolution Mechanism of Flow-Resistance-Increasing Vortex of Aero-Engine Labyrinth Based on Entropy Generation Analysis" Symmetry 14, no. 5: 881. https://doi.org/10.3390/sym14050881







