Digital Integration of LiDAR System Implemented in a Low-Cost FPGA
Abstract
:1. Introduction
2. Principle of the FPGA-TDC
3. TDC Implementation
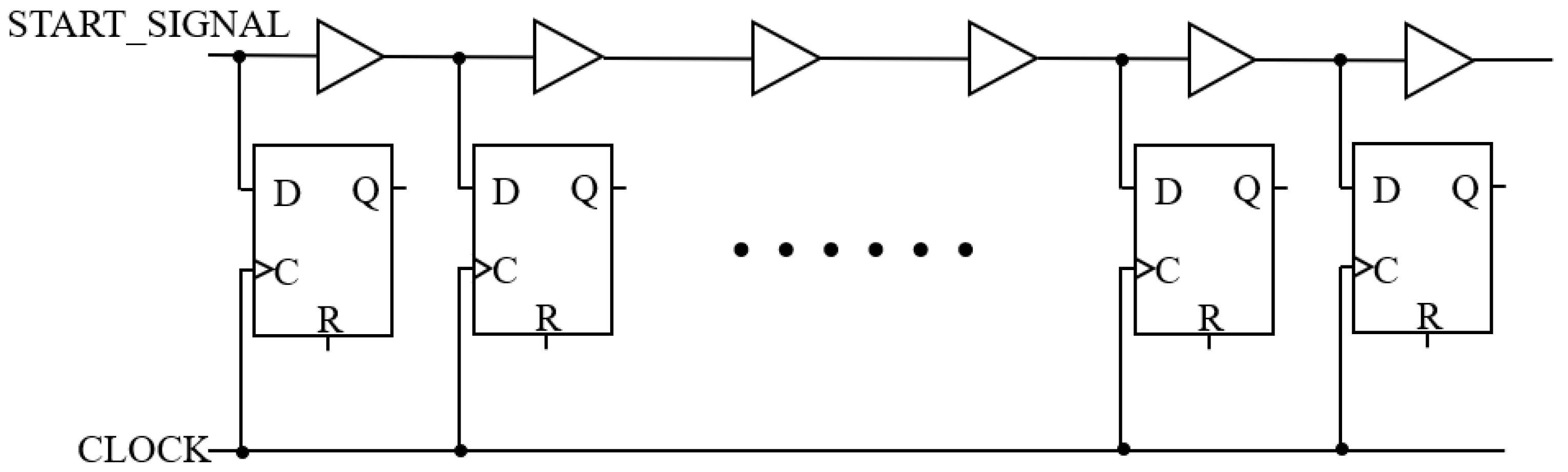
3.1. Input Filter
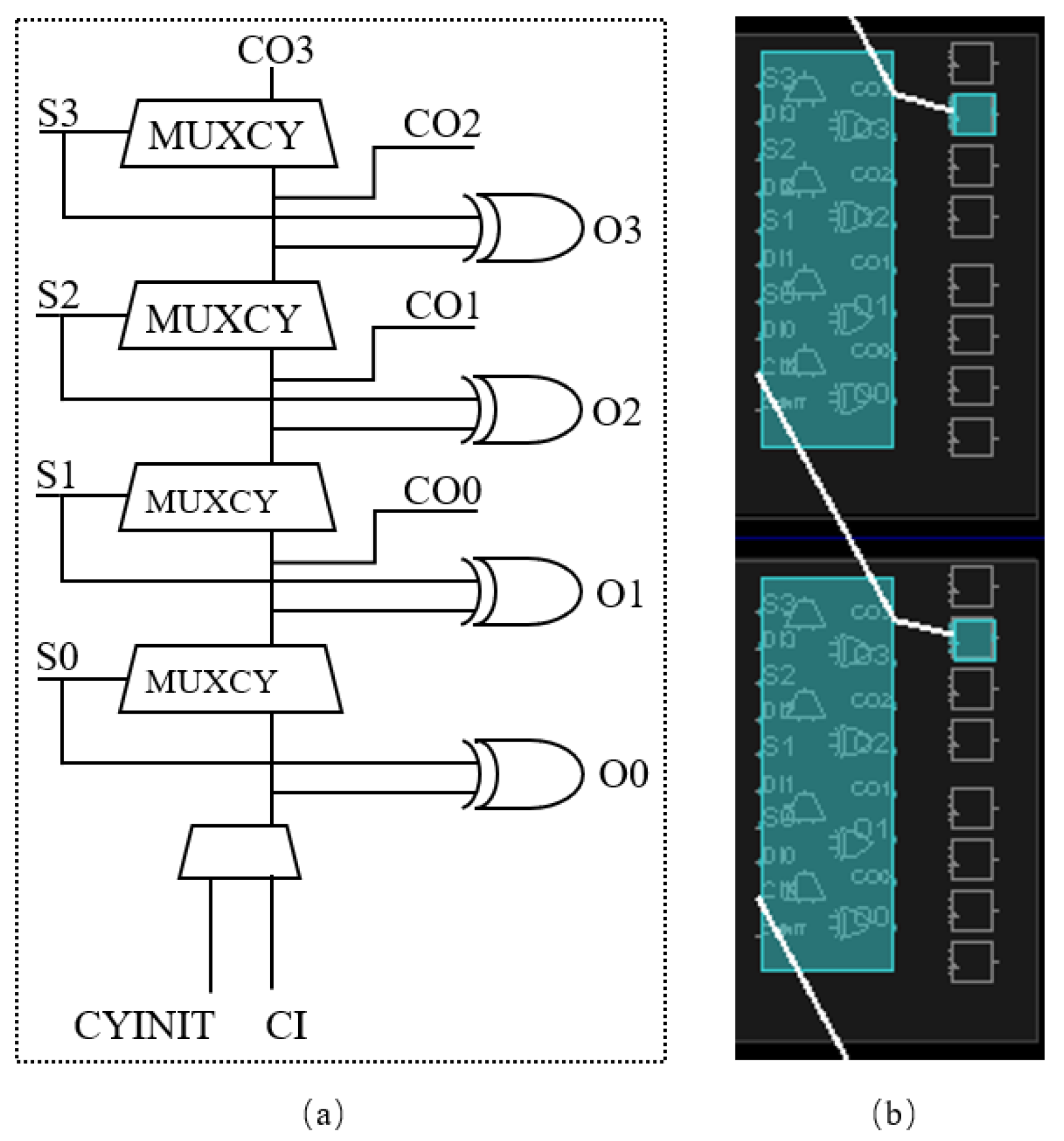
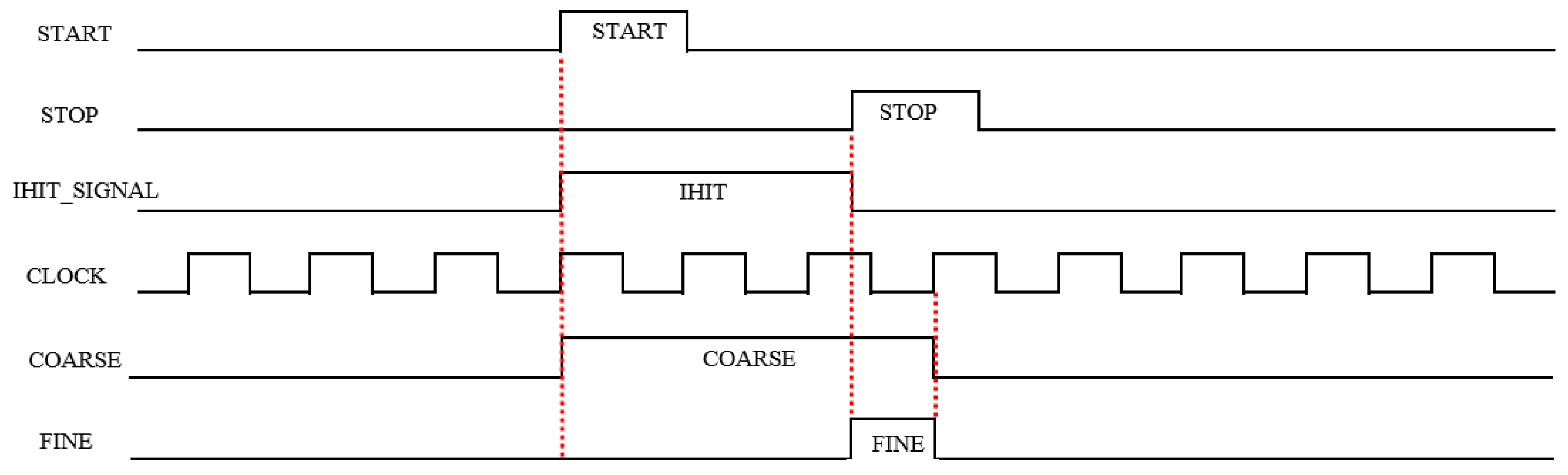
3.2. Implementation of the FPGA-TDC
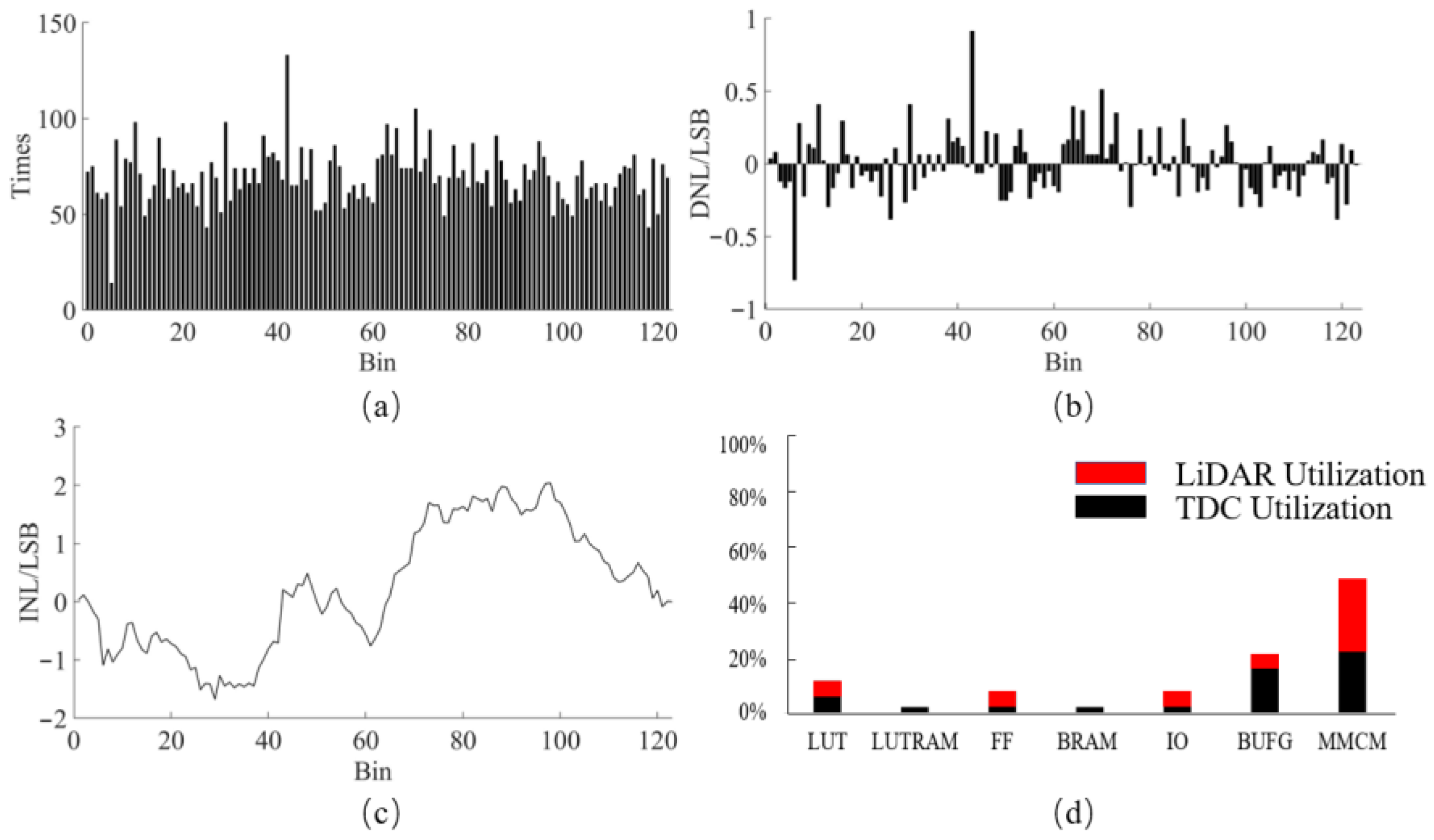
3.3. Evaluation
4. FPGA-Based LiDAR
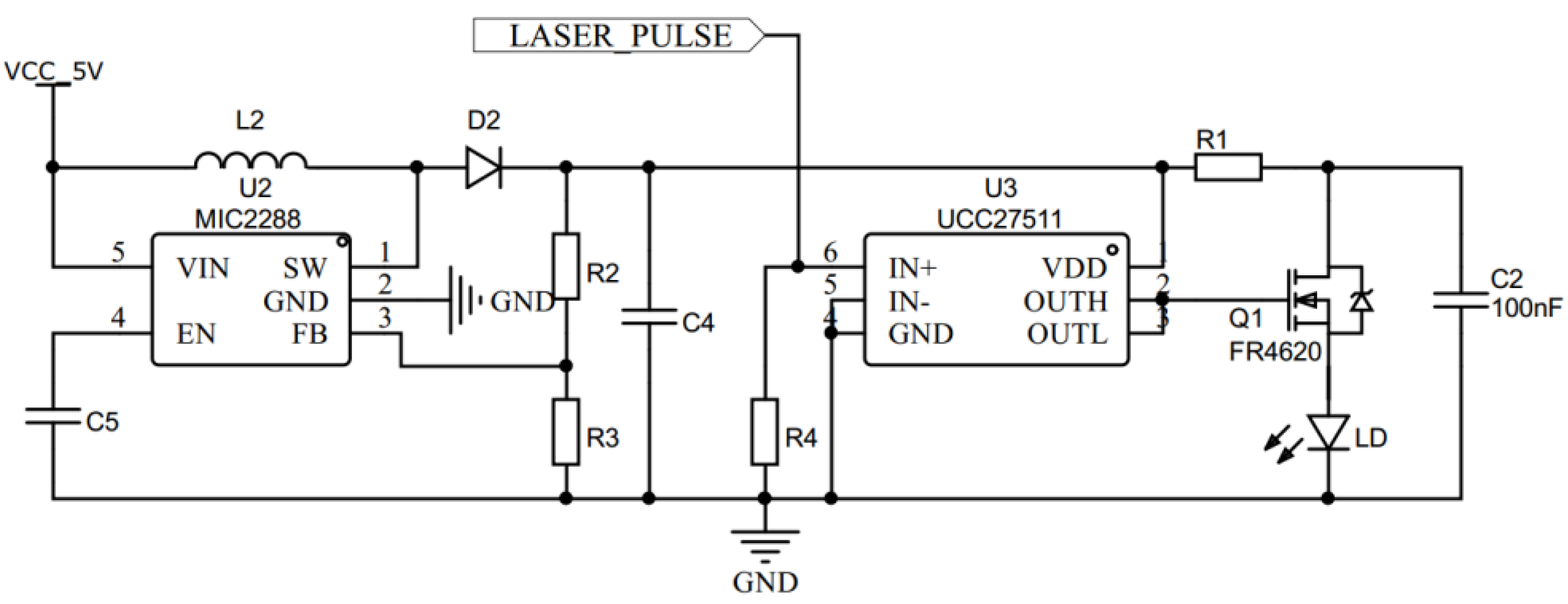
4.1. Laser Driver Circuit
4.2. Receiver Circuit
4.3. Transceiver and LiDAR
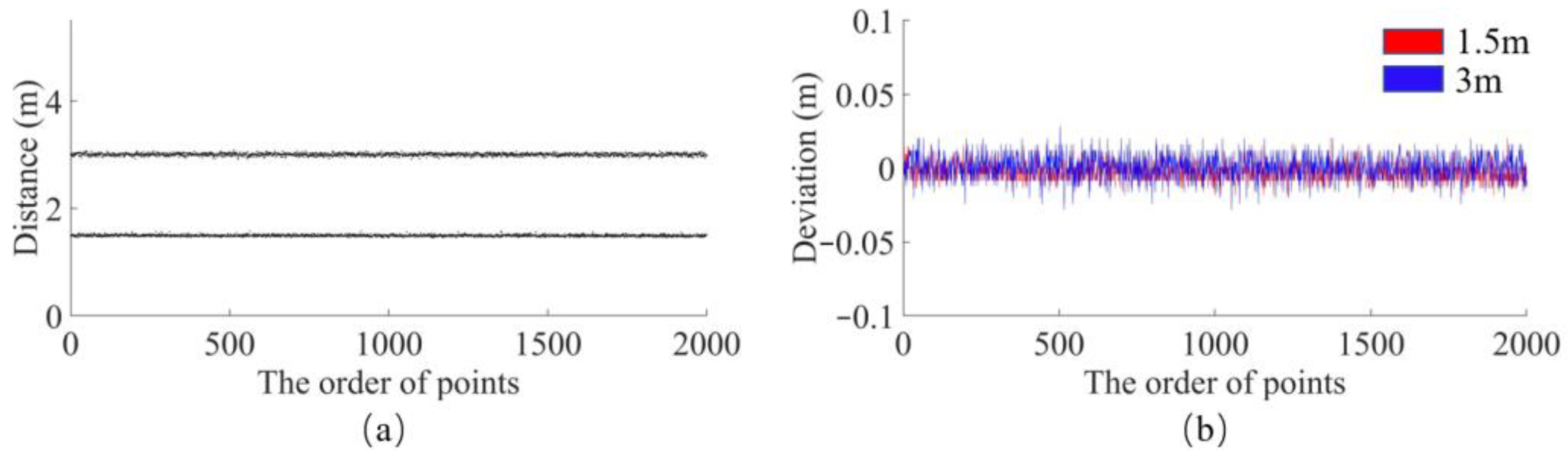
4.4. Experiment Test
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, P.; Liu, D.; Shen, Y.; Chen, Y.; Zhang, H.; Ye, Z.; Jiang, C.; Zhou, Y.; Liu, Q.; Liu, C. Design and validation of a shipborne multiple-field-of-view lidar for upper ocean remote sensing. J. Quant. Spectrosc. Radiat. Transf. 2020, 254, 107201. [Google Scholar] [CrossRef]
- Li, M.; Hu, Y.; Zhao, N.; Qian, Q. Modeling and analyzing point cloud generation in missile-borne LiDAR. Def. Technol. 2020, 16, 69–76. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Wang, J. Map-based localization method for autonomous vehicles using 3D-LIDAR. IFAC-PapersOnLine 2017, 50, 276–281. [Google Scholar] [CrossRef]
- Onda, K.; Oishi, T.; Kuroda, Y. Dynamic environment recognition for autonomous navigation with wide FOV 3D-LiDAR. IFAC-PapersOnLine 2018, 51, 530–535. [Google Scholar] [CrossRef]
- Javanmardi, E.; Javanmardi, M.; Gu, Y.; Kamijo, S. Autonomous vehicle self-localization based on probabilistic planar surface map and multi-channel LiDAR in urban area. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017. [Google Scholar]
- Behroozpour, B.; Sandborn, P.; Wu, M.; Boser, B. Lidar system architectures and circuits. IEEE Commun. Mag. 2017, 55, 135–142. [Google Scholar] [CrossRef]
- Malka, V.; Faure, J.; Glinec, Y.; Rechatin, C. Principle and applications of electron beams produced with laser plasma accelerators. J. Phys. Conf. Ser. 2008, 112, 042029. [Google Scholar] [CrossRef]
- Chen, X.; Kong, W.; Chen, T.; Liu, H.; Huang, G.; Shu, R. High-repetition-rate, sub-nanosecond and narrow-bandwidth fiber-laser-pumped green laser for photon-counting shallow-water bathymetric Lidar. Results Phys. 2020, 19, 103563. [Google Scholar] [CrossRef]
- Wu, D.; Zheng, T.; Wang, L.; Chen, X.; Yang, L.; Li, Z.; Wu, G. Multi-beam single-photon LiDAR with hybrid multiplexing in wavelength and time. Opt. Laser Technol. 2022, 145, 107477. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, R.; Li, X.; Dong, Z.; Zhou, Z.; Ye, G.; Chen, D. Accuracy improvement of imaging lidar based on time-correlated single-photon counting using three laser beams. Opt. Commun. 2018, 429, 175–179. [Google Scholar] [CrossRef]
- Palani, L.; Rajagopal, S.; Rao, Y. Area efficient high-performance time to digital converters. Microprocess. Microsyst. 2020, 73, 102974. [Google Scholar] [CrossRef]
- Christiansen, J. Picosecond stopwatches: The evolution of time-to-digital converters. IEEE Solid-State Circ. Mag. 2012, 4, 55–59. [Google Scholar] [CrossRef]
- Gagnon, H.; Franck, J.; Wisztorski, M.; Day, R.; Fournier, I.; Salzet, M. TARGETED MASS spectrometry imaging: Specific targeting mass spectrometry imaging technologies from history to perspective. Prog. Histochem. Cytochem. 2010, 47, 133–174. [Google Scholar] [CrossRef] [PubMed]
- Maatta, K.; Kostamovaara, J. A high-precision time-to-digital converter for pulsed time-of-flight laser radar applications. IEEE Trans. Instrum. Meas. 1998, 47, 521–536. [Google Scholar] [CrossRef]
- Caram, J.P.; Galloway, J.; Kenney, J.S. Harmonic ring oscillator time-to-digital converter. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 161–164. [Google Scholar]
- Tontini, A.; Gasparini, L.; Pancheri, L.; Passerone, R. Design and characterization of a low-cost FPGA-based TDC. IEEE Trans. Nucl. Sci. 2018, 65, 680–690. [Google Scholar] [CrossRef]
- Sui, T.; Zhao, Z.; Xie, S.; Xie, Y.; Zhao, Y.; Huang, Q.; Xu, J.; Peng, Q. A 2.3-ps RMS resolution time-to-digital converter implemented in a low-cost cyclone V FPGA. IEEE Tran. Instrum. Meas. 2019, 68, 3647–3660. [Google Scholar] [CrossRef] [PubMed]
- Nogrette, F.; Heurteau, D.; Chang, R.; Bouton, Q.; Westbrook, C.; Sellem, R.; Clément, D. Characterization of a detector chain using a FPGA-based time-to-digital converter to reconstruct the three-dimensional coordinates of single particles at high flux. Rev. Sci. Instrum. 2015, 86, 113105. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; An, Q.; Liu, S. A high-resolution time-to-digital converter implemented in field-programmable-gate-arrays. IEEE Trans. Nucl. Sci. 2006, 53, 236–241. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, X.; Liu, S.; Wang, J.; Shen, Q.; Fan, H.; An, Q. The design of a 16-channel 15 ps TDC implemented in a 65 nm FPGA. IEEE Trans. Nuc. Sci. 2013, 60, 3532–3536. [Google Scholar] [CrossRef]
- Kwiatkowski, P.; Szplet, R. Efficient implementation of multiple time coding lines-based TDC in an FPGA device. IEEE Trans. Instrum. Meas. 2020, 69, 7353–7364. [Google Scholar] [CrossRef]
- Dadouche, F.; Turko, T.; Uhring, W.; Malass, I.; Dumas, N.; Normand, J. New design-methodology of high-performance TDC on a low cost FPGA targets. Sens. Transducers 2015, 193, 123–134. [Google Scholar]
- Wang, J.; Liu, S.; Shen, Q.; Li, H.; An, Q. A fully fledged TDC implemented in field-programmable gate arrays. IEEE Trans. Nucl. Sci. 2020, 57, 446–450. [Google Scholar] [CrossRef]
- Lusardi, N.; Garzetti, F.; Geraci, A. Digital instrument with configurable hardware and firmware for multi-channel time measures. Rev. Sci. Instrum. 2019, 90, 055113. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.; Ye, M.; He, J. A novel TDC/ADC hybrid reconstruction ROIC for LiDAR. IEICE Electron. Express 2019, 16, 20181076. [Google Scholar] [CrossRef] [Green Version]
- Seo, H.; Yoon, H.; Kim, D.; Kim, J.; Choi, J. A 36-Channel SPAD-Integrated Scanning LiDAR Sensor with Multi-Event Histogramming TDC and Embedded Interference Filter. In Proceedings of the 2020 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 16–19 June 2020. [Google Scholar]
- Lesani, A.; Nateghinia, E.; Miranda-Moreno, L.F. Development and evaluation of a real-time pedestrian counting system for high-volume conditions based on 2D LiDAR. Transp. Res. Part C Emerg. Technol. 2020, 114, 20–35. [Google Scholar] [CrossRef]
- Tai, T.S.; Zuo, H.; He, S. 3D LIDAR based on FPCB mirror. Mechatronics 2022, 82, 102720. [Google Scholar] [CrossRef]
- Seferiadis, G.; Pouchet, M.; Gough, M. FPGA implementation of a delay-line readout system for a particle detector. Measurement 2006, 39, 90–99. [Google Scholar] [CrossRef]
- Lusardi, N.; Los, J.; Gourgues, R.; Geraci, A. Photon counting with photon number resolution through superconducting nanowires coupled to a multi-channel TDC in FPGA. Rev. Sci. Instrum. 2017, 88, 035003. [Google Scholar] [CrossRef] [Green Version]
- Machado, R.; Cabral, J.; Alves, F.S. Recent developments and challenges in FPGA-based time-to-digital converters. IEEE Trans. Instrum. Meas. 2019, 68, 4205–4221. [Google Scholar] [CrossRef]
- Maamoun, M.; Arami, S.; Beguenane, R.; Benbelkacem, A.; Meraghni, A. A 3 ps resolution time-to-digital converter in low-cost FPGA for laser rangefinder. Proc. World Congr. Eng. 2017, 1, 7–11. [Google Scholar]
- Chen, P.; Hsiao, Y.; Chung, Y. A high resolution FPGA TDC converter with 2.5 ps bin size and -3.79~6.53 LSB integral nonlinearity. In Proceedings of the 2016 2nd International Conference on Intelligent Green Building and Smart Grid (IGBSG), Prague, Czech Republic, 27–29 June 2016. [Google Scholar]
- Prasad, K.; Chandratre, V.; Sukwani, M. An FPGA based 33-channel, 72 ps LSB time-to-digital converter. Nucl. Instrum. Methods Phys. Res. A 2022, 1027, 166052. [Google Scholar] [CrossRef]
- OSRAM Opto Semiconductors, SPL PL90_3_EN Datasheet, Radial T1 3/4. Available online: https://dammedia.osram.info/media/resource/hires/osram-dam-6189135/SPL%20PL90_EN.pdf (accessed on 11 July 2018).
- First Sensor APD Data Sheet, Part Description AD500-9 SMD, Order # 501122; 501818, Version 20-06-11. Available online: https://www.first-sensor.com/cms/upload/datasheets/AD500-9_SMD_3001495.pdf (accessed on 11 June 2020).







| Resource | Used | Utilization |
|---|---|---|
| LUTs | 1056 | 6% |
| DFFs | 2112 | 6% |
| IO | 8 | 6% |
| Name | Consumption |
|---|---|
| Dynamic | 0.193 W |
| Clocks | 0.029 W |
| Signals | 0.038 W |
| Logic | 0.031 W |
| MMCM | 0.095 W |
| I/O | <0.001 W |
| Total | 0.288 W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Ran, S.; Wei, W.; Yu, Q. Digital Integration of LiDAR System Implemented in a Low-Cost FPGA. Symmetry 2022, 14, 1256. https://doi.org/10.3390/sym14061256
Huang J, Ran S, Wei W, Yu Q. Digital Integration of LiDAR System Implemented in a Low-Cost FPGA. Symmetry. 2022; 14(6):1256. https://doi.org/10.3390/sym14061256
Chicago/Turabian StyleHuang, Jiajian, Shengyao Ran, Wei Wei, and Qun Yu. 2022. "Digital Integration of LiDAR System Implemented in a Low-Cost FPGA" Symmetry 14, no. 6: 1256. https://doi.org/10.3390/sym14061256
APA StyleHuang, J., Ran, S., Wei, W., & Yu, Q. (2022). Digital Integration of LiDAR System Implemented in a Low-Cost FPGA. Symmetry, 14(6), 1256. https://doi.org/10.3390/sym14061256





