On a Novel Dynamics of SEIR Epidemic Models with a Potential Application to COVID-19
Abstract
:1. Introduction
2. Background
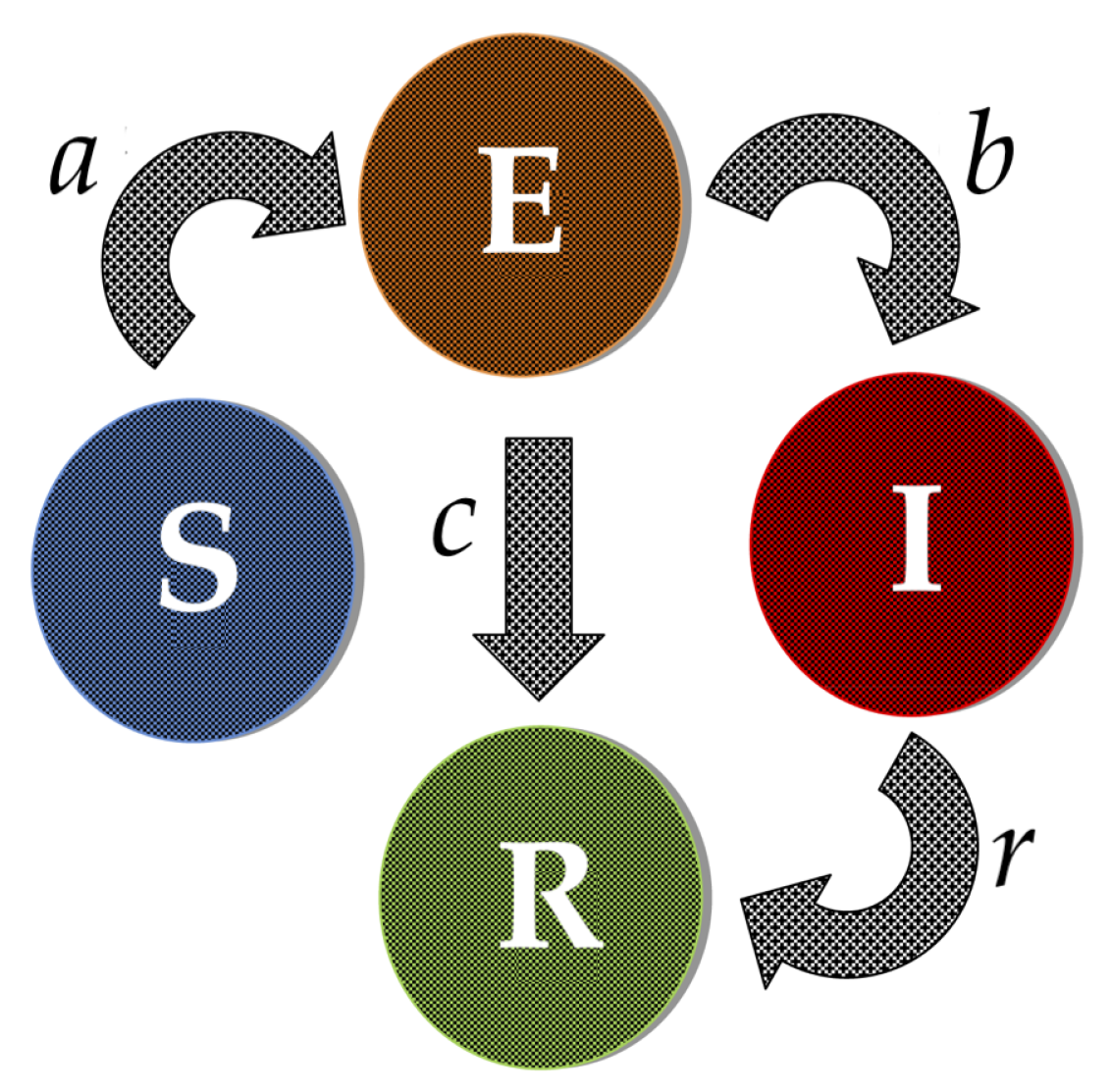
2.1. SEIR Epidemic Model
2.2. Contextualization of the New Epidemic Model
2.3. Preliminaries on Fractional Differential Equations
3. Mathematical Analysis
3.1. Basic Reproduction Number
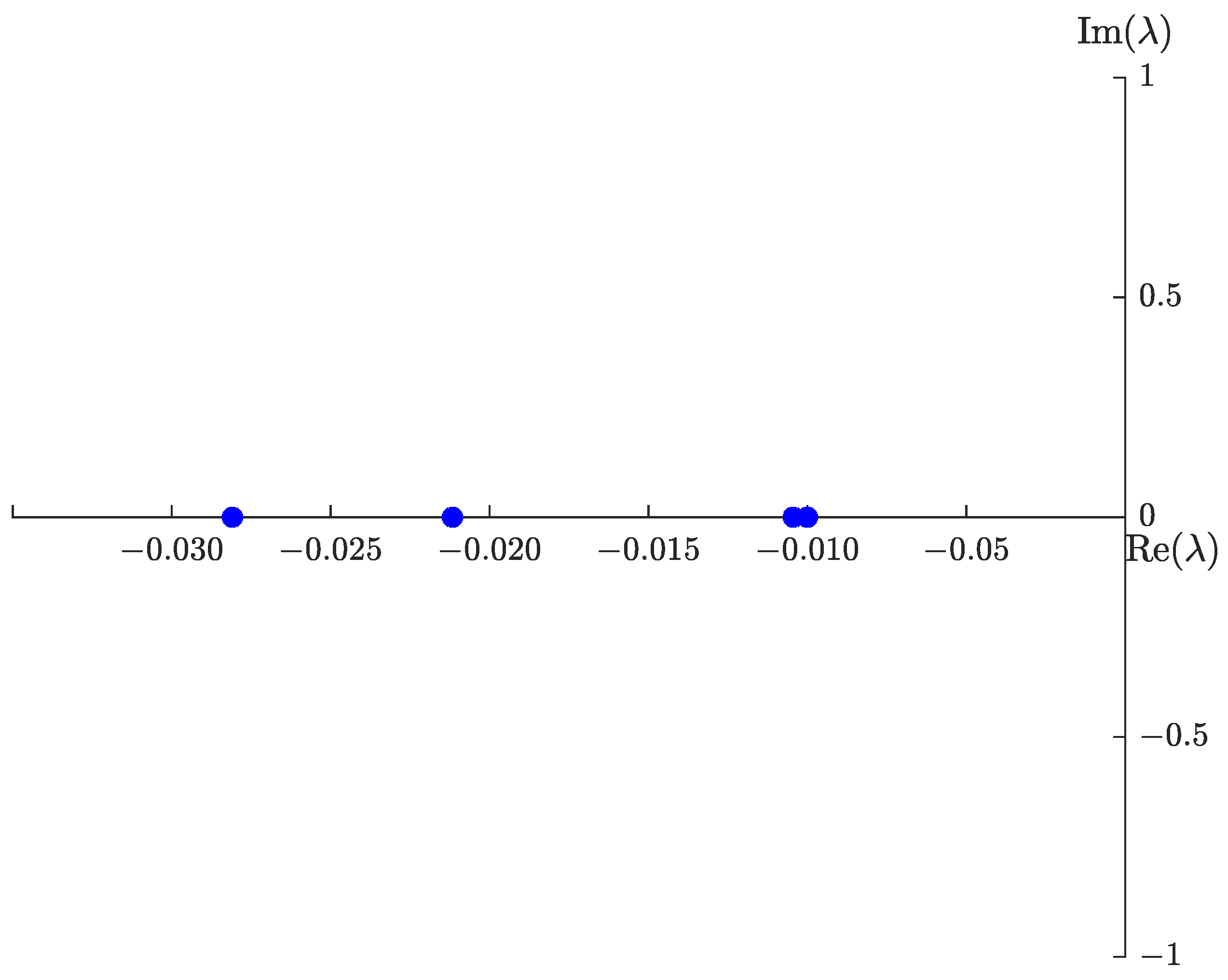
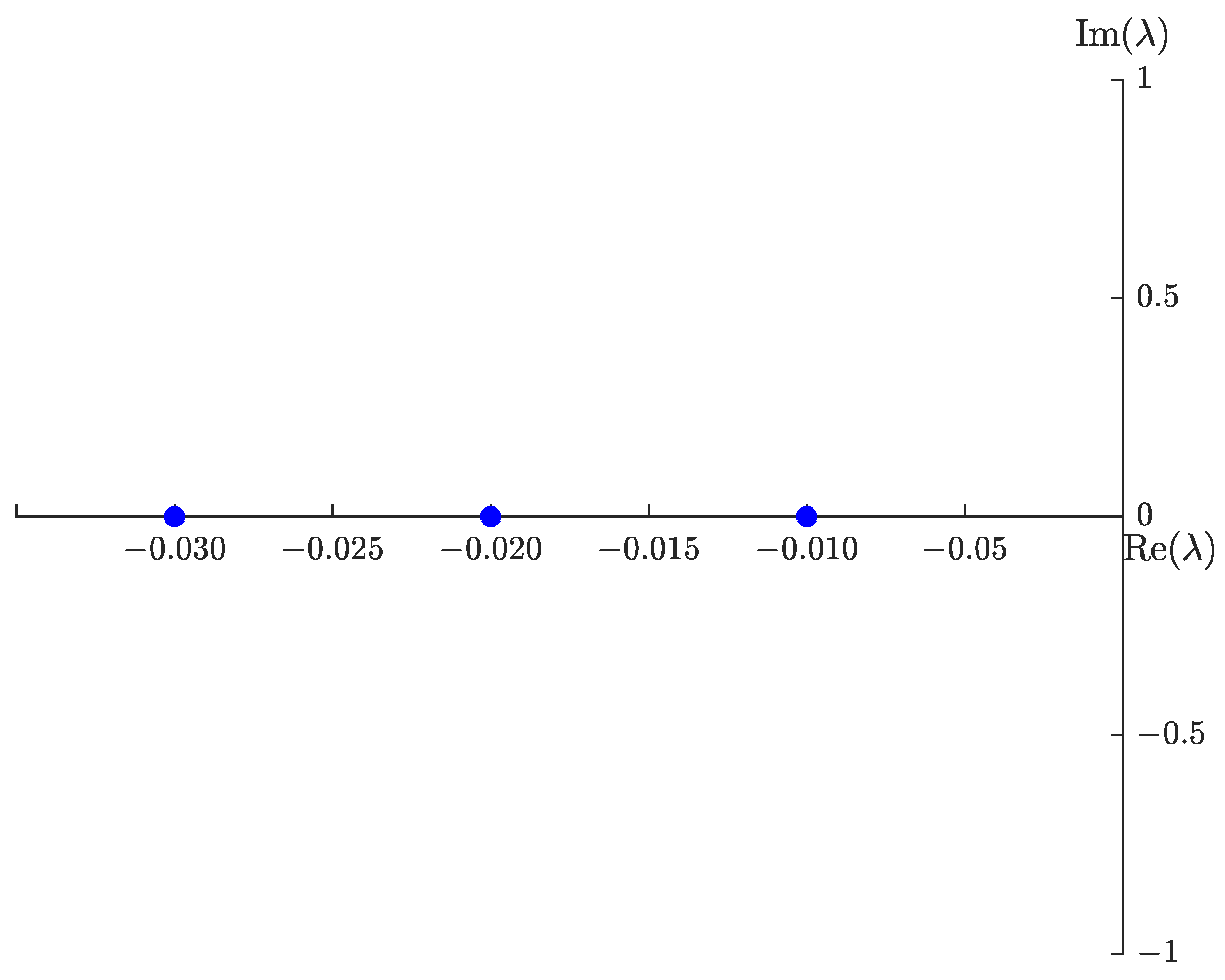
3.2. Equilibrium Points
3.3. Feasibility Region Analysis
- (i)
- The initial populations.
- (ii)
- All possible disease-free equilibrium points.
- (iii)
- The disease-dependent equilibrium points.
4. Positivity in Solutions and Sensitivity Analysis
4.1. Existence of Positivity in Solutions
- (i)
- The solution of the SEIR model is positive for any non-negative initial conditions and for all t.
- (ii)
- The total population remains unvaried even for a long time, which holds for any given arbitrary non-negative initial conditions.
- (iii)
- All the solutions are positively bounded.
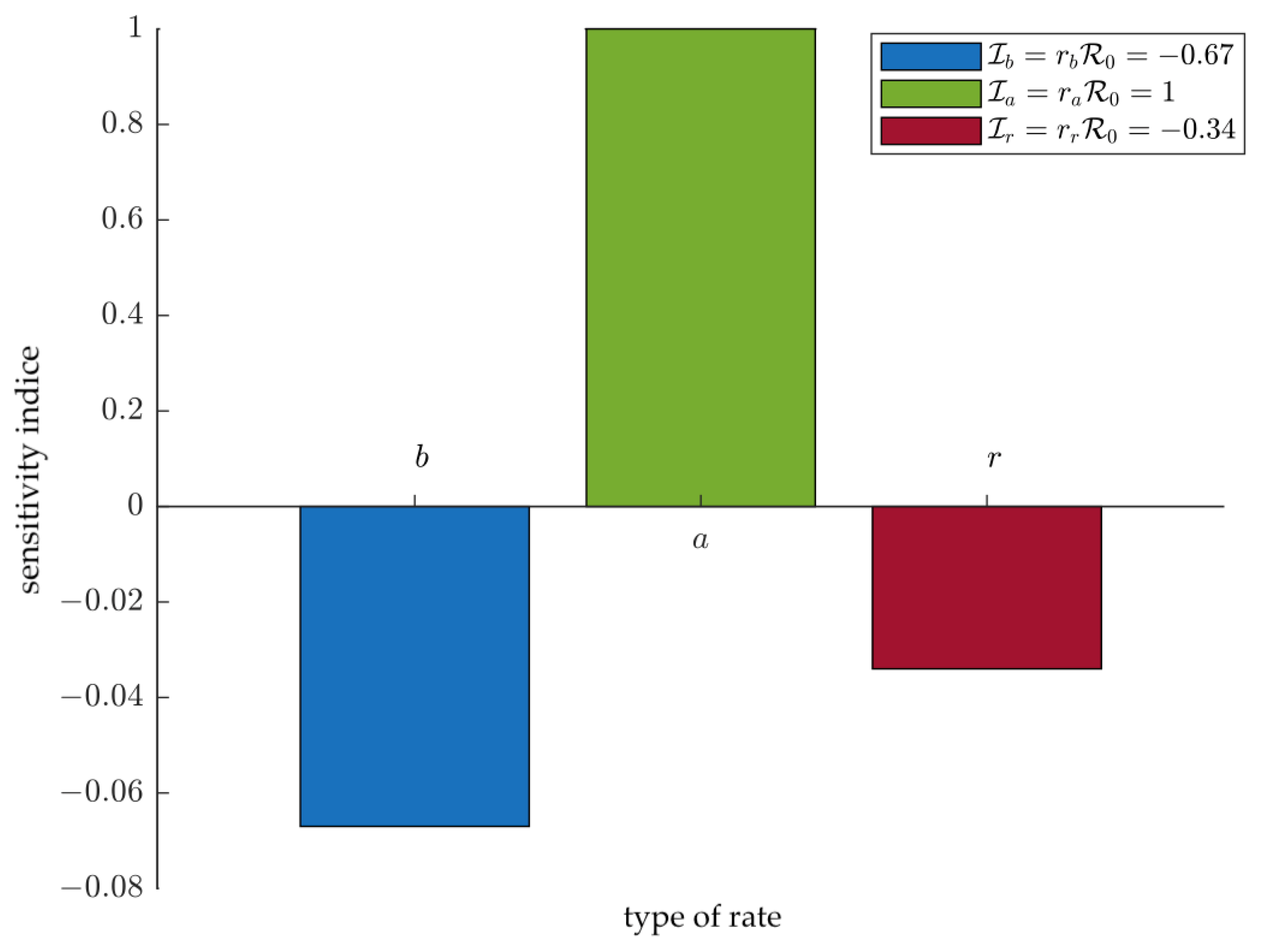
4.2. Sensitivity Analysis
5. Numerical Results
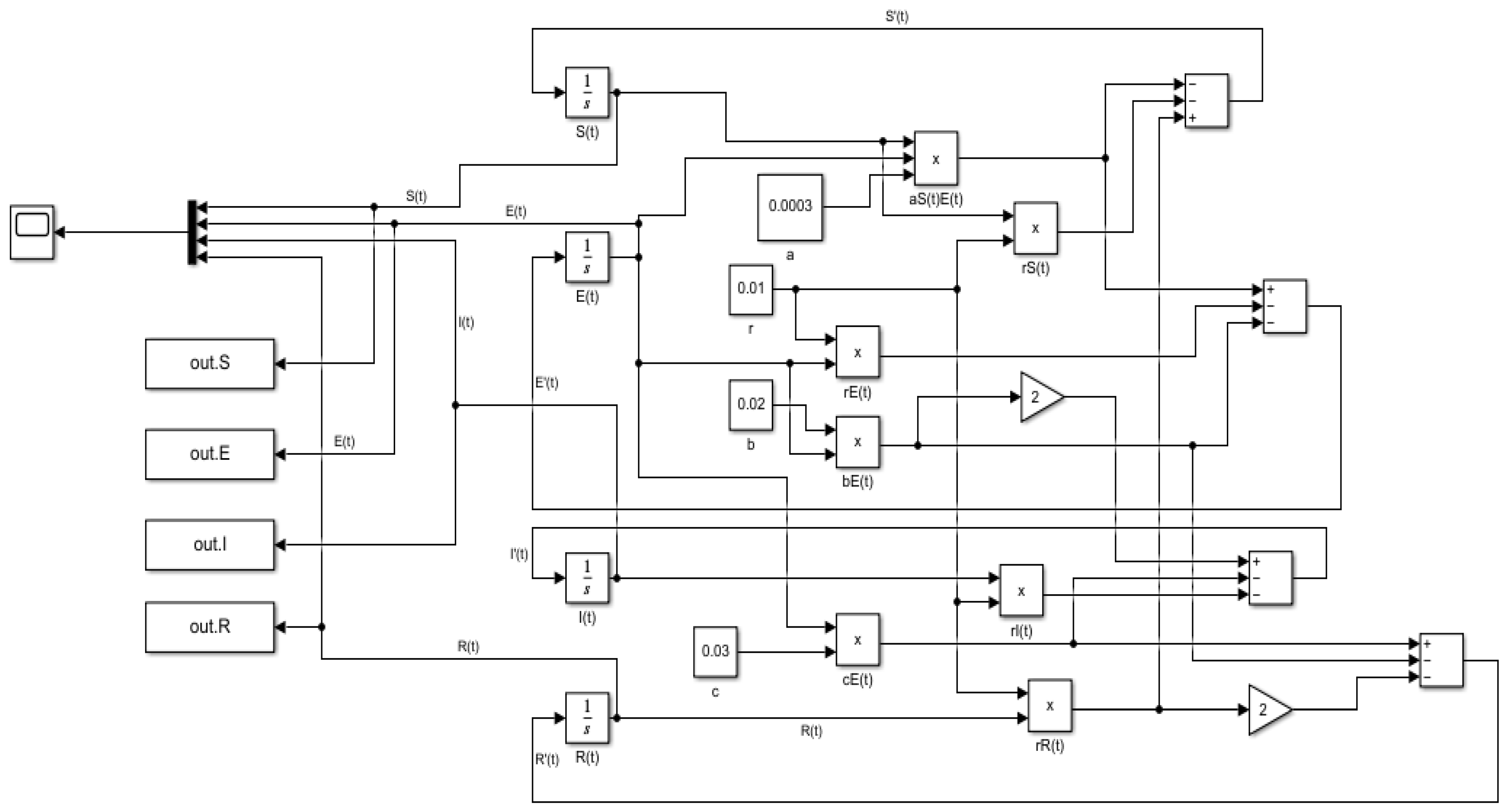
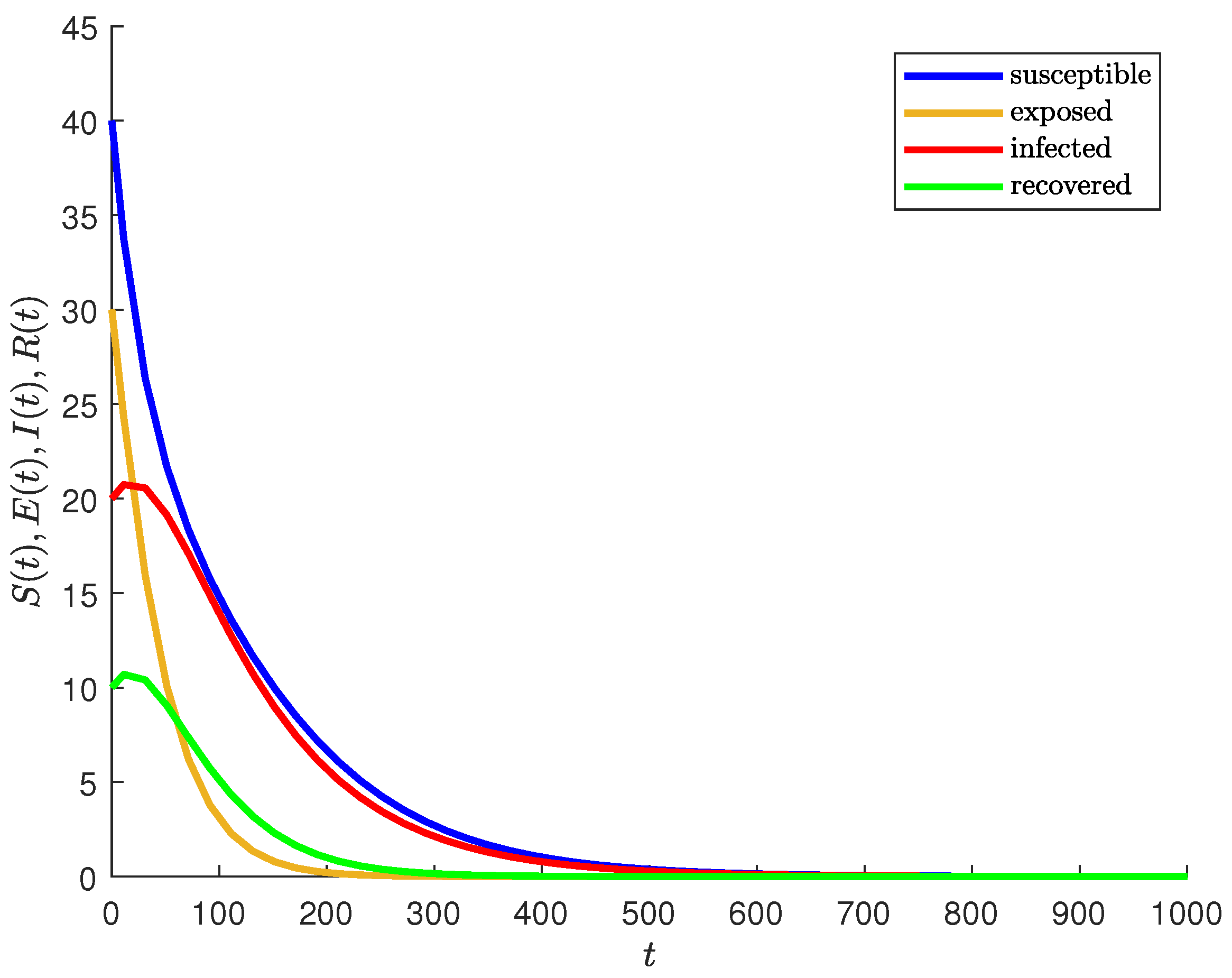
5.1. Graphical Representation of , , , and
5.2. Laplace Adomian Decomposition Method
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kermack, W.O.; Mckendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A 1927, 115, 700–721. [Google Scholar]
- Allen, L.J.S. An Introduction to Mathematical Biology; Prentice-Hall: New Jersey, NJ, USA, 2007. [Google Scholar]
- Fierro, R.; Leiva, V.; Balakrishnan, N. Statistical inference on a stochastic epidemic model. Commun. Stat. Simul. Comput. 2015, 44, 2297–2314. [Google Scholar] [CrossRef]
- Esquivel, M.L.; Krasii, N.P.; Guerreiro, G.R.; Patricio, P. The multi-compartment SI (RD) model with regime switching: An application to COVID-19 pandemic. Symmetry 2021, 13, 2427. [Google Scholar] [CrossRef]
- Jerez-Lillo, N.; Lagos-Alvarez, B.; Munoz-Gutierrez, J.; Figueroa-Zuniga, J.; Leiva, V. A statistical analysis for the epidemiological surveillance of COVID-19 in Chile. Signa Vitae 2022, 18, 19–30. [Google Scholar]
- Molin, R.M.H.D.; Gomes, D.S.R.; Cocco, M.V.; Santos, C.L.D. Short-term forecasting COVID-19 cumulative confirmed cases: Perspectives for Brazil. Chaos Solitons Fractals 2020, 135, 109853. [Google Scholar]
- Ospina, R.; Leite, A.; Ferraz, C.; Magalhaes, A.; Leiva, V. Data-driven tools for assessing and combating COVID-19 out-breaks based on analytics and statistical methods in Brazil. Signa Vitae 2022, 18, 18–32. [Google Scholar]
- Alkadya, W.; ElBahnasy, K.; Leiva, V.; Gad, W. Classifying COVID-19 based on amino acids encoding with machine learning algorithms. Chemom. Intell. Lab. Syst. 2022, 224, 104535. [Google Scholar] [CrossRef]
- Martin-Barreiro, C.; Ramirez-Figueroa, J.A.; Cabezas, X.; Leiva, V.; Galindo-Villardon, M.P. Disjoint and functional principal component analysis for infected cases and deaths due to COVID-19 in South American countries with sensor-related data. Sensors 2021, 21, 4094. [Google Scholar] [CrossRef]
- Chahuan-Jimenez, K.; Rubilar, R.; de la Fuente-Mella, H.; Leiva, V. Breakpoint analysis for the COVID-19 pandemic and its effect on the stock markets. Entropy 2021, 23, 100. [Google Scholar] [CrossRef]
- De la Fuente-Mella, H.; Rubilar, R.; Chahuan-Jimenez, K.; Leiva, V. Modeling COVID-19 cases statistically and evaluating their effect on the economy of countries. Mathematics 2021, 9, 1558. [Google Scholar] [CrossRef]
- Mahdi, E.; Leiva, V.; Mara’Beh, S.; Martin-Barreiro, C. A new approach to predicting cryptocurrency returns based on the gold prices with support vector machines during the COVID-19 pandemic using sensor-related data. Sensors 2021, 21, 6319. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Basti, B.; Hammami, N.; Berrabah, I.; Nouioua, F.; Djemiat, R.; Benhamidouche, N. Stability analysis and existence of solutions for a modified SIRD model of COVID-19 with fractional derivatives. Symmetry 2021, 13, 1431. [Google Scholar] [CrossRef]
- Chintamani, P.; Ankush, B.; Vaibhav, R. Investigating the dynamics of COVID-19 pandemic in India under lockdown. Chaos Solitons Fractals 2020, 138, 109988. [Google Scholar]
- Dhandapani, P.B.; Baleanu, D.; Jayakumar, T.; Vinoth, S. On stiff fuzzy IRD-14 day average transmission model of COVID-19 pandemic disease. AIMS Bioeng. 2020, 7, 208–223. [Google Scholar] [CrossRef]
- Sha, H.; Sanyi, T.; Libinin, R. A discrete stochastic model for COVID-19 outbreak: Forecast and control. Math. Biosci. Eng. 2020, 14, 2792–2804. [Google Scholar]
- Zhou, Z.W.; Aili, W.; Fan, X.; Yanni, X.; Sanyi, T. Effects of media reporting on mitigating spread of COVID-19 in the early phase of the outbreak. Math. Biosci. Eng. 2020, 17, 2693–2707. [Google Scholar]
- Rong, R.X.; Yang, Y.L.; Huidi, C.; Meng, F. Effect of delay in diagnosis on transmission of COVID-19. Math. Biosci. Eng. 2020, 17, 2725–2740. [Google Scholar] [CrossRef]
- Palese, P.; Young, J.F. Variation of influenza A, B, and C. Science 1982, 215, 1468–1474. [Google Scholar] [CrossRef]
- Abbasbandy, S. Extended Newton’s method for a system of nonlinear equations by modified Adomian decomposition method. Appl. Math. Comput. 2005, 170, 648–656. [Google Scholar] [CrossRef]
- Adda, F.B.; Cresson, J. Fractional differential equations and the Schrodinger equation. Appl. Math. Comput. 2005, 161, 323–345. [Google Scholar]
- Makinde, O.D. Adomian decomposition approach to an SIR epidemic model with constant vaccination strategy. Appl. Math. Comput. 2007, 184, 842–848. [Google Scholar] [CrossRef]
- Lakshmikantham; Leela, S. Nagumo-type uniqueness result for fractional differential equations. Nonlinear Anal. Theory Methods Appl. 2009, 71, 2886–2889. [Google Scholar] [CrossRef]
- Liang, Y.S. Box dimensions of Riemann–Liouville fractional integrals of continuous functions of bounded variation. Nonlinear Anal. Theory Methods Appl. 2010, 72, 4304–4306. [Google Scholar] [CrossRef]
- Arafa, A.A.M.; Rida, S.Z.; Khalil, M. Solutions of the fractional-order model of Childhood disease with constant vaccination strategy. In Proceedings of the 2nd International Conference on Mathematics and Information Sciences, Sohag, Egypt, 10–13 September 2011; pp. 9–13. [Google Scholar]
- Moustafa, E.S.; Ahmed, A. The fractional SIRC model and influenza. Math. Probl. Eng. 2011, 2011, 480378. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivative with non-local and non-singular kernel theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, F.; Muhammed, U.S.; Aqueel, A.; Ahamed, M.O. Analysis and numerical solution of SEIR epidemic model of measles with non-integer time fractional derivatives by using Laplace Adomian decomposition method. Ain Shams Eng. J. 2018, 9, 3391–3397. [Google Scholar]
- Baleanu, D.; Jajarmi, A.; Sajjadi, S.S.; Mozyrska, D. A new fractional model and optimal control of tumour immune surveillance with non-singular derivative operator. Chaos 2019, 29, 083127. [Google Scholar] [CrossRef]
- Abishek, K.; Kanica, G.; Nilam. A deterministic time-delayed SIR epidemic model: Mathematical modelling and analysis. Theory Biosci. 2020, 139, 67–76. [Google Scholar]
- Abdeljawad, T. A Lyapunov type inequality for fractional operators with non-singular Mittag–Leffler kernel. J. Inequalities Appl. 2017, 2017, 130. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. Nonlinear equations with global differential and integral operators: Existence, uniqueness with application to epidemiology. Results Phys. 2021, 20, 103593. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Ongun, M.Y. The Laplace Adomian decomposition method for solving a model for HIV infection of CD4+T cells. Math. Comput. Model. 2011, 53, 597–603. [Google Scholar] [CrossRef]
- Dhandapani, P.B.; Baleanu, D.; Jayakumar, T.; Vinoth, S. New fuzzy fractional epidemic model involving death population. Comput. Syst. Sci. Eng. 2021, 37, 331–346. [Google Scholar] [CrossRef]
- Dhandapani, P.B.; Jayakumar, T.; Baleanu, D.; Vinoth, S. On a novel fuzzy fractional retarded delay epidemic model. AIMS Math. 2022, 7, 10122–10142. [Google Scholar] [CrossRef]
- Qian, D.; Li, C.; Agarwal, R.P.; Wong, P.J.Y. Stability analysis of fractional differential system with Riemann–Liouville derivative. Math. Comput. Model. 2010, 52, 862–874. [Google Scholar] [CrossRef]
- Jan, R.; Khan, M.A.; Gomez-Aguilar, J.F. Asymptotic carriers in transmission dynamics of dengue with control interventions. Optim. Control Appl. Methods 2020, 41, 430–447. [Google Scholar] [CrossRef]
- Velasco, H.; Laniado, H.; Toro, M.; Catano-Lopez, A.; Leiva, V.; Lio, Y. Modeling the risk of infectious diseases transmitted by Aedes aegypti using survival and aging statistical analysis with a case study in Colombia. Mathematics 2021, 9, 1488. [Google Scholar] [CrossRef]
- Wanjun, X.; Soumen, K.; Sarit, M. Dynamics of a delayed SEIQ epidemic model. Adv. Differ. Equations 2018, 2018, 336. [Google Scholar]
- Wei, Z.; Dong, W.; Che, J. Periodic boundary value problems for fractional differential equations involving a Riemann- Liouville fractional derivative. Nonlinear Anal. Theory Methods Appl. 2010, 73, 3232–3238. [Google Scholar] [CrossRef]
- Wei, Z.; Li, Q.; Che, J. Initial value problems for fractional differential equations involving Riemann–Liouville sequential fractional derivative. J. Math. Anal. Appl. 2010, 367, 260–272. [Google Scholar] [CrossRef] [Green Version]
- Windarto; Khan, M.A. Fatmawati Parameter estimation and fractional derivatives of dengue transmission model. AIMS Math. 2020, 5, 2758–2779. [Google Scholar] [CrossRef]
- Zaman, G.; Kang, Y.; Jung, I.H. Stability analysis and optimal vaccination of an SIR epidemic model. Biosystems 2008, 93, 240–249. [Google Scholar] [CrossRef] [PubMed]
- De la Sen, M.; Ibeas, A.; Agarwal, R.P. On confinement and quarantine concerns on an SEIAR epidemic model with simulated parameterizations for the COVID-19 pandemic. Symmetry 2020, 12, 1646. [Google Scholar] [CrossRef]
- Ralston, A.; Rabinowitz, P. First Course in Numerical Analysis; MCGraw-Hill: London, UK, 1978. [Google Scholar]
- Blower, S.M.; Dowlatabadi, H. Sensitivity and uncertainty analysis of complex models of disease transmission: An HIV model, as an example. Int. Stat. Rev. 1994, 62, 229–243. [Google Scholar] [CrossRef]




| Notations/Symbols | Definition |
|---|---|
| t | Time instant |
| Susceptible population at t | |
| Exposed population at t | |
| Infected population at t | |
| Recovered population at t | |
| Total population at t | |
| Initial susceptible population, (fixed) | |
| Initial exposed population, (fixed) | |
| Initial infected population, (fixed) | |
| Initial recovered population, (fixed) | |
| Initial total population | |
| Basic reproduction number | |
| a | Rate at which susceptible become exposed, (fixed) |
| b | Rate at which exposed become infected, (fixed) |
| c | Rate at which exposed become recovered, (fixed) |
| r | Rate at which infected become recovered, (fixed) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rangasamy, M.; Chesneau, C.; Martin-Barreiro, C.; Leiva, V. On a Novel Dynamics of SEIR Epidemic Models with a Potential Application to COVID-19. Symmetry 2022, 14, 1436. https://doi.org/10.3390/sym14071436
Rangasamy M, Chesneau C, Martin-Barreiro C, Leiva V. On a Novel Dynamics of SEIR Epidemic Models with a Potential Application to COVID-19. Symmetry. 2022; 14(7):1436. https://doi.org/10.3390/sym14071436
Chicago/Turabian StyleRangasamy, Maheswari, Christophe Chesneau, Carlos Martin-Barreiro, and Víctor Leiva. 2022. "On a Novel Dynamics of SEIR Epidemic Models with a Potential Application to COVID-19" Symmetry 14, no. 7: 1436. https://doi.org/10.3390/sym14071436









