The Prospects of Utilizing Geometrical Visual Illusions as Tools for Neuroscience

Abstract

Geometrical visual illusions have long been used as tools in neuroscience. Most commonly, researchers have taken illusions as a given and attempted to explain phenomenal impressions in terms of known neural mechanisms. In a psychophysical approach to this topic, it is customary to modify stimuli until conditions for which illusions are enhanced, attenuated, or annihilated have been found. Additionally, the focus is not exclusively on response bias but equally on sensitivity, because observers may fall prey to an illusion but at the same time be able to discriminate between stimuli perfectly. For the T-figure, the length of the undivided line is usually overestimated relative to the length of the divided line, and evidence has accrued that suggests that the illusion may be due to the processing of the figure as a coherent unit (a “T-schema”). Dissecting the T or tilting its lines influenced the amount of illusion, suggesting that interactions between orientation-sensitive and end-inhibited neurons are at work. Examples of cognate research with the Ponzo, Ebbinghaus, and Müller-Lyer illusions are also discussed.

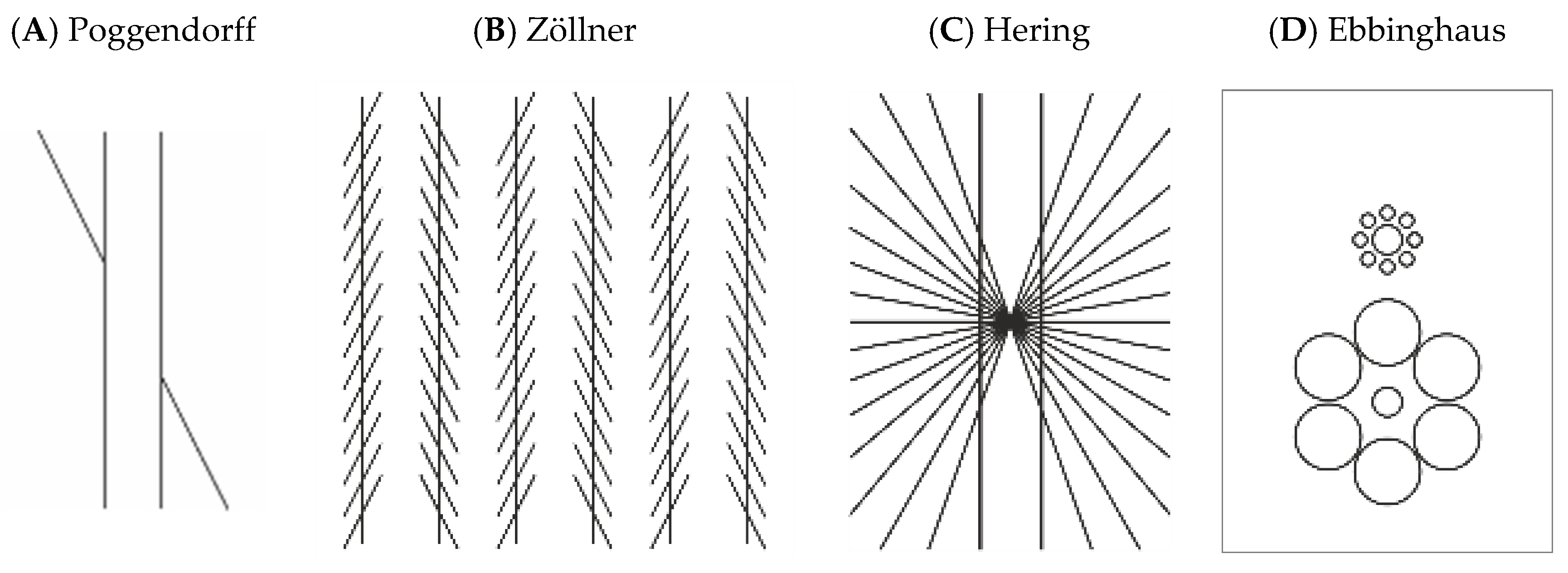
1. Introduction

Eagleman [1] has compiled a brief history of research that used visual illusions to study the human brain. Although his overview contains examples of geometrically defined stimuli, his emphasis was on illusions of light and color, and on ambiguous figures. Similarly, Hamburger [2], in his recent plea for a new classification scheme for visual illusions, also focused on such kinds of illusions, plus illusions of motion from static stimulus displays. The rationale for this selective bias, in both cases, may have been that much is known about the neural underpinnings of these illusions. By contrast, I shall explore the utility of geometrical visual illusions as tools in neuroscience. For the purpose of this study, this class of illusions will be defined in terms of judgmental errors about isometries in figural illustrations that are composed of the elements of Euclidean geometry, that is, points (minuscule dots, visible), lines, and unfilled plane areas. Examples are shown in Figure 1 and Figure 2.

Different approaches have been taken to make use of geometrical visual illusions for neuroscientific purposes. Fermüller and Malm [3], capitalizing on the idea that the formation and processing of images are compromised by uncertainty or “noise”, developed mathematical models to predict (or retrodict) the visual appearances of the line arrangements shown in Figure 2A,B, plus some other patterns that are not considered geometric here because they contain areas filled with achromatic colors. Similarly, Franceschiello et al. [4], starting from observations about simple cortical cells’ receptive profiles, developed a neuromathematical model for the Zöllner and Hering displays (Figure 2B,C) with the same goal in mind (viz., the reconstruction of subjective impressions from specific stimuli).

Axelrod et al. [5] performed veritable neuroscientific research by using structural magnetic resonance imaging (MRI scanning). They used the Ebbinghaus, the Ponzo, a one-line Müller-Lyer, and the ⊥-figures (Figure 1A,C,D and Figure 2D) as well as an achromatic contrast display as stimuli, and focused on the parahippocampal cortex (PHC) as the region of interest—based on the hypothesis that the illusions might be caused by “inconsistency in visuospatial context integration and the construction of a spatial scene” [5] (pp. 2–3). Observers’ susceptibility to expected illusions was determined with the method of adjustment, and illusion magnitudes were correlated with grey matter volume, obtained from the voxel-based morphometry, in subdivisions of PHC. Medium-sized correlations were seen for the Ebbinghaus and the Müller-Lyer illusions (with Spearman’s rho varying between 0.42 and 0.50).

The conclusions that Axelrod et al. [5] drew from their study are compromised by three issues. According to Ward et al. [6], the ⊥- and the Ponzo figures do not elicit associations of depth, so the hypothesis which the authors based their work on does not apply. In the work of Coren et al. [7], the authors found correlations between illusion magnitudes as a measure of the illusion figures’ perceptual similarity, which was not justified. Last, their evidence is circumstantial. Correlations do not allow us to decide between cause and effect, i.e., that specific illusion figures may induce activity in specific brain areas, which, in turn, may not be involved in the generation of the observed illusory responses.

2. Psychophysics

Modern psychophysics studies the relation between well-defined stimuli and the observable responses of experimental subjects [8]. Although, nowadays, most psychologists are also interested in the neural basis of behavior, the scope of inquiry is much wider. In order to understand behavioral coordination, extensive analyses of stimulus conditions are performed. Concerning illusions, stimuli are typically varied to identify the conditions under which illusions are enhanced, attenuated, or annihilated. Additionally, a distinction is made between sensitivity and response bias [9], because observers may well be able to discriminate stimuli but nonetheless fall prey to illusions by making constant errors. Both parameters can be read using a psychometric function [10], which is obtained by plotting response frequencies against an abscissa defined by the differences between stimuli with regard to a specified dimension. Frequency distributions are then fitted by probabilistic functions (most commonly, a cumulative Gaussian) to make them amenable to statistical analyses. The response bias (or amount of “illusion”) is found in the displacement of the 50% point of such a function relative to true zero, and the sensitivity (or “discrimination threshold”) is found in the function’s slope between the 25% and 75% points (although some authors follow other conventions).

In what follows, I shall provide a brief summary of my own work on illusions, which was aimed at generating hypotheses about possible neural mechanisms that might explain the observed effects. The focus will be on answering the following questions: (1) Are all effects local, or are there global interactions? (2) What is the role of an illusion figure’s orientation? (3) What is the role of an illusion figure’s integrity? (4) What is the role of an illusion figure’s symmetry? (5) How do different illusions interact within a single illusion figure? All experiments described used a high-resolution computer screen for stimulus presentation, and a constant width of dots and lines of 9 arc min. For each experiment, there were at least ten observers (mostly psychology undergraduates); this number was decided upon a priori in order to achieve a statistical power of 1 − β ≥ 0.95 for repeated-measures analyses of variance with α = β = 0.05, and f ≥ 1 [11]. Written, informed consent was obtained from all participants, and they were treated in accordance with the Declaration of Helsinki [12].

The experimental paradigm was two alternative forced-choice throughout. It was chosen because it is known to discourage response bias [8]. The psychophysical procedure was the method of constant stimuli, because this method fits best with the optimum control technique in experimental methodology (randomization). Two dependent measures were used: verbal and haptic responses (spreading thumb and index finger to indicate linear extents). In this study, the focus was on verbal responses.

2.1. The T-Illusion

The T-illusion (Figure 1A), first described by the French philosopher Malebranche (1638–1715) [13], and rediscovered in the form of an inverted T (i.e., a ⊥) by Schumann [14] and Titchener [15], consists of the overestimation of the length of the figure’s undivided line as compared to the length of its divided line (the amount of illusion does not differ between the T and the ⊥). Mathematically, the stimulus is composed of two lines, where the endpoint of one bisects the other line orthogonally, so that the whole figure has symmetry group d1 (one axis of mirror symmetry, which coincides with the undivided line). It is well known that the illusion can be decomposed into two components: bisection and horizontal or vertical orientation [16]. The illusion is attenuated with lateral and oblique orientations of the figure, or when the bisecting line is moved away from the bisected line’s midpoint, transforming the ⊥ into an L [17]. The importance of the T’s symmetry was detected only later by tilting the figure’s lines relative to each other [18].

2.1.1. Ts in Contexts

In order to see whether the T-illusion is affected by other figures surrounding it, a target-T was put into the context of other Ts. With periodic patterns of symmetry groups pm, pmm, and pmg, there were no effects. The same was true for random patterns—even when the Ts intersected each other. In delimited, centrosymmetric patterns of four Ts (symmetry group c4), the direction of the comparison between a given T’s two lines sometimes mattered, the illusion being greater when the undivided line had to be compared to the divided line rather than vice versa [19]. However, the effect may have been due to retinal eccentricity, because the effect was more likely to occur when the undivided lines of the Ts pointed inwards the patterns. More interestingly, perhaps, all illusion vanished when the discrete patterns had been turned into branching patterns, with the Ts abutting or crossing one another, and a haptic response measure used. With a verbal response measure, the illusion persisted. This difference required no explanation in terms of differently specialized visual systems [20], because it can also be explained by different task demands or by a different understanding of the task by observers: haptic responses are directed at one item at a time (“absolute perception”), whereas verbal responses normally require an explicit comparison (“relative perception”) [21]. Additionally, observers need not necessarily conceive the haptic task as one of the estimating sizes or lengths, but rather think in terms of target positions to which they have to move their hands and fingers [22]. Either way, the near absence of context effects suggested that the T-illusion is mainly tied to the T as such.

2.1.2. Modified Ts

The simplest modification of the T (or ⊥) as a prototype illusion figure is to rotate it to lateral or oblique orientations. It is well known that the illusion is much attenuated at lateral orientations [16]. The psychological explanation for this effect has been that the two components of the illusion—bisection and orientation—now work against each other. A horizontal undivided line is lengthened due to the bisection component, but a vertical divided line is also lengthened due to the orientation component [17]. The prediction for oblique orientations, therefore, was that the amount of illusion should be intermediate because these orientations would isolate the bisection factor and, cum grano salis, this is what was observed [23]. The ultimate causes of the bisection effect and the so-called horizontal–vertical illusion are still unknown.

Three modifications of the T were made to reveal the importance of the T’s integrity: The lines of the T were replaced by dashes or dots, or the lines were torn apart [24]. Replacing the T’s lines with dashed lines or dots left the illusion unaffected, suggesting that an expressly drawn T-junction is not required. This conclusion was further corroborated by the observation that the illusion also occurred in triangles and beehive figures, in which the T’s undivided line was specified only implicitly [19]. Taken together, these findings suggested that the T may be processed as a coherent unit. To test whether such a kind of processing might be understood as an adaptation to a letter schema [25], asymmetric and near-symmetric Ts were constructed from J-, C-, and S-type curves to mimic handwritten Ts. Since the amounts of illusion were greater, the Ts were more symmetric, and it was concluded that wholistic processing must be due to a more general, nonliterate schema [26]. Although the origin of such a schema seems elusive (see [27] for interesting speculations), there is neurophysiological evidence for specifically tuned neurons in the cat’s striate cortex [28].

Dissecting a T into two separate lines led to an attenuation of the illusion—roughly, the more so, the larger the gap [24]. Although this finding might be interpreted in terms of a decreasing similarity of the modified stimuli to a T-schema, it appears more intelligible if interpreted in terms of interactions between orientation-sensitive and end-stopped neurons, as first identified by Hubel and Wiesel [29,30,31,32], because such interactions should be less pronounced at more extreme variations of the stimuli [33,34]. However, there was also evidence for the idea of a T-schema: at the smallest gap size and upright orientations of the T (or ⊥), the illusion was still about as strong as with a zero gap [17,23].

Building upon and extending the work of Cormack and Cormack [18], the role of the T’s symmetry was investigated by tilting its lines relative to one another [35]. Tilting an upright ⊥’s undivided line relative to the divided line diminished the illusion—in step with the angle of tilt. Adding a gap eradicated all illusions at extreme angles of tilt (20° and 160°). Tilting the divided line of a laterally oriented T relative to the now horizontal undivided line abolished all illusion at all angles of tilt except 90°, and the illusion was inverted after the introduction of a gap. While the first set of effects is ambiguous with regard to the working of a T-schema and local neural interactions, the second set is more in line with the idea of a T-schema. Comparing these data to Cormack and Cormack’s [18], who used the method of adjustment, it was revealed that for laterally oriented ⊥s, the effect of dissecting the ⊥ into two separate lines was roughly equivalent to that when using this method instead of the method of constant stimuli, suggesting that “orientation-sensitive mechanisms may be activated in a similar manner when confronted with dissected ⊥s or when confronted with the task to … adjust the lengths of the lines of nondissected ⊥s” [35] (p. 228).

2.1.3. Interactions of Different Illusions within a Single Illusion Figure

The occurrence of more than one illusion within a single illusion figure has already been alluded to in the description of the T-illusion (Section 2.1). According to Künnapas’ [17] measurements, the two elements of the illusion—bisection and orientation—combine additively. Such a finding is usually interpreted to mean that the effects are caused by independent mechanisms. The same was found for dissection and tilt [35]. It is tempting to regard bisection as the limiting case of dissection, and tilt as a special case of orientation. This would reduce the number of mechanisms to be searched for to a minimum of two. As suggested in Section 2.1.2, interactions between orientation-sensitive and end-stopped neurons may explain many of the findings obtained with modified Ts—although the nature of such interactions still needs to be specified.

2.2. Other Illusion Figures

Although many of the other illusions shown in Figure 1 and Figure 2 attracted more research than the T, most studies tested psychological theories with little or no interest in neural mechanisms. Fisher [36], by inserting more than two lines of equal length into a Ponzo figure (Figure 1D), observed a “gradient of distortion” in that the lines farther away from the implied apex of the converging lines appeared to be increasingly shorter. Since the endpoints of the inserted lines are also necessarily increasingly distant from the converging lines, the effect, in analogy to what was observed with dissected Ts with tilted lines, might be interpreted in terms of interactions between end-stopped and orientation-sensitive neurons.

For the Ebbinghaus illusion (Figure 2D), Jaeger [37] expressly proposed contour interaction as a better explanation of this illusion than psychologically defined size contrast (similar to [38]). For the Müller-Lyer illusion, Pollack and Jaeger [39] found the illusion for isoluminant stimuli, defined by red or blue hues, to be greater than for stimuli that involved differences in light, suggesting that “contour interactions within parvocellular channels that are specialized for coding color” were responsible for the differential effect [39] (p. 225). Although this last example involved color, it may still be regarded as dealing with geometrical illusions because the critical elements of the stimuli were still thin lines (also cf. [40]).

So far, I have restricted my discussion to illusion figures that afford the study of comparative ordinal judgments of linear extents or plane areas. The illusions shown in Figure 2A–C invite dichotomous yes–no decisions: For the Poggendorff, observers have to decide on collinearity, and for the Zöllner and the Hering, on parallelism. These figures are also amenable to psychophysical investigations by varying amounts of misalignment, tilt, and curvature to find points of subjective alignment and parallelism, but, as far as I am aware, this has seldom been carried out (see [41]).

3. Conclusions

So, what are the prospects of utilizing geometrical visual illusions for the purpose of neuroscience? In this paper, I gave examples of psychophysical research that seem suggestive of the existence and working of dedicated neural mechanisms. Neuroscientists may use this evidence as “food” for their investigations. However, an exhaustive account of observers’ behavior requires going beyond response bias; sensitivity, task demands, and different dependent measures of observers’ performance also have to be considered.