Orbits of Particles and Photons around Regular Rotating Black Holes and Solitons
Abstract
:1. Introduction
2. Internal Structure of de Sitter–Kerr Compact Objects
3. Circular Equatorial Orbits and Light Rings
3.1. Particle Orbits
3.2. Light Rings
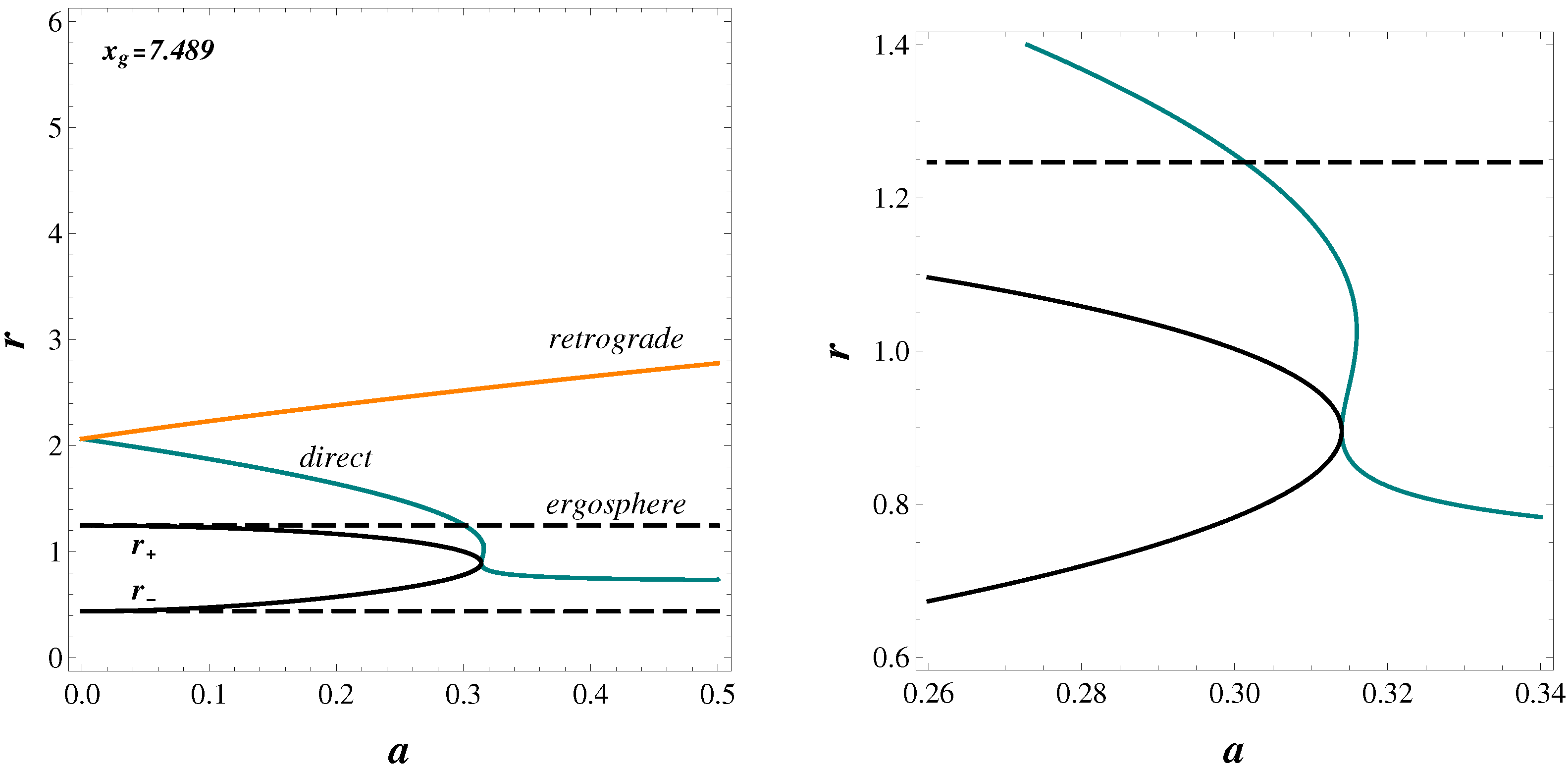
3.3. All Limiting Orbits
4. Observational Signatures
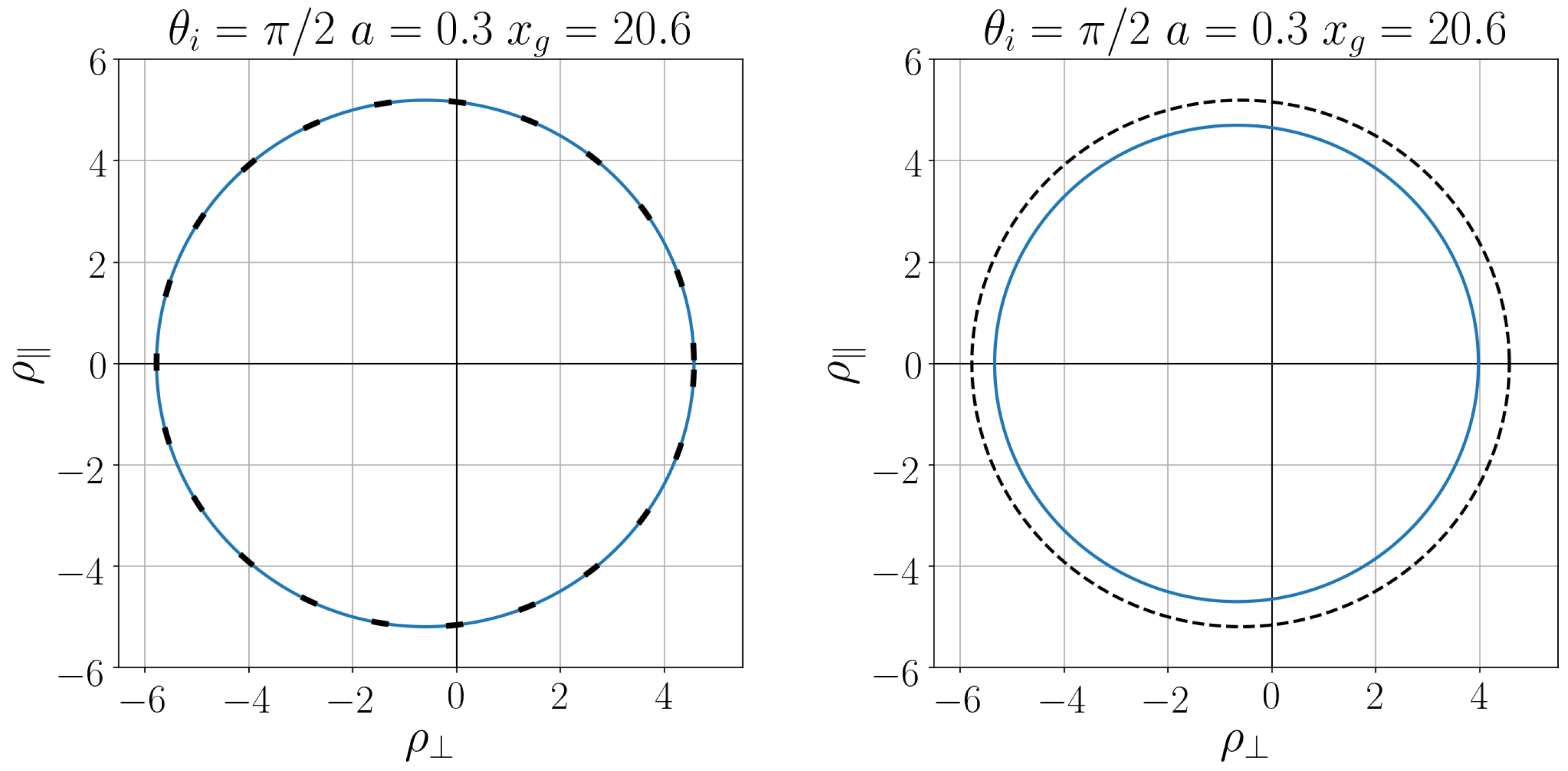
Shadows of de Sitter–Kerr Black Holes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24–62. [Google Scholar] [CrossRef] [Green Version]
- Rivera, A.B.; Garcia-Farieta, J.E. Exploring the Dark Universe: Constraint on dynamical dark energy models from CMB, BAO and Growth Rate Measurements. Int. J. Mod. Phys. D 2019, 28, 1950118. [Google Scholar] [CrossRef]
- Olive, K. Inflation. Phys. Rep. 1990, 190, 309–403. [Google Scholar] [CrossRef]
- Bassett, B.A.; Kunz, M.; Silk, J.; Ungarelli, C. A late-time transition in the cosmic dark energy? Mon. Not. R. Astron. Soc. 2002, 336, 1217–1222. [Google Scholar] [CrossRef] [Green Version]
- Corasaniti, P.S.; Kunz, M.; Parkinson, D.; Copeland, E.J.; Bassett, B.A. Foundations of observing dark energy dynamics with the Wilkinson Microwave Anisotropy Probe. Phys. Rev. D 2004, 70, 083006:1–083006:15. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.; Aikin, R.W.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Bicep2 Collaboration. Detection of B-Mode Polarization at Degree Angular Scales by BICEP2. Phys. Rev. Lett. 2014, 112, 241101:1–241101:25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E. Measurements of Ω and ∧ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Supernova Cosmology Project. The Hubble Space Telescope Cluster Supernova Survey: Improving the Dark Energy Constraints and Building an Early-Type-Hosted Supernova Sample. Astrophys. J. 2012, 746, 85–109. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef] [Green Version]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar]
- Nojiri, S.I.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Sp. Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef] [Green Version]
- Sahni, V.; Shafiello, A.; Starobinsky, A.A. Model-independent Evidence for Dark Energy Evolution from Baryon Acoustic Oscillations. Astrophys. J. 2014, 793, L40–L44. [Google Scholar] [CrossRef] [Green Version]
- Gliner, E.B.; Dymnikova, I.G. Nonsingular Friedmann cosmology. Sov. Astron. Lett. 1975, 1, 93–95. [Google Scholar]
- Bronnikov, K.A.; Dobosz, A.; Dymnikova, I. Nonsingular vacuum cosmologies with a variable cosmological term. Class. Quant. Grav. 2003, 20, 3797–3814. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Dymnikova, I. Regular homogeneous T-models with vacuum dark fluid. Class. Quant. Grav. 2007, 24, 5803–5816. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Dymnikova, I.; Galaktionov, E. Multihorizon spherically symmetric spacetimes with several scales of vacuum energy. Class. Quant. Grav. 2012, 29, 095025:1–0950:22. [Google Scholar] [CrossRef]
- Dymnikova, I.; Dobosz, A.; Sołtysek, B. Lemaître Class Dark Energy Model for Relaxing Cosmological Constant. Universe 2017, 3, 39. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Dobosz, A. Spacetime Symmetry and LemaîTre Class Dark Energy Models. Symmetry 2019, 11, 90. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. The algebraic structure of a cosmological term in spherically symmetric solutions. Phys. Lett. B 2000, 472, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Galaktionov, E. Vacuum dark fluid. Phys. Lett. B 2007, 645, 358–364. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Galaktionov, E. Dark ingredients in one drop. Central Europ. J. Phys. 2011, 9, 644–653. [Google Scholar] [CrossRef]
- Coleman, S. Classical lumps and their quantum descendants. In New Phenomena in Subnuclear Physics; Zichichi, A., Ed.; Plenum: New York, NY, USA, 1977; p. 297. [Google Scholar]
- Dymnikova, I. Dark Energy and Spacetime Symmetry. Universe 2017, 3, 20. [Google Scholar] [CrossRef] [Green Version]
- Anderson, P.R. Attractor states and infrared scaling in de Sitter space. Phys. Rev. D 2000, 62, 124019:1–124019:30. [Google Scholar] [CrossRef] [Green Version]
- Petrov, A.Z. Einstein Spaces; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Stephani, H.; Kramer, D.; MacCallum, V.; Hoenselaers, C.; Herlt, E. Exact Solutions of Einstein’s Field Equations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Rel. Grav. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Dymnikova, I. The cosmological term as a source of mass. Class. Quant. Grav. 2002, 19, 725–740. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. Spherically symmetric space-time with regular de Sitter center. Int. J. Mod. Phys. D 2003, 12, 1015–1034. [Google Scholar] [CrossRef] [Green Version]
- Poisson, E.; Israel, W. Structure of the black hole nucleus. Class. Quant. Grav. 1988, 5, L201–L205. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Black holes as possible sources of closed and semiclosed worlds. Phys. Rev. D 1990, 41, 383–394. [Google Scholar] [CrossRef]
- Dymnikova, I. Internal structure of nonsingular spherical black holes. In Internal Sructure of Black Holes and Spacetime Singularities; Burko, M., Ori, A., Eds.; Annals of the Israel Physical Society; Bristol Insitute of Physics Pulishing: Bristol, UK; Philadelphia, PA, USA; Jerusalem, Israel, 1997; Volume 13, pp. 422–440. [Google Scholar]
- Perez, A. Spin foam models for quantum gravity. Class. Quant. Grav. 2003, 20, R43–R104. [Google Scholar] [CrossRef] [Green Version]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bonanno, A.; Reuter, M. Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. D 2006, 73, 083005–083017. [Google Scholar] [CrossRef] [Green Version]
- Nicolini, P. Noncommutative black holes, the final appeal to quantum gravity: A review. Int. J. Mod. Phys. A 2009, 24, 1229–1308. [Google Scholar] [CrossRef]
- Kerr, R.P.; Schild, A. Some algebraically degenerate solutions of Einstein’s gravitational field equations. Proc. Symp. Appl. Math. 1965, 17, 199. [Google Scholar]
- Gürses, M.; Gürsey, F. Lorentz covariant treatment of the Kerr-Schild geometry. J. Math. Phys. 1975, 16, 2385–2390. [Google Scholar] [CrossRef] [Green Version]
- Newman, E.T.; Janis, A.J. Note on the Kerr Spinning Particle Metric. J. Math. Phys. 1965, 6, 915–917. [Google Scholar] [CrossRef]
- Iso, S.; Umetsu, H.; Wilczek, F. Anomalies, Hawking radiations, and regularity in rotating black holes. Phys. Rev. D 2006, 74, 044017. [Google Scholar] [CrossRef] [Green Version]
- Caravelli, F.; Modesto, L. Spinning loop black holes. Class. Quant. Grav. 2010, 27, 245022. [Google Scholar] [CrossRef]
- Bambi, C.; Modesto, L. Rotating regular black holes. Phys. Lett. B 2013, 721, 329–334. [Google Scholar] [CrossRef] [Green Version]
- Balart, L.; Vagenas, E.C. Regular black hole metrics and the weak energy condition. Phys. Lett. B 2014, 730, 14–17. [Google Scholar] [CrossRef] [Green Version]
- Toshmatov, B.; Ahmedov, B.; Abdujabbarov, A.; Stuchlik, Z. Rotating regular black hole solution. Phys. Rev. D 2014, 89, 104017. [Google Scholar] [CrossRef] [Green Version]
- Neves, J.C.S.; Saa, A. Regular rotating black holes and the weak energy condition. Phys. Lett. B 2014, 734, 44–48. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.G. A nonsingular rotating black hole. Eur. Phys. J. C 2015, 75, 532. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, S. Hawking fluxes and Anomalies in Rotating Regular Black Holes with a Time-Delay. Class. Quant. Grav. 2016, 33, 225016. [Google Scholar] [CrossRef]
- de Lorenzo, T.; Giusti, A.; Speziale, S. Non-singular rotating black hole with a time delay in the center. Gen. Rel. Grav. 2016, 48, 31. [Google Scholar] [CrossRef] [Green Version]
- Torres, R.; Fayos, F. On regular rotating black holes. Gen. Rel. Grav. 2017, 49, 2. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Galaktionov, E. Basic Generic Properties of Regular Rotating Black Holes and Solitons. Adv. Math. Phys. 2017, 2017, 1035381. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. Spinning self-gravitating electrovacuum soliton. Phys. Lett. B 2006, 639, 368–372. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Galaktionov, E. Regular rotating electrically charged black holes and solitons in nonlinear electrodynamics minimally coupled to gravity. Class. Quant. Grav. 2015, 32, 165015. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Galaktionov, E. Regular rotating de Sitter-Kerr black holes and solitons. Class. Quant. Grav. 2016, 33, 145010. [Google Scholar] [CrossRef]
- Dymnikova, I. Dark Matter Candidates with Dark Energy Interiors Determined by Energy Conditions. Symmetry 2020, 12, 662. [Google Scholar] [CrossRef] [Green Version]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Rubin, S.G. Black Holes, Cosmology and Extra Dimensions; World Scientific: Singapore, 2013. [Google Scholar]
- Schnittman, J.D. The Collisional Penrose Process. Gen. Rel. Grav. 2018, 50, 77. [Google Scholar] [CrossRef] [PubMed]
- Toshmatov, B.; Abdujabbarov, A.; Ahmedov, B.; Stuchlik, Z. Particle motion and Penrose processes around rotating regular black hole. Astroph. Sp. Sci. 2015, 357, 41. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlik, Z.; Ahmedov, B. Generic rotating regular black holes in general relativity coupled to nonlinear electrodynamics. Phys. Rev. D 2017, 95, 084037. [Google Scholar] [CrossRef] [Green Version]
- Hayward, S.A. Formation and evaporation of non-singular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [Green Version]
- Chiba, T.; Kimura, M. A note on geodesics in the Hayward metric. Prog. Theor. Exp. Phys. 2017, 2017, 043E01. [Google Scholar] [CrossRef] [Green Version]
- Bautista-Olvera, B.; Degollado, J.C.; German, G. Geodesic structure of a rotating regular black hole. arXiv 2019, arXiv:1908.01886. [Google Scholar]
- Teo, E. Spherical orbits around a Kerr black hole. Gen. Rel. Grav. 2021, 53, 10. [Google Scholar] [CrossRef]
- Cao, W.; Liu, W.; Wu, X. Integrability of Kerr-Newman spacetime with cloud strings, quintessence and electromagnetic field. Phys. Rev. D 2022, 105, 124039. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, N.; Liu, W.; Wu, X. Charged Particle Motions near Non-Schwarzschild Black Holes with External Magnetic Fields in Modified Theories of Gravity. Universe 2021, 7, 488. [Google Scholar] [CrossRef]
- Yang, D.; Cao, W.; Zhou, N.; Zhang, H.; Liu, W.; Wu, X. Chaos in a Magnetized Modified Gravity Schwarzschild Spacetime. Universe 2022, 8, 320. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. III. Reissner-Nordström-(anti)-de Sitter Black Holes. Astrophys. J. J. Suppl. Ser. 2021, 254, 8. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, N.; Liu, W.; Wu, X. Equivalence between two charged black holes in dynamics of orbits outside the event horizons. Gen. Rel. Grav. 2022, 54, 110. [Google Scholar] [CrossRef]
- Teo, E. Spherical Photon Orbits Around a Kerr Black Hole. Gen. Rel. Grav. 2003, 35, 1909–1926. [Google Scholar] [CrossRef]
- Johannsen, T. Photon rings around Kerr and Kerr-like black holes. Astrophys. J. 2013, 777, 170. [Google Scholar] [CrossRef] [Green Version]
- Mokdad, M. Reissner-Nordstrøm-de Sitter Manifold: Photon Sphere and Maximal Analytic Extension. arXiv 2017, arXiv:1701.06982. [Google Scholar] [CrossRef] [Green Version]
- Dolan, S.R.; Shipley, J.O. Stable photon orbits in stationary axisymmetric electrovacuum spacetimes. Phys. Rev. D 2016, 94, 044038. [Google Scholar] [CrossRef] [Green Version]
- Hod, S. On the number of light rings in curved spacetimes of ultra-compact objects. Phys. Lett. B 2018, 776, 1–4. [Google Scholar] [CrossRef]
- Hod, S. Analytic study of self-gravitating polytropic spheres with light rings. Eur. Phys. J. C 2018, 78, 417. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Berti, E.; Herdeiro, C.A.R. Light-Ring Stability for Ultracompact Objects. Phys. Rev. Lett. 2017, 119, 251102. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R. Stationary Black Holes and Light Rings. Phys. Rev. Lett. 2020, 124, 181101. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.; Gao, S. Universal properties of light rings for stationary axisymmetric spacetimes. Phys. Rev. D 2021, 103, 104031. [Google Scholar] [CrossRef]
- Ghosh, R.; Sarkar, S. Light rings of stationary spacetimes. Phys. Rev. D 2021, 104, 044019. [Google Scholar] [CrossRef]
- Dymnikova, I.; Dobosz, A.; Sołtysek, B. Classification of Circular Equatorial Orbits around Regular Rotating Black Holes and Solitons with the de Sitter/Phantom Interiors. Universe 2022, 8, 65. [Google Scholar] [CrossRef]
- Cardoso, V.; Crispino, L.C.B.; Macedo, C.F.B.; Okawa, H.; Pani, P. Light rings as observational evidence for event horizons: Long-lived modes, ergoregions and nonlinear instabilities of ultracompact objects. Phys. Rev. D 2014, 90, 044069. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. De Sitter-Schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529–540. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon Press: Oxford, UK, 1983. [Google Scholar]
- Dymnikova, I. Mass, Spacetime Symmetry, de Sitter Vacuum, and the Higgs Mechanism. Symmetry 2020, 12, 634. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Khlopov, M. Regular black hole remnants and graviatoms with de Sitter interior as heavy dark matter candidates probing inhomogeneity of early universe. Int. J. Mod. Phys. D 2015, 24, 1545002. [Google Scholar] [CrossRef]
- Dymnikova, I. The Fundamental Roles of the de Sitter Vacuum. Universe 2020, 6, 101. [Google Scholar] [CrossRef]
- Dymnikova, I.G. Motion of particles and photons in the gravitational field of a rotating body. Sov. Phys. Uspekhi 1986, 29, 215–237. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the Galactic Center. Astrophys. J. Lett. 2000, 528, L13–L16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takahashi, R. Shapes and positions of black hole shadows in accretion disks and spin parameters of black holes. Astrophys. J. 2004, 611, 996–1004. [Google Scholar] [CrossRef]
- Hioki, K.; Maeda, K. Measurement of the Kerr spin parameter by observation of a compact object’s shadow. Phys. Rev. D 2009, 80, 024042. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Bambi, C. Measuring the Kerr spin parameter of regular black holes from their shadow. J. Cosmol. Astropart. Phys. 2014, 2014, 041–061. [Google Scholar] [CrossRef]
- Mars, K.; Paganini, C.F.; Oancea, M.A. The fingerprints of black holes - shadows and their degeneracies. Class. Quant. Grav. 2018, 35, 025005. [Google Scholar] [CrossRef] [Green Version]
- Grenzebach, A.; Perlick, V.; Lámmerzahl, C. Photon regions and shadows of Kerr-Newman-NUT black holes with a cosmological constant. Phys. Rev. D 2014, 89, 124004. [Google Scholar] [CrossRef] [Green Version]
- Repin, S.V.; Kompaneets, D.A.; Novikov, I.D.; Mityagina, V.A. Shadow of rotating black holes on a standard background screen. arXiv 2018, arXiv:1802.04667. [Google Scholar]
- Doeleman, S.S.; Weintroub, J.; Rogers, A.E.; Plambeck, R.; Freund, R.; Tilanus, R.P.; Woody, D. Event-horizon-scale structure in the supermassive black hole candidate at the Galactic Center. Nature 2008, 455, 78–80. [Google Scholar] [CrossRef] [Green Version]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1–L8. [Google Scholar] [CrossRef]
- Ayon-Beato, A.; Garcia, A. The Bardeen model as a nonlinear magnetic monopole. Phys. Lett. B 2000, 493, 149–152. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Deng, C.; Wu, X.; Liang, E. Observational signatures of Schwarzschild-MOG black holes in scalar-tensor-vector gravity: Shadows and rings with different accretions. Eur. Phys. J. C 2022, 82, 885. [Google Scholar] [CrossRef]
- Atamurotov, F.; Hussain, I.; Mustafa, G.; Jusufi, K. Shadow and quasinormal modes of the Kerr–Newman–Kiselev–Letelier black hole. Europ. Phys. J. C 2022, 82, 831. [Google Scholar] [CrossRef]
- Adler, S.L.; Virbhadra, K.S. Cosmological constant corrections to the photon sphere and black hole shadow radii. Gen. Rel. Grav. 2022, 54, 93. [Google Scholar] [CrossRef]
- Wu, M.-H.; Guo, H.; Kuang, X.-M. Shadow Cast of Rotating Charged Black Hole with Scalar Q-Hair. Symmetry 2022, 14, 2237. [Google Scholar] [CrossRef]
- Mizuno, Y.; Younsi, Z.; Fromm, C.M.; Porth, O.; De Laurentis, M.; Olivares, H.; Falcke, H.; Kramer, M.; Rezzolla, L. The current ability to test theories of gravity with black hole shadows. Nat. Astron. Lett. 2018, 2, 585–590. [Google Scholar] [CrossRef]
- Garca, A.; Galtsov, D.; Kechkin, O. Class of stationary axisymmetric solutions of the Einstein-Maxwell-dilaton-axion field equations. Phys. Rev. Lett. 1995, 74, 1276–1279. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, Y.; Younsi, Z.; Wu, K.; Fuerst, S.V. General relativistic radiative transfer: Formulation and emission from structured tori around black holes. Astron. Astrophys. 2012, 545, A13. [Google Scholar]
- Chan, C.-K.; Psaltis, D.; Oezel, F.; Narayan, R.; Sadowski, A. The power of imaging: Constraining the plasma properties of GRMHD simulations using EHT observations of Sgr A. Astrophys. J. 2015, 799, 1. [Google Scholar] [CrossRef] [Green Version]
- Rezzolla, L.; Zhidenko, A. New parametrization for spherically symmetric black holes in metric theories of gravity. Phys. Rev. D 2014, 90, 084009. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R. Shadows and strong gravitational lensing: A brief review. Gen. Rel. Grav. 2018, 50, 42–51. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Kraav, K. Identification of a Regular Black Hole by Its Shadow. Universe 2019, 5, 163. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dymnikova, I.; Dobosz, A. Orbits of Particles and Photons around Regular Rotating Black Holes and Solitons. Symmetry 2023, 15, 273. https://doi.org/10.3390/sym15020273
Dymnikova I, Dobosz A. Orbits of Particles and Photons around Regular Rotating Black Holes and Solitons. Symmetry. 2023; 15(2):273. https://doi.org/10.3390/sym15020273
Chicago/Turabian StyleDymnikova, Irina, and Anna Dobosz. 2023. "Orbits of Particles and Photons around Regular Rotating Black Holes and Solitons" Symmetry 15, no. 2: 273. https://doi.org/10.3390/sym15020273