The Analysis of Bifurcation, Quasi-Periodic and Solitons Patterns to the New Form of the Generalized q-Deformed Sinh-Gordon Equation
Abstract
:1. Introduction
2. The Mathematical Analysis
3. Lie Symmetry Analysis
4. Symmetry Reductions
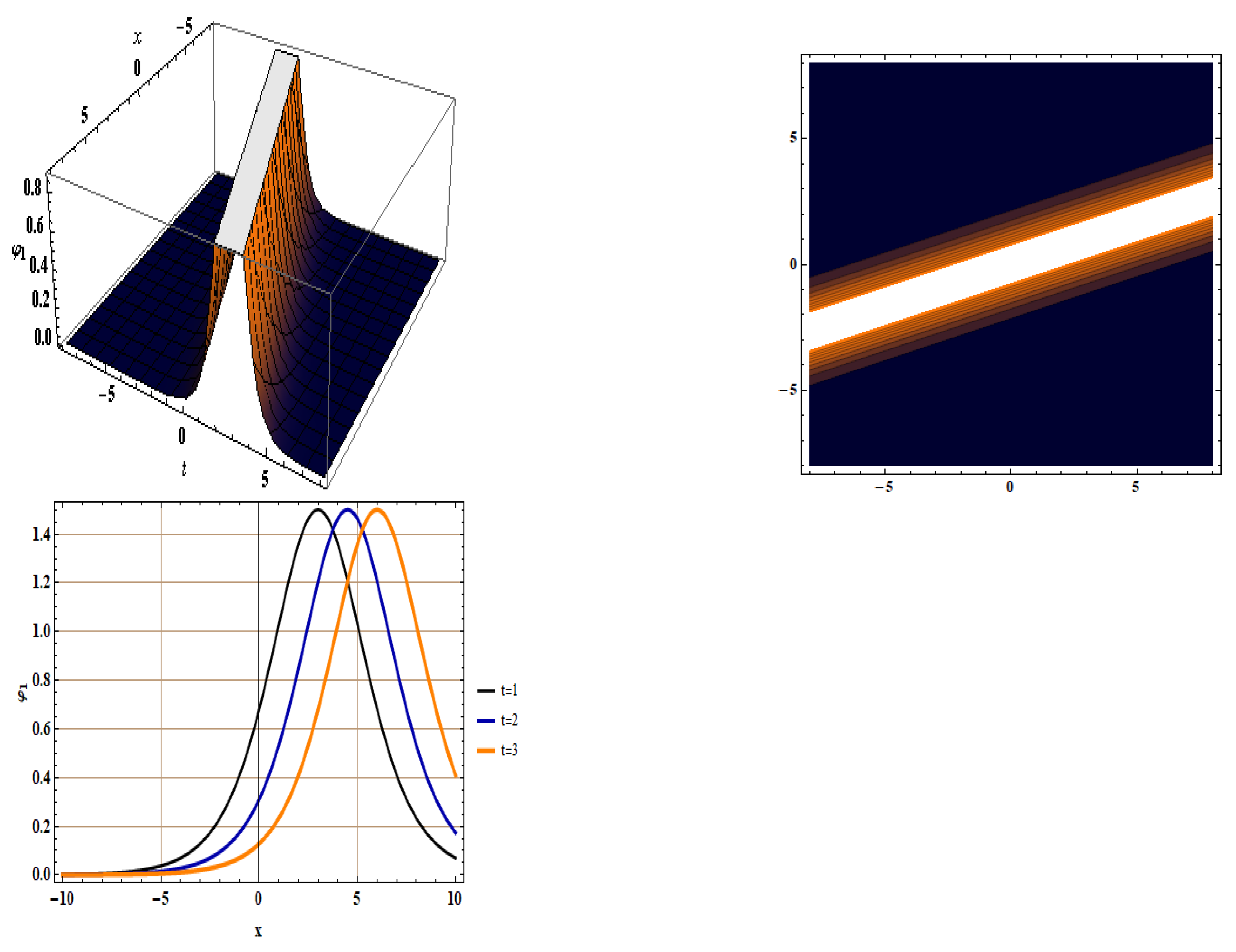
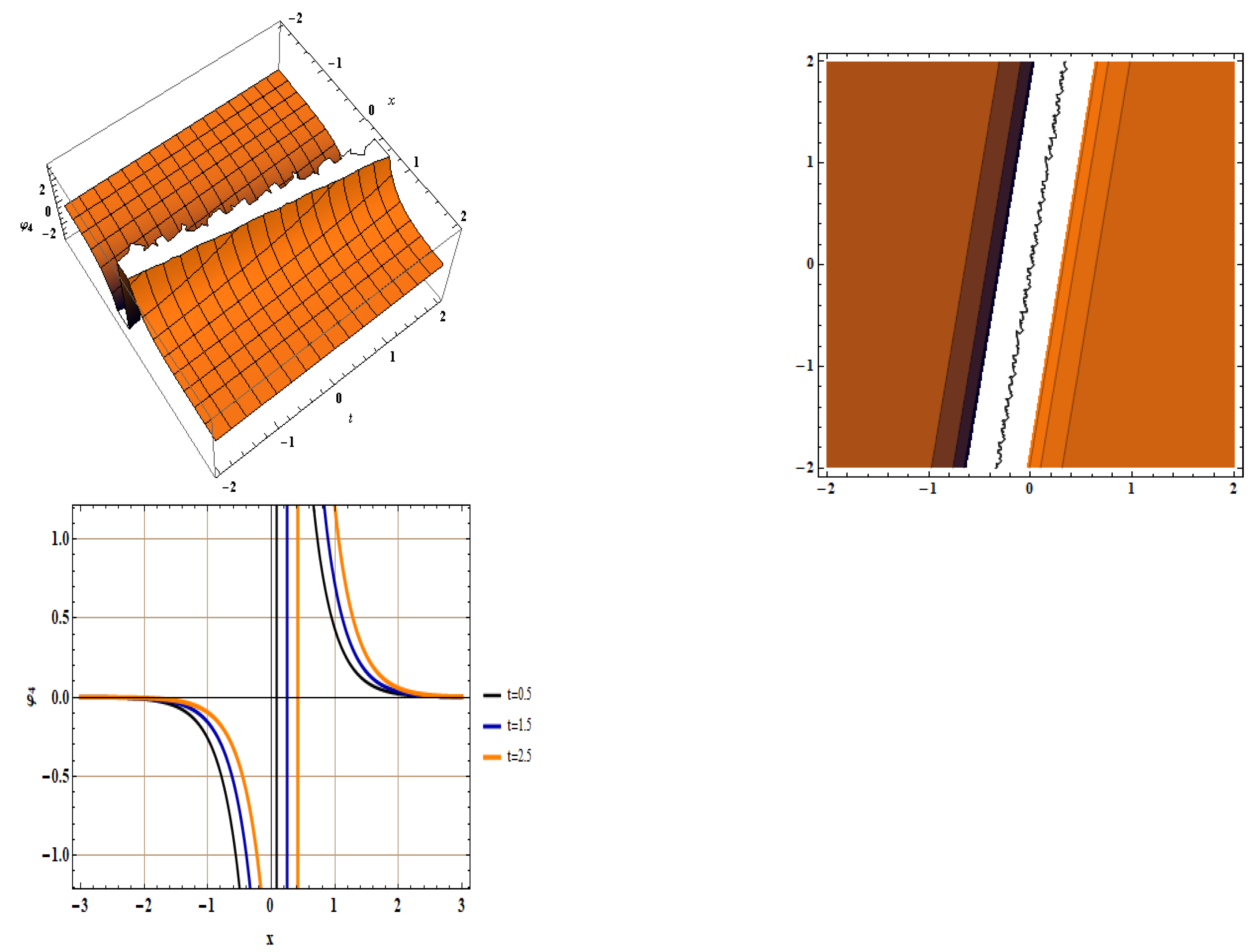
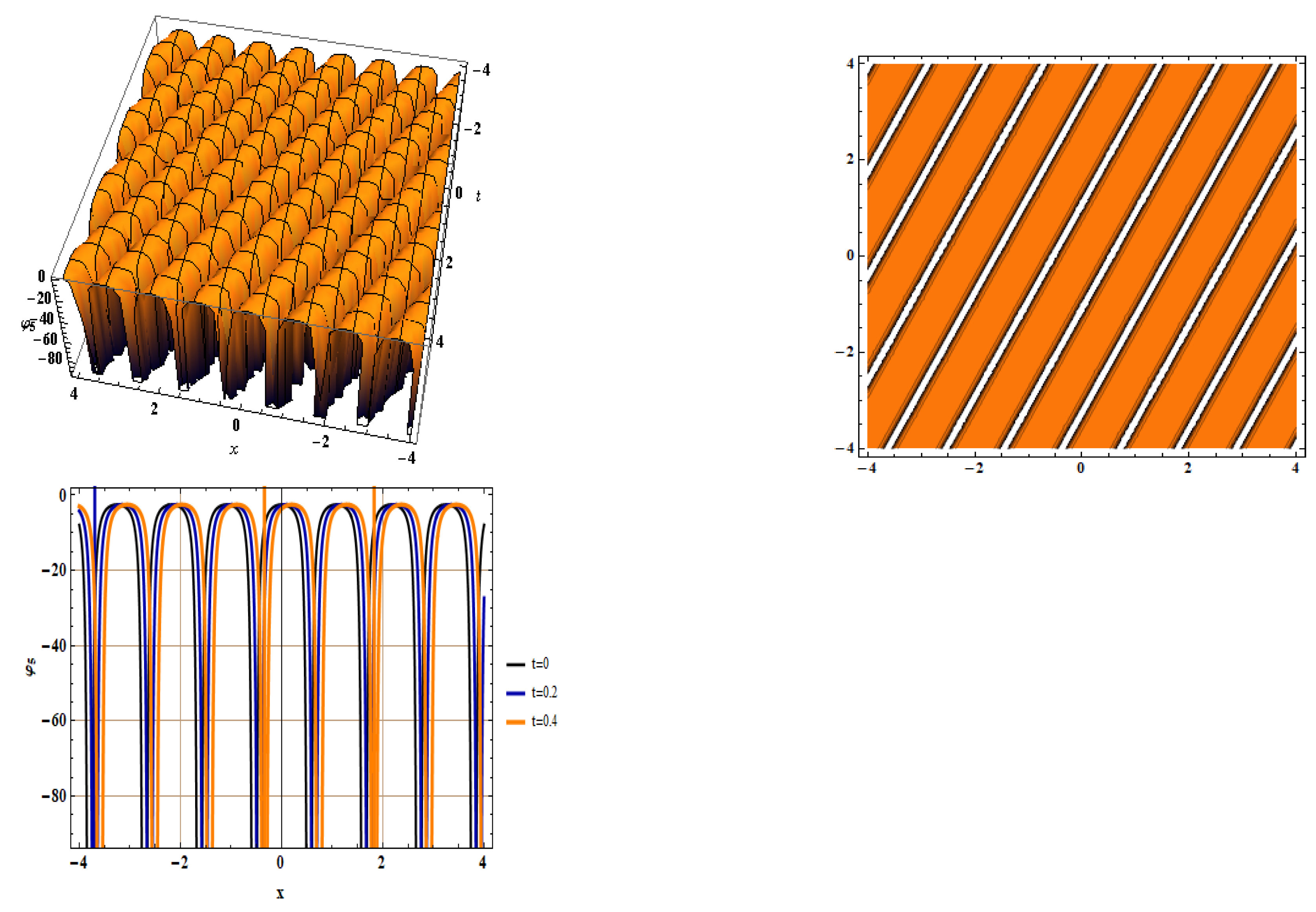
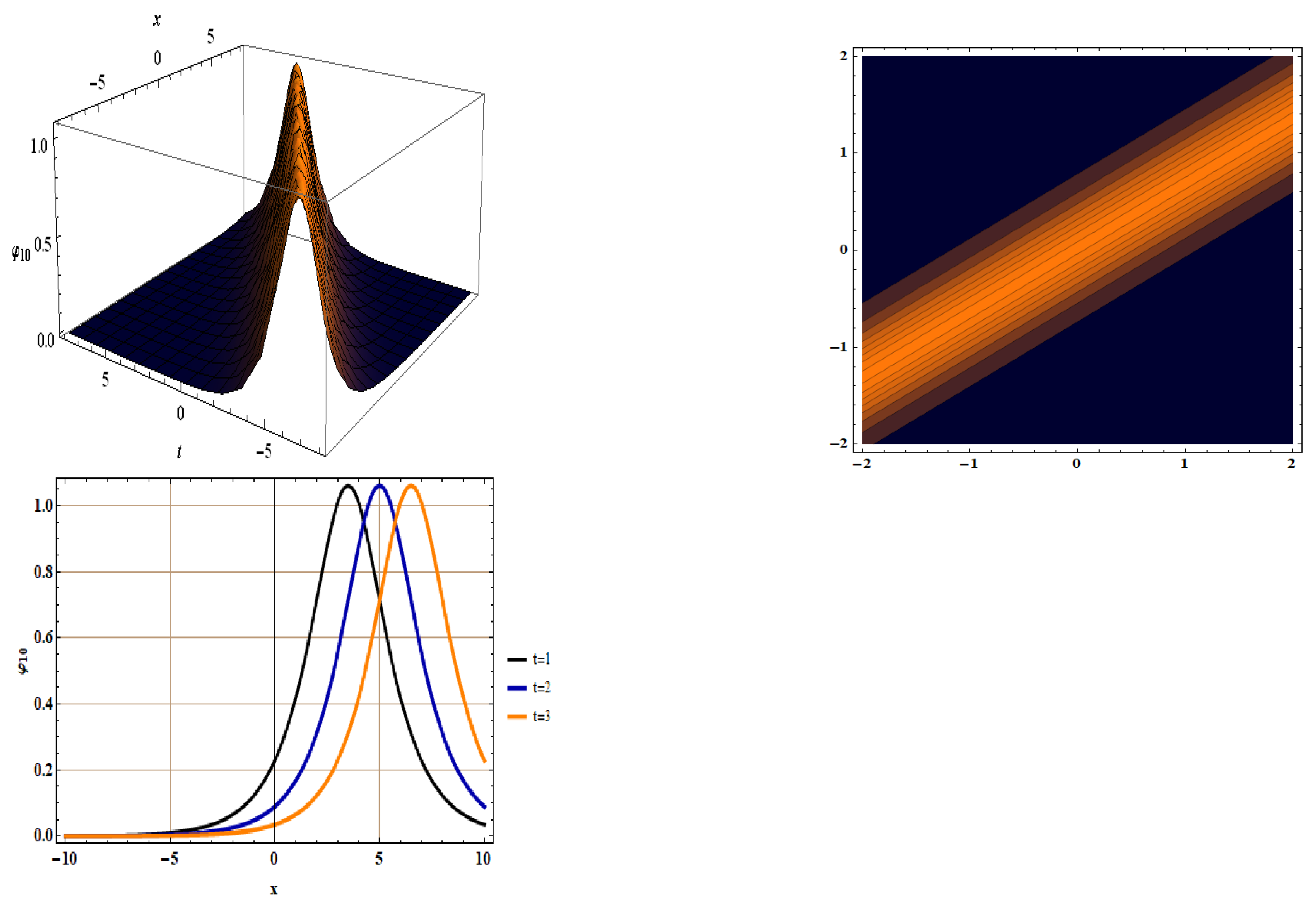
5. Soliton Solutions for Equation (5)
- Type 1: For and , we have
- Type 2: For and , we have
- Type 3: For and , we have
- Type 4: For and , we have
- Type 5: For , we have
- Type 6: For and , we have
- Type 7: For and , we havewith and .
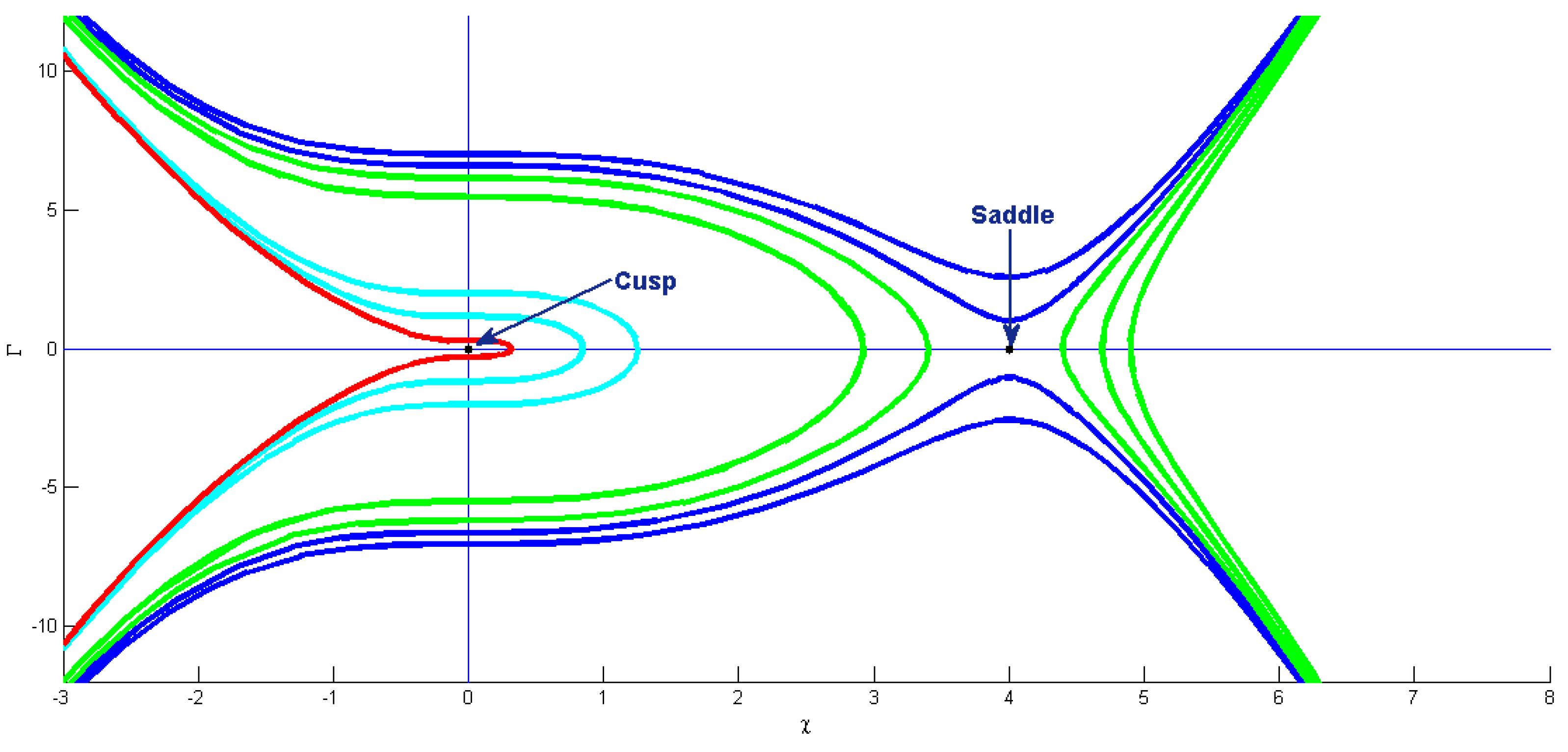
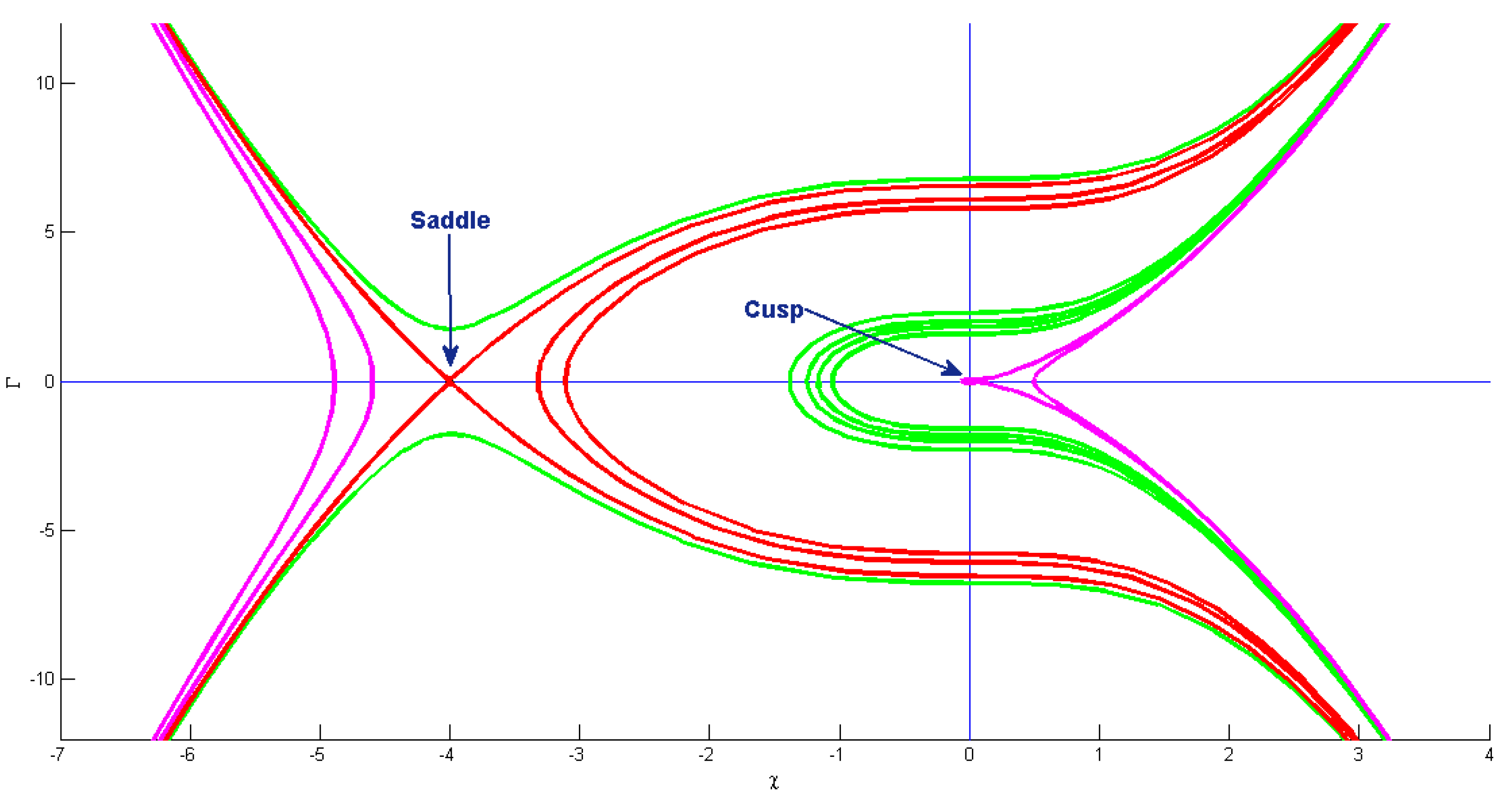
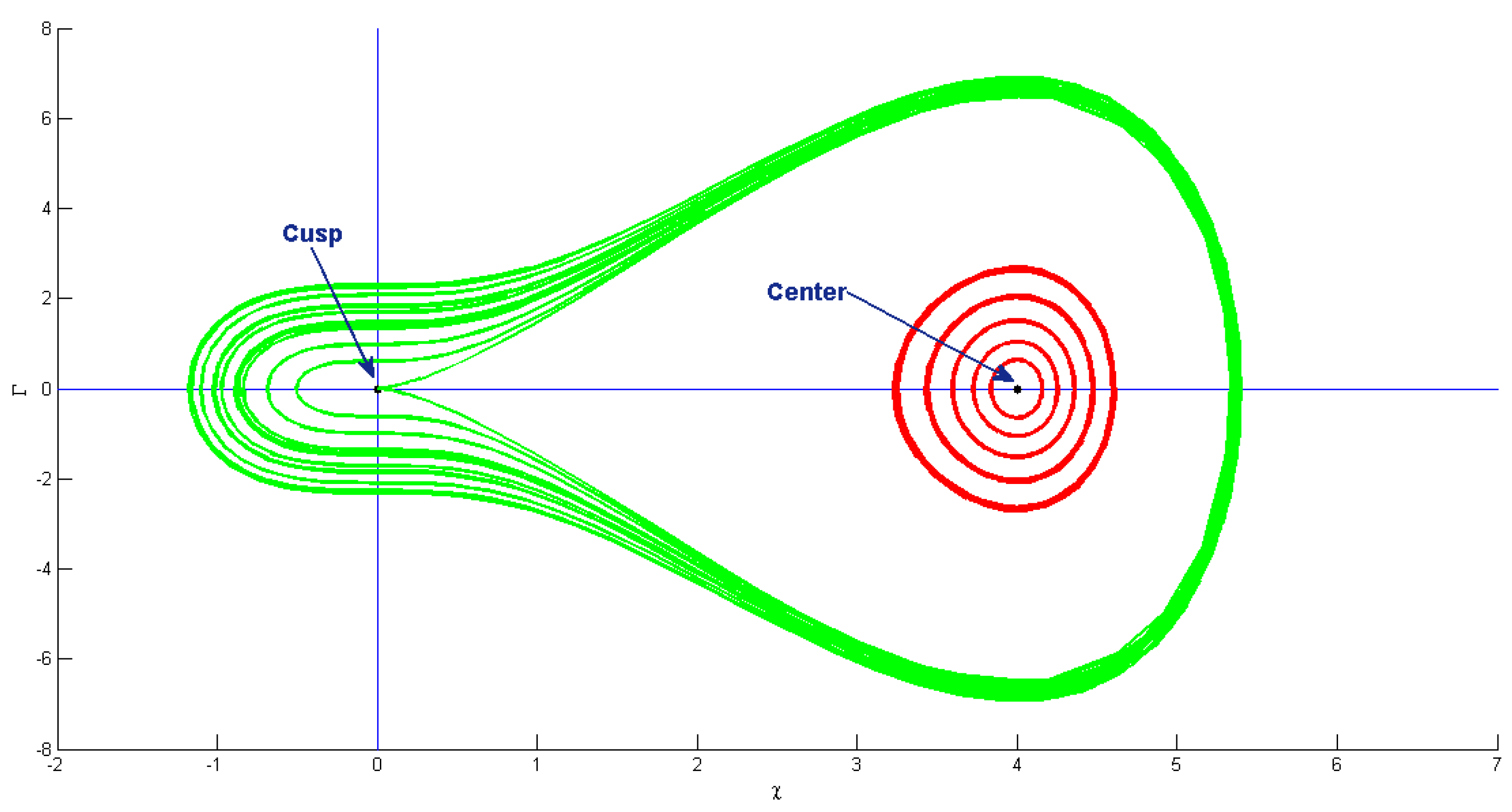
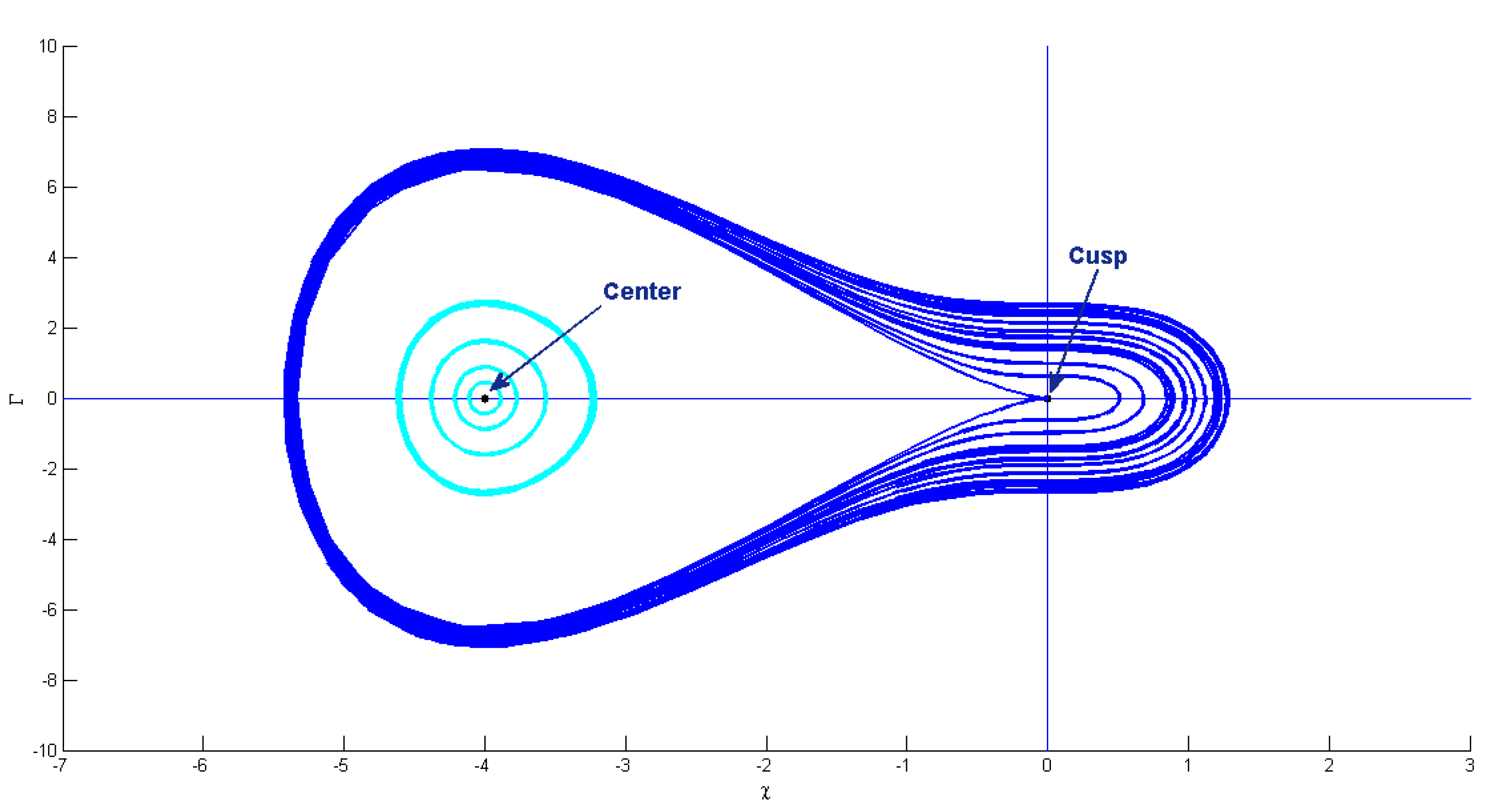
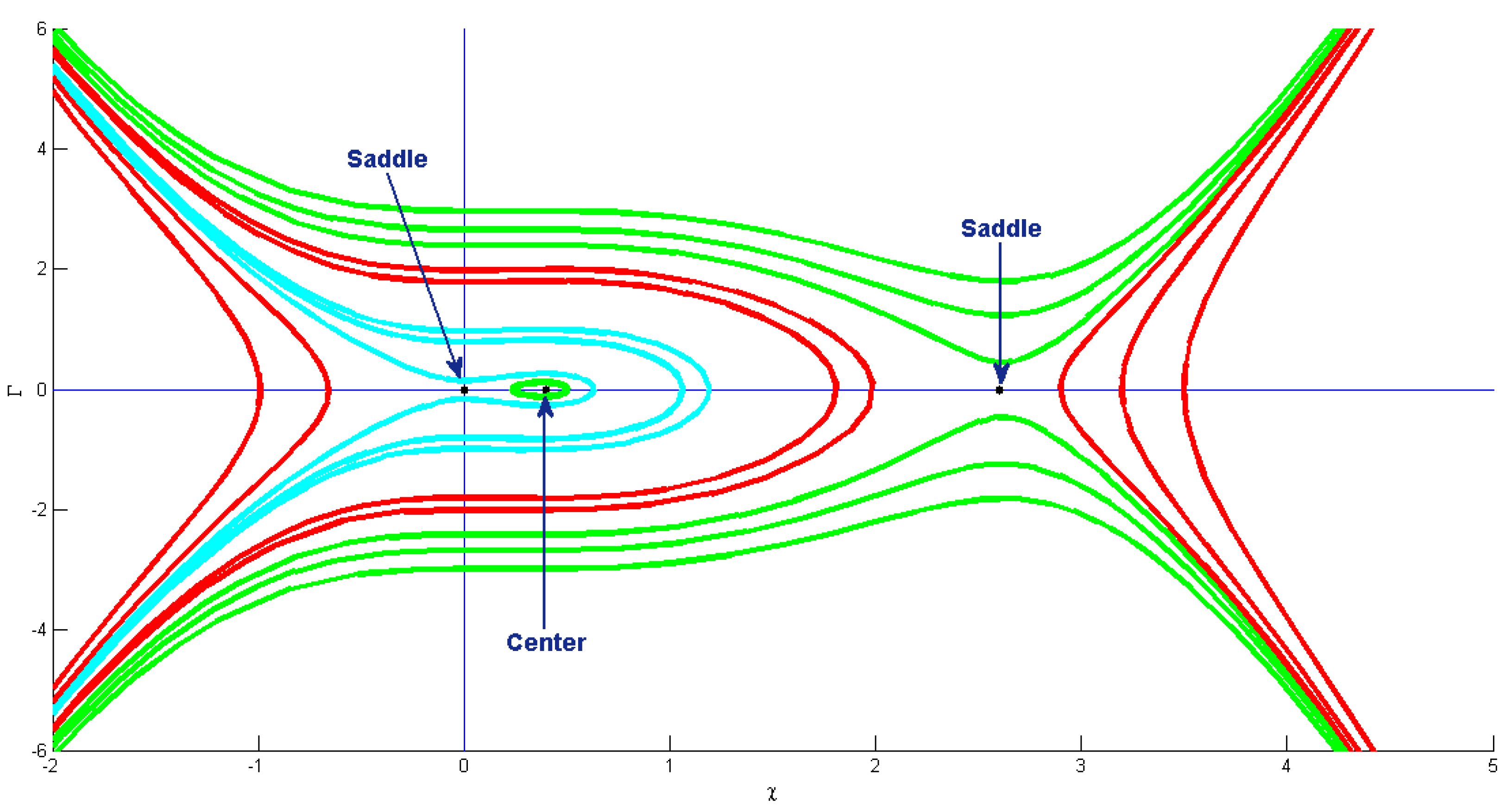
6. Bifurcation Analysis of Equation (5)
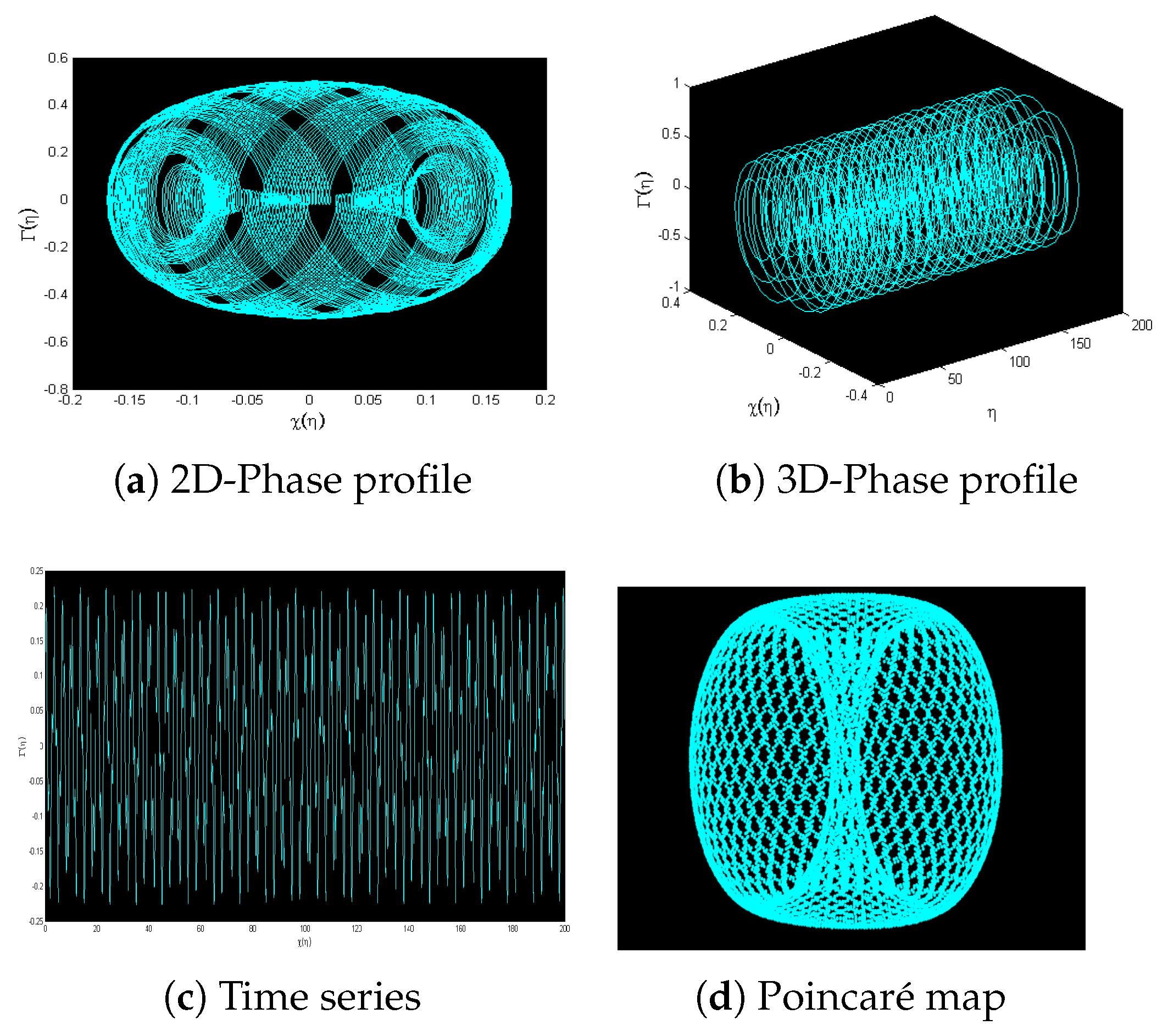
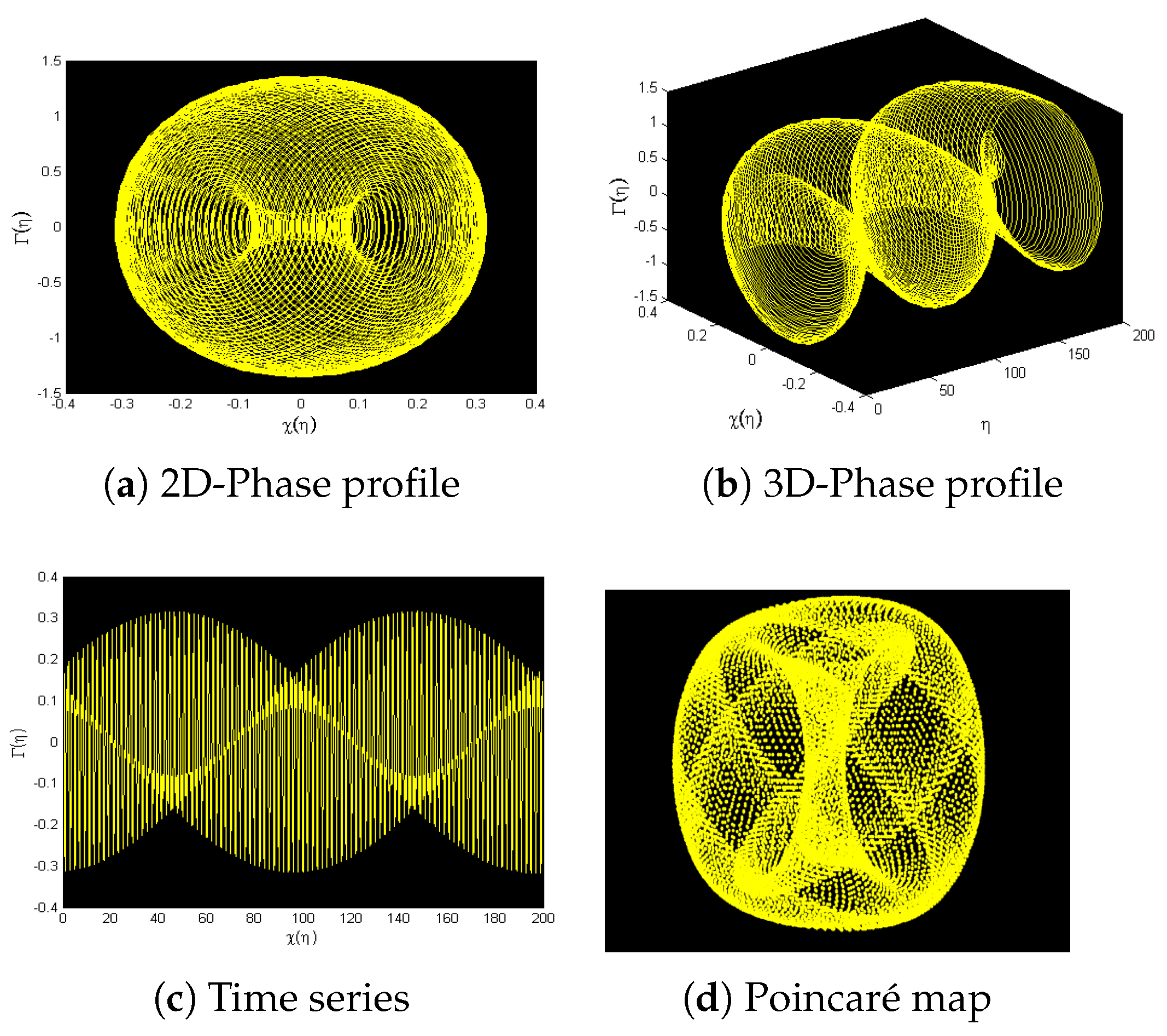
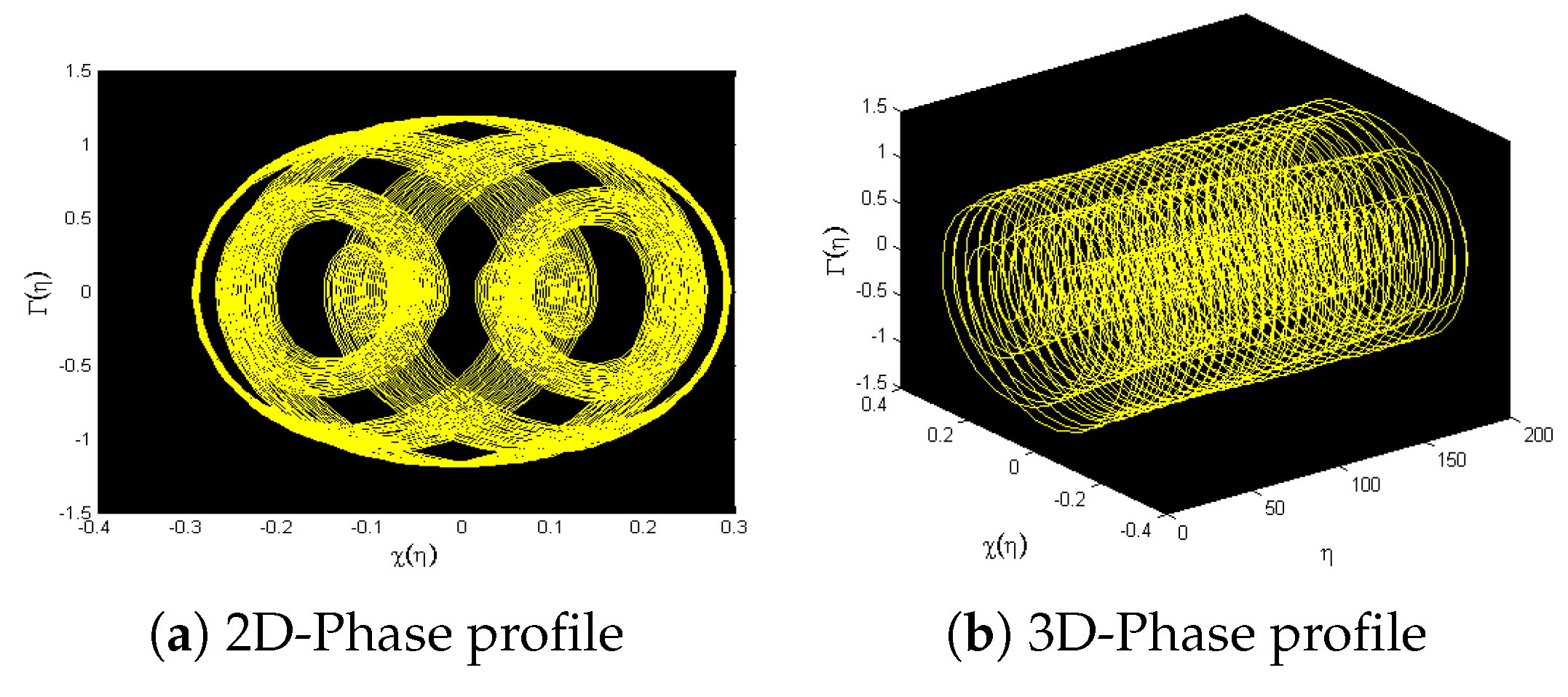
7. Phase Patterns for Quasi-Periodic Behavior
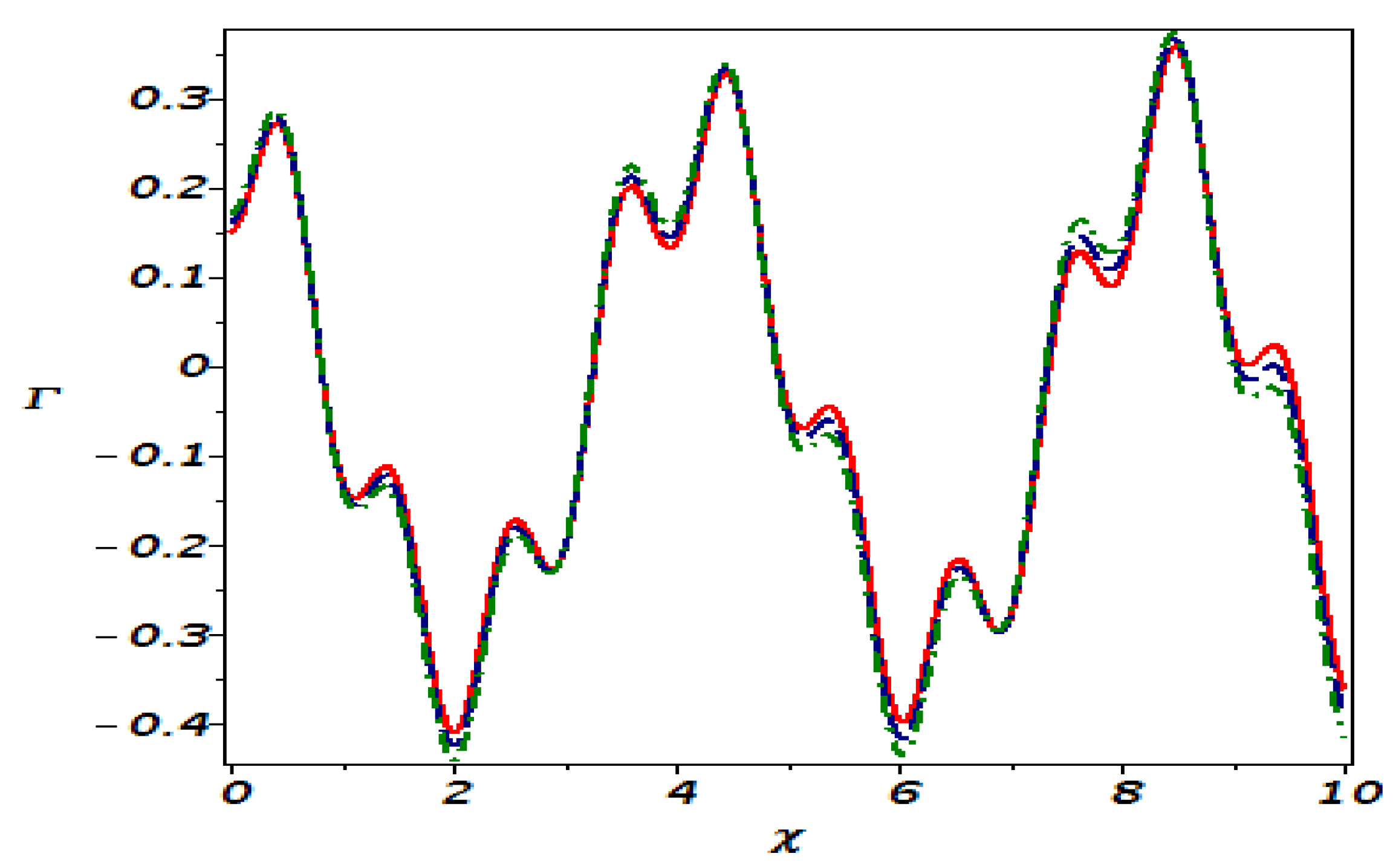
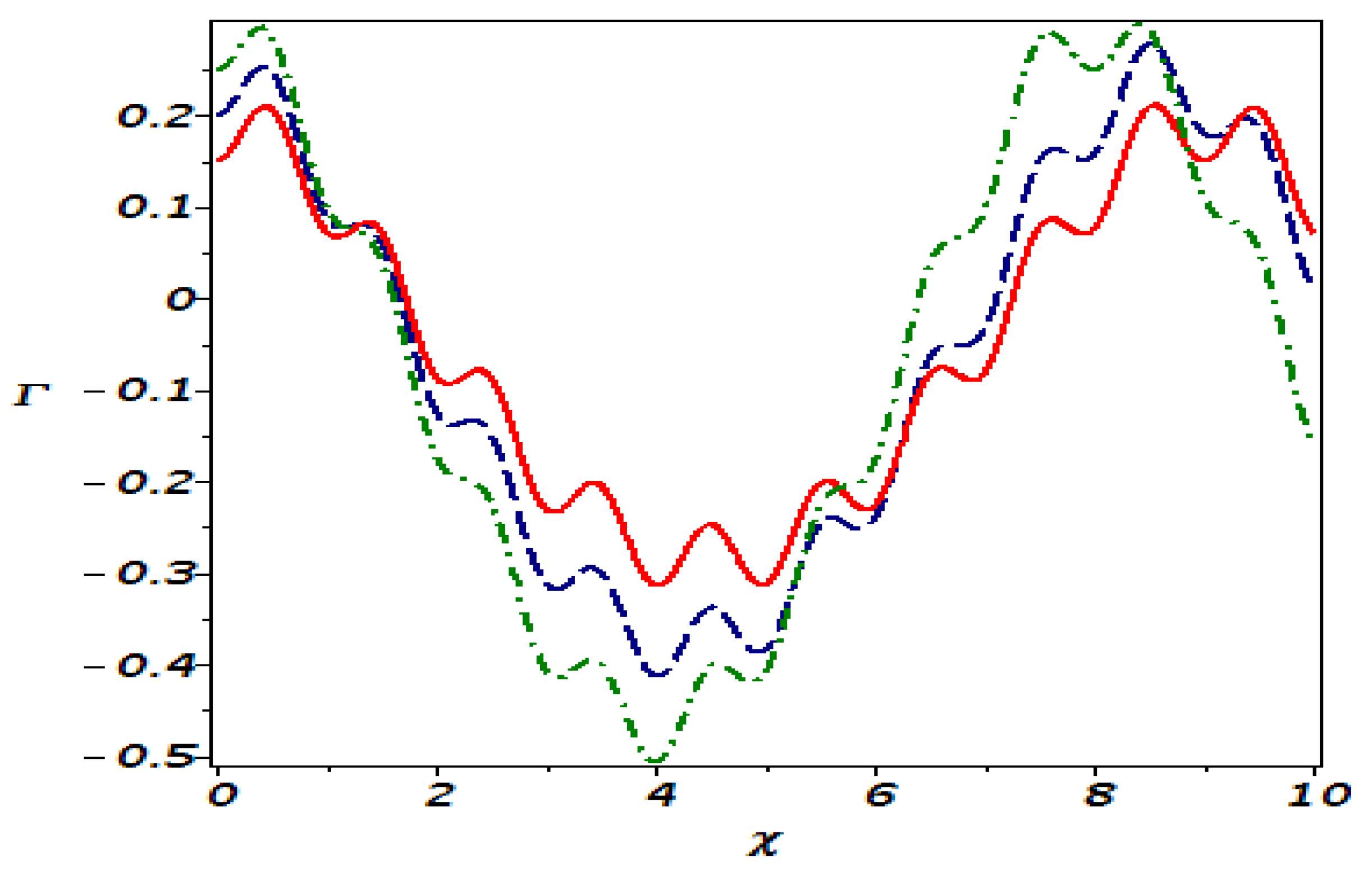
8. Sensitivity Analysis
9. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bruzzone, O.A.; Perri, D.V.; Easdale, M.H. Vegetation responses to variations in climate: A combined ordinary differential equation and sequential Monte Carlo estimation approach. Ecol. Inform. 2023, 73, 101913. [Google Scholar] [CrossRef]
- Zhou, T.Y.; Tian, B.; Zhang, C.R.; Liu, S.H. Auto-Bäcklund transformations, bilinear forms, multiple-soliton, quasi-soliton and hybrid solutions of a (3 + 1)-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov equation in an electron-positron plasma. Eur. Phys. J. Plus 2022, 137, 912. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Akinyemi, L.; Rezazadeh, H.; Yao, S.W.; Akbar, M.A.; Khater, M.M.; Jhangeer, A.; Inc, M.; Ahmad, H. Nonlinear dispersion in parabolic law medium and its optical solitons. Results Phys. 2021, 26, 104411. [Google Scholar] [CrossRef]
- Hassan, S.M.; Altwaty, A.A. Optical Solitons of The Extended Gerdjikov-Ivanov Equation in DWDM System by Extended Simplest Equation Method. Appl. Math. Inf. Sci. 2020, 14, 901–907. [Google Scholar]
- Khater, M.M.A.; Attia, R.A.M.; Abdel-Aty, A. Computational analysis of a nonlinear fractional emerging telecommunication model with higher–order dispersive cubic–quintic. Inf. Sci. Lett. 2020, 9, 83–93. [Google Scholar]
- Nguyen, L.T.K. Wronskian formulation and Ansatz method for bad Boussinesq equation. Vietnam J. Math. 2016, 44, 449–462. [Google Scholar] [CrossRef]
- Hirota, R. Direct methods in soliton theory. Solitons 1980, 44, 157–176. [Google Scholar]
- Raza, N.; Seadawy, A.R.; Kaplan, M.; Butt, A.R. Symbolic computation and sensitivity analysis of nonlinear Kudryashov’s dynamical equation with applications. Phys. Scr. 2021, 96, 105216. [Google Scholar] [CrossRef]
- Zainab, I.; Akram, G. Effect of derivative on time fractional Jaulent-Miodek system under modified auxiliary equation method and exp(−g(O))-expansion method. Chaos Solitons Fractals 2023, 168, 113147. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Mirzazadeh, M. Optical solitons of the perturbed nonlinear Schrödinger equation using Lie symmetry method. Optik 2023, 281, 170816. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Kumar, A. Lie symmetry analysis for obtaining the abundant exact solutions, optimal system, and dynamics of solitons for a higher-dimensional Fokas equation. Chaos Solitons Fractals 2021, 142, 110507. [Google Scholar] [CrossRef]
- Cimpoiasu, R.; Rezazadeh, H.; Florian, D.A.; Ahmad, H.; Nonlaopon, K.; Altanji, M. Symmetry reductions and invariant-group solutions for a two-dimensional Kundu-Mukherjee-Naskar model. Results Phys. 2021, 28, 104583. [Google Scholar] [CrossRef]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer Science and Business Media: Berlin, Germany, 2013; Volume 81. [Google Scholar]
- Kosmann-Schwarzbach, Y. Groups and Symmetries; Springer: New York, NY, USA, 2010. [Google Scholar]
- Dorodnitsyn, V.A.; Kaptsov, E.I.; Kozlov, R.V.; Meleshko, S.V. One-dimensional MHD flows with cylindrical symmetry: Lie symmetries and conservation laws. Int. J.-Non-Linear Mech. 2023, 148, 104290. [Google Scholar] [CrossRef]
- Jhangeer, A.; Raza, N.; Rezazadeh, H.; Seadawy, A. Nonlinear self-adjointness, conserved quantities, bifurcation analysis and travelling wave solutions of a family of long-wave unstable lubrication model. Pramana 2020, 94, 87. [Google Scholar] [CrossRef]
- Hussain, A.; Usman, M.; Al-Sinan, B.R.; Osman, W.M.; Ibrahim, T.F. Symmetry analysis and closed-form invariant solutions of the nonlinear wave equations in elasticity using optimal system of Lie subalgebra. Chin. J. Phys. 2023, 83, 1–13. [Google Scholar] [CrossRef]
- Abdalla, A.; Abbas, I.; Sapoor, H. The Effects of Fractional Derivatives of Bio-Heat Model in Living Tissues using Analytical-Numerical Method. Inf. Sci. Lett. 2022, 11, 7–13. [Google Scholar]
- Zada, L.; Al-Hamami, M.; Nawaz, R.; Jehanzeb, S.; Morsy, A.; Abdel-Aty, A.; Nisar, K.S. A New Approach for Solving Fredholm Integro-Differential Equations. Inf. Sci. Lett. 2021, 10, 407–415. [Google Scholar]
- Akinyemi, L. A fractional analysis of Noyes-Field model for the nonlinear Belousov-Zhabotinsky reaction. Comput. Appl. Math. 2020, 39, 175. [Google Scholar] [CrossRef]
- Nguyen, L.T.K. Soliton solution of good Boussinesq equation. Vietnam J. Math. 2016, 44, 375–385. [Google Scholar] [CrossRef]
- Nguyen, L.T.K.; Smyth, N.F. Modulation Theory for Radially Symmetric Kink Waves Governed by a Multi-Dimensional Sine-Gordon Equation. J. Nonlinear Sci. 2023, 33, 11. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the sine-Gordon equation for multiple collisions of solitons. J. Phys. Soc. Jpn. 1972, 33, 1459–1463. [Google Scholar] [CrossRef]
- Lavagno, A.; Scarfone, A.; Narayana Swamy, P. Classical and quantum q-deformed physical systems. Eur. Phys. J. C 2006, 47, 253–261. [Google Scholar] [CrossRef]
- Kaniadakis, G.; Lavagno, A.; Quarati, P. Kinetic model for q-deformed bosons and fermions. Phys. Lett. 1997, 227, 227–231. [Google Scholar] [CrossRef] [Green Version]
- Eleuch, H.; Ben Nessib, N.; Bennaceur, R. Quantum model of emission in a weakly non ideal plasma. Eur. Phys. J. D 2004, 29, 391–395. [Google Scholar] [CrossRef]
- Aganagic, M.; Ooguri, H.; Saulina, N.; Vafa, C. Black holes, q-deformed 2d Yang–Mills, and non-perturbative topological strings. Nuclear Phys. B 2005, 715, 304–348. [Google Scholar] [CrossRef] [Green Version]
- Dil, E.; Kolay, E.; Ersanli, C.C. On the deformed Einstein equations and quantum black holes. J. Phys. Conf. Ser. 2016, 766, 012004. [Google Scholar] [CrossRef] [Green Version]
- Arai, A. Exact solutions of multi-component nonlinear Schrödinger and Klein-Gordon equations in two-dimensional space-time. J. Phys. Math. Gen. 2001, 34, 4281. [Google Scholar] [CrossRef]
- Chai, N.; Dymarsky, A.; Smolkin, M. Model of persistent breaking of discrete symmetry. Phys. Rev. Lett. 2022, 128, 011601. [Google Scholar] [CrossRef]
- Berra-Montiel, J.; Molgado, A. Coherent representation of fields and deformation quantization. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050166. [Google Scholar] [CrossRef]
- Holmes, D.P. Elasticity and stability of shape-shifting structures. Curr. Opin. Colloid Interface Sci. 2019, 40, 118–137. [Google Scholar] [CrossRef] [Green Version]
- Eleuch, H. Some analytical solitary wave solutions for the generalized q-deformed Sinh-Gordon equation. Adv. Math. Phys. 2018, 2018, 5242757. [Google Scholar] [CrossRef] [Green Version]
- Raza, N.; Arshed, S.; Alrebdi, H.I.; Abdel-Aty, A.H.; Eleuch, H. Abundant new optical soliton solutions related to q-deformed Sinh-Gordon model using two innovative integration architectures. Results Phys. 2022, 35, 105358. [Google Scholar] [CrossRef]
- Ali, K.K.; Abdel-Aty, A.H. An extensive analytical and numerical study of the generalized q-deformed Sinh-Gordon equation. J. Ocean. Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Raza, N.; Butt, A.R.; Arshed, S.; Kaplan, M. A new exploration of some explicit soliton solutions of q-deformed Sinh-Gordon equation utilizing two novel techniques. Opt. Quantum Electron. 2023, 55, 200. [Google Scholar] [CrossRef]
- Ali, K.K.; Alrebdi, H.I.; Alsaif, N.A.; Abdel-Aty, A.H.; Eleuch, H. Analytical Solutions for a New Form of the Generalized q-Deformed Sinh-Gordon Equation: . Symmetry 2023, 15, 470. [Google Scholar] [CrossRef]
- Almusawa, H.; Jhangeer, A. A study of the soliton solutions with an intrinsic fractional discrete nonlinear electrical transmission line. Fractal Fract. 2022, 6, 334. [Google Scholar] [CrossRef]
- Rafiq, M.H.; Raza, N.; Jhangeer, A. Dynamic study of bifurcation, chaotic behavior and multi-soliton profiles for the system of shallow water wave equations with their stability. Chaos Solitons Fractals 2023, 171, 113436. [Google Scholar] [CrossRef]
- Li, Z.; Huang, C. Bifurcation, phase portrait, chaotic pattern and optical soliton solutions of the conformable Fokas-Lenells model in optical fibers. Chaos Solitons Fractals 2023, 169, 113237. [Google Scholar] [CrossRef]
- Zhang, X.; Min, F.; Dou, Y.; Xu, Y. Bifurcation analysis of a modified FitzHugh-Nagumo neuron with electric field. Chaos Solitons Fractals 2023, 170, 113415. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer Science and Business Media: Berlin, Germany, 1993; Volume 107. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1995; Volume 3. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazmi, S.S.; Jhangeer, A.; Raza, N.; Alrebdi, H.I.; Abdel-Aty, A.-H.; Eleuch, H. The Analysis of Bifurcation, Quasi-Periodic and Solitons Patterns to the New Form of the Generalized q-Deformed Sinh-Gordon Equation. Symmetry 2023, 15, 1324. https://doi.org/10.3390/sym15071324
Kazmi SS, Jhangeer A, Raza N, Alrebdi HI, Abdel-Aty A-H, Eleuch H. The Analysis of Bifurcation, Quasi-Periodic and Solitons Patterns to the New Form of the Generalized q-Deformed Sinh-Gordon Equation. Symmetry. 2023; 15(7):1324. https://doi.org/10.3390/sym15071324
Chicago/Turabian StyleKazmi, Syeda Sarwat, Adil Jhangeer, Nauman Raza, Haifa I. Alrebdi, Abdel-Haleem Abdel-Aty, and Hichem Eleuch. 2023. "The Analysis of Bifurcation, Quasi-Periodic and Solitons Patterns to the New Form of the Generalized q-Deformed Sinh-Gordon Equation" Symmetry 15, no. 7: 1324. https://doi.org/10.3390/sym15071324







