Construction-Monitoring Analysis of a Symmetrical Rigid Frame Tied Steel Box Arch Bridge in Southwest China Based on Segmental Assembly Technique
Abstract
1. Introduction
2. Materials and Methods
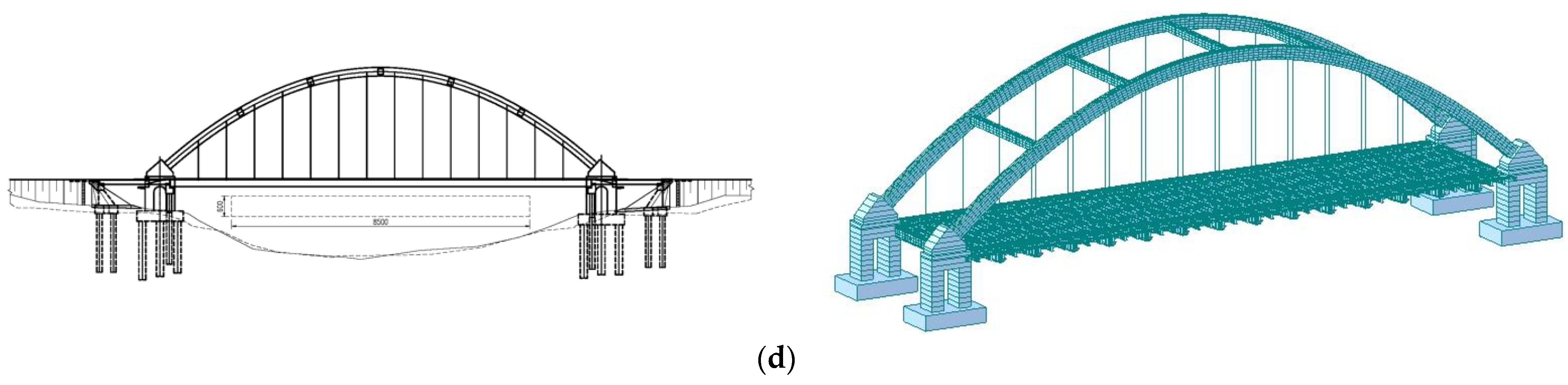
2.1. Bridge Overview
2.1.1. Structural Form
2.1.2. Structural Finite Element and Material Properties of Bridge Construction Process
2.2. Construction-Monitoring Methods Applied to Dafeng River Bridge
2.2.1. Objectives of Bridge Construction Monitoring
2.2.2. Methods and Objects of Bridge Construction Monitoring
- Geometric monitoring
- 2.
- Stress and cable force monitoring
- Cable force detection of long suspender hinged at both ends
- Cable force detection of thick and short suspenders hinged at both ends
- Tension detection of thick and short suspenders fixed at both ends
3. Results and Discussion
3.1. Construction Monitoring and Analysis of Arch Rib Sections and Bridge Deck Elevation
3.1.1. Monitoring Point Arrangement of Arch Rib Section
3.1.2. Measuring Monitoring Regarding Bridge Deck Elevation
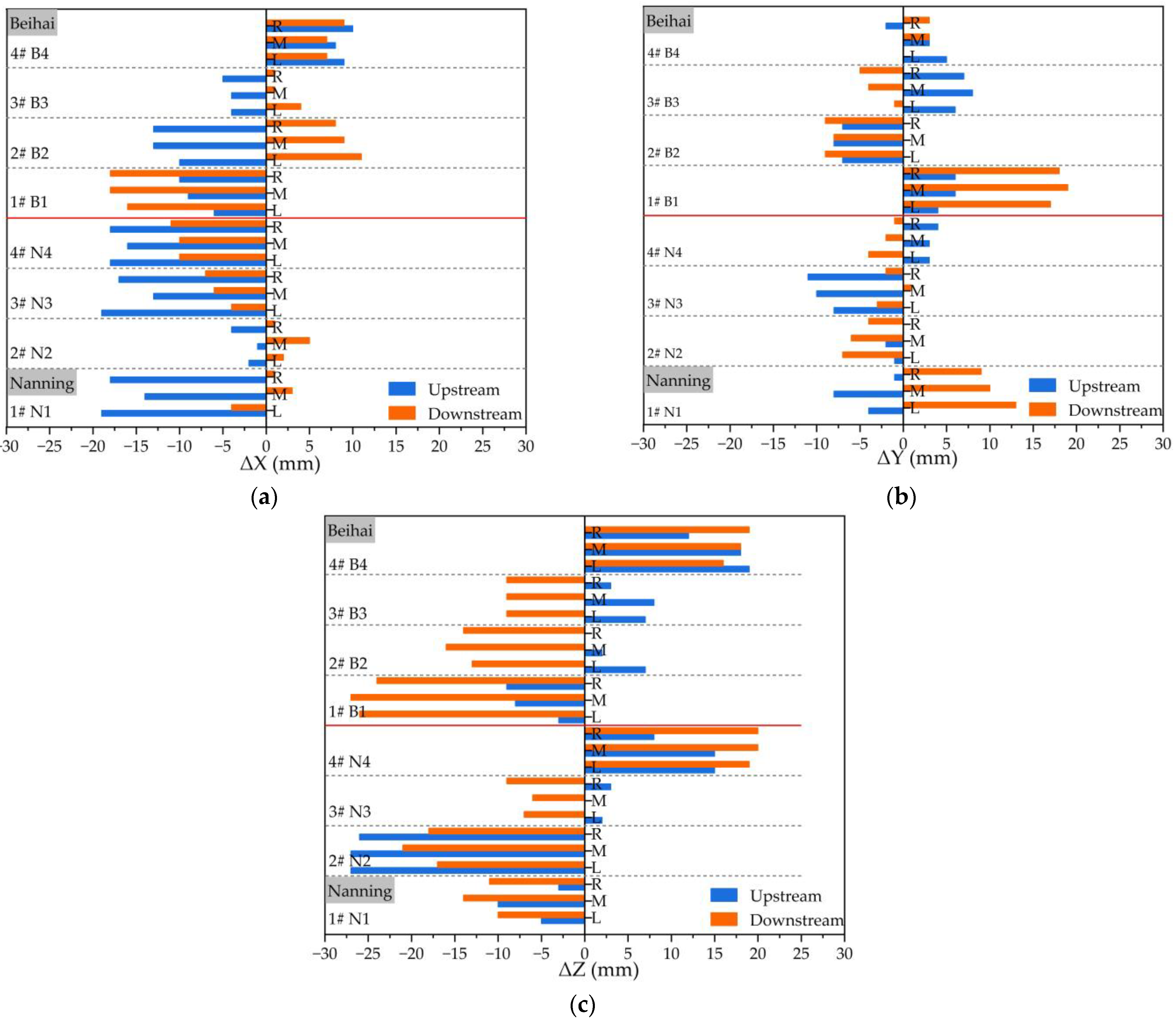
3.1.3. Position-Monitoring Analysis of Arch Rib during Hoisting
3.1.4. Alignment Measurement Monitoring of Arch Rib after Closure
3.2. Force Monitoring of Main Arch, Deck Lattice Beam, Suspender Cable, and Tie Rod Cable
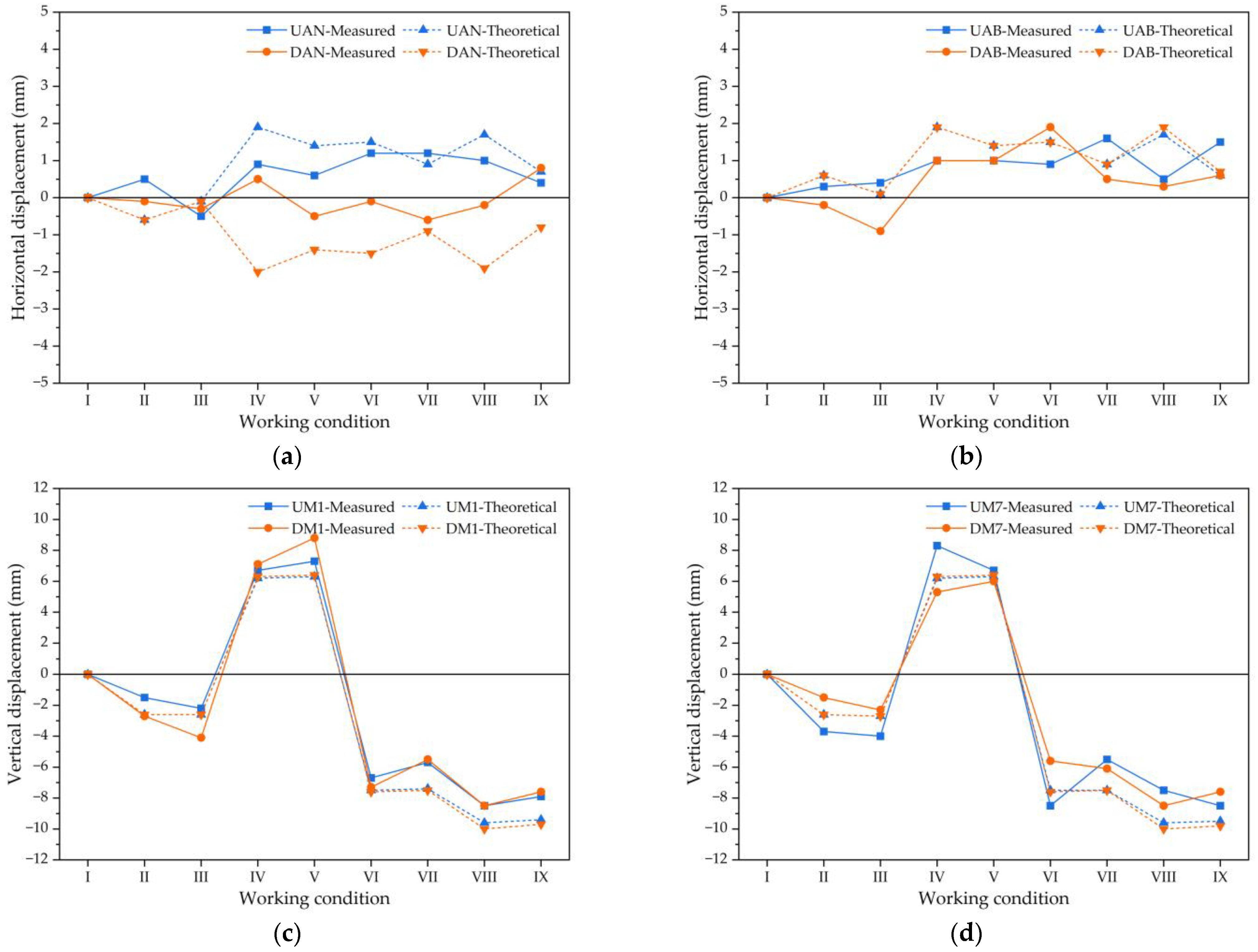
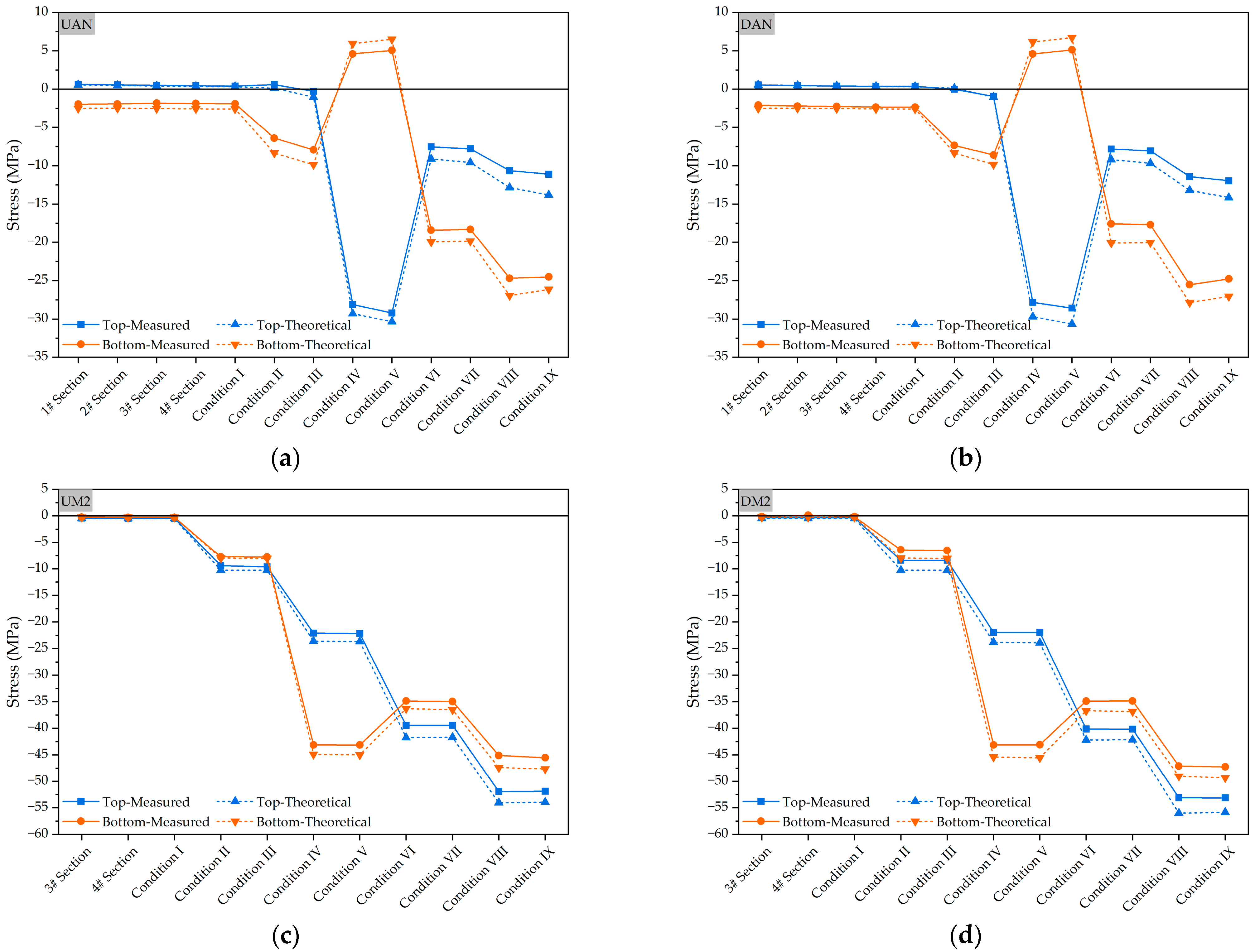
3.2.1. Stress-Monitoring Analysis of Main Arch
3.2.2. Stress-Monitoring Analysis of Deck Lattice Beam
3.2.3. Cable-Force-Monitoring Analysis of Suspender and Tie Rod
4. Conclusions
- (1)
- The maximum total deformation of the steel platform was 5.97 mm downwards. The maximum deviation value for the arch rib axis during hoisting was 19~27 mm. The maximum deviation values for axis and elevation were (−6~5) mm and (−3~4) mm.
- (2)
- The construction-monitoring results of the arch rib sections and bridge deck elevation indicate that accurate calculation and control ensured the precise positioning of the arch rib and lattice beam. The overall degree of bridge alignment was smooth, and the measured alignment aligns well with the theoretical alignment.
- (3)
- The measured stress of the main arch and lattice beam was generally consistent with the theoretical stress results, determined through finite element calculation, at each stage. This consistency was confirmed by the control section stress measurements across the entire bridge. The deviation between the measured cable force and the theoretical value was within 10%, indicating good stress reserve and that overall construction control was satisfactory.
- (4)
- An FE model of the entire bridge during the construction process was established using MIDAS Civil software, and simulation calculations were performed for the entire construction process in accordance with the construction scheme of the bridge. Using this method, the key parameters, including displacement and internal force status, during bridge construction can be determined, and a comparison and analysis with the construction monitoring data can provide useful guidance for the segmental assembly construction technique.
- (5)
- The symmetrical construction for this bridge results in symmetric displacement, stress, and cable force measurements at monitoring points under different working conditions. This confirms the effectiveness of the segmental assembly technique for construction monitoring.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Q.; Wu, X.G.; Zhang, Y.F.; Ma, M. Proposed New Analytical Method of Tower Load in Large-Span Arch Bridge Cable Lifting Construction. Appl. Sci. 2022, 12, 9373. [Google Scholar] [CrossRef]
- Tan, G.J.; Li, H.; Wang, W.S.; Kong, Q.W.; Jiang, L.; Zhang, S.F.; Wei, X.L. A rapid evaluation method based on natural frequency for post-earthquake traffic capacity of small and medium span bridges. Eng. Struct. 2023, 280, 115681. [Google Scholar] [CrossRef]
- Tian, Z.C.; Zhang, Z.J.; Peng, W.P.; Dai, Y.; Cai, Y.; Xu, B.L. Research on the Method of Temporary Prestressing to Regulate the Stress in the Section during the Construction of the Main Arch Ring of the Cantilever Cast Arch Bridge. Appl. Sci. 2022, 12, 10070. [Google Scholar] [CrossRef]
- Granata, M.F. Stressing Sequence for Hanger Replacement of Tied-Arch Bridges with Rigid Bars. J. Bridge Eng. 2022, 27, 04021099. [Google Scholar] [CrossRef]
- Yang, K.K.; Gao, L.Q.; Zheng, K.K.; Shi, J. Mechanical behavior of a novel steel-concrete joint for long-span arch bridges-Application to Yachi River Bridge. Eng. Struct. 2022, 265, 114492. [Google Scholar] [CrossRef]
- Deng, N.C.; Yu, M.S.; Yao, X.Y. Intelligent Active Correction Technology and Application of Tower Displacement in Arch Bridge Cable Lifting Construction. Appl. Sci. 2021, 11, 9808. [Google Scholar] [CrossRef]
- Gao, H.Y.; Zhang, K.; Wu, X.Y.; Liu, H.J.; Zhang, L.Z. Application of BRB to Seismic Mitigation of Steel Truss Arch Bridge Subjected to Near-Fault Ground Motions. Buildings 2022, 12, 2147. [Google Scholar] [CrossRef]
- Mao, W.Z.; Gou, H.Y.; He, Y.N.; Pu, Q.H. Local Stress Behavior of Post-Tensioned Prestressed Anchorage Zones in Continuous Rigid Frame Arch Railway Bridge. Appl. Sci. 2018, 8, 1833. [Google Scholar] [CrossRef]
- Huang, Q.; Wu, X.G.; Wei, H.; Chen, Q.D. Innovative Design of Novel Main and Secondary Arch Collaborative Y-Shaped Arch Bridge and Research on Shear Lag Effect of Its Unconventional Thin-Walled Steel Box Arch Ribs. Appl. Sci. 2022, 12, 8370. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Sun, T.F.; Wang, J.; Liu, Q.L. Deflection distribution estimation of the main arch of arch bridges based on long-gauge fiber optic sensing technology. Adv. Struct. Eng. 2019, 22, 3341–3351. [Google Scholar] [CrossRef]
- Alvarez, J.J.; Aparicio, A.C.; Jara, J.M.; Jara, M. Seismic assessment of a long-span arch bridge considering the variation in axial forces induced by earthquakes. Eng. Struct. 2012, 34, 69–80. [Google Scholar] [CrossRef]
- Morcous, G.; Hanna, K.; Deng, Y.; Tadros, M.K. Concrete-Filled Steel Tubular Tied Arch Bridge System: Application to Columbus Viaduct. J. Bridge Eng. 2012, 17, 107–116. [Google Scholar] [CrossRef]
- Xie, K.Z.; Wang, H.W.; Guo, X.; Zhou, J.X. Study on the safety of the concrete pouring process for the main truss arch structure in a long-span concrete-filled steel tube arch bridge. Mech. Adv. Mater. Struct. 2021, 28, 731–740. [Google Scholar] [CrossRef]
- Lederman, G.; You, Z.; Glisic, B. A novel deployable tied arch bridge. Eng. Struct. 2014, 70, 1–10. [Google Scholar] [CrossRef]
- De Backer, H.; Outtier, A.; Van Bogaert, P. Buckling design of steel tied-arch bridges. J. Constr. Steel Res. 2014, 103, 159–167. [Google Scholar] [CrossRef]
- Peng, Y.C.; Zhang, Z.X. Development of a Novel Type of Open-Web Continuous Reinforced-Concrete Rigid-Frame Bridge. J. Bridge Eng. 2020, 25, 05020005. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.W.; Xu, S.Y.; Shou, W.C.; Peng, C.M.; Lv, D.F. Vision-Based Methods for Relative Sag Measurement of Suspension Bridge Cables. Buildings 2022, 12, 667. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, Y.; Zhang, J. Laser-scan based pose monitoring for guiding erection of precast concrete bridge piers. Autom. Constr. 2022, 140, 104347. [Google Scholar] [CrossRef]
- Puri, N.; Turkan, Y. Bridge construction progress monitoring using lidar and 4D design models. Autom. Constr. 2020, 109, 102961. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Lin, F.Z.; Wang, W.G.; Zhang, J. Vision-based trajectory monitoring for assembly alignment of precast concrete bridge components. Autom. Constr. 2022, 140, 104350. [Google Scholar] [CrossRef]
- Kim, D.; Kwak, Y.; Sohn, H. Accelerated cable-stayed bridge construction using terrestrial laser scanning. Autom. Constr. 2020, 117, 103269. [Google Scholar] [CrossRef]
- Chen, Z.H.; Sun, H.X.; Zhou, S.X.; Chen, Z.S.; Xue, X.Y.; Peng, Y.J. A Hybrid Algorithm for Cable Force Calculation of Cfst Arch Bridges during Construction. Int. J. Robot. Autom. 2022, 37, 192–199. [Google Scholar] [CrossRef]
- Gou, H.Y.; Liu, C.; Bao, Y.; Han, B.; Pu, Q.H. Construction Monitoring of Self-Anchored Suspension Bridge with Inclined Tower. J. Bridge Eng. 2021, 26, 05021011. [Google Scholar] [CrossRef]
- Li, X.X.; Ren, W.X.; Bi, K.M. FBG force-testing ring for bridge cable force monitoring and temperature compensation. Sens. Actuators A Phys. 2015, 223, 105–113. [Google Scholar] [CrossRef]
- Ren, W.X.; Lin, Y.Q.; Peng, X.L. Field load tests and numerical analysis of Qingzhou cable-stayed bridge. J. Bridge Eng. 2007, 12, 261–270. [Google Scholar] [CrossRef]
- Gaute-Alonso, A.; Garcia-Sanchez, D.; Alonso-Cobo, C.; Calderon-Uriszar-Aldaca, I. Temporary cable force monitoring techniques during bridge construction-phase: The Tajo River Viaduct experience. Sci. Rep. 2022, 12, 7689. [Google Scholar] [CrossRef]
- Sanaeiha, A.; Rahimian, M.; Marefat, M.S. Field Test of a Large-Span Soil–Steel Bridge Stiffened by Concrete Rings during Backfilling. J. Bridge Eng. 2017, 22, 06017002. [Google Scholar] [CrossRef]
- Maleska, T.; Beben, D. Numerical analysis of a soil-steel bridge during backfilling using various shell models. Eng. Struct. 2019, 196, 109358. [Google Scholar] [CrossRef]
- Kunecki, B. Field Test and Three-Dimensional Numerical Analysis of Soil–Steel Tunnel during Backfilling. Transp. Res. Rec. J. Transp. Res. Board. 2014, 2462, 55–60. [Google Scholar] [CrossRef]
- Bayraktar, A.; Akkose, M.; Tas, Y.; Erdis, A.; Kursun, A. Long-term strain behavior of in-service cable-stayed bridges under temperature variations. J. Civ. Struct. Health 2022, 12, 833–844. [Google Scholar] [CrossRef]
- Jin, H.W.; Wang, G.A.; Chen, Z.M. Temperature Control Technology for Construction of Jinsha River Bridge. Adv. Civ. Eng. 2021, 2021, 3452167. [Google Scholar] [CrossRef]
- Mei, X.D.; Lu, Y.Y.; Shi, J. Temperature monitoring and analysis of a long-span cable-stayed bridge during construction period. Struct. Monit. Maint. 2021, 8, 203–220. [Google Scholar]
- Zhu, L.; Wang, Y.; Zhou, G.P.; Han, B. Structural health monitoring on a steel-concrete composite continuous bridge during construction and vehicle load tests. Mech. Adv. Mater. Struct. 2022, 29, 1370–1385. [Google Scholar] [CrossRef]
- Grace, N.F.; Mohamed, M.E.; Kasabasic, M.; Chynoweth, M.; Ushijima, K.; Bebawy, M. Design, Construction, and Monitoring of US Longest Highway Bridge Span Prestressed with CFRP Strands. J. Bridge Eng. 2022, 27, 04022047. [Google Scholar] [CrossRef]
- Pan, J.; Wang, X.; Huang, K.; Wang, W. Symmetrically Construction Monitoring Analysis and Completed State Evaluation of a Tied Steel Box Arch Bridge Based on Finite Element Method. Symmetry 2023, 15, 932. [Google Scholar] [CrossRef]








| No. | Component | Material | Elastic Modulus | Linear Expansion Coefficient | Unit Weight |
|---|---|---|---|---|---|
| 1 | Arch rib, transverse brace, lattice beam | Q355C | 2.06 × 105 | 1.20 × 105 | 76.98 |
| 2 | Steel deck | Q235C | 2.06 × 105 | 1.20 × 105 | 76.98 |
| 3 | Concrete for main pier, deck, sidewalk, and access slab | C40 | 3.25 × 104 | 1.00 × 105 | 26.00 |
| 4 | Cushion cap concrete | C35 | 3.15 × 104 | 1.00 × 105 | 26.00 |
| 5 | Arch abutment concrete | C50 | 3.45 × 104 | 1.00 × 105 | 26.00 |
| 6 | Suspender and tie rod | φs15.24 | 1.90 × 105 | 1.20 × 105 | 78.50 |
| Location | Section | Positioning Point No. | Location (Displacement Measuring Point No.) | ||||
|---|---|---|---|---|---|---|---|
| Left | Middle | Right | |||||
| Upstream | Nanning | 1# | UN1-L | UN1-M | UN1-R | A * (Nanning/Beihai) | (UAN/UAB) |
| 2# | UN2-L | UN2-M | UN2-R | L/8 | (UM1) | ||
| 3# | UN3-L | UN3-M | UN3-R | L/4 | (UM2) | ||
| 4# | UN4-L | UN4-M | UN4-R | 3L/8 | (UM3) | ||
| Beihai | 1# | UB1-L | UB1-M | UB1-R | L/2 | (UM4) | |
| 2# | UB2-L | UB2-M | UB2-R | 5L/8 | (UM5) | ||
| 3# | UB3-L | UB3-M | UB3-R | 3L/4 | (UM6) | ||
| 4# | UB4-L | UB4-M | UB4-R | 7L/8 | (UM7) | ||
| Downstream | Nanning | 1# | DN1-L | DN1-M | DN1-R | A * (Nanning/Beihai) | (DAN/DAB) |
| 2# | DN2-L | DN2-M | DN2-R | L/8 | (DM1) | ||
| 3# | DN3-L | DN3-M | DN3-R | L/4 | (DM2) | ||
| 4# | DN4-L | DN4-M | DN4-R | 3L/8 | (DM3) | ||
| Beihai | 1# | DB1-L | DB1-M | DB1-R | L/2 | (DM4) | |
| 2# | DB2-L | DB2-M | DB2-R | 5L/8 | (DM5) | ||
| 3# | DB3-L | DB3-M | DB3-R | 3L/4 | (DM6) | ||
| 4# | DB4-L | DB4-M | DB4-R | 7L/8 | (DM7) | ||
| No. | Steel Pipe Pile Deformation (mm) | Steel Platform Settlement (mm) | Lattice Beam Settlement (mm) | ||
|---|---|---|---|---|---|
| X | Y | Z | |||
| 0 | / | / | / | −5.97~0.61 | / |
| 1 | −4.9~4.8 | −3.3~4.5 | −5.0~3.4 | −2.90~1.03 | |
| 2 | −4.6~1.8 | −1.9~2.7 | −3.9~3.9 | −4.27~0.81 | / |
| 3 | −4.7~3.0 | −2.0~3.0 | −2.5~3.0 | −3.70~1.18 | / |
| 4 | −4.8~3.6 | −2.6~4.0 | −4.2~4.7 | −4.18~3.04 | / |
| 5 | −4.7~−4.0 | −1.6~2.6 | −3.7~4.1 | −4.19~1.85 | / |
| 6 | −5.7~5.2 | −3.9~3.3 | −3.4~5.9 | −1.45~5.76 | / |
| 7 | −5.8~5.2 | −3.9~4.0 | −4.3~5.9 | −1.69~4.07 | −4.07~0.98 |
| 8 | −4.5~3.5 | −3.9~3.9 | −4.6~3.9 | −2.80~0.56 | |
| 9 | −4.1~4.4 | −2.1~4.7 | −4.3~2.0 | / | −3.53~−0.06 |
| 10 | −4.0~3.9 | −2.1~3.2 | −4.8~4.8 | / | −2.64~1.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, L.; Nong, Y.; Wang, W. Construction-Monitoring Analysis of a Symmetrical Rigid Frame Tied Steel Box Arch Bridge in Southwest China Based on Segmental Assembly Technique. Symmetry 2023, 15, 1437. https://doi.org/10.3390/sym15071437
Zhang Y, Wang L, Nong Y, Wang W. Construction-Monitoring Analysis of a Symmetrical Rigid Frame Tied Steel Box Arch Bridge in Southwest China Based on Segmental Assembly Technique. Symmetry. 2023; 15(7):1437. https://doi.org/10.3390/sym15071437
Chicago/Turabian StyleZhang, Yuanchong, Longlin Wang, Yu Nong, and Wensheng Wang. 2023. "Construction-Monitoring Analysis of a Symmetrical Rigid Frame Tied Steel Box Arch Bridge in Southwest China Based on Segmental Assembly Technique" Symmetry 15, no. 7: 1437. https://doi.org/10.3390/sym15071437
APA StyleZhang, Y., Wang, L., Nong, Y., & Wang, W. (2023). Construction-Monitoring Analysis of a Symmetrical Rigid Frame Tied Steel Box Arch Bridge in Southwest China Based on Segmental Assembly Technique. Symmetry, 15(7), 1437. https://doi.org/10.3390/sym15071437






