Al₂O₃-Cu\Ethylene Glycol-Based Magnetohydrodynamic Non-Newtonian Maxwell Hybrid Nanofluid Flow with Suction Effects in a Porous Space: Energy Saving by Solar Radiation

Abstract

Nanotechnology is well-known for its versatile and general thermal transport disciplines, which are used in semiconductors, spacecraft, bioengineering, functional electronics, and biosensors. As a result, process optimization has attracted the interest of scientists and technologists. The main aim of the current analysis is to explore the enhancement of energy/heat transfer via the dispersion of cylindrical-shaped nanoparticles of alumina and copper in ethylene glycol as a base fluid using a non-Newtonian Maxwell fluid model. In the current study, the effects of solar radiation, plate suction, and magnetohydrodynamics on a Maxwell hybrid nanofluid are encountered. The flow is induced by linearly stretching a sheet angled at $\xi =\pi /6$, embedded in a porous space. The proposed problem is converted into a mathematical structure in terms of partial differential equations and then reduced to ordinary differential equations by using appropriate similarity variables. In the similarity solution, all the curves for the velocity field and temperature distribution remain similar, which means that the symmetry between the graphs for the velocity and temperature remains the same. Therefore, there is a strong correlation between similarity variables and symmetry. The obtained model, in terms of ordinary differential equations, is solved using the built-in numerical solver bvp4c. It is concluded that more nanoparticles in a fluid can make it heat up faster, as they are typically better at conducting heat than the fluid itself. This means that heat is transferred more quickly, raising the temperature of the fluid. However, more nanoparticles can also slow the flow speed of the fluid to control the boundary layer thickness. The temperature field is enhanced by increasing the solar radiation parameter, the magnetic field parameter, and the porous medium parameter at an angle of$\xi =\pi /6$, which serves the purpose of including radiation and the Lorentz force. The velocity field is decreased by increasing the values of the buoyancy parameter and the suction parameter effects at an angle of$\xi =\pi /6$. The current study can be used in the improvement of the thermal efficiency of nanotechnological devices and in renewable energy sources to save energy in the energy sector. The present results are compared with the published ones, and it is concluded that there is excellent agreement between them, which endorses the validity and accuracy of the current study.

1. Introduction

The thermal conductivity of conventional fluids such as water and ethylene glycol is low. The suspension of nanoparticles in base fluids like water and ethylene glycol leads to enhancements in the thermal conductance of these fluids, which ensure the thermal efficiency of the fluids; these new fluids are called nanofluids. This class of fluid has many engineering applications. Researchers are implementing these nanofluids in different fields for their respective applications. This suspension of nanoparticles gives the required thermal efficiency for the better transportation of energy. These fluids with extraordinary thermo-physical properties are called nanofluids, whose name was coined by Choi and Eastman [1] for the first time. The earliest investigations of thermal conductivity enhancement were performed by Masuda et al. [2] in 1993. An experimental investigation [3] has shown that nanofluids need only a five percent volumetric fraction of nanoparticles for effective heat transfer enhancement. Buongiorno [4] developed an analytical model for convective transport in nanofluids in which the Brownian motion and the thermophoresis effect are taken into account. The most advanced type of nanofluid is hybrid nanofluids, which have a combination of two nanoparticles (NPs) in the base fluid. The thermal performance of hybrid nanofluids is better than that of nanofluids and simple base fluids [5]. Lee et al. [6] experimentally verified that the suspension of a small number of nanoparticles has substantially higher thermal conductivities than fluids with no nanoparticles. Choi [7] explored nanofluids as a new field of research and applications. He concluded that nanofluids have a higher magnitude of thermal conductivity, which leads to enhanced heat transfer. For the first time, hybrid nanofluids were prepared using single-wall carbon nanotubes (CNTs) and multi-wall carbon nanotubes (MWCNs) on magnetic hybrid nanoparticles (NPs) by Turuce et al. [8]. Jha and Ramaprabhu [9] carried out structural and morphological characterizations of metal-dispersed MWNTs using X-ray diffraction analysis, energy-dispersive X-ray analysis, and Fourier-transform infrared spectroscopy. Lee [10] penned applications of nanofluids in domestic heat exchangers. Similar studies on nanofluids and hybrid nanofluids are presented in [11,12,13,14,15].

The behavior of Newtonian-based fluids that change to non-Newtonian fluids via the suspension of nanoparticles, however, entirely depends on the nanoparticles’ concentration, size, shape, and the interactions between them. This leads to the construction of non-Newtonian models for a better understanding of heat transfer and fluid flow mechanisms. The viscosity and thermal conductivity are no longer constant when the nanofluids undergo sudden motion and temperature variations. Numerous industrial and technical systems frequently employ non-Newtonian fluid flow. Several studies are confined to theoretical research on fluid dynamics based on symmetry concepts, which are drawn from group examination, as well as numerical and analytical studies of Newtonian and non-Newtonian fluid flows. Therefore, the research community has focused its attention on the thermo-physical properties of nanofluids and hybrid nanofluids. Aziz et al. [16] carried out analysis on a ferro-copper-ethylene glycol-based hybrid nanofluid using the Maxwell fluid model. They considered the influence of the entropy phenomenon, the slip condition, the inclined magnetic field, Joule heating, and thermal radiation in their study. Ahmad et al. [17] explored a Maxwell hybrid nanofluid that was prepared using graphene oxide and silver with kerosene oil as the base fluid over a stretching sheet in porous space. They encountered the impacts of viscous dissipation, heat generation, the magnetic field, and convective boundary conditions in their study. Arif, with his research fellows [18], paid attention to the thermal performance of a hybrid nanofluid prepared by suspending a mixture of molybdenum disulfide and grapheme in engine oil using the Maxwell fluid model. They considered the oscillating cylindrical geometry with regard to fluid flow generation. Chu et al. [19] studied the influence of copper and alumina on sodium alginate hybrid nanofluid using the Maxwell fluid model. They used the fractional model using the Caputo time fractional differential operator. Ramzan et al. [20] discussed the hybrid nanofluid flow in rotating disks using thermal stratification. Studies relevant to the use of hybrid nanofluids on different geometries with distinct characteristics are given in [21,22,23,24,25,26,27,28,29,30,31,32].

There are three ways that heat can be transported: conduction, convection, and radiation. Thermal radiation is one of these very important processes. In some cases, the contribution of radiation to the total heat transfer is small or negligible compared with the other modes, but in other cases, it is comparable to or larger than the other modes. There are many examples in which thermal radiation plays an important role, such as when direct sunlight is exploited in solar heating panels and solar farms, and it is necessary to understand the interaction between radiation, the atmosphere, and the device in glass manufacturing, in furnaces and boilers at power stations, in the thermal dynamics of buildings, etc. Researchers have included this effect in their research work many times. Cortell [33] paid attention to solar radiation’s effects on the Sakiad is flow and heat transfer. Khan and Pop [34] discussed the nanofluid flow, heat, and mass transfer phenomena using a single-phase model for a nanofluid over a stretching sheet. The influence of thermophoretic particle deposition and solar radiation on a carbon nanotube hybrid nanofluid with a stagnation point was studied by Rasmesh et al. [35]. Zhang et al. [36] scrutinized the Falkner’s–Skan hybrid nanofluid flow with radiation and magnetic field effects in a porous space. The influence of the diameter of nanoparticles on the heat transfer in micro-polar nanofluid past the stretching sheet was discussed by Ali et al. [37]. Radiation and thermal convective boundary conditions were also encountered. The tangent hyperbolic nanofluid flow with thermal radiation, a magnetic field, a heat source, and convective boundary conditions was tackled numerically by Kumar et al. [38]. Ashraf et al. [39] explored numerically the optically dense gray fluid flow and heat transfer in nanofluid along the surface of a sphere using the finite difference method. Abbas et al. [40] investigated the generalized Fourier’s and Fick’s laws in a non-Maxwell fluid flow over an inclined stretching sheet. Abbas et al. [41] investigated the solar radiation effects on non-Newtonian Casson fluid flow along the surface of an exponentially stretching sheet. Studies in [42,43] cover the radiation effects with variable density and the thermophoresis effects over inclined moving surfaces and spheres.

Magnetohydrodynamics (MHD), also called magnetofluid dynamics or hydromagnetics, is the study of electrically conducting fluids. Examples of such fluids involve plasma, salt water, electrolytes, or liquid metals. This factor has many applications in engineering, medical, and industrial fields; therefore, it grabbed a lot of attention from researchers. Yaseen et al. [44] proposed the study of ternary hybrid nanofluid flow and heat transfer along the flat plate, wedge, and cone. In this study, the authors considered gyrotactic microorganisms with generalized heat and mass transfer laws. Kavya et al. [45] discussed non-Newtonian Williamson hybrid nanofluids past stretching and shrinking cylinders. Kavya and his co-researchers considered the effects of variable thermal conductivity, the magnetic field, and transpiration. Wakif and Nehad [46] investigated magnetohydrodynamics and chemical reaction effects on Von Karman nanofluid flow. They considered zero mass flux and convective boundary conditions in their study. Ragupathi et al. [47] explored the influence of slip conditions on bioconvective flow in the presence of nanoparticles passing through curved stretching sheets. Abbas et al. [48] explored the magneto dynamics of non-Newtonian Williamson fluid in the presence of nanoparticles over an inclined moving plate in a porous space. Ali et al. [49] examined the magnetohydrodynamics and bio-convective micro-polar nanofluid flow over a stretching sheet under mass and thermal convective boundary conditions. Eswaramoorthi et al. [50] examined the heat transfer processes in Williamson fluid flow in a Darcy–Forchheimer porous medium over a Riga plate. They discussed heat generation, generalized heat and mass transfer laws, and chemical reactions. Abbas et al. [51] discussed reduced gravity effects combined with a magnetic field and solar radiation along the sphere.

A porous medium is a good candidate for improving combustion efficiency and reducing pollution formation. It is crucial for many industrial applications, including glass tampering procedures, painting, and drying paper. In [52,53], Darcy–Forchheimer porous medium effects reduced gravity fluid flow of Newtonian fluid with magnetic field effects along the sphere surface. Quintard et al. [54] studied the numerical mechanism of two-equation model heat transfer in porous media. Badruddin and Khan [55] carried out the heat transfer processes in $L$-shaped porous media using the finite element method. Ghalambaz et al. [56] documented the convective heat transfer in hybrid nanofluids with cavity-shaped geometry in porous space under solar radiation and magnetic field effects. In Refs. [57,58,59,60], the studies in porous media with different fluid flows and their characteristics are presented.

In light of published work and the physical significance of the discussed mechanisms, the main aim of the currently proposed model is to examine the thermal efficiency of cylindrical-shaped nanoparticles $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$-$\mathrm{C}\mathrm{u}$ in Ethylene glycol using the Maxwell fluid model. The work also concentrates on the effects of solar radiation and magneto-hydrodynamics. Furthermore, it is considered an inclined stretching sheet with suction effects in a porous space. As per our best knowledge, all of the above characteristics in one frame have never been discussed before this study, so we claim that it is the novelty of the work. In the current study, the solution of physical properties under sundry parameters indicates solar radiation, magnetohydrodynamics, suction parameters, porous space, and angle of inclination. It presents its graphical and tabular aspects with detailed discussion and physical reasoning. This study has several applications in industry and engineering fields. In the coming sections, the modeling statement, the solution procedure, and the results and discussion. In the coming sections, the modeling statement, the solution procedure, the results, and the discussion will be given.

2. Mathematical Modeling

Consider viscous, incompressible, and two-dimensional hybrid Maxwell fluid flow and heat transfer over a stretching sheet angled at an angle $\xi =\pi /6$ embedded in a porous medium. The flow direction is in the $x$-axis and the normal to the flow is in the $y$-axis. The flow diagram representing the flow structure is shown in Figure 1. In Figure 1, the flow pattern is shown, in which the surface is kept inclined at an angle $\xi =\pi /6$ as an appropriate choice. Stretching of the plate induces flow.It has been considered a porous surface with suction effects to control the boundary layer’s thickness. The surface is embedded in a porous medium, and the fluid is saturated with $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$and $\mathrm{C}\mathrm{u}$cylindrical shaped nanoparticles, as shown in Figure 1. The flow direction is in the $x$-axis, and $u$ is $x$-component of velocity. The $y$-axis is taken in the normal direction of fluid flow, and suction of plat is in $y$-direction shown in Figure 1. The magnetic field of strength $B_o$ is applied to the vertical direction to control flow speed and maximize the temperature by generating the current. As a renewable energy source for energy savings, solar radiation is included in the energy equation shown in Figure 1. By following [31,32], we have the following flow equations:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{\beta }{{\rho }_{hnf}}\left(u^2\frac{{\partial }^{2}u}{\partial x^2}+v^2\frac{{\partial }^{2}u}{\partial y^2}+2uv\frac{{\partial }^{2}u}{\partial x\partial y}\right)-\frac{g{\left(\rho {\beta }_T\right)}_{hnf}}{{\rho }_{hnf}}\left(T-T_{\infty }\right){Cos\left(\xi \right)-\sigma }_{hnf}/{\rho }_{hnf}{B}_o^{2}u-\frac{{\nu }_{hnf}}{K_o}u$$

(2)

$${\left(\rho C_p\right)}_{hnf}\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=k_{hnf}\frac{{\partial }^{2}T}{\partial y^2}-\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{\partial q_r}{\partial y}$$

(3)

Equations (1)–(3) are subjected to the following boundary conditions:

$$\left.\begin{array}{c}u=U_w\left(x\right)=cx,v=-v_o,T=T_w,aty=0,\\ u\to 0,T\to T_{\infty },as\eta \to \infty .\end{array}\right\}$$

(4)

Here, $x$ and $y$ are horizontal and vertical coordinates, respectively, and accordingly, velocity components are $u$ and $v$, respectively. The symbols, ${\mu }_{hnf},{\nu }_{hnf},{\rho }_{hnf,}{k}_{hnf},{\left(C_P\right)}_{hnf},{\sigma }_{hnf}$, and ${\left({\beta }_T\right)}_{hnf}$ are dynamic viscosity, kinematic viscosity, density, thermal conductivity, specific heat, electrical conductivity, and thermal expansion of hybrid nanofluid, respectively. The symbols ${\mu }_f,{\nu }_f,{\rho }_{f,}{k}_f,{\left(C_P\right)}_f,{\sigma }_f$, and ${\left({\beta }_T\right)}_f$ are dynamic viscosity, kinematic viscosity, density, thermal conductivity, specific heat, and electrical conductivity of the base, respectively. The notations $T,T_w,T_{\infty },C,C_w,$and $C_{\infty }$ are the temperature of the fluid, the temperature of the surface of the stretching sheet, the temperature of the free stream region, the concentration of the fluid, the concentration at the surface, and the concentration in the free stream region, respectively. The designations $\beta ,\xi ,g,B_o^2,$and $K_o$ are time relaxation constant, angle of inclination of the stretching sheet, gravity force, magnetic field strength, and porosity constant, respectively.

The Roseland approximation for the radiative heat flux vector $q_r$ is given by the following equation given in [33];

$$q_r=-\frac{4\sigma }{3K_R}\frac{\partial T^4}{\partial y}$$

(5)

$K_R$ stands for mean absorption coefficient. Stefan-Boltzmann constant is represented by the symbol$\sigma$. Equation (5)right side $T^4$ is given as follows:

$$T^4\approx 4{T_{\infty }}_{\mathrm{\infty }}^{3}T-3{T^4}_{\mathrm{\infty }}^4.$$

So, Equation $\left(5\right)$ becomes:

$$q_r=-\frac{16T_{\infty }^3\sigma }{3K_R}\frac{\partial T}{\partial y}$$

(6)

So Equation (3) becomes

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{16T_{\infty }^3\sigma }{{\left(\rho C_p\right)}_{hnf}3K_R}\frac{{\partial }^{2}T}{\partial y^2}$$

(7)

After rearrangement the equation becomes

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_f}{{\left(\rho C_p\right)}_f}\left[\frac{\frac{k_{hnf}}{k_f}}{\frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}}+\frac{16T_{\infty }^3\sigma }{3\frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}{k_{f}K}_R}\right]\frac{{\partial }^{2}T}{\partial y^2}.$$

(8)

3. Solution Mythology

In this section, the entire solution methodology is elaborated, in which Equations (1)–(3) with the flow conditions given in Equation (4) are solved. In the next subsections, the formulation procedure by which partial differential Equations (1)–(3) with flow conditions given in Equation (4) are converted to ordinary differential equations is outlined. Also, the solution technique by which ordinary differential equations are solved.

3.1. Similarity Variable Formulation

In this subsection, the similarity formulation given in Equation (9) will be utilized to reduce the system of coupled and non-linear partial differential Equations (1)–(4) into ordinary differential equations. These variables presented in Equation (9) were used by Devi et al. [31].

$$\left.\begin{array}{c}u=cx{f}^{\prime }\left(\eta \right),v=\sqrt{c{\nu }_f}f\left(\eta \right)\\ \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_o-T_{\infty }},\eta =\sqrt{\frac{C}{{\nu }_f}}\end{array}\right\}$$

(9)

By using the similarity variables given in Equation (5) used by [31] in Equations (1)–(4), the continuity equation is satisfied automatically, and the remaining equations take the following forms:

$$\frac{\frac{{\mu }_{hnf}}{{\mu }_f}}{\frac{{\rho }_{hnf}}{{\rho }_f}}{f}^{‴}-f^{{\prime }^2}-f{f}^{″}-\frac{{\lambda }_1}{\frac{{\rho }_{hnf}}{{\rho }_f}}\left(f^2{f}^{‴}-2f{f}^{\prime }{f}^{″}\right)-\frac{\frac{{\left(\rho {\beta }_T\right)}_{hnf}}{{\left(\rho {\beta }_T\right)}_f}}{{\rho }_{\frac{hnf}{{\rho }_f}}}\lambda \theta Cos\left(\xi \right)-\frac{\frac{{\sigma }_{hnf}}{{\sigma }_f}}{{\rho }_{\frac{hnf}{{\rho }_f}}}M{f}^{\prime }-\frac{{\mu }_{hnf}}{{\mu }_f}K{f}^{\prime }=0$$

(10)

$$\left(\frac{\frac{k_{hnf}}{k_f}}{\frac{{\left(\rho C_P\right)}_{hnf}}{{\left(\rho C_P\right)}_f}}+\frac{4}{3Rd\frac{{\left(\rho C_P\right)}_{hnf}}{{\left(\rho C_P\right)}_f}}\right)\frac{1}{Pr}{\theta }^{″}+f{\theta }^{\prime }=0$$

(11)

Considered boundary conditions

$$\left.\begin{array}{c}f=S,f^{\prime }=1,\theta =1,\mathrm{a}\mathrm{t}\eta =0\\ f^{\prime }\to 0,\theta \to 0,\mathrm{a}\mathrm{s}\eta \to \infty \end{array}\right\}$$

(12)

where$Rd=k_f{K}_R/4{\sigma }^{*}{T}_{\infty }^3$ is radiation parameter, ${\lambda }_1=\frac{\beta C}{{\rho }_f}$ is Maxwell fluid parameter, with $\beta$ as time relaxation parameter, $\lambda =\frac{{\mathrm{g}\left({\beta }_T\right)}_f\mathsf{\Delta }T}{C^{2}x}$ is buoyancy parameter with $\mathsf{\Delta }T={(T}_w-T_{\infty })$, $M=\frac{{\sigma }_f{B}_o^2}{C{\rho }_f}$ is magnetic field parameter, $K=\frac{{\nu }_f}{K_{o}C}$ is dimensionless porosity parameter, $Pr=\frac{{\nu }_f}{{\alpha }_f}$ is Prandtl number with $\alpha =\frac{k_f}{{\left(\rho C_P\right)}_f}$ as thermal diffusivity, $S=\frac{v_o}{\sqrt{C{\nu }_f}}$ is suction parameter $(v_o>0)$. Here, $\eta$ is the similarity variable, and prime notation, $\prime$, is differentiation w.r.t, $\eta$.

3.2. Quantities of Engineering

The physical quantities of interest are the skin friction coefficient and the Nusselt number given by Devi et al. [31] is defined as below:

$$C_f=\frac{{\mu }_{hnf}}{{\rho }_f{U}_W^2}{\left(\frac{\partial u}{\partial y}\right)}_{y=0},N{u}_x=-\frac{{xk}_{hnf}}{k_f\left(T_o-T_{\infty }\right)}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}+x{\left(q_r\right)}_{y=0}$$

(13)

Using Equation (5), in Equation (10), and performing the some algebra, we have the following transformed engineering quantities

$${Re}_x^{1/2}{C}_f=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right),{Re}_x^{-1/2}N{u}_x=-\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}Rd\right){\theta }^{\prime }\left(0\right)$$

(14)

where $R{e}_x=\frac{U_{w}x}{{\nu }_f}$ is the local Reynolds number. In the

Table 1. Thermo-physical properties given in [32].

Properties	$\mathit{\rho }(\mathbf{K}\mathbf{g}/\mathbf{m})$	${\mathbf{C}}_{\mathbf{p}}\left({\mathbf{J}\mathbf{K}\mathbf{g}}^{-1}{\mathbf{K}}^{-1}\right)$	$\mathbf{k}\left({\mathbf{W}\mathbf{m}}^{-1}{\mathbf{K}}^{-1}\right)$	$\mathit{\sigma }(\mathbf{S}/\mathbf{m})$	$\mathit{\beta }\times {10}^{-5}{\mathit{K}}^{-1}$
Base fluid Ethylene glycol(EG)	1114.0	2415.5	0.2520	5.5 × ${10}^{-6}$	6.50
$\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$	3970.0	765.0	40.0	59.6 × ${10}^6$	0.850
$\mathrm{C}\mathrm{u}$	8933	385.0	400.0	35.83 × ${10}^6$	1.670

, the thermophysical properties of $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$, $Cu$, and Ethylene glycol(EG) are given.

Thermo-physical properties formulae for hybrid nanofluid used in [32], are given below:

$$\left.\begin{array}{c}\frac{k_{hnf}}{k_{bf}}=\frac{\left(n-1\right)k_f+k_{s2}-\left(n-1\right){\varphi }_2\left(k_{bf}-k_{s2}\right)}{\left(n-1\right)k_{bf}+k_{s2}+{\varphi }_2\left(k_{bf}-k_{s2}\right)},\\ \frac{k_{bf}}{k_f}=\frac{\left(n-1\right)k_f+k_{s2}-\left(n-1\right){\varphi }_2\left(k_f-k_{s2}\right)}{\left(n-1\right)k_f+k_{s1}+{\varphi }_1\left(k_f-k_{s1}\right)},\\ {\left(\rho C_p\right)}_{hnf}={\varphi }_1{\left(\rho C_p\right)}_{s1}+{\varphi }_2{\left(\rho C_p\right)}_{s2}+\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right){\left(\rho C_p\right)}_f\right],\\ {\rho }_{hnf}=\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right){\rho }_f+{\varphi }_1{\rho }_{s1}\right]+{\varphi }_2{\rho }_{s2},\\ \frac{{\sigma }_{hnf}}{{\sigma }_{bf}}=\frac{2{\sigma }_f+{\sigma }_{s2}-2{\varphi }_2\left({\sigma }_{bf}-{\sigma }_{s2}\right)}{{2\sigma }_{bf}+{\sigma }_{s2}+{\varphi }_2\left({\sigma }_{bf}-{\sigma }_{s2}\right)},\\ \frac{{\sigma }_{bf}}{{\sigma }_f}=\frac{2{\sigma }_f+{\sigma }_{s2}-2{\varphi }_2\left({\sigma }_f-{\sigma }_{s2}\right)}{{2\sigma }_f+{\sigma }_{s1}+{\varphi }_1\left({\sigma }_f-{\sigma }_{s1}\right)},\\ \frac{{\mu }_{hnf}}{{\mu }_f}=\frac{1}{{\left(1-{\phi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}},\\ {\left(\rho {\beta }_T\right)}_{hnf}={\varphi }_1{\left(\rho {\beta }_T\right)}_{s1}+{\varphi }_2{\left(\rho {\beta }_T\right)}_{s2}+\left(1-{\varphi }_2\right)\left[(1-{\varphi }_1){\left(\rho {\beta }_T\right)}_f\right].\end{array}\right\}$$

(15)

where ${\phi }_1$ and ${\phi }_2$ are the volume fractions of solid nanoparticles, Alumina ($\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3)$ and Copper ($\mathrm{C}\mathrm{u}$), respectively. Here, $1,s1,$ and $s2$ are used to differentiate the thermophysical characteristics of base fluid, nanoparticles of the first type $\left(\mathrm{A}{\mathrm{L}}_2{\mathrm{O}}_3\right)$, and nanoparticles of the second type $\left(\mathrm{C}\mathrm{u}\right)$, respectively.

3.3. Solution Technique

The Equations (7) and (8) with the imposed boundary conditions given in Equation (9) are solved by using the built-in numerical solver bvp4c. This solver is based on the collocation formula. The Equations (7) and (8) with boundary conditions given in Equation (9) are first transformed into a system of first-order ordinary differential equations and then put into the numerical algorithm of bvp4c in MATLAB for numerical fallout. The solution technique is given below:

$$\mathsf{\Gamma }\left(1\right)=f,\mathsf{\Gamma }\left(2\right)=f^{\prime },\mathsf{\Gamma }\left(3\right)=f^{″},\mathsf{\Gamma }\left(4\right)=\theta ,\mathsf{\Gamma }\left(5\right)={\theta }^{\prime }$$

(16)

$$\mathsf{\Gamma }\mathsf{\Gamma }\mathbf{1}==-\frac{\left(\begin{array}{c}-\\ -\mathsf{\Gamma }{\left(\mathbf{2}\right)}^{\mathbf{2}}-\mathsf{\Gamma }\left(\mathbf{1}\right)\mathsf{\Gamma }\left(\mathbf{3}\right)-\mathbf{2}\frac{{\mathit{\lambda }}_{\mathbf{1}}}{\frac{{\mathit{\rho }}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{\rho }}_{\mathit{f}}}}\mathsf{\Gamma }\left(\mathbf{1}\right)\mathsf{\Gamma }\left(\mathbf{2}\right)\mathsf{\Gamma }\left(\mathbf{3}\right)-\frac{\frac{{\left(\mathit{\rho }{\mathit{\beta }}_{\mathit{T}}\right)}_{\mathit{h}\mathit{n}\mathit{f}}}{{\left(\mathit{\rho }{\mathit{\beta }}_{\mathit{T}}\right)}_{\mathit{f}}}}{{\mathit{\rho }}_{\frac{\mathit{h}\mathit{n}\mathit{f}}{{\mathit{\rho }}_{\mathit{f}}}}}\mathit{\lambda }\mathit{\theta }\mathit{C}\mathit{o}\mathit{s}\left(\mathit{\xi }\right)-\frac{\frac{{\mathit{\sigma }}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{\sigma }}_{\mathit{f}}}}{{\mathit{\rho }}_{\frac{\mathit{h}\mathit{n}\mathit{f}}{{\mathit{\rho }}_{\mathit{f}}}}}\mathit{M}\mathsf{\Gamma }(\mathbf{2})-\frac{{\mathit{\mu }}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{\mu }}_{\mathit{f}}}\mathit{K}\mathsf{\Gamma }(\mathbf{2})\end{array}\right)}{\left(\frac{\frac{{\mathit{\mu }}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{\mu }}_{\mathit{f}}}}{\frac{{\mathit{\rho }}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{\rho }}_{\mathit{f}}}}-\frac{{\mathit{\lambda }}_{\mathbf{1}}}{\frac{{\mathit{\rho }}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{\rho }}_{\mathit{f}}}}\mathsf{\Gamma }{\left(\mathbf{1}\right)}^{\mathbf{2}}\right)},$$

(17)

$$\mathsf{\Gamma }\mathsf{\Gamma }\mathbf{2}=\frac{\mathit{P}\mathit{r}\mathit{f}{\mathit{\theta }}^{\prime }}{\left(\frac{\frac{{\mathit{k}}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{k}}_{\mathit{f}}}}{\frac{{\left(\mathit{\rho }{\mathit{C}}_{\mathit{P}}\right)}_{\mathit{h}\mathit{n}\mathit{f}}}{{\left(\mathit{\rho }{\mathit{C}}_{\mathit{P}}\right)}_{\mathit{f}}}}+\mathbf{3}\frac{{\left(\mathit{\rho }{\mathit{C}}_{\mathit{P}}\right)}_{\mathit{h}\mathit{n}\mathit{f}}}{{\left(\mathit{\rho }{\mathit{C}}_{\mathit{P}}\right)}_{\mathit{f}}}\mathit{R}\mathit{d}\right)}.$$

(18)

Boundary conditions

$$\left.\begin{array}{c}\mathsf{\Gamma }\left(\mathbf{1}\right)=\mathit{S},\mathsf{\Gamma }\left(\mathbf{2}\right)=\mathbf{1},\mathsf{\Gamma }\left(\mathbf{4}\right)=\mathbf{1},\mathbf{a}\mathbf{t}\mathit{\eta }=\mathbf{0}\\ \mathsf{\Gamma }\left(\mathbf{2}\right)\to \mathbf{0},\mathsf{\Gamma }\left(\mathbf{4}\right)\to \mathbf{0},\mathbf{a}\mathbf{s}\mathit{\eta }\to \mathit{\infty }\end{array}\right\}.$$

(19)

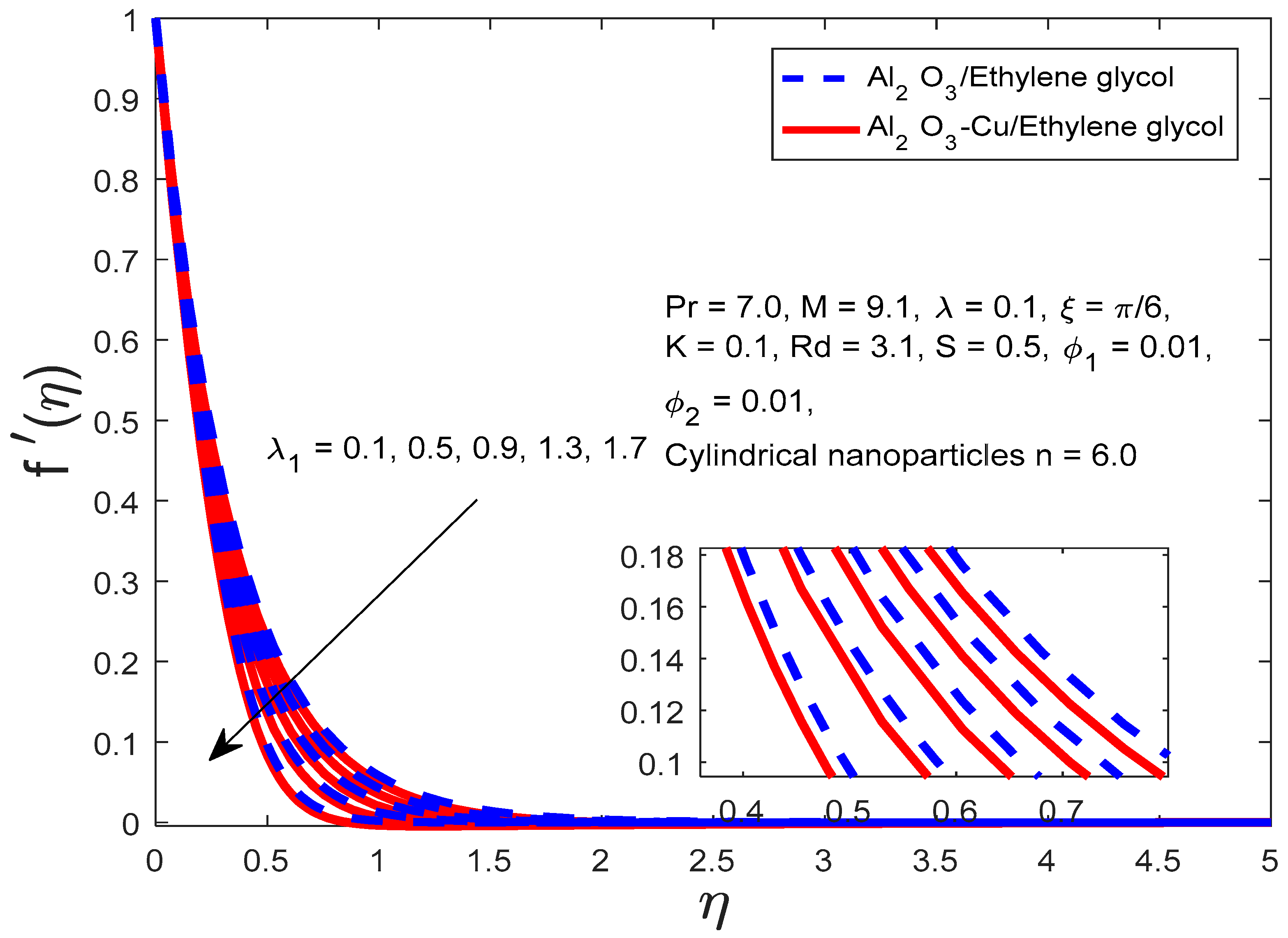
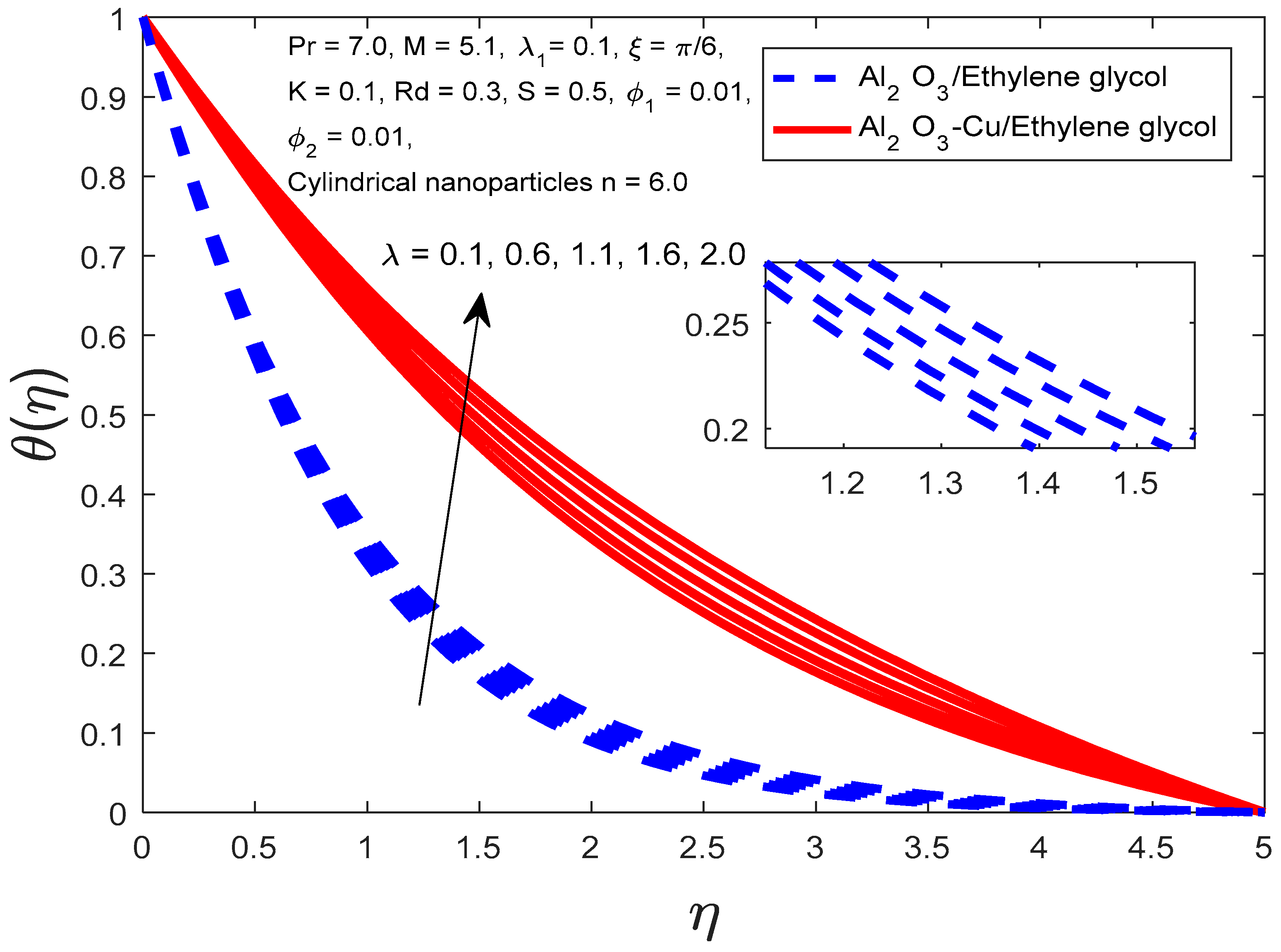
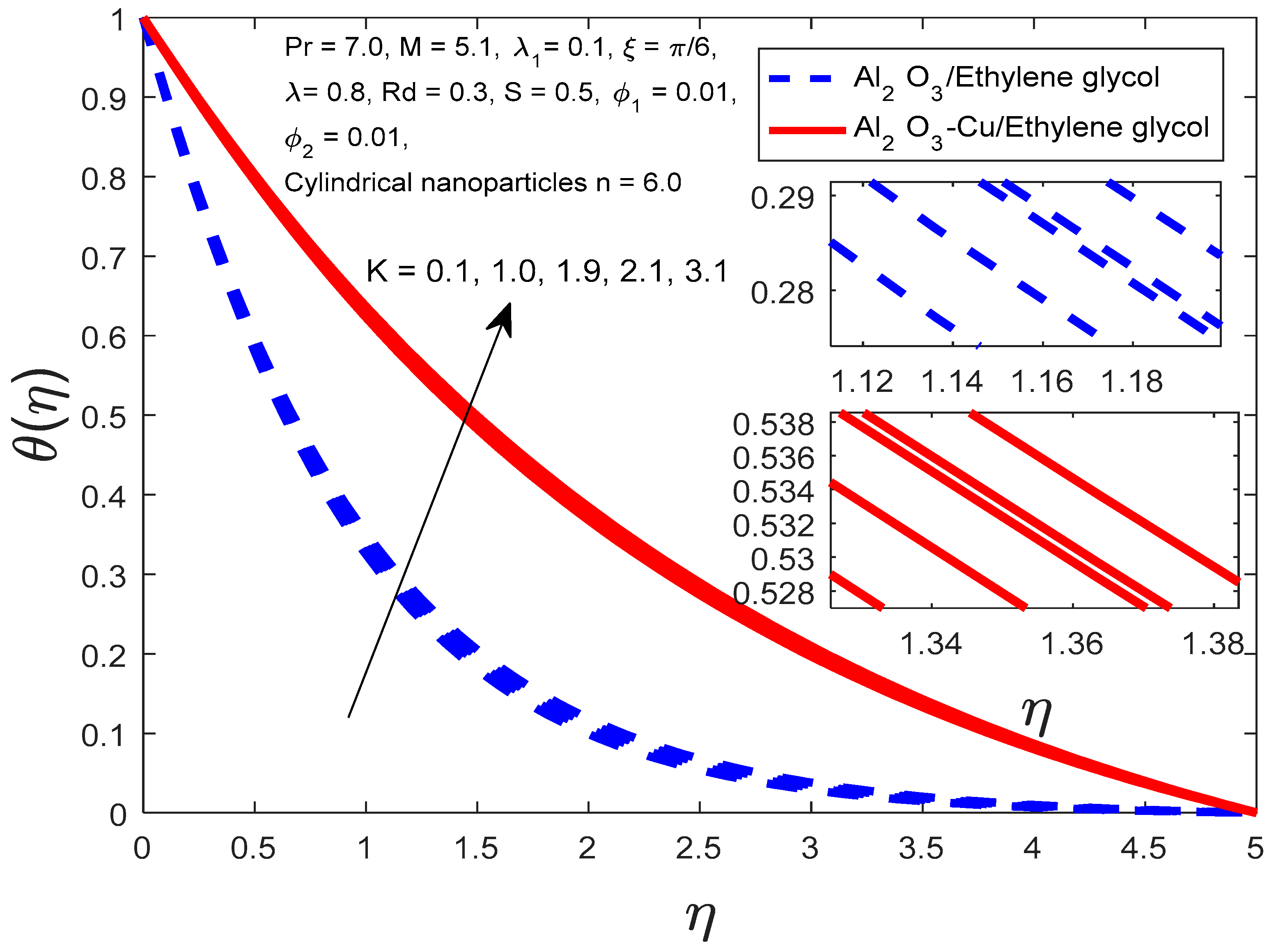
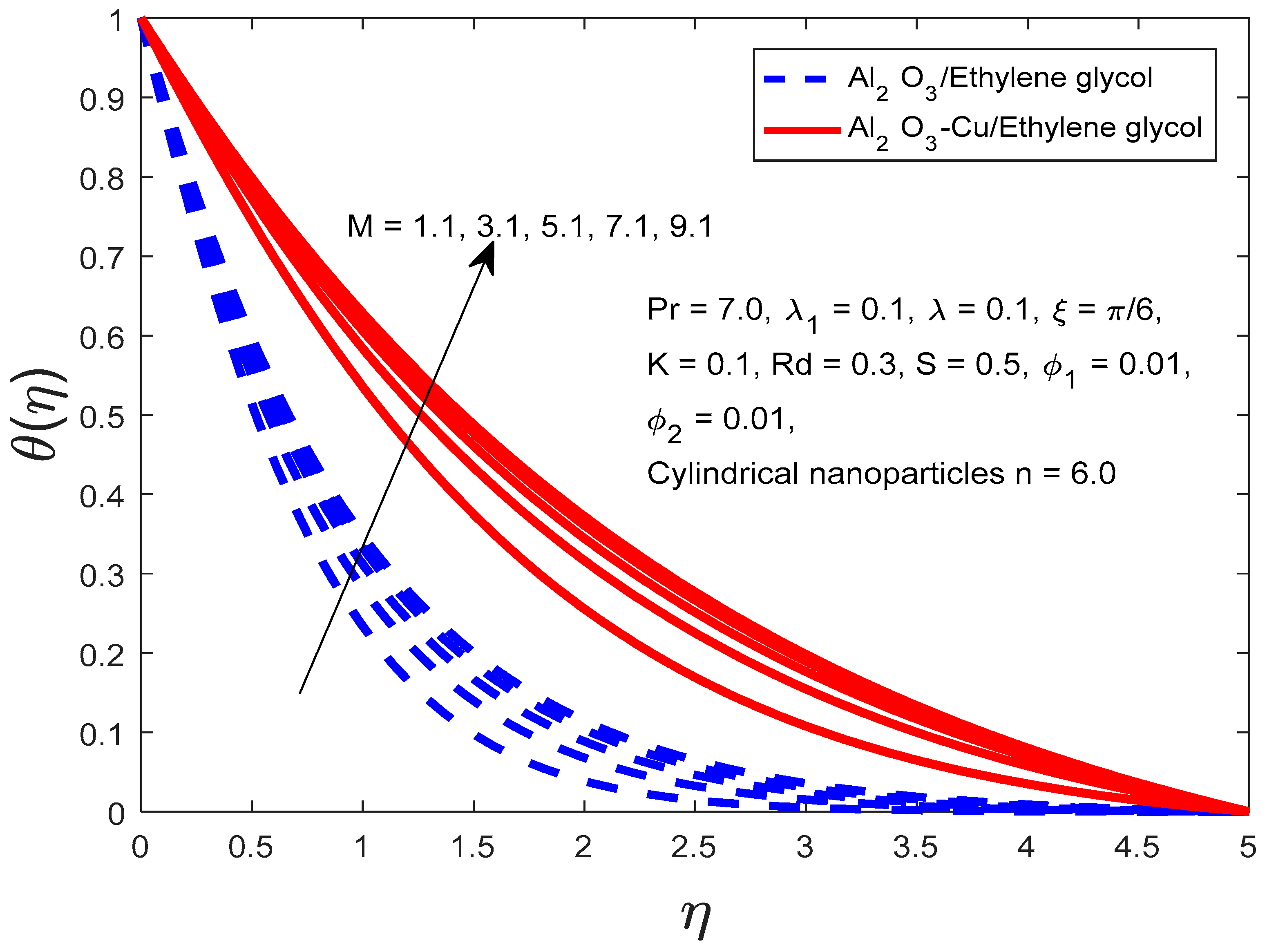
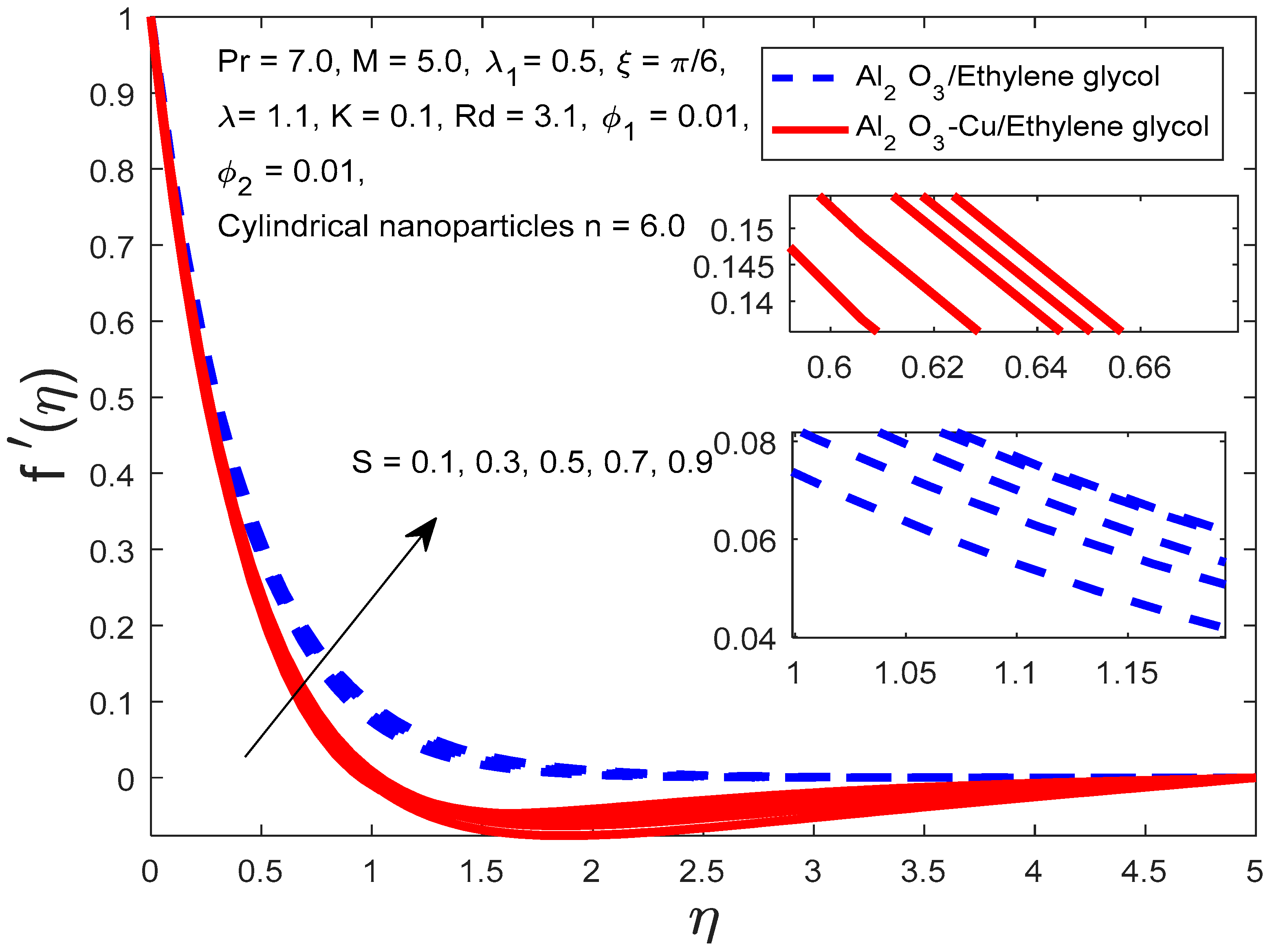
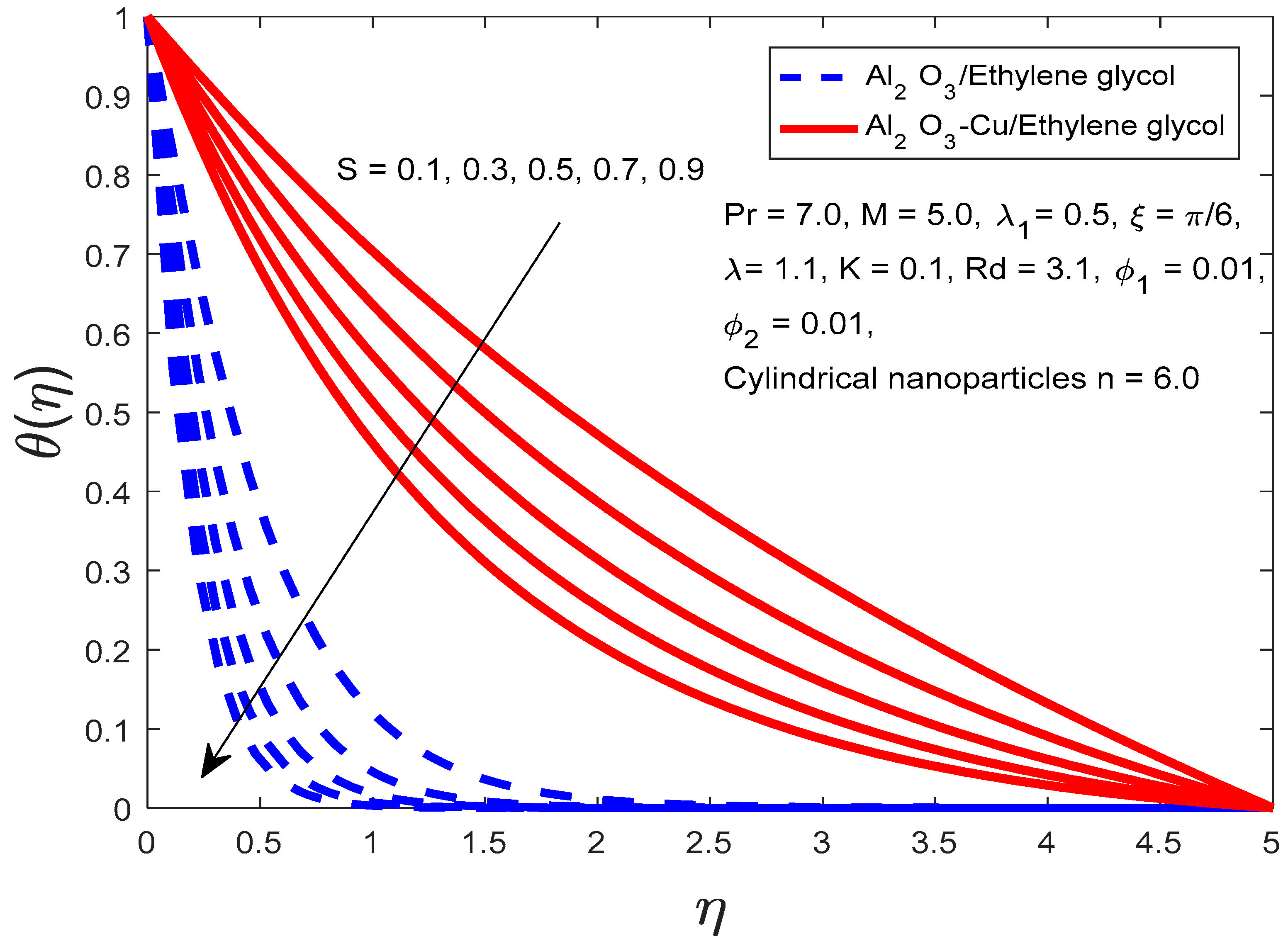
4. Results and Discussion

This section is intended to confine the discussion to the results of the velocity field $f^{\prime }$, temperature field $\theta$, skin friction coefficient $R{e}^{1/2}{C}_f$ and $R{e}^{-1/2}Nu$ under the involved paranetric variations. The parameters appearing in the dimensionless model are the solar radiation parameter $Rd$, suction parameter $(S>0)$, Prandtl number $Pr$, Maxwell fluid parameter ${\lambda }_1$, dimensionless porosity parameter $K$, magnetic field parameter $M$, and buoyancy parameter $\lambda$. The ranges of the parameters are $0.1\le {\lambda }_1\le 1.7,0.1\le \lambda \le 2.0,0.1\le K\le 3.1,0.1\le Rd\le 13.1,1.1\le M\le 9.1,$and $0.1\le S\le 0.9.$

Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 are illustrate the graphical aspects of physical quantities such as velocity field $f^{\prime }$, and temperature field $\theta$ under the pertinent parameters. Figure 2 reveals the non-dimensional velocity $f^{\prime }$ behavior versus increasing inputs of ${\lambda }_1$. Figure 2 illustrates that growing values of ${\lambda }_1$ results in decreasing magnitude of $f^{\prime }$ for both cases mono fluid $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{C}\mathrm{u}\backslash \mathrm{E}\mathrm{t}\mathrm{h}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{e}$ glycol(NF) and $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{C}\mathrm{u}\backslash \mathrm{E}\mathrm{t}\mathrm{h}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{e}$ glycol hybrid nanofluid(HNF).

Figure 3 and Figure 4 depict the influence of buoyancy parameter $\lambda$ on $f^{\prime }$ and $\theta$. It is worth noticing that $\lambda$ has substantial influence on $f$ for both nanofluid and hybrid nanofluid. It can be observed that when $\lambda$ is intensified, then velocity goes to are duction in magnitude for both $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3\backslash \mathrm{E}\mathrm{t}\mathrm{h}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{e}$ glycol(NF) and $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3\backslash \mathrm{E}\mathrm{t}\mathrm{h}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{e}$ glycol hybrid nanofluid(HNF). But a noticeable point is that the magnitudes of the curves for $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3\backslash \mathrm{E}\mathrm{t}\mathrm{h}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{e}$ glycol(NF) are higher than those of $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$-$\mathrm{C}\mathrm{u}$\Ethylene glycol hybrid nanofluid(HNF). On the other hand, the temperature of the fluid demonstrates the entire opposite behavior, unlike the velocity. This is according to the physics of the parameter. The buoyancy parameter is basically the pressure gradient force that retards the motion of fluid. With the intensification in the values of $\lambda$, the thermal expansion parameter is raised, and hence the temperature of the fluid climbs up. Figure 5 and Figure 6, display the effects of the porous medium parameter $K$ on $f^{\prime }$ and $\theta$. When $K$ is enhanced, the velocity gets reduced, and the temperature gets enhanced forboth nanofluid $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3\backslash \mathrm{E}\mathrm{t}\mathrm{h}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{e}$ glycol(NF) and $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3\backslash \mathrm{E}\mathrm{t}\mathrm{h}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{e}$ glycol hybrid nanofluid(HNF). It due to the fact that an increase in $K$ is because of the increment in viscosity causes the velocity to delineate. In the increment of the porosity parameter, the pores sizes are minimized, which compels the fluid flow to slow down. The influence of radiation parameter impact on $\theta$ is displayed in Figure 7. As the radiation parameter is enhanced, the temperature of the fluid flow domain rises. The purpose of the radiation parameter in the energy equation is to raise the temperature of the fluid, hence serving the purpose in Figure 7.

Figure 8 and Figure 9 show the influence of magnetic field number $M$ on $f^{\prime }$ and $\theta$, respectively. When $M$ is augmented, $f^{\prime }$ becomesdelineated and $\theta$ gets raised. This is entirely based on the physics of the magnetic field parameter. The inclusion of $M$ generates the Lorentz force retards the motion of the fluid, and the resistive force creates an enhancement in the temperature. The resistive force intensifies the temperature of the fluid and hinders its flow speed. The effects of the suction parameter $S$ on $f^{\prime }$ and $\theta$ have been shown in Figure 10 and Figure 11, respectively. As the suction parameter is intensified, there is an augmentation in the velocity and are duction in the temperature. By the definition of suction parameter, a rise in suction parameter is due to a reduction in the kinematic viscosity, and hence the speed of the flow is minimized. Figure 12 and Figure 13 is entirely focused on impact of nanoparticles volume fraction of type one ${\varphi }_1$ and types second ${\varphi }_2$ on $f^{\prime }$ and $\theta$. As ${\varphi }_1,{\varphi }_2$ are augmented $f^{\prime }$ decreases and $\theta$ increases. More nanoparticles in a fluid can make it heat up faster, as they are typically better at conducting heat than the fluid itself. This means that heat is transferred more quickly, raising the fluid’s temperature. However, more nanoparticles can also slow the fluid’s flow. This is because they increase the fluid’s thickness or viscosity, making it harder for the fluid to move. For the validation of the current results, the comparison of the present solutions for the Nusselt number with the already published results is given in

Table 2. Comparison of Nusselt number $-{\theta }^{\prime },$ when ${\varphi }_1={\varphi }_2=0,\xi =\frac{\pi }{2},M=0,K=0,{\lambda }_1=0,\lambda =0,Rd=0.0$ against several values of $Pr$.

$\mathit{P}\mathit{r}$	Khan and Pop [34]	Present
2.0	0.9113	0.9112
7.0	1.8954	1.8951
20.0	3.3539	3.3537

. From the comparison, it has been concluded that there is excellent agreement between the present and published solutions, which serves the purpose of ensuring the accuracy of the proposed model.

Table 3. Numerical values of $\left(a\right)R{e}^{1/2}{C}_f\left(b\right)R{e}^{-1/2}NuforM=2.2,M=5.0,{\lambda }_1=0.5,\lambda =0.1,K=1.1,Rd=5.1,S=0.9,{\varphi }_1={\varphi }_2=0.01$ against several values of $Pr$ at angle $\xi =\pi /6$.

Parameter	$\mathbf{A}{\mathbf{l}}_2{\mathbf{O}}_3$/Ethylene Glycol		$\mathbf{A}{\mathbf{l}}_2{\mathbf{O}}_3-\mathbf{C}\mathbf{u}$/Ethylene Glycol
$\mathit{P}\mathit{r}$	$\mathit{R}{\mathit{e}}^{1/2}{\mathit{C}}_{\mathit{f}}$	$\mathit{R}{\mathit{e}}^{-1/2}\mathit{N}\mathit{u}$	$\mathit{R}{\mathit{e}}^{1/2}{\mathit{C}}_{\mathit{f}}$	$\mathit{R}{\mathit{e}}^{-1/2}\mathit{N}\mathit{u}$
1.0	−2.440885780048708	0.937003251099421	−2.496158628810037	0.260514652198284
4.0	−2.433260774141108	3.373926809863024	−2.495086341308096	0.494367779665717
7.0	−2.429131359963453	5.653438109180084	−2.493875082111052	0.776535023741788
10.0	−2.426497007689914	7.878409464833051	−2.492684796970896	1.073507399135452
13.0	−2.424679778344669	10.077134176793365	−2.491578943689763	1.369986830558261

and

Table 4. Numerical values of $\left(a\right)R{e}^{1/2}{C}_f\left(b\right)R{e}^{-1/2}Nu,forPr=7.0,M=5.0,{\lambda }_1=0.5,K=1.1,Rd=5.1,S=0.9,{\varphi }_1={\varphi }_2=0.01$ against several values of $Pr$ at angle $\xi =\pi /6$.

Parameter	$\mathbf{A}{\mathbf{l}}_2{\mathbf{O}}_3$/Ethylene Glycol		$\mathbf{A}{\mathbf{l}}_2{\mathbf{O}}_3-\mathbf{C}\mathbf{u}$/Ethylene Glycol
$\mathit{\lambda }$	$\mathit{R}{\mathit{e}}^{1/2}{\mathit{C}}_{\mathit{f}}$	$\mathit{R}{\mathit{e}}^{-1/2}\mathit{N}\mathit{u}$	$\mathit{R}{\mathit{e}}^{1/2}{\mathit{C}}_{\mathit{f}}$	$\mathit{R}{\mathit{e}}^{-1/2}\mathit{N}\mathit{u}$
0.1	−2.429131359963453	5.653438109180084	−2.493875082111052	0.776535023741788
0.3	−2.458536705009142	5.652062634745575	−2.548458322173527	0.770623015979192
0.5	−2.487980959091588	5.650498254741243	−2.603279067543225	0.764568776805527
0.7	−2.517426119372881	5.649053432490057	−2.658348818265193	0.758363732984885
0.9	−2.546893601939053	5.647544653830980	−2.713675424578194	0.751998460216156

are showing the numerical results of skin friction $R{e}^{1/2}{C}_f$ and Nussle number $R{e}^{-1/2}Nu$ for the Prandtl number and the buoyancy parameter $\lambda$, respectively.Table 3 represents the Prandtl number effects on skin friction and the Nusselt number for nanofluid $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$\Ethylene glycol and hybrid nanofluid $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$-$\mathrm{C}\mathrm{u}$\Ethylene glycol. It has been noted that as $Pr$ is enhanced $R{e}^{1/2}{C}_f$ decreases and $R{e}^{-1/2}Nu$ is increased remarkably. Table 4 is illustrating the effect of buoyancy parameter on $R{e}^{1/2}{C}_f$ and Nussle number $R{e}^{-1/2}Nu$ for nanofluid $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$\Ethylene glycol and hybrid nanofluid $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$-$\mathrm{C}\mathrm{u}$\Ethylene glycol. The varying values of $\lambda$ show that as $\lambda$ is raised $R{e}^{1/2}{C}_f$ rises and $R{e}^{-1/2}Nu$ reduces gradually. All the graphs satisfy the given boundary conditions asymptotically.

5. Conclusions

In the current analysis, the main investigations are on the thermal efficiency of cylindrical-shaped nanoparticles of $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$-$\mathrm{C}\mathrm{u}$ suspended in the base fluid ethylene glycol in non-Newtonian Maxwell fluid flow and heat transfer. Here, the non-Newtonian Maxwell fluid model is considered with solar radiation included in the energy equation along with an applied magnetic field. The suction of the geometry is encountered on the inclined linear stretching sheet angled at $\xi =\pi /6$, which is embedded in a porous medium. The main outcomes of the proposed study for graphical and tabular aspects angle $\xi =\pi /6$ are summarized below:

• It is concluded that more nanoparticles in a fluid can make it heat up faster, as they are typically better at conducting heat than the fluid itself. This means heat is transferred more quickly, raising the fluid’s temperature. However, more nanoparticles can also slow the fluid’s flow at angle $\xi =\pi /6$;
• The presence of a magnetic field results in the Lorentz force. The resistance this force creates slows the fluid down. The temperature of the fluid flow domain is increased by this resistance;
• The stretching rate constant and relaxation time are increasing as a result of a decrease in the density of the base fluid, which helps the fluid climb in speed;
• According to the definition of the porosity parameter, an increase in the porosity parameter results from an increase in kinematic viscosity and a decrease in porous spaces, which impede fluid flow and reduce speed. Additionally, when we compare the cases of nanofluid and hybrid nanofluid, the volume proportion of nanoparticles in nanofluid is lower than that in hybrid nanofluid, which results in stronger velocity curves for nanofluid;
• As the radiation parameter is enhanced, the temperature of the fluid flow domain rises. The purpose of the radiation parameter in the energy equation is to raise the temperature of the fluid, hence serving its purpose;
• Nussle number increases with increasing values of Prandtl number and decreases with increasing values of buoyancy parameter;
• Skin friction coefficient increases values of buoyancy parameter but reduces with rising values of Prandlt number;
• All solutions satisfy the given boundary conditions, which endorses the accuracy of the obtained results at angle $\xi =\pi /6$;
• For the validation of the current results, a comparison of the present solutions for the Nusselt number with already published results is given. From the comparison, it has been concluded that there is excellent agreement between the present and published solutions, which serves the purpose of ensuring the accuracy of the proposed model;
• This study is limited to incorporating the MHD Maxwell fluid model by using a hybrid nanofluid prepared by $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$-$\mathrm{C}\mathrm{u}$\Ethylene glycol. In this study, solar recitation, suction, and porous space over inclined geometry are considered. Further, this study can be extended by adding the reduced gravity effects along with the Soret and Dufour effects. It can also be enhanced to include Fourier’s and Fick’s Laws in future work.