Pseudo-Finsler Radially Symmetric Spaces
Abstract
:1. Introduction
2. Anisotropic Tensor Calculus and Pseudo-Finsler Geometry
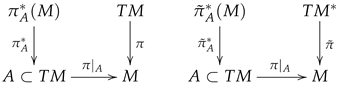
2.1. Anisotropic Connections
- (i)
- , for any ,
- (ii)
- for any , ,
- (iii)
- , for any , ,
2.2. Curvature Tensor
2.3. Parallel Transport
2.4. Pseudo-Finsler Manifolds and Flag Curvature
- It is smooth on ;
- It is positive homogeneous of degree 2;
- For every , the fundamental tensor defined asis a non-degenerate bilinear form.
3. Radially Symmetric Finsler Manifolds
- 1.
- We define as , where γ is the only unit geodesic such that and .
- 2.
- We say that is locally radially symmetric if for all and Ω as above, we have thatis an isometry (as above γ is a unit geodesic, and ) for all .
- (i)
- .
- (ii)
- If V is an observer-parallel vector field along a regular curve α and X is parallel with respect to V, then is also parallel with respect to V along α.
- (iii)
- Flag curvature is invariant under parallel translation.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cartan, É. Sur une classe remarquable d’espaces de Riemann, I. Bull. Soc. Math. Fr. 1926, 54, 214–216. [Google Scholar] [CrossRef]
- Cartan, É. Sur une classe remarquable d’espaces de Riemann, II. Bull. Soc. Math. Fr. 1927, 55, 114–134. [Google Scholar] [CrossRef]
- Deng, S.; Hou, Z. On symmetric Finsler spaces. Isr. J. Math. 2007, 162, 197–219. [Google Scholar] [CrossRef]
- Foulon, P. Locally symmetric Finsler spaces in negative curvature. C. R. Acad. Sci. Paris Sér. I Math. 1997, 324, 1127–1132. [Google Scholar] [CrossRef]
- Egloff, D. Some New Developments in Finsler Geometry. Ph.D. Dissertation, University Fribourg, Fribourg, Switzerland, 1995. [Google Scholar]
- Kim, C.-W. Locally symmetric positively curved Finsler spaces. Arch. Math. 2007, 88, 378–384. [Google Scholar] [CrossRef]
- Matveev, V.S. There exist no locally symmetric Finsler spaces of positive or negative flag curvature. C. R. Math. Acad. Sci. Paris 2015, 353, 81–83. [Google Scholar] [CrossRef]
- Wu, B.Y. Some rigidity theorems for locally symmetrical Finsler manifolds. J. Geom. Phys. 2008, 58, 923–930. [Google Scholar] [CrossRef]
- Deng, S.; Hou, Z. On locally and globally symmetric Berwald spaces. J. Phys. A Math. Gen. 2005, 38, 1691–1697. [Google Scholar] [CrossRef]
- Deng, S.; Hou, Z. Minkowski symmetric Lie algebras and symmetric Berwald spaces. Geom. Dedicata 2005, 113, 95–105. [Google Scholar] [CrossRef]
- Javaloyes, M.Á.; Sánchez, M.; Villaseñor, F.F. Anisotropic connections and parallel transport in Finsler spacetimes. In Developments in Lorentzian Geometry; Springer Proceedings in Mathematics & Statistics Series; Springer: Cham, Switzerland, 2022; Volume 338, 32p, ISBN 978-3-031-05378-8. [Google Scholar]
- Abate, M.; Patrizio, G. Finsler metrics of constant curvature and the characterization of tube domains. Contemp. Math. 1996, 196, 101–107. [Google Scholar]
- Javaloyes, M.A. Anisotropic tensor calculus. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1941001. [Google Scholar] [CrossRef]
- Bao, D.; Chern, S.-S.; Shen, Z. An Introduction to Riemann-Finsler Geometry; Springer: New York, NY, USA, 2000; Volume 200. [Google Scholar]
- Nazim, A. Über Finslersche Räume; Wolf: München, Germany, 1936. [Google Scholar]
- Varga, O. Zur Herleitung des invarianten Differentials in Finslerschen Räumen. Monatsh. Math. Phys. 1941, 50, 165–175. [Google Scholar] [CrossRef]
- Matthias, H.-H. Zwei Verallgemeinerungen eines Satzes von Gromoll und Meyer; Bonner Mathematische Schriften [Bonn Mathematical Publications]; Universität Bonn Mathematisches Institut: Bonn, Germany, 1980; Volume 126. [Google Scholar]
- Shen, Z. Differential Geometry of Spray and Finsler Spaces; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Álvarez Paiva, J.C.; Durán, C.E. Isometric submersions of Finsler manifolds. Proc. Am. Math. Soc. 2001, 129, 2409–2417. [Google Scholar] [CrossRef]
- Rademacher, H.-B. Nonreversible Finsler metrics of positive flag curvature. In A Sampler of Riemann-Finsler Geometry; Cambridge University Press: Cambridge, UK, 2004; Volume 50, pp. 261–302. [Google Scholar]
- Rademacher, H.-B. A sphere theorem for non-reversible Finsler metrics. Math. Ann. 2004, 328, 373–387. [Google Scholar] [CrossRef]
- Kovács, Z.; Tóth, A. On the geometry of two-step nilpotent groups with left invariant Finsler metrics. Acta Math. Acad. Paedagog. Nyházi. 2008, 24, 15–168. [Google Scholar]
- Javaloyes, M.A. Curvature computations in Finsler geometry using a distinguished class of anisotropic connections. Mediterr. J. Math. 2020, 17, 21. [Google Scholar] [CrossRef]
- Foulon, P.; Matveev, M.S. Zermelo deformation of Finsler metrics by Killing vector fields. Electron. Res. Announc. Math. Sci. 2018, 25, 1–7. [Google Scholar] [CrossRef]
- Ambrose, W. Parallel Translation of Riemannian Curvature. Ann. Math. 1956, 64, 337. [Google Scholar] [CrossRef]
- Hicks, N. A theorem on affine connexions. Ill. J. Math. 1959, 3, 24–254. [Google Scholar] [CrossRef]
- Javaloyes, M.A.; Soares, B.L. Geodesics and Jacobi fields of pseudo-Finsler manifolds. Publ. Math. Debr. 2015, 87, 57–78. [Google Scholar] [CrossRef]
- Deng, S. Homogeneous Finsler Spaces; Springer Monographs in Mathematics; Springer: New York, NY, USA, 2012; 240p. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ionel, M.; Javaloyes, M.Á. Pseudo-Finsler Radially Symmetric Spaces. Symmetry 2024, 16, 362. https://doi.org/10.3390/sym16030362
Ionel M, Javaloyes MÁ. Pseudo-Finsler Radially Symmetric Spaces. Symmetry. 2024; 16(3):362. https://doi.org/10.3390/sym16030362
Chicago/Turabian StyleIonel, Marianty, and Miguel Ángel Javaloyes. 2024. "Pseudo-Finsler Radially Symmetric Spaces" Symmetry 16, no. 3: 362. https://doi.org/10.3390/sym16030362




