Constraints on Graviton Mass from Schwarzschild Precession in the Orbits of S-Stars around the Galactic Center
Abstract
:1. Introduction
2. Orbital Precession in Yukawa-like Gravitational Potential
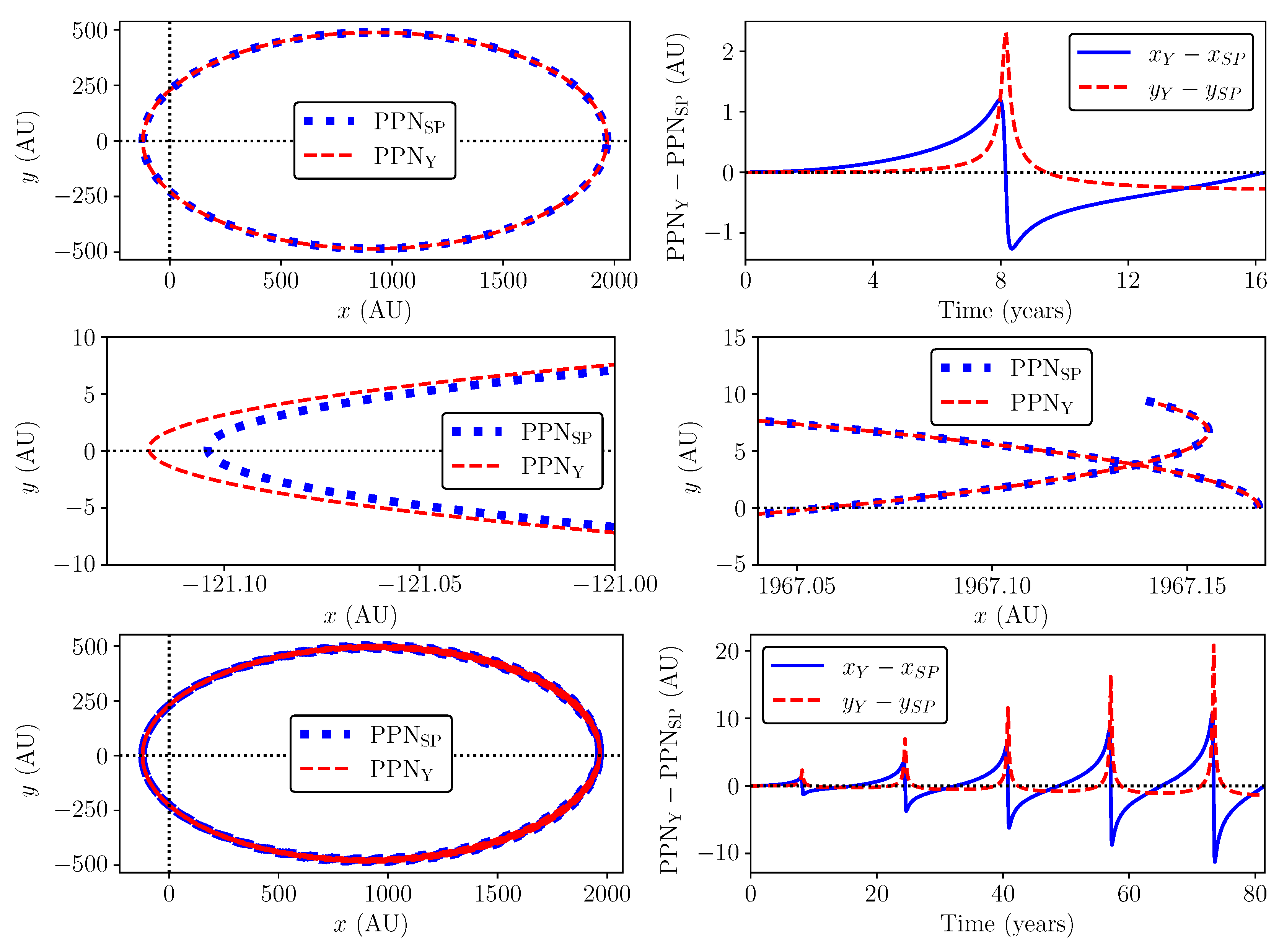
3. Stellar Orbits in Extended/Modified PPN Formalisms
4. Results: Constraints on the Compton Wavelength and Mass of the Graviton
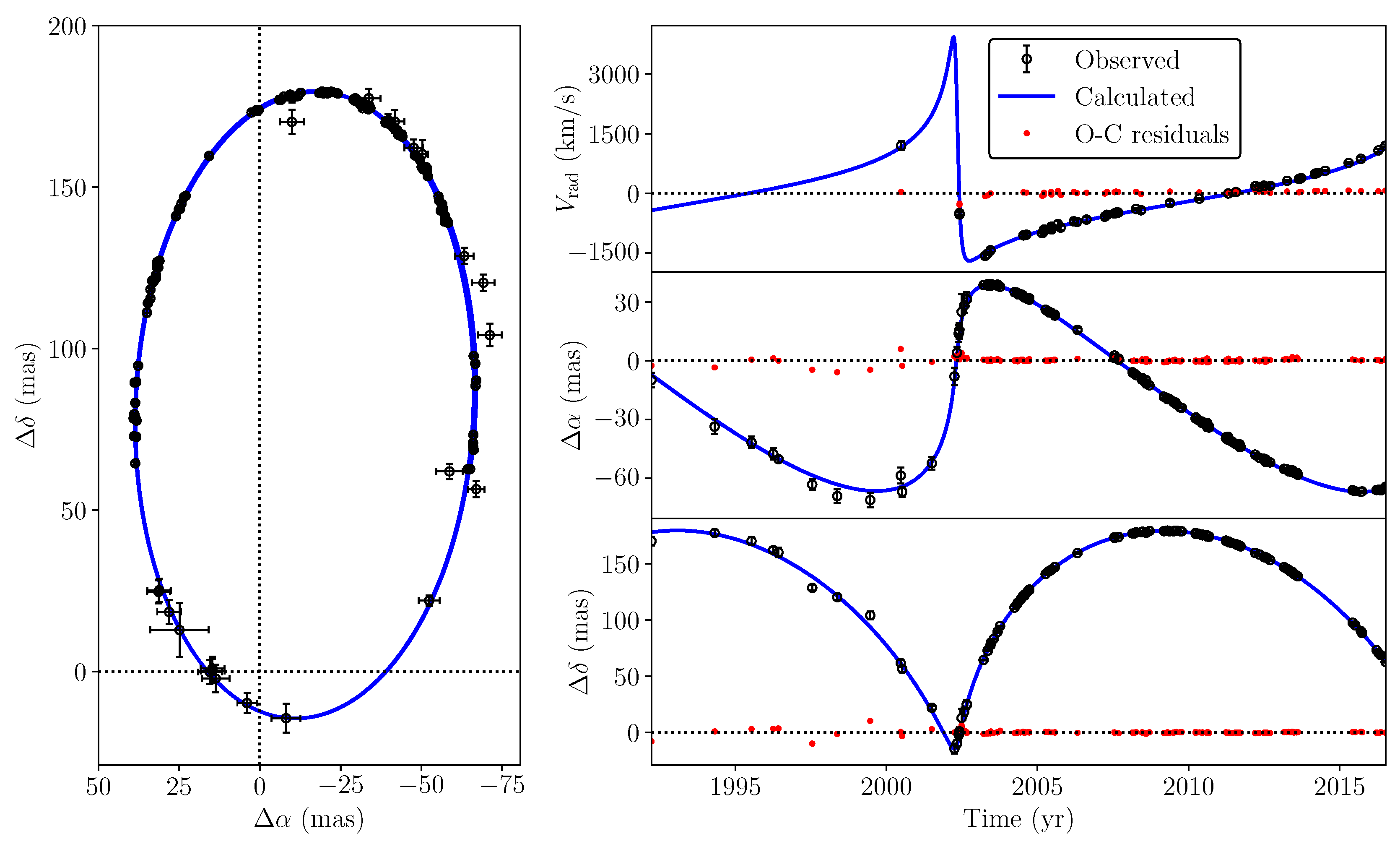
PPN Fit of the Observed Orbit of the S2 Star
- 1.
- First, a simulated orbit of the S2 star in the extended formalism is calculated by numerical integration of the equations of motion (7), starting from initial conditions , where the first two components specify the initial position and the last two the initial velocity in the orbital plane. In our simulations, the initial conditions correspond to the time of apocenter passage, , preceding the first astrometric observation at : , where T is the time of pericenter passage, P is the orbital period, and k is the smallest positive integer (number of periods) for which . Then, the initial conditions are: , , , and where is the apocenter distance and is the corresponding orbital velocity at the apocenter.
- 2.
- The true orbit obtained in the first step, which depends only on , was then projected to the observer’s sky plane using the remaining geometrical orbital elements , in order to obtain the corresponding positions along the apparent orbit,where , and G are the Thiele–Innes elements:In addition, the radial velocities, , are obtained from the corresponding true positions and orbital velocities as (see, e.g., [62] and references therein)where .
- 3.
- Finally, is obtained according to Equation (16), taking into account only those apparent positions that are calculated at the same epochs as the astrometric observations .
5. Conclusions
- 1.
- We found the condition for parameter of the phenomenological Yukawa-like gravitational potential (3) under which the orbital precession in this potential deviates from the Schwarzschild precession in GR by a factor ;
- 2.
- 3.
- Both of the studied PPN formalisms result in close and very similar simulated orbits of S-stars, which practically overlap during the first orbital period and then begin to slowly diverge over time due to some assumed theoretical approximations;
- 4.
- In most cases, the constraints on the upper bound on graviton mass, , and its absolute error, , obtained using the phenomenological potential (3), were improved by ∼30% in respect to our previous corresponding estimates from [55], obtained using a slightly different Yukawa-like potential derived in the frame of theories of gravity, although the relative errors in both cases remained the same;
- 5.
- These results were also confirmed in the case of the S2 star by fitting its observed orbit into the frame of the extended formalism, which resulted in the best-fit value for the graviton Compton wavelength, , within the error intervals of its corresponding estimates obtained according to Equation (14) from the detected values of ;
- 6.
- The least reliable constraints with unrealistically high uncertainties were only obtained from estimates for that were very close to its value predicted by GR, being only slightly larger than 1;
- 7.
- If one compares the results from Table 2 with those from Table 3, it can be seen that the upper bounds on graviton mass, , are very similar. In the case of the S2 star, eV and the relative error is approximately 50%. We can conclude that more precise future observations are required in order to further improve the upper graviton mass bounds.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GC | Galactic Center |
| GR | General Relativity |
| SMBH | Supermassive Black Hole |
| PPN formalism | Parameterized Post-Newtonian formalism |
References
- Will, C.M. Bounding the mass of the graviton using gravitational-wave observations of inspiralling compact binaries. Phys. Rev. D 1998, 57, 2061. [Google Scholar] [CrossRef]
- Will, C.M. Solar system versus gravitational-wave bounds on the graviton mass. Class. Quant. Grav. 2018, 35, 17LT01. [Google Scholar] [CrossRef]
- Fischbach, E.; Talmadge, C.L. The Search for Non–Newtonian Gravity; Springer: Heidelberg, Germany; New York, NY, USA, 1999; 305p. [Google Scholar]
- Kopeikin, S.; Vlasov, I. Parametrized post-Newtonian theory of reference frames, multipolar expansions and equations of motion in the N-body problem. Phys. Rep. 2004, 400, 209. [Google Scholar] [CrossRef]
- Clifton, T. Alternative Theories of Gravity; University of Cambridge: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Fundamental Theories of Physics; Springer: Dordrecht, The Netherlands, 2011; Volume 170. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D. The dark matter problem from f(R) gravity viewpoint. Ann. Phys. 2012, 524, 545. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L.; et al. Einstein, Planck and Vera Rubin: Relevant encounters between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 603190. [Google Scholar] [CrossRef]
- Fierz, M.; Pauli, W. On Relativistic Wave Equations for Particles of Arbitrary Spin in an Electromagnetic Field. Proc. R. Soc. Lond. Ser. A 1939, 173, 211. [Google Scholar]
- Logunov, A.A.; Mestvirishvili, M.A.; Chugreev, Y.V. Graviton Mass and Evolution of a Friedmann Universe. Theor. Math. Phys. 1988, 74, 1. [Google Scholar] [CrossRef]
- Chugreev, Y.V. Cosmological consequences of the relativistic theory of gravitation with massive gravitons. Theor. Math. Phys. 1989, 79, 554. [Google Scholar] [CrossRef]
- Gershtein, S.S.; Logunov, A.A.; Mestvirishvili, M.A. Graviton Mass and the Total Relative Mass Density Ωtot in the Universe. Dokl. Phys. 2003, 48, 282. [Google Scholar] [CrossRef]
- Gershtein, S.S.; Logunov, A.A.; Mestvirishvili, M.A.; Tkachenko, N.P. Graviton mass, quintessence, and oscillatory character of Universe evolution. Phys. Atomic Nucl. 2004, 67, 1596. [Google Scholar] [CrossRef]
- Gershtein, S.S.; Logunov, A.A.; Mestvirishvili, M.A. Gravitational field self-limitation and its role in the Universe. Phys.-Uspekhi 2006, 49, 1179. [Google Scholar] [CrossRef]
- Rubakov, V.A.; Tinyakov, P.G. Infrared-modified gravities and massive gravitons. Phys. Usp. 2008, 51, 759. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C.; Ziour, R. Recovery of general relativity in massive gravity via the Vainshtein mechanism. Phys. Rev. D 2010, 82, 104008. [Google Scholar] [CrossRef]
- de Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 89, 231101. [Google Scholar] [CrossRef] [PubMed]
- de Rham, C. Massive Gravity. Living Rev. Relativ. 2014, 17, 7. [Google Scholar] [CrossRef]
- de Rham, C.; Deskins, J.T.; Tolley, A.J.; Zhou, S.-Y. Massive Gravity. Rev. Mod. Phys. 2017, 89, 025004. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. Can Gravitation Have a Finite Range? Phys. Rev. D 1972, 6, 3368. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration; Virgo Collaboration and KAGRA Collaboration; Abbott, R.; Abe, H.; Acernese, F.; Ackley, K.; Adhikari, N.; Adhikari, R.X.; Adkins, V.K.; Adya, V.B.; et al. Tests of General Relativity with GWTC-3. arXiv 2021, arXiv:2112.06861. [Google Scholar]
- Particle Data Group. Review of particle physics. Progr. Theor. Exper. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Poisson, E.; Will, C.M. Gravity (Newtonian, Post-Newtonian, Relativistic); Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-03286-6. [Google Scholar]
- Sanders, R.H. Anti-gravity and galaxy rotation curves. Astron. Astrophys. 1984, 136, L21. [Google Scholar]
- Talmadge, C.; Berthias, J.-P.; Hellings, R.W.; Standish, E.M. Model-independent constraints on possible modifications of Newtonian gravity. Phys. Rev. Lett. 1988, 61, 1159. [Google Scholar] [CrossRef]
- White, M.J.; Kochanek, C.S. Constraints on the long-range properties of gravity from weak gravitational lensing. Astrophys. J. 2001, 560, 539. [Google Scholar] [CrossRef]
- Amendola, L.; Quercellini, C. Skewness as a test of the equivalence principle. Phys. Rev. Lett. 2004, 92, 181102. [Google Scholar] [CrossRef]
- Reynaud, S.; Jaekel, M.-T. Testing the Newton law at long distances. Int. J. Mod. Phys. A 2005, 20, 2294. [Google Scholar] [CrossRef]
- Sealfon, C.; Verde, L.; Jimenez, R. Limits on deviations from the inverse-square law on megaparsec scales. Phys. Rev. D 2005, 71, 083004. [Google Scholar] [CrossRef]
- Moffat, J.W. Gravitational theory, galaxy rotation curves and cosmology without dark matter. J. Cosmol. Astropart. P. 2005, 5, 22. [Google Scholar] [CrossRef]
- Moffat, J.W. Scalar tensor vector gravity theory. J. Cosmol. Astropart. P. 2006, 03, 004. [Google Scholar] [CrossRef]
- Sereno, M.; Jetzer, P. Dark matter versus modifications of the gravitational inverse-square law: Results from planetary motion in the Solar system. Mon. Not. R. Astron. Soc. 2006, 371, 626. [Google Scholar] [CrossRef]
- Capozziello, S.; Stabile, A.; Troisi, A. Newtonian limit of f(R) gravity. Phys. Rev. D 2007, 76, 104019. [Google Scholar] [CrossRef]
- Iorio, L. Constraints on the range Λ of Yukawa-like modifications to the Newtonian inverse-square law of gravitation from Solar System planetary motions. J. High Energy Phys. 2007, 10, 41. [Google Scholar] [CrossRef]
- Iorio, L. Putting Yukawa-like Modified Gravity (MOG) on the test in the Solar System. Sch. Res. Exch. 2008, 2008, 238385. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoedl, S.; Schlamminger, S. Torsion balance experiments: A low-energy frontier of particle physics. Prog. Part. Nucl. Phys. 2009, 62, 102. [Google Scholar] [CrossRef]
- Capozziello, S.; de Filippis, E.; Salzano, V. Modelling clusters of galaxies by f(R)-gravity. Mon. Not. R. Astron. Soc. 2009, 394, 947. [Google Scholar] [CrossRef]
- Cardone, V.F.; Capozziello, S. Systematic biases on galaxy haloes parameters from Yukawa-like gravitational potentials. Mon. Not. R. Astron. Soc. 2011, 414, 1301. [Google Scholar] [CrossRef]
- Miao, X.; Shao, L.; Ma, B.-Q. Bounding the mass of graviton in a dynamic regime with binary pulsars. Phys. Rev. D 2019, 99, 123015. [Google Scholar] [CrossRef]
- Capozziello, S.; Altucci, C.; Bajardi, F.; Basti, A.; Beverini, N.; Carelli, G.; Ciampini, D.; Di Virgilio, A.D.; Fuso, F.; Giacomelli, U.; et al. Constraining theories of gravity by GINGER experiment. Eur. Phys. J. Plus 2021, 136, 394. [Google Scholar] [CrossRef]
- De Martino, I.; della Monica, R.; De Laurentis, M. f(R)-gravity after the detection of the orbital precession of the S2 star around the Galactic centre massive black hole. Phys. Rev. D 2021, 104, L101502. [Google Scholar] [CrossRef]
- della Monica, R.; De Martino, I.; De Laurentis, M. Constraining MOdified Gravity with the S2 star. Universe 2022, 8, 137. [Google Scholar] [CrossRef]
- Benisty, D. Testing modified gravity via Yukawa potential in two body problem: Analytical solution and observational constraints. Phys. Rev. D 2022, 106, 043001. [Google Scholar] [CrossRef]
- Dong, Y.; Shao, L.; Hu, Z.; Miao, X.; Wang, Z. Prospects for constraining the Yukawa gravity with pulsars around Sagittarius A*. J. Cosmol. Astropart. P. 2022, 11, 51. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, Y. Constraining the Yukawa Gravity with Post Newtonian Approximation using S-star Orbits around the Supermassive Black Hole in our Galactic Center. arXiv 2024, arXiv:2402.00333. [Google Scholar]
- Borka, D.; Capozziello, S.; Jovanović, P.; Borka Jovanović, V. Probing hybrid modified gravity by stellar motion around Galactic Center. Astropart. Phys. 2016, 79, 41. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Jovanović, P.; Borka, D.; Borka Jovanović, V. Constraining the range of Yukawa gravity interaction from S2 star orbits II: Bounds on graviton mass. J. Cosmol. Astropart. Phys. 2016, 5, 45. [Google Scholar] [CrossRef]
- Jovanović, P.; Borka, D.; Borka Jovanović, V.; Zakharov, A.F. Influence of bulk mass distribution on orbital precession of S2 star in Yukawa gravity. Eur. Phys. J. D 2021, 75, 145. [Google Scholar] [CrossRef]
- Jovanović, P.; Borka Jovanović, V.; Borka, D.; Zakharov, A.F. Constraints on Yukawa gravity parameters from observations of bright stars. J. Cosmol. Astropart. Phys. 2023, 3, 056. [Google Scholar] [CrossRef]
- Jovanović, P.; Borka Jovanović, V.; Borka, D.; Zakharov, A.F. Improvement of graviton mass constraints using GRAVITY’s detection of Schwarzschild precession in the orbit of S2 star around the Galactic Center. Phys. Rev. D 2024, 109, 064046. [Google Scholar] [CrossRef]
- Bernus, L.; Minazzoli, O.; Fienga, A.; Gastineau, M.; Laskar, J.; Deram, P. Constraining the Mass of the Graviton with the Planetary Ephemeris INPOP. Phys. Rev. Lett. 2019, 123, 161103. [Google Scholar] [CrossRef] [PubMed]
- Clifton, T. Parametrized post-Newtonian limit of fourth-order theories of gravity. Phys. Rev. D 2008, 77, 24041. [Google Scholar] [CrossRef]
- Alsing, J.; Berti, E.; Will, C.M.; Zaglauer, H. Gravitational radiation from compact binary systems in the massive Brans-Dicke theory of gravity. Phys. Rev. D 2012, 85, 064041. [Google Scholar] [CrossRef]
- Gainutdinov, R.I. PPN Motion of S-Stars around Sgr A*. Astrophysics 2020, 63, 470. [Google Scholar] [CrossRef]
- Gainutdinov, R.; Baryshev, Y. Relativistic Effects in Orbital Motion of the S-Stars at the Galactic Center. Universe 2020, 6, 177. [Google Scholar] [CrossRef]
- Borka, D.; Jovanović, P.; Borka Jovanović, V.; Zakharov, A.F. Constraints on Rn gravity from precession of orbits S2-like stars. Phys. Rev. D 2012, 85, 124004. [Google Scholar] [CrossRef]
- Borka, D.; Jovanović, P.; Borka Jovanović, V.; Zakharov, A.F. Constraining the range of Yukawa gravity interaction from S2 star orbits. J. Cosmol. Astropart. Phys. 2013, 11, 50. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Borka, D.; Borka Jovanović, V.; Jovanović, P. Constraints on Rn gravity from precession of orbits of S2-like stars: A case of a bulk distribution of mass. Adv. Space Res. 2014, 54, 1108. [Google Scholar] [CrossRef]
- Capozziello, S.; Borka, D.; Jovanović, P.; Borka Jovanović, V.B. Constraining Extended Gravity Models by S2 star orbits around the Galactic Centre. Phys. Rev. D 2014, 90, 44052. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Jovanović, P.; Borka, D.; Borka Jovanović, V. Constraining the range of Yukawa gravity interaction from S2 star orbits III: Improvement expectations for graviton mass bounds. J. Cosmol. Astropart. Phys. 2018, 4, 50. [Google Scholar] [CrossRef]
- Dialektopoulos, K.F.; Borka, D.; Capozziello, S.; Borka Jovanović, V.; Jovanović, P. Constraining nonlocal gravity by S2 star orbits. Phys. Rev. D 2019, 99, 044053. [Google Scholar] [CrossRef]
- Borka Jovanović, V.; Jovanović, P.; Borka, D.; Capozziello, S.; Gravina, S.; D’Addio, A. Constraining scalar-tensor gravity models by S2 star orbits around the Galactic Center. Facta Univ. Ser. Phys. Chem. Technol. 2019, 17, 11. [Google Scholar] [CrossRef]
- Borka, D.; Borka Jovanović, V.; Capozziello, S.; Zakharov, A.F.; Jovanović, P. Estimating the Parameters of Extended Gravity Theories with the Schwarzschild Precession of S2 Star. Universe 2021, 7, 407. [Google Scholar] [CrossRef]
- Zakharov, A.F. Testing the Galactic Centre potential with S-stars. Mon. Not. R. Astron. Soc. Lett. 2022, 511, L35. [Google Scholar] [CrossRef]
- Zakharov, A.F. Orbits of Bright Stars Near the Galactic Center as a Tool to Test Gravity Theories. Mosc. Univ. Phys. Bull. 2022, 77, 341. [Google Scholar] [CrossRef]
- Zakharov, A.F. Trajectories of Bright Stars and Shadows around Supermassive Black Holes as Tests of Gravity Theories. Phys. Part. Nucl. 2023, 54, 889. [Google Scholar] [CrossRef]
- Borka, D.; Borka Jovanović, V.; Nikolić, V.N.; Lazarov, N.D.; Jovanović, P. Estimating the parameters of Hybrid Palatini gravity model with the Schwarzschild precession of S2, S38 and S55 stars: Case of bulk mass distribution. Universe 2022, 8, 70. [Google Scholar] [CrossRef]
- Lynden-Bell, D.; Rees, M.J. The Galactic Center. Mon. Not. R. Astron. Soc. 1971, 152, 461. [Google Scholar] [CrossRef]
- Oort, J.H. The Galactic Center. Annu. Rev. Astron. Astrophys. 1977, 15, 295. [Google Scholar] [CrossRef]
- Rees, M.J. The Compact Source at the Galactic Center. AIP Conf. Proc. 1982, 83, 166. [Google Scholar]
- Genzel, R.; Townes, C.H. Physical conditions, dynamics, and mass distribution in the center of the Galaxy. Ann. Rev Astron. Astrophys. 1987, 25, 377. [Google Scholar] [CrossRef]
- Townes, C.H.; Genzel, R. What is Happening at the Center of Our Galaxy? Sci. Am. 1990, 262, 46. [Google Scholar] [CrossRef]
- Ghez, A.M.; Morris, M.; Becklin, E.E.; Tanner, A.; Kremenek, T. The accelerations of stars orbiting the Milky Way’s central black hole. Nature 2000, 407, 349. [Google Scholar] [CrossRef] [PubMed]
- Schodel, R.; Ott, T.; Genzel, R.; Hofmann, R.; Lehnert, M.; Eckart, A.; Mouawad, N.; Alexander, T.; Reid, M.J.; Lenzen, R.; et al. Closest star seen orbiting the supermassive black hole at the Centre of the Milky Way. Nature 2002, 419, 694. [Google Scholar] [CrossRef] [PubMed]
- Ghez, A.M.; Salim, S.; Weinberg, N.N.; Lu, J.R.; Do, T.; Dunn, J.K.; Matthews, K.; Morris, M.R.; Yelda, S.; Becklin, E.E.; et al. Measuring distance and properties of the Milky Way’s central supermassive black hole with stellar orbits. Astrophys. J. 2008, 689, 1044. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Fritz, T.K.; Bartko, H.; Dodds-Eden, K.; Pfuhl, O.; Ott, T.; Genzel, R. The orbit of the star S2 around Sgr A* from very large telescope and Keck data. Astrophys. J. 2009, 707, L114. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Trippe, S.; Alexander, T.; Genzel, R.; Martins, F.; Ott, T. Monitoring stellar orbits around the massive black hole in the Galactic Center. Astrophys. J. 2009, 692, 1075. [Google Scholar] [CrossRef]
- Genzel, R.; Eisenhauer, F.; Gillessen, S. The Galactic Center massive black hole and nuclear star cluster. Rev. Mod. Phys. 2010, 82, 3121. [Google Scholar] [CrossRef]
- Meyer, L.; Ghez, A.M.; Schödel, R.; Yelda, S.; Boehle, A.; Lu, J.R.; Do, T.; Morris, M.R.; Becklin, E.E.; Matthews, K. The Shortest-Known-Period Star Orbiting Our Galaxy’s Supermassive Black Hole. Science 2012, 338, 84. [Google Scholar] [CrossRef]
- Gillessen, S.; Plewa, P.M.; Eisenhauer, F.; Sari, R.E.; Waisberg, I.; Habibi, M.; Pfuhl, O.; George, E.; Dexter, J.; von Fellenberg, S.; et al. An Update on Monitoring Stellar Orbits in the Galactic Center. Astrophys. J. 2017, 837, 30. [Google Scholar] [CrossRef]
- Hees, A.; Do, T.; Ghez, A.M.; Martinez, G.D.; Naoz, S.; Becklin, E.E.; Boehle, A.; Chappell, S.; Chu, D.; Dehghanfar, A.; et al. Testing General Relativity with Stellar Orbits around the Supermassive Black Hole in Our Galactic Center. Phys. Rev. Lett. 2017, 118, 211101. [Google Scholar] [CrossRef]
- Hees, A.; Ghez, A.M.; Do, T.; Lu, J.R.; Morris, M.R.; Becklin, E.E.; Witzel, G.; Boehle, A.; Chappell, S.; Chen, Z.; et al. Testing the gravitational theory with short-period stars around our Galactic Center. In Proceedings of the 52th Rencontres de Moriond, 2017 Gravitation, La Thuile, Italy, 25 March–1 April 2017; Auge, E., Dumarchez, J., Van, J.T.T., Eds.; ARISF: Lausanne, Switzerland, 2017; pp. 283–286. Available online: https://moriond.in2p3.fr/Proceedings/2017/Moriond_Gravitation_2017.pdf (accessed on 1 February 2024).
- Chu, D.S.; Do, T.; Hees, A.; Ghez, A.; Naoz, S.; Witzel, G.; Sakai, S.; Chappell, S.; Gautam, A.K.; Lu, J.R.; et al. Investigating the Binarity of S0-2: Implications for Its Origins and Robustness as a Probe of the Laws of Gravity around a Supermassive Black Hole. Astrophys. J. 2018, 854, 12. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Anugu, N.; Bauböck, M.; Benisty, M.; Berger, J.P.; Blind, N.; Bonnet Brandner, W.; Buron, A.; et al. Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Clénet, Y.; Du Foresto, V.C.; De Zeeuw, P.T.; et al. A geometric distance measurement to the Galactic center black hole with 0.3% uncertainty. Astron. Astrophys. 2019, 625, L10. [Google Scholar]
- Do, T.; Hees, A.; Ghez, A.; Martinez, G.D.; Chu, D.S.; Jia, S.; Sakai, S.; Lu, J.R.; Gautam, A.K.; O’Neil, K.K.; et al. Relativistic redshift of the star S0-2 orbiting the Galactic Center supermassive black hole. Science 2019, 365, 664. [Google Scholar] [CrossRef]
- GRAVITY Collaboration. Scalar field effects on the orbit of S2 star. Mon. Not. R. Astron. Soc. 2019, 489, 4606. [Google Scholar] [CrossRef]
- Saida, H.; Nishiyama, S.; Ohgami, T.; Takamori, Y.; Takahashi, M.; Minowa, Y.; Najarro, F.; Hamano, S.; Omiya, M.; Iwamatsu, A.; et al. A significant feature in the general relativistic time evolution of the redshift of photons coming from a star orbiting Sgr A*. Astron. Soc. Japan 2019, 71, 126. [Google Scholar] [CrossRef]
- Hees, A.; Do, T.; Roberts, B.M.; Ghez, A.M.; Nishiyama, S.; Bentley, R.O.; Gautam, A.K.; Jia, S.; Kara, T.; Lu, J.R.; et al. Search for a Variation of the Fine Structure Constant around the Supermassive Black Hole in Our Galactic Center. Phys. Rev. Lett. 2020, 124, 81101. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Cardoso, V.; Clénet, Y.; de Zeeuw, P.T.; et al. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar]
- Genzel, R. Nobel Lecture: A forty-year journey. Rev. Mod. Phys. 2022, 94, 020501. [Google Scholar] [CrossRef]
- Dokuchaev, V.I.; Eroshenko, Y.N. Physical laboratory at the center of the Galaxy. Phys. Uspekhi 2015, 58, 772. [Google Scholar] [CrossRef]
- De Martino, I.; Lazkoz, R.; De Laurentis, M. Analysis of the Yukawa gravitational potential in f(R) gravity I: Semiclassical periastron advance. Phys. Rev. D 2018, 97, 104067. [Google Scholar] [CrossRef]
- De Laurentis, M.; De Martino, I.; Lazkoz, R. Analysis of the Yukawa gravitational potential in f(R) gravity II: Relativistic periastron advance. Phys. Rev. D 2018, 97, 104068. [Google Scholar] [CrossRef]
- Kalita, S. The Galactic Center Black Hole, Sgr A*, as a Probe of New Gravitational Physics with the Scalaron Fifth Force. Astrophys. J. 2020, 893, 31. [Google Scholar] [CrossRef]
- Lalremruati, P.C.; Kalita, S. Periastron shift of compact stellar orbits from general relativistic and tidal distortion effects near Sgr A*. Mon. Not. R. Astron. Soc. 2021, 502, 3761. [Google Scholar] [CrossRef]
- D’Addio, A. S-star dynamics through a Yukawa-like gravitational potential. Phys. Dark Universe 2021, 33, 100871. [Google Scholar] [CrossRef]
- Lalremruati, P.C.; Kalita, S. Is It Possible to See the Breaking Point of General Relativity near the Galactic Center Black Hole? Consideration of Scalaron and Higher-dimensional Gravity. Astrophys. J. 2022, 925, 126. [Google Scholar] [CrossRef]
- Benisty, D.; Davis, A.-C. Dark energy interactions near the Galactic Center. Phys. Rev. D 2022, 105, 024052. [Google Scholar] [CrossRef]
- Benisty, D.; Mifsud, J.; Levi Said, J.; Staicova, D. Strengthening extended gravity constraints with combined systems: f(R) bounds from cosmology and the galactic center. Phys. Dark Universe 2023, 42, 101344. [Google Scholar] [CrossRef]
- Bambhaniya, P.; Joshi, A.B.; Dey, D.; Joshi, P.S.; Mazumdar, A.; Harada, T.; Nakao, K.I. Relativistic orbits of S2 star in the presence of scalar field. Eur. Phys. J. C 2024, 84, 124. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 2018; 360p. [Google Scholar]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef] [PubMed]
- GRAVITY Collaboration; Abuter, R.; Aimar, N.; Amorim, A.; Ball, J.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Bourdarot, G.; Brandner, W.; et al. Mass distribution in the Galactic Center based on interferometric astrometry of multiple stellar orbits. Astron. Astrophys. 2022, 657, L12. [Google Scholar]

| R.E. | ||||||||
|---|---|---|---|---|---|---|---|---|
| (AU) | (%) | |||||||
| 1.100 | 0.190 | 66361.5 | ± | 63890.7 | 124.9 | ± | 120.2 | 96.3 |
| 1.010 | 0.160 | 209853.4 | ± | 1681506.5 | 39.5 | ± | 316.5 | 801.3 |
| 1.141 | 0.144 | 55886.4 | ± | 29251.3 | 148.3 | ± | 77.6 | 52.3 |
| Star | R.E. | R.E. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (AU) | (%) | (AU) | (%) | |||||||||||
| S1 | 1.6e+06 | ± | 1.6e+06 | 5.1 | ± | 5.1 | 100.7 | 1.2e+06 | ± | 6.6e+05 | 7.0 | ± | 3.9 | 55.7 |
| S2 | 6.6e+04 | ± | 6.4e+04 | 124.9 | ± | 120.2 | 96.3 | 4.8e+04 | ± | 2.5e+04 | 172.1 | ± | 88.3 | 51.3 |
| S4 | 8.8e+05 | ± | 8.5e+05 | 9.4 | ± | 9.1 | 96.7 | 6.4e+05 | ± | 3.3e+05 | 13.0 | ± | 6.7 | 51.7 |
| S6 | 1.0e+06 | ± | 9.5e+05 | 8.3 | ± | 7.9 | 95.2 | 7.2e+05 | ± | 3.6e+05 | 11.5 | ± | 5.8 | 50.2 |
| S8 | 5.5e+05 | ± | 5.4e+05 | 15.0 | ± | 14.7 | 98.0 | 4.0e+05 | ± | 2.1e+05 | 20.6 | ± | 10.9 | 53.0 |
| S9 | 4.5e+05 | ± | 4.4e+05 | 18.6 | ± | 18.6 | 99.7 | 3.2e+05 | ± | 1.8e+05 | 25.7 | ± | 14.0 | 54.7 |
| S12 | 2.4e+05 | ± | 2.3e+05 | 34.9 | ± | 33.6 | 96.4 | 1.7e+05 | ± | 8.9e+04 | 48.1 | ± | 24.7 | 51.4 |
| S13 | 5.5e+05 | ± | 5.2e+05 | 15.1 | ± | 14.5 | 95.5 | 4.0e+05 | ± | 2.0e+05 | 20.9 | ± | 10.5 | 50.5 |
| S14 | 7.3e+04 | ± | 7.8e+04 | 114.1 | ± | 122.4 | 107.3 | 5.3e+04 | ± | 3.3e+04 | 157.2 | ± | 98.0 | 62.3 |
| S17 | 8.7e+05 | ± | 8.5e+05 | 9.5 | ± | 9.2 | 97.1 | 6.3e+05 | ± | 3.3e+05 | 13.1 | ± | 6.8 | 52.1 |
| S18 | 4.5e+05 | ± | 4.3e+05 | 18.4 | ± | 17.8 | 96.5 | 3.3e+05 | ± | 1.7e+05 | 25.4 | ± | 13.1 | 51.5 |
| S19 | 9.4e+05 | ± | 1.1e+06 | 8.8 | ± | 10.2 | 116.4 | 6.8e+05 | ± | 4.9e+05 | 12.1 | ± | 8.7 | 71.4 |
| S21 | 2.5e+05 | ± | 2.5e+05 | 33.3 | ± | 33.2 | 99.6 | 1.8e+05 | ± | 9.9e+04 | 45.9 | ± | 25.1 | 54.6 |
| S22 | 5.9e+06 | ± | 6.7e+06 | 1.4 | ± | 1.6 | 114.1 | 4.3e+06 | ± | 3.0e+06 | 1.9 | ± | 1.3 | 69.1 |
| S23 | 4.5e+05 | ± | 5.2e+05 | 18.5 | ± | 21.4 | 115.6 | 3.2e+05 | ± | 2.3e+05 | 25.5 | ± | 18.0 | 70.6 |
| S24 | 1.3e+06 | ± | 1.3e+06 | 6.6 | ± | 6.8 | 103.2 | 9.2e+05 | ± | 5.3e+05 | 9.1 | ± | 5.3 | 58.2 |
| S29 | 7.4e+05 | ± | 8.1e+05 | 11.1 | ± | 12.2 | 109.1 | 5.4e+05 | ± | 3.5e+05 | 15.4 | ± | 9.8 | 64.1 |
| S31 | 1.1e+06 | ± | 1.0e+06 | 7.8 | ± | 7.5 | 96.4 | 7.8e+05 | ± | 4.0e+05 | 10.7 | ± | 5.5 | 51.4 |
| S33 | 1.8e+06 | ± | 1.9e+06 | 4.7 | ± | 5.0 | 107.0 | 1.3e+06 | ± | 7.9e+05 | 6.5 | ± | 4.0 | 62.0 |
| S38 | 1.1e+05 | ± | 1.0e+05 | 76.9 | ± | 73.3 | 95.4 | 7.8e+04 | ± | 3.9e+04 | 106.0 | ± | 53.4 | 50.4 |
| S39 | 2.5e+05 | ± | 2.5e+05 | 33.2 | ± | 32.8 | 98.8 | 1.8e+05 | ± | 9.7e+04 | 45.8 | ± | 24.6 | 53.8 |
| S42 | 3.2e+06 | ± | 4.0e+06 | 2.6 | ± | 3.1 | 122.7 | 2.4e+06 | ± | 1.8e+06 | 3.5 | ± | 2.7 | 77.7 |
| S54 | 1.9e+06 | ± | 3.5e+06 | 4.4 | ± | 8.4 | 188.3 | 1.4e+06 | ± | 1.9e+06 | 6.1 | ± | 8.8 | 143.3 |
| S55 | 9.6e+04 | ± | 9.3e+04 | 86.5 | ± | 84.5 | 97.6 | 6.9e+04 | ± | 3.7e+04 | 119.3 | ± | 62.7 | 52.6 |
| S60 | 6.6e+05 | ± | 6.4e+05 | 12.6 | ± | 12.3 | 97.7 | 4.8e+05 | ± | 2.5e+05 | 17.4 | ± | 9.2 | 52.7 |
| S66 | 8.5e+06 | ± | 8.6e+06 | 1.0 | ± | 1.0 | 101.4 | 6.2e+06 | ± | 3.5e+06 | 1.3 | ± | 0.8 | 56.4 |
| S67 | 5.2e+06 | ± | 5.2e+06 | 1.6 | ± | 1.6 | 100.1 | 3.8e+06 | ± | 2.1e+06 | 2.2 | ± | 1.2 | 55.1 |
| S71 | 1.3e+06 | ± | 1.4e+06 | 6.4 | ± | 6.8 | 107.3 | 9.4e+05 | ± | 5.9e+05 | 8.8 | ± | 5.5 | 62.3 |
| S83 | 7.6e+06 | ± | 8.4e+06 | 1.1 | ± | 1.2 | 110.3 | 5.5e+06 | ± | 3.6e+06 | 1.5 | ± | 1.0 | 65.3 |
| S85 | 2.3e+07 | ± | 4.9e+07 | 0.4 | ± | 0.8 | 211.0 | 1.7e+07 | ± | 2.8e+07 | 0.5 | ± | 0.8 | 166.0 |
| S87 | 2.0e+07 | ± | 2.1e+07 | 0.4 | ± | 0.4 | 102.4 | 1.5e+07 | ± | 8.5e+06 | 0.6 | ± | 0.3 | 57.4 |
| S89 | 3.6e+06 | ± | 3.8e+06 | 2.3 | ± | 2.5 | 107.8 | 2.6e+06 | ± | 1.6e+06 | 3.2 | ± | 2.0 | 62.8 |
| S91 | 1.2e+07 | ± | 1.2e+07 | 0.7 | ± | 0.7 | 101.9 | 8.4e+06 | ± | 4.8e+06 | 1.0 | ± | 0.6 | 56.9 |
| S96 | 8.4e+06 | ± | 8.4e+06 | 1.0 | ± | 1.0 | 100.0 | 6.1e+06 | ± | 3.3e+06 | 1.4 | ± | 0.7 | 55.0 |
| S97 | 1.5e+07 | ± | 1.9e+07 | 0.6 | ± | 0.7 | 125.9 | 1.1e+07 | ± | 8.8e+06 | 0.8 | ± | 0.6 | 80.9 |
| S145 | 4.5e+06 | ± | 6.1e+06 | 1.9 | ± | 2.5 | 136.7 | 3.2e+06 | ± | 3.0e+06 | 2.6 | ± | 2.4 | 91.7 |
| S175 | 8.2e+04 | ± | 9.0e+04 | 101.4 | ± | 111.8 | 110.3 | 5.9e+04 | ± | 3.9e+04 | 139.7 | ± | 91.2 | 65.3 |
| R34 | 7.6e+06 | ± | 9.2e+06 | 1.1 | ± | 1.3 | 120.5 | 5.5e+06 | ± | 4.2e+06 | 1.5 | ± | 1.1 | 75.5 |
| R44 | 3.3e+07 | ± | 5.2e+07 | 0.2 | ± | 0.4 | 156.2 | 2.4e+07 | ± | 2.7e+07 | 0.3 | ± | 0.4 | 111.2 |
| Star | R.E. | R.E. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (AU) | (%) | (AU) | (%) | |||||||||||
| S1 | 1.3e+06 | ± | 7.2e+05 | 6.4 | ± | 3.6 | 55.7 | 1.4e+06 | ± | 7.6e+05 | 6.1 | ± | 3.4 | 55.7 |
| S2 | 5.2e+04 | ± | 2.7e+04 | 158.0 | ± | 81.0 | 51.3 | 5.5e+04 | ± | 2.8e+04 | 149.9 | ± | 76.8 | 51.3 |
| S4 | 7.0e+05 | ± | 3.6e+05 | 11.9 | ± | 6.1 | 51.7 | 7.4e+05 | ± | 3.8e+05 | 11.3 | ± | 5.8 | 51.7 |
| S6 | 7.9e+05 | ± | 4.0e+05 | 10.5 | ± | 5.3 | 50.2 | 8.3e+05 | ± | 4.2e+05 | 10.0 | ± | 5.0 | 50.2 |
| S8 | 4.4e+05 | ± | 2.3e+05 | 18.9 | ± | 10.0 | 53.0 | 4.6e+05 | ± | 2.4e+05 | 17.9 | ± | 9.5 | 53.0 |
| S9 | 3.5e+05 | ± | 1.9e+05 | 23.6 | ± | 12.9 | 54.7 | 3.7e+05 | ± | 2.0e+05 | 22.3 | ± | 12.2 | 54.7 |
| S12 | 1.9e+05 | ± | 9.7e+04 | 44.1 | ± | 22.7 | 51.4 | 2.0e+05 | ± | 1.0e+05 | 41.8 | ± | 21.5 | 51.4 |
| S13 | 4.3e+05 | ± | 2.2e+05 | 19.2 | ± | 9.7 | 50.5 | 4.6e+05 | ± | 2.3e+05 | 18.2 | ± | 9.2 | 50.5 |
| S14 | 5.7e+04 | ± | 3.6e+04 | 144.3 | ± | 89.9 | 62.3 | 6.1e+04 | ± | 3.8e+04 | 136.9 | ± | 85.3 | 62.3 |
| S17 | 6.9e+05 | ± | 3.6e+05 | 12.0 | ± | 6.3 | 52.1 | 7.3e+05 | ± | 3.8e+05 | 11.4 | ± | 5.9 | 52.1 |
| S18 | 3.6e+05 | ± | 1.8e+05 | 23.3 | ± | 12.0 | 51.5 | 3.8e+05 | ± | 1.9e+05 | 22.1 | ± | 11.4 | 51.5 |
| S19 | 7.4e+05 | ± | 5.3e+05 | 11.1 | ± | 8.0 | 71.4 | 7.8e+05 | ± | 5.6e+05 | 10.6 | ± | 7.5 | 71.4 |
| S21 | 2.0e+05 | ± | 1.1e+05 | 42.2 | ± | 23.0 | 54.6 | 2.1e+05 | ± | 1.1e+05 | 40.0 | ± | 21.8 | 54.6 |
| S22 | 4.7e+06 | ± | 3.2e+06 | 1.8 | ± | 1.2 | 69.1 | 4.9e+06 | ± | 3.4e+06 | 1.7 | ± | 1.2 | 69.1 |
| S23 | 3.5e+05 | ± | 2.5e+05 | 23.4 | ± | 16.5 | 70.6 | 3.7e+05 | ± | 2.6e+05 | 22.2 | ± | 15.7 | 70.6 |
| S24 | 1.0e+06 | ± | 5.8e+05 | 8.3 | ± | 4.8 | 58.2 | 1.1e+06 | ± | 6.1e+05 | 7.9 | ± | 4.6 | 58.2 |
| S29 | 5.9e+05 | ± | 3.8e+05 | 14.1 | ± | 9.0 | 64.1 | 6.2e+05 | ± | 4.0e+05 | 13.4 | ± | 8.6 | 64.1 |
| S31 | 8.5e+05 | ± | 4.3e+05 | 9.8 | ± | 5.0 | 51.4 | 8.9e+05 | ± | 4.6e+05 | 9.3 | ± | 4.8 | 51.4 |
| S33 | 1.4e+06 | ± | 8.6e+05 | 6.0 | ± | 3.7 | 62.0 | 1.5e+06 | ± | 9.1e+05 | 5.6 | ± | 3.5 | 62.0 |
| S38 | 8.5e+04 | ± | 4.3e+04 | 97.3 | ± | 49.0 | 50.4 | 9.0e+04 | ± | 4.5e+04 | 92.3 | ± | 46.5 | 50.4 |
| S39 | 2.0e+05 | ± | 1.1e+05 | 42.0 | ± | 22.6 | 53.8 | 2.1e+05 | ± | 1.1e+05 | 39.8 | ± | 21.4 | 53.8 |
| S42 | 2.6e+06 | ± | 2.0e+06 | 3.2 | ± | 2.5 | 77.7 | 2.7e+06 | ± | 2.1e+06 | 3.1 | ± | 2.4 | 77.7 |
| S54 | 1.5e+06 | ± | 2.1e+06 | 5.6 | ± | 8.0 | 143.3 | 1.6e+06 | ± | 2.2e+06 | 5.3 | ± | 7.6 | 143.3 |
| S55 | 7.6e+04 | ± | 4.0e+04 | 109.5 | ± | 57.6 | 52.6 | 8.0e+04 | ± | 4.2e+04 | 103.8 | ± | 54.6 | 52.6 |
| S60 | 5.2e+05 | ± | 2.7e+05 | 16.0 | ± | 8.4 | 52.7 | 5.5e+05 | ± | 2.9e+05 | 15.2 | ± | 8.0 | 52.7 |
| S66 | 6.7e+06 | ± | 3.8e+06 | 1.2 | ± | 0.7 | 56.4 | 7.1e+06 | ± | 4.0e+06 | 1.2 | ± | 0.7 | 56.4 |
| S67 | 4.1e+06 | ± | 2.3e+06 | 2.0 | ± | 1.1 | 55.1 | 4.4e+06 | ± | 2.4e+06 | 1.9 | ± | 1.0 | 55.1 |
| S71 | 1.0e+06 | ± | 6.4e+05 | 8.1 | ± | 5.0 | 62.3 | 1.1e+06 | ± | 6.8e+05 | 7.6 | ± | 4.8 | 62.3 |
| S83 | 6.0e+06 | ± | 3.9e+06 | 1.4 | ± | 0.9 | 65.3 | 6.4e+06 | ± | 4.2e+06 | 1.3 | ± | 0.8 | 65.3 |
| S85 | 1.8e+07 | ± | 3.0e+07 | 0.5 | ± | 0.8 | 166.0 | 1.9e+07 | ± | 3.2e+07 | 0.4 | ± | 0.7 | 166.0 |
| S87 | 1.6e+07 | ± | 9.3e+06 | 0.5 | ± | 0.3 | 57.4 | 1.7e+07 | ± | 9.8e+06 | 0.5 | ± | 0.3 | 57.4 |
| S89 | 2.8e+06 | ± | 1.8e+06 | 3.0 | ± | 1.9 | 62.8 | 3.0e+06 | ± | 1.9e+06 | 2.8 | ± | 1.8 | 62.8 |
| S91 | 9.1e+06 | ± | 5.2e+06 | 0.9 | ± | 0.5 | 56.9 | 9.6e+06 | ± | 5.5e+06 | 0.9 | ± | 0.5 | 56.9 |
| S96 | 6.6e+06 | ± | 3.6e+06 | 1.2 | ± | 0.7 | 55.0 | 7.0e+06 | ± | 3.8e+06 | 1.2 | ± | 0.7 | 55.0 |
| S97 | 1.2e+07 | ± | 9.6e+06 | 0.7 | ± | 0.6 | 80.9 | 1.2e+07 | ± | 1.0e+07 | 0.7 | ± | 0.5 | 80.9 |
| S145 | 3.5e+06 | ± | 3.2e+06 | 2.4 | ± | 2.2 | 91.7 | 3.7e+06 | ± | 3.4e+06 | 2.2 | ± | 2.0 | 91.7 |
| S175 | 6.5e+04 | ± | 4.2e+04 | 128.2 | ± | 83.7 | 65.3 | 6.8e+04 | ± | 4.4e+04 | 121.6 | ± | 79.4 | 65.3 |
| R34 | 6.0e+06 | ± | 4.6e+06 | 1.4 | ± | 1.0 | 75.5 | 6.4e+06 | ± | 4.8e+06 | 1.3 | ± | 1.0 | 75.5 |
| R44 | 2.6e+07 | ± | 2.9e+07 | 0.3 | ± | 0.3 | 111.2 | 2.8e+07 | ± | 3.1e+07 | 0.3 | ± | 0.3 | 111.2 |
| Parameter | Value | Fit Error | Unit |
|---|---|---|---|
| 82,175.7 | 9828.05 | AU | |
| M | 4.15 | 0.27 | |
| R | 8.33 | 0.198 | kpc |
| a | 0.1229 | 0.00430 | arcsec |
| e | 0.8797 | 0.01597 | |
| i | 134.89 | 1.984 | ° |
| 224.57 | 5.208 | ° | |
| 62.78 | 4.562 | ° | |
| P | 15.98 | 0.362 | yr |
| T | 2018.12219 | 0.696709 | yr |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jovanović, P.; Borka Jovanović, V.; Borka, D.; Zakharov, A.F. Constraints on Graviton Mass from Schwarzschild Precession in the Orbits of S-Stars around the Galactic Center. Symmetry 2024, 16, 397. https://doi.org/10.3390/sym16040397
Jovanović P, Borka Jovanović V, Borka D, Zakharov AF. Constraints on Graviton Mass from Schwarzschild Precession in the Orbits of S-Stars around the Galactic Center. Symmetry. 2024; 16(4):397. https://doi.org/10.3390/sym16040397
Chicago/Turabian StyleJovanović, Predrag, Vesna Borka Jovanović, Duško Borka, and Alexander F. Zakharov. 2024. "Constraints on Graviton Mass from Schwarzschild Precession in the Orbits of S-Stars around the Galactic Center" Symmetry 16, no. 4: 397. https://doi.org/10.3390/sym16040397
APA StyleJovanović, P., Borka Jovanović, V., Borka, D., & Zakharov, A. F. (2024). Constraints on Graviton Mass from Schwarzschild Precession in the Orbits of S-Stars around the Galactic Center. Symmetry, 16(4), 397. https://doi.org/10.3390/sym16040397










