A Review of New Analytic Techniques for Quantifying Symmetry in Locomotion
Abstract
:1. Introduction
1.1. Gait Symmetry
1.2. Multivariate Analyses of Human and Animal Gait and Motion
1.3. Need for New Analysis Tools
2. New Tools for Capturing the Multivariate and Dynamic Nature of Gait
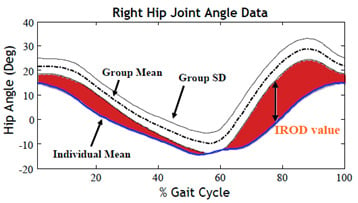
2.1. Regions of Deviation Analysis (ROD)
2.2. Complexity and Variability of Phase Portraits
2.3. Shape-alignment and Decomposition Analyses
2.4. Application beyond Gait: Manual Wheelchair Propulsion
3. Conclusions
3.1. Advantages of New Methods
3.2. Summary
Acknowledgements
References and Notes
- Lai, K.A.; Lin, C.J.; Jou, I.M.; Su, F.C. Gait analysis after total hip arthroplasty with leg-length equalization in women with unilateral congenital complete dislocation of the hip-comparison with untreated patients. J. Orthopaed. Res. 2001, 19, 1147–1152. [Google Scholar] [CrossRef]
- Sutherland, D. The development of mature gait. Gait Posture 1997, 6, 162–170. [Google Scholar] [CrossRef]
- Arsenault, A.B.; Winter, D.A.; Marteniuk, R.G. Bilateralism of EMG profiles in human locomotion. Am. J. Phys. Med. Rehabil. 1986, 65, 1–16. [Google Scholar]
- Ounpuu, S.; DeLuca, P.; Davis, R.; Romness, M. Long-term effects of femoral derotation osteotomies: An evaluation using three-dimensional gait analysis. J. Pediat. Orthoped. 2002, 22, 139–145. [Google Scholar] [CrossRef]
- Ounpuu, S.; Gage, J.R.; Davis, R.B. 3-Dimensional lower-extremity joint kinetics in normal pediatric gait. J. Pediat. Orthoped. 1991, 11, 341–349. [Google Scholar] [CrossRef]
- Sadeghi, H.; Allard, P.; Prince, F.; Labelle, H. Symmetry and limb dominance in able-bodied gait: A review. Gait Posture 2000, 12, 34–45. [Google Scholar] [CrossRef]
- DeVita, P.; Hortobagyi, T.; Barrier, J.; Torry, M.; Glover, K.L.; Speroni, D.L.; Money, J.; Mahar, M.T. Gait adaptations before and after anterior cruciate ligament reconstruction surgery. Med. Sci. Sport. Exercise 1997, 29, 853–859. [Google Scholar] [CrossRef]
- Griffin, M.P.; Olney, S.J.; McBride, I.D. Role of symmetry in gait performance of stroke subjects with hemiplegia. Gait Posture 1995, 3, 132–142. [Google Scholar] [CrossRef]
- Skinner, H.B.; Effeney, D.J. Gait analysis in amputees. Am. J. Phys. Med. 1985, 64, 82–89. [Google Scholar]
- Visser, E.D.; Veth, R.P.H.; Schreuder, H.W.B.; Duysens, J.; Mulder, T. Reorganization of gait after limb-saving surgery of the lower limb. Am. J. Phys. Med. Rehabil. 2003, 825–831. [Google Scholar] [CrossRef]
- Becker, H.P.; Rosenbaum, D.; Kriese, T.; Gerngross, H.; Claes, L. Gait asymmetry following successful surgical-treatment of ankle fractures in young-adults. Clin. Orthop. Related Res. 1995, 262–269. [Google Scholar]
- Mittlmeier, T.; Weiler, A.; Sohn, T.; Kleinhans, L.; Mollbach, S.; Duda, G.; Sudkamp, N.P. Functional monitoring during rehabilitation following anterior cruciate ligament reconstruction. Clin. Biomech. 1999, 14, 576–584. [Google Scholar] [CrossRef]
- Tang, S.F.T.; Chen, C.P.C.; Hong, W.H.; Chen, H.T.; Chu, N.; Leong, C.P. Improvement of gait by using orthotic insoles in patients with heel injury who received reconstructive flap operations. Am. J. Phys. Med. Rehabil. 2003, 82, 350–356. [Google Scholar] [CrossRef] [PubMed]
- Grieve, D.W. Gait patterns and the speed of walking. Biomed. Eng. 1968, 119–122. [Google Scholar]
- Craik, R.L.; Oatis, C.A. Clinical Gait Analysis: Theory and Application; Mosby: St. Louis, MO, USA, 1995. [Google Scholar]
- Bruyn, J.; Bryden, P.; Perry, S. The effect of lateral preference on gait symmetry. J. Sport Exercise Psychol. 2003, 25, S32–S32. [Google Scholar]
- Chodera, J.D. Gait analysis from footprints. Physiotherapy 1974, 60, 179–181. [Google Scholar] [PubMed]
- Crowe, A.; Samson, M.M. 3-D analysis of gait: The effects upon symmetry of carrying a load in one hand. Hum. Movement Sci. 1997, 16, 357–365. [Google Scholar] [CrossRef]
- Diop, M.; Rahmani, A.; Belli, A.; Gautheron, V.; Geyssant, A.; Cottalorda, J. Influence off speed variation and age on the asymmetry of ground reaction forces and stride parameters of normal gait in children. J. Pediatr. Orthoped. 2004, 13, 308–314. [Google Scholar] [CrossRef]
- Draper, E.R.C. A treadmill-based system for measuring symmetry of gait. Med. Eng. Phys. 2000, 22, 215–222. [Google Scholar] [CrossRef]
- Hausdorff, J.M. Stride variability: Beyond length and frequency. Gait Posture 2004, 20, 304–304. [Google Scholar] [CrossRef]
- Knoll, Z.; Kocsis, L.; Kiss, R.M. Gait patterns before and after anterior cruciate ligament reconstruction. Knee Surg. Sports Traumatol. Ar. 2004, 12, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Salamon, A.; Nikolic, V.; Jo-Osvatic, A.; Andric, V. Longitudinal gait analysis of injured ankle joint. Period. Biol. 2002, 104, 317–320. [Google Scholar]
- Stefanyshyn, D.J.; Engsberg, J.R. Right-to-left differences in the ankle joint complex range of motion. Med. Sci. Sport. Exercise 1994, 26, 551–555. [Google Scholar] [CrossRef]
- Chodera, J.D.; Levell, R.W. Footprint patterns during walking. In Perspectives in Biomedical Engineering; Kenedi, R.M., Ed.; University Park Press: Baltimore, MD, USA, 1973; pp. 81–90. [Google Scholar]
- Law, H.T. Microcomputer-based low-cost method for measurement of spatial and temporal parameters of gait. J. Biomed. Eng. 1987, 9, 115–120. [Google Scholar] [CrossRef]
- Allard, P.; Lachance, R.; Aissaoui, R.; Duhaime, M. Simultaneous bilateral 3-D able-bodied gait. Hum. Movement Sci. 1996, 15, 327–346. [Google Scholar] [CrossRef]
- Giakas, G.; Baltzopoulos, V. Time and frequency domain analysis of ground reaction forces during walking: An investigation of variability and symmetry. Gait Posture 1997, 5, 189–197. [Google Scholar] [CrossRef]
- Perttunen, J.R.; Anttila, E.; Sodergard, J.; Merikanto, J.; Komi, P.V. Gait asymmetry in patients with limb length discrepancy. Scand. J. Med. Sci. Sports 2004, 14, 49–56. [Google Scholar] [CrossRef] [PubMed]
- Lamoth, C.J.; Meijer, O.G.; Daffertshofer, A.; Wuisman, P.I.; Beek, P.J. Effects of chronic low back pain on trunk coordination and back muscle activity during walking: changes in motor control. Eur. Spine J. 2005, 29, 29. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, H.; Prince, F.; Sadeghi, S.; Labelle, H. Principal component analysis of the power developed in the flexion/extension muscles of the hip in able-bodied gait. Med. Eng. Phys. 2000, 22, 703–710. [Google Scholar] [CrossRef]
- Sadeghi, H.; Prince, F.; Zabjek, K.F.; Sadeghi, S.; Labelle, H. Knee flexors/extensors in gait of elderly and young able-bodied men (II). Knee 2002, 9, 55–63. [Google Scholar] [CrossRef]
- Sadeghi, H. Local or global asymmetry in gait of people without impairments. Gait Posture 2003, 17, 197–204. [Google Scholar] [CrossRef]
- Williams, G.E.; Silverman, B.W.; Wilson, A.M.; Goodship, A.E. Disease-specific changes in equine ground reaction force data documented by use of principal component analysis. Am. J. Vet. Res. 1999, 60, 549–555. [Google Scholar] [PubMed]
- Wilson, J.F.; Rochelle, R.D.; Bischoff, J.E. Identification and correlation of human footfall load parameters using multivariate analysis. J. Biomech. Eng. 1997, 119, 115–123. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, H.; Allard, P.; Barbier, F.; Sadeghi, S.; Hinse, S.; Perrault, R.; Labelle, H. Main functional roles of knee flexors/extensors in able-bodied gait using principal component analysis (I). Knee 2002, 9, 47–53. [Google Scholar] [CrossRef]
- Dien, J.; Beal, D.J.; Berg, P. Optimizing principal components analysis of event-related potentials: Matrix type, factor loading weighting, extraction, and rotations. Clin. Neurophysiol. 2005, 116, 1808–1825. [Google Scholar] [CrossRef] [PubMed]
- Weber, W.E. Mechanik der Menschlichen Gehwerkzeuge; Dietrichschen Buchhandlung: Gottingen, Germany, 1836. [Google Scholar]
- Hurmuzlu, Y.; Basdogan, C.; Carollo, J.J. Presenting joint kinematics of human locomotion using phase plane portraits and poincare maps. J. Biomech. 1994, 27, 1495–1499. [Google Scholar] [CrossRef]
- Goswami, A. A new gait parameterization technique by means of cyclogram moments: Application to human slope walking. Gait Posture 1998, 8, 15–36. [Google Scholar] [CrossRef]
- Wu, W.H.; Meijer, O.G.; Lamoth, C.J.C.; Uegaki, K.; van Dieen, J.H.; Wuisman, P.; de Vries, J.I.P.; Beek, P.J. Gait coordination in pregnancy: transverse pelvic and thoracic rotations and their relative phase. Clin. Biomech. 2004, 19, 480–488. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; 2nd Edition; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Palmitier, R.A.; An, K.N.; Scott, S.G.; Chao, E.Y. Kinetic chain exercise in knee rehabilitation. Sport. Med. 1991, 11, 402–413. [Google Scholar] [CrossRef]
- Chu, D.A. Rehabilitation of the lower extremity. Clin. Sport. Med. 1995, 14, 205–222. [Google Scholar]
- Morrissey, M.C.; Hudson, Z.L.; Drechsler, W.I.; Coutts, F.J.; Knight, P.R.; King, J.B. Effects of open versus closed kinetic chain training on knee laxity in the early period after anterior cruciate ligament reconstruction. Knee Surg. Sports Traumatol. Ar. 2000, 8, 343–348. [Google Scholar] [CrossRef] [PubMed]
- Macintyre, J.G. 5-year follow-up of open or closed kinetic chain exercises for patellofemoral pain. Clin. Sport. Med. 2005, 15, 199–200. [Google Scholar] [CrossRef]
- Maffiuletti, N.A.; Bizzini, M.; Schatt, S.; Munzinger, U. A multi-joint lower-limb tracking-trajectory test for the assessment of motor coordination. Neurosci. Lett. 2005, 384, 106–111. [Google Scholar] [CrossRef] [PubMed]
- Fleming, B.C.; Oksendahl, H.; Beynnon, B.D. Open- or closed-kinetic chain exercises after anterior cruciate ligament reconstruction? Exerc. Sport Sci. Rev. 2005, 33, 134–140. [Google Scholar] [CrossRef] [PubMed]
- Polk, J.D.; Spencer-Smith, J.; DiBerardino, L.; Ellis, D.; Downen, M.; Rosengren, K.S. Quantifying variability in phase portraits: Application to gait ontogeny. Infant Behav. Develop. 2008, 31, 302–306. [Google Scholar] [CrossRef] [PubMed]
- Rosengren, K.S.; Deconinck, F.J.; Diberardino, L.A., 3rd; Polk, J.D.; Spencer-Smith, J.; De Clercq, D.; Lenoir, M. Differences in gait complexity and variability between children with and without developmental coordination disorder. Gait Posture 2009, 29, 225–229. [Google Scholar] [CrossRef] [PubMed]
- Shorter, K.A.; Polk, J.D.; Rosengren, K.S.; Hsiao-Wecksler, E.T. A new approach to detecting asymmetries in gait. Clin. Biomech. 2008, 23, 459–467. [Google Scholar] [CrossRef] [PubMed]
- DiBerardino, L.A., 3rd; Polk, J.D.; Rosengren, K.S.; Spencer-Smith, J.B.; Hsiao-Wecksler, E.T. Quantifying complexity and variability in phase portraits of gait. Clin. Biomech. 2010, 25, 552–556. [Google Scholar] [CrossRef] [PubMed]
- Helwig, N.E.; Hong, S.; Polk, J.D.; Lague, M.R. Analysis of Gait Cycle Shapes Using Parallel Factor Analysis. In Proceedings of the 34th Annual Meeting of the American Society of Biomechanics, Providence, RI, USA, 18–21 August, 2010. [Google Scholar]
- DiBerardino, L.A.; Ragetly, C.A.; Hong, S.; Griffon, D.J.; Hsiao-Wecksler, E.T. Improving Regions of Deviation Gait Symmetry Analysis with Pointwise T-Tests. In Proceedings of the 34th Annual Meeting of the American Society of Biomechanics, Providence, RI, USA, 18–21 August, 2010. [Google Scholar]
- DiBerardino, L.A.; Hong, S.; Ragetly, C.A.; Thomas, E.J.; Hsiao-Wecksler, E.T. Analysis and Classification Methods for Healthy and Cruciate-Deficient Dogs. In Proceedings of the 45th Annual Society of Engineering Science Conference, Urbana, IL, 12–15 October, 2008. [Google Scholar]
- Prieto, T.E.; Myklebust, J.B.; Hoffmann, R.G.; Lovett, E.G.; Myklebust, B.M. Measures of postural steadiness: Differences between healthy young and elderly adults. IEEE Trans. Biomed. Eng. 1996, 43, 956–966. [Google Scholar] [CrossRef]
- Thomas, D. Elliptical Fourier shape descriptors. Available online: http://www.mathworks.com/matlabcentral/fileexchange/12746 (Accessed on 1 June 2010).
- Kuhl, F.P.; Giardina, C.R. Elliptic Fourier features of a closed contour. Comput. Graph. Image Process. 1982, 18, 236–258. [Google Scholar] [CrossRef]
- Larkin, D.; Hoare, D. Out of step: Coordinating kids movement. Active Life Foundation: Perth, Australia, 1991. [Google Scholar]
- Collard, M.; O’Higgins, P. Ontogeny and homoplasy in the papionin monkey face. Evol. Dev. 2001, 3, 322–331. [Google Scholar] [CrossRef] [PubMed]
- Hennessy, R.J.; Moss, J.P. Facial growth: Separating shape from size. Eur. J. Orthodont. 2001, 23, 275–285. [Google Scholar] [CrossRef]
- Lague, M.R. Another look at shape variation in the distal femur of Australopithecus afarensis: Implications for taxonomic and functional diversity at Hadar. J. Hum. Evol. 2002, 42, 609–626. [Google Scholar] [CrossRef] [PubMed]
- Kaliontzopoulou, A.; Carretero, M.A.; Llorente, G.A. Multivariate and geometric morphometrics in the analysis of sexual dimorphism variation in Podarcis lizards. J. Morphol. 2007, 268, 152–165. [Google Scholar] [CrossRef] [PubMed]
- Gunz, P.; Bookstein, F.L.; Mitteroecker, P.; Stadlmayr, A.; Seidler, H.; Weber, G.W. Early modern human diversity suggests subdivided population structure and a complex out-of-Africa scenario. Proc. Nat. Acad. Sci.USA 2009, 106, 6094–6098. [Google Scholar] [CrossRef] [PubMed]
- Gower, J.C. Generalized procrustes analysis. Psychometrika 1975, 40, 33–51. [Google Scholar] [CrossRef]
- Ten Berge, J.M.F. Orthogonal Procrustes rotation for two or more matrices. Psychometrika 1977, 42, 267–276. [Google Scholar] [CrossRef]
- Schonemann, P.H.; Carroll, R.M. Fitting one matrix to another under choice of a central dilation and a rigid motion. Psychometrika 1970, 35, 245–256. [Google Scholar] [CrossRef]
- Harshman, R.A.; Lundy, M.E. The PARAFAC model for three-way factor analysis and multidimensional scaling. In Research Methods for Multimode Data Analysis; Law, H.G., Snyder, C.W., Jr., Hattie, J., McDonald, R.P., Eds.; Praeger: New York, NY, USA, 1984; pp. 122–215. [Google Scholar]
- Park, K.; Dankowicz, H.; Hsiao-Wecksler, E.T. Characterization of Spatiotemporally Complex and Coupled Gait Patterns Using Cross-Correlation. In Proceedings of the 16th US National Congress on Theoretical and Applied Mechanics (USNCTAM), State College, PA, USA, 27 June–2 July, 2010. [Google Scholar]
- Sosnoff, J.J.; DiBerardino, L.A.; Park, K.; Rampurawala, Z.; Daigle, S.; Hsiao-Wecksler, E.T. Complexity and Variability in Manual Wheelchair Propulsion. In Proceedings of the 16th US National Congress on Theoretical and Applied Mechanics (USNCTAM), State College, PA, USA, 27 June–2 July, 2010. [Google Scholar]
- Davids, K.; Bennett, S.; Newell, K. Variability in the Movement System: A Multidisciplinary Perspective; Human Kinetics: Champaign, IL, USA, 2006. [Google Scholar]
- Newell, K.; Vaillancourt, D. Dimensional change in motor learning. Hum. Movement Sci. 2001, 20, 695–715. [Google Scholar] [CrossRef]
- Helwig, N.E.; Hong, S.; Hsiao-Wecksler, E.T. Time-Normalization Techniques for Gait Data Curves. In Proceedings of the 33rd Annual Meeting of the American Society of Biomechanics, State College, PA, USA, 26–29 August, 2009. [Google Scholar]
- Helwig, N.E.; Hong, S.; Hsiao-Wecksler, E.T. Partitioning Gait Cycle Curves into Temporal and Intensity Differences. In Proceedings of the 33rd Annual Meeting of the American Society of Biomechanics, State College, PA, USA, 26–29 August, 2009. [Google Scholar]
- Helwig, N.E.; Hong, S.; Hsiao-Wecksler, E.T.; Polk, J.D. Methods to temporally align gait cycle data. 2010; in preparation. [Google Scholar]





© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hsiao-Wecksler, E.T.; Polk, J.D.; Rosengren, K.S.; Sosnoff, J.J.; Hong, S. A Review of New Analytic Techniques for Quantifying Symmetry in Locomotion. Symmetry 2010, 2, 1135-1155. https://doi.org/10.3390/sym2021135
Hsiao-Wecksler ET, Polk JD, Rosengren KS, Sosnoff JJ, Hong S. A Review of New Analytic Techniques for Quantifying Symmetry in Locomotion. Symmetry. 2010; 2(2):1135-1155. https://doi.org/10.3390/sym2021135
Chicago/Turabian StyleHsiao-Wecksler, Elizabeth T., John D. Polk, Karl S. Rosengren, Jacob J. Sosnoff, and Sungjin Hong. 2010. "A Review of New Analytic Techniques for Quantifying Symmetry in Locomotion" Symmetry 2, no. 2: 1135-1155. https://doi.org/10.3390/sym2021135