The Symmetry Group of the Non-Isothermal Navier–Stokes Equations and Turbulence Modelling
Abstract
1. Introduction
2. The Symmetry Group of the Equations
- the group of time translations, corresponding to :
- the group of pressure translations, corresponding to :
- the group of pressure-temperature translations, corresponding to :
- the group of horizontal rotations, corresponding to :where is a 2D (constant) rotation matrix, with and , being the identity matrix,
- the (three-parameter) group of generalized Galilean transformations, spanned by the ’s, :
- the group of the first scaling transformations generated by :which shows how , p and change when the spatio-temporal scale is multiplied by ,
- and the group of the second scaling transformations corresponding to :which shows the consequence of the modification of the spatial scale.
- the reflections which are discrete symmetries:where is a reflection matrix:
- and the material indifference in the limit of a 2D horizontal flow in a simply connected domain [17] which is a time-dependent rotation:withwhere is an horizontal 2D rotation matrix with angle , a real parameter, the usual 2D stream function defined by:and indicates the Euclidian norm. The material indifference constitutes a non-local symmetry of the equations.
- –
- the time, the pressure and the generalized Galilean translations,
- –
- the pressure-temperature translations,
- –
- the reflections, the horizontal (constant or time-dependent) rotations,
- –
- the scaling transformations.
3. Model Analysis
3.1. Subgrid Models
- The most widely used model is the Smagorinsky model, which was derived by adopting the concept of turbulent viscosity for and an analogy for :where is a norm of defined byis the Smagorinsky constant, and the subgrid Prandtl number which is a constant. The superscript d stands for the deviatoric operator, i.e.,:being the identity matrix.
- Using Germano–Lilly procedure ([18]), the model constants can be calculated in a dynamic way to give more flexibility to the model. This leads to the dynamic model:where , andThe tilde symbolizes a test filtering, with a width .
- Another model, which introduces the buoyancy term, is the Eidson model ([19]):where is a constant. In practice, when the term under the root sign is negative, the model is set to zero.
- To avoid having a negative radicand, Peng and Davidson ([20]) propose a modified version of the Eidson model:
- Another model, based on the scale-similarity hypothesis, is the scale-similarity model, adapted from Bardina model to the non-isothermal case:
- The scale similarity hypothesis can be used to obtain others models which are combined with the Smagorinsky model to give a mixed model in the following form ([21,22,23,24]):From the point of view of the symmetries, these models behave generally in the same way; so, we study only the following generic model:
3.2. Time, Pressure and Galilean Translations
3.3. Pressure-Temperature Translations
- Next,The scale-similarity model (38) is then invariant.
- For the dynamic model (34), , and are unchanged. And since , remains also unchanged. The model is then invariant.
- At last, the invariance of the Smagorinsky and the scale-similarity models leads to the invariance of the mixed model (40) under the pressure-temperature translations.
3.4. Reflections and Rotations
- For this reflection, we have:These relations imply the invariance of the Smagorinsky model (31).
- In addition,
- For the scale-similarity model (38),This model is then invariant.
- Next, for the dynamic model (34),Hence, and . It follows that the dynamic model is invariant under the third reflection.
- Lastly, the invariance of the mixed model (40) under the third reflection follows from the invariance of the Smagorinsky and the scale-similarity models.
3.5. Scaling Transformations
- Since and , we have, for the Smagorinsky model (31):The model verifies (58) neither when nor when . Thus, it is invariant neither under the first nor under the second scaling transformations.
- The scale-similarity model (38) is invariant under the two types of scaling transformations becauseCondition (58) is verified.
- For the dynamic model (34), we have:This implies thatThus,The dynamic model is invariant.
- At last, the mixed model (40) is not invariant under the scaling transformations because of the Smagorinsky part. However, the (Leonard) terms which correspond to the scale-similarity model are invariant.
4. Symmetry-Invariant LES Models
5. Model Simplification
5.1. Strongly Coupled Model
5.2. Decoupled Model
5.3. Linear Model
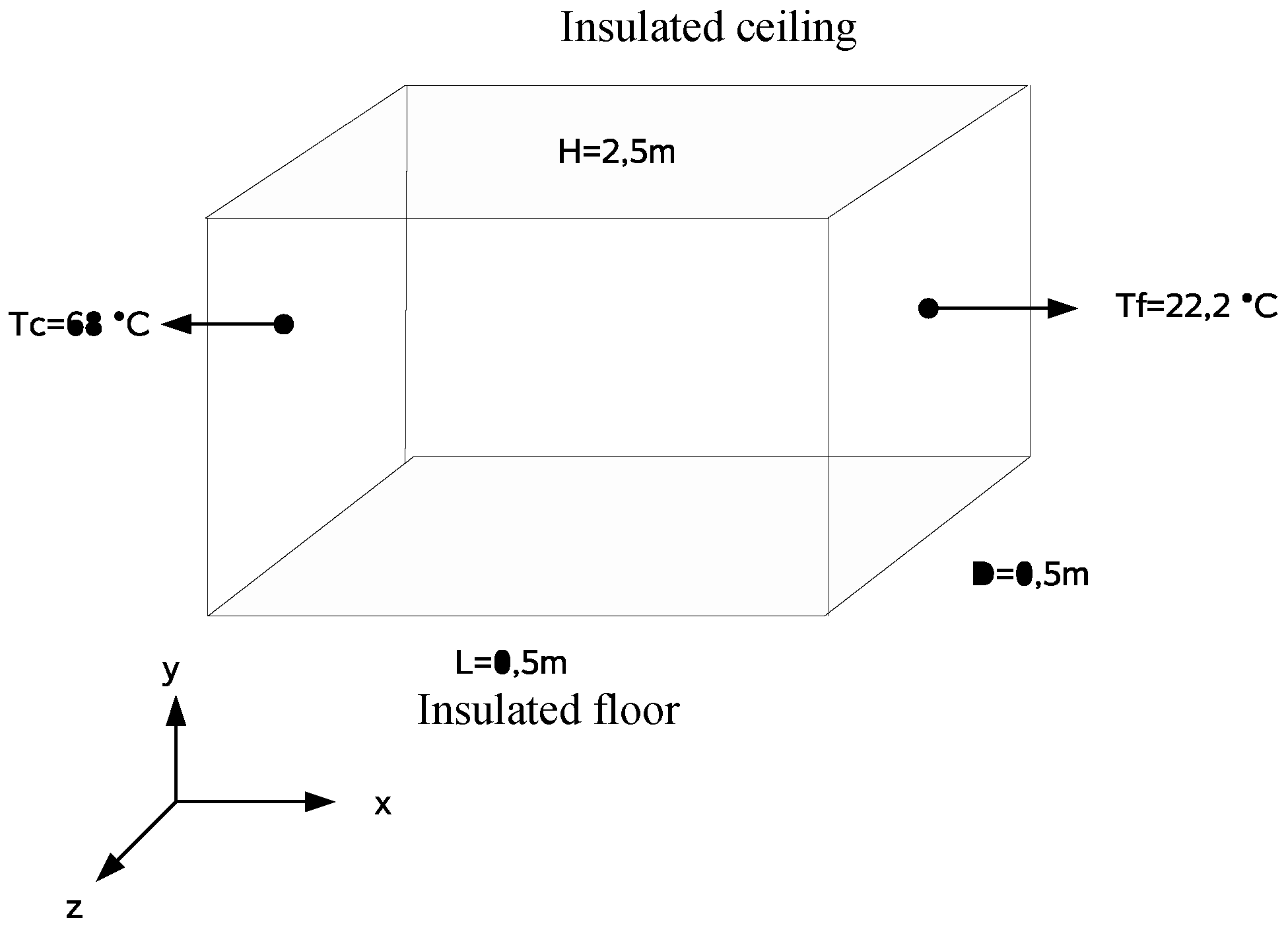
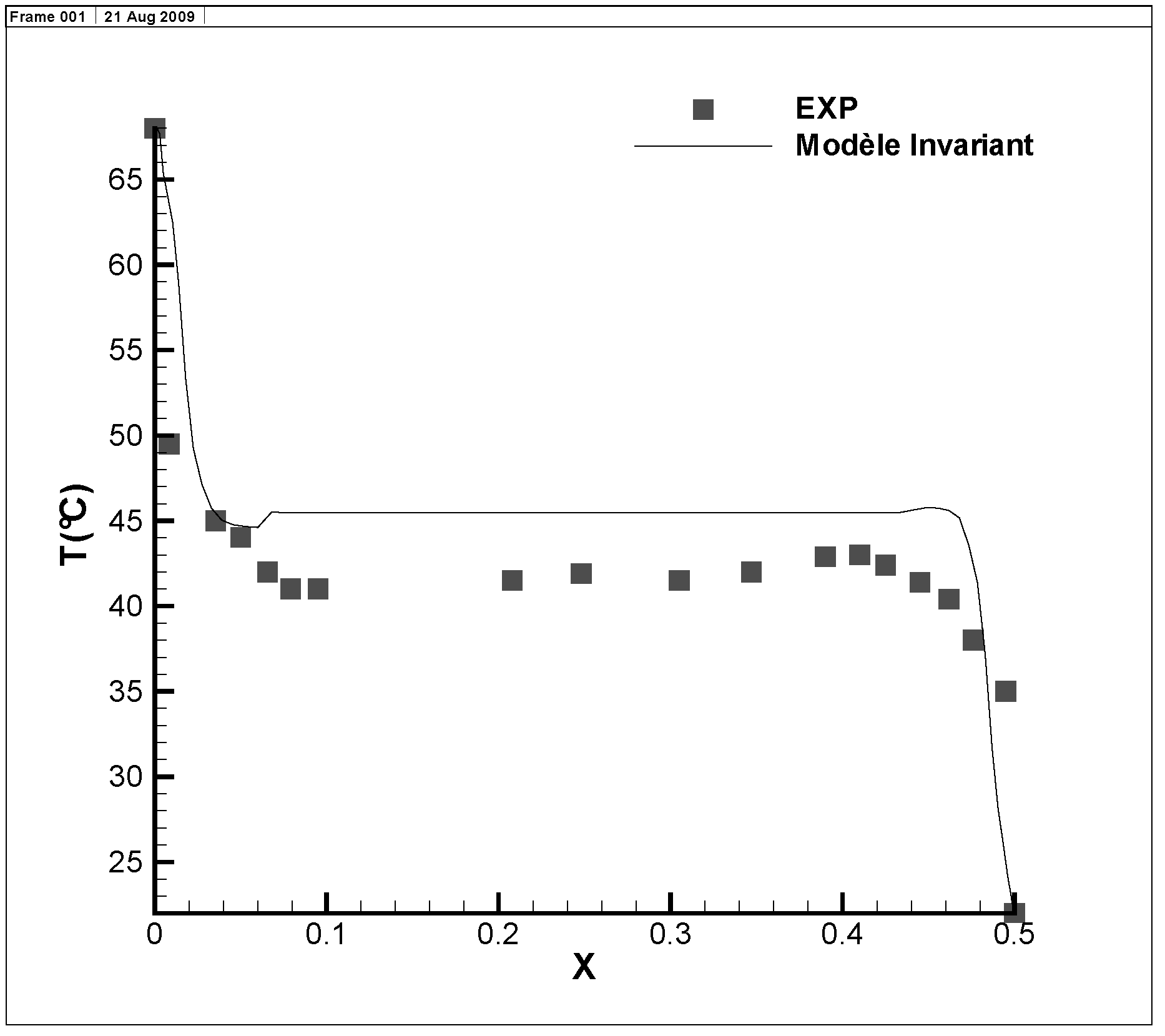
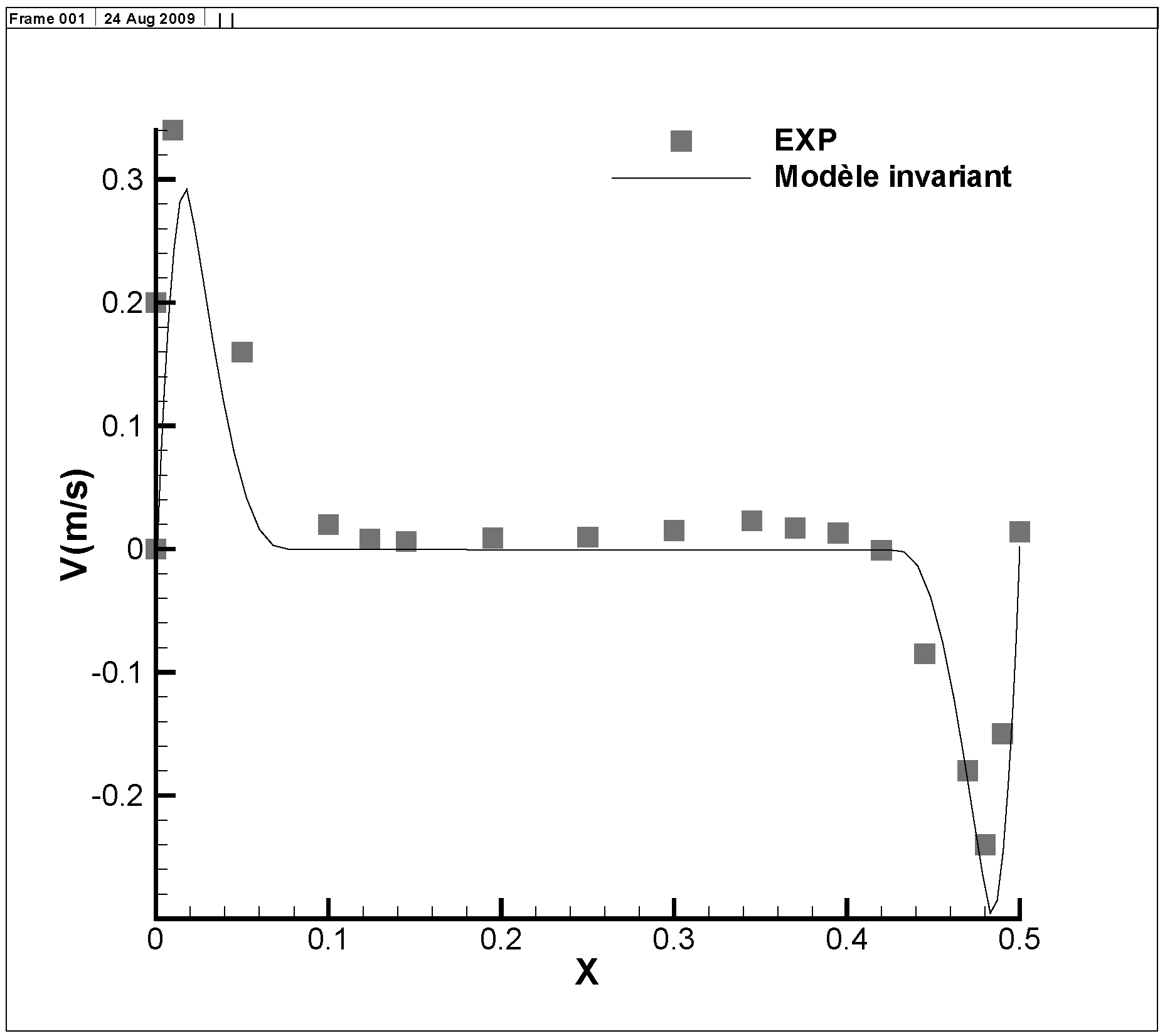
6. Numerical Example
7. Conclusions
References
- Nœther, E. Invariante Variationsprobleme. Königliche Gesellschaft der Wissenschaften 1918, 235–257. [Google Scholar][Green Version]
- Olver, P. Applications of Lie groups to differential equations (Graduate texts in mathematics); Springer-Verlag: New York, NY, USA, 1986. [Google Scholar][Green Version]
- Oberlack, M. A unified Approach for Symmetries in Plane Parallel Turbulent Shear Flows. J. Fluid Mech. 2001, 427, 299–328. [Google Scholar] [CrossRef]
- Oberlack, M.; Cabot, W.; Pettersson Reif, B.; Weller, T. Group analysis, direct numerical simulation and modelling of a turbulent channel flow with streamwise rotation. J. Fluid Mech. 2006, 562, 355–381. [Google Scholar] [CrossRef]
- Grassi, V.; Leo, R.; Soliani, G.; Tempesta, P. Vorticies and invariant surfaces generated by symmetries for the 3D Navier-Stokes equation. Physica A 2000, 286, 79–108. [Google Scholar] [CrossRef]
- Ünal, G. Application of equivalence transformations to inertial subrange of turbulence. Lie Group Appl. 1994, 1, 232–240. [Google Scholar]
- Speziale, C. Invariance of turbulent closure models. Phys. Fluids 1979, 22, 1033–1037. [Google Scholar] [CrossRef]
- Speziale, C. Some interesting properties of two-dimensional turbulence. Phys. Fluids 1981, 24, 1425–1427. [Google Scholar] [CrossRef]
- Fureby, C.; Tabor, G. Mathematical and physical constraints on large-eddy simulations. Theor. Comput. Fluid Dyn. 1997, 9, 85–102. [Google Scholar] [CrossRef]
- Wang, L. Frame-indifferent and positive-denite Reynolds stress-strain relation. J. Fluid Mech. 1997, 352, 341–358. [Google Scholar] [CrossRef]
- Spalart, P.; Speziale, C. A note on constraints in turbulence modelling. J. Fluid Mech. 1999, 391, 373–376. [Google Scholar] [CrossRef]
- Pukhnachev, V. Invariant solution of Navier-Stokes equations describing motions with free boundary. Dokl. Akad. Nauk SSSR 1972, 202–302. [Google Scholar][Green Version]
- Oberlack, M. Symmetries of the Navier-Stokes equations and their applications for subgrid-models in large eddy simulation of turbulence. In Fundamental Problematic Issues in Turbulence; Gyr, A., Kinzelbach, W., Tsinober, A., Eds.; Birkhäuser Verlag: Basel, Switzerland, 1999. [Google Scholar][Green Version]
- Razafindralandy, D.; Hamdouni, A.; Oberlack, M. Analysis and development of subgrid turbulence models preserving the symmetry properties of the Navier–Stokes equations. Eur. J. Mech. B 2007, 26, 531–550. [Google Scholar] [CrossRef]
- Razafindralandy, D.; Hamdouni, A.; Béghein, C. A class of subgrid-scale models preserving the symmetry group of Navier-Stokes equations. Commun. Nonlinear Sci. Numer. Simulat. 2007, 12, 243–253. [Google Scholar] [CrossRef]
- Ibragimov, N. CRC handbook of Lie group analysis of differential equations. Vol 1: Symmetries, exact solutions and conservation laws; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar][Green Version]
- Cantwell, B. Similarity transformations for the two-dimensional, unsteady, stream-function equation. J. Fluid Mech. 1978, 85, 257–271. [Google Scholar] [CrossRef]
- Lilly, D. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids 1992, A4, 633–635. [Google Scholar] [CrossRef]
- Eidson, T. Numerical simulation of the turbulent Rayleigh-Bénard problem using subgrid modelling. J. Fluid Mech. 1985, 158, 245–268. [Google Scholar] [CrossRef]
- Peng, S.H.; Davidson, L. Comparison of Subgrid-Scale Models in LES for Turbulent Convection Flow With Heat Transfer. In 2nd EF Conference in Turbulent Heat Transfer; Manchester, UK, 1998; Vol. 1, pp. 5.25–5.35. [Google Scholar]
- Bardina, J.; Ferziger, J.; Reynolds, W. Improved turbulence models based on large eddy simulation of homogeneous, incompressible, turbulent flows. Technical Report Report TF-19; Stanford University: Standford, CA, USA, 1983. [Google Scholar][Green Version]
- Horiuti, K. The Role of the Bardina Model in Large Eddy Simulation of Turbulent Channel Flow. Phys. Fluids A 1989, 1, 426–428. [Google Scholar] [CrossRef]
- Winckelmans, G.; Wray, A.; Vasilyev, O. Testing of a new mixed model for LES: the Leonard model supplemented by a dynamic Smagorinsky term. In Summer Program; Center for Turbulence Research, NASA Ames/Standford University: Standford, CA, USA, 1998; pp. 367–388. [Google Scholar][Green Version]
- Keating, A.; Piomelli, U.; Bremhorst, K.; Nesic, S. Large-Eddy Simulation of Heat Transfer Downstream of a Backward-Facing Step. J. Turbulence 2004, 5. [Google Scholar] [CrossRef]
- Oberlack, M. Invariant modeling in large-eddy simulation of turbulence. In Annual Research Briefs; Stanford University: Standford, CA, USA, 1997. [Google Scholar]
- Oberlack, M. Symmetries, Invariance and Scaling-Laws in Inhomogeneous Turbulent Shear Flows. Flow Turbul. Combust. 1999, 62, 111–135. [Google Scholar] [CrossRef]
- Lindgren, B.; Österlund, J.; Johansson, A. Evaluation of Scaling Laws Derived from Lie Group Symmetry Methods in Zero-Pressure-Gradient Turbulent Boundary Layers. J. Fluid Mech. 2004, 502, 127–152. [Google Scholar] [CrossRef]
- Razafindralandy, D.; Hamdouni, A. Invariant subgrid modelling in large-eddy simulation of heat convection turbulence. Theor. Comput. Fluid Dyn. 2007, 21, 231–244. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, Y.; Béghein, C.; Su, M. Particulate Dispersion and Transportation in Buildings with Large Eddy Simulation. Technical report. Massachusetts Institute of Technology, 2001. [Google Scholar]
- Zhang, W.; Chen, Q. Large eddy simulation of indoor airflow with a filtred dynamic subgrid scale model. Int. J. Heat Mass Transfer 2000, 43, 3219–3231. [Google Scholar] [CrossRef]
| Time, pressure, Galilean | Pressure-temperature | Rotation, reflection, material indifference | Scaling | |
|---|---|---|---|---|
| Smagorinsky | invariant | invariant | invariant | non-invariant |
| Dynamic | invariant | invariant | invariant | invariant |
| Eidson | invariant | invariant | invariant | non-invariant |
| Modified Eidson | invariant | invariant | invariant | non-invariant |
| Similarity | invariant | invariant | invariant | invariant |
| Mixed | invariant | invariant | invariant | non-invariant |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Al Sayed, N.; Hamdouni, A.; Liberge, E.; Razafindralandy, D. The Symmetry Group of the Non-Isothermal Navier–Stokes Equations and Turbulence Modelling. Symmetry 2010, 2, 848-867. https://doi.org/10.3390/sym2020848
Al Sayed N, Hamdouni A, Liberge E, Razafindralandy D. The Symmetry Group of the Non-Isothermal Navier–Stokes Equations and Turbulence Modelling. Symmetry. 2010; 2(2):848-867. https://doi.org/10.3390/sym2020848
Chicago/Turabian StyleAl Sayed, Nazir, Aziz Hamdouni, Erwan Liberge, and Dina Razafindralandy. 2010. "The Symmetry Group of the Non-Isothermal Navier–Stokes Equations and Turbulence Modelling" Symmetry 2, no. 2: 848-867. https://doi.org/10.3390/sym2020848
APA StyleAl Sayed, N., Hamdouni, A., Liberge, E., & Razafindralandy, D. (2010). The Symmetry Group of the Non-Isothermal Navier–Stokes Equations and Turbulence Modelling. Symmetry, 2(2), 848-867. https://doi.org/10.3390/sym2020848




