Abstract
Chemists use one set of orbitals when comparing to a structural formula, hybridized AOs or NBOs for example, and another for reasoning in terms of frontier orbitals, MOs usually. Chemical arguments can frequently be made in terms of energy and/or electron density without the consideration of orbitals at all. All orbital representations, orthogonal or not, within a given function space are related by linear transformation. Chemical arguments based on orbitals are really energy or electron density arguments; orbitals are linked to these observables through the use of operators. The Valency Interaction Formula, VIF, offers a system of chemical reasoning based on the invariance of observables from one orbital representation to another. VIF pictures have been defined as one-electron density and Hamiltonian operators. These pictures are classified in a chemically meaningful way by use of linear transformations applied to them in the form of two pictorial rules and the invariance of the number of doubly, singly, and unoccupied orbitals or bonding, nonbonding, and antibonding orbitals under these transformations. The compatibility of the VIF method with the bond pair – lone pair language of Lewis is demonstrated. Different electron lone pair representations are related by the pictorial rules and have stability understood in terms of Walsh’s rules. Symmetries of conjugated ring systems are related to their electronic state by simple mathematical formulas. Description of lone pairs in conjugated systems is based on the strength and sign of orbital interactions around the ring. Simple models for bonding in copper clusters are tested, and the bonding of O2 to Fe(II) in hemoglobin is described. Arguments made are supported by HF, B3LYP, and MP2 computations.
1. Introduction
The Lewis structure [] is central to a great deal of chemical reasoning and therefore has been the inspiration for chemically intuitive analysis of quantum computations on molecules. Pauling immediately recognized the compatibility of Lewis’s rule of two with Valence Bond theory and wrote this in a 1928 letter to Lewis.
You have no doubt seen London’s recent paper in the Zeitschrift für Physik and have observed the results which he derived from the quantum mechanics the sharing of electrons are in the main equivalent to the rules which you had previously postulated [].
Slater and Pauling extended VB theory to larger molecules with the technique of hybridization of valence atomic orbitals [,]. Molecular Orbital, MO, theory, an early alternative to VB theory, has a less obvious connection to molecular structural formulas and has been more usually associated with electronic spectroscopy. It was shown in 1935 by Van Vleck and Sherman that VB theory and MO theory are different starting points to better approximations []. In some cases VB and MO treatments are equivalent. Linnett, in his 1956 study of binding in diatomic molecules showed that the MO configuration is equivalent to the VB configuration where both electrons have the same spin []. MO and VB treatments of the three electron bond [] are also equivalent []. Linnett’s work with odd number electron molecules lead him to modify the Lewis-Langmuir octet rule to a double quartet rule, each quartet consisting of electrons with parallel spin []. These modified Lewis structures, considered along with notions of electron repulsion and electron spin correlation allow the properties of molecules with odd numbers of electrons to be rationalized more clearly. Harcourt, inspired by Linnett’s approach, has shown further equivalence between VB and MO treatments of the three electron bond and using a VB approach has shown how fractional electron pair bonds in “increased valence structures” are applied to give insight into a number of important examples [,,,]. VB and MO theories are not equivalent in all cases. Methods for analyzing results of MO and DFT computations in terms of chemical bonds and lone pair electrons have also been developed; examples are Natural Bond Orbital Analysis [], NBO, and Atoms in Molecules, AIM [].
Natural Bond Orbitals, NBOs, are optimized to match the bond pair – lone pair depictions of a Lewis structure. NBOs that do not match Lewis’s “rule of two” still fit chemical intuition and quantify chemical concepts such as electron delocalization and donor-acceptor interactions. Atoms in Molecules (AIM), does not focus on orbitals but on electron density, an observable that it characterizes in a mathematically defined way to match chemical intuition and sometimes to locate supposed chemical bonds. Chemical arguments based on orbitals are in fact energy or electron density arguments. Orbitals are linked to these observables through the use of operators. The Valency Interaction Formula, VIF, method is based on quantum operators and is a link between reasoning in terms of orbitals and observables.
Valency Interaction Formulas, VIFs, are molecular structural formulas that are themselves quantum mechanical operators, one-electron density or one-electron Hamiltonian. They allow molecules to be classified based on an invariance property according to two pictorial rules, linear transformations, applied to the VIF pictures. The number of doubly, singly, and unoccupied valence orbitals or the number of bonding, nonbonding, and antibonding orbitals are preserved under these transformations. The resulting pictures relate molecular geometry and distribution of electrons in molecules to the energetic behavior of frontier orbitals [,,,]. The method for drawing VIF pictures as one electron Hamiltonian operators comparable to the results of MO computations was developed in the mid 1990’s []. Since then, the theory has been broadened in its application by definition of VIF pictures as one-electron density operators and subsequent development of the system of chemical reasoning based on the two pictorial rules [,,].
While a variety of orbital pictures are useful for chemical reasoning and can be related to traditional MO and VB approaches, the VIF method is based on a property of invariance that relates one orbital representation to another while leaving observable properties of the molecule unchanged. It is a way of understanding why a wide variety of orbital pictures describe molecular properties. At the same time the VIF method emphasizes what is common and important about these pictures, their relationship to observables such as energy and distribution of electrons in molecules.
1.1. Three Dimensional Molecular Structural Formulas
Lewis structures as they are typically used today are at first two-dimensional and then given three-dimensional interpretation according to hybridization of atomic orbitals or Valence Shell Electron Pair Repulsion, VSEPR, theory []. By Lewis’s own 1923 account, three-dimensional thinking was a distinguishing feature between his theory of atomic structure and other theories of atomic structure available at the time []. Lewis’s sketches from 1902 shows how electrons represented as dots placed at the corners of a cube describe the valency of second and third period elements. See Figure 1. The tetrahedral geometry of carbon centers is clear in Lewis’s pictorial reasoning.
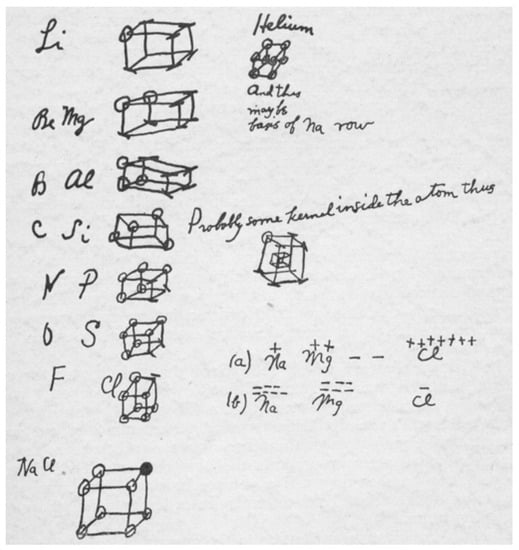
Figure 1.
G. N. Lewis’s 1902 sketch showing valence electrons at the corners of cubic valence shells in atoms. Copied from Lewis [].
Harcourt has found a remarkable way to unite the idea of Bohr orbits with the electron cube structure of Lewis in a three-dimensional theory of the molecular structural formula []. Harcourt’s Bohr orbit model is shown side to side with Linnett’s model both for O2 triplet in Figure 2. Both of these models have a physically intuitive basis; electrons with the same spin stay as far apart as possible. In Linnet’s model electrons of the same spin are arranged at the indices of a tetrahedron. In O2, spin-up electrons, o, are arranged in tetrahedrons that join at an index bisecting the inter-nuclear axis. Seven electrons are spin up. The remaining five spin-down electrons are at the indices of tetrahedrons that join face-to-face in the plane that bisects the molecule. Both spin-up and spin down electrons are symmetrically distributed around the inter-nuclear axis and bisecting plane consistent with the cylindrical, D∞h, symmetry of the molecule. According to Harcourt’s Bohr orbit bonding theory, atoms have quantum number n Bohr orbits in their valence shell. Each orbit can have a maximum of 2n electrons that are positioned with alternating spin around the orbit. For O2 triplet there are seven electrons of one spin and five of the other. In the Bohr orbit model for triplet O2, there are also unequal numbers of electrons in orbit planes of the molecule. See Figure 2. The orbits in the horizontal plane have three electrons each and one shared for a total of five while those in the vertical plane have four electrons each with one shared for a total of seven.
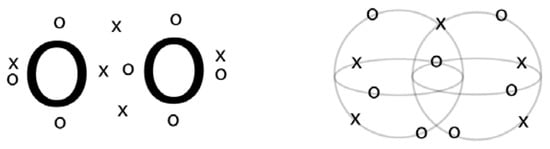
Figure 2.
Linnett-Lewis structure for O2 triplet (left). Harcourt’s Bohr orbit model for O2 triplet (right).
Both the Linnett and Harcourt Bohr orbit models of triplet O2 have four bonding electrons roughly between the nuclei and two unpaired electrons with parallel spin for the triplet. Various VB bonding models have been inspired by the Linnet approach [,,,]. The Bohr orbit model with a maximum of 2n electrons in planar circular orbits is restricted from matching molecular symmetry properties and hence chemical and physical properties in some cases, O2 triplet for example. Application of symmetry properties to orbital (wave) models of chemical bonding has been extremely successful.
It would be interesting to compare Harcourt’s Bohr orbit molecular structural formulas or perhaps a related elliptical orbit approach based on orbits corresponding to AOs, HAOs, or MOs to the “posmom” density analysis of Gill [] which is a quantitative link between thinking in terms of orbitals and orbits. Particle reasoning and wave reasoning applied in an educated way to the atomic and molecular level have been extremely fruitful, a tribute to the achievement of Niels Bohr. Quantum operators are the link between the wavefunction and possible results of an experiment and are an integral part of quantum theory.
The focus in this paper is the VIF method, a pictorial MO theory based on the fact that physical observables remain unchanged with transformation from one orbital representation to another. VIF is alternative to the way that chemists normally think about molecules; VIF molecular structural formulas are one-electron density or Hamiltonian operators. At the same time, there are many aspects of the VIF method that are very much the way that chemists think about molecules. Three dimensional geometry and interaction between valence orbitals are of paramount importance in the VIF method. The VIF picture for methane is shown in Figure 3. Dots, Valency points, VP, represent orbitals. Lines that connect the dots, Valency Interactions, VI, are interactions between the orbitals. The importance of the relationship between the VIF picture and molecular geometry is emphasized by the molecular models shown in Figure 4. The VIF method will be described in the following section and applied to a variety of molecules throughout this paper.
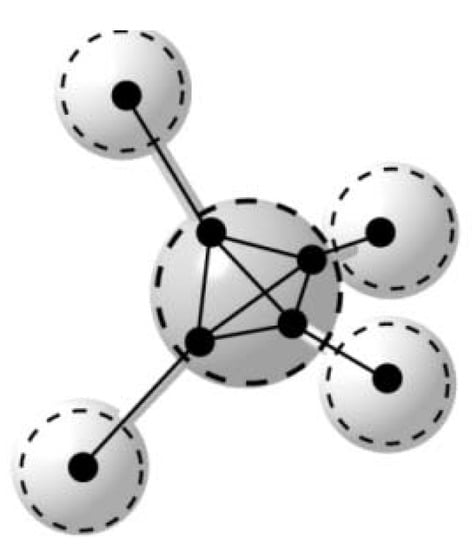
Figure 3.
VIF picture for methane. Valency Points (VP), dots, represent valence orbitals, 1s for hydrogen and sp3 for carbon. Solid lines show interactions, energy or electron density.

Figure 4.
VIF molecular models of methane, ammonia, and water. Black, blue, or red pieces represent sp3 orbitals for C, N, or O, white pieces represent H1s orbitals and interactions represented with tygon tubing.
2. Quantum-Based Molecular Structural Formulas
The Valency Interaction Formula, VIF, is a molecular structural formula and one-electron operator drawn with respect to a reference orbital occupancy or reference energy. The number of positive, zero, and negative eigenvalues with respect to the reference is found using two pictorial rules and is invariant under application of these rules. VIF pictures as one-electron density operators are drawn with respect to a reference orbital occupation of one electron per orbital. VIF pictures as one-electron Hamiltonian operators are frequently drawn with respect to reference energy, αref, frequently −½Eh. See [] and [].
2.1. VIF Mathematical Definitions
A Valency Interaction Formula is a one-electron operator, . Raised and lowered indices refer to Sinanoğlu’s covariant formulation that makes quantum equations invariant under the general linear group, GL(n, C) []. Valency Points, VP, dots on a piece of paper, are projectors,, for valence basis orbitals,{φμ}. All are implicit [].
The VIF operator is drawn with respect to a reference, αref, so corresponding matrix elements are where {Sμν} are elements of the overlap matrix. when . All elements of the overlap matrix are implicit []. If , then the VIF picture is a one-electron density operator and αref is an orbital occupation of one electron per orbital. If , the VIF picture is a one-electron Hamiltonian operator and a useful value for αref is frequently ½ Eh [].
Valency Interactions, VI, lines that connect valency points, are drawn according to chemical intuition but can be tested for accuracy using the two pictorial rules to be presented shortly [,]. Valency Interactions have strength . A usual choice for βo is βspn for molecules with hybridized atomic centers. A default value of κ = 1 gives simple pictures and accurate chemical deductions in most cases. The significance of relative interaction strengths can be tested with the two rules []. Valency Points can be given electronegativity loops with strength . Loops also result from application of the two pictorial rules.
2.2. The Two Pictorial Rules
Chemical deductions are made using two pictorial rules applied to the VIF picture. These are linear transformations applied to the operator. The two rules are given below and demonstrated in Figure 5 (top left) for the H2 molecule. Figure 6 shows the two rules side-by-side with the corresponding linear transformations. The two pictorial rules are the multiplication rule and the addition rule.
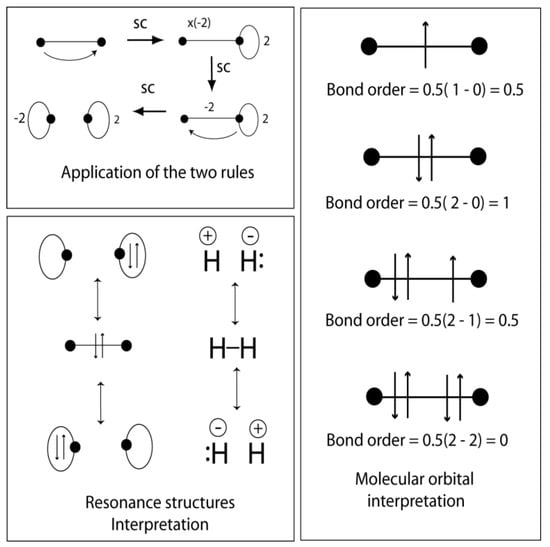
Figure 5.
VIF method applied to the H2 molecule. The multiplication rule and addition rule demonstrated (top left). Pictures related by the rules can be interpreted as resonance structures, (bottom left). If the VIF picture represents a one-electron Hamiltonian operator, electrons can be filled and bond order calculated (right).
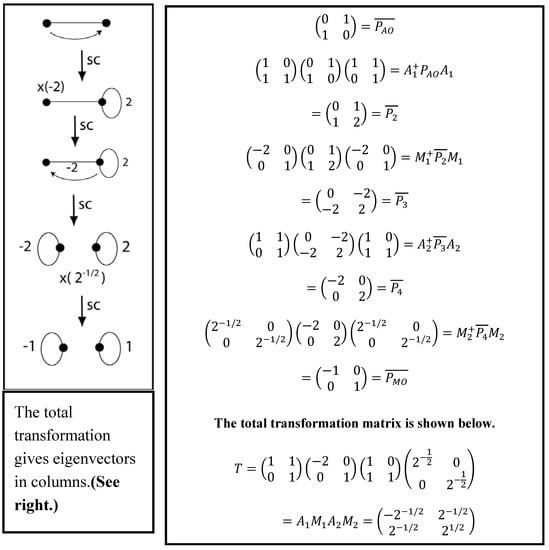
Figure 6.
The two pictorial rules shown side-to-side with the corresponding linear transformations applied to the one-electron density matrix transformed from the AO representation to the MO basis frame.
- The multiplication rule: A Valency Point may be multiplied by a nonzero constant in which case all interactions emanating from the point are multiplied by that constant. A loop is multiplied by the constant squared.
- The addition rule: A Valency Point may be “lifted” and, bringing all its interactions and loops with it, superimposed on another Valency Point. The strengths of superimposed Valency Interactions and loops add. Loops formed by curling up a VI have strength of twice the strength of the VI. The original Valency Point moved and its Valency Interactions and loop if it has one are left like chalk marks.
In a fully simplified VIF picture all of the Valency Interactions, VI, have been cancelled and Valency Points, VP, have loops with positive loop constants, negative loop constants, or no loops, corresponding to eigenvalues that are positive, negative, or zero respectively. If the VIF picture is a one-electron density operator disconnected VP with positive loops represent orbitals with two electrons, those with negative loops, empty orbitals, and those without loops, orbitals with one electron. Likewise, if the VIF picture represents a one-electron Hamiltonian operator positive loops in a fully simplified picture represent bonding orbitals, negative loops, antibonding orbitals, and disconnected VP with no loops, nonbonding orbitals.
VIF pictures related by the two rules are structurally covariant, sc, shown in Figure 5 and Figure 6 and belong to an equivalence class with the same numbers of positive, zero, and negative eigenvalues. Sets of structurally covariant VIF pictures have four key interpretations that can be used to make chemical deductions.
- Sets of structurally covariant VIF pictures are interpreted as the same quantum operator represented in linearly related basis frames.
- VIF density pictures related by the rules can be used as resonance structures but have topological meaning beyond usual resonance structures.
- Structurally covariant VIF pictures can be interpreted as sets of molecular species with similar energy.
- The same VIF picture can sometimes be interpreted as different quantum operators, one-electron density or Hamiltonian for example.
According to these interpretations, bond pair, lone pair, and free radical electrons understood in terms of a localized orbital representation are recognized as having energies above, below, or equal to the predetermined reference, frequently −½Eh [].
2.3. Comparison to Valence Bond Resonance Structures
With valency points representing orbitals, a VIF picture represents a one-electron operator in a minimal valence orbital basis set. VIF resonance structures related by the two pictorial rules are a set of one-electron density operators that all correspond to the same number of doubly, singly, and unoccupied valence natural orbitals. This is a fundamentally different set of definitions than for resonance structures in VB theory. The determinant wave functions that correspond to sets of structurally covariant VIF resonance structures are not in general equivalent to VB wavefunctions. VIF and VB resonance structures are therefore not equivalent in general. There are special cases for which qualitative MO and VB theories are equivalent. This is the case for the three electron bond to be discussed later in this paper. VIF and VB resonance structures show agreement in these cases and also in cases for which VB and MO determinant wavefunctions are not equivalent. VIF resonance structures also have a topological meaning that allows them to be used for making predictions about the behavior of frontier orbitals. See [,,].
2.4. VIF Resonance Structures for Dative, 3e/2c, and 3-Centered Bonds.
Donor-acceptor bonding, three-electron bonding, and three-center boding have been significant in the development of bonding concepts [,]. Figure 7 shows sets of VIF resonance structures related by the pictorial rules (left) and their corresponding matrix transformations (right) for a donor-acceptor dative bond (top) and for a three electron – two center bond (bottom). The donor-acceptor bond is structurally covariant with covalent bonds. Compare Figure 5 with Figure 7. The three electron bond which has two bonding electrons and one antibonding electron from the MO point of view, Figure 5 (right), has structurally covariant resonance structures, Figure 7 (bottom left). Qualitative MO and VB approaches are known to be equivalent in this case [,]. These resonance structures look similar to three electron bond Valence Bond configurations of Green and Linnet [], and Harcourt [,,,] that result from delocalizing an A or B atom lone pair electron into the ΨAB bonding molecular orbital. (. Harcourt [] has also shown that the electrons on the A and B atoms will have parallel spin while the electron delocalized in ΨAB has the opposite spin. Using the notation of Green and Linnet and Linnet [], x and for electrons with opposed spins gives x. We will follow this result when filling electrons into the VIF picture. See Figure 7 (bottom left).
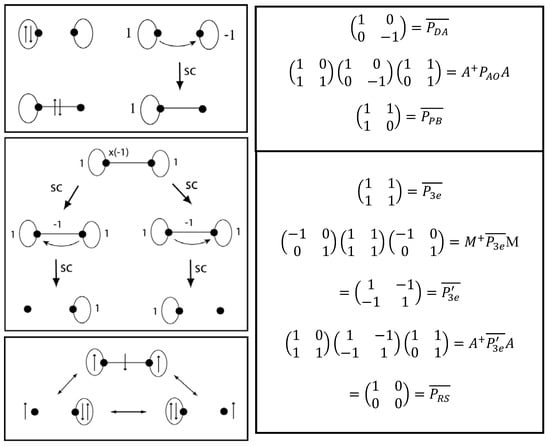
Figure 7.
Structurally covariant VIF resonance structures (left) with corresponding matrix transformations (right) describe a dative bond (top) and three electron — two center bond (bottom), for a doubly occupied donor orbital and unoccupied acceptor orbital; is for the polar bond related to it by the rules, for a three electron bond, and is for the structurally covariant resonance structures.
Structurally covariant resonance structures for three center bonds correspond to cations, anions, or radicals according to whether their topology is Hückel or Möbius []. Figure 8 shows how VIF resonance structures represent the π-systems for allyl cation, anion, or radical depending on whether the density element between the terminal orbitals, a, has a positive, negative, or zero sign. Topological properties based on the sign of density have been known to give chemical insight []. Positive density interactions are bonding, zero are nonbonding, and negative are antibonding. VIF pictures provide a simple approach for the explanation and prediction of conjugated ring symmetries according to the sign of π-system density elements [,]. Application to the study of concerted reactions is the subject of on-going work. We will use VIF pictures similar to those in Figure 8 for the description of small copper clusters and the bonding of O2 to Fe(II) later in this paper.

Figure 8.
The two pictorial rules are used to relate resonance structures for the π-system ally cation, anion, and radical to the topology of the one-electron density matrix; a is positive for a cation, negative for an anion, and zero for the radical.
2.5. VIF Pictures for Hybridized Atomic Centers
VIF pictures for hybridized atomic centers are one-electron operators transformed into a hybridized atomic orbital basis frame [,]. When hybridization transformations are applied to one-electron operators for atomic centers in AO representations, the operators in the resulting HAO representation typically have interactions between them. Energy or electron density elements that result from a hybridization transformation are easy to calculate by hand given the initial AO energies or electron configuration. Line and loop constants for the VIF pictures are likewise easy to calculate too [,]. Intrahybrid or germinal hybrid interactions were used by Dewar in his σ-conjugation and σ-aromaticity PMO theory [].
If The VIF picture is a one-electron density operator, line constants are calculated based on average s and p orbital electron occupations using αspn = (αs + nαp)/(n+1), βspn = (αs – αp)/(n + 1), and loop constants ξspn = (αspn – 1 )/βspn, and line constants κspn = βspn/βspn = 1. Hybridized carbon centers, with an average of one valence electron per valence orbital and ξspn = (αspn – 1) = 0 have no loops. The VIF pictures for hybridized carbon centers are shown in Figure 9. The carbon sp3 VIF picture in Figure 9 is a representation of the ground state electron configuration of a carbon atom with averaged p-orbital occupations that has been transformed into a hybridized orbital frame. It does not represent a quartet of electrons as in Linnett’s theory []. There is therefore no promotion energy in this approach. When the VIF picture is a one-electron Hamiltonian operator, line and loop constants are calculated with αs and αp as valence orbital ionization energies, VOIE.
Figure 9.
VIF depiction of the spn hybridizations of a carbon center shows interacting sets of hybrid orbitals. Valency Points for orbitals centered on the same atom are included within a dotted circle.
The VIF picture for methane shown in Figure 3 is reduced using the two pictorial rules in Figure 10. The valency points for the four carbon sp3 hybrid orbitals are all within the central circle for the methane carbon and interact with each other equally. Each has a Valency Interaction with the nearest H1s Valency Point. The rules are applied yielding four C-H single bonds as expected. Because the number of bonding, nonbonding, and antibonding orbitals is invariant for structurally covariant VIF pictures, and because the molecular orbitals are related to this and other localized frames by linear transformation, this picture also corresponds to four bonding molecular orbitals lower in energy than -½Eh that do not lie along specific C-H bond lines. Each bonding MO has two electrons. Four empty antibonding molecular orbitals also result one from each segment in the reduced picture [,].
Figure 10.
The methane VIF is reduced using the two pictorial rules.
The VIF method is easily applied to describe the bonding in the methonium ion, CH5+. Figure 11 (top) shows the VIF picture for the CH5+ ion. The two rules applied as they were in the case of methane lead to three two center — two electron bonds and a three center two electron bond. Figure 11 (bottom left) shows how the VIF picture for the three center bond is reduced to an antibonding orbital and two VP connected by a VI which, as we have seen in Figure 5 and Figure 6, is further reduced to one bonding and an additional antibonding orbital. The three center bond in CH5+ leads to one doubly occupied bonding orbital and two unoccupied antibonding orbitals. See Figure 8. The natural bond orbitals, NBOs, for the three center — two electron bond in CH5+ are also shown in Figure 11 (bottom right). These were calculated using Gaussian 03 for Windows [] and the NBO options [] included with this suite of programs. The 3c-2e bond presents difficulty for conventional Lewis structures but not for VIFs.
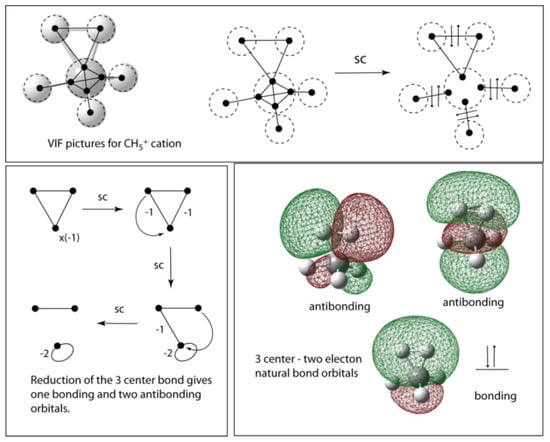
Figure 11.
The VIF picture for CH5+ is easily simplified yielding a three center — two electon bond (top) that is further reduced to one doubly occupied and two unoccupied orbitals or two antibonding and one bonding orbital (bottom). The NBOs (bottom right) were calculated using G03W and displayed using GaussView.
3. VIF Representation of Diatomic Molecules
The order of the molecular orbital energies and the resulting ground sate electron configuration for the C2 molecule has been confirmed in several studies [,,]. A level of theory including some degree of electron correlation is needed in order to compute an accurate potential energy curve for the singlet ground state, 1Σg+, with the π-bonding orbitals each doubly occupied for bond lengths near the equilibrium geometry. According to this picture, the overall bond order is 2 though the σ-bond order is zero.
The VIF treatment for C2 is shown in Figure 12 (top right). Notice that each of the carbon centers was given sp hybridization and no electronegativity loops are needed. The σ-bond interaction in the initial VIF for C2 is immediately canceled using the rules, consistent with the simple MO diagram. See Figure 12 (top left). Jug [] using his Maximum Bond order Principle finds C2 to have a triple bond, in agreement with the fact that the C2 bond length is close to that of acetylene.
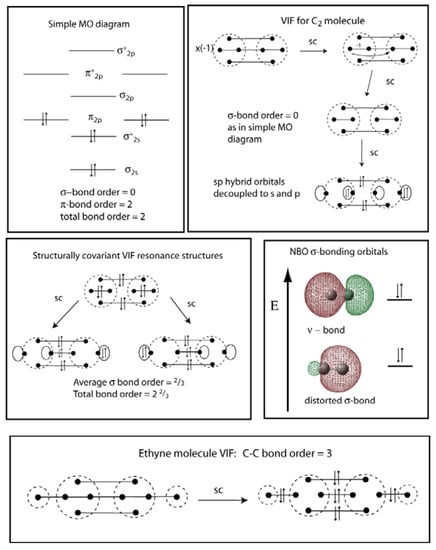
Figure 12.
The simple MO diagram for C2 (top left) is shown with its VIF picture reduced by the two rules (top right). Both approaches indicate a C-C double bond. The stabilization of carbon 2s electrons by interaction with the empty σ-p orbital on the neighboring carbon is shown using VIF resonance structures (middle left) and NBOs (middle right). A C-C triple bond results when hydrogen atoms are added on either end to form ethyne (bottom).
The two coupled sp hybrid orbitals on each carbon atom are decoupled using the two rules to a doubly occupied carbon 2s orbital and unoccupied 2p orbital, Figure 12 (top right). The 2s electrons on each carbon are then further stabilized by interaction with the empty σ 2p orbital on the other carbon atom. This interaction is shown by the structurally covariant VIF resonance structures in Figure 12 (middle left). These allow calculation of a modified bond order, 2 2/3. According the NBO method, the interaction of the 2s electrons with the σ-p orbital on the adjacent carbon atom results in a ν-bond, Figure 12 (middle right).
The C2 molecule has a dissociation energy, De = 610 ± 2.0 kJ/mol, greater than that of O2, 498 ± 0.17 kJ/mol [], less than the ethylene double bond, 728.4 ± 6.3 kJ/mol [], and substantially less than the acetylene triple bond, 960.2 ± 4.2 kJ/mol [], and N2 triple bond, 945.33 ± 0.59 kJ/mol []. The spectroscopic bond length for the C2 molecule is 1.2425 Å [] slightly longer than the C-C bond length in acetylene, 1.203 Å [], and shorter than the C-C bond length in ethylene, 1.339 Å according to MP2/6-311++Gdp. The side to side overlap of p-orbitals on adjacent carbon atoms requires a short bond length. The ν-bonding in C2 does not stabilize the molecule as much as the strong C-C σ-bond in acetylene or in ethylene stabilizes these molecules. Bond order of somewhere between 2 and 3 for C2 does not seem unreasonable considering the experimental evidence and theoretical literature on this topic. Bonding a hydrogen atom to each carbon to form ethyne increases the C-C bond order to three with the formation of a C-C σ-bond. This is shown clearly in the VIF picture of ethyne, Figure 12 (bottom).
The bonding in N2 and O2 molecules is more familiar than that in C2. The bond formation from electron configurations in sp hybridized N and O atoms respectively is shown in Figure 13 (top). The σ-systems for these require loops in their VIF pictures []. Loop constants, ξ, are calculated according to electron configuration and hybridization: αspn = (αs + nαp)/(n + 1), βspn = (αs-αp)/(n + 1) and ξ = (αspn − 1)/βo. βo is frequently βspn but is chosen to get the simplest possible picture that is accurate. The sp hybrid orbitals on each atom are constructed from a doubly occupied 2s orbital and a singly occupied 2p orbital yielding αsp = (2 + 1)/2 = 3/2 and βsp = (2 − 1)/2 = 1/2. The loop constant is calculated with respect to reference of one electron per orbital so the loop constant has a value ξ = (3/2 − 1)2 = 1 and κ = (1/2)/(1/2) = 1. See Figure 13 (middle). These are reduced to a lone pair orbital on either end of the molecule and a σ-bond. The O2 π-bonds are the classic example of two center — three electron bonds, with two electrons in π-bonding orbitals and one electron in π-antibonding and bond order of ½ in each case. O2 is in its triplet ground state with bond order of 2. The three electron bonds can also be described using resonance structures as in Figure 7 (Bottom left).
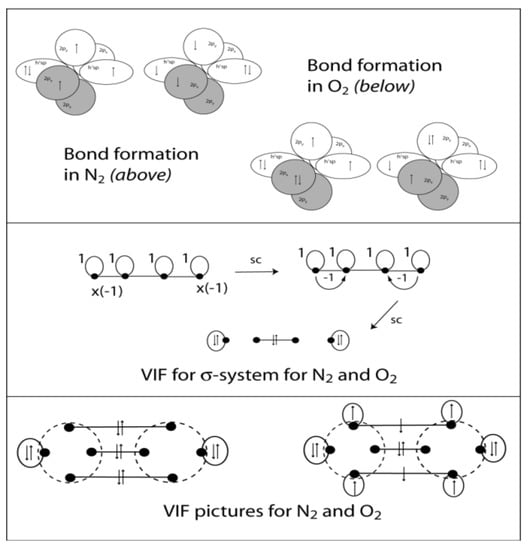
Figure 13.
Orbital interaction diagrams are shown for bond formation in N2 and O2 molecules (top). The σ-system for these molecules consists of four sp hybrid orbitals and six electrons. The VIF picture for the σ-systems reduces to a σ-bond and lone pairs on either end (middle). Including π-bonds with electrons filled in yields expected bond orders and spin multiplicities in each case.
Carbon monoxide is both a familiar and an unusual example with its exceptionally strong bond, Do298 = 1076.5 ± 0.4 kJ/mol [], and small dipole moment. The electron configuration for the symmetry allowed formation of the CO bond is shown in Figure 14 (top). The VIF picture for carbon monoxide requires electronegativity loops for oxygen but not for carbon. See Figure 14 (middle) The sp hybrid orbitals on oxygen are constructed from the doubly occupied 2s and 2p orbitals. αsp = (2+2)/2 = 2 and βsp = (2-2)/2 = 0. The loop constants for the oxygen sp orbitals are ξ = (2-1) = 1 and there is no intrahybrid interaction since βsp = 0. Reduction of the VIF picture for carbon monoxide correctly shows that all ten valence electrons are in bonding orbitals. The σ-bonding interaction is a donor-acceptor interaction or dative bond. The dative bond notation for carbon monoxide was shown as early as 1931 by Sidgwick []. The VIF picture for HCO+ shows that the bond order increases when protonation at carbon occurs. See Figure 14 (bottom). There is no such increase in bond order indicated with protonation at oxygen. See Figure 15. The effects on C-O stretching frequency of protonation at the carbon or oxygen in CO are consistent with the increase in C-O bond order n HCO+ but not COH+. See Frenking [].
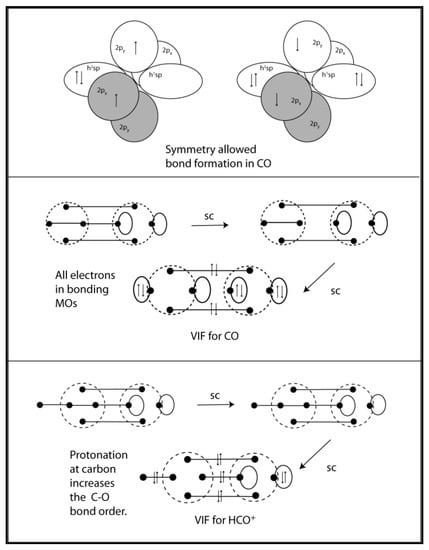
Figure 14.
Orbital interaction diagrams are shown for bond formation CO (top). The VIF depiction of CO (middle) is consistent with the donor-acceptor interpretation of the σ-bond. Protonation of the carbon lone pair results in a C-O triple bond in HCO+ (bottom).
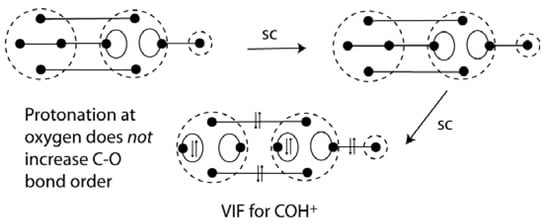
Figure 15.
Protonation of the CO oxygen lone pair does not result in a triple bond in COH+.
4. Bond Angle, Hybridization, and Walsh’s Rules
The technique of hybridization allows prediction of strong directed bonds. From the point of view of localized bond pairs and lone pairs, predictions about bond angles can be made according to Valence Shell Electron Pair Repulsion, VSEPR, ideas. One considers the oxygen atom is in water to be a nearly tetrahedral, sp3, center with bond pair and lone pair electrons exerting repulsive forces on each other. The order of repulsive strength is LP-LP > LP-BP > BP-BP and this trend explains why the bond angle in water is somewhat less than the tetrahedral angle.
Bond angles can also be understood in terms of the stabilization of molecular orbitals. Molecules like water with C2v symmetry have a1, a2, b1, and b2 symmetry species in their irreducible representation. The two lone pair molecular orbitals are not the sp3 hybrid orbitals that one considers when applying VSEPR. The lower energy lone pair molecular orbital is in the plane of the molecule and has a1 symmetry and the higher energy molecular orbital is a p-orbital centered on oxygen in the case of water, and has b1 symmetry. Analysis of how the energy of these orbitals change with bond angle is the basis of Walsh’s rules given below in Walsh’s words for the generic AH2 molecule [].
- (i)
- In the 90° molecule the SA orbital does not mix ("hybridize") with the other orbitals.
- (ii)
- Whether or not an orbital becomes more tightly bound with change of angle is determined primarily by whether or not it changes from being built from a p orbital of A to being built from an s orbital of A.
- (iii)
- If no change of A valencies from which the orbital is built occurs when the angle is changed, the following subsidiary effect determines whether the orbital becomes more or less tightly bound: if the orbital is anti-bonding between the end atoms it is most tightly bound when the latter are as far apart as possible (i.e.in the linear molecule); if it is bonding between the end atoms it is most tightly bound when the latter are as near together as possible (i.e., in the 90° molecule).
According to Walsh’s rules, the bond angle in water, 104.51°, is explained not by repulsion between electron pairs but by the composition of MOs. Specifically the a1 lone pair orbital which is stabilized with a higher percentage of sA character than it would have at 120° or even 109.5°.
In applying the VIF method to AHn molecules, one starts by choosing hybridization for the central atom appropriate for the known or tentative geometry of the molecule. One may choose a tetrahedral hybridization for oxygen in water and then test this choice with application of the two rules. See Figure 16. Electronegativity loops are included for the oxygen sp3 valency points. The pictorial rules are applied and it is shown that the sp3 lone pair orbitals are coupled by an intrahybrid valency interaction. Decoupling results in two lone pair molecular orbitals.
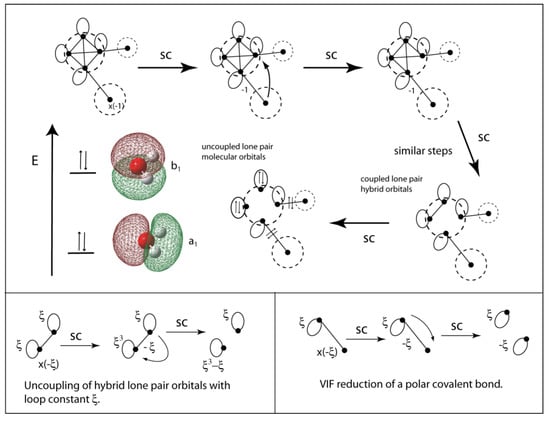
Figure 16.
The VIF picture for a water molecule with sp3 hybridized oxygen includes electronegativity loops on oxygen. Application of the two rules leads to two polar covalent bonds and hybrid lone pair orbitals which are decoupled to lone pair molecular orbitals with a1 and b1 symmetry (top). The rules are used to decouple the lone pair orbitals and reduce the polar covalent bonds (bottom). The loop constant has a value of .
From the symmetry of the water molecule we know that the higher energy lone pair molecular orbital is a 2p orbital on oxygen. This means that the remaining lone pair orbital, the one with a1 symmetry, has all of the s-character from the two lone pair sp3 hybrids so is 50% 2s and 50% 2p. The a1 lone pair MO is approximately a sp hybrid orbital. If sp2 hybridization were used, there would be no decoupling and the a1 lone pair orbital would have only 33% 2s character. Consistent with Walsh’s rules, as the bond angle increases from 90° to 180°, the sA character of the a1 lone pair MO decreases from 100% to 0%.
Figure 16 (bottom left) shows the decoupling of the sp3 lone pair orbitals using the two rules. The loop constant has a value ξ = 3 so both lone pair orbitals are doubly occupied and lower in energy than the refrence −½ Eh []. Figure 16 (bottom right) shows polar covalent bonds reduced to one doubly occupied and one unoccupied orbital or in terms of energy a bonding MO and an antibonding MO.
VIF pictures for singlet methylene are shown in Figure 17. The carbon valence orbitals have an average of one electron per orbital so no electronegativity loops are needed on the sp3 orbitals. Like in water, we see that the sp3 hybrids are coupled but in this case, decoupling leads to one doubly occupied lone pair orbital and an unoccupied orbital. From the energy point of view, one orbital lower in energy than −½ Eh and the unoccupied orbital, a carbon 2p orbital, higher in energy than −½Eh. Once again we know that the a1 lone pair orbital, in this case the HOMO, is roughly a sp hybrid orbital stabilized relative to the original sp3 hybrids by increased s-character. On the other hand, by choosing sp2 hybridization for triplet carbene we start with a singly occupied unhybridized carbon 2p orbital, Figure 18. Application of the two rules shows the other singly occupied molecular orbital, SOMO, is the a1 MO. From the VIF approach we know that the triplet carbene has a wider bond angle than singlet carbene. By application of Walsh’s rule (iii) we know that the highest doubly occupied MO which is bonding with respect to the hydrogen 1s is stabilized by an even wider bond angle than 120°. Either by this reasoning or by applying VSEPR we expect a bond angle greater than 120°. The triplet carbene bond angle is predicted to be 135.37° using B3LYP/6-311++Gdp.
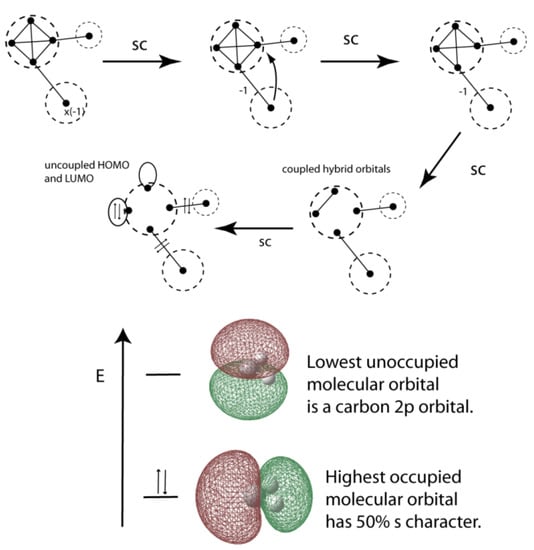
Figure 17.
VIF picture for singlet methylene is reduced using the rules (top). Coupled sp3 lone pair orbitals are decoupled to and doubly occupied a1 lone pair orbital and an unoccupied b1 lone pair orbital (bottom).
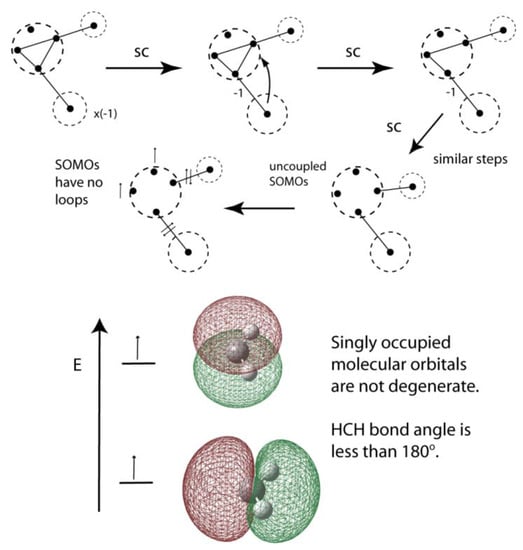
Figure 18.
VIF depiction and reduction of triplet methylene. Disconnected VP without loops are singly occupied molecular orbitals, nonbonding from the energetic viewpoint.
VIF treatment of the NH2 radical is depicted in Figure 19. The nitrogen atom requires the use of electronegativity loops. Nitrogen in its ground state electron configuration is [He]2s2sp3 so αsp3 = (2 + 3(3/3))/4 = 5/4, βsp3 = (2 – (3/3))/4 = 1/4, and the loop constant is ξsp3 = (5/4 – 1)∙4 = 1. In this case the coupled hybrid orbitals are simplified to a doubly occupied lone pair MO with a1 symmetry and a SOMO which is the nitrogen 2p orbital. The a1 lone pair orbital is roughly 50% N 2s so is approximately a nitrogen sp orbital. The bond angle in NH2 radical is predicted to be 103.07° using UB3LYP/6-311++Gdp.
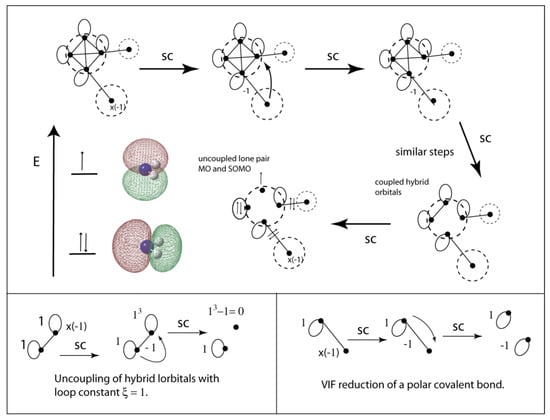
Figure 19.
VIF picture for the NH2 radical reduced. Tetrahedral hybridization is used on nitrogen and the sp3 lone pair orbitals are decoupled to form a lone pair MO and SOMO (top). The sp3 lone pair orbitals are decoupled and N-H polar covalent bonds reduced using the two rules (bottom).
VIF pictures for ammonia, NH3, are shown in Figure 20. The Nsp3 electronegativity loops are ξ = 1, same as the NH2 radical example. The nitrogen lone pair molecular orbital is uncoupled from the three N-H bonding orbitals by use of the two rules. The nitrogen lone pair orbital is roughly an Nsp3 hybrid orbital and gains slightly more 2s character according to Walsh’s rules when the HNH bond angles are made more acute than the tetrahedral angle. The VIF method applied to the understanding of molecules with heavier atoms, third period and higher, is a subject of ongoing research. It is well known that heavier p-block atomic centers display a wider variety of chemical bonding possibilities and initial studies show that the VIF method with its sensitivity to molecular geometry and hybridization describe these cases well.
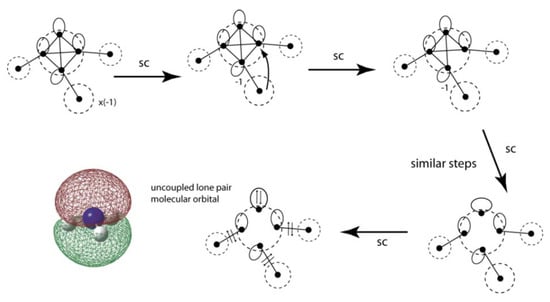
Figure 20.
VIF picture for ammonia, NH3 reduced using the two rules.
5. Depiction of Ring Systems
The benzene and other unsaturated and saturated hydrocarbons have had a special role in the development of the molecular structural formula and application of chemical bonding theories. The VIF method has been used to predict the π-distortivity of benzene, distinct single and double bonds in cyclobutadiene, and symmetries of cyclopentadienyl cation, radical, and anion []. The consideration of relative interaction energies is important in these cases and a formula relating the effect of relative interaction strength to the number of carbon atoms in σ-ring systems has been derived []. Figure 21 shows the reduction of the VIF for the π-system of cyclobutadiene. The constant, a, is used to test the relevance of alternating interactions of different strength around the ring. Application of the two rules yields two segments. If a = 1 as would be the case for a square, D4h symmetry for the molecule, then from the point of view of electron density, there are two unpaired electrons or from the point of view of energy, there are two degenerate molecular orbitals which result in a triplet state according to Hund’s rule when the 4 π-electrons are filled in. The singlet state with a pair of doubly occupied π molecular orbitals is therefore Jahn-Teller distorted as is well known.
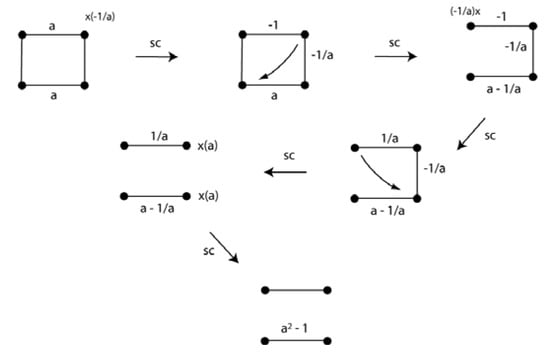
Figure 21.
The cyclobutadiene π-system includes the relative interactions strength to test the effect of distortion of the molecular geometry on the frontier orbitals.
The reduction for the benzene π-system is shown in Figure 22. The third segment in the reduced bottom picture has strength of a3 + 1. This means that if a > −1, the picture indicates singlet state with three doubly occupied π-bonding orbitals. A wide range of values for a are possible for the benzene singlet state consistent with the π-distortivity of this molecule.
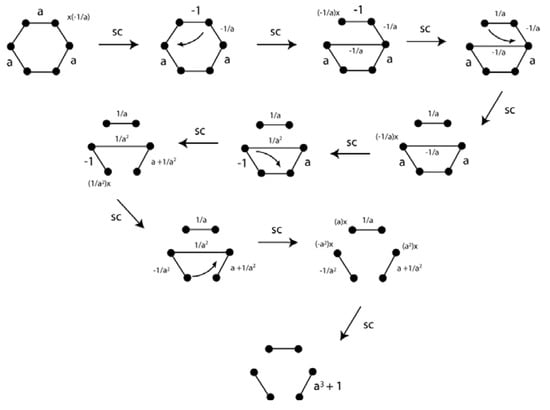
Figure 22.
VIF depiction and reduction of the benzene π-system indicate that frontier orbitals energies are not changed much with a wide range of geometric distortions.
The same approach can be used for σ-systems. Figure 23 shows the VIF method applied to cyclopropane. The relative interactions, strength a, indicate the difference in strength of sp3 carbon intrahybrid interactions and σ-bonding interactions around the ring. The constant a is greater than 1 so one concludes that all of cycloproprane’s valence electrons are in doubly occupied molecular orbitals. No assertions need be made about σ-aromaticity []. When VIF is applied to σ-systems of hydrocarbon rings, the last interaction has strength of an + (−1)(n–1) []. This formula can be applied quickly and easily to larger ring systems. The VIF results for benzene are shown in Figure 24. Using the formula from above, the last σ-interaction has strength of a6 − 1. Since a > 1, all of benzene’s valence electrons are paired in bonding molecular orbitals. The two benzene resonance structures are structurally covariant because they are related by the two pictorial rules.
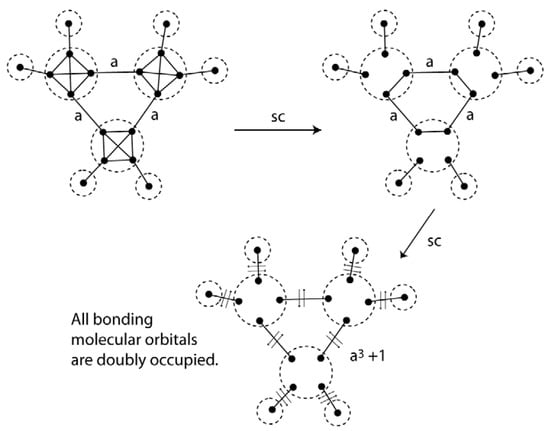
Figure 23.
The VIF picture for cyclopropane when reduced indicates that all valence electrons are in doubly occupied bonding orbitals. No assertions about aromaticity are made.
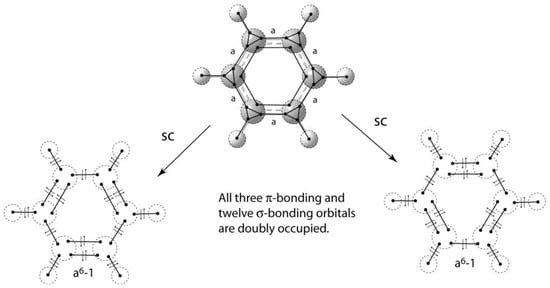
Figure 24.
All valence electrons in the benzene molecule are in bonding molecular orbitals. Benzene’s resonance structures are structurally covariant.
The VIF picture for phenyl radical, anion, and cation is shown in Figure 25. From the point of view of electron density, the radical, anion, and cation are distinguished by the value of the relative interaction strength, a. The final loop has strength of a6 − 1. This is not an application of the rule for ring σ-systems but required separate derivation. If a = 1, the final loop strength is zero and the picture represents the phenyl radical. If |a| > 1 the final orbital is a lone pair orbital and phenyl anion is represented. With |a| < 1, the picture represents phenyl cation. From the energy point of view a > 1 and the last orbital is a bonding molecular orbital. This is consistent with the electron density interpretation because as electrons fill into bonding molecular orbitals, bond order increases.
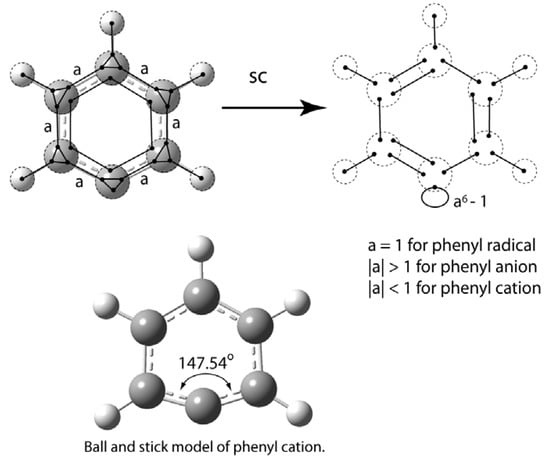
Figure 25.
VIF depiction of the phenyl radical, anion, and cation shows that the SOMO, LP, or unoccupied orbital is sensitive to the degree of C-C bonding in the σ-framework.
Walsh’s rules can be applied to understand the change in bond angel between phenyl anion, 112.3°, radical, 126.0°, and cation, 147.5° calculated using B3LYP 6-311++Gdp with the G03W package []. The empty orbital in the phenyl cation increases in p-character and the bonding orbitals are then lowered in energy having increased s-character. A simpler depiction of the phenyl cation uses sp hybridization for the carbon that does not have a hydrogen atom attached. The an + (−1)(n – 1) rule can be used and bonding interactions are increased so a > 1. Bonding character in the σ-system of the cation is increased with increased bond angle at the phenyl carbon consistent with Walsh’s rules.
A similar increase in bond angle is found in the double aromatic [] C6H3+ cation. The VIF treatment of the σ-system for this cation is shown in Figure 26. The carbon atoms with hydrogen atoms attached are given sp hybridization. The unhybridized p-orbitals in the σ-plane interact to form the three centered — two electron bond. The remaining σ-system is reduced using the an + (−1)(n–1) rule and the π-system is the same as for benzene. The CCC bond angles centered on the carbon atoms without hydrogen are 149.4° according to B3LYP/6-311++Gdp.
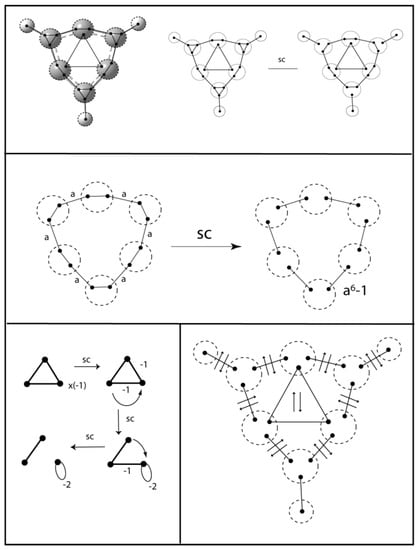
Figure 26.
The σ-system for the C6H3+ double aromatic cation includes a two center – three electron bond resulting from the three carbon 2p orbitals in the the σ-plane.
6. Cyclopentadienylidene
An unusual molecule with a high degree of distortion and low degree of symmetry, C1, is singlet cyclopentadienylidene. One may wonder whether the singlet state of this neutral carbene with formula C5H4 will be π-aromatic with 6 π-electrons and the empty orbital in the sigma plane or π-antiaromatic with 4 π-electrons and the carbene lone pair in a σ-lone pair orbital stabilized with a higher degree of s-character. Frenking [] using the EDA analysis considers cyclopentadienylidene to be antiaromatic, a classification that in itself does not explain the puckering and twisting of the ring to give C1 symmetry. The cyclopentadienyl cation with its 4π electrons is planar though JT distorted in the plane.
VIF pictures for this case are shown in Figure 27, (top). Interaction of the lone pair electrons with the π-system are neglected in this picture. The full reduction of this VIF picture by the two rules is not shown in Figure 27. The reduction results in the sp3 lone pair orbitals being coupled by a line strength of κ = a5 – 1. The constant, a, is the relative interaction strength between carbon — carbon σ-bonding interactions and carbon intrahybrid interactions. This is greater than one so κ is also greater than one. The VIF approach does not neglect the significance of the ring system on the lone pair. The lone pair orbitals are decoupled to yield a roughly sp lone pair MO in the σ-plane, and an empty carbon 2p orbital, similar to Figure 17. Before considering interactions with the π-system, we will place the lone pair electrons in the lower energy σ-LP orbital and refer to the empty carbon 2p orbital as LP*. These are depicted in Figure 27 (middle right).

Figure 27.
VIF pictures for cyclopentadienylidene are shown (top). Explanation of the distorted geometer is made using frontier orbital donor-acceptor arguments (middle and bottom).
The geometry of cyclopentadienylidene is distorted; the ring is puckered and twisted to give C1 symmetry. Carbon – carbon bond lengths around the ring according to a geometry optimization carried out using MP2/6-311++Gdp are shown in Figure 27 (middle left). Figure 27 (bottom) shows how interaction of the lone pair orbitals with the π-system distorts the geometry of the ring. Puckering of the five membered carbon ring allows donation of the σ-LP orbital into the π* orbital. This also decreases the electron density in the σ-LP orbital. According to an NBO calculation based on the B3LYP/6-311++Gdp level of theory this orbital has an electron occupation of 1.54 electrons and a hybridization of sp1.7. Consistent with Walsh’s rules, removal of electron density from this orbital results in a reduction of s-character in the NBOs from sp and a widening of the bond angle from 109.5° to 116.7° according to B3LYP and 122.6° according to MP2, both with the 6-311++Gdp basis set. The NBO algorithm available with the G03W package includes calculation of the energies of donor acceptor-interactions. The σ-LP orbital donates into the two localized π-antibonding NBOs with donor-acceptor interaction energies of 15.04 kcal/mol and 11.63 kcal/mol. The puckering of the cyclopentadienylidene singlet ring is clearly attributable to stabilization of the lone pair by a donation of LP density into the π-system because protonation leads to the planar cyclopentadienyl cation.
The cyclopentadienylidene π-system is stabilized by donation into the LP* orbital, the otherwise empty carbene carbon 2p orbital causing a conrotatory twist of the ring from Cs to C1 symmetry. See Figure 27 (bottom right). According to the NBO calculations performed based on B3LYP/6-311++Gdp, the electron occupation of this orbital is 0.35 electrons. The interaction is depicted in Figure 27 (bottom right). Because the ring is also puckered the interaction is stronger on one side of the ring than the other causing the carbon-carbon bond length on one side of the carbene carbon to be shorter than on the other, 1.354 Å as opposed to 1.426 Å according to the MP2 calculation. The donor-acceptor interactions are likewise different on either side of the carbene carbon, 102 kcal/mol compared to 33 kcal/mol. Both of these donor-acceptor interactions are 63 kcal/mol in the optimized Cs transition structure identified by one imaginary vibrational frequency. The unusual puckered and twisted geometry of singlet cyclopentadienylidene can thus be understood in terms of donation of electron density from the carbene LP orbital into the π-LUMO and donation from the π-HOMO into the otherwise empty LP* orbital.
The donation of electron density into the LP* carbon 2p orbital is the stronger of the two donor-accepter interactions discussed above. To describe this and the resulting twisting of the ring using VIF, one considers a basis set of the four 2p orbitals in the double bonds and the LP* orbital. See Figure 28 (top). The ring puckering allows only one lobe of LP* to interact with the nearest neighbor 2p orbitals. A conrotatory twist therefore requires one negative interaction around the ring. See Figure 28 (top). Reduction using the two rules leads to two doubly occupied or bonding orbitals and three unoccupied or antibonding orbitals, consistent in a system that stabilizes the 4 π electrons. If interaction with the LP orbital is included, the VIF picture correctly describes this 6 π electron system Figure 28 (bottom).
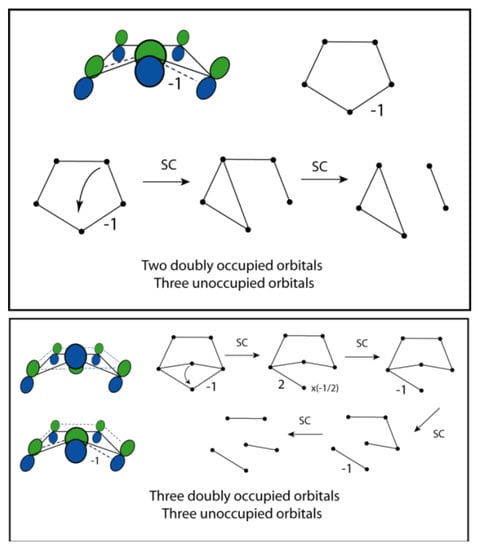
Figure 28.
Interacting π-system 2p orbitals in cyclopentadienylidene interact with each other and LP* (top left). Conrotatory twisting results in a negative VI. Reduction by the two rules leads to two doubly occupied orbitals, a 4 π-electron system (top). If interactions of the π-system with σ-LP are included a 6 π-electron system is correctly described (bottom).
7. Copper Atom Clusters
A long term goal with regard to the VIF method is to be able to apply it more widely through the periodic table. A challenge in doing this is to maintain visually simplicity while studying molecules with heavier atoms that have more valence orbitals. Jug [] has found that simple bonding pictures can be used to understand small copper clusters. The 3d sublevel is full in copper atoms in their ground electronic state so bonding in copper clusters takes place largely through copper 4s orbitals. Qualitative electronic properties of the symmetrical Cu3+ and Jahn-Teller distorted Cu3 can be understood according to three-center bonding models. See Figure 8 for the VIF treatment. With a = 0 in the VIF density picture one doubly and one singly occupied MOs result. The SOMO is antibonding (a > 0) according to the VIF Hamiltonian energy picture if only 4s orbitals are included. Aside from consideration of increased binding due to dispersion effects, one would expect the distorted Cu3 cluster to dissociate into Cu2 + Cu as is the case for H3. Inspection of the Cu3 HOMO indicates a small degree of bonding 3d orbital contribution to this orbital. See []. These create a stabilizing effect for the Cu3 cluster.
The Cu4+ and Cu4 clusters are no less interesting. Figure 29 shows the VIF treatment for Cu4+. The VIF pictures as one-electron density and one-electron Hamiltonian operators are the same in this case. The resulting SOMO is nonbonding. One would expect a hypothetical H4+ molecule to dissociate to a stable H3+ cation and H atom. Aside from increased binding due to dispersion, one can attribute relative stability of the Cu4+ cluster to small but important bonding contributions from 3d orbitals. See Figure 3 in Jug []. When an electron is added to make a Cu4 cluster, all of the bonds in the cluster become shorter according to HF/LanL2DZ, an indication that the LUMO has bonding character. The VIF treatment shown in Figure 29 only considers valence 4s orbitals and indicates that the LUMO is nonbonding. The bonding character is therefore attributable to 3d orbital contributions. In analogy to a hypothetical H4 molecule one might expect Cu4 to dissociate to two Cu2 molecules. This is predicted by the analogous VIF treatment in Figure 21. According to HF/LanL2DZ, the rhomboid Cu4 cluster is 11 kcal/mol lower in energy than 2 Cu2. Jug has studied Cun clusters n = 2–10 []. Three member rings are a structural motif in these. The author is planning to study more of these examples.

Figure 29.
VIF depiction of Cu4+ including Valency Points only for Cu 4s orbitals. As one-electron density operators, these pictures indicate one doubly occupied, one singly occupied, and two unoccupied orbitals for a total of 3 electrons. As one-electron Hamiltonian operators one bonding, one nonbonding, and two antibonding orbitals are indicated.
8. VIF Description of the Binding of O2 to Fe(II)
The binding of the O2 molecule to the Fe(II) center in hemoglobin is an interesting and important example. The treatment here is inspired by Harcourt’s approach utilizing Increased Valence structures []. See structures 24–29 in []. In this bonding model O2 in its ground triplet state binds to Fe2+ in an intermediate spin t2g5e1 triplet state. The well known bent Fe-O-O geometry results from binding through the O2 π* orbitals. The Fe-O bond is not a double bond and this is accounted for through the inclusion of resonance structures with “long bonds” also called “formal bonds” between the terminal O atom and Fe atom. “Formal bonds” have negligible strength but indicate that the associated electrons are paired [].
A VIF depiction of this bonding situation is shown in Figure 30. The bonding of O2 to Fe(II) is described by two three-center four-electron bonds each analogous to the π-system of allyl anion. Also see Figure 8. The density interactions between Fe and the terminal O atom p-orbitals are antibonding, a < 0, resulting in two doubly occupied MO’s for this system. One expects greater electron charge density on the Fe and terminal O atoms from this type of bonding. The geometry of heme with distal imidazol and bound O2 molecule was optimized using B3LYP/LanL2Z. The APT partial charges on Fe, the O atom bonded to Fe, and the terminal O atom are 0.357, 0.263, and -0.350 respectively. Without the O2 bound, the APT partial charge on the Fe(II) atom increases to +0.585 also using B3LYP/LanL2Z. The computed negative partial charge on the terminal oxygen atom while the oxygen atom bonded to iron has a positive partial charge and increased charge on the Fe atom is evidence that supports this bonding description three-center four- electron MO bonding description. See resonance structures in Figure 8.
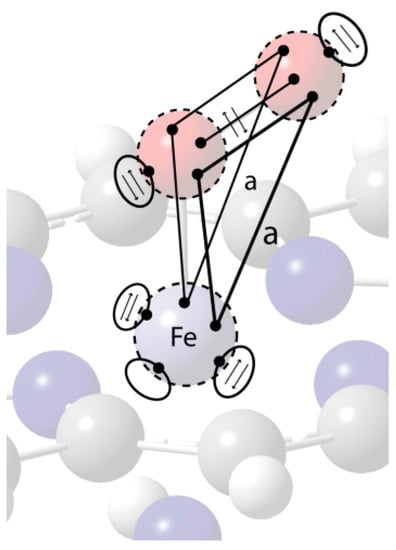
Figure 30.
VIF density operator depiction of O2 bonding to Fe(II) through two three-center four-electron bonds. Constant a has “a” is an antibonding density interaction, a < 0, to give four electrons in each three-center bond. See Figure 8.
9. Conclusions
Bond and lone electron pair concepts applied to the three-dimensional geometry of molecules are central in chemical reasoning. These are emphasized in this presentation of the Valency Interaction Formula, a quantum based molecular structural formula. The VIF method has been presented in detail here. It offers a method of chemical reasoning based on the invariance of observable properties under linear transformations applied in the form of two pictorial rules. VIF pictures related by the rules are structurally covariant, sc, and have four interpretations.
- Sets of structurally covariant VIF pictures are interpreted as the same quantum operator represented in linearly related basis frames.
- VIF density pictures related by the rules can be used as resonance structures but have topological meaning beyond usual resonance structures.
- Structurally covariant VIF pictures can be interpreted as sets of molecular species with similar energy.
- The same VIF picture can sometimes be interpreted as different quantum operators, one-electron density or Hamiltonian for example.
The theory was applied to well known and interesting molecules and ions, methane, methonium cation, C2, N2, O2, and CO, water, singlet and triplet methylene, NH2 radical, and ammonia, cyclobutadiene singlet and triplet, benzene, cyclopropane, phenyl anion, cation, and radical, the double aromatic C6H3+ ring, and cyclopentadienylidene, Cu3+, Cu3, Cu4+, and Cu4 copper atom clusters, and the bonding of O2 to Fe(II) in hemoglobin.
The VIF pictures as one-electron density and one-electron Hamiltonian operators for these examples have been analyzed according to the invariance of the number of doubly, singly, and unoccupied orbitals and/or numbers of bonding, nonbonding, and antibonding orbitals. The results have been compared to familiar bond pair — lone pair concepts, Walsh’s rules, and frontier orbital donor-acceptor methods as well as to results of HF, B3LYP, and MP2 computations with LanL2Z or 6-311++Gdp basis set and NBO analysis of these. Bonding pictures have also been compared to the VB structural formulas of Linnet and Harcourt.
The VIF method, a pictorial MO theory, incorporates some of the advantages of VB pictures and at the same time gives insight into the behavior of MO frontier orbitals. A major goal of this and previous work has been to develop methods of chemical reasoning using VIF pictures, demonstrate their agreement with other theoretical methods. This foundation is the basis of ongoing work being done to apply the method through more of the periodic table and toward the understanding of a wide range of chemical reactions.
Acknowledgements
I am grateful to my colleagues in the chemistry discipline at UMM for their kind support and encouragement and in particular to James Togeas for many stimulating discussions and for the generosity he has shown with his books, many of them classics. I thank the editorial board of the open access journal Symmetry for inviting me to submit this article and the reviewers for introducing me to a great deal of important literature and for their suggestions for improving the manuscript.
References and Notes
- Lewis, G.N. The atom and the molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef]
- Pauling, L. Linus Pauling in a letter to Gilbert N. Lewis. Available online: http://osulibrary.oregonstate.edu/specialcollections/coll/pauling/bond/corr/corr216.1-lp-lewis-19280307.html (accessed on 9 July 2010).
- Slater, J.C. Directed valence in polyatomic molecules. Phys. Rev. 1931, 37, 481–489. [Google Scholar] [CrossRef]
- Pauling, L. The nature of the chemical bond. Application of the results obtained from the quantum mechanics and from the theory of paramagnetic susceptibility to the structure of molecules. J. Am. Chem. Soc. 1931, 53, 1367–1400. [Google Scholar] [CrossRef]
- Van Vleck, J.H.; Sherman, A. The quantum theory of valence. Rev. Mod. Phys. 1935, 7, 167–228. [Google Scholar] [CrossRef]
- Linnett, J.W. Binding in diatomic molecules. J. Chem. Soc. 1956, 275–287. [Google Scholar] [CrossRef]
- Pauling, L. The nature of the chemical bond. II. The one-electron bond and the three-electron bond. J. Am. Chem. Soc. 1931, 53, 3225–3237. [Google Scholar] [CrossRef]
- Green, M.; Linnett, J.W. Molecules and ions containing and odd number of electrons. J. Chem. Soc. 1960, 4959–4965. [Google Scholar] [CrossRef]
- Linnett, J.W. A modification of the Lewis-Langmuir octet rule. J. Am. Chem. Soc. 1961, 83, 2643–2653. [Google Scholar] [CrossRef]
- Harcourt, R.D. Qualitative, Valence-Bond Descriptions of Electron-Rich Molecules: Pauling “3-Electron Bonds” and “Increased-Valence” Theory. In Lecture Notes in Chemistry; Springer: Berlin, Germany, 1982; Volume 30, Chapter 3. [Google Scholar]
- Harcourt, R.D. Valence bond and molecular orbital descriptions of the three-electron bond. J. Phys. Chem. A 1997, 101, 2496–2501, 5962. [Google Scholar] [CrossRef]
- Harcourt, R.D. Increased-valence structures for qualitative valence-bond representations of electronic structure for electron-rich molecules. Eur. J. Inorg. Chem. 2000, 9, 1901–1916. [Google Scholar] [CrossRef]
- Harcourt, R.D. Valence bond structures for three-electron three-center and four-electron three center bonding units: some further examples. J. Phys. Chem. A 2010. http://pubs.acs.org/doi/abs/10.1021/jp911294x (accessed on 9 July 2010). [CrossRef] [PubMed]
- Weinhold, F.; Landis, C. Valency and Bonding, A Natural Bond Orbital Donor-Acceptor Perspectvie; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Bader, R.F.W.; Hernández-Trujillo, J.; Cortés-Guzmán, F. Chemical bonding: from Lewis to atoms in molecules. J. Comp. Chem. 2006, 28, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Sinanoğlu, O.; Alia, J.; Hastings, M. Valency Interactions in AHm 0,±, (Hydrides of Main Group Elements, Radicals, Cations, Anions), and MO Energy Level Patterns Directly from the Pictorial “VIF’ Method Compared with Computer Calculations. J. Phys. Chem. US 1994, 98, 5867–5877. [Google Scholar] [CrossRef]
- Alia, J.D. Molecular structural formulas as one-electron density and Hamiltonian operators: the VIF method extended. J. Phys. Chem. A 2007, 111, 2307–2318. [Google Scholar] [CrossRef] [PubMed]
- Alia, J.D.; Vlaisavljevich, B.; Abbot, M.; Warneke, H.; Mastin, T. Prediction of molecular properties including symmetry from quantum-based molecular structural formulas. J. Phys. Chem. A 2008, 112, 9784–9795. [Google Scholar] [CrossRef] [PubMed]
- Alia, J. Graph representation of quantum mechanical operators as molecular structural formulas. IJPAM 2008, 49, 467–474. [Google Scholar]
- Gillespie, R.J.; Hargittai, I. The VSEPR Model of Molecular Geometry; Allyn and Bacon: Boston, MA, USA, 1991. [Google Scholar]
- Lewis, G.N. Valence and the structure of atoms and molecules. American Chemical Society Monograph Series; The Chemical Catalogue Company, Inc.: Derbyshire, UK, 1923. [Google Scholar]
- Harcourt, R.D. Chemical bonding via Bohr circular orbits and a 2nxn factorization of 2n(2). J. Mol. Struc-Theochem 1995, 338, 195–213. [Google Scholar] [CrossRef]
- Bernard, Y.A.; Gill, P.M.W. Posmom: The unobservable obsrvable. J. Phys. Chem. Lett. 2010, 1, 1254–1258. [Google Scholar] [CrossRef]
- Sinanoğlu, O. A principal of linear covariance for quantum mechanics and electronic structure theory of molecules and other atom clusters. Theoret. Chim. Acta Berl. 1984, 6, 233–242. [Google Scholar] [CrossRef]
- Pauling, L.; Wilson, E.B. Introduction to Quantum Mechanics; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1935; p. 362. [Google Scholar]
- Shaik, S.S.; Hiberty, P.C. A Chemist’s Guide to Valence Bond Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; p. 57. [Google Scholar]
- Jug, K. A maximum bond order principle. J. Am. Chem. Soc. 1977, 99, 7800–7805. [Google Scholar] [CrossRef]
- Dewar, M.J.S. σ-conjugation and σ-aromaticity. Bull. Soc. Chim. Belg. 1979, 88, 957–967. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A.; Vreven, T., Jr.; Kudin, K.N.; Burant, J.C.; Millam, J.M.; Iyengar, S.S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G.A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J.E.; Hratchian, H.P.; Cross, J.B.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R.E.; Yazyev, O.; Austin, A.J.; Cammi, R.; Pomelli, C.; Ochterski, J.W.; Ayala, P.Y.; Morokuma, K.; Voth, G.A.; Salvador, P.; Dannenberg, J.J.; Zakrzewski, V.G.; Dapprich, S.; Daniels, A.D.; Strain, M.C.; Farkas, O.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Ortiz, J.V.; Cui, Q.; Baboul, A.G.; Clifford, S.; Cioslowski, J.; Stefanov, B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong, M.W.; Gonzalez, C.; Pople, J.A. Gaussian 03, Revision C.02; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Mulliken, R.S. Note on electronic states of diatomic carbon, and the carbon-carbon bond. Phys. Rev. 1939, 56, 778–781. [Google Scholar] [CrossRef]
- Simons, J.; Boldyrev, A.I.; Gonzales, N. Periodicity and peculiarity in 120 first- and second-row diatomic molecules. J. Phys. Chem. 1994, 98, 9931–9944. [Google Scholar]
- Paldus, J.; Li, X. Symmetry breaking in spin-restricted hartree-fock solutions: the case of the C2 molecule and the N2+ and F2+ cations. Phys. Chem. Chem. Phys. 2009, 11, 5281–5289. [Google Scholar]
- Lide, D.R. Bond Dissociation Energies. In The CRC Handbook of Chemistry and Physics, 85th ed.; CRC Press: New York, NY, USA, 2004–2005. [Google Scholar]
- Luo, Y.R. Handbook of Bond Dissociation Energies in Organic Compounds; CRC Press: New York, NY, USA 2003; p. 101. [Google Scholar]
- Sidgwick, N.V. Structure of divalent carbon compounds. Chem. Rev. 1931, 9, 77–88. [Google Scholar] [CrossRef]
- Frenking, G.; Loschen, C.; Krapp, A.; Fau, S.; Strauss, S. Electronic structure of CO—an exercise in modern chemical bonding theory. J. Comp. Chem. 2006, 28, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Walsh, A.D. The electronic orbitals, shapes, and spectra of polyatomic molecules, part I: AH2 molecules. J. Chem. Soc. 1953, 22, 60–66. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Wu, W.; Ma, B.; I-Chia Wu, J.; Mo, Y. Is cyclopropane really the σ-aromatic paradigm? Chem. Eur. J. 2009, 15, 9730–9736. [Google Scholar]
- Wodrich, M.D.; Corminboeuf, C.; Park, S.S.; Schleyer, P.v.R. Double aromaticity in monocyclic carbon, boron, and borocarbon rings based on magnetic criteria. Chem. Eur. J. 2007, 13, 4582–4593. [Google Scholar] [CrossRef]
- Frenking, G.; Fernandez, I. Direct estimate of conjugation and aromaticity in cyclic compounds with the EDA method. Faraday Discuss. 2007, 135, 403–421. [Google Scholar]
- Jug, K.; Zimmermann, B.; Köster, A.M. Growth pattern and bonding in copper clusters. Int. J. Quantum Chem. 2002, 90, 594–602. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).