Frame Transformation Relations and Symmetry Analysis of Fluxional Symmetric Rotor Dimers
Abstract
:1. Introduction
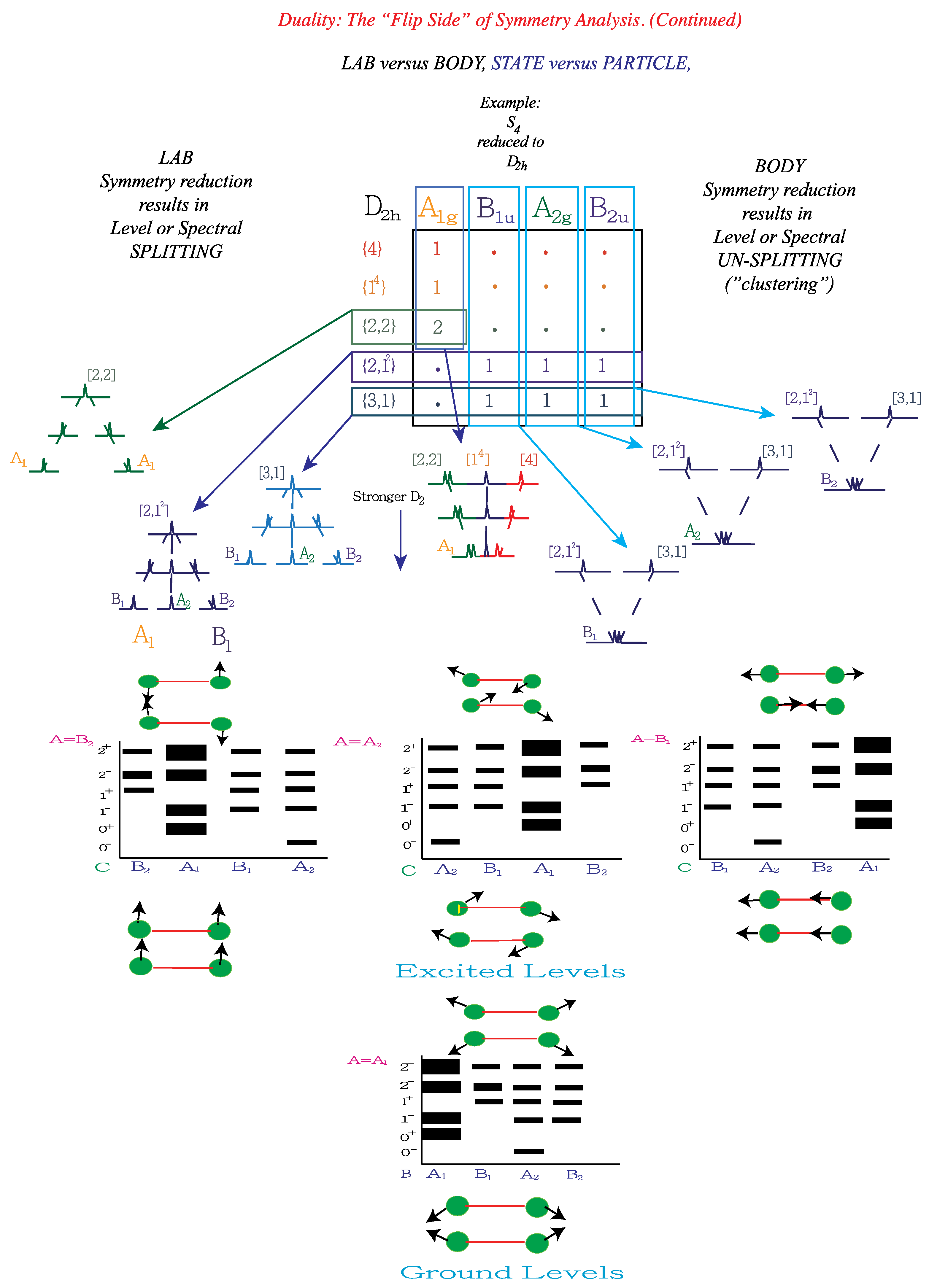
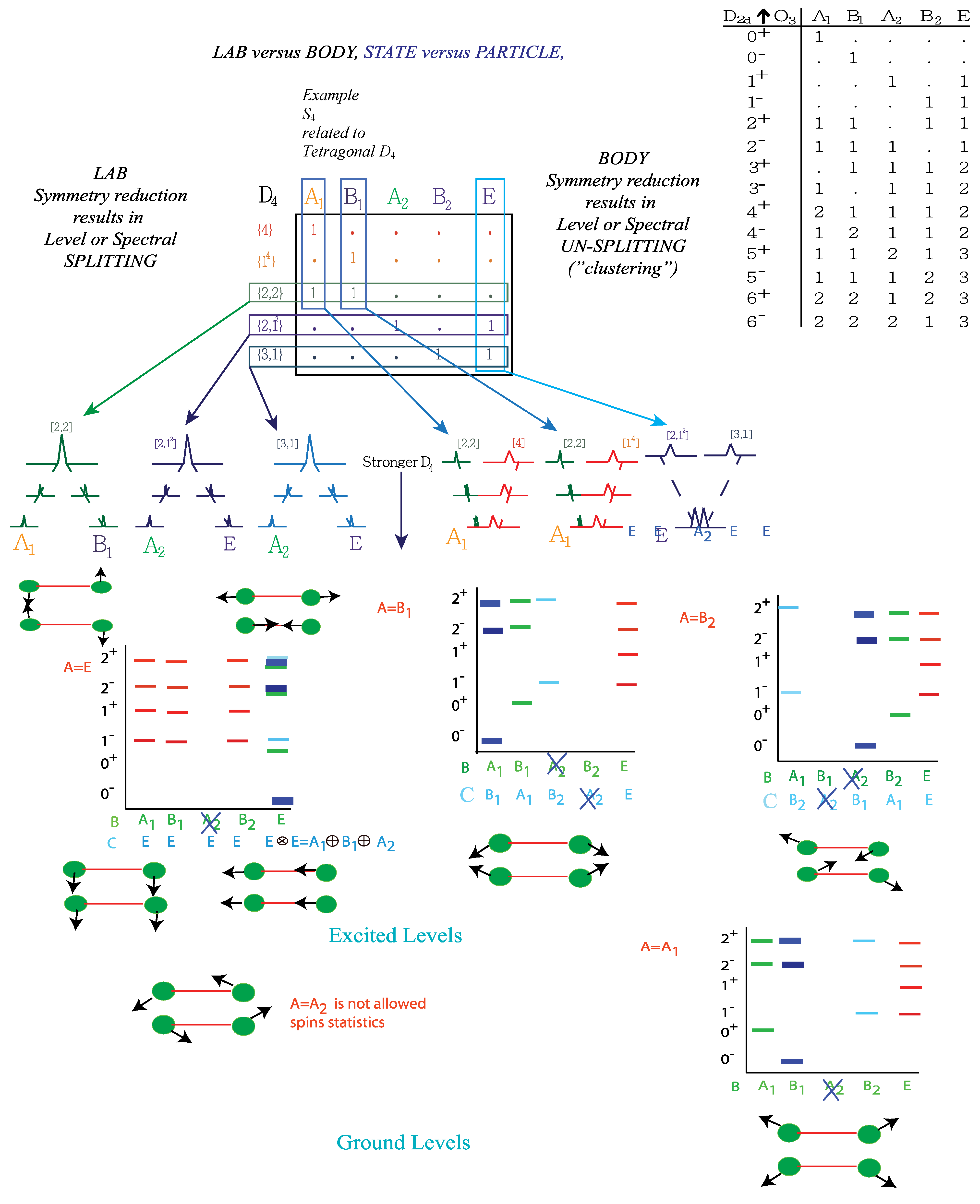
2. Symmetry Relation for a Coupled System
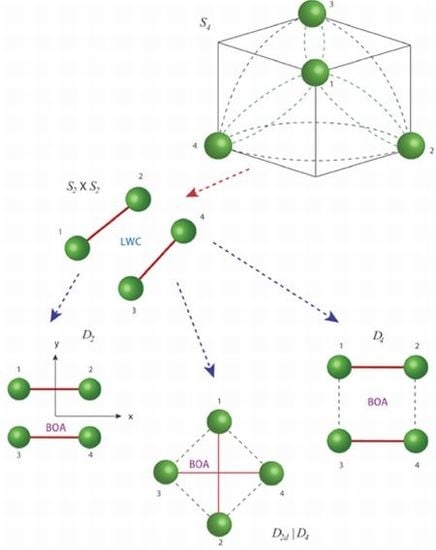
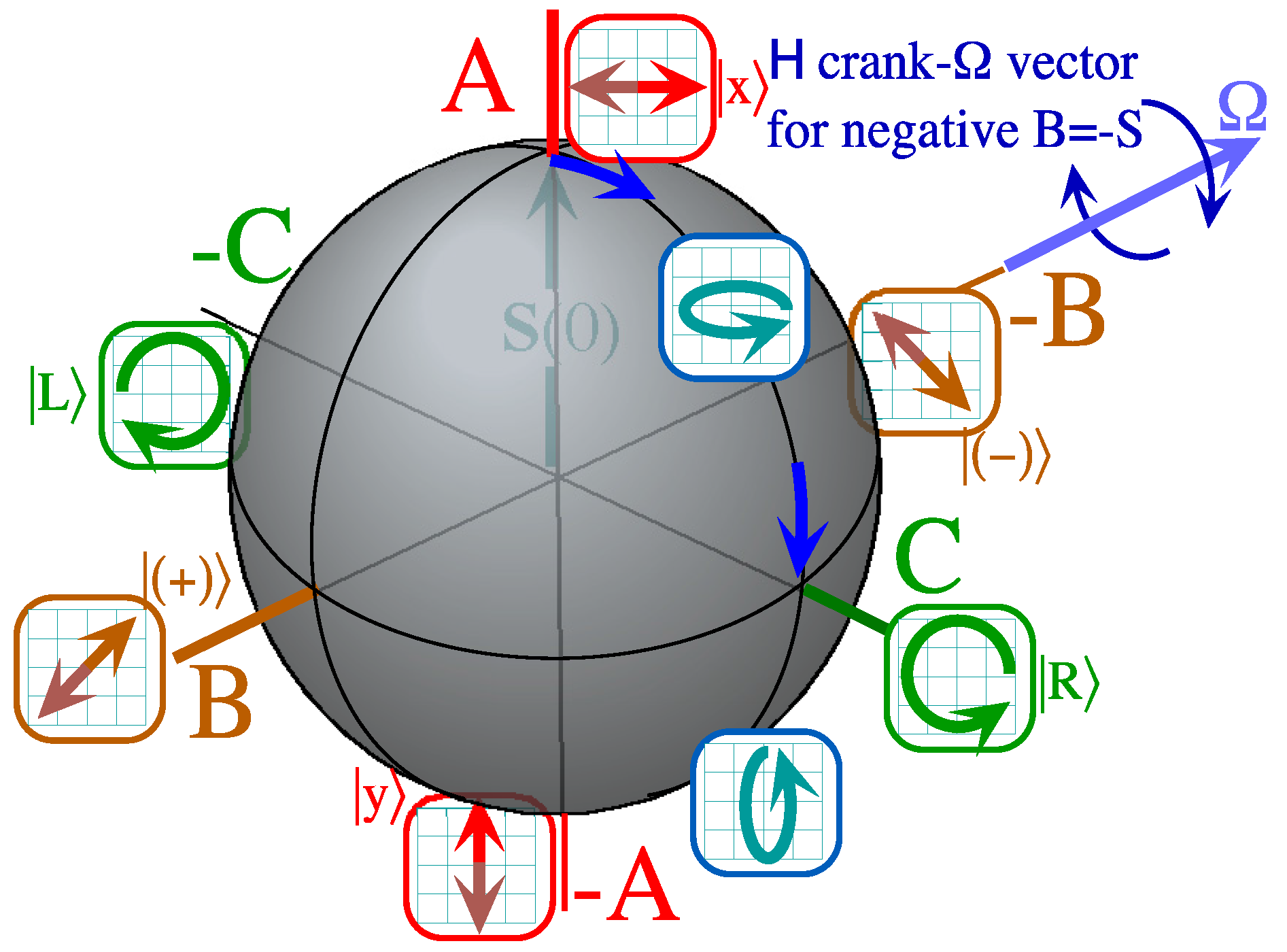
2.1. Symmetry Effects for Two Coupled Rotors
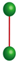 and
and 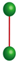 form a molecule
form a molecule 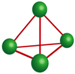 .
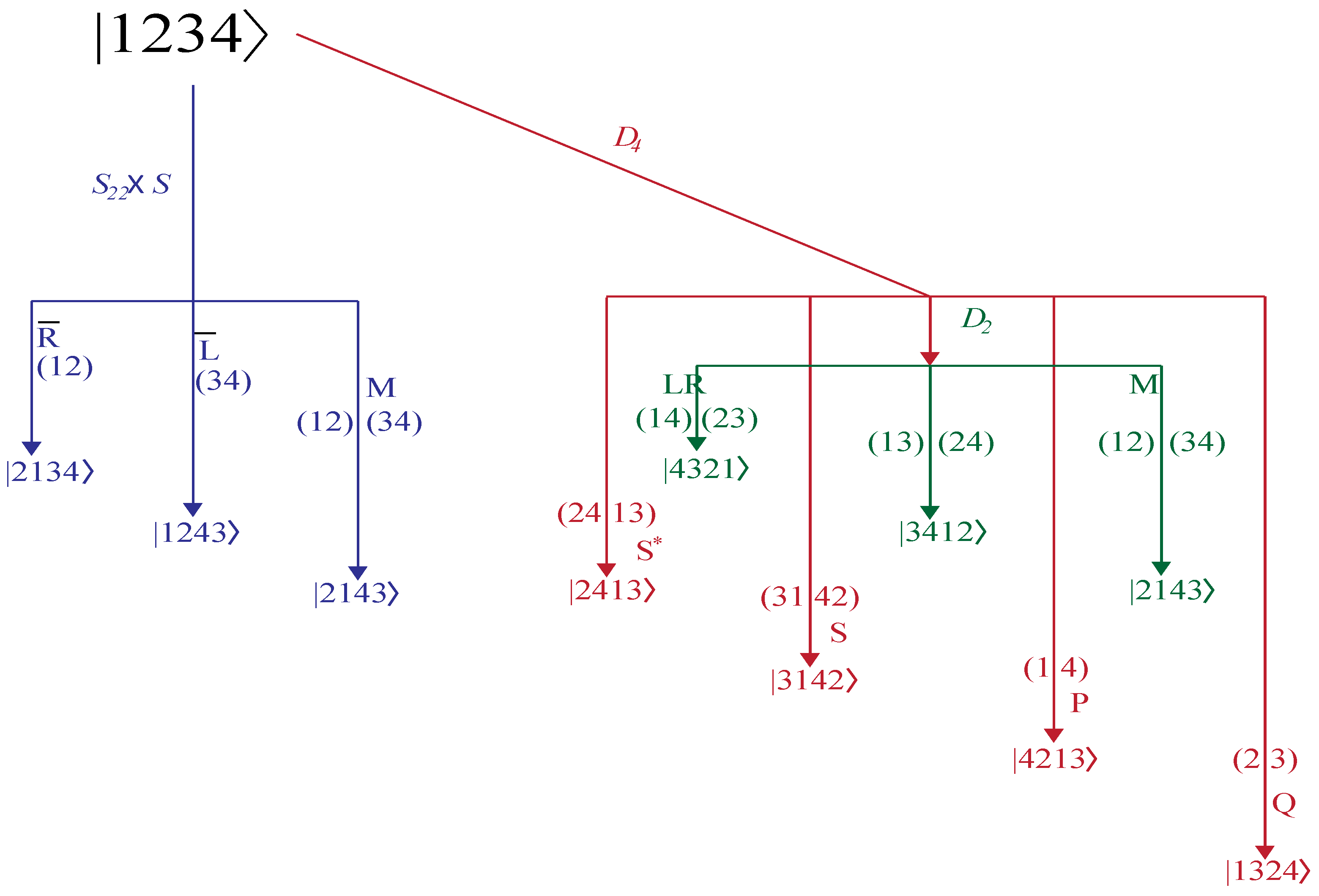
.2.2. (ABC) Operators and Nuclear Exchange Symmetry
2.3. Theory of ABC Symmetry Selection

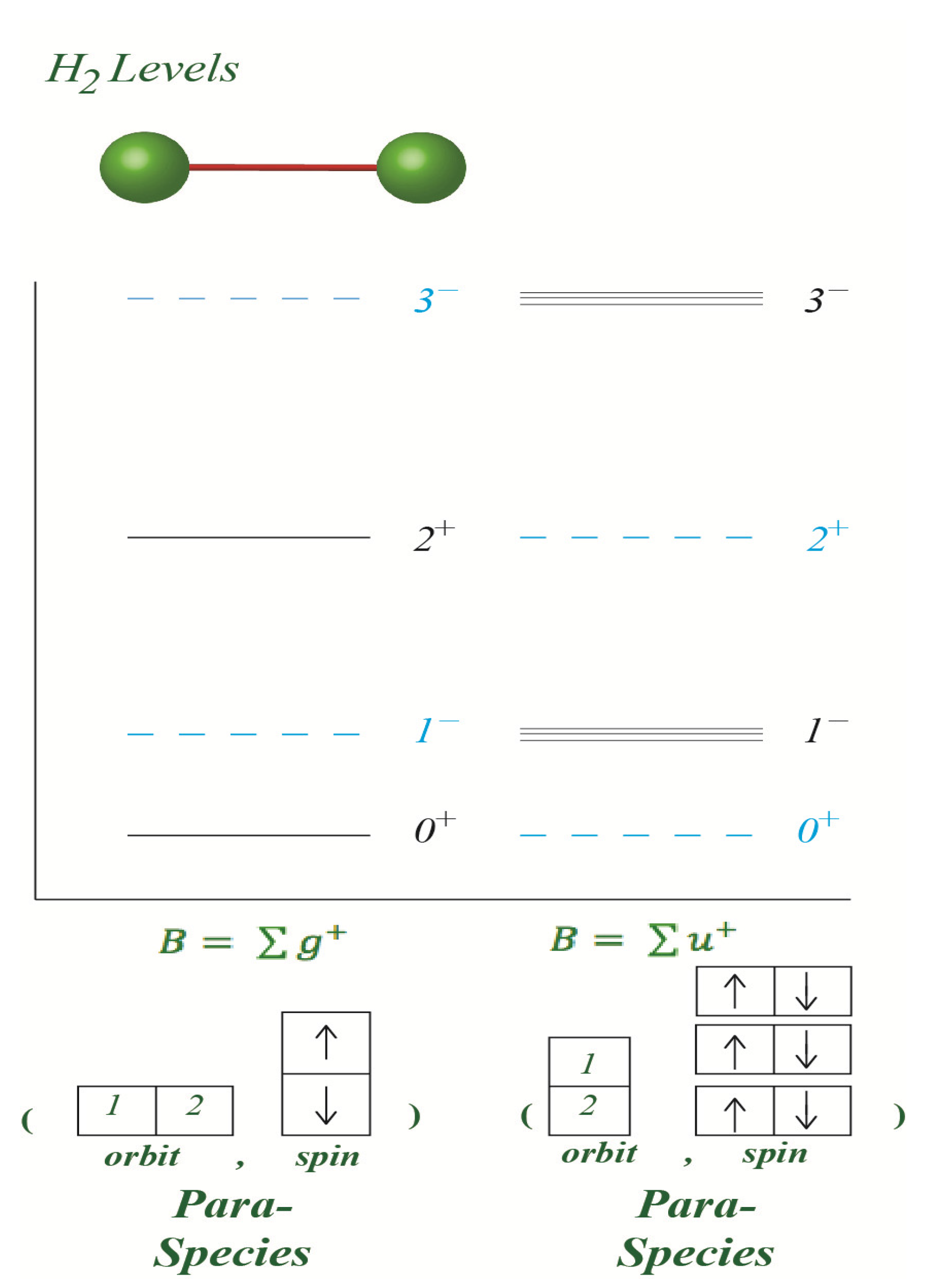
3. Spin Statistical Weights
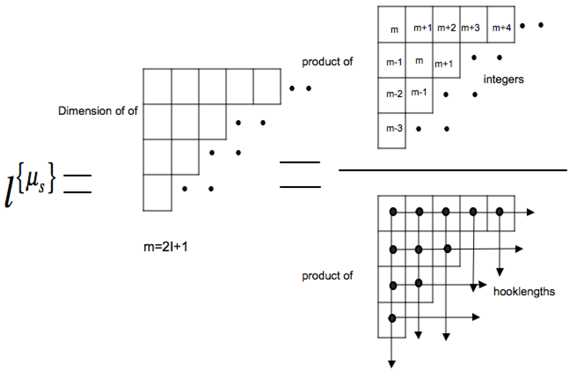
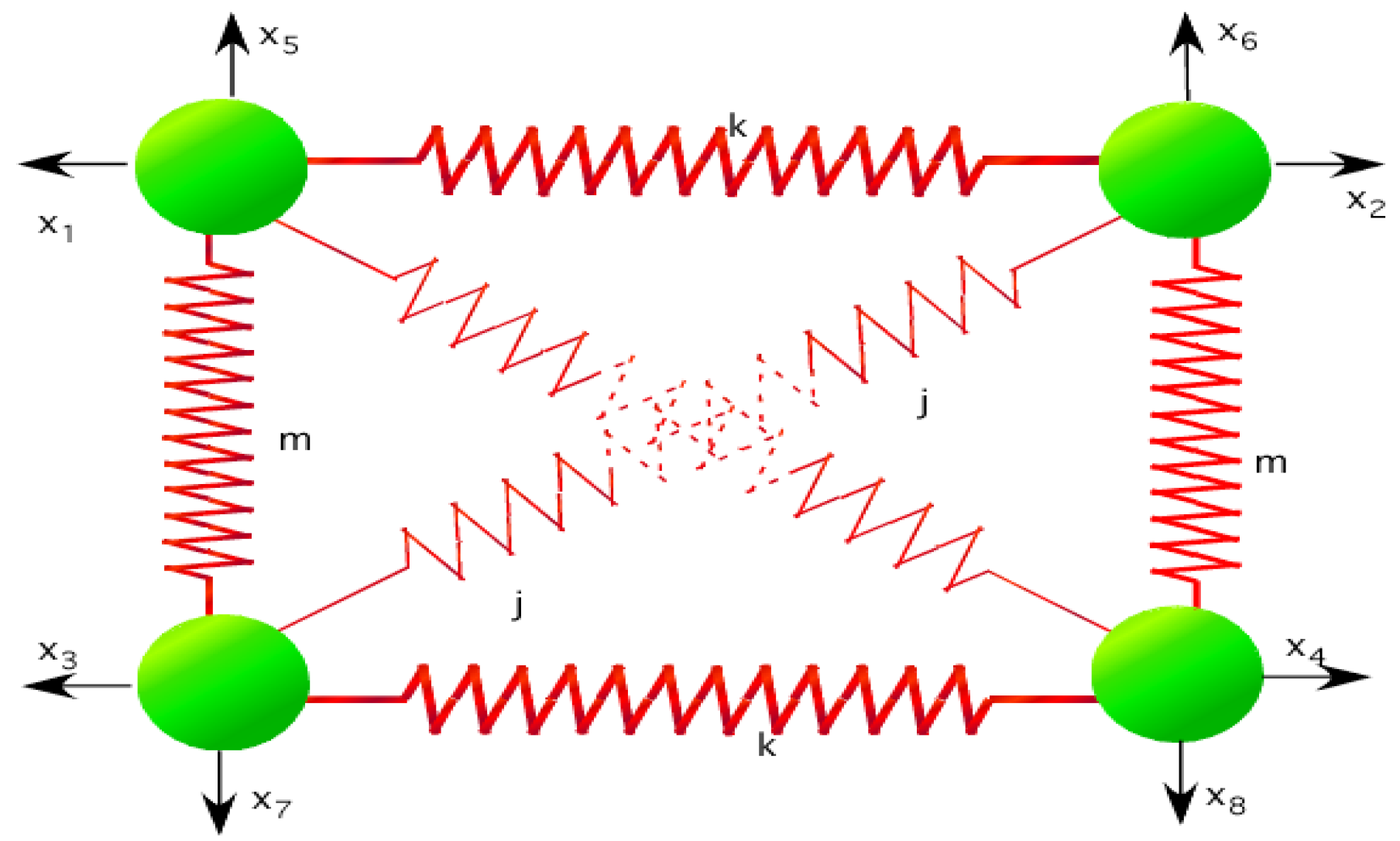
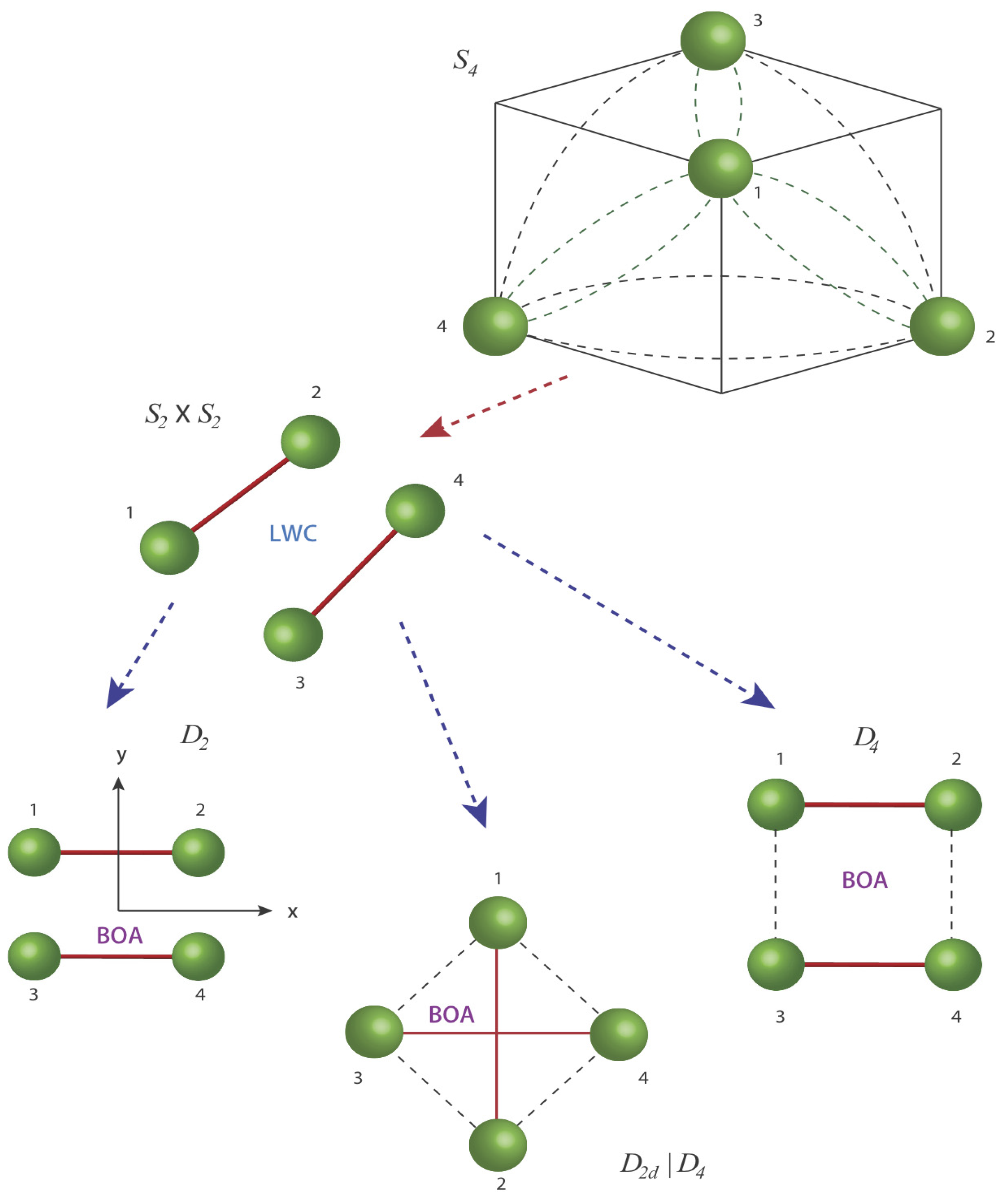
4. Coupling between Two Diatomic Molecules
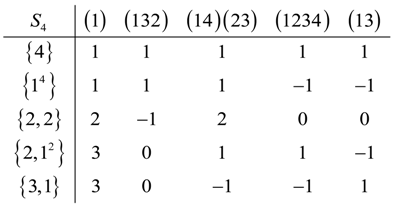

4.1. Point Group
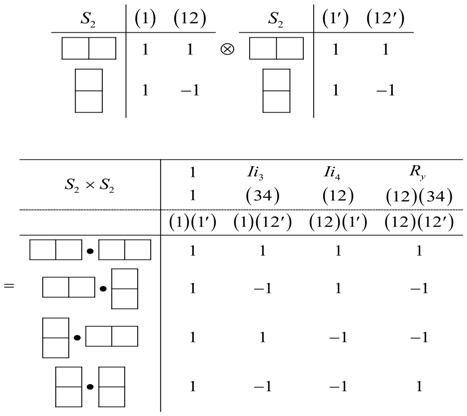
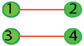 where the numbers label the position of the atoms of the molecules. Under the operation (34), the previous configuration changes to
where the numbers label the position of the atoms of the molecules. Under the operation (34), the previous configuration changes to 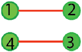 .
.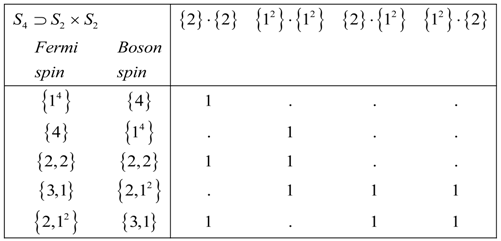
4.2. Statistical Weight
 ,
,  , and
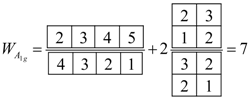
, and  . The Frobenius Reciprocity theorem gives the correlation frequencies and using Equations (20a) and (20b) we compute the statistical weight for to be,
. The Frobenius Reciprocity theorem gives the correlation frequencies and using Equations (20a) and (20b) we compute the statistical weight for to be, 
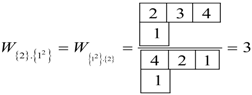
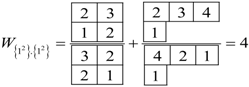
4.3. Point Group
 . This operator works by inverting the spatial coordinates of all nuclei through the center of mass. The overall symmetry of configuration is the outer product of and that is contains three 180° degrees rotations about the xyz axes, an I inversion, a horizontal refection , and two vertical planes (), . The character table for symmetry group is given by Equation (27).
. This operator works by inverting the spatial coordinates of all nuclei through the center of mass. The overall symmetry of configuration is the outer product of and that is contains three 180° degrees rotations about the xyz axes, an I inversion, a horizontal refection , and two vertical planes (), . The character table for symmetry group is given by Equation (27).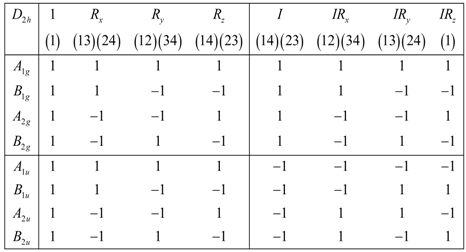
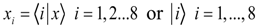
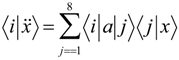




4.4. Statistical Weight for

4.5. . Point Group

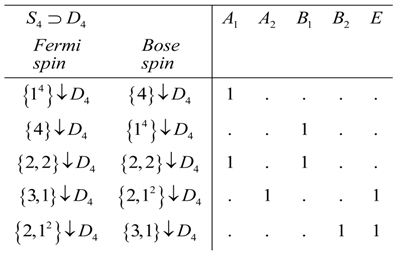
4.6. Statistical Weight for

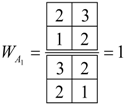
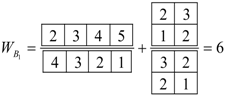
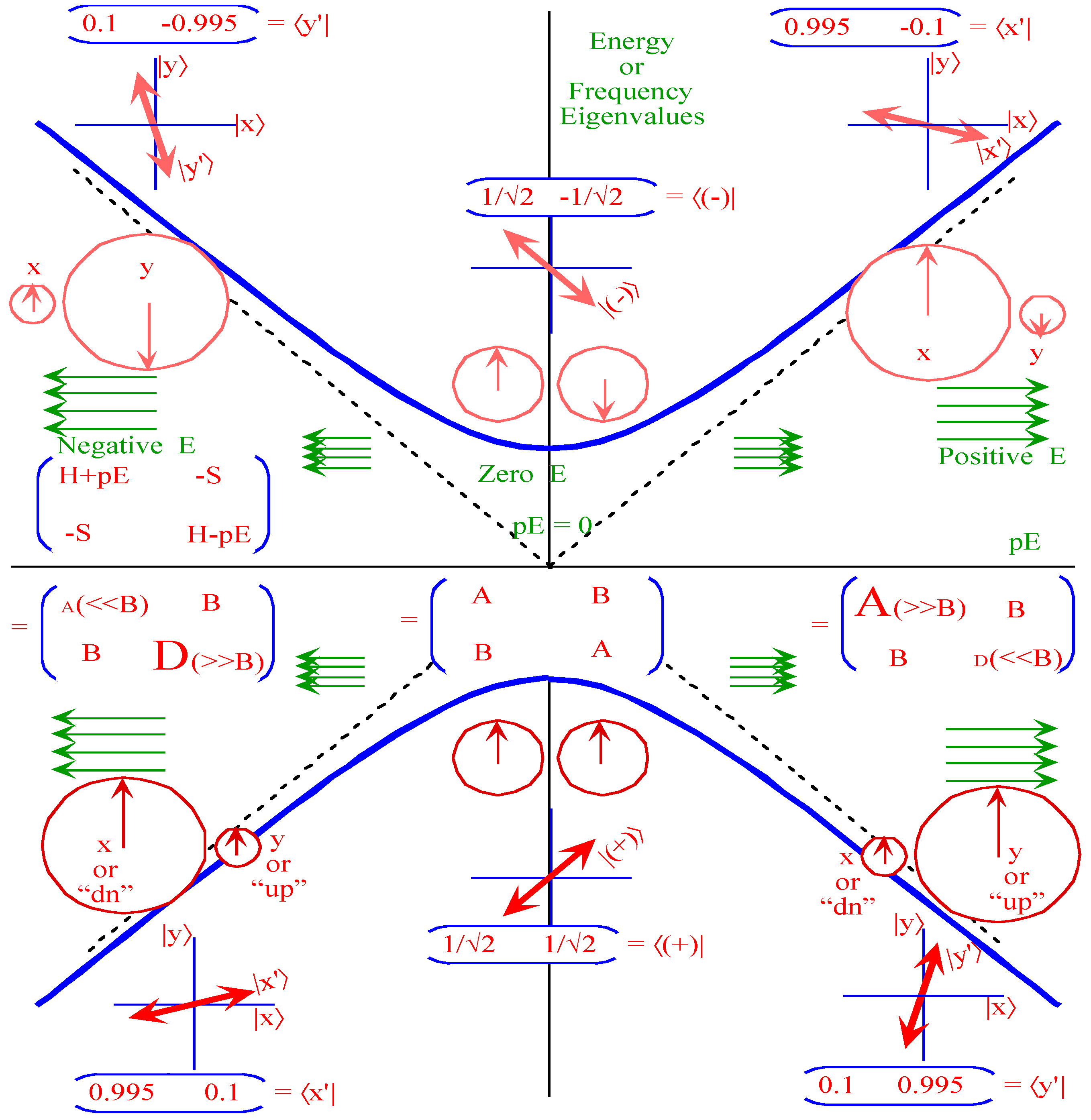
5. Tunneling Hamiltonians
5.1. Tunneling Hamiltonian for Point Symmetry
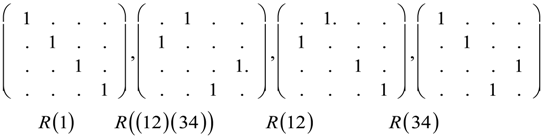


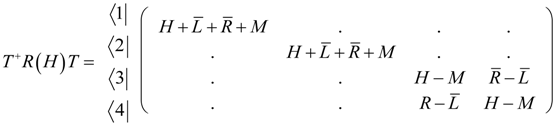
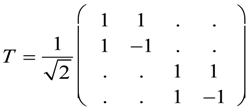
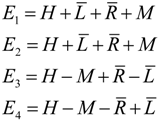
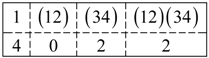
5.2. Tunneling Hamiltonian for D2 Point Symmetry
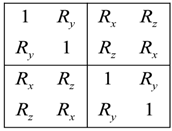

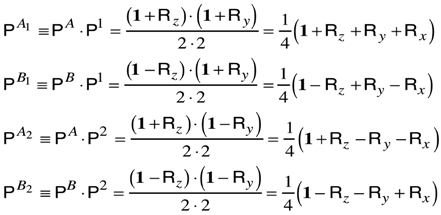
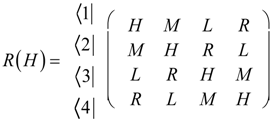

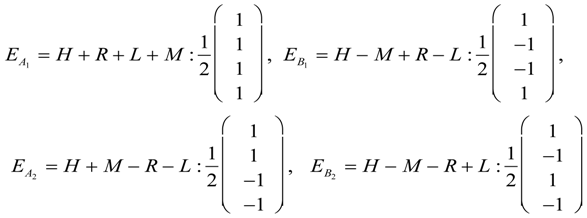
5.3. Tunneling Hamiltonian for Point Symmetry



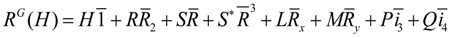

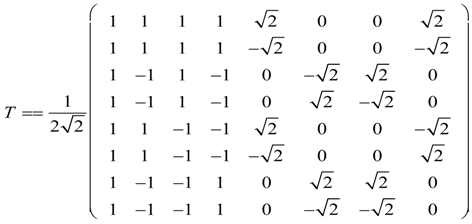

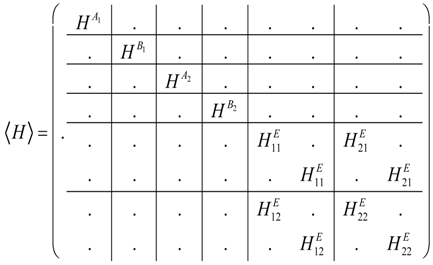
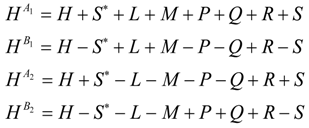
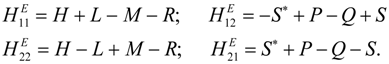
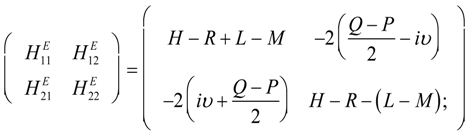

6. Conclusions
Acknowledgments
References
- Young, A. On quantitative substitutional analysis IX. Proc. Lond. Math. Soc. 1952, 54, 219–253. [Google Scholar] [CrossRef]
- Yamanouchi, T. On the construction of unitary irreducible representation of the symmetric group. Proc. Phys. Math. Soc. Jpn. 1937, 19, 436–450. [Google Scholar]
- Yamanouchi, T. The Application of the Rotational Group and Symmetric Group; Beijing Science Press: Beijing, China, 1966. [Google Scholar]
- Littlewood, D.E. The Theory of Group Characters and Matrix Representations of Groups; Oxford Press: Oxford, UK, 1950. [Google Scholar]
- Gel’fand, M.I. The center of an infinitesimal group algebra. Mat. Sb. 1950, 26, 103–112. [Google Scholar]
- Gel’fand, M.I. Matrix elements for the unitary groups. Dokl. Akad. Nauk. 1950, 71, 825–828. [Google Scholar]
- Gel’fand, M.I. Representations of the Rotation and Lorentz and Their Applications; Pergamon Press: New York, NY, USA, 1963. [Google Scholar]
- Shur, I. Neue anwendungen der Intergralrechnung auf Probleme der Invariantentheorie; Sitzungsberichte Akademie der Wissenschaften: Berlin, Germany, 1924; pp. 189–208. [Google Scholar]
- De Beauregard Robinson, G. Representation Theory of the Symmetric Group; University of Toronto Press: Toronto, Canada, 1960. [Google Scholar]
- Coleman, A.J. Induced Representations and Applications; Queens University Press: Kingston, Ontario, Canada, 1971. [Google Scholar]
- Harter, W. Theory of hyperfine and super levels in symmetric polyatomic molecules. II Elementary cases in octahedral hexafluoride molecules. Phys. Rev. A 1981, 24, 192–263. [Google Scholar] [CrossRef]
- Harter, W.G.; Patterson, C.W.; da Paixao, F.J. Frame transformation relations and multiple transitions in symmetric polyatomic molecules. Rev. Mod. Phys. 1978, 50, 37–83. [Google Scholar] [CrossRef]
- Harter, W.; Patterson, C.W. Theory of hyperfine and super levels in symmetric polyatomic molecules. Trigonal and tetrahedral: Elementary spin ½ cases vibronic ground states. Phys. Rev. A 1979, 19, 2277–2303. [Google Scholar] [CrossRef]
- Streater, R.F.; Wightman, A.S. PCT, Spin and Statistics, and All That; Princeton University Press: Princeton, NJ, USA, 1964. [Google Scholar]
- Longuet-Higgins, H.C. The symmetry groups of non-rigid molecules. Mol. Phys. 1963, 6, 445–460. [Google Scholar] [CrossRef]
- Hougen, J.T. Classification of rotational energy levels for symmetric—Top molecules. J. Chem. Phys. 1962, 37, 1433–1441. [Google Scholar] [CrossRef]
- Harter, W.G. Alternative basis for the theory of complex spectra. Phys. Rev. A 1973, 8, 2819–2827. [Google Scholar] [CrossRef]
- Harter, W.G.; Patterson, C.W. Alternative basis for the theory of complex spectra. II. Phys. Rev. A 1976, 13, 1067–1082. [Google Scholar] [CrossRef]
- Patterson, C.W.; Harter, W.G. Canonical symmetrization for unitary bases. I. Canonical Weyl bases. J. Math. Phys. 1976, 17, 1125–1136. [Google Scholar] [CrossRef]
- Harter, W.G.; Patterson, C.W. Simple model for asymptotic level clusters in SF6 rotational spectra. Phys. Rev. Lett. 1977, 5, 224–227. [Google Scholar] [CrossRef]
- Harter, W.G.; Weeks, D.E. Rotation-vibration spectra of icosahedral molecules. I. Icosahedral symmetry analysis and fine structure. J. Chem. Phys. 1989, 90, 4727–4743. [Google Scholar] [CrossRef]
- Harter, W.G.; Patterson, C.W. Alternative basis for the theory of complex spectra. III. Phys. Rev. A 1976, 15, 2372–2379. [Google Scholar]
- Bunker, P.R.; Jensen, P. Molecular Symmetry and Spectroscopy, 2nd ed.; NRC Research Press: Ottawa, Canada, 1998. [Google Scholar]
- Groner, P. Effective rotational Hamiltonian for molecules with two periodic large-amplitude motions. J. Chem. Phys. 1997, 107, 4483–4498. [Google Scholar] [CrossRef]
- Crogman, H.T.; Harter, W.G. Frame transformation relations for fluxional symmetric rotor dimmers. J. Chem. Phys. 2004, 121, 9297–9312. [Google Scholar] [CrossRef] [PubMed]
- Chang, E.S.; Fano, U. Theory of electron-molecule collisions by frame transformations. Phys. Rev. A 1972, 6, 173–185. [Google Scholar] [CrossRef]
- Junger, C.H. Highly excited molecular states: Quantum defect and ab initio theory. Proceedings of International Symposium on Molecular and Spectroscopy, Ohio State University, Columbus, OH, USA, 16–20 June 2003. [Google Scholar]
- Junger, C.H.; Atabek, O. Rovibronic interactions in the photoabsorption spectrum of molecular hydrogen and deuterium: An application of multichannel quantum defect methods. J. Chem. Phys. 1976, 66, 5584–5609. [Google Scholar] [CrossRef]
- Chen, J.Q. Group Representation Theory for Physicist; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1989. [Google Scholar]
- Kung, P.S.J. Young Tableaux in Combinatorics Invariant Theory and Algebra; Academic Press: University of Michigan, Ann Arbor, MI, USA, 1982. [Google Scholar]
- Lemus, R. A general method to obtain vibrational symmetry adapted bases in a local scheme. Mol. Phys. 2003, 101, 2511–2528. [Google Scholar] [CrossRef]
- Crogman, H.T. A rotational energy surface study for low polyad structures of the general rovibrational Hamiltonian. Mol. Phys. 2010, 108, 705–721. [Google Scholar] [CrossRef]
- Crogman, H.T.; Harter, W.G. The emergence of a single frame and effects on quantum states and levels for rotor-rotor interactions. Proceedings of 59th Ohio State University International Symposium on Molecular Spectroscop, Ohio State University, Columbus, OH, USA, 21–24 June 2004. [Google Scholar]
- Hougen, J.T. Classification of rotational energy levels. II. J. Chem. Phys. 1971, 39, 358–365. [Google Scholar] [CrossRef]
- Alvarez-Bajo, O.; Lemus, R.; Carvajal, M.; Perez-Bernal, F. Equivalent rotations associated with the permutation inversion group revisited: Symmetry projection of the rotational functions of methane. Mol. Phys. 2011, 109, 797–812. [Google Scholar] [CrossRef]
- Lederer, C.M.; Hollander, J.M.; Perlman, I. Table of Isotopes, 6th ed.; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Hougen, J.T.; Merer, A.J. Extended permutation-inversion groups for simultaneous treatment of the rovibronic states of trans-acetylene, cis-acetylene, and vinylidene. J. Mol. Spectrosc. 2011, 267, 200–221. [Google Scholar] [CrossRef]
- Harter, W.G. The Quantum Computer Age; University of Arkansas: Fayetteville, NC, USA, 2004. [Google Scholar]
- Harter, W.G. Principle of Symmetry, Dynamics & Spectroscopy; Wiley: New York, NY, USA, 1993. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Crogman, H.T.; Choi, B.; Chen, H.B.; Harter, W.G. Frame Transformation Relations and Symmetry Analysis of Fluxional Symmetric Rotor Dimers. Symmetry 2013, 5, 86-118. https://doi.org/10.3390/sym5010086
Crogman HT, Choi B, Chen HB, Harter WG. Frame Transformation Relations and Symmetry Analysis of Fluxional Symmetric Rotor Dimers. Symmetry. 2013; 5(1):86-118. https://doi.org/10.3390/sym5010086
Chicago/Turabian StyleCrogman, Horace T., Bumgyunmiga Choi, Harrison B. Chen, and William G. Harter. 2013. "Frame Transformation Relations and Symmetry Analysis of Fluxional Symmetric Rotor Dimers" Symmetry 5, no. 1: 86-118. https://doi.org/10.3390/sym5010086
APA StyleCrogman, H. T., Choi, B., Chen, H. B., & Harter, W. G. (2013). Frame Transformation Relations and Symmetry Analysis of Fluxional Symmetric Rotor Dimers. Symmetry, 5(1), 86-118. https://doi.org/10.3390/sym5010086