Analyzing Fluctuating Asymmetry with Geometric Morphometrics: Concepts, Methods, and Applications
Abstract
: Approximately two decades after the first pioneering analyses, the study of shape asymmetry with the methods of geometric morphometrics has matured and is a burgeoning field. New technology for data collection and new methods and software for analysis are widely available and have led to numerous applications in plants and animals, including humans. This review summarizes the concepts and morphometric methods for studying asymmetry of shape and size. After a summary of mathematical and biological concepts of symmetry and asymmetry, a section follows that explains the methods of geometric morphometrics and how they can be used to analyze asymmetry of biological structures. Geometric morphometric analyses not only tell how much asymmetry there is, but also provide information about the patterns of covariation in the structure under study. Such patterns of covariation in fluctuating asymmetry can provide valuable insight about the developmental basis of morphological integration, and have become important tools for evolutionary developmental biology. The genetic basis of fluctuating asymmetry has been studied from empirical and theoretical viewpoints, but serious challenges remain in this area. There are many promising areas for further research that are only little explored at present.1. Introduction
Studies of fluctuating asymmetry have long primarily used measurements of lengths or perhaps angles on the left and right sides of organisms [1–6]. More recently, however, many new tools have been developed in the field of geometric morphometrics [7–10], including methods for studying asymmetry of shape [11–14]. These methods have been used increasingly for studies of fluctuating asymmetry in a wide range of organisms.
To some extent, the results from asymmetry studies using geometric morphometrics have confirmed the findings from studies with traditional morphometric methods focusing on length measurements and similar measures of size [2–5]. In other instances, however, the results from analyses of shape asymmetry differ considerably from those of size asymmetry. For instance, studies of size measurements have found directional asymmetry only sporadically, whereas directional asymmetry for shape appears to be nearly ubiquitous in all animals that have been examined in sufficiently large studies [15].
Geometric morphometric methods have also brought some significant conceptual changes and additions to the field. Geometric morphometrics is therefore not just a set of new analytical tools to address the same questions that have always been the focus of asymmetry studies, but they have led investigators to ask new questions and to use fluctuating asymmetry in new research contexts, most notably for the study of developmental integration [11,16,17].
This article is a survey of geometric morphometric studies of fluctuating asymmetry. It reviews the concepts and methods that underlie these studies and compiles some of the results that have emerged from them.
2. Symmetry
Before considering asymmetry, it is helpful to think briefly about symmetry, because asymmetry is simply a deviation from symmetry. Symmetry of biological structures can be defined as the repetition of parts in different positions and orientations to each other. Such symmetry is a fundamental feature of the body plans of most organisms and of many of their parts.
Most animals are bilaterally symmetric, with left and right sides that are mirror images of each other. Bilateral symmetry, however, is not the only type of symmetry in biological structures. In particular, plants show a wide variety of different kinds of symmetries in flowers and other organs [18–21]. This section gives a brief overview of some of this diversity and provides the fundamental concepts concerning symmetry that will be used throughout the paper.
2.1. Types of Symmetry in Biological Structures
Because symmetry of morphological structures is the repetition of parts in different positions and orientations, it is useful to consider the number and arrangement of repeated parts as a way to understand the different types of symmetry. For instance, the familiar bilateral symmetry of most animals is associated with the repetition of parts as pairs, located on the left and right sides as mirror images of each other. For each pair of parts, a reflection about the median plane maps the left part onto the right part and vice versa. Therefore, this reflection about the median plane is fundamentally important for bilateral symmetry and can be used to characterize it.
Other types of asymmetry are based on different arrangements of parts (Figure 1). Because these types of symmetry usually are more complex than bilateral symmetry, for instance because most include more than two parts, they are subsumed under the umbrella term “complex symmetry”—any type of symmetry other than bilateral symmetry. This term is useful because structures with complex symmetry require special methods for morphometric analysis [14], which are a generalization of the simpler methods routinely used for bilateral symmetry [11–13].
Reflection is not only important for bilateral symmetry, but also occurs in various types of complex symmetry. Disymmetry or biradial symmetry, where there are two perpendicular axes or planes of symmetry, is another type of symmetry that is widespread, for instance, in unicellular algae (Figure 1a) [22–24] or in many flowers, particularly in the Brassicaceae [25–29]. The two axes of symmetry can be different in developmental and functional aspects (left–right axis versus dorsal–ventral or adaxial–abaxial axes), which can be a focus of specific interest [23,24,27].
Rotation is also involved in many symmetries, either alone, as in the rotational or “pinwheel” symmetry of some flowers (Figure 1b) or in combination with reflection, so that each of the parts is mirror-symmetric, as in the familiar radial symmetry of many flowers or in some invertebrate animals such as sea urchins and jellyfish. Each rotation has a center or axis and each rotation has an order, the number of repetitions of parts that are arranged around a full circle (e.g., Figure 1b shows a rotation of order 5, or 72° per step).
A further possible arrangement is the repetition of parts along an axis, with a translation as the change between the repeated parts. Such translational symmetry is perhaps more familiar to biologists under the name serial homology. It occurs widely in the body plans of many animals that show segmentation in some form (e.g., the spine of vertebrates, Figure 1c) and also in many plants, where leaves and other organs are repeated along shoots. In these examples, translation is often combined with rotation or reflection.
Spiral symmetries, where rotation and translation occur together with an expansion, is another type of symmetry that is frequently seen in morphological structures (e.g., the shells of snails and other mollusks, Figure 1d). These examples are not a complete enumeration of the many symmetries that are found in morphological structures, but they represent the most widespread types and therefore are useful as an overview of the most important types.
2.2. Mathematics of Symmetry
There is an extensive and powerful mathematical theory concerning symmetry [30–33], which is crucial for understanding complex symmetries. This theory offers a formal definition of symmetry that relates closely to the ideas used intuitively in the preceding introduction of complex asymmetries.
In particular, transformations play an important role in this theory. A transformation maps every point of an object onto some point in the plane or space of the object and is reversible (there is a transformation that can undo the effect of the first one; this is a one-to-one relation between the points before and after applying the transformation). Transformations with particular interest for symmetry are reflection, rotation and translation, which define the arrangement of repeated parts in a symmetric structure (Figure 1). Also, a further transformation that is quite important is the identity, the transformation that leaves every point unchanged (it could also be described as a rotation by 360° or as the result of two reflections about the same axis or plane).
An object is symmetric if a transformation leaves the object unchanged. For instance, reflection about the median plane leaves a bilaterally symmetric structure unchanged. Similarly, in Figure 1b, a rotation by 72° (or by 144° or 216° …) leaves the flower looking the same. The transformations that leave the object unchanged are called its symmetry transformations.
The symmetry of an object can be characterized by the set of all its symmetry transformations. This is a set with some special properties, called a group, and therefore is called the symmetry group. Each type of symmetry has its characteristic symmetry group [30–33].
One of the properties of symmetry groups is that the result of combining two transformations in the group (or also just one with itself) is also a transformation contained in the symmetry group. For instance, if we combine a rotation by 72° and one by 144°, the resulting rotation by 216° must also be in the symmetry group. For this example with rotation of order 5, it follows that the symmetry group will contain the rotations by 72°, 144°, 216°, 288° and by 360° (or 0°, the identity). In this case, once we have come full circle, any further combinations will just yield rotations already included in the set, so these five rotations are sufficient for the symmetry group.
For bilateral symmetry, the symmetry group clearly contains the reflection about the median plane. If we combine this reflection with itself, that is, if we perform the reflection twice in a row, the result is the original position. Therefore, the symmetry group for bilateral symmetry contains the refection and the identity.
Symmetry groups can also combine rotations and reflection. The symmetry group of the equilateral triangle is such an example (Figure 2). In this case, the rotation is of order 3, or by 120°, which means that the symmetry group also includes rotations by 240° and by 360° (or 0°, the identity again). Each of these rotations can further be combined with a reflection (Figure 2; this changes whether the corners of the triangle are labeled in clockwise or counter-clockwise order). Because each rotation can either occur with or without the reflection, the symmetry group includes six transformations in total (Figure 2).
Note that not all symmetry groups have a finite number of transformations, where there is only a certain set of symmetry transformations, and combining these transformations in any conceivable way always yields transformations already included in that set. Consider the example of Figure 1c, the translation symmetry of the spine, there the possible transformations are moving forward by one vertebra or moving backward by one vertebra. If we repeatedly apply one of these, we never return to the same transformation because we always can add one more step, and then another and another. Of course, in the example (Figure 1c) we’ll run out of vertebrae at either the anterior or posterior end of the spine, but that only tells us that the spine as a whole is not really symmetric under translations. Symmetry groups involving translation contain an infinite number of symmetry transformations. The same applies to spiral symmetry: in the nautilus shall (Figure 1d), it is possible to start at the center and then step along the spiral of the shell from chamber to chamber, but this sequence never ends because it could always be repeated one more time. The distinction between these finite and infinite symmetry groups is relevant for morphometric studies, namely, to determine which kinds of analyses can be used for different types of symmetry.
2.3. Matching Symmetry and Object Symmetry
For the analysis of asymmetry of shape, it is useful to make a further distinction between two kinds of symmetry or, perhaps more helpfully, two perspectives on symmetry. First, there is the type of symmetry where a structure is present as two separate copies, one on each side of the body, which are mirror images of each other. Familiar examples of this type of symmetry are human hands or insect wings (Figure 3a). The axis or plane of symmetry runs between the two copies, but is not part of either copy. As a result, the arrangement of the two parts relative to each other is not an aspect of their symmetry. This type of symmetry is called matching symmetry [12,13], because the left and right copies can be moved and matched to each other, for instance, by putting the palms of the left and right hands together.
The alternative is object symmetry, where the object of interest is symmetric in itself [12,13]. For instance, the human face is symmetric because its left and right halves are mirror images of each other (Figure 3b). For structures with object symmetry, the axis or plane of symmetry runs through the structure. Therefore, the relative arrangement of the two halves is an integral aspect of the symmetry of the whole structure.
This distinction has important implications for analyses of asymmetry. For matching symmetry, the possibility of matching together the left and right copies also offers a straightforward method for characterizing asymmetry: try to match the left and right copies together as well as possible, and the remaining differences are due to asymmetry. For object symmetry, the situation is slightly more complex because the left and right halves must be compared as part of the whole structure, but an elegant method uses a superimposition of the original and a mirror-image copy of the object for characterizing symmetry and asymmetry (Section 4.3, below). Object symmetry is important for morphometric studies even if asymmetry is not the focus of interest, because left and right halves of the structure are interdependent, which potentially can cause problems for analyses [34]. For structures with object symmetry, investigators therefore should always use methods that take the symmetry into account [12,13].
Distinguishing matching symmetry and object symmetry is easy in most cases. The key question is whether the median axis or plane is passing between the left and right halves so that it leaves them free to move relative to each other, or whether it goes through the structure so that the two halves are linked together solidly. Usually, this question is easy to answer and it is thus clear which type of analysis should be used. In rare cases, however, both analyses can be informative in combination—for addressing some specific question in studies of asymmetry, it can be useful to conduct analyses for object symmetry for the whole structure and separate analyses for matching symmetry of the halves [35].
The distinction between matching and object symmetry is particularly important for how size differences between the left and right sides are treated. For matching symmetry, a difference in the size of left and right copies results in an asymmetry for centroid size, but it has no necessary implication for the asymmetry of shape, unless they happen to be correlated. The asymmetries of size and of shape are two logically separate issues, which can be addressed in separate analyses. By contrast, for structures with object symmetry, a difference in size between the left and right halves is an aspect of the shape of the whole structure (e.g., imagine that one half of the face in Figure 3b is smaller than the other: this difference will be an feature of shape of the whole face). For object symmetry, because the entire configuration is considered as a whole and not as the two halves separately, all asymmetries between the left and right halves are aspects of shape of the whole configuration [13]. For this reason, studies of asymmetry in structures with matching symmetry normally carry out separate analyses of asymmetry for centroid size and for shape, whereas studies in structures with object symmetry conduct analyses of asymmetry only for shape.
I have focused on bilateral symmetry to introduce matching and object symmetry, but both apply as well for complex symmetries [14]. Matching symmetry applies to all possible types of symmetry. It consists of considering the repeated parts that make up the structure separately, without considering their relative arrangement to one another. For instance, for studying the symmetry and asymmetry in a flower, an analysis of matching symmetry might divide the flower into its petals and then analyze the similarities and differences among petals. By contrast, object symmetry considers the structure as a whole, including the relative arrangement of parts. For the flower example (Figure 1b), an analysis of object symmetry would consider the flower as a whole and the relative positions of the petals would be important aspects of symmetry and asymmetry. The flower in this example is symmetric as a whole because a rotation by 72°, or by a multiple of 72°, leaves the flower unchanged. Likewise, the algal cell in Figure 1a has object symmetry because reflections about either the vertical or horizontal axes (or the combination of both reflections, a rotation by 180°) leave the cell unchanged. Whereas the perspective of matching symmetry is feasible for all possible types of symmetry, there are some types of symmetry for which object symmetry is not applicable, namely the symmetries that have infinite symmetry groups [14]. In practice, this means that analyses of object symmetry are not possible for symmetries like translational or spiral symmetry (Figure 1c,d): there are clearly problems with the comparisons at the ends of the spine or shell. For these types of symmetry, matching symmetry is the only available approach.
3. Distributions of Asymmetry
Traditionally, three types of asymmetry have been distinguished according to the distribution of left–right differences in a population: directional asymmetry, fluctuating asymmetry, and antisymmetry (Figure 4) [1,2]. These types most often have been applied in analyses of scalar measurements, for instance lengths, angles, or counts of structures such as bristles, but they can be applied similarly to multidimensional features such as shape. In a seminal paper that laid the foundation for many modern studies of asymmetry, including this distinction, Van Valen (page 126 in [1]) stated clearly that these three types of asymmetry are not mutually exclusive categories, but can occur together in the same trait.
Directional asymmetry, fluctuating asymmetry and antisymmetry are observable patterns in the distribution of left–right differences in populations of organisms. Because three types of asymmetry are defined in a population, not for single individuals, identifying and separating the three categories requires measurements of many individuals. The types of asymmetry have different statistical properties as well as distinct biological origins and implications.
It is also worth remembering that these patterns of asymmetry are observable manifestations of biological processes, but that they are not the processes themselves. Inference from the patterns of asymmetry to biological processes is very limited and usually requires additional evidence.
In keeping with the bulk of the literature on shape asymmetry, most of the discussion in this section will focus on bilateral asymmetry, which is much more widespread than any of the types of complex asymmetry. The general concepts, nevertheless, apply to complex symmetry in the same way. Some special aspect of morphometric analyses of complex symmetry will be discussed below in a special section, which will also provide an overview of empirical results from studies of this kind (Section 4.6).
3.1. Directional Asymmetry
Directional asymmetry is a tendency for a trait to be consistently developed in different manners on the left and right body sides. Directional asymmetry can be quantified by the difference between left and right averages. The difference between left and right sides may be large or small, but the average left–right difference differs from zero.
The prime example of directional asymmetry is the arrangement of internal organs in most animals, including humans, where the heart is on the left side, the intestine is coiled in a constant and asymmetric manner, and other organs such as the lungs or liver are also asymmetric in a consistent way. The mirror-image arrangement of all internal organs, situs inversus, is rare in humans and heterotaxy, or situs ambiguus, is also a rare condition in humans where only some but not all internal organs occur in mirror-image orientation and is associated with malformations and causes serious morbidity or mortality in affected persons [36].
Most traits assessed by traditional morphometric methods have shown no significant directional asymmetry, so that it was long considered a phenomenon that sporadically occurs in some traits, but is not a regular feature of many organisms [2]. Occasionally, directional asymmetry has been reported for various linear measurements in diverse animals including insects [37] or humans [38,39].
With the advent of geometric morphometric methods in the 1990s, subtle but statistically significant directional asymmetry has been found virtually in every early study of shape asymmetry [11,40,41] and has been recognized as a real and possibly widespread phenomenon [15]. More recently, dozens of studies in a wide range of different animal taxa have found statistically significant directional asymmetry of shape [13,16,42–110]. Even in snails where morphs with opposite directions of shell coiling occur within populations, a subtle directional pattern of asymmetry is superimposed on the dimorphism, because the average shell shapes of the two morphs are not precise mirror images of each other [111–114]. Therefore, just as conspicuous directional asymmetry of internal organs is near-ubiquitous among bilaterian animals, it seems that, for a wide range of animals, even structures that seem superficially symmetric show a subtle directional asymmetry of shape.
There appear to be remarkably few exceptions to this pattern. A few studies of shape in Drosophila found no significant directional asymmetry of wing shape [115–119] or mixed results [120–126], although a series of other studies did find it [15,16,54,56,62,77,85,123]. Similarly, one study on human skulls [127] found no directional asymmetry of shape, whereas several others reported directional asymmetry of the skull [47,68,84,86,90,94,109] and soft tissues of the face and ears [38,66,98,104,105,108]. Further non-significant results were reported from mites [128] and wings of Trichogramma egg parasitoids [129]—but both studies reported results only from relatively small subsamples (≤30 specimens per sample) and tiny organisms, raising questions about statistical power and possible artifacts from mounting very small specimens. Further negative results come from two datasets of wings from Chironomus midges [116], whereas other studies found mixed results for wings and larval mouthparts [103,130,131]. Some studies, in a variety of species, have found mixed results, with some structures or subgroups yielding significant results, but others not [132–138]. Because these studies with negative results are relatively few and some are based on relatively small samples, the question arises whether negative results really indicate the absence of directional asymmetry or whether they result from limitations of statistical power. Yet, there are other studies where negative results might reflect differences in the biology of those organisms. A study of two parts of the predatory appendage of a mantis shrimp, carried out separately in males and females, found that only one of the four tests showed marginally significant directional asymmetry [139]. It is unclear whether this may relate to the sometimes accentuated antisymmetry of crustaceans [140], although no evident antisymmetry appears to occur in mantis shrimp. Overall, the vast majority of studies using geometric morphometric methods indicate that subtle, but measurable directional asymmetry of shape is very widespread in the animal kingdom.
Directional asymmetry requires systematic developmental differences between the left and right sides. Such differences have been investigated extensively for the conspicuous directional asymmetries of internal organs that exist in most phyla of bilaterian animals, and a variety of molecular mechanisms have been found that can establish an initial distinction between left and right sides and transmit this information to developing organs [141–144]. Some of the mechanisms and the genes involved in producing directional asymmetry of internal organs seem to be highly conserved, suggesting that left–right asymmetry is an ancestral feature of bilaterian animals [141–144]. Clearly, with changes in body plans during evolution of different animal clades, the expression of directional asymmetry has changed as well. But it is plausible that developing organs in most animals possess the mechanisms necessary to sense on which body side they are positioned and can modulate development accordingly, potentially producing directional asymmetry. This directional asymmetry of shape may be conspicuous or it may require measurement and analysis with powerful statistical methods to be detected, but according to the available results it is very widespread. The possible functional and adaptive significance of directional asymmetry is unclear [15,145,146] and it is conceivable, for instance, that the subtle directional asymmetry of many external structures is a non-adaptive consequence of developmental constraints relating to the conspicuous directional asymmetry of internal organs.
By contrast to animals, there are only few studies that use geometric morphometric methods to study asymmetry in plants. There are some reports of directional asymmetry of leaf shape [147], but there are also examples where no directional asymmetry was found [148]. Also, directional asymmetry has been found in flower shape [27,149]. More systematic searches are required before it is possible to assess how widespread directional asymmetry is in plants.
3.2. Fluctuating Asymmetry
Fluctuating asymmetry denotes small differences between the left and right sides due to random imprecisions in developmental processes [150]. If a morphological trait is expected, on average, to be expressed in a particular way under the control of a particular genome, under particular environmental conditions, and for the body side in question, a real trait will usually deviate by a greater or lesser amount from this expectation (or “target phenotype” [151]). These deviations exist because developmental processes are not entirely deterministic, but have an inherent component of random variation [150]. For an individual, the deviations of a trait from the target phenotype that occur on the two body sides will usually differ and therefore give rise to a degree of asymmetry. This random or residual component of asymmetry is fluctuating asymmetry [2,3,150].
A practical problem with this reasoning is that the target phenotype is normally not known, but must be estimated. If the target phenotype is estimated by the average of each side in a population of genetically homogeneous organisms raised in the same environment, then fluctuating asymmetry can be obtained as the difference of each individual’s asymmetry from the average of directional asymmetry. In other words, fluctuating asymmetry is the individual variation of the left–right differences of trait values. This definition has the advantage that it is easy to integrate into a statistical framework for analyses of fluctuating asymmetry [2,152–156].
Fluctuating asymmetry of a scalar-valued trait usually is associated with a bell-shaped distribution of left–right differences (e.g., Figure 4a). Some authors have suggested that this should be a normal distribution and that tests of kurtosis might be useful to distinguish fluctuating asymmetry from antisymmetry or for making inferences about underlying biological processes [1,155–159]. The assumption that fluctuating asymmetry follows a normal distribution is widely accepted but there is surprisingly little justification for it. Palmer and Strobeck ([157], p. 59) explain that a normal distribution of left–right differences emerges if the deviations from the target phenotype are the result of many small random effects that are additive and independent of one another. This is a biological translation of the central limit theorem from statistics. Whereas it is plausible that developmental fluctuations are random in their directions, it is doubtful that they are additive and independent, because nonlinear (non-additive) processes and mutual interdependence are prominent features of developmental processes [150,160]. Empirical comparisons of the distributions of left–right differences to different parametric distributions have yielded variable results [161–164]. While this information certainly useful for the statistical analysis of specific datasets, such comparisons also raise the question what insight into the underlying biological processes can be gained from knowing that the asymmetries follow a particular type of parametric distribution. This kind of question is particularly relevant for analyses of shape. Very little is known about the characteristics of distributions of shape asymmetry. Therefore, for the time being, it seems advisable to avoid inferences that make any assumption about the specific distribution of shape asymmetry.
Many studies have used fluctuating asymmetry as a measure of developmental instability [2,3,150,153,155,165] and have tried to correlate it with measures of exposure to stress or other adverse conditions, inbreeding or hybridization, or fitness. Developmental instability is the amount of variation among structures for which the same target phenotype is expected: it is the result of imprecision of developmental processes and therefore a measure of developmental regulation. Because the left and right sides of the same organism share the same genome and usually nearly the same environment, organs on the left and sides can be expected to share the same target phenotype (assuming that there is no directional asymmetry) and therefore differ only by developmental instability. This reasoning is based on a number of assumptions, which will be discussed below (Section 5.1). Whether fluctuating asymmetry, following this reasoning, is indeed a good measure of developmental instability and whether it correlates with exposure to adverse conditions or genetic challenges are questions that continue to be debated. In this paper, these questions will be addressed to the extent they have been used in studies using geometric morphometrics (Sections 4.5 and 5).
A different type of application of fluctuating asymmetry is used mostly within the framework of geometric morphometrics. This is to use fluctuating asymmetry for inferring the developmental origins of integration within or between morphological structures [17,166]. The reasoning behind the method is that fluctuating asymmetry originates from random variation in developmental processes. Therefore, traits that develop separately from each other will have no correlation in their asymmetries. For the asymmetries of two traits to be correlated, there needs to be a developmental interaction between the precursors of the traits, so that the effects of developmental fluctuations can be transmitted between traits. If there is no such developmental interaction, the asymmetries of the two traits will be uncorrelated. Analyses of covariation in the asymmetries of landmark configurations thus can be used to infer whether such developmental interactions exist (Section 6). This approach has been applied in a growing number of studies [11,16,44,49,51,56,59,63,67,72,74,75,78,79,82,139,167–174].
A somewhat different perspective is to use the comparison of patterns of covariance for fluctuating asymmetry and for variation among individuals to infer whether the same processes are contributing to developmental stability and canalization [42,175,176]. Developmental stability is the ability of the developmental system to achieve a phenotype close to the target despite fluctuations in developmental processes. In other words, it is a type of developmental buffering that counteracts the effects of random developmental variation. Similarly, canalization is a kind of developmental buffering against the effects of variation in environmental conditions or genetic variation. Whether the same processes provide buffering against both kinds of variation or whether distinct processes act against intrinsic or extrinsic variation clearly is an important question (Section 5.2). The studies that have used geometric morphometrics to address this question have produced mixed results [42,54–56,62,73,117,124,135,177,178].
In summary, the use of geometric morphometrics in studies of fluctuating asymmetry both has provided new methods for studying questions that were already addressed in studies of fluctuating asymmetry in traditional traits such as length measurements [2,3] and it has opened up new directions of research addressing questions concerning subjects such as morphological integration [179].
3.3. Antisymmetry
Antisymmetry is a pattern of asymmetry where most individuals are asymmetric, but differ in the directions of the asymmetries so that there is a mix of “left-sided” and “right-sided” individuals. As a result of this mix, the distribution of left–right differences may be bimodal (Figure 4c). Weaker cases of antisymmetry, with smaller asymmetries, may not produce a clearly bimodal distribution. Indeed, it seems reasonable to envision a gradual transition between antisymmetry and fluctuating asymmetry. Several authors have pointed out that antisymmetry requires some sort of negative correlation or feedback between trait values on the left and right sides [1,140,180], whereas there is no such correlation for fluctuating asymmetry. The continuous transition between antisymmetry and fluctuating asymmetry therefore can be seen as corresponding to a gradual change from a strong negative correlation towards a correlation of zero.
Antisymmetry is quite widespread in animals and plants. Palmer [140] assembled an extensive review of antisymmetry and reported numerous examples from many animal phyla. Well-known examples include snails with dextral and sinistral morphs, differing in the direction of shell coiling, and many crustaceans such as fiddler crabs, which have claws of two very different sizes. A morphometric analysis of fiddler crab claws showed that the major and minor claws differ very clearly within a species [181]. This separation of major and minor claw shapes also holds in a separate analysis at the evolutionary level, comparing species averages of claw shapes across the genus [182].
Antisymmetry can be combined with a directional component of asymmetry. It manifests itself in a difference between the average phenotypes of each morph and the mirror image of the other morph. Such differences have been found for snail shells in species with dimorphism due to sinistral and dextral coiling [111–114] as well as for the “left-sided” and “right-sided” forms of the European flounder [183].
Some studies have found that antisymmetry can be fairly difficult to demonstrate with geometric morphometrics, even in famous examples such as the orientation of the mouth in scale-eating cichlid fish [184]. Different studies found either bimodal [184,185] or unimodal [186,187] distributions of measures of asymmetry in the mouth region. Also, there is evidence that the distribution of asymmetry in larvae is unimodal [188] and that both genetic factors [188,189] and plasticity [186] influence the asymmetry of the mouth in adults. Accordingly, multiple factors need to be considered in the design of studies, data collection and analysis, which may partly account for the discrepancies in the results.
A remarkably clear example of antisymmetry was found in a morphometric analysis of leaf shapes of the plant Montrichardia linifera (Araceae), where multivariate analysis revealed two distinct clusters in the leaf asymmetry [190]. These clusters were not due to differentiation between populations, but the division occurred within populations, indicating a consistent bimodal distribution of asymmetry in leaf shape.
Subtle antisymmetry might be fairly widespread in plants, because leaf asymmetry relates to leaf phyllotaxis [191], the arrangement of leaves along the shoot. In the shoot meristem, where there leaves originate, leaf primordia are arranged in a spiral, and each primordium therefore has one side that faces up the spiral and one side that faces down the spiral. The directions up and down the spiral correspond to local differences in auxin concentrations, a plant hormone that has a powerful and lasting effect on leaf development [191]. Depending on whether the spiral has a clockwise or counter-clockwise direction, the directions up or down the spiral are the left or right sides of the developing leaves. Morphometric analyses of the shape of mature leaves in tomato and Arabidopsis showed differences in leaf asymmetry between shoots with clockwise and counter-clockwise phyllotaxis, and experiments showed that the differences in auxin concentration were indeed responsible for such asymmetries [191]. These results provide an elegant demonstration of a mechanism that can generate antisymmetry in plant structures, provided populations contain a mix of plants with meristems spiraling in a clockwise and counter-clockwise direction. It is not clear how widespread such asymmetries of plant organs are, but the developmental mechanism that was demonstrated should be widely applicable.
4. Geometric Morphometrics
Geometric morphometric methods, which were invented repeatedly at different times during the 20th century [192,193] but became widely known and used only since the 1990s [7,194,195], have recently become an important research tool for evolutionary and developmental biology and allied fields in the life sciences [8–10]. They offer a rigorous and flexible approach for quantifying morphological variation, which can also be used for quantifying asymmetry. The statistical methods for studying fluctuating asymmetry [2,153,155], mostly developed for single measurements such as lengths or angles, can be extended in a fairly straightforward manner to a multivariate framework, as it is required for analyses of shape [11,13]. As a benefit, the results from such analyses come with the various options for visualizing results that are a central component of geometric morphometrics [196]. Moreover, studies of fluctuating asymmetry in the context of geometric morphometrics have stimulated the development of new approaches and applications, such as methods for morphometric analyses of complex symmetry [14] and the use or fluctuating asymmetry as a tool for investigating the developmental basis of morphological integration [17,166].
All the main methods in geometric morphometrics are based on an explicit geometric definition of shape: shape encompasses all the geometric features of an object except for its size, position and orientation [7]. Features that are aspects of shape include proportions, angles, and the relative arrangement of parts in a structure. The geometric definition provides a clear logical separation between size and shape: size and shape are conceptually distinct from each other, although they may be correlated in biological data. For studies of asymmetry, analyses of size can use the traditional methods developed for measurements of lengths [2,153,155]. By contrast, because of the multifaceted nature of shape, analyses of asymmetry of shape require multivariate extensions of these methods. Analyses of asymmetry of size and of shape are distinct from each other, focusing on complementary aspects of morphological variation, and can provide different results. It is often sensible to conduct analyses for both size and shape as different parts of the same study.
There have been a few studies using alternatives to the Procrustes methods that are the main focus of this article, such as Euclidean distance matrix analysis (EDMA), in which all the pairwise distances between landmarks are considered [197,198]. Methods for studying fluctuating asymmetry using this approach have been developed [199], but have been used in only relatively few studies [38,39,47,52,68,138,178,200,201]. The vast majority of studies, however, have used Procrustes approaches and this review therefore is focusing mainly on these.
This section reviews the principal concepts and methods of geometric morphometrics primarily as they apply to the study of fluctuating asymmetry of shape.
4.1. Landmarks, Procrustes Methods, and Shape Spaces
Landmarks are points that can be located precisely and correspond in a one-to-one manner among all the specimens included in a study. If the landmarks cover most of the important anatomical parts in a structure, the relative positions of the landmarks can provide a concise and reasonably complete characterization of the main features of shape in a morphological structure. The coordinates of the landmarks contain all the information that is needed to characterize these relative positions. Therefore, a set of pairs (for data in two dimensions, or 2D) or triplets (for three dimensions, 3D) of numbers is sufficient to summarize the morphology of a specimen. Different specimens are described by collecting the coordinates of the same set of landmarks on every specimen in the sample. This set of landmarks is therefore crucially important for all comparisons across specimens.
Collecting coordinates of the same set of landmarks in all specimens implies that the investigator makes decisions about the correspondence of points among specimens in the sample. Because the coordinates of the landmarks serve as variables in the subsequent analyses, it is important that each variable is a coordinate of the same point for all the specimens in the sample. This correspondence of landmarks, or homology in the context of comparative evolutionary studies, is a central assumption of geometric morphometric methods [9], even for semilandmarks and similar methods that use points selected along a smooth outline or surface [104,202–205]. Because fluctuating asymmetry is usually investigated within populations and the scale of variation is normally relatively small, correspondence of landmarks tends to be a less serious problem than in studies of evolutionary or ontogenetic variation. Nevertheless, occasionally there can be considerable differences even between left and right sides of the same individual or among individuals, which should be taken into account when the landmarks are defined at the outset of a study.
To extract the shape information from the data, the Procrustes superimposition (or Procrustes fit) can be used [7,9,206,207]. This approach is so widespread in geometric morphometrics that a recent review of the field [10] has labeled the current framework of morphometric methods as the “Procrustes paradigm”. It is also at the core of methods for analyzing asymmetry of shape [11,13]. Most often, the Procrustes superimposition is explained as a method for removing the components of variation that are not part of shape from the coordinate data, but there is an alternative and equally important explanation that sees it as a tool for obtaining a local linear approximation of Kendall’s shape space [7,208,209] for the data at hand. Because of the central role of the Procrustes fit in geometric morphometrics, I briefly present both explanations and some additional facts that are important for understanding geometric morphometrics.
The Procrustes superimposition aims to extract shape variation by eliminating the non-shape components of variation, that is, size, position and orientation. There are two types of Procrustes fit: the ordinary Procrustes superimposition, where one configuration (I will call it the movable configuration) is fitted onto another (target) configuration, and the generalized Procrustes superimposition, where multiple configurations are fitted onto a common consensus or average configuration.
The ordinary Procrustes superimposition eliminates differences in size, position and orientation between the movable and target configurations in a step-by-step procedure (Figure 5). First, both configurations are scaled to the same size (Figure 5a). The measure of size that is used is centroid size [7], the square root of the sum of squared distances of all the landmarks to their center of gravity (the centroid; the point whose coordinates are the averages of the respective coordinates of all the landmarks). Centroid size can be viewed as a measure of spread of the landmarks around the center of gravity. Second, the movable configuration is shifted so that it has the same center of gravity as the target configuration (Figure 5b). Finally, the movable configuration is rotated until the sum of squared distances between corresponding landmarks in the two configurations is minimal. In other words, this procedure eliminates variation in size, position and orientation to find an optimal fit, using the sum of squared distances between corresponding landmarks as the optimality criterion.
The sum of squared distances between corresponding landmarks of the optimally superimposed configurations reflects the discrepancies in shape between the configurations. It is that amount of difference between configurations that cannot be removed, no matter how the configurations are aligned relative to each other. Therefore, it can be used as a measure of the shape difference between the two configurations. The sum of squared distances between corresponding landmarks can itself be viewed as a squared distance (this extends the use of the Pythagorean theorem, normally used to sum up squared coordinate differences to obtain a squared distance, to sum up squared differences across all landmarks). The square root of the sum is called the Procrustes distance between the shapes of the configurations [7].
The ordinary Procrustes fit explained above (Figure 5) can be used to superimpose two configurations of landmarks. But what if there are more than two configurations? In that case, an iterative procedure of repeated ordinary Procrustes fits is used, which is called a generalized Procrustes fit [7,206,210]. In a first round, one configuration (e.g., the first one in the dataset) is chosen as the target configuration and every other configuration is superimposed on it. A consensus configuration is then computed by averaging the superimposed configurations (including the one used as the target) and rescaling this average to have a centroid size of 1.0. This consensus is then used as the target configuration in a second round, where every configuration in the dataset is fitted to the consensus, and a new consensus is computed as the average of the superimposed configurations (this time without the target, because it is not one of the landmark configurations in the dataset) and rescaled to a centroid size of 1.0. This procedure is repeated until the consensus is no longer changed, which usually happens after a few rounds (often, as few as two or three rounds are sufficient). The result of the procedure is a set of configurations that are superimposed as closely as possible to their overall average shape. The landmark coordinates of the superimposed configurations (called Procrustes coordinates) contain the complete information on shape variation in the data. Therefore, these coordinates can be used as shape variables in multivariate analyses to address a wide range of research questions.
Removing variation in size, position and orientation also has an effect on the dimensionality of the variation. For each landmark, the original data contain two coordinates for 2D data or three coordinates for 3D coordinates. Therefore, the total dimensionality of the data is two or three times the number of landmarks (imagine the data in a coordinate system in which all the landmark coordinates are separate dimensions). Because the Procrustes fit imposes a standard size, position, and orientation, the landmark coordinates cannot vary in every possible way, but there are some restrictions. These restrictions can be described as a loss of degrees of freedom or a loss of dimensionality of the data, and as such they can be counted. Removing variation in size comes at a cost of one dimension. Removing variation in position causes a loss of one dimension per coordinate, that is, two dimensions for 2D data and three dimensions for 3D data. Finally, removing variation in orientation removes one dimension for 2D data, because there is one angle of rotation, but it removes three dimensions for 3D data, because there are three rotations (about the anterior–posterior, dorsal–ventral, and left–right axes). In total, therefore, four dimensions are lost for 2D data and seven dimensions are lost for 3D data. This has practical implications for subsequent analyses.
Kendall’s shape space, for a particular number of landmarks in either two or three dimensions, is the multidimensional space in which there is a point for every possible shape and where the distances between points are the Procrustes distances between the corresponding points. The dimensionality is that of the Procrustes-superimposed data: for k landmarks, it is 2k–4 for 2D data and 3k–7 for 3D data. For triangles, for example, Kendall’s shape space happens to be the surface of a sphere (Figure 6; this is true for both 2D and 3D data, because three points are always in a plane, no matter how many coordinates are used to specify their positions). The surface of the sphere is two-dimensional, corresponding to the dimensionality of the shape data, but it is embedded in a three-dimensional space. This is a feature shared with other shape spaces, for configurations with more landmarks, which are also multidimensional curved surfaces (known in mathematics as manifolds), but tend to be much more complex and much harder to visualize than a sphere [7,208,209]. Each point in a shape space corresponds to one particular shape, and each possible shape corresponds to one point in the appropriate shape space (Figure 6).
Kendall’s shape spaces are complex, but in practice, most analyses do not need to use them. Just as the curved surface of the Earth can be successfully approximated by a flat map, as long as it only covers a region that is small by comparison with the Earth’s radius, it is possible to approximate the shape space locally by a linear tangent space [7,206,211]. This raises the question whether shape changes encountered by morphometric studies are sufficiently small for the tangent space approximation to be successful. The answer, fortunately, is that biological data usually are quite concentrated in relatively small regions of shape space, even comparisons at large taxonomic scale involve shape variation that is sufficiently small for the tangent approximation to be remarkably exact [212]. That is particularly reassuring for studies of fluctuating asymmetry, which usually focus on fairly subtle shape differences. The projection from the shape space to tangent space is mathematically quite straightforward [7] and is done automatically by the widely used software packages for geometric morphometrics. The usual procedure uses the average shape, obtained by the Procrustes fit, as the point where the tangent space touches Kendall’s shape space, and then projects all the data points into this tangent space. The shape tangent space has exactly the correct dimensionality (2k–4 for 2D data and 3k–7 for 3D data) and can be used with the standard methods of multivariate statistics.
It is useful to ask how Kendall’s shape spaces and tangent spaces relate to the Procrustes superimposition. Recall that the shape space was defined as a space in which the distances between points are identical to the Procrustes distances between the corresponding shapes. Similarly, if the Procrustes coordinates from a generalized Procrustes fit of a set of configurations are used as a coordinate system, the Euclidean distances between data points are very nearly the same as the Procrustes distances between the shapes of the corresponding configurations. Therefore, the Procrustes superimposition, with the appropriate projection to the tangent space, provides a local linear approximation of Kendall’s shape space. No matter how many landmarks there are, and thus how complex Kendall’s shape space is as a whole, the Procrustes fit and tangent projection provide a good approximation of the relative arrangement of the data in the relatively small patch of the shape space that contains the actual data. The investigator therefore does not need to deal with the complexity of the entire shape space, but still obtains all the information that is relevant to the data at hand.
Perhaps it is most helpful to think of the Procrustes superimposition in terms of this second explanation. It is not just a method to extract shape information from coordinate data by removing the variation of size, position and orientation, but it also provides a local approximation of the shape (tangent) space in the neighborhood of the data. It is important to note that this somewhat abstract characterization of what the Procrustes superimposition does is central for understanding geometric morphometrics: it provides a direct link between the theoretical foundations such as Kendall’s shape space and the day-to-day application to real data.
4.2. Morphometric Analysis of Matching Symmetry
The analyses of shape in the context of matching symmetry use the tools of geometric morphometrics in a fairly straightforward way—the main question is what to do with the left and right copies of the landmark configurations. For matching symmetry (Figure 3a), the parts from the left and right sides can be moved relative to each other and their shapes can be compared. Asymmetry is manifest as the differences between the left and right copies, and it can be studied for size and shape separately. For studying asymmetry in the size of a morphological structure, the centroid size can be computed for the landmarks configurations from the left and right sides of each individual included in the study. Centroid size is a measure of overall size for which asymmetry can be analyzed with the same methods as for conventional measurements [2,153,155]. For shape, the comparison of left and right sides can be done with the Procrustes approach explained above, by computing differences of the landmark coordinates after a Procrustes superimposition of the configurations from both sides.
For bilateral symmetry, the left and right copies of a morphological structure are mirror images of each other. Therefore, the landmark configurations from one body side (e.g., all configurations from the left side) need to be reflected before all the data can be entered in a Procrustes superimposition. Such a reflection can be done by simply changing the sign of one coordinate for all the landmarks (e.g., for all x coordinates; some software packages for geometric morphometrics do this reflection automatically). This reflection ensures that the landmark configurations from both sides fit together and that asymmetry of shape is separated from the shape difference that is due simply to the fact that the left and right sides are mirror images of each other. A joint Procrustes fit for all the left and right configurations provides a local approximation to the shape space as well as an alignment of specimens and common coordinate system in which shape variation and asymmetry can be examined [11,40,41,195]. Asymmetry of shape can then be characterized as the differences between the two superimposed landmark configurations of each individual.
To partition the total asymmetry into components of directional and fluctuating asymmetry, it is useful to recall the definitions of those types of asymmetry. Directional asymmetry is the mean asymmetry in the population, and therefore can be estimated as the average of individual left–right shape differences over all the individuals in the sample or, equivalently, as the difference between the average of all left configurations and the average of all right configurations. Fluctuating asymmetry is the variation of individual asymmetries around the average of directional asymmetry, and thus can be computed as each individual’s left–right shape difference minus the overall average of the left–right shape differences. Variation among individuals, what we tend to consider just as “shape” in day-to-day life, can be characterized by the variation among the averages of the left and right landmark configurations.
To quantify these different components of variation, it is convenient to compute sums of squares by summing the squared deviations across the coordinates of all landmarks for a particular difference, and then taking the square root of the sum. Due to the properties of the Procrustes fit, the squared distances for individual variation and fluctuating and directional asymmetry add up to the total sum of squared deviations from the average shape that remained after the Procrustes fit. Therefore, the relative contributions of the different components of variation can be quantified separately. This topic will be explored in more detail below (Section 4.4). These computations, established in the 1990s in a series of studies [11,40,41,195], remain a fundamental basis for studies of asymmetry with the methods of geometric morphometrics.
Because shape is a multidimensional feature, the results from analyses of shape asymmetry are somewhat more complex than the results of an analysis of asymmetry of traditional traits (or centroid size, which uses the same type of analysis as for traditional measurements). Whereas traditional analyses can characterize directional asymmetry, fluctuating asymmetry and individual variation as a single number each (the average left–right difference and the variances for fluctuating asymmetry and individual variation), these results are vectors or matrices for shape data. Directional asymmetry, for shape data, is a vector of coordinate differences that indicates the average shape change from the left to the right side (or vice versa). For instance, if the red and blue wings in Figure 5 correspond to the average shapes of the left and right sides, the coordinate differences of corresponding landmarks in the last diagram of the figure are the estimate of directional asymmetry. As a shape change vector, directional asymmetry has a magnitude, which can be quantified as the Procrustes distance between the average shapes for the left and right sides [11,40,41,195], but it also has a direction in shape (tangent) space, which reflects the relative magnitudes and directions of the displacements of landmarks. Both fluctuating asymmetry and individual variation concern variation in the sample, and both can therefore be represented as covariance matrices [11]. Because fluctuating asymmetry is the variation of individual asymmetries around the average of directional asymmetry, it can be characterized with the covariance matrix of the individual left–right differences (centered, to take into account directional asymmetry). Similarly, individual variation of shape can be represented by the covariance matrix of the individual left–right averages. The amounts of shape variation for fluctuating asymmetry and individual variation can be quantified as the Procrustes variance (or Procrustes total variance), the sum of the variances of all the landmark coordinates, which are the diagonal elements in the respective covariance matrix (i.e., the trace of the respective covariance matrix). An important aspect of analyses of shape asymmetry is that the covariance matrices for fluctuating asymmetry and individual variation can be used in further analyses to access the information in the patterns of covariation.
4.3. Morphometric Analysis of Object Symmetry
Analyses of object symmetry need to take into account the fact that every landmark configuration consists of two halves that are arranged to each other as mirror images. As a consequence of this, there are two different types of landmarks: there are some single landmarks that are located in the median axis or plane, whereas the remaining landmarks occur as pairs on either side of the median axis or plane. We are familiar with this from human faces (Figure 3c), where the tip of the nose, the bridge of the nose and the tip of the chin are single landmarks on the midline, whereas the corners of the mouth, the inner and outer corners of the eyes, and similar landmarks appear as pairs on either side of the face.
Instead of combining separate left and right sides in a Procrustes fit, as for matching symmetry, the analysis of object symmetry combines the entire configuration of landmarks with a copy that has been reflected to its mirror image (Figure 7) [12,13,34,213,214]. In a way, this combining of mirror images also brings together the left and right sides of the configuration. Further, because the method does not change how the left and right halves are attached to each other, the method also takes into account the relative arrangement of the two halves.
When the original configuration of landmarks and its mirror image are combined for a Procrustes fit, there is one difficulty. The reflection brings the landmarks from the left side to the right side and vice versa. For instance, in Figure 7, landmark 6 of the original configuration (blue) will be on the opposite side near landmark 14 of the reflected copy (red). If these two points are considered to be corresponding landmarks, there will be problems with the Procrustes fit. Therefore, the paired landmarks in the reflected configuration must be relabeled so that, for each pair of landmarks, the landmark that is reflected from the left side and ends up on the right side has the same label as the landmark on the right side of the original configuration (and likewise for the opposite side). The landmarks on the midline are not relabeled. After relabeling, all the original and the reflected and relabeled configurations together are entered into a Procrustes fit (Figure 7, which shows an example with only a single configuration and its reflected and relabeled copy).
The Procrustes fit produces an average shape (purple in Figure 7) and an optimal alignment of all the configurations, which minimizes the sum of squared deviations from the consensus configuration. Both results are useful for the analysis of symmetry and asymmetry. Because the Procrustes fit treats all the landmarks equally, the complete information about symmetry and asymmetry that every landmark contributes is used in the analysis.
The consensus shape from the Procrustes fit of original and reflected and relabeled configurations is perfectly symmetric [12,13,214]. This is true both for the overall average across multiple configurations and their reflected and relabeled copies, as well as for the average of the original and reflected and relabeled copies of each configuration. As a consequence, all unpaired landmarks of these consensus shapes are lying exactly on a straight line or in a plane that is the anatomical midline or midplane (for 2D and 3D data, respectively; this is not visible in Figure 7 because there are only to unpaired landmarks). Furthermore, the lines that connect pairs of landmarks are exactly perpendicular on this midline and the two landmarks of each pair have equal distances to the midline. Therefore, the consensus shape from this Procrustes fit yields an estimate of the median axis or plane that takes into account the information from all the landmarks. This approach avoids the need for any ad-hoc assumptions that some landmarks, for instance those at anterior and posterior extremes of the midline, are more “reliable” than others and are therefore better suited for identifying the median line or plane [215–221].
The reason why the consensus shape is symmetric is fairly easy to see by recalling the mathematical definition of symmetry (Section 2.2): an object is symmetric if it does not change when some transformation is applied to it, in this case reflection (and relabeling). If we apply this transformation to the data used to compute the consensus shape, the original configurations and their reflected and relabeled copies, we obtain the same data. Transforming an original configuration yields its reflected and relabeled copy, whereas transforming a reflected and relabeled copy simply reverses the transformation and yields the corresponding original configuration. If we perform a Procrustes fit with these transformed data, we obtain the same consensus as in the initial analysis because the Procrustes fit is done on the same data (the order of the configurations does not make a difference to the average shape that results). Therefore, the consensus shape does not change under reflection and relabeling, and is thus symmetric.
After the Procrustes fit, the differences of the original (or of the reflected and relabeled copy) from the symmetric consensus indicate asymmetry of shape (Figure 7). Equivalently, asymmetry can also be read from the difference between the original and the reflected copies of each landmark configuration. Both measures are equivalent up to a factor of 2.0, because the landmark positions for the consensus shape are midway between those for the original and the reflected and relabeled copies (Figure 7). Directional asymmetry is the average of the individual asymmetries and can be computed from the difference of the average of all the original copies minus the overall symmetric consensus in the entire sample (or, equivalent but twice the magnitude, the average shape of all the original minus the average of all the reflected and relabeled copies). Fluctuating asymmetry is the variation of individual asymmetries around the average of directional asymmetry, as for matching symmetry.
An example of the possible results of an analysis of object symmetry is presented in Figure 8. The example uses data from pharyngeal jaws of Amphilophus citrinellus, a cichlid fish [13]. There is one landmark on the median line and four pairs of landmarks on either side. As expected, the overall consensus shape is perfectly symmetric (Figure 8a). The average asymmetry (Figure 8b) is subtle and needs to be exaggerated to be visibly different from the symmetric consensus shape. It is convenient to display the effects of variation among individuals and fluctuating asymmetry with principal component analyses of the respective covariance matrices, because the first few principal components provide the main patterns of shape variation at these two levels (Figure 8c,d). It is clearly visible that the shape changes differ between variation among individuals (Figure 8c) and fluctuating asymmetry (Figure 8d). The shape changes for individual variation are symmetric (Figure 8c): the relative shifts of paired landmarks on both sides are the same (e.g., if the left landmark moves anteriorly, so does the right one). By contrast, the shape changes for fluctuating asymmetry are asymmetric (Figure 8d), with relative shifts of paired landmarks in opposite directions (e.g., if the left landmark moves proximally, the right one moves distally).
Symmetric variation originates from differences among individuals in the consensus shapes of the original and reflected copies of the landmark configurations. (Figure 8c). This origin imposes some constraints on the possible patterns of variation. The median landmarks are limited to movements within the axis or plane of symmetry, as any lateral deviation would be asymmetric. The paired landmarks on the left and right sides can move in any anatomical direction, but the relative displacements of the left and right landmarks are exactly the same—for instance, if the left landmark of a pair moves in a lateral and anterior direction, the right landmark also moves in the corresponding lateral and anterior direction as an exact mirror image.
Asymmetric variation stems from the differences between the original and reflected and relabeled copies of each configuration. Accordingly, there are constraints on the asymmetric shape changes too (Figures 7 and 8d). For the median landmarks, such differences can only exist in the direction perpendicular to the median axis or plane (Figure 7), and asymmetric variation of these landmarks is thus confined to that direction. For the paired landmarks, differences can be in any direction, but the two landmarks of each pair have differences that are exactly opposite to each other and have the same magnitude (see the opposite arrangements of red, purple and blue dots for the paired landmarks in Figure 7). Therefore, from the change in one landmark, the change in the other landmark of the same pair is predictable exactly.
The symmetric and asymmetric components of variation are not only distinct because they are associated with different shape changes, but these two components of variation also occupy two distinct, mutually orthogonal subspaces of the shape tangent space of the whole configuration of landmarks [12,13,214]. Together, the two subspaces add up to the complete shape tangent space. Because of the various constraints that apply to the symmetric and asymmetric components of variation, each of them has fewer dimensions than the entire shape tangent space, but together, the dimensions in the two subspaces add up to the total dimensionality of the whole shape tangent space. This structure of shape variation for landmark configurations with object symmetry has important implications for morphometric studies.
That the symmetric and asymmetric shape changes occupy two different subspaces can be understood intuitively by looking again at Kendall’s shape space for triangles (Figure 6). In the particular orientation of the shape space in Figure 6, one of the “meridians” of the spherical shape space is visible as a vertical line through the center of the diagram. The shapes that are located on this line are all isosceles triangles, with equal lengths of the left and right sides, which also means that these triangles are all symmetric about the vertical axis. The shape of isosceles triangles can only vary in one aspect: the ratio of height to width of the triangle. The vertical line in the diagram shows the entire spectrum, from top to bottom, from extremely flat and wide to extremely tall and narrow isosceles triangles (in the two extremes, all three points of the triangle lie on a single line). Therefore, the vertical direction in Figure 6 is the symmetric component of the shape space of the triangles. To find triangles that are asymmetric, it is sufficient to go from this vertical line to the left or right side, corresponding to “pulling” the upper vertex of the triangle to the left or to the right. Therefore, the direction from left to right is the asymmetry component. Accordingly, the symmetric component and the asymmetry component each have a single dimension. Together they sum up to the two dimensions of Kendall’s shape space for triangles.
To derive the dimensionalities of the subspaces containing the symmetric and asymmetry components for shapes with more than three landmarks, it is possible to enumerate the degrees of freedom by considering the constraints of landmark displacements for the symmetric and asymmetric components of variation [12,13]. Assume there are k pairs of landmarks on both sides and l single landmarks in the median axis or plane, in either 2D or 3D data (2k + l ≥ 3 must hold, so that there is at least a triangle of landmarks; the restriction [13] that k ≥ 1 is unnecessary). The dimensionality of the complete shape space is then 4k + 2l − 4 for 2D data and 6k + 3l − 7 in 3D data (the total number of all landmark coordinates, minus the number of degrees of freedom lost to standardize size, position and orientation in the Procrustes fit). The paired landmarks, for both symmetric variation and asymmetry, can shift in any direction, but for each pair, the displacement of the landmark on one side completely determines the landmark displacement on the other side. Therefore, for each subspace, the paired landmarks contribute 2k dimensions for 2D data or 3k dimensions for 3D data. The median landmarks can move in the median axis or plane for the symmetric component of variation, which corresponds to l dimensions for 2D data and 2l dimensions for 3D data. For the asymmetry component, the median landmarks can only move in the single direction perpendicular to the median axis or plane, and there are therefore l degrees of freedom. The constraints imposed by the Procrustes fit also need to be taken into consideration. For the symmetric component of variation, there are three such constraints: (i) one degree of freedom is lost for scaling to standard centroid size, both for 2D and for 3D data; (ii) the landmark displacements in the direction of the median axis or plane must sum up to zero, removing one degree of freedom for 2D data and two for 3D data, and, for 3D data only; (iii) there is a further constraint on rotation in the plane of symmetry (no “pitch”), removing one degree of freedom. There are two further constraints concerning asymmetry: (i) the lateral displacements in all landmarks must sum to zero, removing one degree of freedom for both 2D and 3D data; and (ii) an additional constraint concerns rotations (no “roll” or “yaw”), eliminating one degree of freedom for 2D data and two for 3D data. Altogether, the constraints for the Procrustes fit eliminate two degrees of freedom each from the symmetric and the asymmetric component of variation in 2D data. In 3D data, these constraints remove four degrees of freedom for the symmetric component and three degrees of freedom for asymmetry. For 2D data, therefore, the two subspaces of the shape space each contain 2k + l − 2 dimensions, whereas for 3D data, the symmetric component has 3k + 2l − 4 dimensions and the asymmetry component has 3k + l − 3 dimensions [13]. For most practical applications, it is sufficient to remember that each subspace has about half the dimensionality of the entire shape space (this holds exactly for 2D data, and is approximately so for 3D data including a reasonable number of paired landmarks).
The structure of the symmetric and asymmetric components of shape variation of a landmark configuration with object symmetry can be explored by multivariate analyses of the variation in the averages and differences of original and reflected and relabeled copies of the landmark configurations (Figure 8c,d). An alternative method is to use the combined dataset of original as well as reflected and relabeled configurations in a principal component analysis [222]. The resulting principal components are aligned either with the symmetric component or with the asymmetry component, but not at an oblique angle to them, and the shape features associated with the principal components are therefore either symmetric or asymmetric shape changes, but not a mix of the two. This method was used in a study of human faces [223], but because the more conventional analysis (as in Figure 8c,d) is fairly straightforward for bilateral symmetry, the technique is perhaps better suited for more complex types of asymmetry [14,23,27].
The fact that the symmetric and asymmetric components of shape variation occupy orthogonal subspaces of the overall shape space has some consequences for subsequent analyses of variation. For instance, comparisons of the patterns of covariation between the two subspaces need to make some adjustments in the methods used [13] (additional information concerning specific methods is given in Section 5).
The symmetric and asymmetric components of variation have fundamentally different biological interpretations and relevance, and should therefore be distinguished in studies of shapes with object symmetry even if symmetry and asymmetry are not of primary interest [13]. The separation of shape variation into the two components is biologically and statistically sound because it reduces or removes the effect of possibly confounding factors. Further, it is mathematically exact and rigorous. Due to the orthogonal nature of the two subspaces of shape tangent space, each of the two subspaces provides the complete variation of the respective component with the correct dimensionality, which facilitates further analyses. Because the symmetric and asymmetry component each have only about half the dimensionality of the shape space of the complete configuration, using only the one component relevant for the research question at hand is also an effective method of dimension reduction.
The symmetric component of variation is what many biologists informally think of as “shape” and is therefore the optimal choice for further analyses addressing a wide range of questions in ecology, evolution or ontogeny [224–226]. Alternative approaches, such as using various ad-hoc procedures for identifying a median axis from just some landmarks [215–221] or ignoring the symmetry of the structure altogether [227–230], seem clearly inferior to the Procrustes approach for object symmetry. Using only half of a symmetric structure, which was a reasonable recommendation before methods to deal with object symmetry were available [34], is still sometimes used [231–234], but also has a number or disadvantages because it offers no principled way of removing potentially confounding asymmetry in the structure [13,235].
4.4. Quantifying Shape Variation and Asymmetry: Procrustes ANOVA
Traditional analyses of fluctuating asymmetry have long used a two-factor, mixed-effect ANOVA with individuals and sides as the two factors [2,152,153]. The main effect of individuals results from variation in their left–right averages of trait values. The main effect of side reflects the average difference between left and right sides, and therefore represents directional asymmetry. The individual-by-side interaction is due to differences among individuals in their left–right asymmetries, and therefore stands for fluctuating asymmetry or antisymmetry. Because measurement error is often a serious concern for studies of fluctuating asymmetry, the ANOVA model can be expanded by including replicate measurements [2,153].
This ANOVA model has been incorporated into studies of fluctuating asymmetry using the methods of geometric morphometrics [11,13]. This is straightforward because the algebra that underlies the computations of the Procrustes superimposition is based on sums of squared deviations, and is therefore directly compatible with the sums of squares used in conventional ANOVA. The key point is that, in the calculation of Procrustes distances, squared coordinate differences are added up across all coordinates of all the landmarks. Goodall [206] established the use of ANOVA designs in the context of Procrustes methods, which provides the statistical foundation for Procrustes ANOVA in studies of shape asymmetry. Table 1 provides an example of a Procrustes ANOVA for a small sample of Drosophila wings, including replication for estimating the error from imaging and digitizing.
Procrustes ANOVA uses the coordinates of landmarks after a joint Procrustes superimposition of all the data in the sample (all individuals, both sides or original and reflected/relabeled configurations, all replicate measurements). The computation of sums of squares proceeds in the same way as in conventional ANOVA [2,153,236], with the difference that squares of coordinate differences are added up for all coordinates of all landmarks [11,13,206]. As a result of this summation over coordinates, there are more degrees of freedom associated with the sums of squares than in the corresponding sums of squares for a conventional ANOVA: the degrees of freedom in Procrustes ANOVA can be obtained for each ANOVA effect by multiplying the degrees of freedom for the respective effect in conventional ANOVA by the shape dimension [11,13]. The ANOVA degrees of freedom are a result of the design and reflect the sample size, number of replicate measurements, etc. The shape dimension, for matching symmetry, is the dimensionality of the shape space (with k landmarks, 2k − 4 for 2D data and 3k − 7 for 3D data) [11,13]. For data with object symmetry, the shape dimension depends on the ANOVA effect, because some effects concern the symmetric and others the asymmetry component of shape variation. For the main effect of individuals, the shape dimension is the dimensionality of the subspace for symmetry (with k pairs and l single landmarks, 2k + l − 2 for 2D data and 3k + 2l − 4 for 3D data), whereas the shape dimension for the main effect of side and for the individual-by-side interaction is the dimensionality of the asymmetry subspace (2k + l − 2 for 2D data and 3k + l − 3 for 3D data) [13]. Measurement error affects every aspect of shape, and its shape dimension is therefore the dimensionality of the entire shape space, even for object symmetry [13].
The approach of calculating Procrustes sums of squares and using them to compute Goodall’s F is an option for conducting statistical tests of the effects in a Procrustes ANOVA that directly extends Goodall’s [206] use of ANOVA in the context of asymmetry analyses [11,13]. Mean squares can be obtained by dividing the Procrustes sums of squares by the degrees of freedom for the respective effects. Dividing the mean square of each effect by the mean square for the appropriate error effect (the same as in the univariate ANOVA for asymmetry [2,153]) yields the F-value. The tests can use either a parametric [206] or a nonparametric permutation approach [237,238]. Using the parametric F test makes the assumption that the distribution of data points in shape tangent space is approximately multivariate normal and that variation is isotropic (equal amounts of variation in all directions). Multivariate normality is probably a reasonable proposition for intra-population data as they are often used in studies of asymmetry, but the assumption of isotropic variation is biologically unrealistic [13,239]. The assumption of multivariate normality can be avoided by using the permutation approach, but even that method implies the assumption of isotropic variation as long as it uses Goodall’s F or another test statistic derived from Procrustes sums of squares. Also, permutation tests can involve tedious programming, particularly with unbalanced designs, which may be why they have been used only rarely [11,13,16,44,132]. A direct comparison of parametric and permutation results yielded similar P-values for both approaches [13].
To avoid the assumption of isotropic variation, it is possible to conduct tests with the classical test statistics for MANOVA, such as Pillai’s trace, the Lawley-Hotelling trace, or Wilks lambda [240–242]. These statistics are computed from matrices of sums of squares and cross products, rather than Procrustes sums of squares, and therefore preserve information about the directionality of variation [239]. This comes at a cost, however, because these methods require large sample sizes to perform well, and there are some serious limitations in the presence of object symmetry [13]. Because the symmetric and asymmetric components reside in orthogonal subspaces of the shape tangent space, both the effect of interest and its error effect must be from the same component of variation. For instance, using the individual-by-side interaction as the error effect for the main effect of individuals, as it is usual for univariate ANOVA of asymmetry [2,153], is therefore not possible in the MANOVA framework [13]. The Procrustes approach can overcome this problem by assuming that isotropy holds across the entire shape tangent space. In practice, tests using the Procrustes and MANOVA statistics often yield similar P-values, so this distinction is usually not a serious concern (but very few direct comparisons have been published [13]).
For scalar traits containing size information, such as distance measurements or centroid size of landmark configurations (with matching symmetry), fluctuating asymmetry is usually very subtle, on the order of 1% of the trait average or even less, and is normally also much smaller than the variation among individuals [3,153,155,243]. By contrast, many analyses of shape have shown that the difference in the amounts of fluctuating asymmetry and individual variation is less pronounced (as can be assessed by the ratio of the Procrustes mean squares of the main effect of individuals and of the individual-by-side interaction). No systematic comparison has been done, but this is a pattern that seems to be rather widespread among published Procrustes ANOVAs.
An important function of Procrustes ANOVAs is to provide a simple means to gauge the possible effect of measurement error on estimates of fluctuating asymmetry (see also Section 4.9.2). If each of the landmark coordinates has been digitized multiple times, the residual effect in the Procrustes ANOVA indicates the variation among these replicate measurements. The question is whether fluctuating asymmetry is sufficiently large relative to the measurement error so that the error is negligible. This requires more than just an effect of fluctuating asymmetry that is statistically significant, because that only indicates that there is some effect of fluctuating asymmetry in addition to the measurement error. For the error to be negligible, the magnitude of fluctuating asymmetry needs to be much bigger than the magnitude of measurement error. A useful measure for this is the ratio of the respective mean squares in the Procrustes ANOVA, which is also the F ratio for the effect of fluctuating asymmetry [11,13]. Under favorable conditions, this ratio can be high (e.g., 25 in the example of Table 1, or also in published examples [44,56,93]), indicating that the measurement error makes up no more than a few percent of the estimate of fluctuating asymmetry and is therefore negligible. More often, however, this ratio is lower, with fluctuating asymmetry just a few times bigger than the error term, suggesting that replication and other measures to reduce the effect of measurement error are necessary.
4.5. Individual Measures of Fluctuating Asymmetry of Shape
For many applications, a population estimate of the quantity and pattern of fluctuating asymmetry is not sufficient, but investigators need a measure of the asymmetry for individuals. This applies particularly to observational studies that examine the association of fluctuating asymmetry, as an estimate of developmental instability, with various environmental, genetic, or behavioral variables. In experimental studies, the “treatment” and “control” groups can be compared to each other. In many observational studies, however, there are no clear groups, and such studies therefore tend to focus on the variation of asymmetry and external factors among individuals within a population. For these studies, an estimate of individual asymmetry is required.
Because fluctuating asymmetry is the result of random irregularities during development, the specific direction of the left–right difference is not informative, but the magnitude of the shape asymmetry can be used as an estimate of developmental instability. A straightforward choice for a measure of the amount of overall asymmetry is therefore the Procrustes distance (or squared Procrustes distance) between left and right sides [11,41,53,116,128,129,132,161,162,164] or, for object symmetry, between the original and the reflected and relabeled landmark configurations [110,244–249]. Some researchers made minor adjustments to obtain modified indices of asymmetry, for instance, by dividing by the number of landmarks [245].
In the presence of directional asymmetry, which is very widespread (Section 3.1), the Procrustes distance between left and right sides is the combined result of fluctuating and directional asymmetry. To separate the two effects, it is possible to subtract the mean asymmetry to remove the effect of directional asymmetry before computing the Procrustes distance between the left and right shapes, so that the resulting distance indicates exclusively the magnitude of fluctuating asymmetry [11,41,239]. This measure of asymmetry, again, is available for both matching symmetry, where it is obtained from differences between the left and right sides [40,61,250,251], and for object symmetry, where it quantifies differences between original and reflected and relabeled configurations [86,94,102,105,134,148,252].
Quantifying fluctuating asymmetry as Procrustes distance provides an absolute magnitude of the shape difference between the left and right sides (possibly adjusting for directional asymmetry, as appropriate). This approach does not take into account that fluctuating asymmetry usually is not distributed equally in all directions, but some shape features are more variable than others (Figure 9a). Therefore, the question arises whether an intermediate-sized left–right difference is equivalent in a direction in which there is much asymmetry, where this difference may appear relatively small, and in a direction where there is little asymmetry, where the same left–right difference might be unusually large.
To address this problem, it is possible to use the Mahalanobis distance between left and right sides, rather than the Procrustes distance, as an individual measure of fluctuating asymmetry [239]. The transformation uses the distribution of left–right differences around the average of directional asymmetry (Figure 9a; this is the sample distribution of fluctuating asymmetry), and scales each direction by the inverse of its variation of asymmetries, so that the shape tangent space is transformed into a new space in which there is an equal amount of fluctuating asymmetry in every direction (Figure 9b). As a result, distances are fully comparable regardless of the directions of the corresponding left–right differences in the shape tangent space (Figure 9c). This comes at a cost, however, because the transformation requires a sufficient sample size for estimating the covariance matrix reliably, which can be a problem in practice. Also, the asymmetry scores are not in units of Procrustes distance, and therefore are not easily related to other measures of shape variation in the data. The asymmetry measure using Mahalanobis distance is used in an increasing number of studies, comparing levels of fluctuating asymmetry between groups or correlating it with factors that might influence developmental instability, both for structures with matching symmetry [77,124] and with object symmetry [90,98,108,137,253].
4.6. Morphometric Analysis of Complex Symmetry
Bilateral symmetry is just one of many types of symmetry in living organisms (Figure 1). The natural question, then, is whether the methods outlined above for bilateral symmetry can be generalized for complex symmetries. A framework of morphometric methods for the analysis of any type of symmetry has been proposed [14], which uses the theory of symmetry groups (Section 2.2) as its conceptual basis. It might therefore be useful to review briefly the morphometric methods for bilateral symmetry, discussed in the preceding sections, from the perspective of symmetry groups.
The symmetry group for bilateral symmetry contains just two transformations: a reflection and the identity, the transformation that produces no change. Using a description that focuses on symmetry transformations, we can therefore explain the morphometric analysis for matching symmetry (Section 4.2) as follows: for each pair of landmark configurations, the configuration of one side is transformed using the reflection, the configuration of the other side is transformed with the identity (which has no effect), and all pairs of transformed configurations are entered together in a generalized Procrustes superimposition. For object symmetry (Section 4.3), the analysis is based on two copies of the each landmark configuration in the sample, of which one copy is transformed using the reflection and the other copy using the identity, and both copies of all configurations are then superimposed in a joint Procrustes fit. For both matching and object symmetry, asymmetry can be computed from the differences between the Procrustes coordinates of the configurations transformed with the reflection and identity (i.e., the two sides for matching symmetry and the reflected and original copies for object symmetry). Also, a symmetric consensus or left–right average can be computed by averaging both configurations for each individual in the sample. These descriptions in terms of symmetry transformations are helpful both to put the preceding accounts of the procedures for bilateral symmetry into the perspective of the more general mathematical approach and as a starting point for discussing morphometric analyses of complex symmetry.
4.6.1. Analyses of Matching Symmetry for Complex Symmetries
The perspective of matching symmetry focuses on the repeated parts, for instance the wings of a fly (Figure 3) or the human hands. For complex symmetry, there are usually more than two copies that are repeated in various spatial arrangements (Figure 1). Examples are the petals of flowers (Figure 1b), vertebrae in the spine of a fish (Figure 1c), chambers in a nautilus shell (Figure 1d), or even the quadrants of an algal cell (Figure 1a).
The first step in an analysis of matching symmetry is therefore to identify the repeated units and to collect coordinates of a set of corresponding landmarks in each repeated unit (Figure 10). Configurations of each of these parts are considered separately. This may require that landmarks shared on the boundary between two units are duplicated, so that each of the configurations has a complete set of landmarks. Depending on the arrangement of parts, the landmark configurations of some of the parts may need to be reflected before they can be superimposed. Finally, the configurations of all parts and all individuals are entered together into a joint Procrustes superimposition (Figure 10).
The Procrustes superimposition extracts the variation in the shapes of the repeated parts in all the configurations. As for bilateral symmetry, averaging over the parts of each individual produces an estimate of a consensus that can be used to characterize individual variation, whereas differences among the repeated parts of each individual provide estimates of asymmetry. The difference is that, with complex symmetry, there may be more than one aspect of asymmetry. For instance, for a structure with disymmetry (Figure 10), it might be of interest to compare the left–right asymmetry to the dorsal–ventral (or adaxial–abaxial) asymmetry. For doing this, an estimate of left–right asymmetry can be obtained as the difference between the average shape of the two left parts (A, C) and the average shape of two right parts (B, D), whereas the dorsal–ventral asymmetry can be computed as the difference between the average shape of the two dorsal parts (A, B) and the average shape of the two ventral parts (C, D). Which types of asymmetries are of interest, and how they are calculated from contrasts of repeated parts included in the joint Procrustes superimposition, depends on the number and arrangement of parts and therefore on the type of symmetry.
For morphological structures with matching symmetry, all the components of asymmetry and of variation among individuals are occupying the same shape space: the shape space of the repeated parts. Therefore, all components will have the same dimensionality and further analyses of the patterns of variation can be compared with the usual morphometric tools [11,254].
Note that the repeated parts themselves may be symmetric, with object symmetry of some kind. For instance, the vertebrae that make up the spine show translation symmetry as a whole (Figure 1c), but each of them is bilaterally symmetric [14]. Likewise, the petals of many flowers, which may be chosen as the repeated parts in studies of floral symmetry, often are also bilaterally symmetric. In cases like this, the investigator has the choice of redefining the unit of the analysis, and focus on half-vertebrae or half-petals instead whole vertebrae or petals. This choice, of course, will increase the number of parts (in the examples, this would be a doubling of the number of parts included in the Procrustes fit). Alternatively, the object symmetry of the parts can be addressed directly, which requires that two or more copies of each landmarks configuration are included in the overall Procrustes fit, each appropriately transformed and relabeled (e.g., if each part is bilaterally symmetric, each will have one unchanged and one reflected and relabeled copy). The choice between these two alternatives depends on the specific system at hand and on the biological question that the analysis is intended to answer.
To my knowledge, there are no fully worked examples of this approach yet. There is considerable potential for studies of structures repeated as a sequence along some axis, like vertebrae in the spinal column of fish or snakes [255,256], plant leaves along a shoot axis [257–260], leaflets within compound leaves [173,191,260], or flowers within an inflorescence [261]. In plants, particularly, the modular body plan provides many opportunities for exploring variation among repeated parts within individuals [262].
4.6.2. Analyses of Object Symmetry for Complex Symmetries
Analyses of object symmetry consider variation in a symmetric structure as a whole and thus take into account both the variation of repeated parts and their relative arrangement. Examples are algal cells with disymmetry (Figure 1a) or flowers with rotational symmetry (Figure 1b). Note that object symmetry is not applicable to all types of symmetry, but only to those with finite symmetry groups [14]. This excludes, for example, translational symmetry (Figure 1c) and spiral symmetry (Figure 1c), where it is impossible to superimpose transformed copies of the entire structure because of problems at the ends of the axis of translation or the spiral. For the vast majority of studies of complex symmetry in biological structures, it is sufficient to limit the discussion to symmetries that include a single rotation with or without a reflection [14]. There are types of biological structures with different symmetries (e.g., radiolarians with symmetries of the Platonic solids), but for practical reasons these are unlikely to be used in morphometric studies.
Morphometric analyses of object symmetry for complex types of symmetry [14] are based on the theory of symmetry groups (Section 2.2). The principal idea of the analysis is to make copies of the landmark configurations and to use each symmetry transformation in the symmetry group to transform one copy (Figure 11). These copies are then entered into a joint Procrustes fit and components of symmetric shape variation and asymmetry are extracted from the resulting Procrustes coordinates. This approach is a direct extension of the method for object symmetry with bilateral symmetry [12,13,214]. The first study that used the approach, for a dataset with disymmetry, did not refer to symmetry groups but was a direct extension of the idea of a combined Procrustes fit with multiple copies per specimen [22].
The first step in the analysis is to record landmarks so that each repeated part contains a set of corresponding landmarks. Shared landmarks on the boundaries between repeated parts are not a problem—it does not really matter to which part each landmark belongs. What is important, however, is that each landmark has exactly one corresponding landmark when any of the transformations in the symmetry group is applied (even if the landmark is mapped onto itself, e.g., for the central point of a structure under reflection or rotation).
The second step, as for bilateral symmetry (Section 4.3), is to make copies of the original landmark configuration of each individual in the sample. The number of copies is the same as the number of transformations in the symmetry group, and therefore depends on the type of symmetry. For instance, it is four for disymmetry: a left–right reflection, a dorsal–ventral reflection, the combination of both reflections (which is the same as a rotation by 180°), and the identity (Figure 11). For the equilateral triangle, there are six symmetry transformations (Figure 2) and six copies are therefore required. Each copy then needs to be transformed with one of the transformations in the symmetry group and the landmarks need to be relabeled accordingly. Relabeling of landmarks is critically important and is based on the correspondences of landmarks among repeated units in the structure as a whole [14].
The Procrustes superimposition then uses the entire set of transformed and relabeled copies of landmark configurations. The resulting average shape, both for the sample as a whole and for the set of copies of each specimen, is perfectly symmetric. For instance, for a triangle to which the analysis for the symmetry group of the equilateral triangle (Figure 2) was applied, the consensus shape is an equilateral triangle (Figure 12). The variation among the symmetric averages of the copies of landmark configurations for all individuals defines a component of shape variation that is completely symmetric (symmetric under every transformation in the symmetry group; Figure 13a).
Depending on the type of symmetry, and therefore on the structure of the symmetry group, one or more components of asymmetry can be extracted from the Procrustes-superimposed coordinates by computing differences between copies of the same configurations that were transformed differently. For instance, to compute a component of dorsal–ventral asymmetry in a configuration with disymmetry (Figure 11), it is the difference between configurations that have or have not been reflected in the dorsal–ventral direction that are of interest. Averaging across the copies that have or have not been reflected in the left–right direction makes the resulting shape changes left–right symmetric (Figure 13b). Other components of asymmetry can be obtained in similar ways (Figure 13c,d). Depending on the type of symmetry, therefore, there can be multiple types of asymmetry with different characteristics.
The fact that the total shape variation is organized into several distinct components according to symmetry or asymmetry has consequences for the structure of variation in shape tangent space. The different components of variation occupy orthogonal subspaces in the shape tangent space [14]. It is possible to work out the dimensionality of the subspaces by enumerating degrees of freedom [14], but this is fairly tedious. As an easier alternative, for particular datasets, there is an exploratory approach using principal component analysis, which is an extension from the corresponding method for bilateral symmetry [222]. This method uses a principal component analysis of the combined data of all transformed copies of landmark configurations after the Procrustes fit [14]. Each of the resulting principal components is aligned with just one of the subspaces and the corresponding shape change can be used to identify its type of symmetry or asymmetry [14,23,24,27]. The associated eigenvalue indicates the amount of variation for which it accounts. An example is shown in Figure 13, which shows the results of an analysis of corolla shape in Erysimum mediohispanicum [27]. Like other members of the family Brassicaceae, Erysimum has disymmetric flowers, which are symmetric under reflection about the adaxial–abaxial (upper versus lower petals) as well as left–right axes.
The different components of symmetry and asymmetry of shape are not only geometrically distinct from each other, but also can have different biological significance. For the Erysimum example (Figure 13), the symmetric component is mostly featuring variation in the shape and relative arrangement of petals (Figure 13a). The adaxial–abaxial component of variation shows differentiation of the upper and lower petals (Figure 13b). Remarkably similar patterns of shape changes emerged in studies of selection by pollinators on corolla shape in Erysimum [26,263–266], even though the analyses did not explicitly take into account floral symmetry, suggesting that the differentiation of upper and lower petals is a floral feature that is important for pollinators. Also, differentiation of adaxial and abaxial parts of flowers is a prominent aspect of floral evolution and is under specific developmental genetic control [18–21,28,29,267]. The third component of variation, left–right asymmetry (Figure 13c), has the usual interpretation, but the analysis separates it clearly from the other components of asymmetry. Finally, there is an additional component of asymmetry, transversal asymmetry [24], which is asymmetric with respect to reflections about both the vertical and horizontal axes, but symmetric under rotation by 180° (Figure 13d). The biological significance of this type of asymmetry is unclear and will need to be examined as additional studies in structures with disymmetry become available.
The biological significance of the different components, even for the same type of symmetry, can differ from one study system to another. Another study system with disymmetry is the unicellular alga Micrasterias rotata [23,24]. Because these cells multiply by splitting and re-growing the missing half of the cell, the asymmetry between half-cells is inherently associated with variation due to cell growth and differentiation. By contrast, the left–right asymmetry has no such special significance, but is presumably due to random fluctuations in the processes of growth and formation of the cell wall. Finally, again, the biological significance of the transversal component is unclear.
Neustupa [24] computed the four components of symmetric and asymmetric shape variation and used them in analyses comparing different Micrasterias taxa and found that the symmetric component separated the taxa much more than any of the three components of asymmetry. Whether this finding can be generalized to other taxa remains to be seen—similar analyses in other study systems are clearly needed. If this result holds generally, then using just the symmetric component of variation for taxonomic studies of structures with complex symmetry (or maybe studies in other contexts as well) would be an excellent way of drastically reducing the dimensionality of the data and eliminating statistical noise from asymmetry that is irrelevant to that kind of study.
4.7. Alternative Methods for Complex Symmetry
Two alternative methods for the analysis of landmark configurations with complex symmetries have been proposed. One is a general framework for identifying symmetries of objects that has been developed primarily for chemistry [268], but has also been further developed for applications such as image analysis [269], whereas the other is a variant of this method, specifically intended for the study of deviations from rotational symmetry in flowers [270]. Here I briefly introduce the two approaches here and outline their relationship to the Procrustes approach.
4.7.1. Continuous Symmetry Measure
In a series of papers, Zabrodsky et al. [268,269,271,272] proposed a general framework for quantifying the degree of asymmetry in structures defined by a set of points, such as positions of atoms in a molecule. This framework is based on the mathematical theory of symmetry groups (Section 2.2) just as the Procrustes approach outlined above. Because the principal focus was on applications in chemistry, however, the main goal of the approach is to quantify the symmetry of a single object rather than the variation within a sample.
The approach is based on the idea of “folding” and “unfolding” a configuration of points according to the transformations of the symmetry group (Figure 14). For the folding step, the transformations in the symmetry group are applied to bring corresponding points from the repeated parts of the structure together. For instance, for disymmetry, the points from all four quadrants are brought together in a single quadrant (Figure 14b). The positions of the points can then be averaged to obtain a consensus position (red dot in Figure 14b). In the unfolding step, the consensus point is copied back into all repeated parts of the configuration, using the appropriate symmetry transformation for each copy, so that a completely symmetric configuration results (Figure 14c). If there are multiple landmarks per repeated part of the structure, the folding and unfolding can be performed for each of them separately.
The measure of asymmetry is the average of the squared distances of the points in the original configuration from the corresponding points in the symmetric consensus configuration (Figure 14b,d). The details of symmetry transformations such as the axes or planes of reflection and centers or axes of rotation are chosen to minimize the sum of squared distances between the original and symmetric configurations (accordingly, the centroid of the configuration serves as the center of rotations and axes of reflection and rotation symmetry pass through the centroid). The measure of asymmetry uses a scaling so that the longest distance between the centroid of the configuration and any of the landmarks is set to 10 [269] or 100 [268,271,272]. An alternative scaling method sets the average of the distances between the centroid and each of the landmarks to 1.0 [273].
Because this measure of asymmetry is based on a minimization of the sum of squared distances between the original and symmetrized configurations of points, it is, up to a scaling factor that is specific to each configuration, identical to the Procrustes distance between the original configuration and the symmetric consensus computed with the Procrustes approach for complex symmetry [14]. The symmetric shape produced by the folding and unfolding algorithm is the same as that produced, for the same starting configuration and its transformed and relabeled copies, by the Procrustes approach. In essence, the folding and unfolding algorithm does the same as the Procrustes approach, but uses transformed copies of just one of the repeated parts instead of the whole configuration.
A major difference to the Procrustes approach [14] is that the measure of asymmetry indicates the magnitude of difference to perfect symmetry for each configuration, but because it considers one configuration at a time, it has no way to distinguish fluctuating and directional asymmetry [273]. For that purpose, the Procrustes approach is much better suited because it can handle any number of configurations simultaneously and thus derive averages of asymmetry and characterize the variation among the symmetric consensus configurations for the different specimens.
One of the major purposes of the measure in the context of chemistry was to choose between different types of symmetry. The measure of symmetry was designed to help select a type of symmetry that best fits a configuration of points [268]. The type of symmetry may be unclear for molecular structures, but for most morphological structures, anatomical or developmental evidence is decisive about the type of symmetry. Therefore, searching for a best-fitting type of symmetry is not a frequent task in biological applications.
4.7.2. Measure of Asymmetry for Rotational Symmetry in Flowers
A variant of this method was developed specifically for quantifying floral asymmetry [270,274]. This method is using the deviations from a regular polygon for a single set of landmarks that correspond to each other under the rotations in the symmetry group [270]. The resulting measure of asymmetry is also based on squared deviations of landmarks from a regular polygon obtained by a computation that is similar to the folding–unfolding algorithm [268]. As long as a single landmark per petal is used, this method does not distinguish between purely rotational symmetry and radial symmetry (including rotation and reflection).
This method has been applied to quantify the asymmetry in flowers of Geranium robertianum [270,274], which are radially symmetric and have five petals. One landmark at the tip of each petal was used and the asymmetry measure was computed for each flower as the deviation from a regular pentagon. To evaluate the method, this measure was compared with an alternative measure that considers the variation among petal lengths within each flower, and both measures were significantly correlated in a sample of flowers [270]. The asymmetry measure was correlated with measures of reproductive investment, as flower size and amount of pollen decreased with increasing asymmetry [274].
4.8. Outline Methods
When morphological structures have no or very few landmarks that can be located precisely, an alternative is to use morphometric methods that characterize variation of biological shapes using outlines or surfaces. Examples of methods for this include Fourier analyses [275–277], eigenshape analysis [278–280], semilandmarks [202,205,281,282], and a variety of methods of superimposing 3D surfaces to an overall best fit [104,203,204,283,284]. Note that, even though some authors have claimed that such methods are “homology-free” [285], all these approaches are based in one way or another on a one-to-one correspondence of points on the outline or surface, which is the basis for the computations of mutual fit or difference between shapes [286]. Different methods are making different assumptions about this correspondence or use it in different ways. As a consequence of these assumptions about the correspondence of points and of the calculations used by the different methods, some of them are related to each other and produce similar or identical results, whereas others may provide different results when applied to the same data [277,287–290].
When applied to structures with matching symmetry, analyses of outline or surface data do not differ fundamentally from the landmark methods discussed above. Asymmetry can be computed as left–right averages of the scores in an outline analysis, and variation among individuals can be characterized as the averages of both sides after the outline or surface on one side has been reflected. Studies of this kind have been done using elliptic Fourier analysis [291,292], eigenshape analysis [293], semilandmarks [87,169,171], and 3D-surface superimposition [104].
For structures with object symmetry, the information regarding symmetry and asymmetry is contained in a single outline or surface. It is possible to apply the same strategy as for landmark data (Figure 7): for each specimen, the original outline or surface and its mirror image are included together in the analysis that superimposes outlines or surfaces. If identified landmarks are playing a role in the superimposition procedure, these need to be relabeled before the superimposition. Following this, asymmetry can be quantified as the difference between the original and reflected outline or surface. This method has been used with semilandmarks for 2D outlines [148,294,295] and with 3D surfaces [204,296]. A similar idea was the basis for an ad-hoc method to determine the asymmetry in a single outline contour using image analysis [297].
For analyses of symmetric outlines using elliptical Fourier analysis, Iwata et al. [298] observed that one set of parameters from the Fourier decomposition of the total variation contains a component of perfectly symmetric variation, whereas the remaining parameters characterize asymmetric variation. This method for separating symmetric and asymmetric components of variation has been used in studies to characterize asymmetry and shape variation in plant leaves and other structures [191,260,299–304].
4.9. Practical Problems for Analyses of Shape Asymmetry
There are a few practical problems that concern many morphometric studies, but are especially important in studies of fluctuating asymmetry because they focus on variation that is fairly subtle. For this reason, investigators should pay attention to possible artifacts from specimen preparation and to measurement error. How specimens are aligned in relation to a camera or other measuring device is a particularly important factor, especially when collecting 2D data from specimens that are actually three-dimensional. Finally, there are a few organisms where it is not entirely clear what is up or down, left or right—clearly a crucial problem when a study is about asymmetry.
Another practical point of the utmost importance for studies of asymmetry, if there is matching symmetry, is that the parts of the left and right sides must be identified correctly and kept separate. This can be tricky, for instance, for the wings of small insects that need to be mounted on microscope slides, but it is crucial for the further steps in the study. Mix-ups among sides can invalidate the analyses and may lead to failure to detect directional asymmetry even if it exists in the sample at hand, and they also confound fluctuating and directional components of asymmetry. If samples have been collected for purposes where the effects of side are not of interest, for instance taxonomy, and it is not certain that the sides have been distinguished properly for all specimens, such samples should better not be used in studies of asymmetry. If using such samples is inevitable, investigators should make clear this fact and note that it is not possible to disentangle the effects of fluctuating and directional asymmetry.
4.9.1. Preparation and Preservation of Specimens
Many studies of fluctuating asymmetry use museum specimens or newly collected specimens that have been preserved in various ways. For instance, many studies have used dried material such as herbarium specimens, dried insects or bones. For delicate specimens, drying can result in serious distortions, for instance bending of the legs, antennae and wings of dried insects or warping of delicate bones (e.g., fish). Similarly, pressing and drying plant leaves can affect their shape noticeably [305] and may therefore have serious effects on studies of asymmetry. Many other types of specimens need to be stored in liquids such as ethanol or formalin, which changes tissue properties and also affects length measurements [306] and shape [307,308]. Even freezing can affect the shape of fish significantly [308]. Naturally, such artifacts from preservation are most serious for soft tissues such as embryos [309] or brain tissue [310]. Similarly, very small specimens such as mites [128] or the wings of parasitoid wasps [129] need to be mounted on microscope slides, which may produce artifacts due to the positioning of specimens on the slide or distortions due to the pressure from the coverslip.
To avoid misleading results in studies of fluctuating asymmetry, it is sometimes possible to prevent such artifacts altogether by using fresh specimens. If that is not possible, it is often feasible to minimize artifacts by choosing different procedures and to quantify the magnitude of effects. For instance, it is possible to humidify dried insect specimens to flatten their wings before taking images [311], a procedure that, at least to a large extent, reverses the effects of drying.
A particularly vexed problem about artifacts from preparation or preservation is that they tend to be irreversible, and therefore cannot be quantified by repeating the procedure and measurements. It may be possible to make measurements before and after preservation [305,307–310], which makes it possible to quantify any artifacts and to their magnitude in relation to the biological effects under study. An even better option is to avoid preservation altogether. For instance, for morphometric studies of leaf shape it is often feasible to use fresh material, possibly placing leaves under a glass plate to flatten them gently before taking images. All the steps in the procedure of positioning a leaf and taking images are repeatable, so that it is possible to estimate explicitly the effect of positioning in relation to the shape variation and asymmetry in the data. Such repeats can be analyzed in the same way as other components of measurement error.
The effect of preparation procedures is not always negative. Treatments such as removing scales or hairs from morphological structures or staining to enhance the contrast of different tissues can enhance the precision of landmark positions [312]. The decisions about such procedures are probably best based on pilot studies exploring different options of preparation.
4.9.2. Measurement Error
The literature on fluctuating asymmetry has long considered measurement error as a serious issue and therefore discussed possible procedures to quantify and minimize its effects [2,153,155,313]. With the advent of geometric morphometrics, the same concerns need to be addressed in studies of shape [11,13,314–317]. Measurements result from an interaction of the objects under study, the equipment used and the observer making the measurements. In addition, various steps of preparing specimens can also have an influence on the outcome. Therefore, all these factors need to be taken into consideration as possible sources of measurement error and for devising strategies to minimize it.
There are two types of measurement error: systematic error and random error. Systematic error affects all measurements made by a particular observer with the give equipment in the same way—there is a consistent, systematic deviation from the true values. By contrast, random error affects each individual measurement differently, and deviations of measurements from true values are in all directions (but not necessarily in equal amounts in all directions). The distinction of systematic and random error is useful because dealing with them requires different strategies. In general, systematic error can be reduced by appropriate set-up of equipment and careful calibration, whereas the effects of random error can be mitigated by making repeat measurements and averaging the resulting values. Both kinds of error can affect studies of asymmetry.
There are several sources of systematic error that can affect asymmetry studies. Some of them are widely known [315], such as the distortions by low-quality lenses, particularly wide-angle lenses, and parallax (the effects of viewing a specimen at an oblique angle, not exactly in alignment with the median plane; particularly relevant are the inclined optical paths of standard dissecting microscopes that are designed to provide 3D vision of objects, but not exact photography). It is relatively easy to avoid optical distortion by not using wide-angle lenses and positioning the camera as far as possible from the object, so that optical paths to all parts of the object are nearly parallel. Also, taking an image of a rectangular grid can provide a useful test for distortions (particularly near the margins of the image). 3D measuring equipment should be calibrated with objects of known dimensions (simple shapes such as cubes are particularly suitable). Not only the optics, but also other equipment can produce systematic errors: for instance, light sources that result in unequal illumination of different parts of the specimens.
There are some sources of systematic errors that are particularly relevant for studies of asymmetry. For digitizing equipment that is operated by hand, such as the MicroScribe 3D digitizer, the handedness of the observer conceivably can make a difference: a right-handed observer might point the tip of a digitizing arm to the positions of landmarks on the left and right sides of a skull in slightly different ways. Digitizing a perfectly symmetric object (if the structure has object symmetry) or exact mirror images (if the structure has matching symmetry) is a test for this effect (the test object should be as similar as possible to the structure under study—such objects might be generated with a 3D printer, provided it is sufficiently precise itself). Likewise, there might be subconscious biases when locating landmarks on images or scans of the left and right sides of biological structures. To assess this effect, it is useful to compare the landmark data to data digitized on images or scans that have been transformed to mirror images (for matching symmetry, it is even possible to reflect all images from one side in this way to avoid such a bias). This kind of systematic error is particularly serious for asymmetry studies because it could conceivably generate a systematic bias in the data that would be impossible to distinguish from subtle directional asymmetry.
A different source of systematic error that is important for morphometric studies is the definition of landmarks. Different observers may pick slightly different points based on the same definition of a landmark. Intersections of linear features such as cranial sutures of vertebrates or wing veins of insects seem to offer very precise definitions of landmarks, but even these structures have a certain width (and there are other complicating factors in many cases), so that there is a degree of ambiguity about the definition. It is helpful to write down a very precise description of the procedure used to locate each landmark. This will help to minimize the differences between the actual landmark definitions used by different observers or the changes over time for each individual observer. But even these detailed descriptions cannot completely eliminate this sort of difference. The effect of such differences can be tested by comparisons between measurements of the same objects made by different observers or by the same observer at different times.
Random error originates from many steps in the procedures for acquiring images or scans of specimens and locating landmarks. This can include the positioning of specimens relative to a camera, variation in the level of focus or inaccurately focused images, heterogeneous illumination, the pixelation of images (this is no longer a real problem with optical images, as high-resolution digital cameras now are inexpensive, but it can be a real problem for computed tomography and especially magnetic resonance images), and the accuracy of the observer in locating the landmarks. Different factors can interact: for instance, the observer may be less accurate for images that are somewhat blurred or badly illuminated.
To quantify random errors and to reduce their effects on subsequent analyses, investigators can repeat measurements of the same specimens [2,11,13,153,155,315]. Differences between replicates result from measurement error and averages of the repeats can provide values that are less affected by measurement error. It is important that all the steps of the data acquisition procedure are repeated, because all of them can contribute to measurement error. If just the digitizing of landmarks from images or scans is repeated, all components of error that stem from the other steps are ignored and the resulting estimates of measurement error may be grossly overoptimistic. For instance, in a simple study where the investigator first takes images of specimens and then locates landmarks in the images, both steps should be replicated (Figure 15).
A key question in the design of such an analysis of measurement error is how many replicates should be used at each level. In the example, two replicates are used for both the imaging and digitizing steps (Figure 15). This is the minimum of replication, which allows the investigator to use a bigger sample of specimens for the analysis with a given amount of total effort. Because measurement error should be assessed relative to fluctuating asymmetry and possibly the variation among individuals, a reasonable possibility is to use two replicates for each level in the hierarchy (Figure 15). Therefore, two replicates of each lower-level effect provide one degree of freedom within each level of the next-higher effect (e.g., one degree of freedom for the digitizing error within each image, one degree of freedom for the imaging effect within each specimen). With two replicates per level, a relatively large number of specimens can be included, so that the estimates for fluctuating asymmetry and variation among individuals also are reasonably precise. This design is preferable over analyses using one or a few specimens with many replications—such a design produces a good estimate for measurement error, but not for the biological variation. Also, taking many replicates of the same few specimens brings the danger that the observer, consciously or subconsciously, remembers peculiarities of landmarks on those few specimens and therefore may obtain measurements that appear more precise than those made on unfamiliar specimens. This would yield overoptimistic estimates of measurement error.
To analyze the repeated measurements and quantify components of measurement error, both for specimens with matching and object symmetry, Procrustes ANOVA (Section 4.4) is a flexible and powerful tool [11,13]. The hierarchical nature of the replicated data (Figure 15) implies that measurement error enters the ANOVA model as one or more nested effects, as it has been done traditionally in ANOVAs for studies of asymmetry of length measurements [2,153,155]. For instance, if two images of each specimen are taken and each image is digitized twice (Figure 15), the effect of images is nested within the individual-by-side interaction and the digitizing effect is nested within images (Table 1).
The key question concerning measurement error is not whether fluctuating asymmetry is statistically significant in the Procrustes ANOVA, because that means only that some fluctuating asymmetry is discernible despite the measurement error. Of course, such statistical significance is required for subsequent analyses to make sense, but it is not enough (if fluctuating asymmetry is not statistically significant, measurement procedures should be improved, and more replicates and ideally a larger sample size should be used). The main question of interest is how much greater fluctuating asymmetry is than the measurement error. The answer can be obtained from the F ratio for the individual-by-side effect (the ratio between the mean square of the individual-by-side interaction and the highest measurement error effect). If this ratio is high, such as the value of 25 in the example of Table 1, it is reasonable to say that measurement error is negligible. If such a result is obtained in a pilot study, it is debatable whether replicates are really necessary for the main data collection. If the ratio is lower, however, replication and averaging of the resulting values is necessary throughout the whole data collection in order to obtain sufficiently precise estimates of fluctuating asymmetry.
For pilot studies, a sample size in the order of 20–30 individuals, with twofold replication of the measurement and replication steps, is usually reasonable. Such a sample size is sufficient to provide reasonable estimates of Procrustes sums of squares and mean squares for fluctuating asymmetry and variation among individuals (note, however, that bigger samples are required for estimating the multivariate patterns of covariation for those effects). If the estimates of measurement error from such a pilot study turn out to be relatively big, replicating three or four times for the main data collection may be reasonable. Conversely, if measurement error is negligible relative to fluctuating asymmetry, the main data collection may be conducted without replicate measurements, to enable the researchers to use larger sample sizes with comparable effort (this seems reasonable for the example in Table 1, where fluctuating asymmetry exceeds imaging error by a factor of 25).
The ANOVA design with replicate measurements can further be used to compute matrices of sums of squares and cross products (SSCP) for the different levels of measurement error. Multivariate analyses of SSCP matrices of measurement error, for instance, principal component analyses, can reveal patterns of relative landmark shifts in the variation due to measurement error. These patterns can be informative about the nature of the measurement error. For instance, if the first or the first few principal components for digitizing error are dominated by relative displacements of a single landmark or a few landmarks, this is an indication that those landmarks may be difficult to localize. Improving the definition of the landmarks or, at worst, excluding the landmarks may reduce the level of error.
The analyses described here have all focused on the effect of measurement error on shape, rather than measurement error of individual landmarks, which has also been called “landmark error” [314,317,318]. Because such studies often focus on a few specimens that remain fixed over a series of repeats, these studies capture only a part of the total measurement error that occurs during normal data collection. Such analyses can be useful for refining landmark definitions or for evaluating measuring equipment. They are perhaps less suited, however, for evaluating measurement error such as it applies to studies of fluctuating asymmetry, where the primary question of interest is to understand the error that occurs during the routine data collection. Also, because the main concern is about the possible consequences of measurement error on the results of morphometric analyses, the effect on overall shape is more directly relevant than the imprecision at individual landmarks.
4.9.3. Two- versus Three-Dimensional Data
There are some biological structures that are flat, such as many (but not all) insect wings and plant leaves, so that morphological variation can be captured as 2D coordinates of landmarks without loss of any relevant information. The majority of biological structures, however, are fully three-dimensional. Representing them in 2D images involves a projection from the original three dimensions to two, resulting in an obvious loss of information. That 3D data should be used for studying 3D biological structures has long been pointed out in the morphometrics literature [319]. Yet, because 2D images are cheaper and quicker to collect than 3D morphometric data [320] and because the results from analyses of 2D data are easier to visualize [196], many morphometric studies continue to use 2D data for 3D structures.
A particularly serious problem is how to align the specimen relative to the camera or microscope. For morphometric analyses in 3D, this is not a problem because the Procrustes superimposition will find the optimal rotation in 3D, but if 2D images are made, the effects of the alignment are irreversible because the third dimension is irretrievably lost. For an intuitive appreciation of the problem, imagine a football with various areas of different colors and consider how they change if you rotate the ball slightly in different directions. The rotations produce various complex distortions of the shapes of the colored areas. Similar complex distortions occur if the alignment of a 3D morphological structure relative to a camera is altered.
The best option seems to use a set of specific landmarks to align the specimen in a precisely specified orientation—for instance, it is possible to align all specimens so that the plane defined by three specific landmarks is perpendicular to the axis of view of the camera (parallel to the image plane). A consequence of this procedure is that variation in the positions of those three landmarks relative to the other landmarks results in a change of the alignment of the whole structure. Therefore, even strict standardization of the alignment is not necessarily a complete solution to the problem (unpublished data indicate that this effect can be serious for analyses of fluctuating asymmetry).
Some studies, although concerned with variation among individuals and not asymmetry, have tried to remove the effects of variable alignment by projecting the shape data onto a subspace orthogonal to the effects of those rotations [321,322]. Because the effects of rotations are expected to be some trigonometric functions of the angles of rotation and trigonometric functions are markedly nonlinear, the linear approach of eliminating variation in some directions is at best an approximation. Moreover, because this method eliminates all the shape variation in the directions deemed to represent the effects of rotation, it harbors the danger that some genuine biological variation is also eliminated. For studies of asymmetry, which need to consider subtle morphological variation, this approach appears to be too crude.
In summary, while using 2D data for 3D structures may be possible for studies of variation among individuals and taxa with the appropriate caution [320], this is problematic for studies of fluctuating asymmetry. Equipment and methods for 3D data acquisition have become much more efficient and affordable in recent years, so that many of the arguments for using 2D data no longer apply. The perils of “flattening” 3D structures into 2D images appear to be substantial, making 3D the better choice for studies of fluctuating asymmetry.
4.9.4. Structures Lacking a Clear Orientation
Some structures or entire organisms do not have unambiguous front and back, up and down, or left and right sides. Examples are some unicellular algae [24], which appear identical when they are flipped over and where thus the left and right sides are interchangeable (as an equivalent, imagine a coin with heads on both sides). Similar problems apply to some flowers that are radially or rotationally symmetric and grow in terminal positions on a shoot, so that they do not have a clear adaxial or abaxial side.
These structures cause problems for the data collection and analysis. For the data collection, this situation has the consequence that the correspondence of landmarks is ambiguous. Defining a correspondence of landmarks therefore usually involves some arbitrary decision, such as assigning the side that is at the top of an image to be the “dorsal” side. Other correspondences then follow automatically (e.g., the “left” and “right” sides).
For the analysis, the ambiguity of correspondence makes it impossible to separate the components of fluctuating and directional asymmetry. The only possibility is to consider just the total asymmetry as the deviation from perfect symmetry. For the Procrustes ANOVA, this means that the effect that relates to ambiguous correspondence of landmarks (usually the effect of “side”) should be included as an effect nested within the effect of individuals (and not as a fixed effect as usual).
5. Fluctuating Asymmetry and Developmental Instability
Traditionally, fluctuating asymmetry has been used as a measure of developmental instability [1–6,153,155], which can be correlated to various environmental or genetic factors. Such studies have mostly used measurements of different lengths as traits. It is therefore of interest how the justifications for such a use of fluctuating asymmetry applies to shape.
This section first revisits the central argument that fluctuating asymmetry is an expression of developmental instability by reviewing its developmental origins. I then review applications that have related fluctuating asymmetry of shape to measures of stress and genetic quality. Since the advent of geometric morphometric studies of fluctuating asymmetry, many studies have used these methods to investigate whether developmental stability and canalization share the same patterns or whether they may be based on distinct sets of processes. Finally, this section provides an overview of studies that have investigated the genetic basis of fluctuating asymmetry of shape, and it examines some ideas on the special role of plasticity for fluctuating asymmetry of sessile organisms.
5.1. The Central Argument: Fluctuating Asymmetry as a Measure of Developmental Instability
The central argument why fluctuating asymmetry is a measure of developmental instability [150] is based on the assumption that corresponding structures on the left and right side are independent copies of a structure that develop under the control of the same genome and under the same environmental conditions. If development were a completely deterministic process, corresponding organs on different body sides would develop as identical copies of each other, both showing the “target phenotype” [151] for the particular genome and environment of a given individual. Because developmental processes are not completely deterministic, however, random fluctuations in developmental processes can cause deviations from the target phenotype. Such differences can occur because of the stochasticity of molecular processes due to the low number of copies of DNA and many other molecular species within cells and can translate to variability across developing tissues and organs [323–327]. Because the two copies of a structure on the left and right side (or different numbers and arrangements of copies for complex symmetries) develop separately from each other, the random fluctuations of developmental processes affect each copy separately and are thus likely to produce deviations from the target phenotype that are different from copy to copy. As a result, even if the copies of the same organ share the same genome and environment, there inevitably will be small phenotypic differences between them that manifest themselves as measurable asymmetries. Those asymmetries can be used as indicators of developmental instabilities.
This argument makes several assumptions that are not necessarily met by real biological systems. The first of these assumptions is that the left and right copies of a structure are equivalent and thus have the same target phenotype. This is the same as assuming that there is no directional asymmetry, an assumption that is clearly wrong in many instances, because directional asymmetry has been found in many empirical studies and seems to be a very widespread phenomenon [15] (see Section 3.1). As a result, the argument needs to be modified slightly: the target phenotypes for the left and right sides are not equal, but can differ. As long as a homogeneous population is available so that the target phenotypes can be estimated as the average values (an estimate of the expected phenotypic value), the deviations of individual asymmetries from the average asymmetry, fluctuating asymmetry, can be used as an indicator of developmental instability. This is the correction for directional asymmetry that is inherent in the two-factor ANOVA model that has traditionally been used in studies of fluctuating asymmetry [2,152,153,155], including studies of shape asymmetry using geometric morphometrics [11,13] and in the measures of fluctuating asymmetry based on Procrustes or Mahalanobis distance [239].
The assumption that the left and right sides share the same genome implies that somatic mutations are negligible. This may be a reasonable assumption, although somatic mutations have been demonstrated in genome-wide surveys and are known to accumulate with age in mammals [328–330], but it is unclear how much they may contribute to normal phenotypic variation. For plants, where ample opportunity for somatic mutation exists and extensive research on genetic mosaicism has been conducted, Herrera [262] reviewed the available evidence and concluded that such genetic variation is only rarely responsible for appreciable portion of within-individual variation. Overall, with some caution, it is thus plausible that left and right sides share essentially the same genetic control of developmental processes.
The assumption that the left and right side share the same environment is more problematic. Many environmental factors are heterogeneous at a spatial scale that might generate within-individual variation, including differences between the left and right sides of individuals. If phenotypic traits show a plastic response to such heterogeneity, some of the observable fluctuating asymmetry may be due to phenotypic plasticity rather than developmental instability. This possibility has been emphasized in the literature on fluctuating asymmetry before and is especially acute for sessile organisms such as plants [27,151,155,173,243]. For motile organisms, which move through their environment during their development, it is plausible that such heterogeneities will average out so that plastic responses to environmental differences between sides are negligible. With appropriate caveats, for many organisms, fluctuating asymmetry can indeed be viewed as the result of minor random variations in developmental processes and is therefore appropriate for quantifying developmental instability.
The reasoning presented here is based on the assumption that developmental differences between sides are small and both sides of an individual are within the range of normal development and phenotypic outcomes. Asymmetries due to more serious disruption of developmental processes, which may lead to malformations of organs, are likely to be different in their origin as well as their consequences. An example are deformities of the opercle in fish that can lead to pronounced asymmetries of head shape, but also have consequences on the shape of the whole body [331]. These changes may be closer to the consequences of mutations that disrupt developmental processes and thus can result in gross morphological defects [62,332,333]. Nevertheless, such phenotypes can provide valuable insights into development and evolution [334].
5.2. Developmental Instability versus Canalization: One or more Mechanisms for Developmental Buffering?
In many instances, fluctuating asymmetry is very subtle, as there seems to be a high degree of developmental precision in achieving target phenotypes. A study that quantified these effects on the positions of wing veins in flies reared under controlled laboratory conditions calculated that their scale was less than the diameter of a single cell [335]. Accordingly, the developmental processes that form the structure seem to be remarkably precise.
This precision raises the question of the nature of the processes involved. Are developmental processes inherently stable, so that there is little variation in the first place, or are there specific processes that act as buffers so that variation in earlier stages of development is not expressed as observable variation in the resulting phenotype? Are there specific processes that generate and buffer against such variation or are developmental “noise” and robustness simply a side-product of the functioning of developmental systems? The answers to these questions are still unclear. Some theoretical simulation studies have pointed out the remarkable robustness of specific systems [336], whereas others suggested that the nonlinear interactions in developmental systems are sufficient to control developmental buffering [160].
Some empirical studies, using geometric morphometric methods, focused on molecular chaperones such as Hsp90 and other heat shock proteins [124,126,177,337] and genes involved in various ways in the development of the structures under study [62,332,338] and found variable effects of those genes on shape asymmetry. Additional studies have found pronounced effects of mutations in various genes on the fluctuating asymmetry in the size of structures and, even though they have not specifically investigated shape, sometimes found evident asymmetries of shape [333,339,340]. The observation that some of these effects depend on the genetic background [177] suggests that interactions among multiple components of the developmental system are important. In addition to these experiments based on candidate genes, studies using genome scans have tended to find distributed effects with unclear relations to specific processes [77,125]. Overall, therefore, a variety of processes may be involved in generating and buffering against developmental variation that manifests itself as fluctuating asymmetry.
It is important to keep in mind that the fluctuating asymmetry observable in morphological structures is the combined effect of the developmental fluctuations and any mechanisms that might buffer against them. Untangling the contributions of the developmental “noise” and the effects of buffering is very difficult, because they are inevitably intertwined in the observable variation. Some rare glimpses on the relative contributions of the two processes are provided by quasi-experimental situations like diseases causing localized perturbations of development [35] or actual experimental manipulation altering development on one side of the structure [341,342]. Nevertheless, much about the specific mechanisms involved in the origin of developmental fluctuations and the buffering processes that counteract them remains unclear.
It is possible, however, to gain useful biological insights even from the aggregate effect of developmental noise and buffering. Some further evidence on the nature of developmental stability and canalization is available from comparisons of fluctuating asymmetry and individual variation over different ages [343–348]. Studies using the methods of geometric morphometrics found fluctuating asymmetry of fetal mice to decrease with age [251] or reported diminishing individual variation over early postnatal development in various rodents [219,349,350]. There is also unexplored potential for future analyses of the regulation of shape variation, because some studies used longitudinal data [349,351]. Analyses that explicitly address the covariation among the changes between successive ontogenetic stages can shed light on regulatory phenomena, but so far have only been used with traditional morphometric data [352–357].
Because geometric morphometric approaches offer the possibility to visualize and compare the patterns of covariation among landmarks, they have been used prominently to investigate the nature of developmental buffering and have stimulated new questions and ways to answer them. In particular, morphometric methods have been used widely to address the question whether developmental stability, the buffering against intrinsic developmental fluctuations, and canalization, the buffering against environmental and genetic variation among individuals, are based on the same process or whether different mechanisms are involved. Because morphometric analyses of asymmetry provide separate estimates of the patterns of individual variation and fluctuating asymmetry [11,13], it is possible to use comparisons of these patterns as a way of examining whether canalization and developmental stability are based on distinct processes or whether they may have a common origin [42,175,176]. If the same processes are involved at both levels, similar patterns of variation are expected. By contrast, a discrepancy between the patterns of fluctuating asymmetry and individual variation indicates that different processes must be involved.
Many studies have examined the relation between developmental stability and canalization by comparing covariance matrices for fluctuating asymmetry and individual variation, because the patterns of covariation at the two levels provide information on the underlying processes. Comparisons are usually conducted with matrix correlations and statistical significance is assessed with matrix permutation tests, adapted for landmark morphometrics [11,13,254]. Matrix correlations can either be computed from the entire covariance matrix or they can exclude the diagonal blocks of variances and covariances of the coordinates of each landmark, depending on whether the variation across the whole structure or just the pattern of covariation among landmarks is of interest [13,56]. The matrix permutation test uses permutations of landmarks rather than individual coordinates (i.e., the x, y, and possibly z coordinates of each landmark are kept together because they are not interchangeable among landmarks) [11]. Some special steps are necessary for covariance matrices between symmetric and asymmetric components of variation if the structure under study has object symmetry [13]. Because the symmetric and asymmetry components occupy orthogonal subspaces of the shape space of the whole structure, whenever there is variation in one of them, there cannot be corresponding variation in the other, and all matrix correlations are zero. To avoid this problem and still examine whether the patterns of symmetric variation and asymmetry are similar, it is possible to focus just on the covariation among the paired landmarks on one side of the structure [13].
This approach has been applied in a growing number of studies, with somewhat mixed results. Many studies have found matrix correlations between covariance matrices for fluctuating asymmetry and individual variation that are statistically significant, but of rather variable strengths [11,16,44,49,55,56,67,72,79,82,97,106,119,139,167–169,172,173,177,358]. A few studies have reported a mix of significant and non-significant results for analyses of multiple samples or structures [54,75,120,174], and some other studies found only non-significant test results [13,42,73,78]. In a majority of studies, therefore, there seems to be some degree of resemblance between the patterns of fluctuating asymmetry and individual variation, but usually no perfect congruence, and in some cases it is not possible to rule out the null hypothesis that they are altogether unrelated.
What conclusion can be drawn from these studies? The variable outcomes of different analyses have led authors to draw different conclusions, ranging from the possibility that developmental stability and canalization are independent of each other [42] to the suggestion that they may share the same developmental basis [56]. Just counting the number of studies that did or did not find significant matrix correlations between covariance matrices of fluctuating asymmetry and individual variation cannot settle the debate because it ignores the great variation in the strength of association among the studies with positive results. It is therefore preferable to withhold general conclusions on the relation between developmental stability and canalization for the time being.
5.3. Developmental Instability of Shape in Relation to Stress and Genetic Quality
The goal of many studies of fluctuating asymmetry has been to use it as a measure of developmental instability for correlating it with various measures of stress, individual quality, and fitness [2,153,155,165,243,359–366]. The idea that drives such studies is that stress or inferior quality of individuals leads to greater amounts of developmental noise or a diminished capacity to buffer against developmental fluctuations, and that individuals with better ability to buffer against developmental perturbations are generally more vigorous or resilient and therefore have higher fitness.
A well-known practical problem with this approach is that developmental instability is difficult to estimate from just one measurement each from the left and right sides of an organism—it is essentially the same as estimating a variance from just two data points, which is possible but very imprecise [6,158,159,367,368]. A possible solution for this problem is to use the fluctuating asymmetry of multiple traits simultaneously to improve this estimate [155,369]. Of course, a condition for this approach to work is that the fluctuating asymmetries of different traits provide independent information concerning developmental instability, which means that the traits should be developmentally independent of each other [155].
Because geometric morphometrics considers all aspects of the shape variation in a structure, not just particular traits, using it seems an attractive idea to use indices of fluctuating asymmetry of the shape of entire structures as measures of developmental instability. The individual measures of fluctuating asymmetry for shape based on Procrustes distance or Mahalanobis distance [11,239] are indices that can be used for this purpose (Section 4.5). It is important to note, however, that morphological integration is likely to be a significant problem for such studies. Because the parts of morphological structures are developing in a coordinated manner, the fluctuating asymmetries of different aspects of shape are not mutually independent, but are correlated to a greater or lesser extent. Often, much of the total variation is concentrated in just a few of the dimensions of the shape space [179,254], so that the data do not occupy much of the theoretically available dimensionality. In other words, morphological integration acts as a constraint that makes some aspects of shape variation biologically inaccessible. Whereas this structured variation provides an opportunity for using fluctuating asymmetry to investigate the developmental basis of morphological integration (Section 6), it can impede the use of individual measure of fluctuating asymmetry as estimates of developmental instability.
Nevertheless, a growing number of studies have used the individual measures of fluctuating asymmetry of shape and correlated them with various measures of environmental or genetic stresses and individual quality. Because of the wide range of questions that have been addressed and the diverse organisms used in these studies, it is fairly difficult to summarize the results.
Environmental stress has been the focus of many studies of shape asymmetry. Several studies found greater fluctuating asymmetry in disturbed than in undisturbed habitats for skull shape of voles [250], in areas of worse rather than better climatic suitability for skull shape of Akodon rodents [370], in urban than in rural habitats for head shape of lizards [106], in polluted than unpolluted habitats for crab carapace shape [253] and for mandible shape of shrews [371]. Studies of the larval mentum and adult wings in chironomid midges showed that pollution in the rearing environment had no or only limited effects on fluctuating asymmetry [130,131] or that there was more fluctuating asymmetry in offspring reared in unpolluted sediment in the laboratory than in the parental generation collected from polluted sediment in the field [103]. Temperature stress had no significant effect on fluctuating asymmetry of body shape in bulb mites [372], but fluctuating asymmetry of shape has been shown to be influenced by temperature in aphid [164] and Drosophila wings [62,121]. Fluctuating asymmetry for skull shape in yellow-necked mice was found to be higher in sites with high radioactive contamination from the Chernobyl nuclear disaster than in less contaminated sites [53].
A number of studies have investigated the effects of toxins on fluctuating asymmetry of shape. In experiments with cactus-breeding species of Drosophila, one species had increased fluctuating asymmetry of wing shape in the non-preferred cactus host, but other species showed no difference or even had greater fluctuating asymmetry in the primary host [118,123]. Additional experiments demonstrated that alkaloids in the cactus tissue can cause increased fluctuating asymmetry and abnormal wing phenotypes [119]. Not all toxins affect fluctuating asymmetry of shape: an experiment showed that even applications of sodium pentachlorophenate that were sufficiently severe to suppress cranial growth of zebrafish did not produce increased fluctuating asymmetry of shape [137]. Administering TCDD had no effect on fluctuating asymmetry of shape in mouse mandibles, but affected average shape [43], whereas the same toxin both increased fluctuating asymmetry and changed the average shape of molar teeth [373].
Disease can be viewed as a different kind of stress. A very large study examined the correlation between fluctuating asymmetry of facial shape in children and their past record for various categories of ill-health, but found no association between facial asymmetry and health [252]. A study of asymmetry of human skull shape found that persons who died from degenerative diseases, on average, had higher fluctuating asymmetry than persons who died from infective diseases or from other causes [90].
In humans, fluctuating asymmetry can reflect the influence of various factors and may correlate with behavioral and reproductive traits. In a study using a large combined sample from different Latin American countries, several factors were correlated to facial asymmetry: the strongest correlation was with age, but ethnic ancestry, heterozygosity, body mass index and height, as well as sex also had appreciable and significant effects [108]. Several studies have examined whether facial asymmetry is related to whether faces are rated as attractive by the subjects themselves or by other viewers, and some found a significant association [57,249,295,374], whereas others found no association [102,105] or a weak association only for male but not female faces [247]. Some analyses showed an association between fluctuating asymmetry and facial femininity or masculinity in humans [375], but others did not [102,374], nor was there a correlation between femininity or masculinity of skull shape and fluctuating asymmetry in baboons, chimpanzees, and gorillas [110]. Also, no correlation was found between facial fluctuating asymmetry and the ratio of second to fourth digits, which relates to prenatal exposure to sex hormones [375,376]. By contrast, short-term effects of hormonal levels on asymmetry have been shown, as the asymmetry of facial shape changes during the menstrual cycle of individual women [294]. Finally, some human behavioral traits are also correlated with fluctuating asymmetry of facial shape, such as the tendency to cooperate or defect in the “prisoner’s dilemma” game [374,375], some aggressive behaviors in adolescents [248], and personality traits [377,378].
Fluctuating asymmetry of shape has also been related to reproductive traits and fitness in a few studies from a very wide range of organisms other than humans. For bulb mites, a negative relation between fluctuating asymmetry and fecundity was found, indicating that more symmetric individuals tend to have more offspring, but it was statistically significant only in one of two generations included in the study [128]. A study of parasitoid wasps yielded no evidence for an association between fitness and fluctuating asymmetry of wing shape [129]. Similarly, in humans, no significant correlation was found between fluctuating asymmetry of facial shape in postmenopausal women and the number of their children or pregnancies [295]. In plants, one study presents evidence that asymmetry of floral shape is correlated with measures of overall plant vigor and pollen number and viability, and also that it may affect the rate of visits by pollinators [274]. Also, asymmetry of the winged fruit of ash trees can affect flight duration and thus dispersal distance [300]. Overall, these few studies suggest that the link between fluctuating asymmetry of shape and reproductive fitness is rather tenuous, but more and larger studies may be worthwhile.
Another traditional field of application for fluctuating asymmetry is its relation to heterozygosity [379]. Several studies have used the shapes of mouse skulls and mandibles from hybrid zones, with rather variable results, including reduced fluctuating asymmetry in hybrids [42], no difference [60] or asymmetric patterns including a gradient [70]. Relations between fluctuating asymmetry of shape and hybridization have also been observed in other systems, including oak leaves [148], Drosophila wings [120,122], but not in some others such as Triatoma bugs [76].
Heterozygosity relates to population genetic structure and has clear implications for conservation, and its relation to fluctuating asymmetry is also of interest in that context. There is a negative correlation between heterozygosity and fluctuating asymmetry of shape for the mandibles of shrews on Scottish islands and the mainland, but this relation is substantially influenced by the population on the smallest island, where heterozygostity and asymmetry are highest [61]. In increasingly fragmented habitats, different species of insects seem to respond differently in terms of the fluctuating asymmetry of shape [81,136]. Finally, heterozygosity is also one of the factors that has been found to influence fluctuating asymmetry of facial shape in humans [108,134], but a large study in a European population found no association between heterozygosity and asymmetry [380].
Overall, these correlations of fluctuating asymmetry with various measures of stress or genetic quality are very heterogeneous and many are rather tenuous. Whereas fluctuating asymmetry of shape is relatively easy to measure, these results suggest that, despite its multivariate nature [369], it is not a reliable indicator of environmental stress or genetic quality.
5.4. Allometry in Fluctuating Asymmetry
One of the factors that can influence the pattern and amount of fluctuating asymmetry is allometry, the relation between size and shape. This can occur in different ways: differences in size of whole organisms can have an effect on the developmental instability and thus the fluctuating asymmetry, or the fluctuating asymmetry of size may be associated via an allometric relation with fluctuating asymmetry of shape.
The first type of size dependence of fluctuating asymmetry, where the size of the whole organism or of the trait under study is related to the amount of asymmetry, has been discussed extensively in the literature on asymmetry of traditional measurements [2,153,155,381]. In the literature on geometric morphometrics and asymmetry, as far as I know, this topic has not been discussed at all. That is understandable because the Procrustes superimposition partly removes effects of the size of the structure (as far as they are isometric) and also because analysis and correction of such allometric effects on asymmetry would be quite difficult (or at least tedious) in the context of geometric morphometrics.
Conversely, studies of fluctuating asymmetry of shape have quite often examined the second type of allometry, which does not exist for analyses of asymmetry of scalar traits such as distances. For asymmetry of shape, it is relevant to ask whether shape differences between the left and right sides might be allometric consequences of the asymmetry of size. To address this question, it is possible to use the standard approach to allometry in geometric morphometrics, a multivariate regression of shape on size [382–384], using the signed left–right difference of the shape variables as the dependent variables and the signed left–right difference of centroid size as the independent variable [11,16,44,49,56,83,95,97]. Note that this approach is applicable only for matching symmetry because, in structures with object symmetry, the two sides do not have separate size measures and size differences between left and right sides are an aspect of shape.
5.5. Inheritance of Fluctuating Asymmetry
The genetic basis of fluctuating asymmetry has been extensively discussed from a range of different perspectives [385–389] because it is important for many of the traditional applications of asymmetry studies. Genetic studies of fluctuating asymmetry are complicated by the fact that the measurable asymmetries themselves are of non-genetic nature: what is of interest, therefore, is the genetic basis of developmental instability, the tendency of organisms with particular genotypes and in the given environment to produce left–right asymmetry. The most direct way to implement experiments that reflect this situation is to use model organisms where it is easy to obtain many individuals with identical genotypes [52,56,77,124–126], but traditional approaches from quantitative genetics can also be used, such as parent–offspring regression [128], analyses of variation among inbred lines [85], or pedigree-based methods [85].
Quantitative genetic analyses for fluctuating asymmetry of shape have obtained low estimates of heritability sometimes statistically indistinguishable from zero [85,128]. This agrees with findings from traditional measurements [388]. Also, experiments in Drosophila using artificial selection for higher or lower fluctuating asymmetry for indices computed from wing measurements found low estimates of heritability that were significant in one experiment [390] but not in another [391]. Results from statistical models suggest that these findings are in line with theoretical expectations and that it is very challenging to estimate the heritability of the developmental instability that underlies the observed fluctuating asymmetry with the sizes of experiments that are normally used [389]. Experiments comparing fluctuating asymmetry among inbred strains have regularly found significant differences, and therefore indicate that there is a genetic basis to fluctuating asymmetry for the shape of Drosophila wings [56,85] and mouse skulls [135].
Several studies have mapped quantitative trait loci with effects on fluctuating asymmetry in mouse mandibles [45,107,392], mouse skulls [64], Drosophila wings [77], and human faces [98]. These studies found at least some loci with effects on fluctuating asymmetry, but it is likely that such analyses have limited statistical power with the experimental sizes that are feasible in most cases. Nevertheless, despite these limitations, it is conspicuous that some of these studies [45,107,392] as well as analyses using distance measurements [393], found that dominance and epistasis played an important role for effects of these loci on fluctuating asymmetry [387,388].
The prominent role of dominance and epistasis matches the results of simulations that used models of developmental processes to investigate the genetic architecture of fluctuating asymmetry [160]. In a simple model of a reaction–diffusion system, the trait is the distance from a morphogen source within which the concentration exceeds a certain threshold [394]. The model parameters (the activity of the morphogen source, background level, decay rate, diffusion rate, concentration threshold, and time from initiation to cessation of the process) are each controlled by a separate locus with two alleles. The result of this is that the phenotypic value is a somewhat nonlinear function of each of the parameters. Because the phenotypic values for heterozygotes are not exactly midway between the homozygotes, there is some dominance for each of the loci [160,395,396]. For different values of each parameter, controlled by one locus, the effects of the loci controlling the other parameters change, so that there is clear epistasis for the phenotypic values [160]. When a small amount of stochastic variation, independent of the genotype, is added to the parameters of the model, fluctuating asymmetry can be simulated by computing pairs of values as the left and right sides and taking their difference. Because of the nonlinear nature of the model, different values of the developmental parameters result in different phenotypic asymmetries. Also, dominance and epistasis are strong for the asymmetry values too [160].
The main results of these simulations do not depend on the specific system, but apply to any model that contains nonlinear developmental mapping, that is, nonlinear relationships between developmental or physiological parameters and the resulting phenotype [150,160,396]. Nonlinear relationships are widespread, not just in reaction–diffusion systems [160,336,394,395,397]. Given a nonlinear developmental mapping function, the slope of the function can differ between different genotypes (Figure 16). The slope of the function at each value matters, because it indicates the sensitivity of the phenotype to small changes in the developmental parameter or, in other words, developmental instability. If the slope differs for different genotypes, the expected phenotypic response to small perturbations of the developmental system differs too. This means that different genotypes can have different developmental instability, and therefore nonlinear developmental mapping is sufficient to explain genetic variation for developmental instability (Figure 16). This reasoning also implies that there is no need for special genes that control developmental instability: any gene affecting a developmental parameter that maps nonlinearly to the phenotypic trait can have an effect on developmental instability [160].
The measure for developmental instability is the absolute value of the slope of the developmental mapping function for the genotype and environmental conditions of interest (Figure 16, blue tangent lines: the slopes for three genotypes). It is the absolute value of the slope that matters for developmental instability because the signs of the perturbations of developmental parameters are random. It matters whether the slope is steep or flat, not whether the curve goes up or down. For instance, both U-shaped and inverse U-shaped functions have regions of high developmental instability on either side of a central section with low developmental instability (at the bottom of the “valley” or top of the “hill” of the developmental mapping function).
Depending on the shape of the developmental mapping function, the heterozygous genotype of a given locus may have a slope that is not exactly intermediate between the two corresponding homozygotes, but closer to one of them (e.g., Figure 16) or more extreme than both (e.g., possible for U-shaped or sigmoid functions). This means there can be dominance as well as over- or underdominance for developmental instability [160]. It also means that the dominance for developmental instability is linked in some way to the dominance for the phenotypic value itself. If there are multiple developmental parameters in the model, the developmental mapping function is a surface over the space of parameters. Depending on the curvature of this surface, changes in the values of one parameter can cause alterations in the mapping function for other parameters [160]. From a genetic perspective, this means that the effects of genes that influence the values of one parameter can alter the phenotypic effects of genes that alter other parameters in the model. In other words, the effects of genes controlling different developmental parameters interact with each other, or there is epistasis between them [160]. And again, the epistasis for the trait value can bring about epistasis for developmental instability because the change of the developmental mapping functions may involve changes of slopes. Also, even for a single developmental parameter that is under the control of two or more loci, nonlinear developmental mapping can bring about epistasis among those loci for developmental instability.
This reasoning has clear implications for studies of the genetic architecture of developmental instability [150,160]. Above all, it can account for the prominent role of dominance and epistasis for fluctuating asymmetry that have been found in searches for quantitative trait loci [387,388]. It also can explain the relationship between fluctuating asymmetry and heterozygosity and the role of coadapted gene complexes, which both have been prominent themes in the literature on fluctuating asymmetry [379,385].
Note a further implication of the model: an environmental change that either changes the shape of the developing mapping functions (the curve in Figure 16) or that can change the values of developmental parameters for a particular genotype (horizontal shifts of the positions of genotypes in Figure 16) can also change the developmental instability of any given genotype or the genetic architecture of developmental instability in a population. This is a somewhat humbling thought with regard to interpreting the results of different empirical studies or the replication of experiments.
So far, this discussion has considered models in which the phenotype is represented by a single scalar trait. Yet organismal shape is an inherently multidimensional feature, so that it is necessary to consider briefly the implications of these models for such complex phenotypes. For simple scalar traits, the slopes indicate the steepness of the inclines of the developmental mapping function and possibly the direction of steepest inclines in relation to the coordinate system of developmental parameters. With multidimensional phenotypes, the developmental mapping function represents the relation between the space of the developmental parameters and the phenotypic space (the shape space in studies using geometric morphometrics). Some aspects of the phenotype might covary most with some set of developmental parameters but less with others, so that different phenotypic aspects might be more or less associated with specific developmental processes and vice versa. Alternatively, there might be less flexibility, but a single dominating set of features accounting for most or all phenotypic variation may be linked with a feature encompassing all developmental variation. The focus has therefore shifted from developmental mapping to the patterns of covariation among traits and parameters. In the context of geometric morphometrics, tools such as partial least squares analysis [398] between shape and developmentally relevant quantities or a multivariate regression [382] of shape on a set of hypothesized developmental parameters could be used for exploring the developmental mapping in empirical data. Also, because phenotypic variation from random perturbations in the developmental system is likely to arise predominantly in the directions of steepest inclines of the developmental mapping functions, these can possibly be identified from the shape features associated with the most fluctuating asymmetry, as they can be estimated from principal component analyses of fluctuating asymmetry [11,13]. In conclusion, it emerges that geometric morphometric analyses can help to provide local estimates of the directions of developing mapping functions for shape. In combination with comparative and experimental approaches, it is also possible that morphometric methods can be used for exploring the larger-scale topography of developmental mapping functions.
6. Fluctuating Asymmetry and Developmental Integration
Because geometric morphometrics offers the possibility to study patterns of covariation among landmarks, it has opened a wide range of new applications for fluctuating asymmetry in the study of morphological integration [179,399]. After some pioneering studies of integration in fluctuating asymmetry [400,401], interest in the topic grew quickly since the late 1990s, mostly in the context of evolutionary developmental biology, where analyses of covariation of fluctuating asymmetry, particularly in combination with the methods of geometric morphometrics, are now a standard tool in the study of morphological integration [11,16,17,42,44,49,51,55,135,168,169,176,251,402,403]. The rationale behind using fluctuating asymmetry in studies of morphological integration is that it can provide information on the developmental origins of covariation among traits [17,404]. This section will summarize the reasoning behind this approach and provide an overview of applications.
6.1. Developmental Origins of Covariation between Morphological Traits
To infer information about the development of traits from morphometric data, the main source of evidence is the covariation among traits. Therefore, it is useful to consider how this covariation originates in development. A range of theoretical models of developmental processes have been developed to consider this and related questions [405,406]. These models contain different scenarios how covariation between traits results from developmental processes.
Riska [405] formulated a model in which a precursor tissue is divided into two parts that subsequently give rise to a different trait each (Figure 17a). Because of the shared development before the partitioning of the precursor, variation that affects those early steps (lightning bolt in Figure 17a) has a joint effect on both traits that can manifest itself as covariation between the traits. Division of a precursor tissue is not the only way of generating such covariation. Another model contains two separate developmental pathways that each produce one trait, and which are connected by a signaling interaction from one pathway to the other (Figure 17b). The signaling interaction can pass variation from “upstream” in the pathway from which the signal originates to the other pathway and thereby generate covariation between the two traits. Both these ways of generating covariation between traits involve direct interactions between the pathways from which the traits originate: the splitting of a single pathway into two or the signaling from one pathway to the other. In both models, the interaction transmits variation, including variation that arises within the “upstream” part of the pathway itself, directly to multiple traits. Therefore, these models can be summarized as mechanisms that generate covariation between traits by direct interactions between developmental pathways [17,404]. Additional models for the origin of covariation from direct interactions between pathways are conceivable (e.g., competition between growing tissues for some resource [342,407]) and will have similar implications.
A different situation is the model of covariation between traits from parallel variation in separate developmental pathways (Figure 17c). The covariation originates from the simultaneous effect of some external source of variation on two separate developmental pathways [17,404]. Sources of variation may be environmental, such as variation in temperature or nutrition, or they may be genetic, such as the occurrence of different alleles for a gene that has some role in both pathways. There is no interaction between the pathways, which may be in distant parts of the organism. Therefore, variation from within one of the pathways can only affect the trait that emerges from that pathway, but cannot generate covariation between traits.
Distinguishing the two modes of covariation clearly is important if the purpose of a study is to identify developmental basis of morphological integration, but it also matters because the two modes of covariation have different evolutionary implications. For covariation by direct interaction of developmental pathways, the source of variation and the origin of the association between traits are separate from each other. The source of variation just needs to act “upstream” of the interaction in order to transmit its effects to multiple traits through the interaction between pathways. This also means that the interaction can affect different sources of variation—genetic, environmental or spontaneous fluctuations of the developmental processes themselves. By contrast, for parallel variation of separate developmental pathways, the source of variation and the association between traits are inseparable because the association originates from the simultaneous effects of variation on different pathways. Therefore, different sources of variation may produce different associations among traits. Both modes of covariation can produce pleiotropy, joint effects of single genes on multiple traits, but they will have different consequences in populations and evolving lineages [404]. Distinguishing the two modes is therefore important for developmental, genetic and evolutionary studies.
In practice, how can the two modes be distinguished? Covariation by parallel variation of separate developmental pathways relies on a source of external genetic or environmental variation. Therefore, strictly controlling for environmental variation by rearing organisms under constant laboratory conditions and using genetically identical individuals is a possibility, but is restricted to the standard model organisms. Another strategy is to try to focus on variation originating from inside the developmental pathways themselves, because this variation can only be transmitted among traits by direct developmental interactions. Fortunately, fluctuating asymmetry meets the requirements of both these strategies: the left and right sides of individuals share the same genome and very nearly the same environmental conditions and, because the differences between the sides originate from random fluctuations in developmental processes, the variation arises from within the developmental pathways that build the structures under study. Therefore, covariation of fluctuating asymmetry in different traits must be exclusively due to direct developmental interactions between pathways that generate those traits [17,404].
The comparison of patterns of variation for fluctuating asymmetry and individual variation therefore is a useful tool for making inferences about the developmental basis of morphological integration. Whereas the covariation in fluctuating asymmetry is exclusively due to direct interactions between developmental pathways, the covariation for individual variation usually is expected to be a mix of contributions from direct interactions between developmental pathways and parallel variation of separate pathways. There is no direct way to quantify the relative contributions of the two modes to the total covariation of traits among individuals, but it is plausible that direct developmental interactions play a primary role for all covariation if the patterns of covariation of fluctuating asymmetry and individual variation are similar [17,404]. This is one of the main rationales for an increasing number of comparisons of the patterns of covariation between fluctuating asymmetry and individual variation [254].
6.2. Morphometric Analyses of Covariation of Fluctuating Asymmetry
The comparisons between patterns of covariation for fluctuating asymmetry and individual variation used in the context of developmental integration are similar to those in the context of developmental stability and canalization (cf. Section 5.2). Accordingly, many studies have used matrix correlation and the associated matrix permutation tests [11,13] or similar statistical approaches. Many such studies have found related patterns for fluctuating asymmetry and individual variation [11,16,44,49,55,56,67,72,79,82,97,106,119,139,167–169,172–174,177,358]. Such results support the idea that direct developmental interactions make a substantial contribution to the patterns of integration among individuals. Nevertheless, the fact that a handful of other studies did not find significant associations between the two levels [13,42,73,78] is a reminder that general conclusions are elusive. Also, some of the matrix correlations found in these studies, although statistically significant, are not very high—the patterns of variation for fluctuating asymmetry and individual variation often are clearly related but they are not the same. Accordingly, it appears that direct developmental interactions do play an important role in shaping the patterns of integration for morphological traits, but parallel variation of separate developmental pathways also contributes some of the covariation.
If there are many covariance matrices to consider, for instance if there are different species or genotypes included in a study, the comparison among them by pairwise matrix correlations is very tedious. An alternative approach is to conduct an ordination analysis by principal coordinate analysis based on a suitable measure of distance between covariance matrices, which yields scatter plots in which the spatial arrangement of points represents the relations among covariance matrices. The first such analysis used a distance measure calculated as one minus the matrix correlation between covariance matrices [177], and alternative measures were proposed subsequently [408,409]. The statistical properties of these distance measures are not well understood, but some empirical comparisons have found somewhat similar but not identical patterns [73,349]. This approach has been applied to comparisons involving fluctuating asymmetry and individual variation [62,73,117,177]. Although no firm conclusions can be drawn from these few studies, they suggested intriguing patterns such as systematic differences between the patterns of fluctuating asymmetry and individual variation [62,117], as well as a possible tendency for less variable patterns of fluctuating asymmetry [177]. Overall, it seems promising to use this approach in conjunction with large-scale experimental or comparative studies.
In addition to these overall comparisons of patterns of variation, geometric morphometrics offers a range of different analyses that focus on different aspects of morphological integration [9,254]. For instance, principal component analysis extracts the main patterns of variation in a structure and provides information about the dimensionality of variation, which are important aspects of integration [254,410]. For this reason, many studies have conducted principal component analyses of fluctuating asymmetry, which provide estimates of the patterns and dimensionality of integration due to direct interactions among developmental pathways [11,16,44,49,52,106,167,168].
An important task in studies of developmental integration, of course, is the analysis of covariation of fluctuating asymmetry between different structures. Both the strength and the pattern of this covariation are of interest. To quantify the strength of integration between the shapes of different parts, the RV coefficient [411] can be used, which is an index of covariation between sets of variables that is a multivariate generalization of a squared correlation coefficient and has properties that make it suitable for geometric morphometrics [170]. Simulation studies [412,413] have shown that the RV coefficient can be upwardly biased, particularly if sample size is small and the dimensionality of the data is high (similar biases also occur for other measures of covariation [414], and notably apply to the squared correlation coefficient as well). Therefore, some caution is advisable when comparing strengths of integration between different structures, particularly if the data differ in sample sizes and dimensionality. Notably, for comparisons of RV coefficients between fluctuating asymmetry and individual variation that are computed from the same datasets, this bias is not a serious problem because the sample sizes and dimensionalities are nearly or exactly the same and the bias therefore has the same effect on both estimates. The RV coefficient has been used to quantify integration of fluctuating asymmetry and individual variation [63,170,415].
The patterns of covariation between structures or between parts of the same structure can be investigated with partial least squares (PLS) analysis [16,44,49,398,414,416,417]. PLS analysis decomposes a matrix of covariances between two blocks of variables into pairs several axes so that the resulting new variables have maximal covariance with each other. Each PLS axis in one block is correlated in the other block only with the PLS axis of the same pair, so that the PLS axes can be inspected pair by pair. In the context of geometric morphometrics, each PLS axis is associated with a particular shape change. The shape changes of the first few pairs of PLS axes are the dominant patterns of covariation between the blocks, and only a few pairs often account for the bulk of the total covariation between blocks. Statistical significance of covariation can be assessed using permutation tests [44,398]. If covariation between two regions within a single configuration of landmarks is the subject of a PLS analysis, so that the two blocks of variables are landmark coordinates that have undergone the same Procrustes superimposition together, the permutation test needs to be adjusted by including the Procrustes fit in each round of the permutation test to take into account the effect of the joint superimposition on the covariation between parts [49,170]. PLS analyses have been widely used to examine patterns of integration between parts, and many studies have compared PLS analyses for fluctuating asymmetry and individual variation [16,44,49,63,74,80,415].
Modularity [418–421] is related to morphological integration: in a modular structure, the modules are integrated internally but relatively independent of one another, so that integration is strong within modules but weaker between them [170,179]. Some authors have argued that modularity facilitates evolutionary change [418–421], a hypothesis that has been investigated with the methods of geometric morphometrics [172,422–424]. Also, some authors have hypothesized that the patterns of genetic and developmental modularity should evolve to match the patterns of functional modularity [399,419,425–427]. Clearly, this “matching hypothesis” [428] provides a rationale for investigating the relation between modularity of fluctuating asymmetry, which indicates the developmental basis of modularity, and modularity among individuals or genotypes. If a hypothesis of modularity is available, based on functional, anatomical or developmental considerations [72,178,179,428], it can be tested using geometric morphometrics [170]. If the hypothesis is true, it is expected that subdividing the landmarks according to the modules to which they belong will result in a weak covariation among the resulting subsets. By contrast, if the landmarks are partitioned haphazardly into subsets that are not congruent with the true modules, the strong within-module integration will produce a strong covariation between these subsets. By comparing a multivariate measure of association, such as the RV coefficient, for the subdivision that corresponds to the hypothesis and a large number of alternative partitions with the same numbers of landmarks it is possible to test the hypothesis of modularity [170]. If the hypothesis holds, the association between subsets corresponding to hypothetical modules should be smaller than the association between random subsets of landmarks. By contrast, if the hypothesis is false, there is no expectation that the covariation between hypothetical modules should be weaker than for random partitions of landmarks. Therefore, the test can be conducted by obtaining the distribution of RV coefficients for a large number of alternative partitions of the landmarks into subsets of the same sizes as the modules in the hypothesis [170]. This method of comparing a measure of association among alternative partitions can be used for fluctuating asymmetry as well as for individual variation, and a growing number of studies have applied it to both levels [67,72,74,75,82,97,101,106,170,172,174].
In summary, this brief overview demonstrates that the standard methods of geometric morphometrics as well as the more specialized tools such as tests for modularity can all be applied to data for fluctuating asymmetry [254]. Analyses of fluctuating asymmetry can therefore be used as an integral part of multilevel analyses of morphological integration [429] including also individual variation, interspecific comparative data providing information on evolutionary diversification and perhaps other levels, if they are available. Some first examples of this kind of study exist [72,168,172,173], and it can be expected that others will soon appear.
6.3. Evolutionary Implications
The distinction between covariation from direct developmental interactions and from parallel variation of separate developmental pathways is not just of interest for its own sake, but has also important evolutionary implications [404]. In an evolutionary context, the focus of attention is the origin of pleiotropy, the genetic association between traits, because it is a key determinant for evolutionary change by natural selection or random drift [425,430–432]. The two modes of covariation have consequences for the evolutionary effects of pleiotropy. It is easiest to appreciate these consequences by considering what happens if there is a change in the mechanisms that produce covariation and how frequent such changes may be [404].
To understand the consequences of changes in direct interactions between pathways, we need to ask how a changed interaction between pathways can affect the covariation between the traits they produce. Therefore, it is useful to reconsider the models used to introduce the idea of direct interactions (Figure 17a,b), but to add a change in the interactions themselves (Figure 18). If there is an evolutionary change of how a precursor tissue is partitioned (orange lightning bolt in Figure 18a), the way in which variation from “upstream” in the pathway (yellow lightning bolt in Figure 18a) is transmitted to the traits may be changed. Such a change has an effect on all the variation passed through the pathway and therefore may alter the patterns of pleiotropic effects for many genes that are active in the pathway. Similarly, a change in the signaling from one pathway to the other (orange lightning bolt in Figure 18b) can affect how variation is transmitted for all the variation originating in the upstream portion of the left pathway (yellow lightning bolt in Figure 18b). Because the source of variation is separate from the origin of covariation, the interaction between pathways, a single change in this interaction can simultaneously change the patterns of pleiotropy of many genes that are active in the upstream portion of the pathway [404]. It is clear that the consequences of such a change for the genetic architecture of the traits can be far-reaching.
Another question is how probable such a change is in a population or in an evolving lineage over a particular time interval. Because developmental processes such as the division of precursor tissues and inductive signaling between pathways are often of fundamental importance for setting up the fundamental structure of an organ, it is likely that changes in such processes have consequences on the morphology of the organ that are relevant to the fitness of the entire organism. It is therefore likely that most changes of this kind are selected against, but that rare advantageous changes may occur and spread through lineages. If so, the developmental interaction is constant over much of evolutionary time, but occasionally may change at a relatively rapid rate. The resulting changes in the patterns of genetic integration will share the same dynamics of extended periods of constancy interspersed with occasional relatively rapid changes. To some extent, therefore, changes in developmental interactions between developmental pathways may contribute to a “punctuational” type of dynamics for the patterns of genetic integration [404].
For covariation of traits from parallel variation of separate developmental pathways, it is helpful to use an example where a single gene encodes a protein that is active in both pathways, but where separate regulatory regions drive expression in the different developmental contexts of the two pathways (Figure 19). If the mutation is in the coding region of the gene and alters the developmental activity of the gene product, it affects both pathways (Figure 19a). If such a mutation is segregating in a population, it produces joint variation of traits 1 and 2 and therefore contributes to their covariation. Accordingly, for this kind of mutation, there is pleiotropy. By contrast, if the mutation is located in one of the two regulatory regions (Figure 19b,c), it only affects the pathway in which the regulatory region drives the expression of the gene, but has no effect on the other pathway. Accordingly, such a mutation produces no covariation between the two traits and has no pleiotropic effect.
Changes in the covariation of traits from parallel variation in separate developmental pathways are likely to be quite abundant because mutations, on an evolutionary time scale, are frequent events. The magnitude of the changes is expected to be variable, with many small changes and few larger ones. Also, changes in allele frequencies of variants with different effects on different pathways produce shifts in the strength of genetic covariation between traits in the population. Altogether, therefore, it is likely that these changes provide a basis for frequent and fairly gradual modification in the amount and pattern of covariation between traits and therefore can contribute flexibly to adaptive evolution of traits [404].
This theoretical argument is largely speculative and clearly requires testing with empirical data. Yet, it offers some intriguing explanations for emerging patterns in empirical studies. If covariation by direct interaction of developmental pathways is evolutionarily conservative or follows punctuational dynamics with long periods of constancy and occasional abrupt change, it offers a possible explanation for the suggestive findings of some studies that the patterns of fluctuating asymmetry may be more constant among genotypes and populations than those of individual variation [73,177]. More systematic comparisons of the patterns of integration of fluctuating asymmetry and individual variation will be necessary to reach firm conclusions on this question.
7. Perspectives
This paper has provided an overview of the concepts and methods for studying fluctuating asymmetry with geometric morphometrics. Some of these ideas are just extensions of analyses that have traditionally been used in the study of asymmetry, but some other aspects are different, and geometric morphometrics offers some completely new possibilities.
Some of the differences are simple facts, such as the prevalence of directional asymmetry (Section 3.1). In studies of asymmetry of distance measurements, directional asymmetry is found occasionally, but geometric morphometric studies have found it in nearly every dataset that was examined. Even though I was aware of this, during the work on this paper, I have been astounded by the sheer number of studies that have found directional asymmetry of shape. This is not just a matter of statistical power, as many of the same studies (if they used structures with matching symmetry) report no directional asymmetry for centroid size. There seems to be a genuine difference between size and shape here, one that only the methods of geometric morphometrics could reveal. This raises some new questions about the developmental basis of directional asymmetry of shape, its possible functional implications, and its evolution.
An important feature of geometric morphometric studies, as a consequence of the multivariate nature of shape, is that fluctuating asymmetry of shape is not just a scalar quantity, as it is for size, but has patterns of variation that are of interest by themselves. Geometric morphometrics offers a range of tools for analyzing these patterns, and such analyses of covariation in fluctuating asymmetry are now an established part of studies of morphological integration [179,254,403]. In turn, the patterns of covariation can also provide information about the nature and developmental origins of asymmetry. A most promising approach combines analyses of fluctuating asymmetry with others such as individual and evolutionary variation into a multilevel approach [429]. This approach is feasible for many studies, as long as multiple specimens from a number of species are measured for left and right sides, and has yielded useful insights in the few examples where it has been used to date [168,172,173]. A greater challenge, in terms of both the requirements of data collection and the problems of the analyses, is the question how the patterns of integration evolve.
Another area with much scope for further work, are structures with complex symmetries, where a few studies have provided first glimpses at the wide range of future possibilities [14,24]. In particular, studies of symmetry and asymmetry of flowers appear to be a promising area for geometric morphometrics, with few examples of such studies at present [25,27]. In general, in plants, studies of symmetry can be seen as a part of or complement to the investigation of within-plant variation [262], and some elegant analyses have used geometric morphometrics to shed light on questions of plant development [191,260].
In conclusion, I would like to express my surprise and delight about the diversity and richness of work in this area. The length of this review and the number of references are a clear sign of this (I expected this paper to be at most half the length it has now). I am also excited about the remarkable number of publications from the last two to three years, which suggests rapid growth in this area and makes me look forward to its future.
Acknowledgments
I thank John Graham for inviting me to contribute a paper to this special issue of Symmetry. I owe a debt of gratitude to Rich Palmer because I started research on the topic of this review because, back in 1996, he hired me to develop analyses of fluctuating asymmetry with the methods of geometric morphometrics. Many of the ideas in this paper first took shape during my time as a postdoc in the labs of Fred Nijhout (Duke University) and Michael Akam (University of Cambridge) and in collaborations with Larry Leamy and Benedikt Hallgrímsson. I further benefitted from discussions with and challenges by students and postdocs who worked with me over the years, including Hugo Benítez, Casper Breuker, Elis Damasceno, Vincent Debat, Abby Drake, Nelly Gidaszewski, Katharina Mebus, Nicolas Navarro, Yoland Savriama, and Emma Sherratt. I am deeply grateful to the late Ruth Flatscher for the data used to prepare Figure 7 and for illuminating discussions on morphometrics and asymmetry in plants. Finally, I thank Elis Damasceno, Hugo Benítez, and two anonymous reviewers for helpful comments on earlier versions of this paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Van Valen, L. A study of fluctuating asymmetry. Evolution 1962, 16, 125–142. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry: Measurement, analysis, patterns. Annu. Rev. Ecol. Syst. 1986, 17, 391–421. [Google Scholar]
- Møller, A.P.; Swaddle, J.P. Asymmetry, Developmental Stability, and Evolution; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Polak, M. Developmental Instability: Causes and Consequences; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating asymmetry: Methods, theory, and applications. Symmetry 2010, 2, 466–540. [Google Scholar]
- Van Dongen, S. Fluctuating asymmetry and developmental instability in evolutionary biology: Past, present and future. J. Evol. Biol. 2006, 19, 1727–1743. [Google Scholar]
- Dryden, I.L.; Mardia, K.V. Statistical Shape Analysis; Wiley: Chichester, UK, 1998. [Google Scholar]
- Klingenberg, C.P. Evolution and development of shape: Integrating quantitative approaches. Nat. Rev. Genet. 2010, 11, 623–635. [Google Scholar]
- Zelditch, M.L.; Swiderski, D.L.; Sheets, H.D. Geometric Morphometrics for Biologists: A Primer, 2nd ed; Elsevier: Amsterdam, The Netherland, 2012. [Google Scholar]
- Adams, D.C.; Rohlf, F.J.; Slice, D.E. A field comes of age: Geometric morphometrics in the 21st century. Hystrix 2013, 24, 7–14. [Google Scholar]
- Klingenberg, C.P.; McIntyre, G.S. Geometric morphometrics of developmental instability: Analyzing patterns of fluctuating asymmetry with Procrustes methods. Evolution 1998, 52, 1363–1375. [Google Scholar]
- Mardia, K.V.; Bookstein, F.L.; Moreton, I.J. Statistical assessment of bilateral symmetry of shapes. Biometrika 2000, 87, 285–300. [Google Scholar]
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape analysis of symmetric structures: Quantifying variation among individuals and asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar]
- Savriama, Y.; Klingenberg, C.P. Beyond bilateral symmetry: Geometric morphometric methods for any type of symmetry. BMC Evol. Biol. 2011, 11, 280. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; McIntyre, G.S.; Zaklan, S.D. Left–right asymmetry of fly wings and the evolution of body axes. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 1255–1259. [Google Scholar]
- Klingenberg, C.P.; Zaklan, S.D. Morphological integration between developmental compartments in the Drosophila wing. Evolution 2000, 54, 1273–1285. [Google Scholar]
- Klingenberg, C.P. Developmental instability as a research tool: Using patterns of fluctuating asymmetry to infer the developmental origins of morphological integration. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 427–442. [Google Scholar]
- Endress, P.K. Symmetry in flowers: Diversity and evolution. Int. J. Plant Sci. 1999, 160, S3–S23. [Google Scholar]
- Endress, P.K. Evolution of floral symmetry. Curr. Opin. Plant Biol. 2001, 4, 86–91. [Google Scholar]
- Citerne, H.; Jabbour, F.; Nadot, S.; Damerval, C. The evolution of floral symmetry. Adv. Bot. Res. 2010, 54, 85–137. [Google Scholar]
- Busch, A.; Zachgo, S. Flower symmetry evolution: Towards understanding the abominable mystery of angiosperm radiation. BioEssays 2009, 31, 1181–1190. [Google Scholar]
- Potapova, M.; Hamilton, P.B. Morphological and ecological variation within the Achnanthidium minutissimum (Bacillariophyceae) species complex. J. Phycol. 2007, 43, 561–575. [Google Scholar]
- Savriama, Y.; Neustupa, J.; Klingenberg, C.P. Geometric morphometrics of symmetry and allometry in Micrasterias rotata (Zygnemophyceae, Viridiplantae). Nova Hedwigia Suppl. 2010, 136, 43–54. [Google Scholar]
- Neustupa, J. Patterns of symmetric and asymmetric morphological variation in unicellular green microalgae of the genus Micrasterias (Desmidiales, Viridiplantae). Fottea 2013, 13, 53–63. [Google Scholar]
- Gómez, J.M.; Perfectti, F.; Camacho, J.P.M. Natural selection on Erysimum mediohispanicum flower shape: Insights into the evolution of zygomorphy. Am. Nat. 2006, 168, 531–545. [Google Scholar]
- Gómez, J.M.; Perfectti, F. Evolution of complex traits: The case of Erysimum corolla shape. Int. J. Plant Sci. 2010, 171, 987–998. [Google Scholar]
- Savriama, Y.; Gómez, J.M.; Perfectti, F.; Klingenberg, C.P. Geometric morphometrics of corolla shape: Dissecting components of symmetric and asymmetric variation in Erysimum mediohispanicum (Brassicaceae). New Phytol. 2012, 196, 945–954. [Google Scholar]
- Busch, A.; Zachgo, S. Control of corolla monosymmetry in the Brassicaceae Iberis amara. Proc. Natl. Acad. Sci. USA 2007, 104, 16714–16719. [Google Scholar]
- Busch, A.; Horn, S.; Mühlhausen, A.; Mummenhoff, K.; Zachgo, S. Corolla monosymmetry: Evolution of a morphological novelty in the Brassicaceae family. Mol. Biol. Evol. 2012, 29, 1241–1254. [Google Scholar]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Martin, G.E. Transformation Geometry: An Introduction to Symmetry; Springer: New York, NY, USA, 1982. [Google Scholar]
- Armstrong, M.A. Groups and Symmetry; Springer: New York, NY, USA, 1988. [Google Scholar]
- Conway, J.H.; Burgiel, H.; Goodman-Strauss, C. The Symmetries of Things; A.K. Peters: Wellesley, MA, USA, 2008. [Google Scholar]
- Bookstein, F.L. Combining the tools of geometric morphometrics. In Advances in Morphometrics; Marcus, L.F., Corti, M., Loy, A., Naylor, G.J.P., Slice, D.E., Eds.; Plenum Press: New York, NY, USA, 1996; pp. 131–151. [Google Scholar]
- Heuzé, Y.; Martínez-Abadías, N.; Stella, J.M.; Senders, C.W.; Boyadjiev, S.A.; Lo, L.-J.; Richtsmeier, J.T. Unilateral and bilateral expression of a quantitative trait: Asymmetry and symmetry in coronal craniosynostosis. J. Exp. Zool. B Mol. Dev. Evol. 2012, 318, 109–122. [Google Scholar]
- Sutherland, M.J.; Ware, S.M. Disorders of left–right asymmetry: Heterotaxy and situs inversus. Am. J. Med. Genet. 2009, 151C, 307–317. [Google Scholar]
- Pither, J.; Taylor, P.D. Directional and fluctuating asymmetry in the black-winged damselfly Calopteryx maculata (Beauvois) (Odonata: Calopterygidae). Can. J. Zool. 2000, 78, 1740–1748. [Google Scholar]
- Ercan, I.; Turan Ozdemir, S.; Etoz, A.; Sigirli, D.; Tubbs, R.S.; Loukas, M.; Guney, I. Facial asymmetry in young healthy subjects evaluated by statistical shape analysis. J. Anat. 2008, 213, 663–669. [Google Scholar]
- DeLeon, V.B. Fluctuating asymmetry and stress in a Medieval Nubian population. Am. J. Phys. Anthropol. 2007, 132, 520–534. [Google Scholar]
- Auffray, J.-C.; Alibert, P.; Renaud, S.; Orth, A.; Bonhomme, F. Fluctuating asymmetry in Mus musculus subspecific hybridization: Traditional and Procrustes comparative approach. In Advances in Morphometrics; Marcus, L.F., Corti, M., Loy, A., Naylor, G.J.P., Slice, D.E., Eds.; Plenum Press: New York, NY, USA, 1996; pp. 275–283. [Google Scholar]
- Smith, D.R.; Crespi, B.J.; Bookstein, F.L. Fluctuating asymmetry in the honey bee, Apis mellifera: Effects of ploidy and hybridization. J. Evol. Biol. 1997, 10, 551–574. [Google Scholar]
- Debat, V.; Alibert, P.; David, P.; Paradis, E.; Auffray, J.-C. Independence between developmental stability and canalization in the skull of the house mouse. Proc. R. Soc. Lond. B Biol. Sci. 2000, 267, 423–430. [Google Scholar]
- Allen, D.E.; Leamy, L.J. 2,3,7,8-tetrachlorodibenzo-p-dioxin affects size and shape, but not asymmetry, of mandibles in mice. Ecotoxicology 2001, 10, 167–176. [Google Scholar]
- Klingenberg, C.P.; Badyaev, A.V.; Sowry, S.M.; Beckwith, N.J. Inferring developmental modularity from morphological integration: Analysis of individual variation and asymmetry in bumblebee wings. Am. Nat. 2001, 157, 11–23. [Google Scholar]
- Klingenberg, C.P.; Leamy, L.J.; Routman, E.J.; Cheverud, J.M. Genetic architecture of mandible shape in mice: Effects of quantitative trait loci analyzed by geometric morphometrics. Genetics 2001, 157, 785–802. [Google Scholar]
- Leamy, L.J.; Meagher, S.; Taylor, S.; Carroll, L.; Potts, W.K. Size and fluctuating asymmetry of morphometric characters in mice: Their associations with inbreeding and the t-haplotype. Evolution 2001, 55, 2333–2341. [Google Scholar]
- McIntyre, G.T.; Mossey, P.A. Asymmetry of the parental craniofacial skeleton in orofacial clefting. J. Orthod. 2002, 29, 299–305. [Google Scholar]
- Workman, M.S.; Leamy, L.J.; Routman, E.J.; Cheverud, J.M. Analysis of quantitative trait locus effects on the size and shape of mandibular molars in mice. Genetics 2002, 160, 1573–1586. [Google Scholar]
- Klingenberg, C.P.; Mebus, K.; Auffray, J.-C. Developmental integration in a complex morphological structure: How distinct are the modules in the mouse mandible? Evol. Dev. 2003, 5, 522–531. [Google Scholar]
- Schneider, S.S.; Leamy, L.J.; Lewis, L.A.; DeGrandi-Hoffman, G. The influence of hybridization between African and European heoneybees, Apis mellifera, on asymmetries in wing size and shape. Evolution 2003, 57, 2350–2364. [Google Scholar]
- Hallgrímsson, B.; Willmore, K.; Dorval, C.; Cooper, D.M.L. Craniofacial variability and modularity in macaques and mice. J. Exp. Zool. B Mol. Dev. Evol. 2004, 302, 207–225. [Google Scholar]
- Hallgrímsson, B.; Dorval, C.J.; Zelditch, M.L.; German, R.Z. Craniofacial variability and morphological integration in mice susceptible to cleft lip and palate. J. Anat. 2004, 205, 501–517. [Google Scholar]
- Oleksyk, T.K.; Novak, J.M.; Purdue, J.R.; Gashchak, S.P.; Smith, M.H. High levels of fluctuating asymmetry in populations of Apodemus flavicollis from the most contaminated areas in Chornobyl. J. Environ. Radioact. 2004, 73, 1–20. [Google Scholar]
- Santos, M.; Fernández Iriarte, P.; Céspedes, W. Genetics and geometry of canalization and developmental stability in Drosophila subobscura. BMC Evol. Biol. 2005, 5, 7. [Google Scholar] [CrossRef]
- Willmore, K.E.; Klingenberg, C.P.; Hallgrímsson, B. The relationship between fluctuating asymmetry and environmental variance in rhesus macaque skulls. Evolution 2005, 59, 898–909. [Google Scholar]
- Breuker, C.J.; Patterson, J.S.; Klingenberg, C.P. A single basis for developmental buffering of Drosophila wing shape. PLoS ONE 2006, 1, e7. [Google Scholar]
- Schaefer, K.; Fink, B.; Grammer, K.; Mitteroecker, P.; Gunz, P.; Bookstein, F.L. Female appearance: Facial and bodily attractiveness as shape. Psychol. Sci. 2006, 48, 187–204. [Google Scholar]
- Stige, L.C.; David, B.; Alibert, P. On hidden heterogeneity in directional asymmetry—Can systematic bias be avoided? J. Evol. Biol. 2006, 19, 492–499. [Google Scholar]
- Breuker, C.J.; Gibbs, M.; van Dyck, H.; Brakefield, P.M.; Klingenberg, C.P.; Van Dongen, S. Integration of wings and their eyespots in the speckled wood butterfly Pararge aegeria. J. Exp. Zool. 2007, 308B, 454–463. [Google Scholar]
- Mikula, O.; Macholán, M. There is no heterotic effect upon developmental stability in the ventral side of the skull within the house mouse hybrid zone. J. Evol. Biol. 2008, 21, 1055–1067. [Google Scholar]
- White, T.A.; Searle, J.B. Mandible asymmetry and genetic diversity in island populations of the common shrew Sorex araneus. J. Evol. Biol. 2008, 21, 636–641. [Google Scholar]
- Debat, V.; Debelle, A.; Dworkin, I. Plasticity, canalization, and developmental stability of the Drosophila wing: Joint effects of mutations and developmental temperature. Evolution 2009, 63, 2864–2876. [Google Scholar]
- Laffont, R.; Renvoisé, E.; Navarro, N.; Alibert, P.; Montuire, S. Morphological modularity and assessment of developmental processes within the vole dental row (Microtus arvalis, Arvicolinae, Rodentia). Evol. Dev. 2009, 11, 302–311. [Google Scholar]
- Burgio, G.; Baylac, M.; Heyer, E.; Montagutelli, X. Genetic analysis of skull shape variation and morphological integration in the mouse using interspecific recombinant congenic strains between C57BL/6 and mice of the Mus spretus species. Evolution 2009, 63, 2668–2686. [Google Scholar]
- Breuker, C.J.; Gibbs, M.; van Dongen, S.; Merckx, T.; van Dyck, H. The use of geometric morphometrics in studying butterfly wings in an evolutionary ecological context. In Morphometrics for Nonmorphometricians; Elewa, A.M.T., Ed.; Springer-Verlag: Berlin, Germany, 2010; pp. 271–287. [Google Scholar]
- Klingenberg, C.P.; Wetherill, L.F.; Rogers, J.L.; Moore, E.S.; Ward, R.E.; Autti-Rämö, I.; Fagerlund, Å.; Jacobson, S.W.; Robinson, L.K.; Hoyme, H.E.; et al. Prenatal alcohol exposure alters the patterns of facial asymmetry. Alcohol 2010, 44, 649–657. [Google Scholar]
- Ivanović, A.; Kalezić, M.L. Testing the hypothesis of morphological integration on a skull of a vertebrate with a biphasic life cycle: A case study of the alpine newt. J. Exp. Zool. B Mol. Dev. Evol. 2010, 314, 527–538. [Google Scholar]
- McIntyre, G.T.; Mossey, P.A. Asymmetry of the craniofacial skeleton in the parents of children with a cleft lip, with or without a cleft palate, or an isolated cleft palate. Eur. J. Orthod. 2010, 32, 177–185. [Google Scholar]
- Milankov, V.; Francuski, L.; Ludoški, J.; Ståhls, G.; Vujić, A. Estimating genetic and phenotypic diversity in a northern hoverfly reveals lack of heterozygosity correlated with significant fluctuating asymmetry of wing traits. J. Insect Conserv. 2010, 14, 77–88. [Google Scholar]
- Mikula, O.; Auffray, J.-C.; Macholán, M. Asymmetric size and shape variation in the Central European transect across the house mouse hybrid zone. Biol. J. Linn. Soc. 2010, 101, 13–27. [Google Scholar]
- Young, R.L.; Badyaev, A.V. Developmental plasticity links local adaptation and evolutionary diversification in foraging morphology. J. Exp. Zool. B Mol. Dev. Evol. 2010, 314, 434–444. [Google Scholar]
- Klingenberg, C.P.; Debat, V.; Roff, D.A. Quantitative genetics of shape in cricket wings: Developmental integration in a functional structure. Evolution 2010, 64, 2935–2951. [Google Scholar]
- Breno, M.; Leirs, H.; van Dongen, S. No relationship between canalization and developmental stability of the skull in a natural population of Mastomys natalensis (Rodentia: Muridae). Biol. J. Linn. Soc. 2011, 104, 207–216. [Google Scholar]
- Jamniczky, H.A.; Hallgrímsson, B. Modularity in the skull and cranial vasculature of laboratory mice: Implications for the evolution of complex phenotypes. Evol. Dev. 2011, 13, 28–37. [Google Scholar]
- Jojić, V.; Blagojević, J.; Vujošević, M. B chromosomes and cranial variability in yellow-necked field mice (Apodemus flavicollis). J. Mammal. 2011, 92, 396–406. [Google Scholar]
- Nouvellet, P.; Ramirez-Sierra, M.J.; Dumonteil, E.; Gourbière, S. Effects of genetic factors and infection status on wing morphology of Triatoma dimidiata species complex in the Yucatán peninsula, Mexico. Infect. Genet. Evol. 2011, 11, 1243–1249. [Google Scholar]
- Takahashi, K.H.; Okada, Y.; Teramura, K.; Tsujino, M. Deficiency mapping of the genomic regions associated with effects on developmental stability in Drosophila melanogaster. Evolution 2011, 65, 3565–3577. [Google Scholar]
- Webster, M.; Zelditch, M.L. Evolutionary lability of integration in Cambrian ptychoparioid trilobites. Evol. Biol. 2011, 38, 144–162. [Google Scholar]
- Webster, M.; Zelditch, M.L. Modularity of a Cambrian ptychoparioid trilobite cranidium. Evol. Dev. 2011, 13, 96–109. [Google Scholar]
- Burgio, G.; Baylac, M.; Heyer, E.; Montagutelli, X. Exploration of the genetic organization of morphological modularity on the mouse mandible using a set of interspecific recombinant congenic strains between C57BL/6 and mice of the Mus spretus species. G3–Genes Genomes Genet. 2012, 2, 1257–1268. [Google Scholar]
- Habel, J.C.; Engler, J.O.; Rödder, D.; Schmitt, T. Contrasting genetic and morphologic responses on recent population decline in two burnet moths (Lepidoptera, Zygaenidae). Conserv. Genet. 2012, 13, 1293–1304. [Google Scholar]
- Jojić, V.; Blagojević, J.; Vujošević, M. Two-module organization of the mandible in the yellow-necked mouse: A comparison between two different morphometric approaches. J. Evol. Biol. 2012, 25, 2489–2500. [Google Scholar]
- Ludoški, J.; Djurakic, M.; Ståhls, G.; Milankov, V. Patterns of asymmetry in wing traits of three island and one continental population of Merodon albifrons (Diptera, Syrphidae) from Greece. Evol. Ecol. Res. 2012, 14, 933–950. [Google Scholar]
- Singh, N.; Harvati, K.; Hublin, J.-J.; Klingenberg, C.P. Morphological evolution through integration: A quantitative study of cranial integration in Homo, Pan, Gorilla and Pongo. J. Hum. Evol. 2012, 62, 155–164. [Google Scholar]
- Tsujino, M.; Takahashi, K.H. Natural genetic variation in fluctuating asymmetry of wing shape in Drosophila melanogaster. Ecol. Res. 2012, 27, 133–143. [Google Scholar]
- Bigoni, L.; Krajíček, V.; Sládek, V.; Velemínsky, P.; Velemínská, J. Skull shape asymmetry and the socioeconomic structure of an early medieval central European society. Am. J. Phys. Anthropol. 2013, 150, 349–364. [Google Scholar]
- Domjanic, J.; Fieder, M.; Seidler, H.; Mitteroecker, P. Geometric morphometric footprint analysis of young women. J. Foot Ankle Res. 2013, 6, 27. [Google Scholar] [CrossRef]
- Gómez-Robles, A.; Hopkins, W.D.; Sherwood, C.C. Increased morphological asymmetry, evolvability and plasticity in human brain evolution. Proc. R. Soc. Lond. B Biol. Sci. 2013, 280, 20130575. [Google Scholar] [CrossRef]
- Sanfilippo, P.G.; Hewitt, A.W.; Mountain, J.A.; Mackey, D.A. A geometric morphometric assessment of hand shape and comparison to the 2D:4D digit ratio as a marker of sexual dimorphism. Twin Res. Hum. Genet. 2013, 16, 590–600. [Google Scholar]
- Weisensee, K.E. Assessing the relationship between fluctuating asymmetry and cause of death in skeletal remains: A test of the developmental origins of health and disease hypothesis. Am. J. Hum. Biol. 2013, 25, 411–417. [Google Scholar]
- Benítez, H.A.; Lemic, D.; Bažok, R.; Gallardo-Araya, C.M.; Mikac, K.M. Evolutionary directional asymmetry and shape variation in Diabrotica virgifera virgifera (Coleoptera: Chrysomelidae): An example using hind wings. Biol. J. Linn. Soc. 2014, 111, 110–118. [Google Scholar]
- Benítez, H.A.; Püschel, T.; Lemic, D.; Čačija, M.; Kozina, A.; Bažok, R. Ecomorphological variation of the wireworm cephalic capsule: Studying the interaction of environment and geometric shape. PLoS ONE 2014, 9, e102059. [Google Scholar]
- Gonzalez, P.N.; Lotto, F.P.; Hallgrímsson, B. Canalization and developmental stability of the fetal skull in a mouse model of maternal nutritional stress. Am. J. Phys. Anthropol. 2014, 154, 544–553. [Google Scholar]
- Lotto, F.P.; Gonzalez, P.N. Inestabilidad del desarrollo en estructuras craneofaciales de poblaciones humanas sudamericanas. Rev. Argent. Antropol. Biol. 2014, 16, 17–29. [Google Scholar]
- Ludoški, J.; Djurakic, M.; Pastor, B.; Martínez-Sánchez, A.I.; Rojo, S.; Milankov, V. Phenotypic variation of the housefly, Musca domestica: Amounts and patterns of wing shape asymmetry in wild populations and laboratory colonies. Bull. Entomol. Res. 2014, 104, 35–47. [Google Scholar]
- Marchiori, A.B.; Bartholomei-Santos, M.L.; Santos, S. Intraspecific variation in Aegla longirostri (Crustacea: Decapoda: Anomura) revealed by geometric morphometrics: Evidence for ongoing speciation? Biol. J. Linn. Soc. 2014, 112, 31–39. [Google Scholar]
- Martínez-Vargas, J.; Muñoz-Muñoz, F.; Medarde, N.; López-Fuster, M.J.; Ventura, J. Effect of chromosomal reorganizations on morphological covariation of the mouse mandible: Insights from a Robertsonian system of Mus musculus domesticus. Front. Zool. 2014, 11, 51. [Google Scholar] [CrossRef]
- Miller, S.F.; Weinberg, S.M.; Nidey, N.L.; Defay, D.K.; Marazita, M.L.; Wehby, G.L.; Moreno Uribe, L.M. Exploratory genotype–phenotype correlations of facial form and asymmetry in unaffected relatives of children with non-syndromic cleft lip and/or palate. J. Anat. 2014, 224, 688–709. [Google Scholar]
- Parés-Casanova, P.M. Proximo-distal gain of asymmetry in lamb metacarpals. Ital. J. Anat. Embryol. 2014, 119, 60–66. [Google Scholar]
- Parés-Casanova, P.M.; Esteve-Puig, Directional. fluctuating asymmetries in domestic pig skulls. Research (Lambertville). 2014, 1, 828. [Google Scholar] [CrossRef]
- Urbanová, P.; Hejna, P.; Zátpková, L.; Safr, M. The asymmetry and modularity of the hyoid bone. Int. J. Morphol. 2014, 32, 251–260. [Google Scholar]
- Van Dongen, S. Associations among facial masculinity, physical strength, fluctuating asymmetry and attractiveness in young men and women. Ann. Hum. Biol. 2014, 41, 205–213. [Google Scholar]
- Arambourou, H.; Branchu, P.; Beisel, J.-N. Increase in developmental instability in a field-collected Chironomus population maintained under laboratory conditions. Bull. Environ. Contam. Toxicol. 2015. [Google Scholar] [CrossRef]
- Claes, P.; Reijniers, J.; Shriver, M.D.; Snyders, J.; Suetens, P.; Nielandt, J.; de Tré, G.; Vandermeulen, D. An investigation of matching symmetry in the human pinnae with possible implications for 3D ear recognition and sound localization. J. Anat. 2015, 226, 60–72. [Google Scholar]
- Farrera, A.; Villanueva, M.; Quinto-Sánchez, M.; González-José, R. The relationship between facial shape asymmetry and attractiveness in Mexican students. Am. J. Hum. Biol. 2015, 27, 387–396. [Google Scholar]
- Lazić, M.; Carretero, M.A.; Crnobrnja-Isailović, J.; Kaliontzopoulou, A. Effects of environmental disturbance on phenotypic variation: An integrated assessment of canalization, developmental stability, modularity, and allometry in lizard head shape. Am. Nat. 2015, 185, 44–58. [Google Scholar]
- Leamy, L.J.; Klingenberg, C.P.; Sherratt, E.; Wolf, J.B.; Cheverud, J.M. The genetic architecture of fluctuating asymmetry of mandible size and shape in a population of mice: Another look. Symmetry 2015, 7, 146–163. [Google Scholar]
- Quinto-Sánchez, M.; Adhikari, K.; Acuña-Alonzo, V.; Cintas, C.; Silva de Cerqueira, C.C.; Ramallo, V.; Castillo, L.; Farrera, A.; Jaramillo, C.; Hünemeier, T.; et al. Facial asymmetry and genetic ancestry in Latin American admixed populations. Am. J. Phys. Anthropol. 2015, 157, 58–70. [Google Scholar]
- Schlager, S.; Rüdell, A. Analysis of the human osseous nasal shape—Population differences and sexual dimorphism. Am. J. Phys. Anthropol. 2015. [Google Scholar] [CrossRef]
- Van Dongen, S. Lack of correlation between fluctuating asymmetry and morphological masculinity/femininity in primate skulls. Int. J. Primatol. 2015, 36, 113–123. [Google Scholar]
- Nakadera, Y.; Sutcharit, C.; Ubukata, T.; Seki, K.; Utsuno, H.; Panha, S.; Asami, T. Enantiomorphs differ in shape in oppsite directions between populations. J. Evol. Biol. 2010, 23, 2377–2384. [Google Scholar]
- Schilthuizen, M.; Haase, M. Disentangling true shape differences and experimenter bias: Are dextral and sinistral snail shells exact mirror images? J. Zool. (Lond.) 2010, 282, 191–200. [Google Scholar]
- Utsuno, H.; Asami, T.; Van Dooren, T.J.M.; Gittenberger, E. Internal selection against the evolution of left–right reversal. Evolution 2011, 65, 2399–2411. [Google Scholar]
- Schilthuizen, M.; Haase, M.; Koops, K.; Looijestijn, S.M.; Hendrikse, S. The ecology of shell shape difference in chirally dimorphic snails. Contrib. Zool. 2012, 81, 95–101. [Google Scholar]
- Fernández Iriarte, P.; Céspedes, W.; Santos, M. Quantitative-genetic analysis of wing form and bilateral asymmetry in isochromosomal lines of Drosophila subobscura using Procrustes methods. J. Genet. 2003, 82, 95–113. [Google Scholar]
- Hoffmann, A.A.; Woods, R.E.; Collins, E.; Wallin, K.; White, A.; McKenzie, J.A. Wing shape versus asymmetry as an indicator of changing environmental conditions in insects. Aust. J. Entomol. 2005, 44, 233–243. [Google Scholar]
- Debat, V.; Cornette, R.; Korol, A.B.; Nevo, E.; Soulet, D.; David, J.R. Multidimensional analysis of Drosophila wing variation in Evolution Canyon. J. Genet. 2008, 87, 407–419. [Google Scholar]
- Soto, I.M.; Carreira, V.P.; Soto, E.M.; Hasson, E. Wing morphology and fluctuating asymmetry depend on the host plant in cactophilic Drosophila. J. Evol. Biol. 2008, 21, 598–609. [Google Scholar]
- Padró, J.; Carreira, V.; Corio, C.; Hasson, E.; Soto, I.M. Host alkaloids differentially affect developmental stability and wing vein canalization in cactophilic Drosophila buzzatii. J. Evol. Biol. 2014, 27, 2781–2797. [Google Scholar]
- Rego, C.; Matos, M.; Santos, M. Symmetry breaking in interspecific Drosophila hybrids is not due to developmental noise. Evolution 2006, 60, 746–761. [Google Scholar]
- Santos, M.; Brites, D.; Laayouni, H. Thermal evolution of pre-adult life history traits, geometric size and shape, and developmental stability in Drosophila subobscura. J. Evol. Biol. 2006, 19, 2006–2021. [Google Scholar]
- Carreira, V.P.; Soto, I.M.; Fanara, J.J.; Hasson, E. A study of wing morphology and fluctuating asymmetry in interspecific hybrids between Drosophila buzzatii and D. koepferae. Genetica (Dordr.) 2008, 133, 1–11. [Google Scholar]
- Soto, I.M.; Carreira, V.P.; Corio, C.; Soto, E.M.; Hasson, E. Host use and developmental instability in the cactophilic sibling species Drosophila gouveai and D. antonietae. Entomol. Exp. Appl. 2010, 137, 165–175. [Google Scholar]
- Takahashi, K.H.; Rako, L.; Takano-Shimizu, T.; Hoffmann, A.A.; Lee, S.F. Effects of small Hsp genes on developmental stability and microenvironmental canalization. BMC Evol. Biol. 2010, 10, 284. [Google Scholar] [CrossRef]
- Takahashi, K.H.; Okada, Y.; Teramura, K. Genome-wide deficiency mapping of the regions responsible for temporal canalization of the developmental processes of Drosophila melanogaster. J. Hered. 2011, 102, 448–457. [Google Scholar]
- Takahashi, K.H.; Daborn, P.J.; Hoffmann, A.A.; Takano-Shimizu, T. Environmental stress-dependent effects of deletions encompassing Hsp70Ba on canalization and quantitative trait asymmetry in Drosophila melanogaster. PLoS ONE 2011, 6, e17295. [Google Scholar]
- Kimmerle, E.H.; Jantz, R.L. Secular trends in craniofacial asymmetry studied by geometric morphometry and generalized Procrustes methods. In Modern Morphometrics in Physical Anthropology; Slice, D.E., Ed.; Kluwer Academic/Plenum: New York, NY, USA, 2005; pp. 247–263. [Google Scholar]
- Radwan, J.; Watson, P.J.; Farslow, J.; Thornhill, R. Procrustean analysis of fluctuating asymmetry in the bulb mite Rhyzoglyphus robini Claparede (Astigmata: Acaridae). Biol. J. Linn. Soc. 2003, 80, 499–505. [Google Scholar]
- Kölliker-Ott, U.M.; Blows, M.W.; Hoffmann, A.A. Are wing size, wing shape and asymmetry related to field fitness of Trichoramma egg parasitoids? Oikos 2003, 100, 563–573. [Google Scholar]
- Arambourou, H.; Beisel, J.-N.; Branchu, P.; Debat, V. Patterns of fluctuating asymmetry and shape variation in Chironomus riparius (Diptera, Chironomidae) exposed to nonylphenol or lead. PLoS ONE 2012, 7, e48844. [Google Scholar]
- Arambourou, H.; Beisel, J.-N.; Branchu, P.; Debat, V. Exposure to sediments from polluted rivers has limited phenotypic effects on larvae and adults of Chironomus riparius. Sci. Total Environ. 2014, 484, 92–101. [Google Scholar]
- Hoffmann, A.A.; Collins, E.; Woods, R.E. Wing shape and wing size changes as indicators of environmental stress in Helicoverpa punctigera (Lepidoptera: Noctuidae) moths: Comparing shifts in means, variances, and asymmetries. Environ. Entomol. 2002, 31, 965–971. [Google Scholar]
- Hennessy, R.J.; Laneb, A.; Kinsella, A.; Larkin, C.; O’Callaghan, E.; Waddington, J.L. 3D morphometrics of craniofacial dysmorphology reveals sex-specific asymmetries in schizophrenia. Schizophr. Res. 2004, 67, 261–268. [Google Scholar]
- Schaefer, K.; Lauc, T.; Mitteroecker, P.; Gunz, P.; Bookstein, F.L. Dental arch asymmetry in an isolated Adriatic community. Am. J. Phys. Anthropol. 2006, 129, 132–142. [Google Scholar]
- Willmore, K.E.; Zelditch, M.L.; Young, N.; Ah-Seng, A.; Lozanoff, S.; Hallgrímsson, B. Canalization and developmental stability in the brachyrrhine mouse. J. Anat. 2006, 208, 361–372. [Google Scholar]
- Habel, J.C.; Reuter, M.; Drees, C.; Pfaender, J. Does isolation affect phenotypic variability and fluctuating asymmetry in the endangered Red Apollo? J. Insect Conserv. 2012, 16, 571–579. [Google Scholar]
- López-Romero, F.; Zúñiga, G.; Martínez-Jerónimo, F. Asymmetric patterns in the cranial skeleton of zebrafish (Danio rerio) exposed to sodium pentachlorophenate at different embryonic developmental stages. Ecotoxicol. Environ. Saf. 2012, 84, 25–31. [Google Scholar]
- Heuzé, Y.; Balzeau, A. Asymmetry of the midfacial skeleton of eastern lowland gorillas (Gorilla beringei graueri) and potential association with frontal lobe asymmetries. J. Hum. Evol. 2014, 74, 123–129. [Google Scholar]
- Claverie, T.; Chan, E.; Patek, S.N. Modularity and scaling in fast movements: Power amplification in mantis shrimp. Evolution 2011, 65, 443–461. [Google Scholar]
- Palmer, A.R. Antisymmetry. In Variation: A Central Concept in Biology; Hallgrímsson, B., Hall, B.K., Eds.; Elsevier: Burlington, MA, USA, 2005; pp. 359–397. [Google Scholar]
- Levin, M. Left–right asymmetry in embryonic development: A comprehensive review. Mech. Dev. 2005, 122, 3–25. [Google Scholar]
- Vandenberg, L.N.; Levin, M. A unified model for left-right asymmetry? Comparison and synthesis of molecular models of embryonic laterality. Dev. Biol. 2013, 379, 1–15. [Google Scholar]
- Coutelis, J.-B.; González-Morales, N.; Géminard, C.; Noselli, S. Diversity and convergence in the mechanisms establishing L/R asymmetry in metazoa. EMBO Rep. 2014, 15, 926–937. [Google Scholar]
- Namigai, E.K.O.; Kenny, N.J.; Shimeld, S.M. Right across the tree of life: The evolutio of left–right asymmetry in the Bilateria. Genesis 2014, 52, 458–470. [Google Scholar]
- Pélabon, C.; Hansen, T.F.; Carter, A.J.R.; Houle, D. Response of fluctuating and directional asymmetry to selection on wing shape in Drosophila melanogaster. J. Evol. Biol. 2006, 19, 764–776. [Google Scholar]
- Pélabon, C.; Hansen, T.F. On the adaptive accuracy of directional asymmetry in insect wing size. Evolution 2008, 62, 2855–2867. [Google Scholar]
- Baranov, S.G. Use of morphometric method for study fluctuating asymmetry in leaves Tiliacordata under industrial pollution. Adv. Environ. Biol. 2014, 8, 2391–2398. [Google Scholar]
- Albarrán-Lara, A.L.; Mendoza-Cuenca, L.; Valencia-Avalos, S.; González-Rodríguez, A.; Oyama, K. Leaf fluctuating asymmetry increases with hybridization and introgression between Quercus magnoliifolia and Quercus resinosa (Fagaceae) through an altitudinal gradient in Mexico. Int. J. Plant Sci. 2010, 171, 310–322. [Google Scholar]
- Baranov, S.G.; Gavrikov, D.E. Use of TPS software for studying fluctuating asymmetry in flowers. Int. J. Biosci. Biochem. Bioinf. 2013, 3, 284–287. [Google Scholar]
- Klingenberg, C.P. A developmental perspective on developmental instability: Theory, models and mechanisms. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 14–34. [Google Scholar]
- Nijhout, H.F.; Davidowitz, G. Developmental perspectives on phenotypic variation, canalization, and fluctuating asymmetry. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 3–13. [Google Scholar]
- Leamy, L. Morphometric studies in inbred and hybrid house mice. V. Directional and fluctuating asymmetry. Am. Nat. 1984, 123, 579–593. [Google Scholar]
- Palmer, A.R. Fluctuating asymmetry analyses: A primer. In Developmental Instability: Its Origins and Implications; Markow, T.A., Ed.; Kluwer: Dordrecht, The Netherlands, 1994; pp. 335–364. [Google Scholar]
- Van Dongen, S.; Molenberghs, G.; Matthysen, E. The statistical analysis of fluctuating asymmetry: REML estimation of a mixed regression model. J. Evol. Biol. 1999, 12, 94–102. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry analyses revisited. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 279–319. [Google Scholar]
- Van Dongen, S.; Lens, L.; Molenberghs, G. Recent developments and shortcomings in the analysis of individual asymmetry: A review and introduction of a Bayesian statistical approach. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 320–342. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry as a measure of developmental stability: Implications of non-normal distributions and power of statistical tests. Acta Zool. Fenn. 1992, 191, 57–72. [Google Scholar]
- Whitlock, M. The heritability of fluctuating asymmetry and the genetic control of developmental stability. Proc. R. Soc. Lond. B Biol. Sci. 1996, 263, 849–854. [Google Scholar]
- Whitlock, M. The repeatability of fluctuating asymmetry: A revision and extension. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 1429–1431. [Google Scholar]
- Klingenberg, C.P.; Nijhout, H.F. Genetics of fluctuating asymmetry: A developmental model of developmental instability. Evolution 1999, 53, 358–375. [Google Scholar]
- Babbitt, G.A.; Kiltie, R.; Bolker, B. Are fluctuating asymmetry studies adequately sampled? Implications of a new model for size distribution. Am. Nat. 2006, 167, 230–245. [Google Scholar]
- Babbitt, G.A. Inbreeding reduces power-law scaling in the distribution of fluctuating asymmetry: An explanation of the basis of developmental instability. Heredity 2006, 97, 258–268. [Google Scholar]
- Van Dongen, S.; Møller, A.P. On the distribution of developmental errors: Comparing the normal, gamma, and log-normal distribution. Biol. J. Linn. Soc. 2007, 92, 197–210. [Google Scholar]
- Babbitt, G.A. How accurate is the phenotype?—An analysis of developmental noise in a cotton aphid clone. BMC Dev. Biol. 2008, 8, 19. [Google Scholar] [CrossRef]
- Parsons, P.A. Fluctuating asymmetry: An epigenetic measure of stress. Biol. Rev. 1990, 65, 131–145. [Google Scholar]
- Klingenberg, C.P. Integration, modules and development: Molecules to morphology to evolution. In Phenotypic Integration: Studying the Ecology and Evolution of Complex Phenotypes; Pigliucci, M., Preston, K., Eds.; Oxford University Press: New York, NY, USA, 2004; pp. 213–230. [Google Scholar]
- Badyaev, A.V.; Foresman, K.R. Evolution of morphological integration. I. Functional units channel stress-induced variation in shrew mandibles. Am. Nat. 2004, 163, 868–879. [Google Scholar]
- Young, R.L.; Badyaev, A.V. Evolutionary persistence of phenotypic integration: Influence of developmental and functional relationships on complex trait evolution. Evolution 2006, 60, 1291–1299. [Google Scholar]
- Zelditch, M.L.; Wood, A.R.; Bonett, R.M.; Swiderski, D.L. Modularity of the rodent mandible: Integrating bones, muscles, and teeth. Evol. Dev. 2008, 10, 756–768. [Google Scholar]
- Klingenberg, C.P. Morphometric integration and modularity in configurations of landmarks: Tools for evaluating a-priori hypotheses. Evol. Dev. 2009, 11, 405–421. [Google Scholar]
- Zelditch, M.L.; Wood, A.R.; Swiderski, D.L. Building developmental integration into functional systems: Function-induced integration of mandibular shape. Evol. Biol. 2009, 36, 71–87. [Google Scholar]
- Drake, A.G.; Klingenberg, C.P. Large-scale diversification of skull shape in domestic dogs: Disparity and modularity. Am. Nat. 2010, 175, 289–301. [Google Scholar]
- Klingenberg, C.P.; Duttke, S.; Whelan, S.; Kim, M. Developmental plasticity, morphological variation and evolvability: A multilevel analysis of morphometric integration in the shape of compound leaves. J. Evol. Biol. 2012, 25, 115–129. [Google Scholar]
- Sorensen, D.W.; Butkus, C.; Cooper, L.N.; Cretekos, C.J.; Rasweiler, J.J., IV; Sears, K.E. Palate variation and evolution in New World leaf-nosed and Old World fruit bats (order Chiroptera). Evol. Biol. 2014, 41, 595–605. [Google Scholar]
- Debat, V.; David, P. Mapping phenotypes: Canalization, plasticity and developmental stability. Trends Ecol. Evol. 2001, 16, 555–561. [Google Scholar]
- Hallgrímsson, B.; Willmore, K.; Hall, B.K. Canalization, developmental stability, and morphological integration in primate limbs. Yearb. Phys. Anthropol. 2002, 45, 131–158. [Google Scholar]
- Debat, V.; Milton, C.C.; Rutherford, S.; Klingenberg, C.P.; Hoffmann, A.A. Hsp90 and the quantitative variation of wing shape in Drosophila melanogaster. Evolution 2006, 60, 2529–2538. [Google Scholar]
- Willmore, K.E.; Leamy, L.; Hallgrímsson, B. Effects of developmental and functional interactions on mouse cranial variability through late ontogeny. Evol. Dev. 2006, 8, 550–567. [Google Scholar]
- Klingenberg, C.P. Morphological integration and developmental modularity. Annu. Rev. Ecol. Evol. Syst. 2008, 39, 115–132. [Google Scholar]
- Graham, J.H.; Freeman, D.C.; Emlen, J.M. Antisymmetry, directional asymmetry, and dynamic morphogenesis. Genetica 1993, 89, 121–137. [Google Scholar]
- Rosenberg, M.S. Evolution of shape differences between the major and minor chelipeds of Uca pugnax (Decapoda: Ocypodidae). J. Crustac. Biol. 1997, 17, 52–59. [Google Scholar]
- Rosenberg, M.S. Fiddler crab claw shape variation: A geometric morphometric analysis across the genus Uca (Crustacea: Brachyura: Ocypodidae). Biol. J. Linn. Soc. 2002, 75, 147–162. [Google Scholar]
- Russo, T.; Pulcini, D.; Constantini, D.; Pedreschi, D.; Palamara, E.; Boglione, C.; Cataudella, S.; Scardi, M.; Mariani, S. “Right” or “wrong”? Insights into the ecology of sidedness in European flounder” Platichthys flesus. J. Morphol. 2012, 273, 337–346. [Google Scholar]
- Hori, M. Frequency-dependent natural selection in the handedness of scale-eating cichlid fish. Science 1993, 260, 216–219. [Google Scholar]
- Hata, H.; Yasugi, M.; Takeuchi, Y.; Takahashi, S.; Hori, M. Measuring and evaluating morphological asymmetry in fish: Distinct lateral dimorphism in the jaws of scale-eating cichlids. Ecol. Evol. 2013, 3, 4641–4647. [Google Scholar]
- Van Dooren, T.J.M.; van Goor, H.A.; van Putten, M. Handedness and asymmetry in scale-eating cichlids: Antisymmetries of different strength. Evolution 2010, 64, 2159–2165. [Google Scholar]
- Kusche, H.; Lee, H.J.; Meyer, A. Mouth asymmetry in the textbook example of scale-eating cichlid fish is not a discrete dimorphism after all. Proc. R. Soc. Lond. B Biol. Sci. 2012, 279, 4715–4723. [Google Scholar]
- Stewart, T.A.; Albertson, R.C. Evolution of a unique predatory feeding apparatus: Functional anatomy, development and a genetic locus for jaw laterality in Lake Tanganyika scale-eating cichlids. BMC Biol. 2010, 8, 8. [Google Scholar] [CrossRef]
- Hori, M.; Ochi, H.; Kohda, M. Inheritance pattern of lateral dimorphism in two cichlids (a scale eater, Perissodus microlepis, and an herbivore, Neolamprologus moorii) in Lake Tanganyika. Zool. Sci. (Tokyo). 2007, 24, 486–492. [Google Scholar]
- Silva, M.F.S.; de Andrade, I.M.; Mayo, S.J. Geometric morphometrics of leaf blade shape in Montrichardia linifera (Araceae) populations from the Rio Parnaíba delta, north-east Brazil. Bot. J. Linn. Soc. 2012, 170, 554–572. [Google Scholar]
- Chitwood, D.H.; Headland, L.R.; Ranjan, A.; Martinez, C.C.; Braybrook, S.A.; Koenig, D.P.; Kuhlemeier, C.; Smith, R.S.; Sinha, N.R. Leaf asymmetry as a developmental constraint imposed by auxin-dependent phyllotactic patterning. Plant Cell. 2012, 24, 2318–2327. [Google Scholar]
- Boas, F. The horizontal plane of the skull and the general problem of the comparison of variable forms. Science 1905, 21, 862–863. [Google Scholar]
- Sneath, P.H.A. Trend-surface analysis of transformatrion grids. J. Zool. 1967, 151, 65–122. [Google Scholar]
- Rohlf, F.J.; Marcus, L.F. A revolution in morphometrics. Trends Ecol. Evol. 1993, 8, 129–132. [Google Scholar]
- Bookstein, F.L. Morphometric Tools for Landmark Data: Geometry and Biology; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Klingenberg, C.P. Visualizations in geometric morphometrics: How to read and how to make graphs showing shape changes. Hystrix 2013, 24, 15–24. [Google Scholar]
- Lele, S.; Richtsmeier, J.T. Euclidean distance matrix analysis: A coordinate-free approach for comparing biological shapes using landmark data. Am. J. Phys. Anthropol. 1991, 86, 415–427. [Google Scholar]
- Lele, S.R.; Richtsmeier, J.T. An Invariant Approach to Statistical Analysis of Shapes; Chapman & Hall/CRC: Boca Raton, FL, USA, 2001; p. 308. [Google Scholar]
- Richtsmeier, J.T.; Cole, T.M., III; Lele, S.R. An invariant approach to the study of fluctuating asymmetry: Developmental instability in a mouse model for Down syndrome. In Modern Morphometrics in Physical Anthropology; Slice, D.E., Ed.; Kluwer Academic/Plenum: New York, NY, USA, 2005; pp. 187–212. [Google Scholar]
- DeLeon, V.B.; Richtsmeier, J.T. Fluctuating asymmetry and developmental instability in sagittal craniosynostosis. Cleft Palate Craniofac. J 2009, 46, 187–196. [Google Scholar]
- Starbuck, J.M.; Cole, T.M., III; Reeves, R.H.; Richtsmeier, J.T. Trisomy 21 and facial developmental instability. Am. J. Phys. Anthropol. 2013, 151, 49–57. [Google Scholar]
- Bookstein, F.L. Landmark methods for forms without landmarks: Morphometrics of group differences in outline shape. Med. Imag. Anal. 1997, 1, 225–243. [Google Scholar]
- Hammond, P.; Hutton, T.J.; Allanson, J.E.; Campbell, L.E.; Hennekam, R.C.M.; Holden, S.; Patton, M.A.; Shaw, A.; Temple, I.K.; Trotter, M.; et al. 3D analysis of facial morphology. Am. J. Med. Genet. 2004, 126A, 339–348. [Google Scholar]
- Claes, P.; Walters, M.; Vandermeulen, D.; Clement, J.G. Spatially-dense 3D facial asymmetry assessment in both typical and disordered growth. J. Anat. 2011, 219, 444–455. [Google Scholar]
- Gunz, P.; Mitteroecker, P. Semilandmarks: A method for quantifying curves and surfaces. Hystrix 2013, 24, 103–109. [Google Scholar]
- Goodall, C.R. Procrustes methods in the statistical analysis of shape. J. R. Statist. Soc. B 1991, 53, 285–339. [Google Scholar]
- Rohlf, F.J.; Slice, D.E. Extensions of the Procrustes method for the optimal superimposition of landmarks. Syst. Zool. 1990, 39, 40–59. [Google Scholar]
- Kendall, D.G.; Barden, D.; Carne, T.K.; Le, H. Shape and Shape Theory; Wiley: Chichester, UK, 1999. [Google Scholar]
- Small, C.G. The Statistical Theory of Shape; Springer-Verlag: New York, NY, USA, 1996. [Google Scholar]
- Gower, J.C. Generalized Procruses analysis. Psychometrika 1975, 40, 33–51. [Google Scholar]
- Rohlf, F.J. Shape statistics: Procrustes superimpositions and tangent spaces. J. Classif. 1999, 16, 197–223. [Google Scholar]
- Marcus, L.F.; Hingst-Zaher, E.; Zaher, H. Application of landmark morphometrics to skulls representing the orders of living mammals. Hystrix 2000, 11, 27–47. [Google Scholar]
- Auffray, J.-C.; Debat, V.; Alibert, P. Shape asymmetry and developmental stability. In On Growth and Form: Spatio-Temporal Pattern Formation in Biology; Chaplain, M.A.J., Singh, G.D., McLachlan, J.C., Eds.; Wiley: Chichester, UK, 1999; pp. 309–324. [Google Scholar]
- Kent, J.T.; Mardia, K.V.; Shape, Procrustes. tangent projections and bilateral symmetry. Biometrika 2001, 88, 469–485. [Google Scholar]
- Corti, M.; Rohlf, F.J. Chromosomal speciation and phenotypic evolution in the house mouse. Biol. J. Linn. Soc. 2001, 73, 99–112. [Google Scholar]
- Corti, M.; Aguilera, M.; Capanna, E. Size and shape changes in the skull accompanying speciation of South American spiny rats (Rodentia: Proechimys spp.). J. Zool. 2001, 253, 537–547. [Google Scholar]
- Webster, M.; Sheets, H.D.; Hughes, N.C. Allometric patterning in trilobite ontogeny: Testing for heterochrony in Nephrolenellus. In Beyond Heterochrony: The Evolution of Development; Zelditch, M.L., Ed.; Wiley-Liss: New York, NY, USA, 2001; pp. 105–144. [Google Scholar]
- Kim, K.; Sheets, H.D.; Haney, R.A.; Mitchell, C.E. Morphometric analysis of ontogeny and allometry of the Middle Ordovician trilobite Triarthrus becki. Paleobiology 2002, 28, 364–377. [Google Scholar]
- Zelditch, M.L.; Lundrigan, B.L.; Garland, T., Jr. Developmental regulation of skull morphology. I. Ontogenetic dynamics of variance. Evol. Dev. 2004, 6, 194–206. [Google Scholar]
- Kaliontzopoulou, A.; Carretero, M.A.; Llorente, G.A. Multivariate and geometric morphometrics in the analysis of sexual dimorphism variation in Podarcis lizards. J. Morphol. 2007, 268, 152–165. [Google Scholar]
- Baab, K.L.; McNulty, K.P. Size, shape, and asymmetry in fossil hominins: The status of the LB1 cranium based on 3D morphometric analyses. J. Hum. Evol. 2009, 57, 608–622. [Google Scholar]
- Kolamunnage, R.; Kent, J.T. Principal component analysis for shape variation about an underlying symmetric shape. In Stochastic Geometry, Biological Structure and Images; Aykroyd, R.G., Mardia, K.V., Langdon, M.J., Eds.; Department of Statistics, University of Leeds: Leeds, UK, 2003; pp. 137–139. [Google Scholar]
- Valentova, J.V.; Kleisner, K.; Havlíček, J.; Neustupa, J. Shape differences between the faces of homosexual and heterosexual men. Arch. Sex. Behav. 2014, 43, 353–361. [Google Scholar]
- Weisensee, K.E.; Jantz, R.L. Secular change in craniofacial morphology of the Portuguese using geometric morphometrics. Am. J. Phys. Anthropol. 2011, 145, 548–559. [Google Scholar]
- Sherratt, E.; Gower, D.J.; Klingenberg, C.P.; Wilkinson, M. Evolution of cranial shape in caecilians (Amphibia: Gymnophiona). Evol. Biol. 2014, 41, 528–545. [Google Scholar]
- Harmon, L.J.; Kolbe, J.J.; Cheverud, J.M.; Losos, J.B. Convergence and the multidimensional niche. Evolution 2005, 59, 409–421. [Google Scholar]
- Netherway, D.J.; Abbott, A.H.; Gulamhuseinwala, N.; McGlaughlin, K.L.; Anderson, P.J.; Townsend, G.C.; David, D.J. Three-dimensional computed tomography cephalometry of plagiocephaly: Asymmetry and shape analysis. Cleft Palate Craniofac. J 2006, 43, 201–210. [Google Scholar]
- Barluenga, M.; Stölting, K.N.; Salzburger, W.; Muschick, M.; Meyer, A. Sympatric speciation in Nicaraguan crater lake cichlid fish. Nature 2006, 439, 719–723. [Google Scholar]
- Weinberg, S.M.; Naidoo, S.D.; Bardi, K.M.; Brandon, C.A.; Neiswanger, K.; Resick, J.M.; Martin, R.A.; Marazita, M.L. Face shape of unaffected parents with cleft affected offspring: Combining three-dimensional surface imaging and geometric morphometrics. Orthod. Craniofac. Res. 2009, 12, 271–281. [Google Scholar]
- Tennant, J.P.; MacLeod, N. Snout shape in extant ruminants. PLoS ONE 2014, 9, e112035. [Google Scholar]
- Cobb, S.N.; O’Higgins, P. The ontogeny of sexual dimorphism in the facial skeleton of the African apes. J. Hum. Evol. 2007, 53, 176–190. [Google Scholar]
- Elmer, K.R.; Lehtonen, T.K.; Kautt, A.F.; Harrod, C.; Meyer, A. Rapid sympatric ecological differentiation of crater lake cichlid fishes within historic times. BMC Biol. 2010, 8, 60. [Google Scholar] [CrossRef]
- Young, M.T.; Brusatte, S.L.; Ruta, M.; de Andrade, M.B. The evolution of Metriorhynchoidea (mesoeucrocodylia, thalattosuchia): An integrated approach using geometric morphometrics, analysis of disparity, and biomechanics. Zool. J. Linn. Soc. 2010, 158, 801–859. [Google Scholar]
- Viscosi, V.; Cardini, A. Leaf morphology, taxonomy and geometric morphometrics: A simplified protocol for beginners. PLoS ONE 2011, 6, e25630. [Google Scholar]
- Bruner, E.; Constantini, D.; Fanfani, A.; Dell’Omo, G. Morphological variation and sexual dimorphism of the cephalic scales in Lacerta bilineata. Acta Zool. (Stockh.) 2005, 86, 245–254. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Biometry, 4th ed; Freeman: New York, NY, USA, 2012. [Google Scholar]
- Good, P. Permutation Tests: A Practical Guide to Resampling Methods for Testing Hypotheses, 2nd ed; Springer: New York, NY, USA, 2000. [Google Scholar]
- Manly, B.F.J. Randomization, Bootstrap and Monte Carlo Methods in Biology; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; p. 455. [Google Scholar]
- Klingenberg, C.P.; Monteiro, L.R. Distances and directions in multidimensional shape spaces: Implications for morphometric applications. Syst. Biol. 2005, 54, 678–688. [Google Scholar]
- Timm, N.H. Applied Multivariate Analysis; Springer: New York, NY, USA, 2002. [Google Scholar]
- Krzanowski, W.J.; Marriott, F.H.C. Multivariate Analysis. Part 1. Distributions, Ordination and Inference; Arnold: London, UK, 1994. [Google Scholar]
- Flury, B. A First Course in Multivariate Statistics; Springer: New York, NY, USA, 1997. [Google Scholar]
- Palmer, A.R. Waltzing with asymmetry. Bioscience 1996, 46, 518–532. [Google Scholar]
- Rivera, G.; Claude, J. Environmental media and shape asymmetry: A case study on turtle shalls. Biol. J. Linn. Soc. 2008, 94, 483–489. [Google Scholar]
- Bock, M.T.; Bowman, A.W. On the measurement and analysis of asymmetry with applications to facial modelling. Appl. Statist. 2006, 55, 77–91. [Google Scholar]
- Hajeer, M.Y.; Ayoub, A.F.; Millett, D.T. Three-dimensional assessment of facial soft-tissue asymmetry before and after orthognathic surgery. Br. J. Oral Maxillofac. Surg. 2004, 42, 396–404. [Google Scholar]
- Komori, M.; Kawamura, S.; Ishihara, S. Averageness or symmetry: Which is more important for facial attractiveness? Acta Psychol. 2009, 131, 136–142. [Google Scholar]
- Muñoz-Reyes, J.A.; Gil-Burmann, C.; Fink, B.; Turiegano, E. Facial asymmetry and aggression in Spanish adolescents. Pers. Individ. Dif. 2012, 53, 857–861. [Google Scholar]
- Abend, P.; Pflüger, L.S.; Koppensteiner, M.; Coquerelle, M.; Grammer, K. The sound of female shape: A redundant signal of vocal and facial attractiveness. Evol. Hum. Behav. 2015, 36, 174–181. [Google Scholar]
- Marchand, H.; Paillat, G.; Montuire, S.; Butet, A. Fluctuating asymmetry in bank vole populations (Rodentia, Arvicolinae) reflects stress caused by landscape fragmentation in the Mont-Saint-Michel Bay. Biol. J. Linn. Soc. 2003, 80, 37–44. [Google Scholar]
- Hallgrímsson, B.; Miyake, T.; Willmore, K.; Hall, B.K. Embryological origins of developmental stability: Size, shape and fluctuating asymmetry in prenatal random bred mice. J. Exp. Zool. B Mol. Dev. Evol. 2003, 296, 40–57. [Google Scholar]
- Pound, N.; Lawson, D.W.; Toma, A.M.; Richmond, S.; Zhurov, A.I.; Penton-Voak, I.S. Facial fluctuating asymmetry is not associated with childhood ill-health in a large British cohort study. Proc. R. Soc. Lond. B Biol. Sci. 2014, 281, 20141639. [Google Scholar] [CrossRef]
- Lezcano, A.H.; Rojas Quiroga, M.L.; Liberoff, A.L.; van der Molen, S. Marine pollution effects on the southern surf crab Ovalipes trimaculatus (Crustacea: Brachyura: Polybiidae) in Patagonia Argentina. Mar. Pollut. Bull. 2015, 91, 524–529. [Google Scholar]
- Klingenberg, C.P. Cranial integration and modularity: Insights into evolution and development from morphometric data. Hystrix 2013, 24, 43–58. [Google Scholar]
- Bruner, E.; Bartolino, V. Morphological variation in the seahorse vertebral system. Int. J. Morphol. 2008, 26, 247–262. [Google Scholar]
- Sarris, I.; Marugán-Lobón, J.; Chamero, B. Buscalioni, Á.D. Shape variation and allometry in the precloacal vertebral series of the snake Daboia russelli (Viperidae). Int. J. Morphol. 2012, 30, 1363–1368. [Google Scholar]
- Jones, C.S. Comparative ontogeny of a wild cucurbit and its derived cultivar. Evolution 1992, 46, 1827–1847. [Google Scholar]
- Jones, C.S. Heterochrony and heteroblastic leaf development in two subspecies of Cucurbita argyrosperma (Cucurbitaceae). Am. J. Bot. 1993, 80, 778–795. [Google Scholar]
- Jones, C.S. Does shade prolong juvenile development? A morphological analysis of leaf shape changes in Cucurbita argyrosperma subsp. sororia (Cucurbitaceae). Am. J. Bot. 1995, 82, 346–359. [Google Scholar]
- Chitwood, D.H.; Headland, L.R.; Kumar, R.; Peng, J.; Maloof, J.N.; Sinha, N.R. The developmental trajectory of leaflet morphology in wild tomato species. Plant Physiol. (Rockv.) 2012, 158, 1230–1240. [Google Scholar]
- Bateman, R.M.; Ruddall, P.J. Evolutionary and morphometric implications of morphological variation among flowers within an inflorescence: A case study using European orchids. Ann. Bot. 2006, 98, 975–993. [Google Scholar]
- Herrera, C.M. Multiplicity in Unity: Plant Subindividual Variation and Interactions with Animals; University of Chicago Press: Chicago, IL, USA, 2009. [Google Scholar]
- Gómez, J.M. Dispersal-mediated selection on plant height in an autochorously dispersed herb. Plant Syst. Evol. 2007, 268, 119–130. [Google Scholar]
- Gómez, J.M.; Bosch, J.; Perfectti, F.; Fernández, J.D.; Abdelaziz, M.; Camacho, J.P.M. Spatial variation in selection on corolla shape in a generalist plant is promoted by the preference patterns of its local pollinators. Proc. R. Soc. Lond. B Biol. Sci. 2008, 275, 2241–2249. [Google Scholar]
- Gómez, J.M.; Perfectti, F.; Bosch, J.; Camacho, J.P.M. A geographic selection mosaic in a generalized plant–pollinator–herbivore system. Ecol. Monogr. 2009, 79, 245–263. [Google Scholar]
- Gómez, J.M.; Abdelaziz, M.; Camacho, J.P.M.; Muñoz-Pajares, A.J.; Perfectti, F. Local adaptation and maladaptation to pollinators in a generalist geographic mosaic. Ecol. Lett. 2009, 12, 672–682. [Google Scholar]
- Kim, M.; Cui, M.-L.; Cubas, P.; Gillies, A.; Lee, K.; Chapman, M.A.; Abbott, R.J.; Coen, E. Regulatory genes control a key morphological and ecological trait transferred between species. Science 2008, 322, 1116–1119. [Google Scholar]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Symmetry as a continuous feature. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 1154–1166. [Google Scholar]
- Frey, F.M.; Robertson, A.; Bukoski, M. A method for quantifying rotational symmetry. New Phytol. 2007, 175, 785–791. [Google Scholar]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. 2. Symmetry groups and the tetrahedron. J. Am. Chem. Soc. 1993, 115, 8278–8289. [Google Scholar]
- Zabrodsky, H.; Avnir, D. Continuous symmetry measures. 4. Chirality. J. Am. Chem. Soc. 1995, 117, 462–473. [Google Scholar]
- Graham, J.H.; Whitesell, M.J.; Fleming, M., II; Hel-Or, H.; Nevo, E.; Raz, S. Fluctuating asymmetry of plant leaves: Batch processing with LAMINA and continuous symmetry measures. Symmetry 2015, 7, 255–268. [Google Scholar]
- Frey, F.M.; Bukoski, M. Floral symmetry is associated with flower size and pollen production but not insect visitation rates in Geranium robertianum (Geraniaceae). Plant Species Biol. 2014, 29, 272–280. [Google Scholar]
- Kuhl, F.P.; Giardina, C.R. Elliptic Fourier features of a closed contour. Comput. Graph. Im. Proc. 1982, 18, 236–258. [Google Scholar]
- Ferson, S.; Rohlf, F.J.; Koehn, R.K. Measuring shape variation of two-dimensional outlines. Syst. Zool. 1985, 34, 59–68. [Google Scholar]
- Rohlf, F.J.; Archie, J.W. A comparison of Fourier methods for the description of wing shape in mosquitoes (Diptera: Culicidae). Syst. Zool. 1984, 33, 302–317. [Google Scholar]
- Lohmann, G.P.; Schweitzer, P.N. On eigenshape analysis. In Proceedings of the Michigan Morphometrics Workshop; Rohlf, F.J., Bookstein, F.L., Eds.; University of Michigan Museum of Zoology: Ann Arbor, MI, USA, 1990; pp. 147–166. [Google Scholar]
- Lohmann, G.P. Eigenshae analysis of microfossils: A general morphometric procedure for describing changes in shape. Math. Geol. 1983, 15, 659–672. [Google Scholar]
- MacLeod, N. Generalizing and extending the eigenshape method of shape space visualization and analysis. Paleobiology 1999, 25, 107–138. [Google Scholar]
- Gunz, P.; Mitteroecker, P.; Bookstein, F.L. Semilandmarks in three dimensions. In Modern Morphometrics in Physical Anthropology; Slice, D.E., Ed.; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2005; pp. 73–98. [Google Scholar]
- McCane, B. Shape variation in outline shapes. Syst. Biol. 2013, 62, 134–146. [Google Scholar]
- Kristensen, E.; Parsons, T.E.; Hallgrímsson, B.; Boyd, S.K. A novel 3-D image-based morphological method for phenotypic analysis. IEEE Trans. Biomed. Eng. 2008, 55, 2826–2831. [Google Scholar]
- Shen, L.; Farid, H.; McPeek, M.A. Modeling three-dimensional morphological structures using spherical harmonics. Evolution 2009, 63, 1003–1016. [Google Scholar]
- Polly, P.D. Developmental dynamics and G-matrices: Can morphometric spaces be used to model phenotypic evolution? Evol. Biol. 2008, 35, 83–96. [Google Scholar]
- Klingenberg, C.P. Novelty and “homology-free” morphometrics: What’s in a name? Evol. Biol. 2008, 35, 186–190. [Google Scholar]
- Rohlf, F.J. Relationships among eigenshape analysis, Fourier analysis, and analysis of coordinates. Math. Geol. 1986, 18, 845–854. [Google Scholar]
- Cannon, C.H.; Manos, P.S. Combining and comparing morphometric shape descriptors with a molecular phylogeny: The case of fruit type evolution in Bornean Lithocarpus (Fagaceae). Syst. Biol. 2001, 50, 860–880. [Google Scholar]
- Navarro, N.; Zatarain, X.; Montuire, S. Effects of morphometric descriptor changes on statistical classification and morphospaces. Biol. J. Linn. Soc. 2004, 83, 243–260. [Google Scholar]
- Perez, S.I.; Bernal, V.; Gonzalez, P.N. Differences between sliding semi-landmark methods in geometric morohometrics, with an application to human craniofacial variation. J. Anat. 2006, 208, 769–784. [Google Scholar]
- Sforza, C.; Michielon, G.; Fragnito, N.; Ferrario, V.F. Foot asymmetry in healthy adults: Elliptic Fourier analysis of standardized footprints. J. Orthop. Res. 1998, 16, 758–765. [Google Scholar]
- Tanaka, H. Numerical analysis of the proximal humeral outline: Bilateral shape differences. Am. J. Hum. Biol. 1999, 11, 343–357. [Google Scholar]
- Polly, P.D.; Killick, L.; Ruddy, M. Using left–right asymmetry to estimate non-genetic variation in vole teeth (Arvicolinae, Muridae, Rodentia). Palaeontol. Electron. 2011, 14, 1–12. [Google Scholar]
- Oberzaucher, E.; Katina, S.; Schmehl, S.F.; Holzleitner, I.J.; Grammer, K. The myth of hidden ovulation: Shape and texture changes in the face during the menstrual cycle. J. Evol. Psychol. 2012, 10, 163–175. [Google Scholar]
- Pflüger, L.S.; Oberzaucher, E.; Katina, S.; Holzleitner, I.J.; Grammer, K. Cues to fertility: Perceived attractiveness and facial shape predict reproductive success. Evol. Hum. Behav. 2012, 33, 708–714. [Google Scholar]
- Hammond, P.; Forster-Gibson, C.; Chudley, A.E.; Allanson, J.E.; Hutton, T.J.; Farrell, S.A.; McKenzie, J.; Holden, J.J.A.; Lewis, M.E.S. Face–brain asymmetry in autism spectrum disorders. Mol. Psychiatry. 2008, 13, 614–623. [Google Scholar]
- DiBiase, A.T.; Elcock, C.; Smith, R.N.; Brook, A.H. A new technique for symmetry determination in tooth morphology using image analysis: Application in the diagnosis of solitary maxillary median central incisor. Arch. Oral Biol. 2006, 51, 870–875. [Google Scholar]
- Iwata, H.; Niikura, S.; Matsuura, S.; Takano, Y.; Ukai, Y. Evaluation of variation of root shape of Japanese radish (Raphanus sativus L.) based on image analysis using elliptic Fourier descriptors. Euphytica 1998, 102, 143–149. [Google Scholar]
- Yoshioka, Y.; Iwata, H.; Ohsawa, R.; Ninomiya, S. Analysis of petal shape variation of Primula sieboldii by elliptic Fourier descriptors and principal component analysis. Ann. Bot. 2004, 94, 657–664. [Google Scholar]
- Goto, S.; Iwata, H.; Shibano, S.; Ohya, K.; Suzuki, A.; Ogawa, H. Fruit shape variation in Fraxinus mandshurica var. japonica characterized using elliptic Fourier descriptors and the effect on flight duration. Ecol. Res. 2005, 20, 733–738. [Google Scholar]
- Lexer, C.; Joseph, J.; van Loo, M.; Prenner, G.; Heinze, B.; Chase, M.W.; Kirkup, D. The use of digital image-based morphometrics to study the phenotypic mosaic in taxa with porous genomes. Taxon 2009, 58, 349–364. [Google Scholar]
- Adebowale, A.; Nicholas, A.; Lamb, J.; Naidoo, Y. Elliptic Fourier analysis of leaf shape in southern African Strychnos section Densiflorae (Loganiaceae). Bot. J. Linn. Soc. 2012, 170, 542–553. [Google Scholar]
- Chitwood, D.H.; Naylor, D.T.; Thammapichai, P.; Weeger, A.C.S.; Headland, L.R.; Sinha, N.R. Conflict between intrinsic leaf asymmetry and phyllotaxis in the resupinate leaves of Alstromeria psittacina. Front. Plant Sci. 2012, 3, 182. [Google Scholar] [CrossRef]
- Chitwood, D.H.; Ranjan, A.; Kumar, R.; Ichihashi, Y.; Zumstein, K.; Headland, L.R.; Ostria-Gallardo, E.; Aguilar-Martínez, J.A.; Bush, S.; Carriedo, L.; et al. Resolving distinct genetic regulators of tomato leaf shape within a heteroblastic and ontogenetic context. Plant Cell. 2014, 26, 3616–3629. [Google Scholar]
- Volkova, P.A.; Kasatskaya, S.A.; Boiko, A.A.; Shipunov, A.B. Stability of leaf form and size during specimen preparation of herbarium specimens. Feddes Repert. 2010, 212, 219–225. [Google Scholar]
- Lee, J.C. Accuracy and precision in anuran morphometrics: Artifacts of preservation. Syst. Zool. 1982, 31, 266–281. [Google Scholar]
- Martinez, P.A.; Berbel-Filho, W.M.; Jacobina, U.P. Is formalin fixation and ethanol preservation able to influence in geomertric morphometric analysis? Fishes as a case study. Zoomorphology (Berl.) 2013, 132, 87–93. [Google Scholar]
- Berbel-Filho, W.M.; Jacobina, U.P.; Martinez, P.A. Preservation effects in geometric morphometric approaches: Freezing and alcohol in a freshwater fish. Ichthyol. Res. 2013, 60, 268–271. [Google Scholar]
- Schmidt, E.J.; Parsons, T.E.; Jamniczky, H.A.; Gitelman, J.; Trpkov, C.; Boughner, J.C.; Logan, C.C.; Sensen, C.W.; Hallgrímsson, B. Micro-computed tomography-based phenotypic approaches in embryology: Procedural artifacts on assessments of embryonic craniofacial growth and development. BMC Dev. Biol. 2010, 10, 18. [Google Scholar] [CrossRef]
- Weisbecker, V. Distortion in formalin-fixed brains: Using geometric morphometrics to quantify the worst-case scenario in mice. Brain Struct. Funct. 2012, 217, 677–685. [Google Scholar]
- Perrard, A.; Villemant, C.; Carpenter, J.M.; Baylac, M. Differences in caste dimorphism among three hornet species (Hymenoptera: Vespidae): Forewing size, shape and allometry. J. Evol. Biol. 2012, 25, 1389–1398. [Google Scholar]
- Lorenz, C.; Suesdek, L. Evaluation of chemical preparation on insect wing shape for geometric morphometrics. Am. J. Trop. Med. Hyg. 2013, 89, 928–931. [Google Scholar]
- Merilä, J.; Björklund, M. Fluctuating asymmetry and measurement error. Syst. Biol. 1995, 44, 97–101. [Google Scholar]
- Corner, B.D.; Lele, S.R.; Richtsmeier, J.T. Measuring precision of three-dimensional landmark data. J. Quant. Anthropol. 1992, 3, 347–359. [Google Scholar]
- Arnqvist, G.; Mårtensson, T. Measurement error in geometric morphometrics: Empirical strategies to assess and reduce its impact on measures of shape. Acta Zool. Acad. Sci. Hung. 1998, 44, 73–96. [Google Scholar]
- Robinson, D.L.; Blackwell, P.G.; Stillman, E.C.; Brook, A.H. Impact of landmark reliability on the planar Procrustes analysis of tooth shape. Arch. Oral Biol. 2002, 47, 545–554. [Google Scholar]
- Von Cramon-Taubadel, N.; Frazier, B.C.; Lahr, M.M. The problem of assessing landmark error in geometric morphometrics: Theory, methods, and modifications. Am. J. Phys. Anthropol. 2007, 134, 24–35. [Google Scholar]
- Sholts, S.B.; Flores, L.; Walker, P.P.; Wärmländer, S.K.T.S. Comparison of coordinate measurement precision of different landmark types on human crania using a 3D laser scanner and a 3D digitiser: Implications for applications of digital morphometrics. Int. J. Osteoarchaeol. 2011, 21, 535–543. [Google Scholar]
- Roth, V.L. On three-dimensional morphometrics, and on the identification of landmark points. In Contributions to Morphometrics; Marcus, L.F., Bello, E., García-Valdecasas, A., Eds.; Museo Nacional de Ciencias Naturales: Madrid, Spain, 1993; pp. 41–61. [Google Scholar]
- Cardini, A. Missing the third dimension in geometric morphometrics: How to assess if 2D images really are a good proxy for 3D structures? Hystrix 2014, 25, 73–81. [Google Scholar]
- Gharaibeh, W.S. Correcting for the effect of orientation in geometric morphometric studies of side-view images of human heads. In Modern Morphometrics in Physical Anthropology; Slice, D.E., Ed.; Kluwer Academic/Plenum: New York, NY, USA, 2005; pp. 117–143. [Google Scholar]
- Posnien, N.; Hopfen, C.; Hilbrant, M.; Ramos-Womack, M.; Murat, S.; Schönauer, A.; Herbert, S.L.; Nunes, M.D.S.; Arif, S.; Breuker, C.J.; et al. Evolution of eye morphology and rhodopsin expression in the Drosophila melanogaster species subgroup. PLoS ONE 2012, 7, e37346. [Google Scholar]
- Losick, R.; Desplan, C. Stochasticity and cell fate. Science 2008, 320, 65–68. [Google Scholar]
- Raj, A.; van Oudenaarden, A. Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell 2008, 135, 216–226. [Google Scholar]
- Huh, D.; Paulsson, J. Non-genetic heterogeneity from stochastic partitioning at cell division. Nat. Genet. 2011, 43, 95–100. [Google Scholar]
- Coulon, A.; Chow, C.C.; Singer, R.H.; Larson, D.R. Eukaryotic transcriptional dynamics: From single molecules to cell populations. Nat. Rev. Genet. 2013, 14, 572–584. [Google Scholar]
- Marinov, G.K.; Williams, B.A.; McCue, K.; Schroth, G.P.; Gertz, J.; Myers, R.M.; Wold, B.J. From single-cell to cell-pool transcriptomes: Stochasticity in gene expression and RNA splicing. Genome Res. 2014, 24, 496–510. [Google Scholar]
- Zhou, W.; Tan, Y.; Anderson, D.J.; Crist, E.M.; Ruohola-Baker, H.; Salipante, S.J.; Horwitz, M.S. Use of somatic mutations to quantify random contributions to mouse development. BMC Genomics. 2013, 14, 39. [Google Scholar] [CrossRef]
- Behjati, S.; Huch, M.; van Boxtel, R.; Karthaus, W.; Wedge, D.C.; Tamuri, A.U.; Matrincorena, I.; Petljak, M.; Alexandrov, L.B.; Gundem, G.; et al. Genome sequencing of normal cells reveals developmental lineages and mutational processes. Nature 2014, 513, 422–425. [Google Scholar]
- Vijg, J. Somatic mutations, genome mosaicism, cancer and aging. Curr. Opin. Genet. Dev. 2014, 26, 141–149. [Google Scholar]
- Verhaegen, Y.; Adriaens, D.; De Wolf, T.; Dhert, P.; Sorgeloos, P. Deformities in larval gilthead sea bream (Sparus aurata): A qualitative and quantitative analysis using geometric morphometrics. Aquaculture 2007, 268, 156–168. [Google Scholar]
- Debat, V.; Bloyer, S.; Faradji, F.; Gidaszewski, N.A.; Navarro, N.; Orozco-terWengel, P.; Ribeiro, V.; Schlötterer, C.; Deutsch, J.S.; Peronnet, F. Developmental stability: A major role for Cyclin G in Drosophila melanogaster. PLoS Genet. 2011, 7, e1002314. [Google Scholar]
- DeLaurier, A.; Huycke, T.R.; Nichols, J.T.; Swartz, M.E.; Larsen, A.; Walker, C.; Dowd, J.; Pan, L.; Moens, C.B.; Kimmel, C.B. Role of mef2ca in developmental buffering of the zebrafish larval hyoid dermal skeleton. Dev. Biol. 2014, 385, 189–199. [Google Scholar]
- Alberch, P. The logic of monsters: Evidence for internal constraint in development and evolution. In Ontogenèse et Évolution; David, B., Marchand, J.-L., Chaline, J., Laurin, B., Eds.; Geobios, mémoire spécial 12: Dijon, France, 1989; pp. 21–57. [Google Scholar]
- Abouchar, L.; Petkova, M.D.; Steinhardt, C.R.; Gregor, T. Fly wing vein patterns have spatial reproducibility of a single cell. J. R. Soc. Interface 2014, 11. [Google Scholar] [CrossRef]
- von Dassow, G.; Meir, E.; Munro, E.M.; Odell, G.M. The segment polarity network is a robust developmental module. Nature 2000, 406, 188–192. [Google Scholar]
- Milton, C.C.; Huynh, B.; Batterham, P.; Rutherford, S.L.; Hoffmann, A.A. Quantitative trait symmetry independent of Hsp90 buffering: Distinct modes of genetic canalization and developmental stability. Proc. Natl. Acad. Sci. USA 2003, 100, 13396–13401. [Google Scholar]
- Debat, V.; Peronnet, F. Asymmetric flies: The control of developmental noise in Drosophila. Fly 2013, 7, 70–77. [Google Scholar]
- Garelli, A.; Gontijo, A.M.; Miguela, V.; Caparros, E.; Dominguez, M. Imaginal discs secrete insulin-like peptide 8 to mediate plasticity of growth and maturation. Science 2012, 336, 579–582. [Google Scholar]
- Talbot, J.C.; Walker, M.B.; Carney, T.J.; Huycke, T.R.; Yan, Y.-L.; BreMiller, R.A.; Gai, L.; DeLaurier, A.; Postlethwait, J.H.; Hammerschmidt, M.; et al. fras1 shapes endodermal pouch 1 and stabilizes zebrafish pharyngeal skeletal development. Development 2012, 139, 2804–2813. [Google Scholar]
- Freeman, D.C.; Brown, M.L.; Dobson, M.; Jordan, Y.; Kizy, A.; Micallef, C.; Hancock, L.C.; Graham, J.H.; Emlen, J.M. Developmental instability: Measures of resistance and resilience using pumpkin (Cucurbita pepo L.). Biol. J. Linn. Soc. 2003, 78, 27–41. [Google Scholar]
- Klingenberg, C.P.; Nijhout, H.F. Competition among growing organs and developmental control of morphological asymmetry. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 1135–1139. [Google Scholar]
- Hallgrímsson, B. Fluctuating asymmetry in Macaca fascicularis: A study of the etiology of developmental noise. Int. J. Primatol. 1993, 14, 421–443. [Google Scholar]
- Swaddle, J.P.; Witter, M.S. On the ontogeny of developmental stability in a stabilised trait. Proc. R. Soc. Lond. B Biol. Sci. 1997, 264, 329–334. [Google Scholar]
- Aparicio, J.M. Patterns of fluctuating asymmetry in developing primary feathers: A test of the compensational growth hypothesis. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 2353–2357. [Google Scholar]
- Hallgrímsson, B. Ontogenetic patterning of skeletal fluctuating asymmetry in Rhesus macaques and humans: Evolutionary and developmental implications. Int. J. Primatol. 1999, 20, 121–151. [Google Scholar]
- Kellner, J.R.; Alford, R.A. The ontogeny of fluctuating asymmetry. Am. Nat. 2003, 161, 931–947. [Google Scholar]
- Pélabon, C.; Hansen, T.F.; Carlson, M.L.; Armbruster, W.S. Patterns of asymmetry in the twining vine Dalechampia scandens (Euphorbiaceae): Ontogenetic and hierarchical perspectives. New Phytol. 2006, 170, 65–74. [Google Scholar]
- Gonzalez, P.N.; Hallgrímsson, B.; Oyhenart, E.E. Developmental plasticity in covariance structure of the skull: Effects of prenatal stress. J. Anat. 2011, 218, 243–257. [Google Scholar]
- Zelditch, M.L. Developmental regulation of variability. In Variation: A Central Concept in Biology; Hallgrímsson, B., Hall, B.K., Eds.; Elsevier: Burlington, MA, USA, 2005; pp. 249–276. [Google Scholar]
- Bulygina, E.; Mitteroecker, P.; Aiello, L. Ontogeny of facial dimorphism and patterns of individual development within one human population. Am. J. Phys. Anthropol. 2006, 131, 432–443. [Google Scholar]
- Cheverud, J.M.; Rutledge, J.J.; Atchley, W.R. Quantitative genetics of development: Genetic correlations among age-specific trait values and the evolution of ontogeny. Evolution 1983, 37, 895–905. [Google Scholar]
- Riska, B.; Atchley, W.R.; Rutledge, J.J. A genetic analysis of targeted growth in mice. Genetics 1984, 107, 79–101. [Google Scholar]
- Kirkpatrick, M.; Lofsvold, D. Measuring selection and constraint in the evolution of growth. Evolution 1992, 46, 954–971. [Google Scholar]
- Björklund, M. Phenotypic variation of growth trajectories in finches. Evolution 1993, 47, 1506–1514. [Google Scholar]
- Klingenberg, C.P.; Neuenschwander, B.E.; Flury, B.D. Ontogeny and individual variation: Analysis of patterned covariance matrices with common principal components. Syst. Biol. 1996, 45, 135–150. [Google Scholar]
- Klingenberg, C.P. Individual variation of ontogenies: A longitudinal study of growth and timing. Evolution 1996, 50, 2412–2428. [Google Scholar]
- Benítez, H.A.; Lemic, D.; Bažok, R.; Bravi, R.; Buketa, M.; Püschel, T. Morphological integration and modularity in Diabrotica virgifera virgifera LeConte (Coleoptera: Chrysomelidae) hindwings. Zool. Anz. 2014, 253, 461–468. [Google Scholar]
- Thornhill, R.; Møller, A.P. Developmental stability, disease and medicine. Biol. Rev. 1997, 72, 497–548. [Google Scholar]
- Møller, A.P. Developmental stability and fitness: A review. Am. Nat. 1997, 149, 916–932. [Google Scholar]
- Møller, A.P.; Thornhill, R. Bilateral symmetry and sexual selection: A meta-analysis. Am. Nat. 1998, 151, 174–192. [Google Scholar]
- Gangestad, S.W.; Thornhill, R. Individual differences in developmental precision and fluctuating asymmetry: A model and its implications. J. Evol. Biol. 1999, 12, 402–416. [Google Scholar]
- Møller, A.P.; Shykoff, J.A. Morphological developmental statibility in plants: Patterns and causes. Int. J. Plant Sci. 1999, 160, S135–S146. [Google Scholar]
- Palmer, A.R.; Hammond, L.M. The emperor’s codpiece: A post-modern perspective on biological asymmetries. Int. Soc. Behav. Ecol. Newsl. 2000, 12, 13–20. [Google Scholar]
- Møller, A.P.; Manning, J.T. Growth and developmental instability. Vet. J 2003, 166, 19–27. [Google Scholar]
- Van Dongen, S.; Gangestad, S.W. Human fluctuating asymmetry in relation to health and quality: A meta-analysis. Evol. Hum. Behav. 2011, 32, 380–398. [Google Scholar]
- Van Dongen, S. How repeatable is the estimation of developmental stability by fluctuating asymmetry? Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 1423–1427. [Google Scholar]
- Houle, D. A simple model of the relationship between asymmetry and developmental stability. J. Evol. Biol. 2000, 13, 720–730. [Google Scholar]
- Leung, B.; Forbes, M.R.; Houle, D. Fluctuating asymmetry as a bioindicator of stress: Comparing efficacy of analyses involving multiple traits. Am. Nat. 2000, 155, 101–115. [Google Scholar]
- Maestri, R.; Fornel, R.; Galiano, D.; de Freitas, T.R.O. Niche suitability affects development: Skull asymmetry increases in less suitable areas. PLoS ONE 2015, 10, e0122412. [Google Scholar]
- Sánchez-Chardi, A.; García-Pando, M.; López-Fuster, M.J. Chronic exposure to environmental stressors induces fluctuating asymmetry in shrews inhabiting protected Mediterranean sites. Chemosphere 2013, 93, 916–923. [Google Scholar]
- Radwan, J. Inbreeding not stress increases fluctuating asymmetry in the bulb mite. Evol. Ecol. Res. 2003, 5, 287–295. [Google Scholar]
- Keller, J.M.; Allen, D.E.; Davis, C.R.; Leamy, L.J. 2,3,7,8-Tetrachlorodibenzo-p-dioxin affects fluctuating asymmetry of molar shape in mice, and an epistatic interaction of two genes for molar size. Heredity 2007, 98, 259–267. [Google Scholar]
- Muñoz-Reyes, J.A.; Pita, M.; Arjona, M.; Sanchez-Pages, S.; Turiegano, E. Who is the fairest of them all? The independent effect of attractive features and self-perceived attractiveness on cooperation among women. Evol. Hum. Behav. 2014, 35, 118–125. [Google Scholar]
- Sanchez-Pages, S.; Turiegano, E. Testosterone, facial symmetry and cooperation in the prisoners’ dilemma. Physiol. Behav. 2010, 99, 355–361. [Google Scholar]
- Fink, B.; Grammer, K.; Mitteroecker, P.; Gunz, P.; Schaefer, K.; Bookstein, F.L.; Manning, J.T. Second to fourth digit ratio and face shape. Proc. R. Soc. Lond. B Biol. Sci. 2005, 272, 1995–2001. [Google Scholar]
- Sanchez-Pages, S.; Turiegano, E. Two studies on the interplay between social preferences and individual biological features. Behaviour 2013, 150, 713–735. [Google Scholar]
- Holtzman, N.S.; Augustine, A.A.; Senne, A.L. Are pro-social or socially aversive people more physically symmetrical? Symmetry in relation to over 200 personality variables. J. Res. Pers. 2011, 45, 687–691. [Google Scholar]
- Woolf, C.M.; Markow, T.A. Genetic models for developmental homeostasis: Historical perspectives. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 99–115. [Google Scholar]
- Windhager, S.; Schaschl, H.; Schaefer, K.; Mitteroecker, P.; Huber, S.; Wallner, B.; Fieder, M. Variation at genes influencing facial morphology are not associated with developmental imprecision in human faces. PLoS ONE 2014, 9, e99009. [Google Scholar]
- Leung, B. Correcting for allometry in studies of fluctuating asymmetry and quality within samples. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 1623–1629. [Google Scholar]
- Monteiro, L.R. Multivariate regression models and geometric morphometrics: The search for causal factors in the analysis of shape. Syst. Biol. 1999, 48, 192–199. [Google Scholar]
- Drake, A.G.; Klingenberg, C.P. The pace of morphological change: Historical transformation of skull shape in St. Bernard dogs. Proc. R. Soc. Lond. B Biol. Sci. 2008, 275, 71–76. [Google Scholar]
- Rodríguez-Mendoza, R.; Muñoz, M.; Saborido-Rey, F. Ontogenetic allometry of the bluemouth, Helicolenus dactylopterus dactylopterus (Teleostei: Scorpaenidae), in the Northeast Atlantic and Mediterranean based on geometric morphometrics. Hydrobiologia 2011, 670, 5–22. [Google Scholar]
- Alibert, P.; Auffray, J.-C. Genomic coadaptation, outbreeding depression, and developmental instability. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 116–134. [Google Scholar]
- Fuller, R.C.; Houle, D. Inheritance of developmental instability. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 157–183. [Google Scholar]
- Leamy, L.J. Dominance, epistasis, and fluctuating asymmetry. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 142–156. [Google Scholar]
- Leamy, L.J.; Klingenberg, C.P. The genetics and evolution of fluctuating asymmetry. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 1–21. [Google Scholar]
- Van Dongen, S. What do we know about the heritability of developmental instability? Answers from a Bayesian model. Evolution 2007, 61, 1033–1042. [Google Scholar]
- Carter, A.J.R.; Houle, D. Artificial selection reveals heritable variation for developmental instability. Evolution 2011, 65, 3558–3564. [Google Scholar]
- Tsujino, M.; Takahashi, K.H. Lack of response to artificial selection on developmental stability of partial wing shape components in Drosophila melanogaster. Genetica (Dordr.) 2014, 142, 177–184. [Google Scholar]
- Leamy, L.J.; Workman, M.S.; Routman, E.J.; Cheverud, J.M. An epistatic genetic basis for fluctuating asymmetry of tooth size and shape in mice. Heredity 2005, 94, 316–325. [Google Scholar]
- Leamy, L.J.; Routman, E.J.; Cheverud, J.M. An epistatic genetic basis for fluctuating asymmetry of mandible size in mice. Evolution 2002, 56, 642–653. [Google Scholar]
- Nijhout, H.F.; Paulsen, S.M. Developmental models and polygenic characters. Am. Nat. 1997, 149, 394–405. [Google Scholar]
- Gilchrist, M.A.; Nijhout, H.F. Nonlinear developmental processes as sources of dominance. Genetics 2001, 159, 423–432. [Google Scholar]
- Klingenberg, C.P. Dominance, nonlinear developmental mapping and developmental stability. In The Biology of Genetic Dominance; Veitia, R.A., Ed.; Landes Bioscience: Austin, TX, USA, 2004; pp. 37–51. [Google Scholar]
- Kacser, H.; Burns, J.A. The molecular basis of dominance. Genetics 1981, 97, 639–666. [Google Scholar]
- Rohlf, F.J.; Corti, M. The use of two-block partial least-squares to study covariation in shape. Syst. Biol. 2000, 49, 740–753. [Google Scholar]
- Olson, E.C.; Miller, R.L. Morphological Integration; University of Chicago Press: Chicago, IL, USA, 1958. [Google Scholar]
- Sakai, K.-I.; Shimamoto, Y. A developmental-genetic study on panicle charaters in rice, Oryza sativa L. Genet. Res. 1965, 6, 93–103. [Google Scholar]
- Leamy, L. Morphological integration of fluctuating asymmetry in the mouse mandible. Genetica 1993, 89, 139–153. [Google Scholar]
- Willmore, K.E.; Hallgrímsson, B. Within individual variation: Developmental noise versus developmental stability. In Variation: A Central Concept in Biology; Hallgrímsson, B., Hall, B.K., Eds.; Elsevier: Burlington, MA, USA, 2005; pp. 191–218. [Google Scholar]
- Goswami, A.; Polly, P.D. Methods for studying morphological integration and modularity. In Quantitative Methods in Paleobiology; Alroy, J., Hunt, G., Eds.; Paleontological Society: Ithaca, NY, USA, 2010; pp. 213–243. [Google Scholar]
- Klingenberg, C.P. Developmental constraints, modules and evolvability. In Variation: A Central Concept in Biology; Hallgrímsson, B., Hall, B.K., Eds.; Elsevier: Burlington, MA, USA, 2005; pp. 219–247. [Google Scholar]
- Riska, B. Some models for development, growth, and morphometric correlation. Evolution 1986, 40, 1303–1311. [Google Scholar]
- Slatkin, M. Quantitative genetics of heterochrony. Evolution 1987, 41, 799–811. [Google Scholar]
- Nijhout, H.F.; Emlen, D.J. Competition among body parts in the development and evolution of insect morphology. Proc. Natl. Acad. Sci. USA 1998, 95, 3685–3689. [Google Scholar]
- Dryden, I.L.; Koloydenko, A.; Zhou, D. Non-Euclidean statistics for covariance matrices, with applications to diffusion tensor imaging. Ann. Appl. Stat. 2009, 3, 1102–1123. [Google Scholar]
- Mitteroecker, P.; Bookstein, F.L. The ontogenetic trajectory of the phenotypic covariance matrix, with examples from craniofacial shape in rats and humans. Evolution 2009, 63, 727–737. [Google Scholar]
- Young, N.M. Function, ontogeny and canalization of shape variance in the primate scapula. J. Anat. 2006, 209, 623–636. [Google Scholar]
- Escoufier, Y. Le traitement des variables vectorielles. Biometrics 1973, 29, 751–760. [Google Scholar]
- Smilde, A.K.; Kiers, H.A.L.; Bijlsma, S.; Rubingh, C.M.; van Erk, M.J. Matrix correlations for high-dimensional data: The modified RV-coefficient. Bioinformatics (Oxf.) 2009, 25, 401–405. [Google Scholar]
- Fruciano, C.; Franchini, P.; Meyer, A. Resampling-based approaches to study variation in morphological modularity. PLoS ONE 2013, 8, e69376. [Google Scholar]
- Mitteroecker, P.; Bookstein, F.L. The conceptual and statistical relationship between modularity and morphological integration. Syst. Biol. 2007, 56, 818–836. [Google Scholar]
- Labonne, G.; Navarro, N.; Laffont, R.; Chateau-Smith, C.; Montuire, S. Developmental integration in a functional unit: Deciphering processes from adult dental morphology. Evol. Dev. 2014, 16, 224–232. [Google Scholar]
- Tabachnick, R.E.; Bookstein, F.L. The structure of individual variation in Miocene Globorotalia. Evolution 1990, 44, 416–434. [Google Scholar]
- Bookstein, F.L.; Gunz, P.; Mitteroecker, P.; Prossinger, H.; Schaefer, K.; Seidler, H. Cranial integration in Homo: Singular warps analysis of the midsagittal plane in ontogeny and evolution. J. Hum. Evol. 2003, 44, 167–187. [Google Scholar]
- Raff, R.A. The Shape of Life: Genes, Development and the Evolution of Animal Form; University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Wagner, G.P.; Altenberg, L. Complex adaptations and the evolution of evolvability. Evolution 1996, 50, 967–976. [Google Scholar]
- Gerhart, J.; Kirschner, M. Cells, Embryos, And evolution: Toward a Cellular and Developmental Understanding of Phenotypic Variation and Evolutionary Adaptability; Blackwell Science: Malden, MA, USA, 1997. [Google Scholar]
- Kirschner, M.; Gerhart, J. Evolvability. Proc. Natl. Acad. Sci. USA 1998, 95, 8420–8427. [Google Scholar]
- Goswami, A.; Polly, P.D. The influence of modularity on cranial morphological disparity in Carnivora and Primates (Mammalia). PLoS ONE 2010, 5, e9517. [Google Scholar]
- Goswami, A.; Smaers, J.B.; Soligo, C.; Polly, P.D. The macroevolutionary consequences of phenotypic integration: From development to deep time. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014, 369, 20130254. [Google Scholar] [CrossRef]
- Sanger, T.J.; Mahler, D.L.; Abzhanov, A.; Losos, J.B. Roles for modularity and constraint in the evolution of cranial diversity among Anolis lizards. Evolution 2012, 66, 1525–1542. [Google Scholar]
- Cheverud, J.M. Quantitative genetics and developmental constraints on evolution by selection. J. Theor. Biol. 1984, 110, 155–171. [Google Scholar]
- Cheverud, J.M. Developmental integration and the evolution of pleiotropy. Am. Zool. 1996, 36, 44–50. [Google Scholar]
- Wagner, G.P. Homologues, natural kinds and the evolution of modularity. Am. Zool. 1996, 36, 36–43. [Google Scholar]
- Breuker, C.J.; Debat, V.; Klingenberg, C.P. Functional evo-devo. Trends Ecol. Evol. 2006, 21, 488–492. [Google Scholar]
- Klingenberg, C.P. Studying morphological integration and modularity at multiple levels: Concepts and analysis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014, 369, 20130249. [Google Scholar] [CrossRef]
- Lande, R. Quantitative genetic analysis of multivariate evolution, applied to brain:body size allometry. Evolution 1979, 33, 402–416. [Google Scholar]
- Roff, D.A. Evolutionary Quantitative Genetics; Chapman & Hall: New York, NY, USA, 1997. [Google Scholar]
- Kruuk, L.E.B.; Slate, J.; Wilson, A.J. New answers for old questions: The evolutionary quantitative genetics of wild animal populations. Annu. Rev. Ecol. Evol. Syst. 2008, 39, 525–548. [Google Scholar]

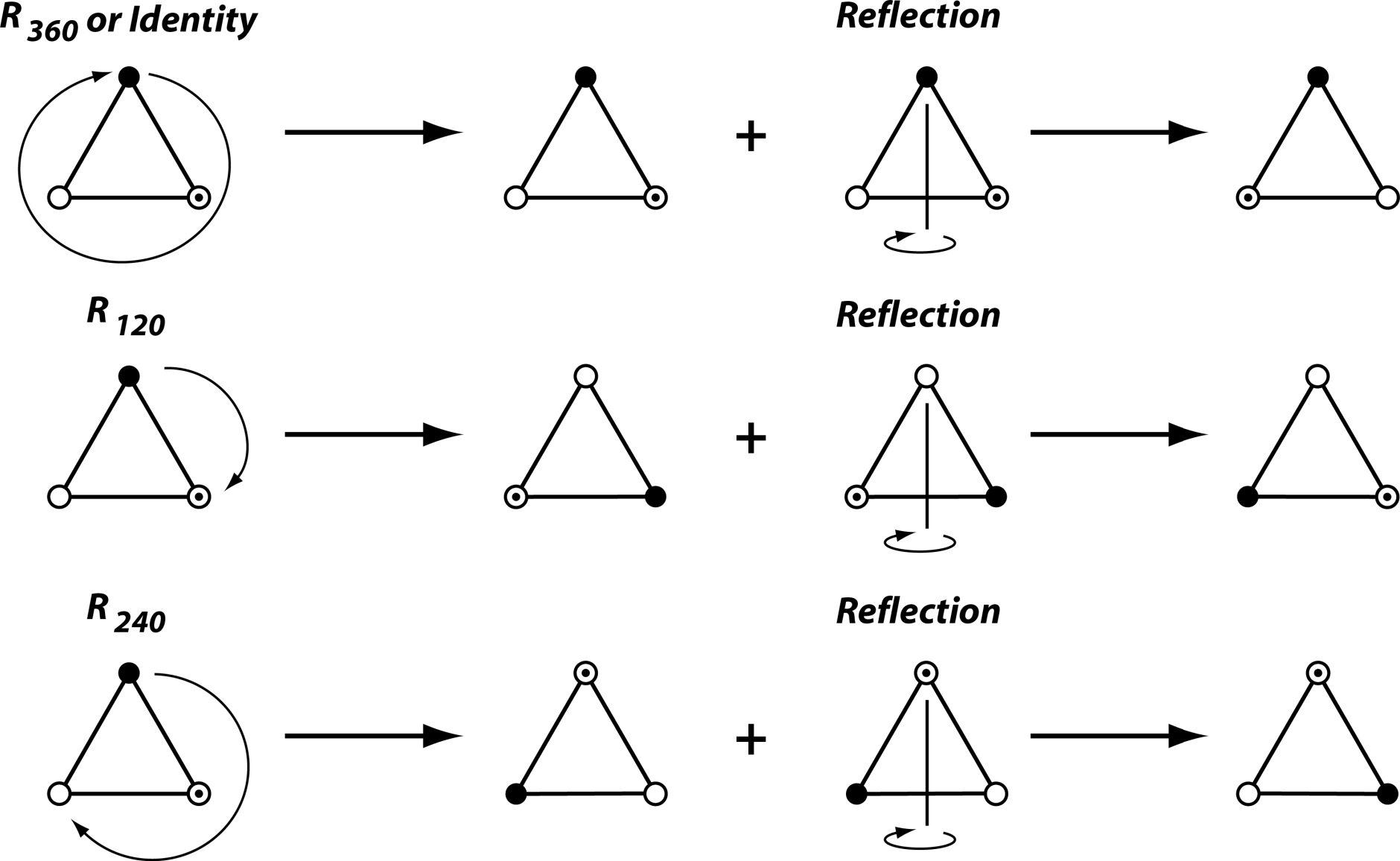

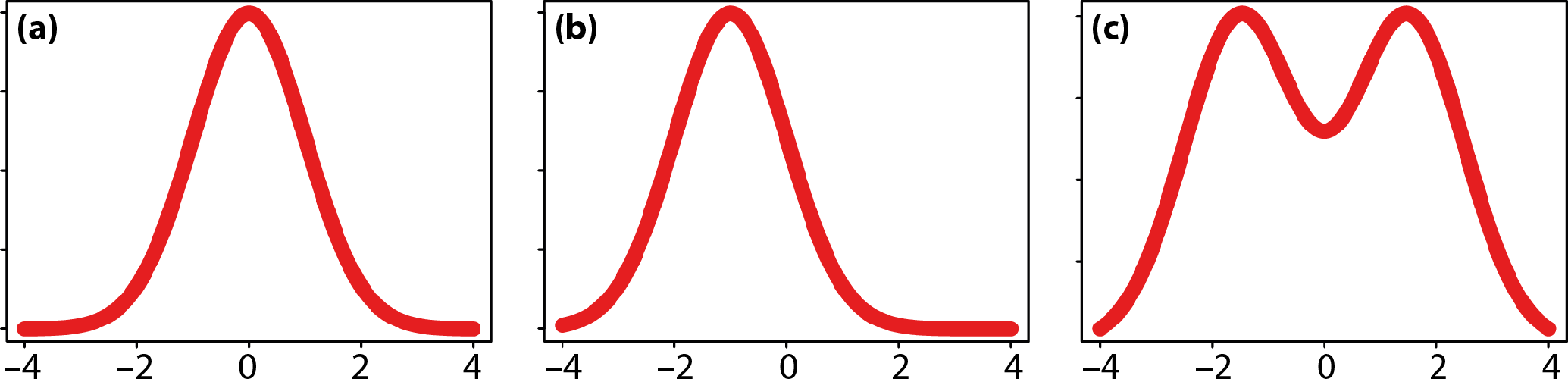

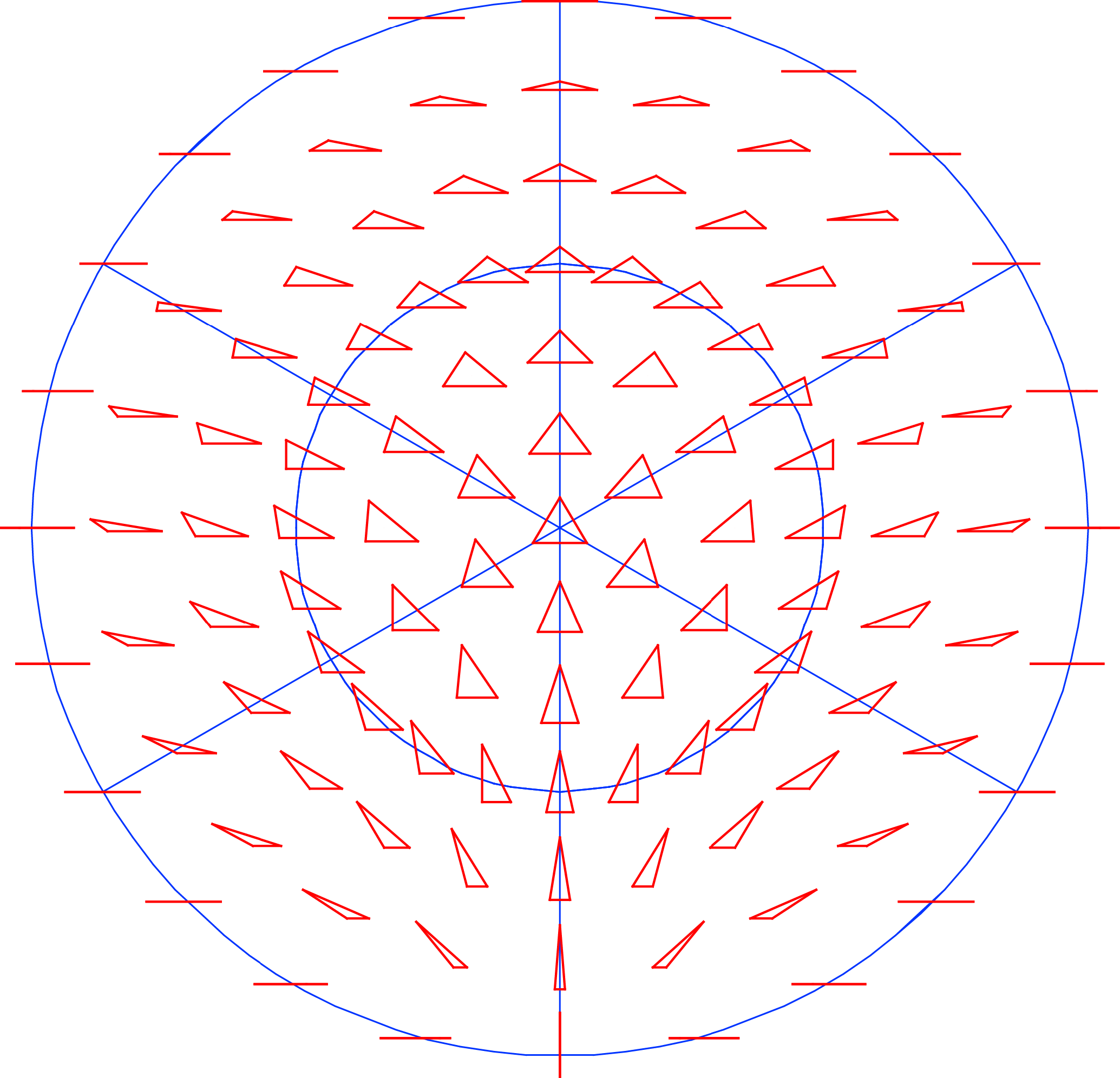

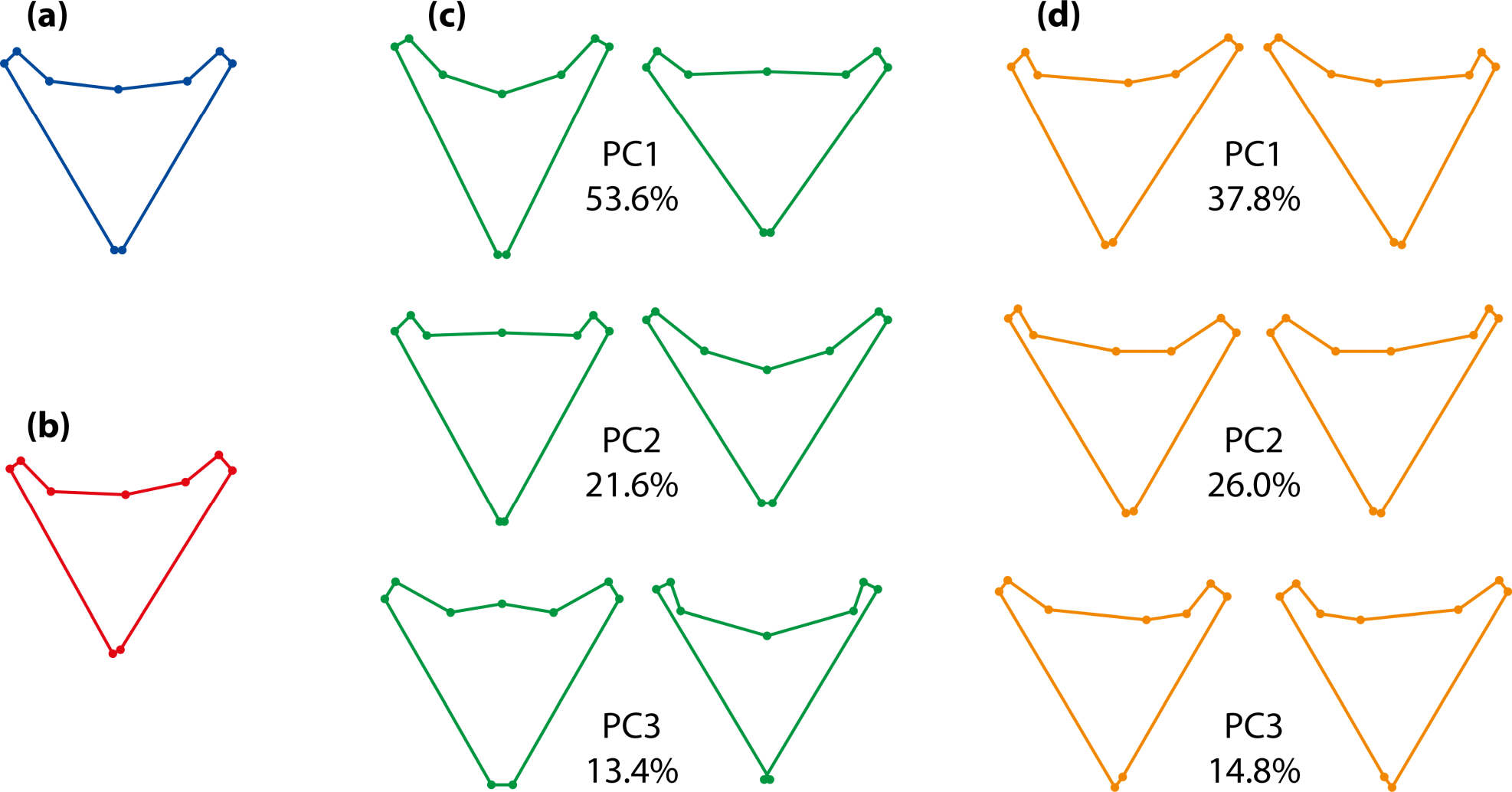





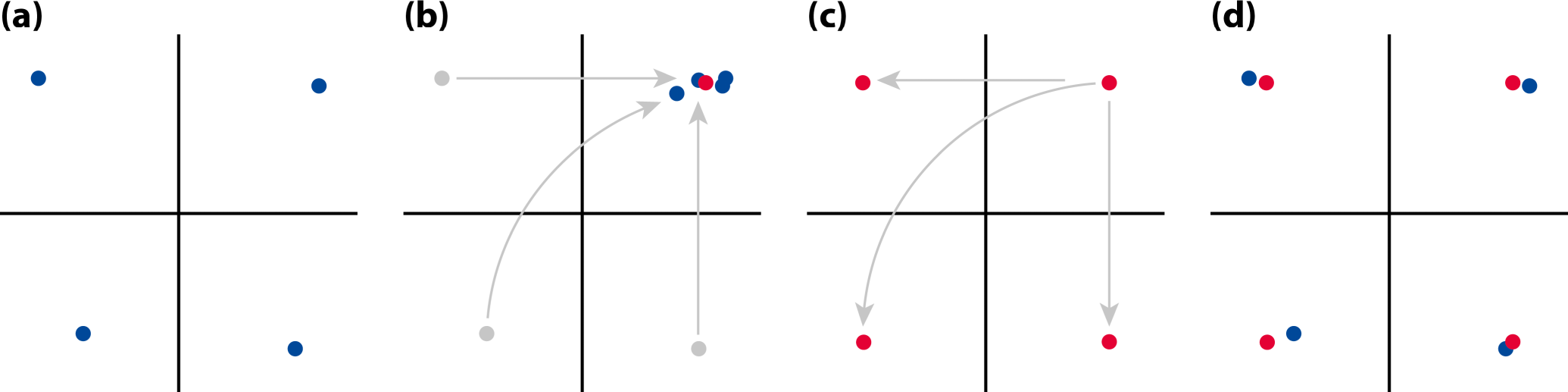
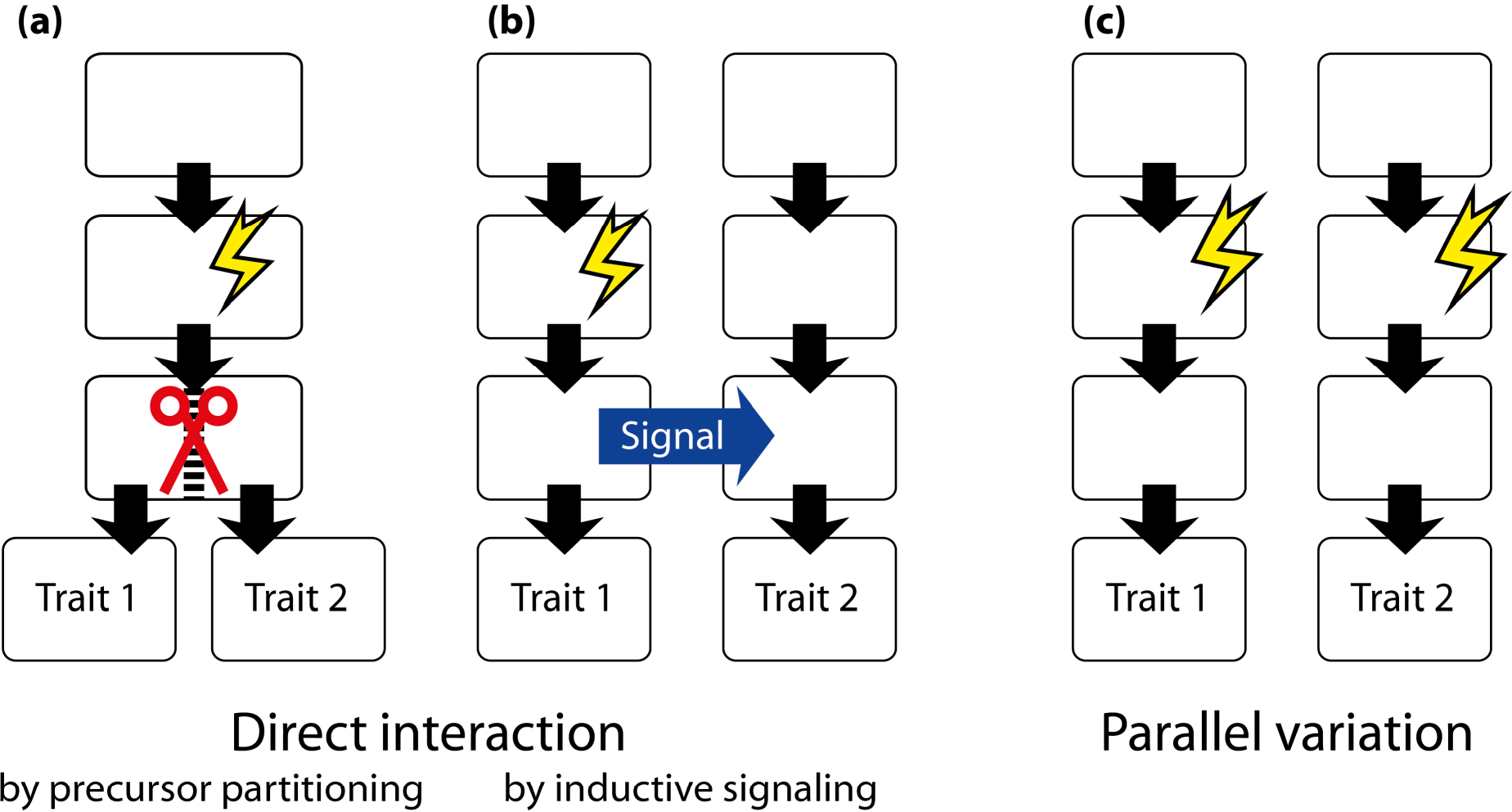

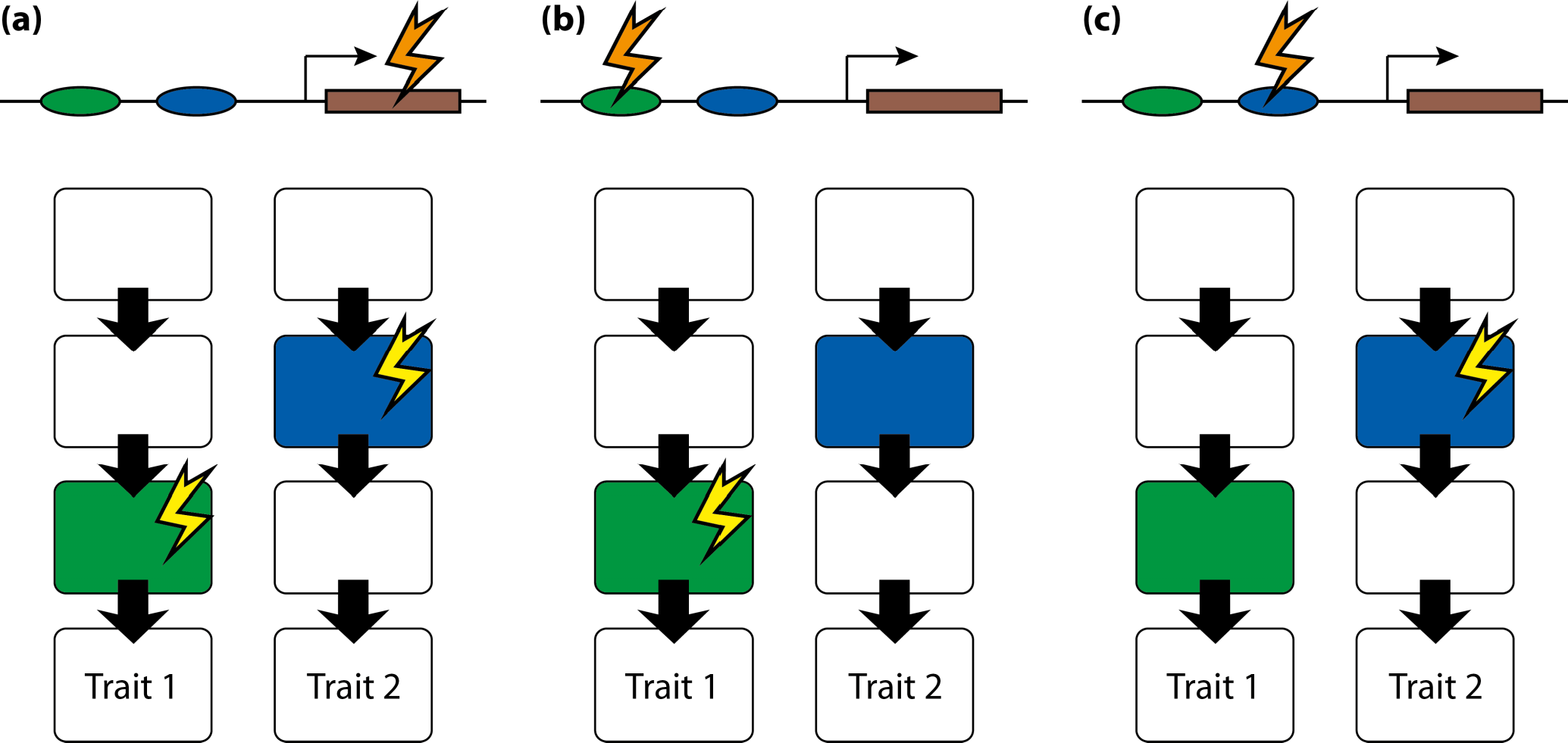
| Effect | Sum of Squares | Mean Squares | df | F | P | Pillai’s trace | P |
|---|---|---|---|---|---|---|---|
| Individual | 0.013438 | 2.25 × 10−5 | 598 | 2.06 | <0.0001 | – | – |
| Side | 0.000487 | 1.87 × 10−5 | 26 | 1.72 | 0.0154 | – | – |
| Ind. × Side | 0.006519 | 1.09 × 10−5 | 598 | 25.16 | <0.0001 | 16.65 | <0.0001 |
| Imaging | 0.000541 | 4.33 × 10−7 | 1248 | 1.16 | 0.0010 | 9.22 | 0.0259 |
| Digitizing | 0.000027 | 3.73 × 10−7 | 2496 | – | – | – | – |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klingenberg, C.P. Analyzing Fluctuating Asymmetry with Geometric Morphometrics: Concepts, Methods, and Applications. Symmetry 2015, 7, 843-934. https://doi.org/10.3390/sym7020843
Klingenberg CP. Analyzing Fluctuating Asymmetry with Geometric Morphometrics: Concepts, Methods, and Applications. Symmetry. 2015; 7(2):843-934. https://doi.org/10.3390/sym7020843
Chicago/Turabian StyleKlingenberg, Christian Peter. 2015. "Analyzing Fluctuating Asymmetry with Geometric Morphometrics: Concepts, Methods, and Applications" Symmetry 7, no. 2: 843-934. https://doi.org/10.3390/sym7020843





