Hierarchical Clustering Using One-Class Support Vector Machines
Abstract
:1. Introduction
2. One-Class Support Vector Machines
3. Hierarchical Clustering Based on OC-SVM
3.1. Nested OC-SVM Decision Sets
3.2. Hierarchical Clustering Using OC-SVM Decision Sets
| Algorithm 1 Hierarchical clustering based on one-class support vector machine (OC-SVM). |
| Input: |
|
- if is connected to none of the clusters, then the singleton cluster is added to the cluster collection ;
- if is connected to exactly one cluster, then the singleton cluster is merged into the cluster;
- if is connected to more than one cluster, then all of these clusters and the singleton cluster are merged.

4. Experiments
4.1. Gaussian Mixture Data



4.2. Benchmark Data
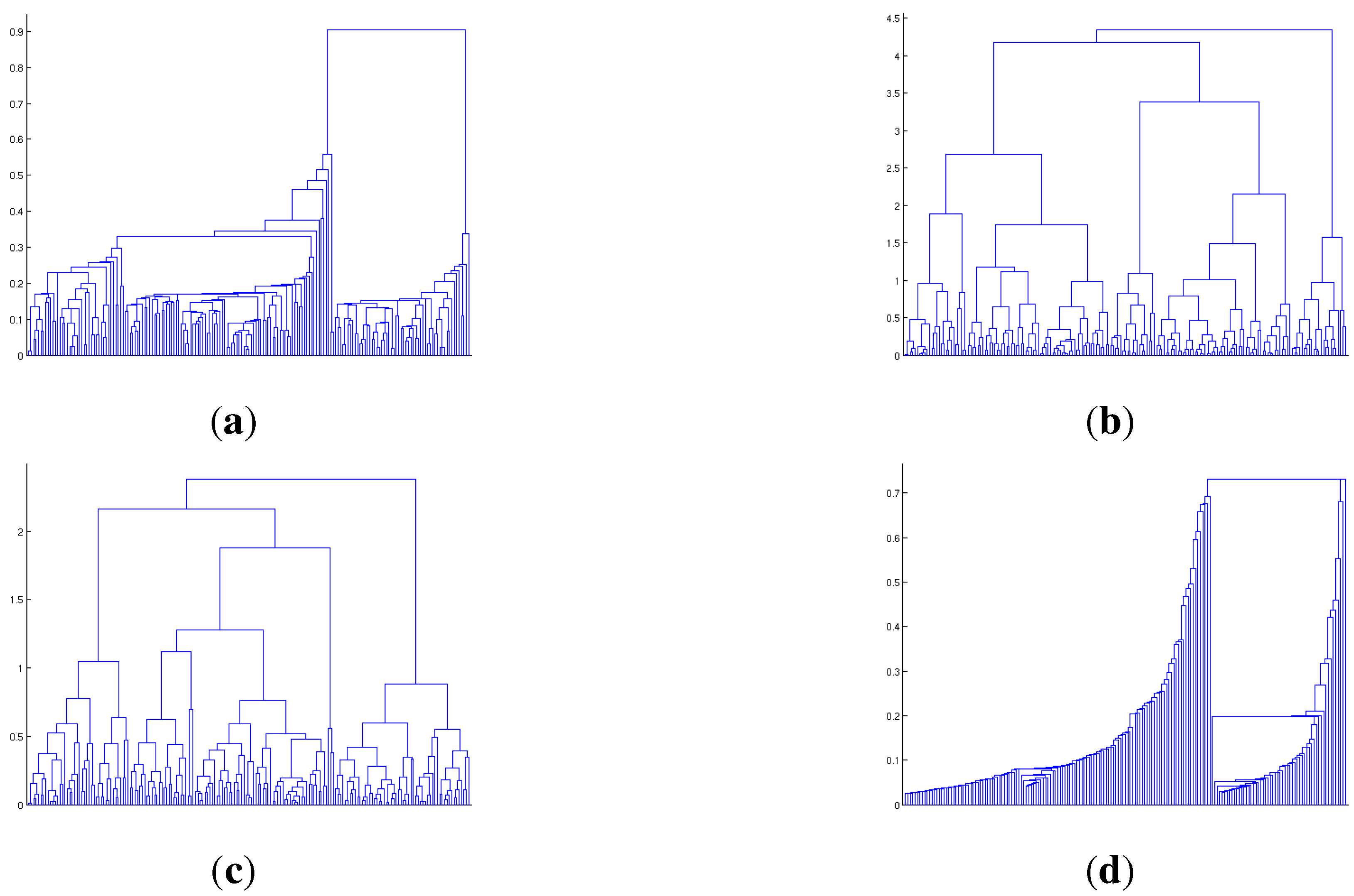

4.3. Computational Costs
| Computational Costs | multi | banana |
|---|---|---|
| # of breakpoints | 504 | 404 |
| OC-SVM path algorithm (sec) | 0.19 | 0.15 |
| Hierarchical clustering (OC-SVM) (sec) | 1.04 | 1.17 |
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix
A. OC-SVM Solution Path Algorithm
A.1. Initialization
A.2. Tracing the Path
- A point enters from or .
- A point leaves to enters or .
A.3. Finding the Next Breakpoint
- Some for which enters the hyperplane so that . From Equation (5), this event occurs at
- Some for which reaches 0 or 1. From equation (4), this case, respectively, corresponds to
References
- Duda, R.; Hart, P.; Stork, D. Pattern Classification, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Data Mining, Inference and Prediction; Springer Verlag: New York, NY, USA, 2001. [Google Scholar]
- Schölkopf, B.; Smola, A. Learning with Kernels; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Qi, Z.; Tian, Y.; Shi, Y. Successive overrelaxation for laplacian support vector machine. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 667–684. [Google Scholar] [CrossRef] [PubMed]
- Qi, Z.; Tian, Y.; Shi, Y. Laplacian twin support vector machine for semi-supervised classification. Neural Netw. 2012, 35, 46–53. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Qi, Z.; Ju, X.; Shi, Y.; Liu, X. Nonparallel support vector machines for pattern classification. IEEE Trans. Cybern. 2014, 44, 1067–1079. [Google Scholar] [CrossRef] [PubMed]
- Qi, Z.; Tian, Y.; Shi, Y. Twin support vector machine with Universum data. Neural Netw. 2012, 36, 112–119. [Google Scholar] [CrossRef] [PubMed]
- Qi, Z.; Tian, Y.; Shi, Y. Structural twin support vector machine for classification. Knowl. Based Syst. 2013, 43, 74–81. [Google Scholar] [CrossRef]
- Qi, Z.; Tian, Y.; Shi, Y. Robust twin support vector machine for pattern classification. Pattern Recognit. 2013, 46, 305–316. [Google Scholar] [CrossRef]
- Tax, D.; Duin, R. Support vector domain description. Pattern Recognit. Lett. 1999, 20, 1191–1199. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.; Shawe-Taylor, J.; Smola, A.; Williamson, R. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1472. [Google Scholar] [CrossRef] [PubMed]
- Vert, R.; Vert, J. Consistency and convergence rates of one-class SVMs and related algorithms. J. Mach. Learn. Res. 2006, 7, 817–854. [Google Scholar]
- Ben-Hur, A.; Horn, D.; Siegelmann, H.; Vapnik, V. Support vector clustering. J. Mach. Learn. Res. 2001, 2, 125–137. [Google Scholar] [CrossRef]
- Hartigan, J. Clustering Algorithms; Wiley: New York, NY, USA, 1975. [Google Scholar]
- De Morsier, F.; Tuia, D.; Borgeaud, M.; Gass, V.; Thiran, J.P. Cluster validity measure and merging system for hierarchical clustering considering outliers. Pattern Recognit. 2015, 48, 1478–1489. [Google Scholar] [CrossRef]
- Yoon, S.H.; Min, J. An intelligent automatic early detection system of forest fire smoke signatures using gaussian mixture model. J. Inf. Process. Syst. 2013, 9, 621–632. [Google Scholar] [CrossRef]
- Manh, H.T.; Lee, G. Small object segmentation based on visual saliency in natural images. J. Inf. Process. Syst. 2013, 9, 592–601. [Google Scholar] [CrossRef]
- Yang, X.; Peng, G.; Cai, Z.; Zeng, K. Occluded and low resolution face detection with hierarchical deformable model. J. Converg. 2013, 4, 11–14. [Google Scholar]
- Lee, G.; Scott, C. The one class support vector machine solution path. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA, 15–20 April 2007; Volume 2, pp. 521–524.
- Machine learning data set repository. Available online: http://mldata.org/repository/tags/data/IDA_Benchmark_Repository/ (accessed on 24 June 2015).
- OC-SVM HC. Available online: http://sites.google.com/site/gyeminlee/codes/ (accessed on 24 June 2015).
- Glower, J.; Ross, G. Minimum spanning trees and single linkage cluster analysis. Appl. Stat. 1969, 18, 54–64. [Google Scholar] [CrossRef]
- Hastie, T.; Rosset, S.; Tibshirani, R.; Zhu, J. The entire regularization path for the support vector machine. J. Mach. Learn. Res. 2004, 5, 1391–1415. [Google Scholar]
- Lee, G.; Scott, C. Nested support vector machines. IEEE Trans. Signal Process. 2010, 58, 1648–1660. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G. Hierarchical Clustering Using One-Class Support Vector Machines. Symmetry 2015, 7, 1164-1175. https://doi.org/10.3390/sym7031164
Lee G. Hierarchical Clustering Using One-Class Support Vector Machines. Symmetry. 2015; 7(3):1164-1175. https://doi.org/10.3390/sym7031164
Chicago/Turabian StyleLee, Gyemin. 2015. "Hierarchical Clustering Using One-Class Support Vector Machines" Symmetry 7, no. 3: 1164-1175. https://doi.org/10.3390/sym7031164
APA StyleLee, G. (2015). Hierarchical Clustering Using One-Class Support Vector Machines. Symmetry, 7(3), 1164-1175. https://doi.org/10.3390/sym7031164





