The Reality of Casimir Friction
Abstract
:1. Introduction
2. Friction between Two Plates
3. Methodologies
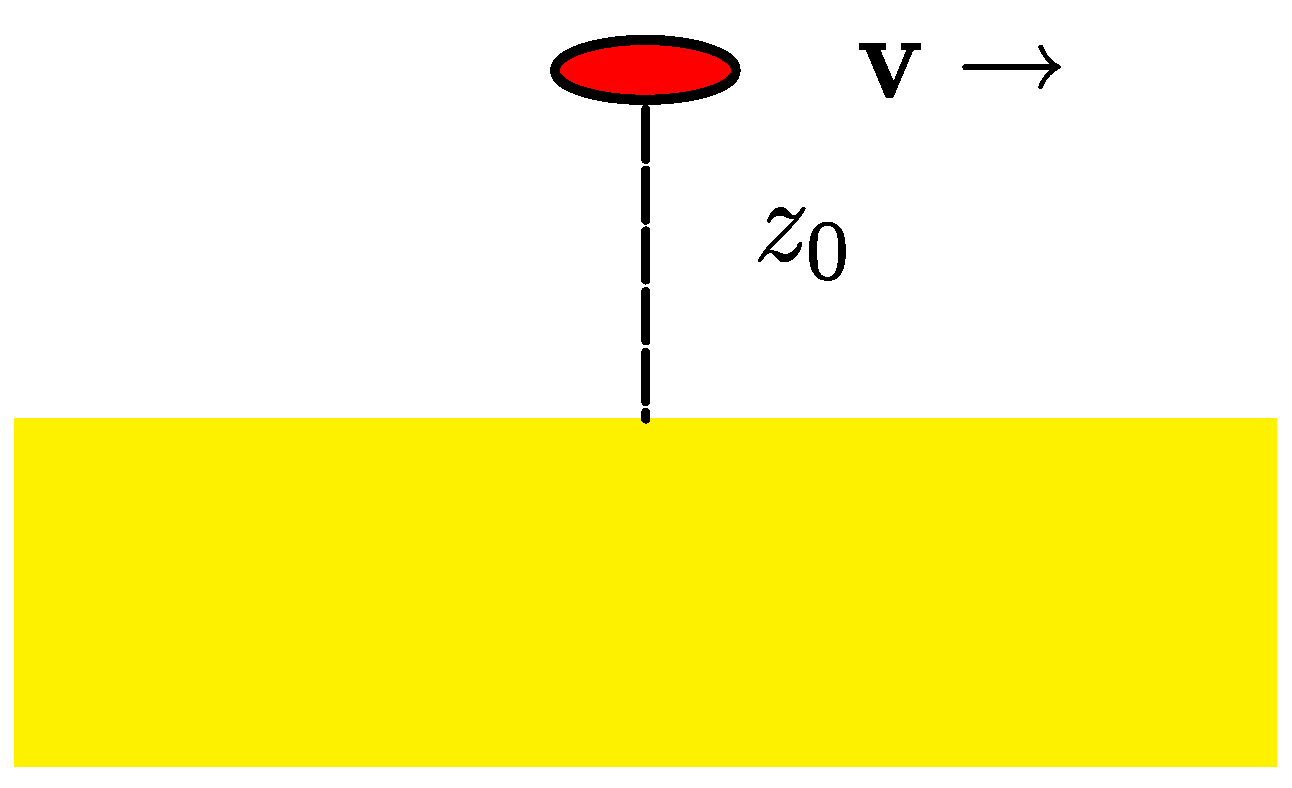
4. Interaction between an Atom and a Plate
5. Friction between Parallel Plates
6. Temperature Dependence
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SI | Système international d’unités |
| TM | Transverse magnetic |
| C | Casimir |
| CP | Casimir-Polder |
| vdW | van der Waals |
References
- Mohr, P.J.; Taylor, B.N.; Newell, D.B. CODATA Recommended Values of the Fundamental Physical Constants: 2006. Rev. Mod. Phys. 2008, 80, 633–730. [Google Scholar] [CrossRef]
- Hanneke, D.; Fogwell, S.; Gabrielse, G. New Measurement of the Electron Magnetic Moment and the Fine Structure Constant. Phys. Rev. Lett. 2008, 100, 120801. [Google Scholar] [CrossRef] [PubMed]
- Casimir, H.B.G.; Polder, D. The Influence of retardation on the London-van der Waals forces. Phys. Rev. 1948, 73, 360. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On the Attraction Between Two Perfectly Conducting Plates. Kon. Ned. Akad. Wetensch. Proc. 1948, 51, 793–795. [Google Scholar]
- Milton, K.A.; Abalo, E.K.; Parashar, P.; Pourtolami, N.; Brevik, I.; Ellingsen, S.Å. Repulsive Casimir and Casimir-Polder Forces. J. Phys. A 2012, 45, 374006. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 2011, 479, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Lähteenmäkia, P.; Paraoanua, G.S.; Hasselb, J.M.; Hakonena, P.J. Dynamical Casimir effect in a Josephson metamaterial. PNAS 2013, 110, 4234–4238. [Google Scholar] [CrossRef]
- Moore, G.T. Quantum theory of the electromagnetic field in a variable-length one-dimensional cavity. J. Math. Phys. 1970, 11, 2679. [Google Scholar] [CrossRef]
- Fullling, S.A. Nonuniqueness of Canonical Field Quantization in Riemannian Space-Time. Phys. Rev. D 1973, 7, 2850. [Google Scholar] [CrossRef]
- Davies, P.C.W. Scalar production in Schwarzschild and Rindler metrics. J. Phys. A 1975, 8, 609. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef]
- Fulling, S.A.; Matsas, G.E.A. Unruh Effect. Scholarpedia 2014, 9, 31789. [Google Scholar] [CrossRef]
- Chen, F.; Mohideen, U.; Klimchitskaya, G.L.; Mostepanenko, V.M. Experimental and theoretical investigation of the lateral Casimir force between corrugated surfaces. Phys. Rev. A 2002, 66, 032113. [Google Scholar] [CrossRef]
- Munday, J.M.; Iannuzzi, D.; Barash, Y.; Capasso, F. Torque on birefringent plates induced by quantum fluctuations. Phys. Rev. A 2005, 71, 042102. [Google Scholar] [CrossRef]
- Guérout, R.; Genet, C.; Lambrecht, A.; Reynaud, S. Casimir Torque between Nanostructured Plate. EPL 2015, 111, 44001. [Google Scholar] [CrossRef]
- Milton, K.A. The Casimir Effect: Physical Manifestations of Zero-Point Energy; World Scientific: Singapore, 2001. [Google Scholar]
- Bordag, M.; Klimchitskaya, G.I.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Dalvit, D.A.R.; Milonni, P.; Roberts, D.; da Rosa, F. (Eds.) Casimir Physics; Springer: Berlin, Germany, 2011.
- Simpson, W.M.R.; Leonhardt, U. Force of the Quantum Vacuum: An Introduction to Casimir Physics; World Scientific: Singapore, 2015. [Google Scholar]
- Mate, C.M.; McClelland, G.M.; Erlandsson, R.; Chiang, S. Atomic-Scale Friction of a Tungston Tip on a Graphite Surface. Phys. Rev. Lett. 1987, 59, 1942. [Google Scholar] [CrossRef] [PubMed]
- Berman, D.; Erdemir, A.; Zinovev, A.V.; Sumant, A.V. Nanoscale friction properties of graphene and graphene oxide. Diam. Rel. Mater. 2015, 54, 91–96. [Google Scholar] [CrossRef]
- Levchenko, A.; Kamenev, A. Coulomb Drag at Zero Temperature. Phys. Rev. Lett. 2008, 100, 026805. [Google Scholar] [CrossRef] [PubMed]
- Persson, B.N.J.; Zhang, Z. Theory of friction: Coulomb drag between two closely spaced solids. Phys. Rev. B 1998, 57, 7327. [Google Scholar] [CrossRef]
- Teodorovich, E.V. Contribution of macroscopic van der Waals interactions to frictional force. Proc. R. Soc. Lond. A 1978, 362, 71–77. [Google Scholar] [CrossRef]
- Levitov, L.S. Van der Waals friction. Europhys. Lett. 1989, 8, 499–504. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Friction force between moving harmonic oscillators. Physica A 1992, 181, 413–426. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Friction force with non-instantaneous interaction between moving harmonic oscillators. Physica A 1993, 196, 241–254. [Google Scholar] [CrossRef]
- Pendry, J.B. Shearing the vacuum—Quantum friction. J. Phys. Condens. Matter 1997, 9, 10301–10320. [Google Scholar] [CrossRef]
- Pendry, J.B. Can sheared surfaces emit light? J. Mod. Opt. 1998, 45, 2389–2408. [Google Scholar] [CrossRef]
- Pendry, J.B. Quantum friction—Fact or fiction? New J. Phys. 2010, 12, 033028. [Google Scholar] [CrossRef]
- Pendry, J.B. Reply to comment on “Quantum friction—Fact or friction?”. New J. Phys. 2010, 12, 068002. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 2; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Lambrecht, A.; Reynaud, S. Casimir force between metallic mirrors. Eur. Phys. J. D 2000, 8, 309–318. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Near-field radiative heat transfer and noncontact friction. Rev. Mod. Phys. 2007, 79, 1291–1329. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon Press: Oxford, UK, 1984. [Google Scholar]
- Rytov, S.M. Theory of Electrical Fluctuations and Thermal Radiation; Academy of Science USSR Publishing House: Moscow, Russia, 1953. [Google Scholar]
- Milonni, P.W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Ginzburg, V.L. Applications of Electrodynamics in Theoretical Physics and Astrophysics; Gordon and Breach Science Publisher: Philadelphia, PA, USA, 1989. [Google Scholar]
- Ginzburg, V.L. Radiation by uniformly moving sources (Vavilov-Cherenkov effect, transition radiation, and other phenomena). Phys. Uspekhi 1996, 39, 973–982. [Google Scholar] [CrossRef]
- Intravaia, F.; Mkrtchian, V.E.; Buhmann, S.; Schell, S.; Dalvit, D.A.R.; Henkel, C. Friction forces on atoms after acceleration. J. Phys. Condens. Matter 2015, 27, 214020. [Google Scholar] [CrossRef] [PubMed]
- Pieplow, G.; Henkel, C. Cherenkov friction on a neutral particle moving parallel to a dielectric. J. Phys. Condens. Matter 2015, 27, 214001. [Google Scholar] [CrossRef] [PubMed]
- Brevik, I.; Kolbenstvedt, H. Quantum point detector moving through a dielectric medium. II. Constant acceleration. Il Nuovo Cimento B 1989, 103, 45–62. [Google Scholar] [CrossRef]
- Brevik, I.; Lautrup, B. Quantum Electrodynamics in Material Media; Munksgaard: Copenhagen, Denmark, 1970; Volume 38, pp. 1–37. [Google Scholar]
- Barnett, S.M. Resolution of the Abraham-Minkowski Dilemma. Phys. Rev. Lett. 2010, 104, 070401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; Ng, J.; Xiao, M.; Chan, C.T. Electromagnetic stress at the boundary: Photon pressure or tension? Sci. Adv. 2016, 2, e1501485. [Google Scholar] [CrossRef] [PubMed]
- Høye, J.S.; Brevik, I. Casimir friction force and energy dissipation for moving harmonic oscillators. EPL 2010, 91, 60003. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Casimir friction force and energy dissipation for moving harmonic oscillators. II. Eur. Phys. J. D 2011, 61, 335–339. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Casimir friction in terms of moving harmonic oscillators: Equivalence between two different formulations. Eur. Phys. J. D 2011, 64, 1–3. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Casimir friction force between polarizable media. Eur. Phys. J. D 2012, 66, 149. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Casimir friction force for moving harmonic oscillators. Int. J. Mod. Phys. A 2012, 27, 1260011. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Casimir friction between dense polarizable media. Entropy 2013, 15, 3045–3064. [Google Scholar] [CrossRef] [Green Version]
- Høye, J.S.; Brevik, I. Casimir friction at zero and finite temperatures. Eur. Phys. J. D 2014, 68, 61. [Google Scholar] [CrossRef]
- Høye, J.S.; Brevik, I. Casimir friction: Relative motion more generally. J. Phys. Condens. Matter 2015, 27, 214008. [Google Scholar] [CrossRef] [PubMed]
- Kubo, R. Lectures in Theoretical Physics; Brittin, W.E., Dunham, L.G., Eds.; Interscience: New York, NY, USA, 1959; Volume 1. [Google Scholar]
- Høye, J.S.; Stell, G. Quantum statistical mechanical model for polarizable fluids. J. Chem. Phys. 1981, 75, 5133. [Google Scholar] [CrossRef]
- Thompson, M.J.; Schweizer, K.S.; Chandler, D. Quantum theory of polarization in liquids: Exact solution of the mean spherical and related approximations. J. Chem. Phys. 1982, 76, 1128–1135. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Theory of friction: The contribution from a fluctuating electromagnetic field. J. Phys. Condens. Matter 1999, 11, 345–359. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Noncontact friction between nanostructures. Phys. Rev. B 2003, 68, 155420. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Theory of the interaction forces and the radiative heat transfer between moving bodies. Phys. Rev. B 2008, 78, 155437. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Quantum friction. Phys. Rev. Lett. 2011, 106, 094502. [Google Scholar] [CrossRef] [PubMed]
- Volokitin, A.I.; Persson, B.N.J. Comment on “Fully covariant radiation force on a polarizable particle”. New J. Phys. 2014, 16, 118001. [Google Scholar] [CrossRef]
- Dedkov, G.V.; Kyasov, A.A. Vacuum attraction, friction and heating of nanoparticles moving nearby a heated surface. J. Phys. Condens. Matter 2008, 20, 354006. [Google Scholar] [CrossRef]
- Dedkov, G.V.; Kyasov, A.A. Conservative-dissipative forces and heating mediated by fluctuating electromagnetic field: Two plates in relative nonrelativistic motion. Surf. Sci. 2010, 604, 562–567. [Google Scholar] [CrossRef]
- Dedkov, G.V.; Kyasov, A.A. Dynamical van der Waals atom-surface interaction. Surf. Sci. 2011, 605, 1077–1081. [Google Scholar] [CrossRef]
- Dedkov, G.V.; Kyasov, A.A. Dynamical Casimir-Polder atom-surface interaction. Surf. Sci. 2012, 606, 46–52. [Google Scholar] [CrossRef]
- Dedkov, G.V.; Kyasov, A.A. A uniformly moving and rotating polarizable particle in thermal radiation field: Frictional force and torque, radiation and heating. 2015; arXiv:1504.01588. [Google Scholar]
- Polevoi, V.G. Tangential molecular forces between moving bodies by a fluctuating electromagnetic field. Sov. Phys. JETP 1990, 71, 1119. [Google Scholar]
- Mkrtchian, V.E. Interaction between moving macroscopic bodies: Viscosity of the electromagnetic vacuum. Phys. Lett. A 1995, 207, 299–302. [Google Scholar] [CrossRef]
- Rytov, S.M.; Kravtsov, Y.A. Elements of Random Fields. In Principles of Statistical Radiophysics; Springer: Berlin, Germany, 1989; Volume 3. [Google Scholar]
- Barton, G. On van der Waals friction: I. Between two atoms. New J. Phys. 2010, 12, 113044. [Google Scholar] [CrossRef]
- Barton, G. On van der Waals friction. II: Between atom and half-space. New J. Phys. 2010, 12, 113045. [Google Scholar] [CrossRef]
- Barton, G. On van der Waals friction between two atoms at nonzero temperature. New J. Phys. 2011, 13, 043023. [Google Scholar] [CrossRef]
- Barton, G. On van der Waals friction between half-spaces at low temperature. J. Phys. Condens. Matter 2011, 23, 335004. [Google Scholar] [CrossRef] [PubMed]
- Barton, G. Van der Waals friction: A Hamiltonian test bed. Int. J. Mod. Phys. A 2012, 27, 1260002. [Google Scholar] [CrossRef]
- Philbin, T.G.; Leonhardt, U. No quantum friction between uniformly moving plates. New J. Phys. 2009, 11, 033035. [Google Scholar] [CrossRef]
- Pieplow, G.; Henkel, C. Fully covariant radiation force on a polarizable particle. New J. Phys. 2013, 15, 023027. [Google Scholar] [CrossRef]
- Maghrebi, M.F.; Golestanian, R.; Kardar, M. Quantum Cherenkov radiation and noncontact friction. Phys. Rev. A 2013, 88, 042509. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Theory of quantum friction. New J. Phys. 2014, 16, 063011. [Google Scholar] [CrossRef]
- Fröhlich, J.; Gang, Z. Emission of Cherenkov Radiation as a Mechanism for Hamiltonian Friction. Adv. Math. 2014, 264, 183–235. [Google Scholar] [CrossRef]
- Nesterenko, V.V.; Nesterenko, A.V. Macroscopic approach to the Casimir friction force. JETP Lett. 2014, 99, 581–584. [Google Scholar] [CrossRef]
- Intravaia, F.; Behunun, R.O.; Dalvit, D.A.R. Quantum friction and fluctuation theorems. Phys. Rev. A 2014, 89, 050101(R). [Google Scholar] [CrossRef]
- Einstein, A.; Hopf, L. Statistische Untersuchung der Bewegung eines Resonators in einem Strahlungsfeld. Ann. Phys. 1910, 338, 1105–1115. (In German) [Google Scholar] [CrossRef]
- Einstein, A. Zur Quantentheorie der Strahlung. Phys. Zeitsch. 1917, 18, 121–128. (In German) [Google Scholar]
- Mkrtchian, V.; Parsegian, V.A.; Podgornik, R.; Saslow, W.N. Universal Thermal Radiation Drag on Neutral Objects. Phys. Rev. Lett. 2003, 91, 220801. [Google Scholar] [CrossRef] [PubMed]
- Høye, J.S.; Brevik, I.; Milton, K.A. Casimir friction between polarizable particle and half-space with radiation damping at zero temperature. J. Phys. A 2015, 48, 365004. [Google Scholar] [CrossRef]
- Maghrebi, M.F.; Golestanian, R.; Kardar, M. Scattering approach to the dynamical Casimir effect. Phys. Rev. D 2013, 87, 025016. [Google Scholar] [CrossRef]
- Scheel, S.; Buhmann, S.Y. Casimir-Polder Forces on Moving Atoms. Phys. Rev. A 2009, 80, 042902. [Google Scholar] [CrossRef]
- Donaire, M.; Lambrecht, A. Velocity-dependent dipole forces on an excited atom. Phys. Rev. A 2016, 93, 022701. [Google Scholar] [CrossRef]
- Volokitin, A.I. Blackbody friction force on a relativistic small neutral particle. Phys. Rev. A 2015, 91, 032505. [Google Scholar] [CrossRef]
- Dedkov, G.V.; Kyasov, A.A. Attraction Force, Frictional Torque, and Heating of a Spherical Particle Rotating in the Evanescent Electromagnetic Field of a Heated Surface. Tech. Phys. Lett. 2013, 39, 609–611. [Google Scholar] [CrossRef]
- Zhao, R.; Manjavacas, A.; Javier García de Abajo, F.; Pendry, J.B. Rotational Quantum Friction. Phys. Rev. Lett. 2012, 109, 123604. [Google Scholar] [CrossRef] [PubMed]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milton, K.A.; Høye, J.S.; Brevik, I. The Reality of Casimir Friction. Symmetry 2016, 8, 29. https://doi.org/10.3390/sym8050029
Milton KA, Høye JS, Brevik I. The Reality of Casimir Friction. Symmetry. 2016; 8(5):29. https://doi.org/10.3390/sym8050029
Chicago/Turabian StyleMilton, Kimball A., Johan S. Høye, and Iver Brevik. 2016. "The Reality of Casimir Friction" Symmetry 8, no. 5: 29. https://doi.org/10.3390/sym8050029





