Cyclotomic Aperiodic Substitution Tilings
Abstract
:1. Introduction
- The tiling shall be aperiodic and repetitive (locally indistinguishable) to have an interesting (psychedelic) appearance.
- The tiling shall have a small inflation multiplier for reasons of economy. Large inflation multipliers either require large areas to be covered or many tiles of a small size to be used.
- The tiling shall yield “individual dihedral symmetry” or with . In other words, it shall contain an infinite number of patches of any size with dihedral symmetry only by iteration of substitution rules on a single tile.Similar to G. Maloney we demand symmetry of individual tilings and not only symmetry of tiling spaces [8].
- A “tile” in is defined as a nonempty compact subset of which is the closure of its interior.
- A “tiling” in is a countable set of tiles, which is a covering as well as a packing of . The union of all tiles is . The intersection of the interior of two different tiles is empty.
- A “patch” is a finite subset of a tiling.
- A tiling is called “aperiodic” if no translation maps the tiling to itself.
- “Prototiles” serve as building blocks for a tiling.
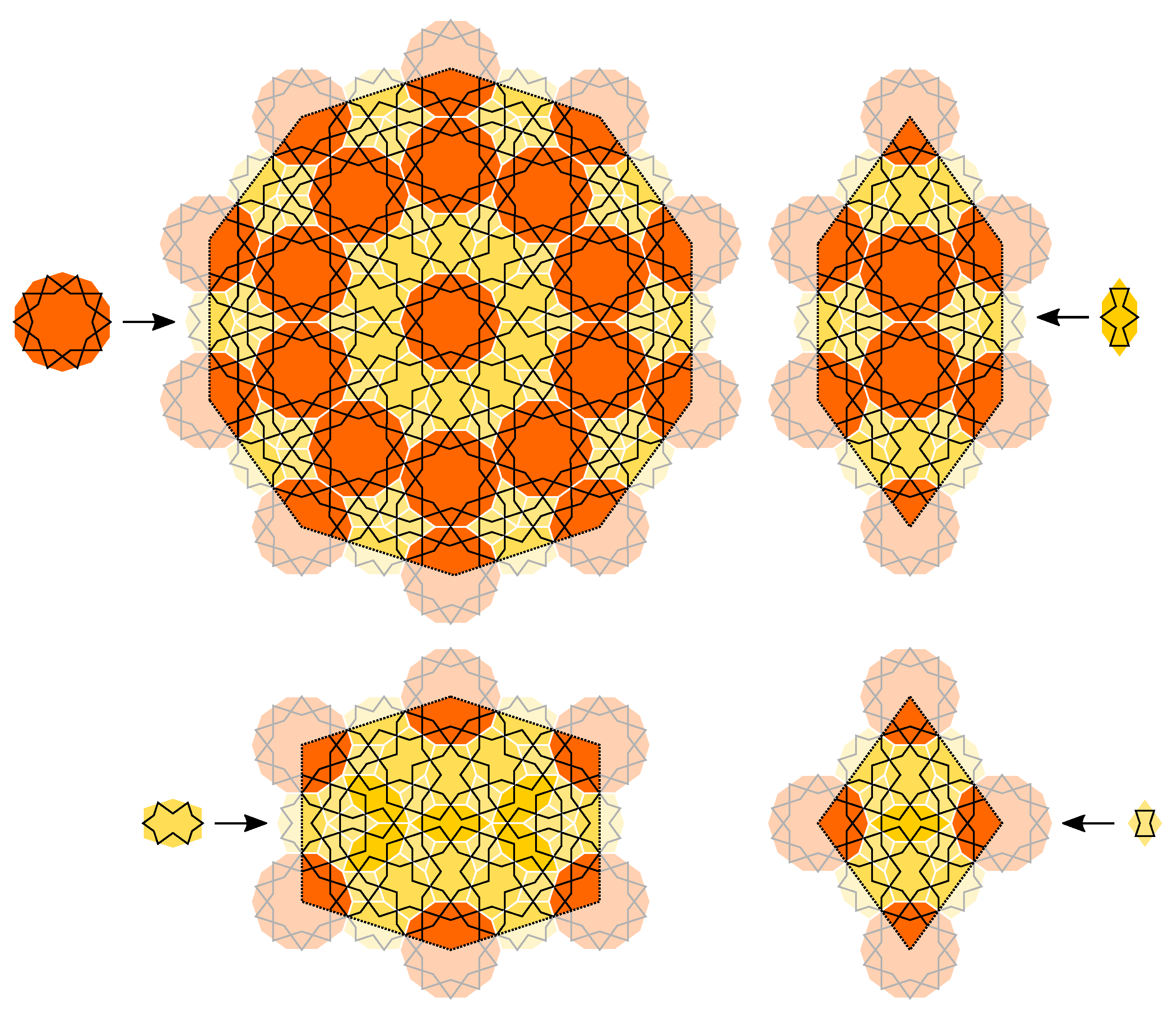
- Within this article the term “substitution” means, that a tile is expanded with a linear map—the “inflation multiplier”—and dissected into copies of prototiles in original size—the “substitution rule”.
- A “supertile” is the result of one or more substitutions, applied to a single tile. Within this article we use the term for one substitutions only.
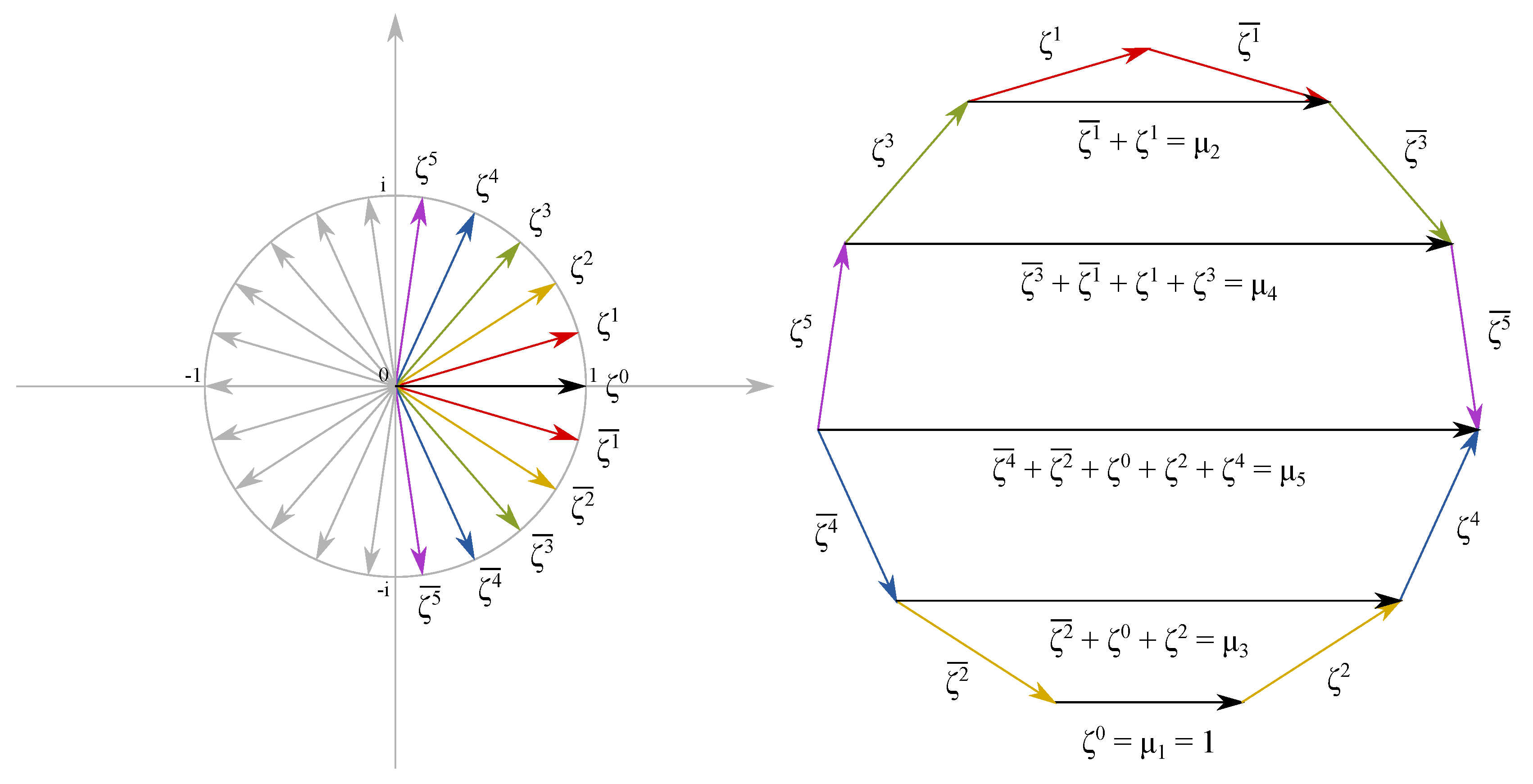
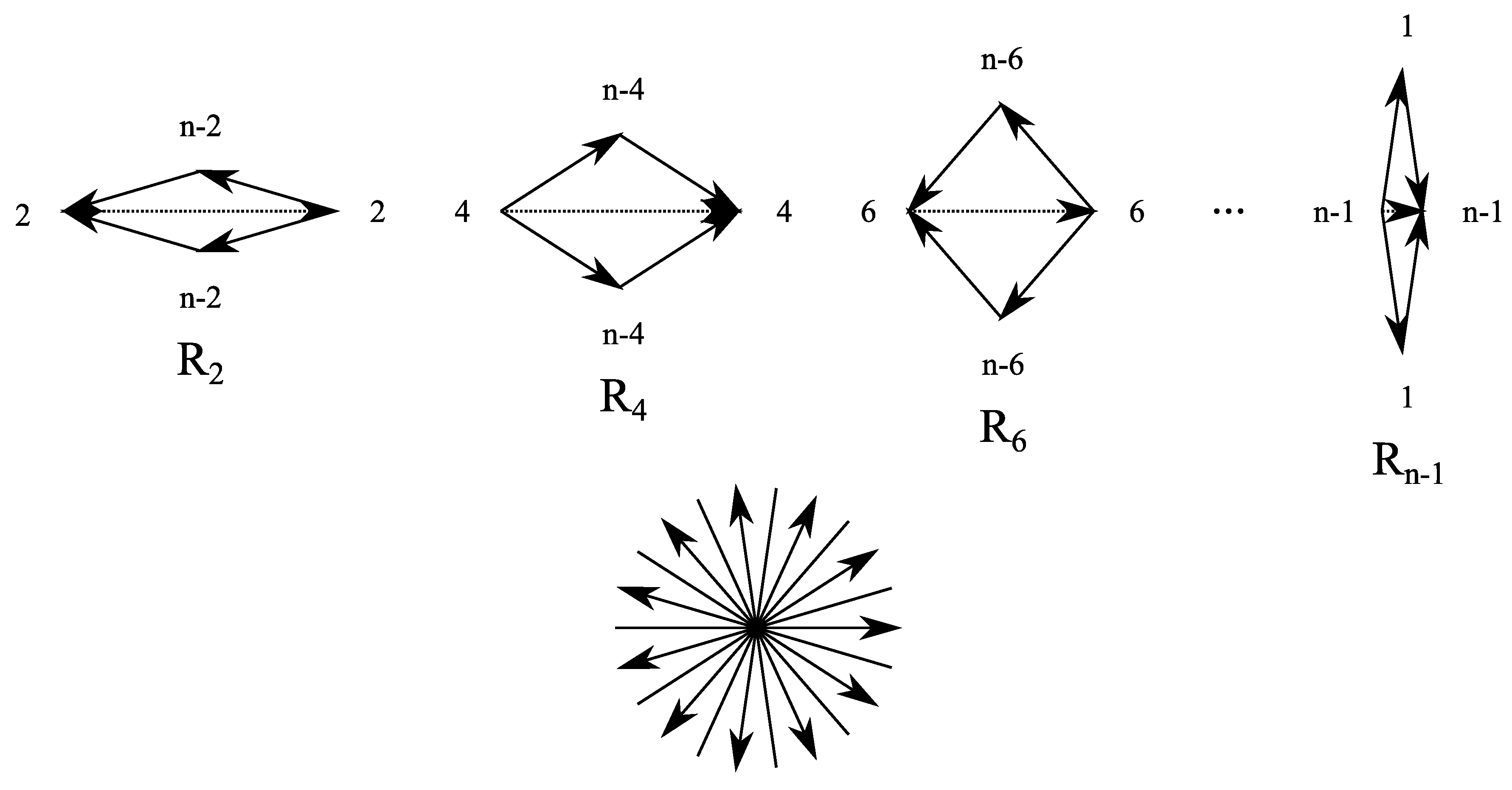
- We use to denote the n-th roots of unity so that and its complex conjugate .
- denotes the n-th cyclotomic field. Please note that for .
- The maximal real subfield of is .
- denotes the the ring of algebraic integers in .
- denotes the the ring of algebraic integers (which are real numbers) in .
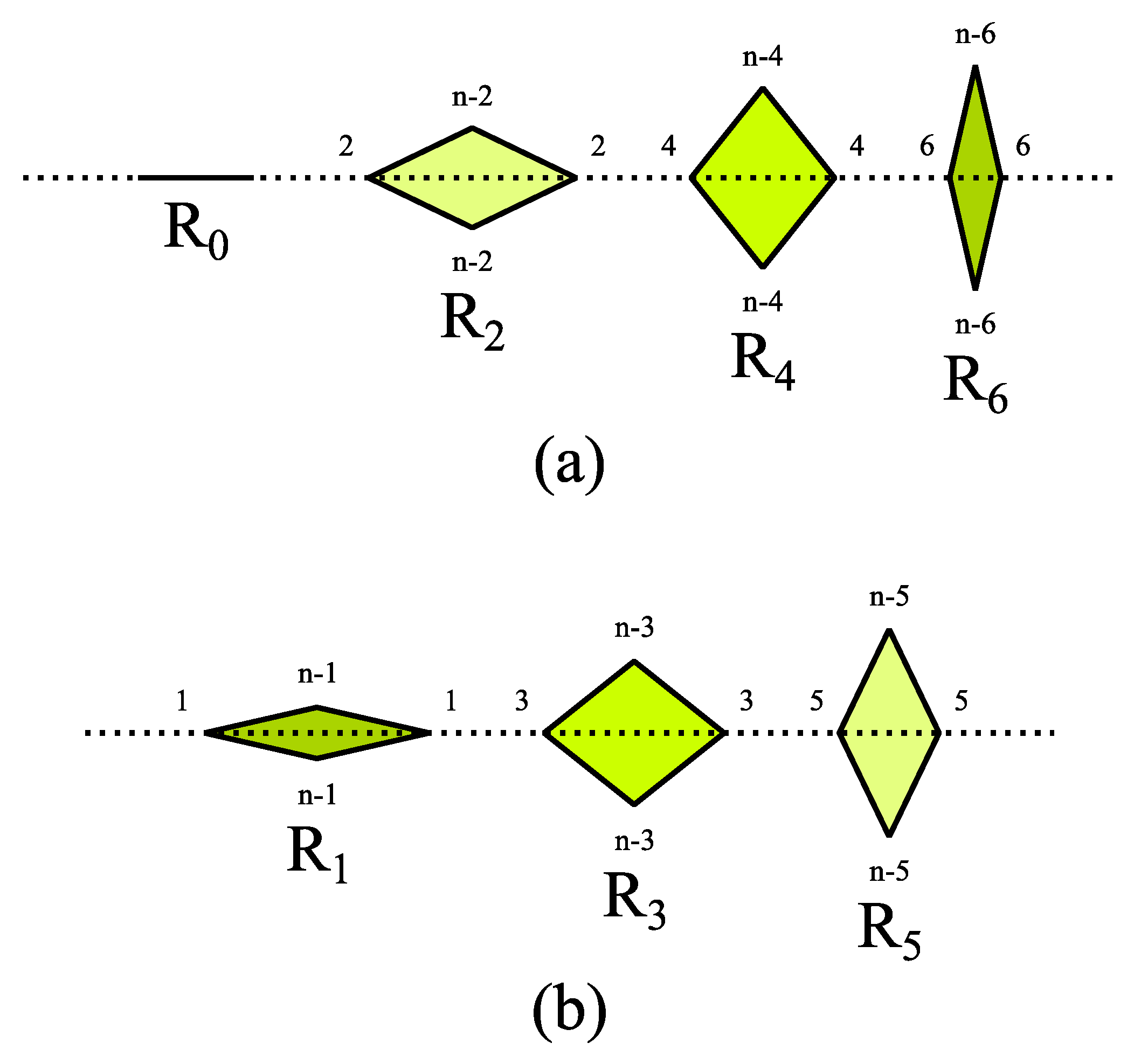
- We use to denote the k-th diagonal of a regular n-gon with side length .
- denotes the ring of the diagonals of a regular n-gon.
2. Properties of Cyclotomic Aperiodic Substitution Tilings
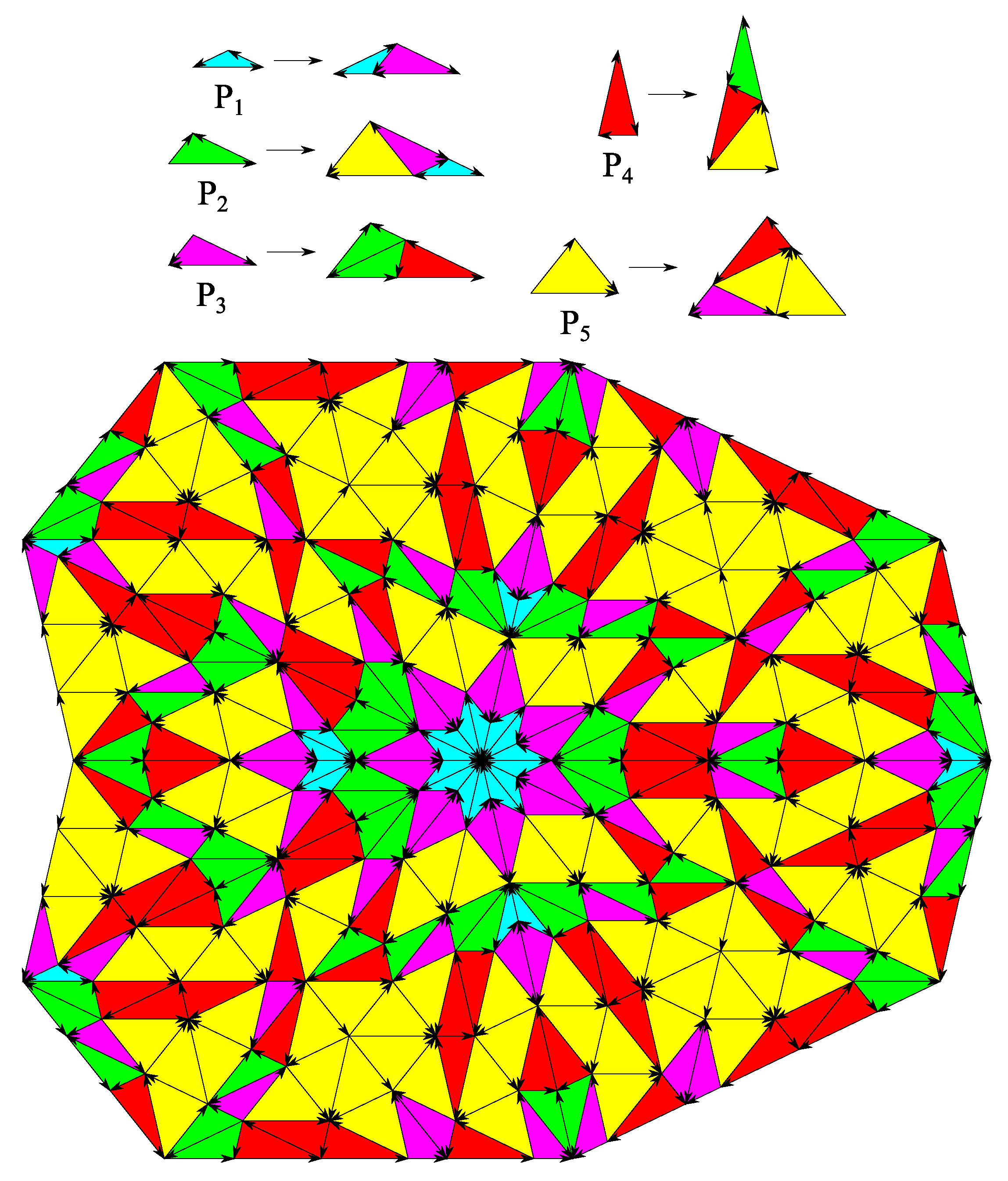
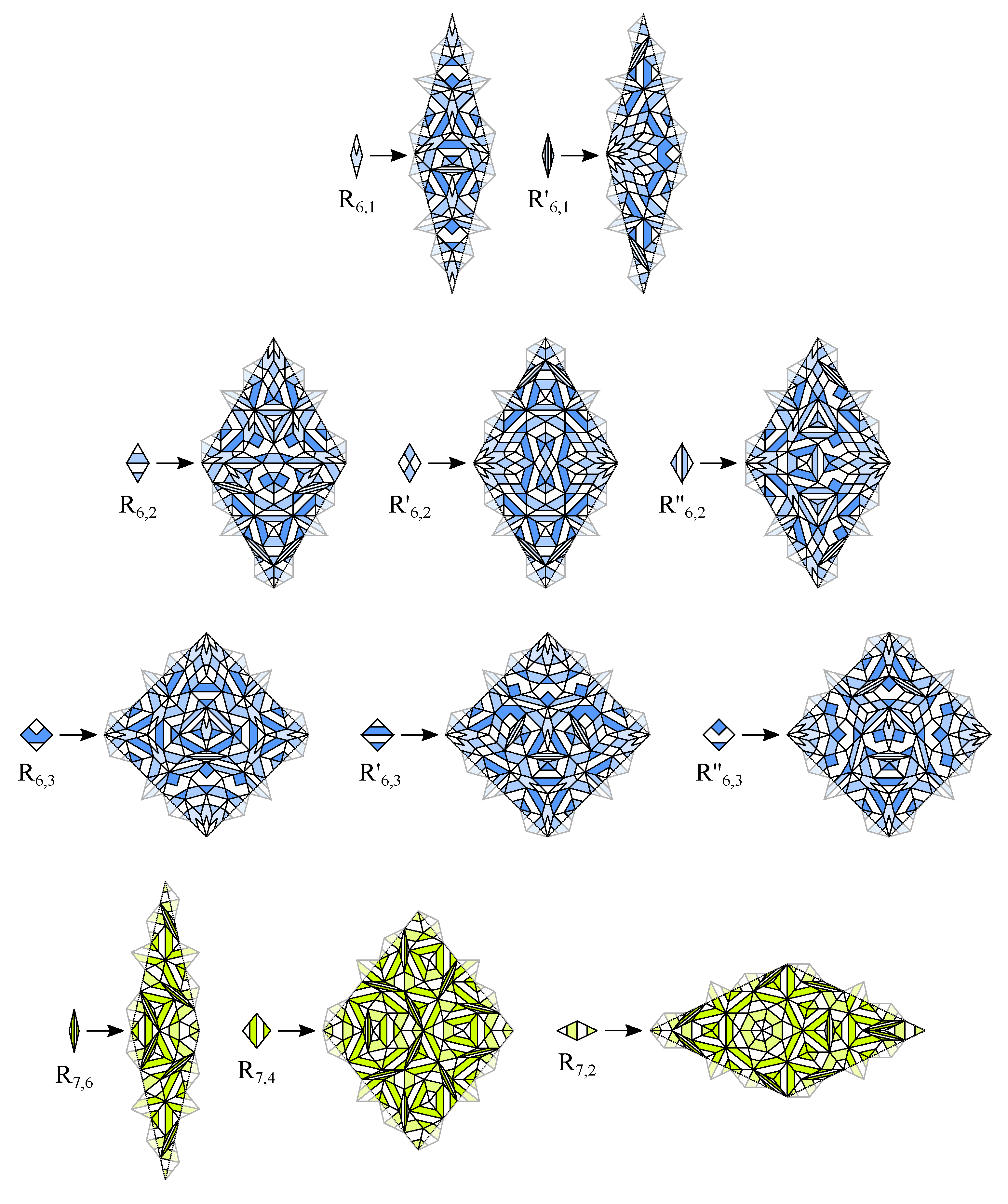
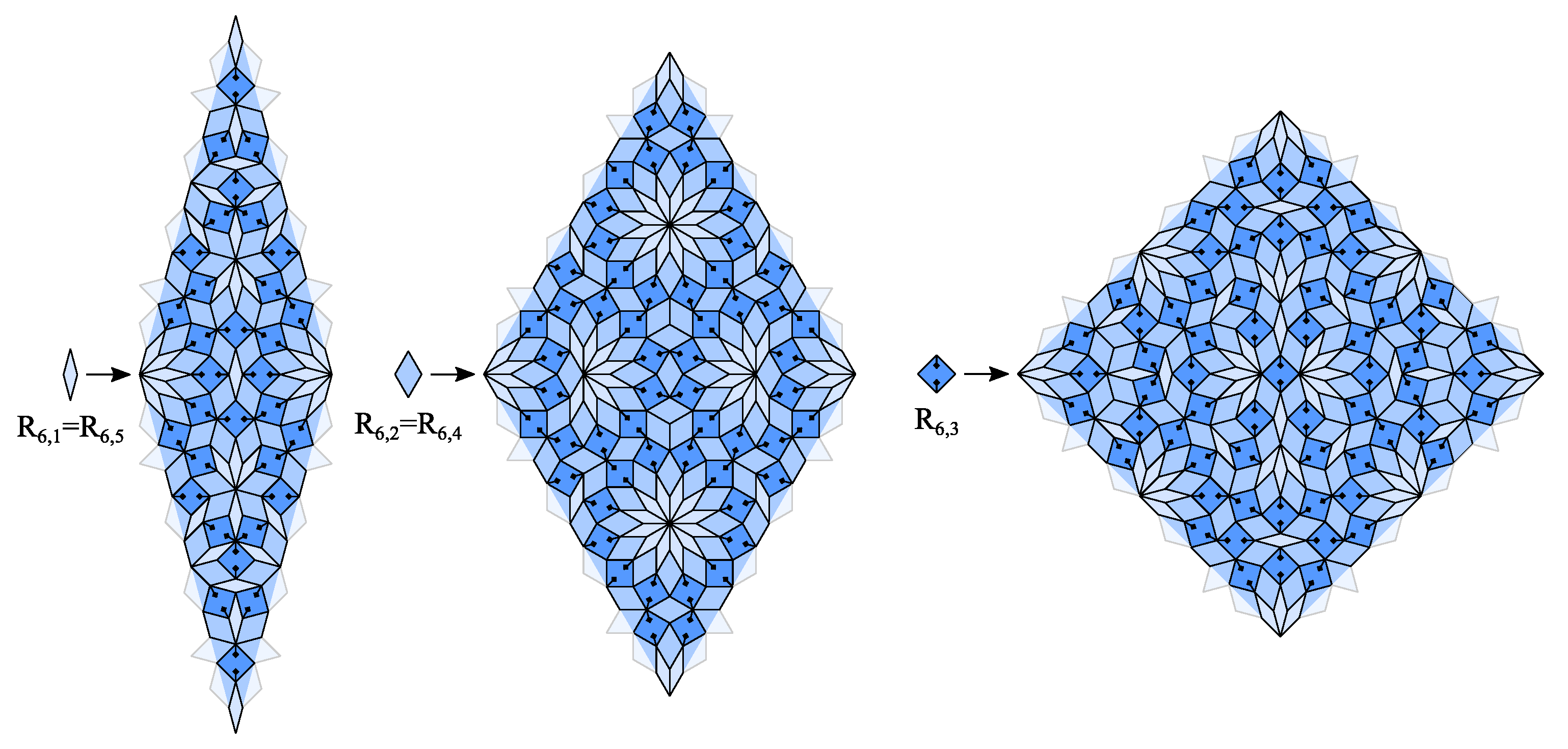
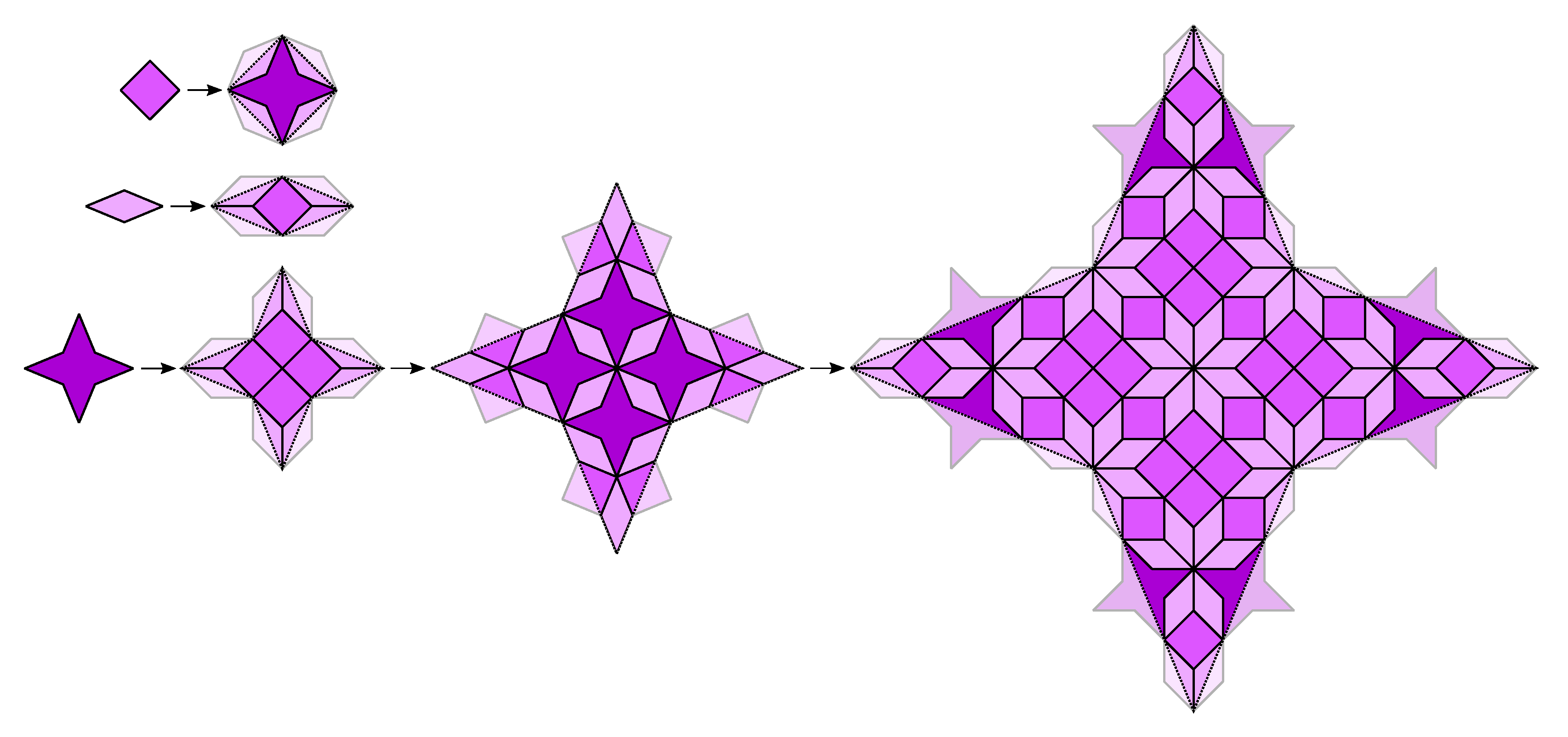
3. CASTs with Minimal Inflation Multiplier
3.1. The Odd n Case
3.2. The Even n Case
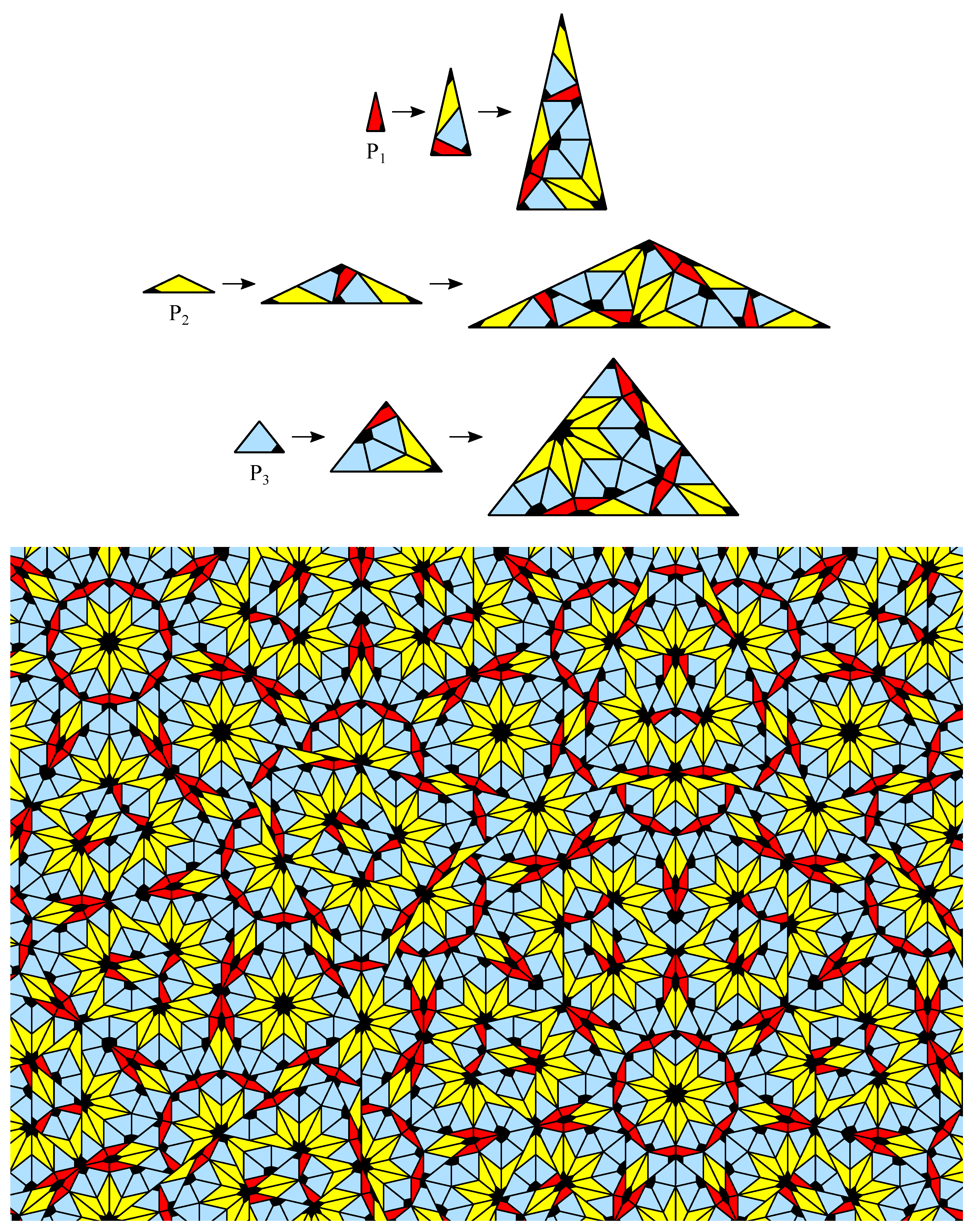
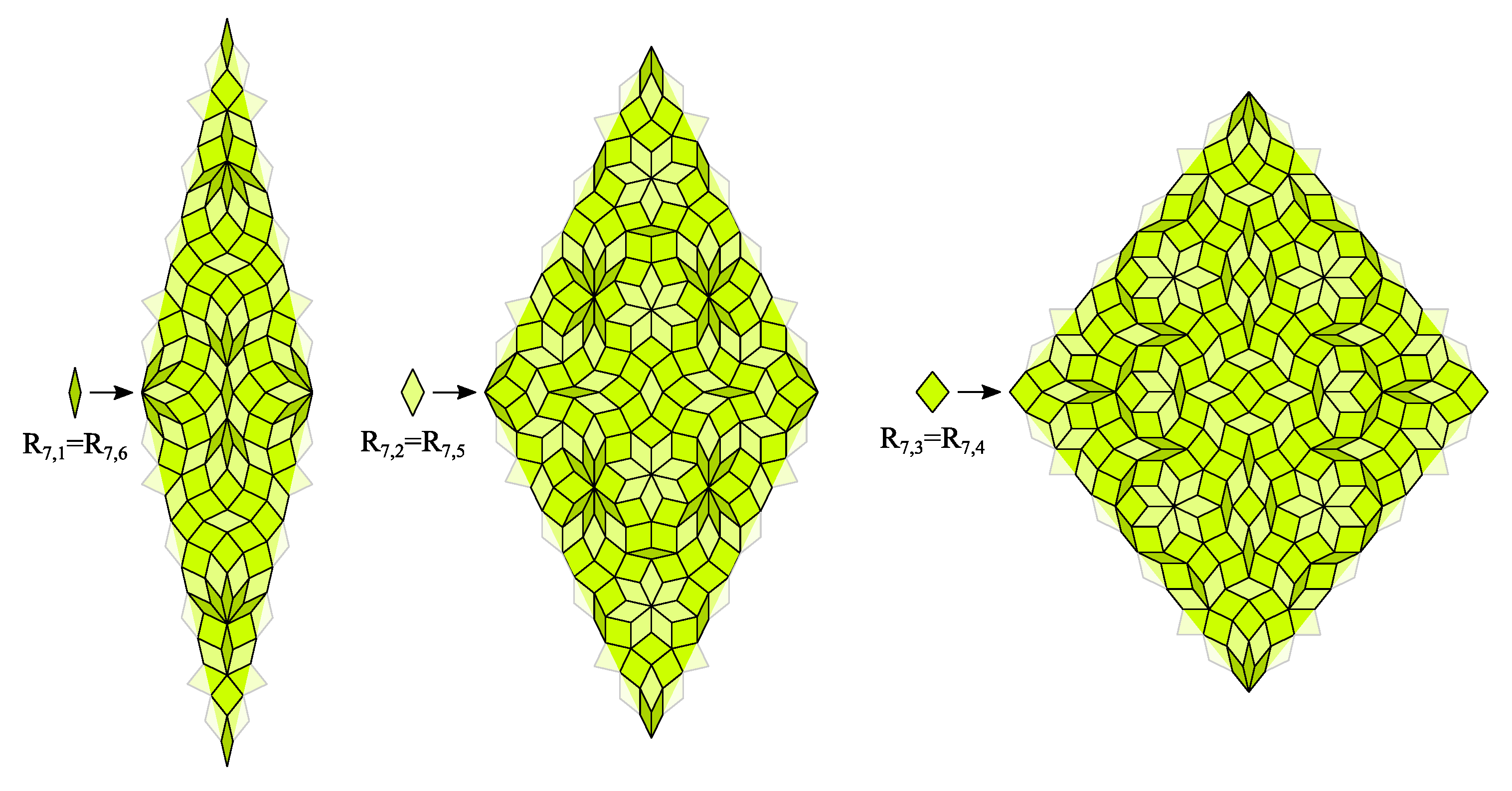
4. CASTs with Inflation Multiplier Equal to the Longest Diagonal of a Regular Odd n-Gon
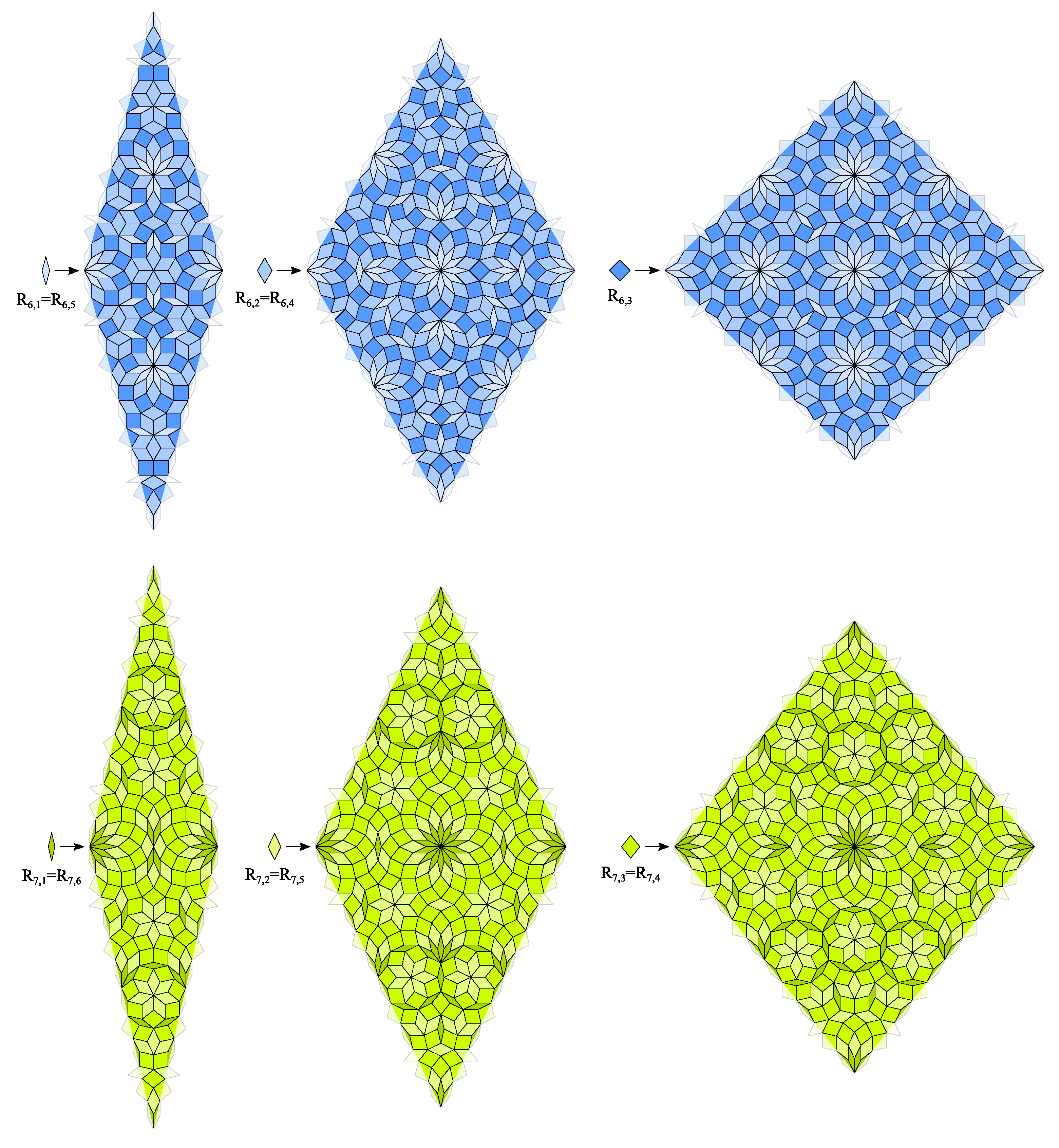
5. Rhombic CASTs with Symmetric Edges and Substitution Rules
- There are two ways to place rhombs on the edge of substitution rules. We recall that the inner angles of the rhombs are integer multiples of . We can place all rhombs on the edge so that the inner angles either with even or odd multiples of are bisected by the boundary of the supertile. We will call these two cases “even” and “odd edge configuration”, for details see Figure 7. A “mixed” configuration is not allowed, because it would force the existence of rhombs with inner angle equal to .
- We can choose the symmetry of the substitution rules and their edges. Possible choices are dihedral symmetry and . Edges with dihedral symmetry can have the boundary of the supertile or its perpendicular bisector as line of symmetry. The smallest nontrivial solution for the latter case is the generalized Goodman-Strauss tiling [39]. Since this example does not provide individual dihedral symmetry or in general, we will focus on the other case.Substitution rules of rhombs which appear on the edge of a substitution rule are forced to have the appropriate dihedral symmetry as well. This is also true for substitution rules of prototiles which lie on the diagonal, i.e., a line of symmetry of a substitution rule. The orientations of the edges have to be considered as well. These three conditions may force the introduction of additional rhomb prototiles and substitution rules. Additionally, the existence of edges with orientations may require additional preconditions.To avoid this problem, a general dihedral symmetry can be chosen for the substitution rules and their edges.
- Parity of the chosen n may require different approaches in some cases, similar to the example of the generalized Lançon-Billard tiling in Section 3.2 and Figure 4.
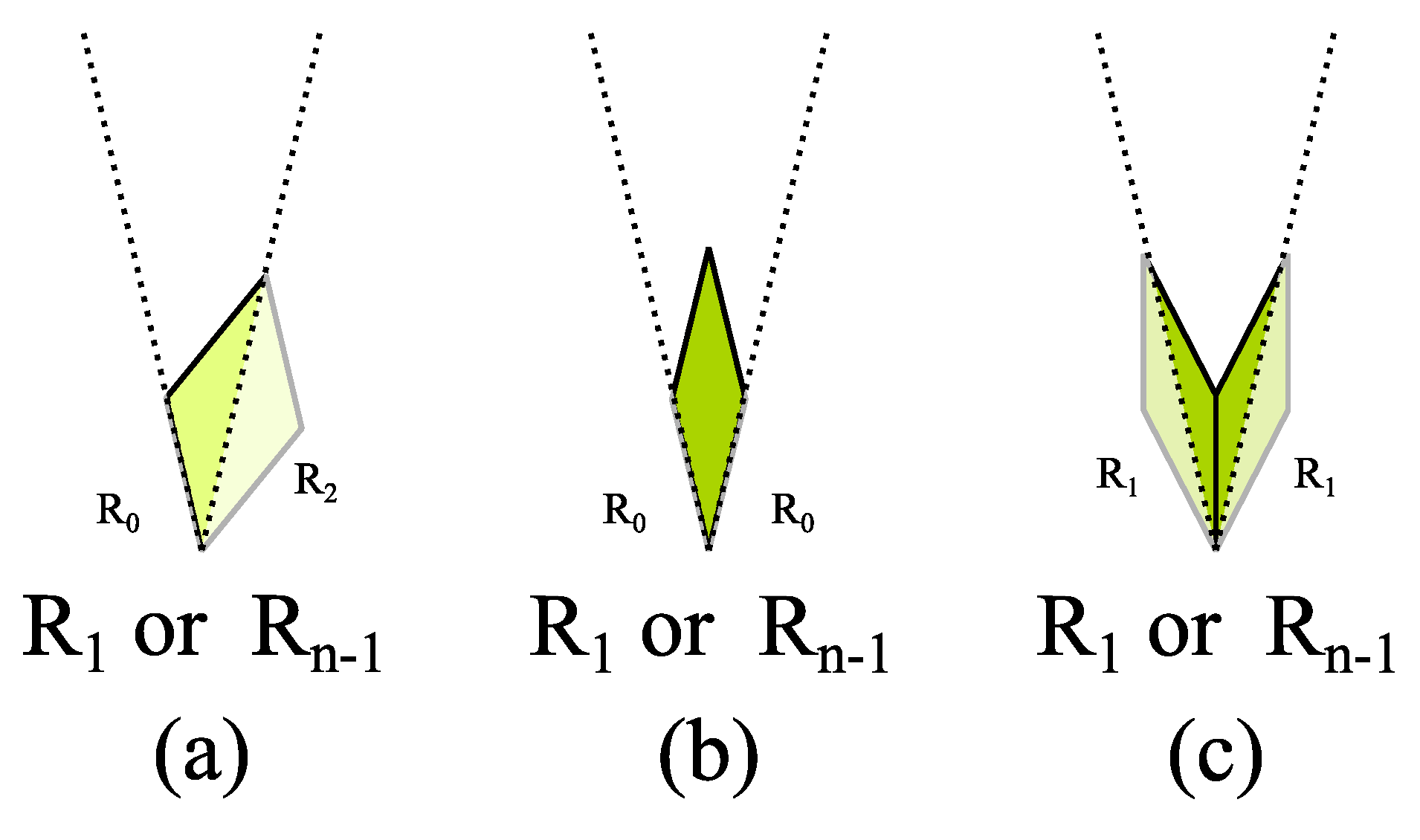
- The rhombs on the edges must not overlap. For this reason, for the tip of the substitution rule, only three configurations are possible as shown in Figure 8. Obviously, a tip as shown in Figure 8c is compliant to the cases 2 and 4 with odd edge configuration and Figure 8b to cases 1 and 3 with even edge configuration. Figure 8a requires the even edge configuration as well. Since all edges are congruent, it must be the start and the end of the same edge, which meet on that vertex. Since start and end of the edge are different, it can not have dihedral symmetry . For this reason, the tip in Figure 8a is not compliant to case 3.
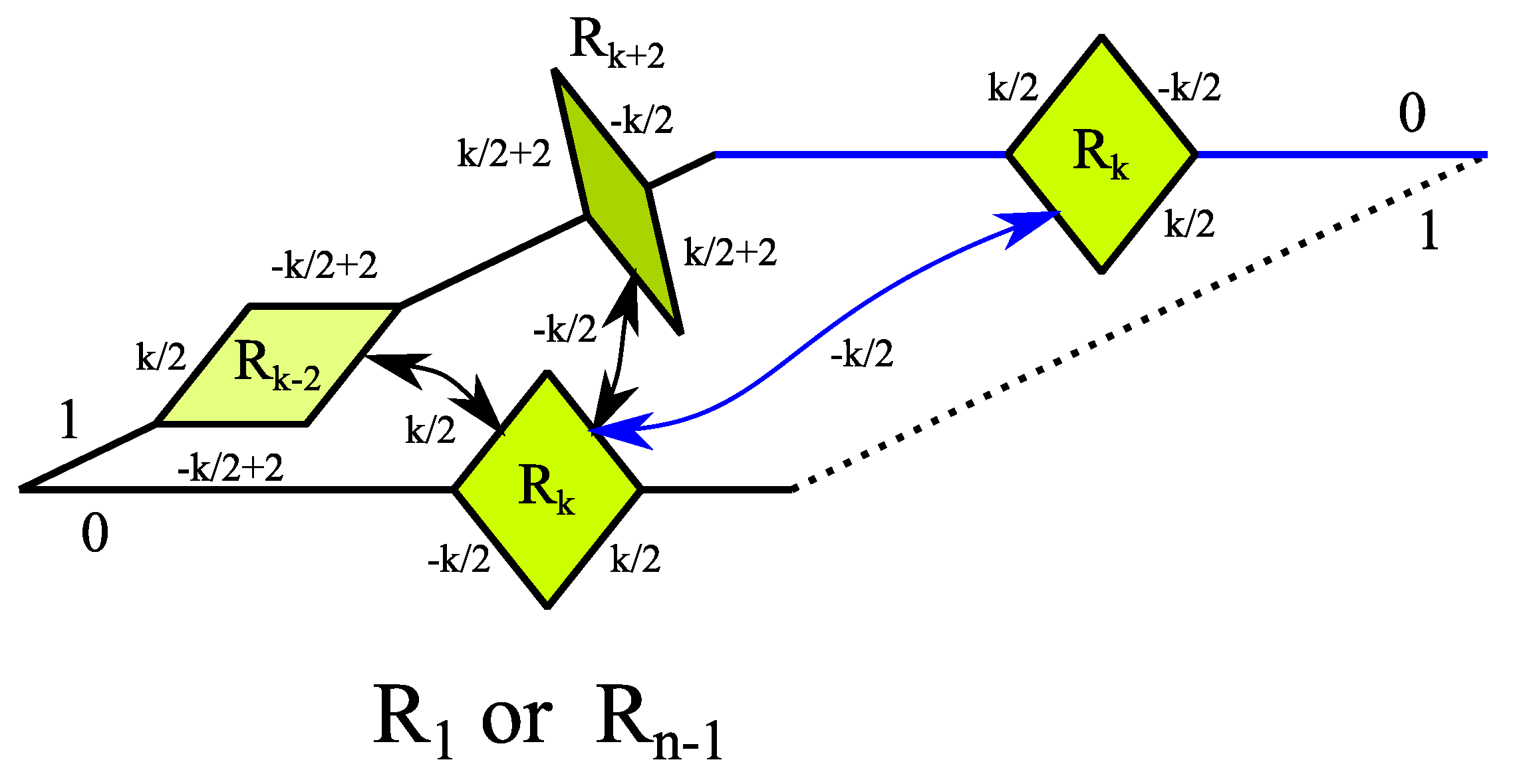
- Any rhomb with on one edge implies the existence of a rhomb on the corresponding edge. In turn, rhomb on one edge is implied by a rhomb on the corresponding edge or a rhomb on the opposite edge. An example is shown in Figure 9.
- Any rhomb on one edge implies the existence of a line segment on the corresponding edge. In turn, rhomb on one edge is implied by a rhomb on the corresponding edge or a rhomb on the opposite edge.
- Any rhomb on one edge implies the existence of a rhomb on the corresponding edge. In turn, rhomb on one edge is implied by a rhomb on the corresponding edge or a rhomb on the opposite edge.
- Any line segment on one edge is implied by a rhomb on the corresponding edge or a line segment on the opposite edge.
- Any rhomb on one edge implies the existence of a rhomb on the corresponding edge. In turn, rhomb on one edge is implied by a rhomb on the opposite edge. (Rhomb does not exist, because the inner angle would be zero.)
- Any rhomb on one edge implies the existence of a rhomb on the corresponding edge. In turn, rhomb on one edge is implied by a rhomb on the opposite edge. (Rhomb does not exist, it would have an inner angle greater than π or smaller the 0.)
- If for a rhomb on one edge two related elements (rhomb or line segment) and exist on the corresponding edge, is closer to the tip than .
- Any line segment on the edge implies the existence of a rhomb on the correspondent edge or a line segment on the opposite edge. As shown in Figure 10a,b, the existence of rhomb on the edge is not required to meet the KSK criterion.
- Any rhomb on the edge implies the existence of a rhomb on the correspondent edge or a rhomb on the opposite edge. As shown in Figure 10c,d, the KSK criterion is only met if at least one exists on the edge.
- The line segment on the edge implies the existence of a line segment on the opposite edge only (rhomb does not exist).
- Any rhomb on the edge implies the existence of a rhomb on the correspondent edge or a rhomb on the opposite edge. So the KSK criterion is only met if at least one exists on the edge.
- Any rhomb on the edge implies the existence of a rhomb on the correspondent edge or a rhomb on the opposite edge. So the KSK criterion is only met if at least one exists on the edge.
- Any rhomb on the edge implies the existence of a rhomb on the correspondent edge or a rhomb on the opposite edge. So the KSK criterion is only met if at least one exists on the edge.
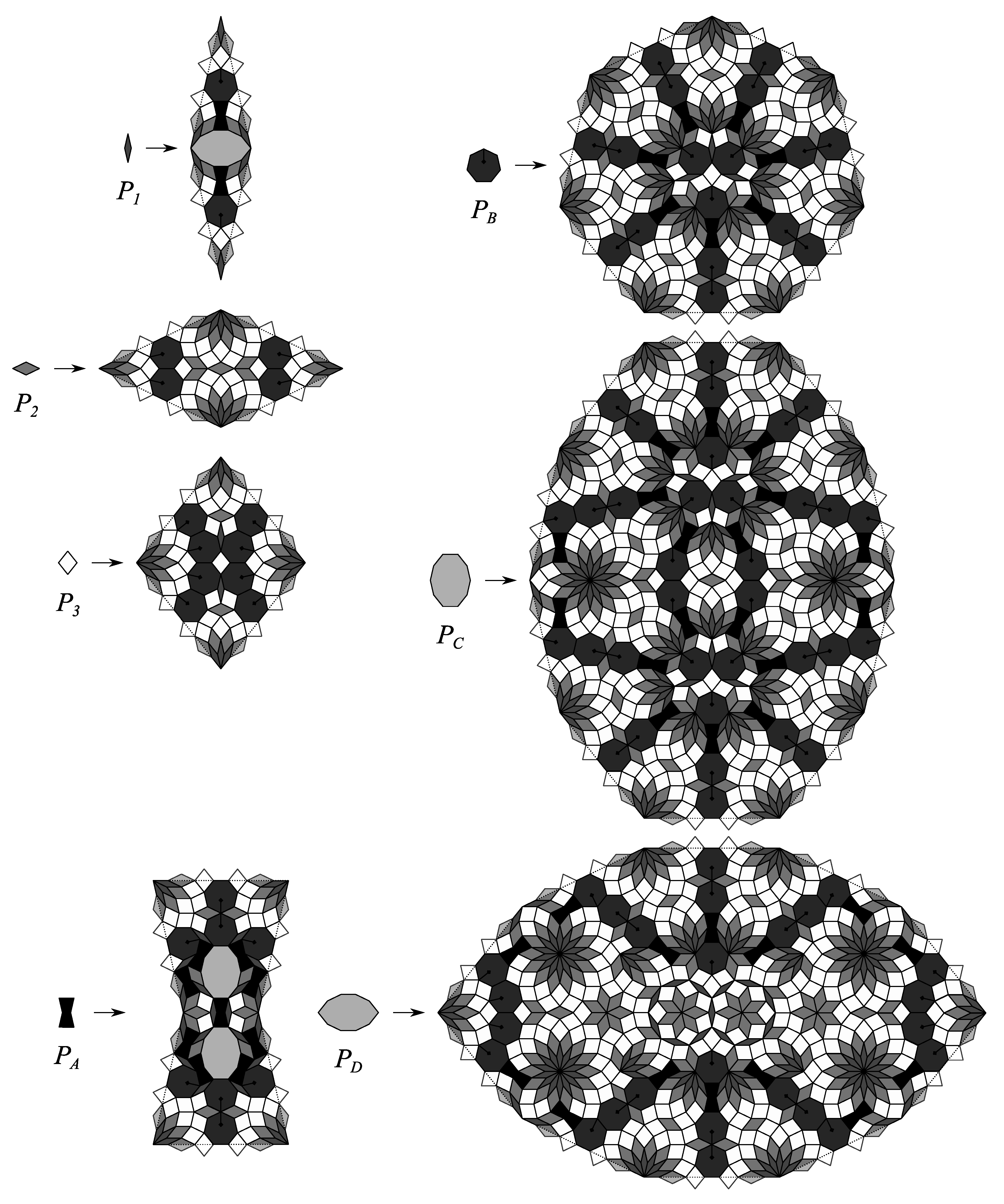
6. Gaps to Prototiles Algorithm
- All prototiles have inner angles equal .
- All edges of all substitution rules are congruent and have dihedral symmetry .
- As discussed in Section 5 the tiles on the edge have to be placed, so that the inner angles either with even or odd multiples of are bisected by the boundary of the supertile.
- The tiles on the edge are bisected by one or two lines of symmetry of the edge. This implies dihedral symmetry or of the corresponding substitution rules.
- The inflation multiplier η must fulfill the conditions in Theorem 1.
- The inflation multiplier η is defined by the sequence of tiles which are part of the edge.
- We start with the prototiles which appear on the edge of the substitution rule.
- We start the construction of the substitution rules by placing the prototiles on the edge.
- If the edge prototiles overlap the algorithm has failed. In this case, we may adjust the sequence of rhombs or other equilateral polygons on the edge and start another attempt.
- We try to “fill up” the substitution rules with existing prototiles under consideration of the appropriate dihedral symmetry or . If gaps remain, they are defined as new prototiles and we go back to step (2). Please note, if a gap lies on one or two lines of symmetry, the substitution rule of the new prototile must also have the appropriate dihedral symmetry or .
- If no gaps remain the algorithm was successful.
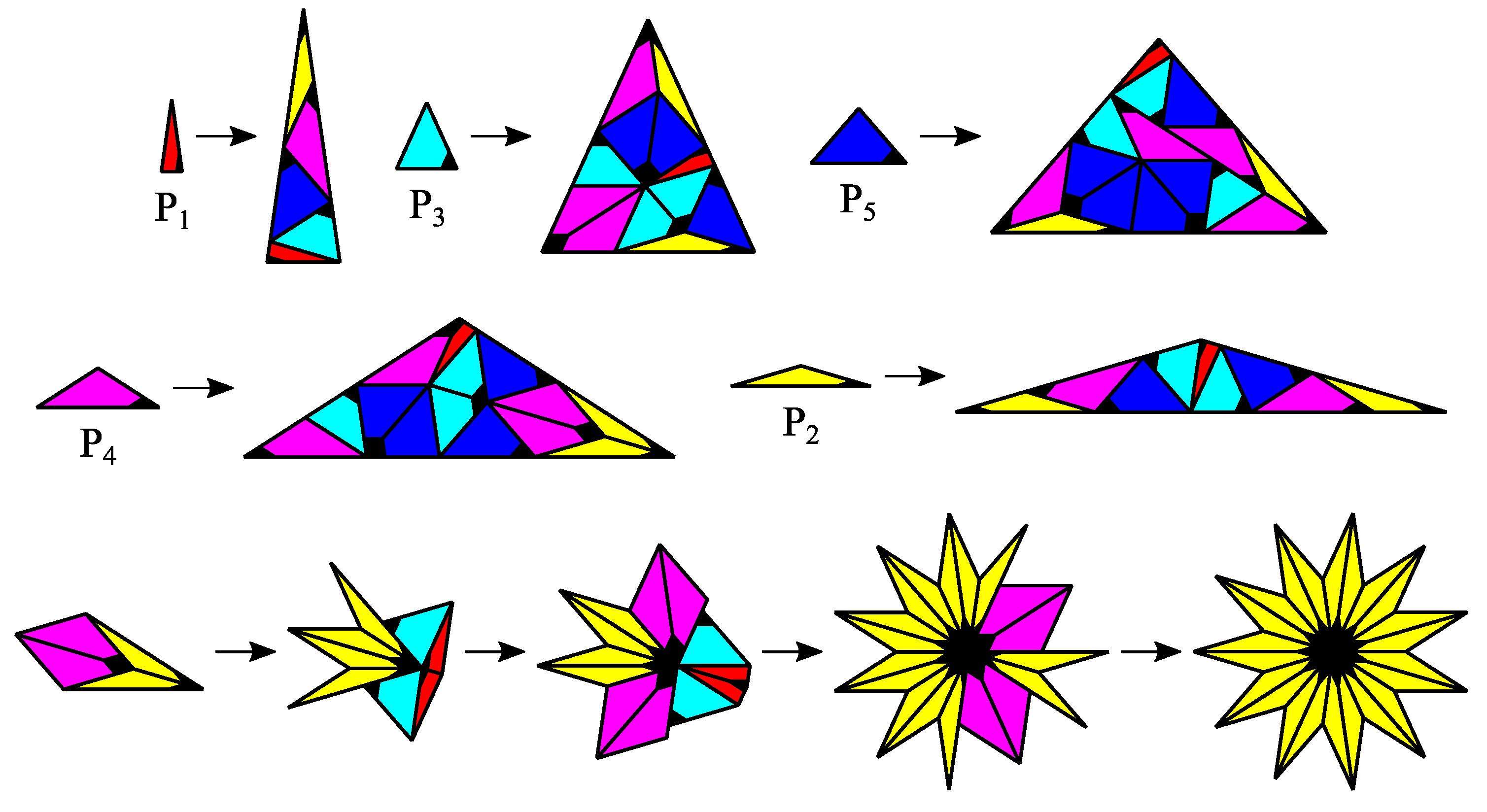
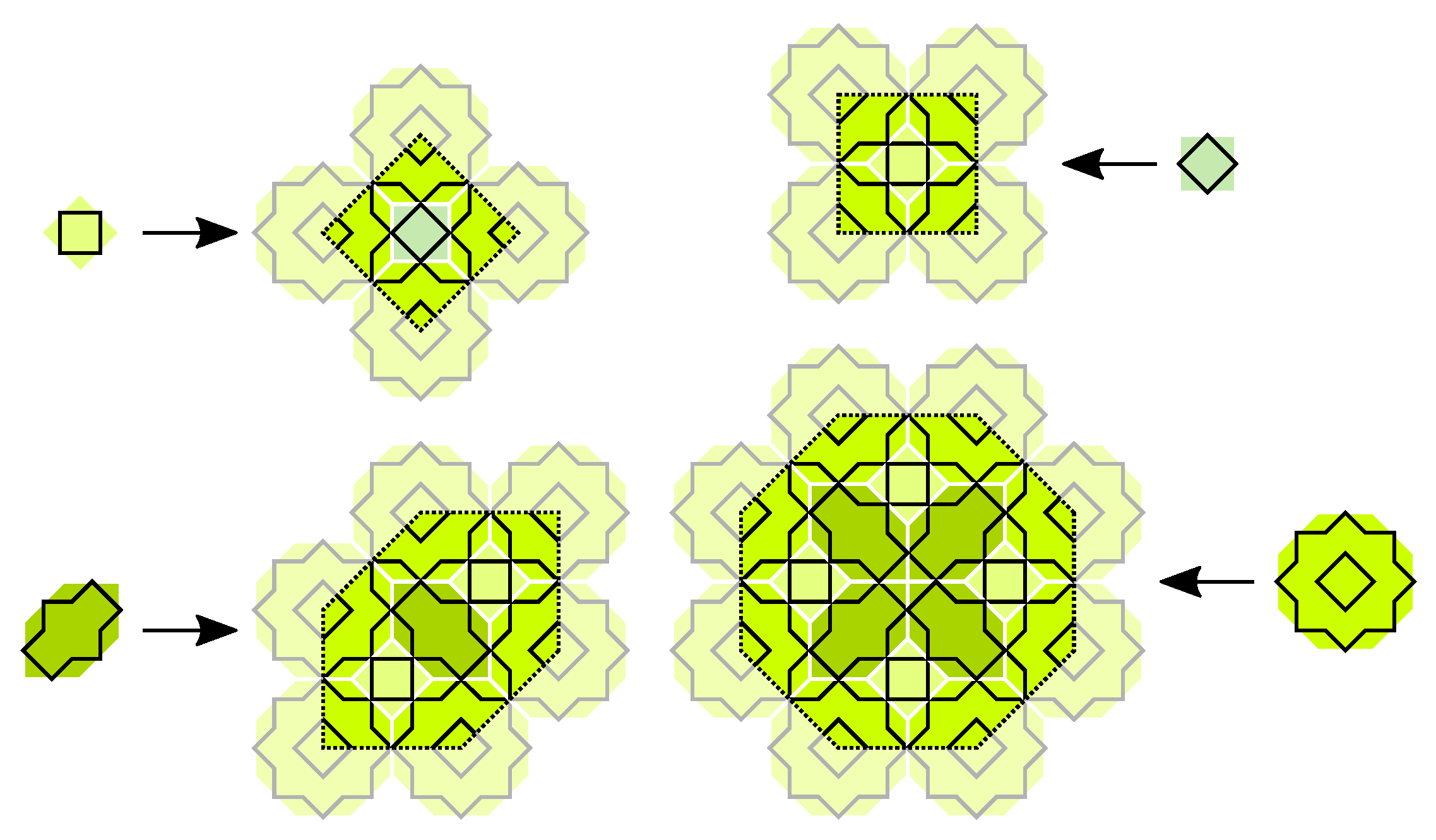
7. Extended Girih CASTs
- Regular decagon with inner angles
- Regular pentagon with inner angles
- Rhomb with inner angles and
- Convex hexagon with inner angles ,,,,,
- Convex hexagon with inner angles ,,,,,
- Nonconvex hexagon with inner angles , , , , ,
- All prototiles of an extended Girih CAST are equilateral polygons with the same side length.
- The inner angles of all prototiles are , .
- One of the prototiles may be a regular n-gon with inner angles .
- One of the prototiles may be a regular -gon with inner angles .
- All edges of the substitution rules are congruent and have dihedral symmetry .
- All substitution rules except those for regular n-gons with have dihedral symmetry .
- The substitution rule of the regular n-gon with has dihedral symmetry .
- The substitution rule of the regular -gon has dihedral symmetry for and for .
- In every corner of every substitution rule a regular -gon is placed.
- Edge and inflation multiplier have been derived from a periodic pattern of regular -gons and their inter space counterparts.
8. Summary and Outlook
Acknowledgments
Conflicts of Interest
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Grünbaum, B.; Shephard, G.C. Tilings and Patterns; W. H. Freeman & Co.: New York, NY, USA, 1987. [Google Scholar]
- Baake, M.; Grimm, U. Aperiodic Order. Vol 1. A Mathematical Invitation. In Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 2013; Volume 149. [Google Scholar]
- Escher, M.C.; Bool, F.; Locher, J.L. M. C. Escher, His Life and Complete Graphic Work: With a Fully Illustrated Catalogue; H. N. Abrams: New York, NY, USA, 1982. [Google Scholar]
- Voderberg, H. Zur Zerlegung der Umgebung eines ebenen Bereiches in kongruente. Jahresber. Deutsch. Math. Ver. 1936, 46, 229–231. [Google Scholar]
- Voderberg, H. Zur Zerlegung der Ebene in kongruente Bereiche in Form einer Spirale. Jahresber. Deutsch. Math. Ver. 1937, 47, 159–160. [Google Scholar]
- Lück, R. Dürer-Kepler-Penrose, the development of pentagon tilings. Mater. Sci. Eng. A 2000, 294–296, 263–267. [Google Scholar] [CrossRef]
- Maloney, G.R. On substitution tilings of the plane with n-fold rotational symmetry. Discret. Math. Theor. Comput. Sci. 2015, 17, 395–412. [Google Scholar]
- Berger, R. The undecidability of the domino problem. Mem. Am. Math. Soc. 1966, 66, 1–72. [Google Scholar] [CrossRef]
- Socolar, J.E.S. Simple octagonal and dodecagonal quasicrystals. Phys. Rev. B 1989, 39, 10519–10551. [Google Scholar] [CrossRef]
- Socolar, J.E.S. Weak matching rules for quasicrystals. Commun. Math. Phys. 1990, 129, 599–619. [Google Scholar] [CrossRef]
- Gähler, F. Matching rules for quasicrystals: The composition-decomposition method. J. Non-Cryst. Solids 1993, 153, 160–164. [Google Scholar] [CrossRef]
- De Bruijn, N.G. Algebraic theory of Penrose’s non-periodic tilings of the plane I and II. Indag. Math. New Ser. 1981, 84, 39–66. [Google Scholar] [CrossRef]
- Lagarias, J.C. Meyer’s concept of quasicrystal and quasiregular sets. Commun. Math. Phys. 1996, 179, 365–376. [Google Scholar] [CrossRef]
- Moody, R.V. The Mathematics of Long-Range Aperiodic Order; Springer: Heidelberg, Germany, 1997. [Google Scholar]
- Meyer, Y. Algebraic Numbers and Harmonic Analysis; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- De Bruijn, N.G. Dualization of multigrids. J. Phys. Colloq. 1986, 47 (C3), 9–18. [Google Scholar] [CrossRef]
- Gähler, F.; Rhyner, J. Equivalence of the generalised grid and projection methods for the construction of quasiperiodic tilings. J. Phys. A Math. Gen. 1986, 19, 267. [Google Scholar] [CrossRef]
- Ingalls, R. Decagonal quasicrystal tilings. Acta Crystallogr. Sect. A 1992, 48, 533–541. [Google Scholar] [CrossRef]
- Ingalls, R. Octagonal quasicrystal tilings. J. Non-Cryst. Solids 1993, 153–154, 177–180. [Google Scholar] [CrossRef]
- Lück, R. Basic ideas of ammann bar grids. Int. J. Mod. Phys. B 1993, 7, 1437–1453. [Google Scholar] [CrossRef]
- Scheffer, M. Festkörperreaktionen in Quasikristallinen Legierungen. Ph.D. Thesis, Universität Stuttgart and Max-Planck-Institut für Metallforschung, Stuttgart, Germany, 1998. [Google Scholar]
- Von Koch, H. Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire. Ark. Mat. 1904, 1, 681–702. [Google Scholar]
- Von Koch, H. Une méthode géométrique élémentaire pour l’étude de certaines questions de la théorie des courbes planes. Acta Math. 1906, 30, 145–174. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Co.: San Francisco, CA, USA, 1977. [Google Scholar]
- Gardner, M. On ‘Rep-tiles’, Polygons that can make larger and smaller copies of themselves. Sci. Am. 1963, 208, 154–164. [Google Scholar] [CrossRef]
- Penrose, R. The role of aesthetics in pure and applied mathematical research. Bull. Inst. Math. Appl. 1974, 10, 266ff. [Google Scholar]
- Gardner, M. Extraordinary nonperiodic tiling that enriches the theory of tiles. Sci. Am. 1977, 236, 110–119. [Google Scholar] [CrossRef]
- Penrose, R. Pentaplexity A Class of Non-Periodic Tilings of the Plane. Math. Intell. 1979, 2, 32–37. [Google Scholar] [CrossRef]
- Goodman-Strauss, C. Matching Rules and Substitution Tilings. Ann. Math. 1998, 157, 181–223. [Google Scholar] [CrossRef]
- Goodman-Strauss, C. Matching Rules for the Sphinx Substitution Tiling. Unpublished Notes. Available online: http://comp.uark.edu/~strauss/ (accessed on 22 June 2016).
- Frettlöh, D.; Gähler, F.; Harris, E.O. Tilings Encyclopedia. Available online: http://tilings.math.uni-bielefeld.de/ (accessed on 22 June 2016).
- Nischke, K.P.; Danzer, L. A construction of inflation rules based on n-fold symmetry. Discret. Comput. Geom. 1996, 15, 221–236. [Google Scholar] [CrossRef]
- Steinbach, P. Golden fields: A case for the heptagon. Math. Mag. 1997, 70, 22–31. [Google Scholar] [CrossRef]
- Frettlöh, D. About substitution tilings with statistical circular symmetry. Philos. Mag. 2008, 88, 2033–2039. [Google Scholar] [CrossRef]
- Frettlöh, D.; Say-Awen, A.L.D.; de las Peñas, M.L.A.N. Substitution tilings with dense tile orientations and n-fold rotational symmetry. Indag. Math. 2016, in press. [Google Scholar]
- Lançon, F.; Billard, L. Two-dimensional system with a quasi-crystalline ground state. J. Phys. 1988, 49, 249–256. [Google Scholar] [CrossRef]
- Godrèche, C.; Lançon, F. A simple example of a non-Pisot tiling with five-fold symmetry. J. Phys. I 1992, 2, 207–220. [Google Scholar] [CrossRef]
- Harriss, E.O. Non-Periodic Rhomb Substitution Tilings that Admit Order n Rotational Symmetry. Discret. Comput. Geom. 2005, 34, 523–536. [Google Scholar] [CrossRef]
- Hibma, T. Generalization of Non-periodic Rhomb Substitution Tilings. arXiv, 2015; arXiv:1509.02053. [Google Scholar]
- Math Pages. Non-Periodic Tilings with n-fold Symmetry. Available online: http://mathpages.com/home/kmath539/kmath539.htm (accessed on 22 June 2016).
- Hibma, T. Aperiodic Rhomb Tiling. Available online: http://www.hibma.org/wpaperiodictiling/ (accessed on 22 June 2016).
- Warrington, D.H. Two Dimensional Inflation Patterns and Corresponding Diffraction Patterns. In Quasicrystalline Materials: Proceedings of the I.L.L./CODEST Workshop; Janot, C., Dubois, J., Eds.; World Scientific: Singapore, 1988; pp. 243–254. [Google Scholar]
- Frettlöh, D.; Harriss, E.O. Parallelogram Tilings, Worms, and Finite Orientations. Discret. Comput. Geom. 2013, 49, 531–539. [Google Scholar] [CrossRef]
- Kannan, S.; Soroker, D. Tiling Polygons with Parallelograms. Discret. Comput. Geom. 1992, 7, 175–188. [Google Scholar] [CrossRef]
- Kenyon, R. Tiling a Polygon with Parallelograms. Algorithmica 1993, 9, 382–397. [Google Scholar] [CrossRef]
- Kari, J.; Rissanen, M. Sub Rosa, A System of Quasiperiodic Rhombic Substitution Tilings with n-Fold Rotational Symmetry. Discret. Comput. Geom. 2016, 55, 972–996. [Google Scholar] [CrossRef]
- Beenker, F.P.M. Algebraic Theory of Non-Periodic Tilings of the Plane by Two Simple Building Blocks: A Square and a Rhombus; Technical Report 82-WSK04; Eindhoven University of Technology: Eindhoven, The Netherlands, 1982. [Google Scholar]
- Ammann, R.; Grünbaum, B.; Shephard, G.C. Aperiodic Tiles. Discret. Comput. Geom. 1992, 8, 1–25. [Google Scholar] [CrossRef]
- Allen, T. Islamic Art and the Argument from Academic Geometry; Solipsist Press: Occidental, CA, USA, 2004. [Google Scholar]
- Lee, A.J. Islamic Star Patterns. Muqarnas 1987, 4, 182–197. [Google Scholar] [CrossRef]
- Bourgoin, J. Arabic Geometrical Pattern and Design; Dover Pictorial Archive Series; Dover Publications: New York, NY, USA, 1973. [Google Scholar]
- Necipoğlu, G.; Al-Asad, M. The Topkapı Scroll: Geometry and Ornament in Islamic Architecture: Topkapı Palace Museum Library MS; Number Bd. 1956 in Sketchbooks & Albums; Getty Center for the History of Art and the Humanities: Santa Monica, CA, USA, 1995. [Google Scholar]
- Lu, P.J.; Steinhardt, P.J. Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture. Science 2007, 315, 1106–1110. [Google Scholar] [CrossRef] [PubMed]
- Tennant, R. Medieval Islamic Architecture, Quasicrystals, and Penrose and Girih Tiles: Questions from the Classroom. In Bridges Leeuwarden: Mathematics, Music, Art, Architecture, Culture; Sarhangi, R., Séquin, C.H., Eds.; Tarquin Publications: London, UK, 2008; pp. 297–304. Available online: http://archive.bridgesmathart.org/2008/bridges2008-297.html (accessed on 22 June 2016).
- Cromwell, P.R. The Search for Quasi-Periodicity in Islamic 5-fold Ornament. Math. Intell. 2008, 31, 36–56. [Google Scholar] [CrossRef]
- Lück, R. Penrose sublattices. J. Non-Cryst. Solids 1990, 117, 832–835. [Google Scholar] [CrossRef]
- Lück, R.; Lu, K. Non-locally derivable sublattices in quasi-lattices. J. Alloys Comp. 1994, 209, 139–143. [Google Scholar] [CrossRef]
- Gähler, F. Crystallography of Dodecagonal Quasicrystals. In Quasicrystalline Materials: Proceedings of the I.L.L./CODEST Workshop; Janot, C., Dubois, J., Eds.; World Scientific: Singapore, 1988; pp. 272–284. [Google Scholar]
- Niizeki, N.; Mitani, H. Two-dimensional dodecagonal quasilattices. J. Phys. A Math. Gen. 1987, 20, L405. [Google Scholar] [CrossRef]
- Franco, B.J.O.; Ferreira, J.R.F.; da Silva, F.W.O. A Third-Order Fibonacci Sequence Associated to a Heptagonal Quasiperiodic Tiling of the Plane. Phys. Status Solidi 1994, 182, K57–K62. [Google Scholar] [CrossRef]
- Gähler, F.; Kwan, E.E.; Maloney, G.R. A computer search for planar substitution tilings with n-fold rotational symmetry. Discret. Comput. Geom. 2015, 53, 445–465. [Google Scholar] [CrossRef]
- Frettlöh, D. Inflationäre Pflasterungen der Ebene Mit D2m+1-Symmetrie und Minimaler Musterfamilie, Betreuer Ludwig Danzer. Diploma Thesis, Universität Dortmund, Dortmund, Germany, 1998. [Google Scholar]
- Watanabe, Y.; Ito, M.; Soma, T.; Betsumiya, T. Nonperiodic Tesselation with Eight-Fold Rotational Symmetry. In Science on Form: Proceedings of the First International Symposium for Science on Form; Ishizaka, S., Kato, Y., Takaki, R., Toriwaki, J., Eds.; KTK Scientific Publishers: Tokyo, Japan, 1986; pp. 471–477. [Google Scholar]
- Watanabe, Y.; Ito, M.; Soma, T. Nonperiodic tessellation with eightfold rotational symmetry. Acta Crystallogr. Sect. A 1987, 43, 133–134. [Google Scholar] [CrossRef]
- Watanabe, Y.; Soma, T.; Ito, M. A new quasiperiodic tiling with dodecagonal symmetry. Acta Crystallogr. Sect. A 1995, 51, 936–942. [Google Scholar] [CrossRef]
- Niizeki, K. A self-similar dodecagonal quasiperiodic tiling of the plane in terms of squares, regular hexagons and thin rhombi. J. Phys. A Math. Gen. 1988, 21, 2167. [Google Scholar] [CrossRef]
- Stampfli, P. A Dodecagonal Quasi-Periodic Lattice in 2 Dimensions. Helv. Phys. Acta 1986, 59, 1260–1263. [Google Scholar]
- Ben-Abraham, S.I.; Gummelt, P.; Lück, R.; Gähler, F. Dodecagonal tilings almost covered by a single cluster. Ferroelectrics 2001, 250, 313–316. [Google Scholar] [CrossRef]
- Hermisson, J.; Richard, C.; Baake, M. A Guide to the Symmetry Structure of Quasiperiodic Tiling Classes. J. Phys. 1997, 7, 1003–1018. [Google Scholar] [CrossRef]
- Baake, M. A guide to mathematical quasicrystals. arXiv, 1999; arXiv:math-ph/9901014. [Google Scholar]
- Baake, M. Quasicrystals: An Introduction to Structure, Physical Properties and Applications; Springer: Berlin/Heidelberg, Germany, 2002; Chapter 2; pp. 17–48. [Google Scholar]
- Frettlöh, D. A fractal fundamental domain with 12-fold symmetry. Symmetry Cult. Sci. 2011, 22, 237–246. [Google Scholar]
- Franco, B.J.O. Third-order Fibonacci sequence associated to a heptagonal quasiperiodic tiling of the plane. Phys. Lett. A 1993, 178, 119–122. [Google Scholar] [CrossRef]
- Franco, B.J.O.; da Silva, F.W.O.; Inácio, E.C. A non-quadratic irrationality associated to an enneagonal quasiperiodic tiling of the plane. Phys. Status Solidi 1996, 195, 3–9. [Google Scholar] [CrossRef]



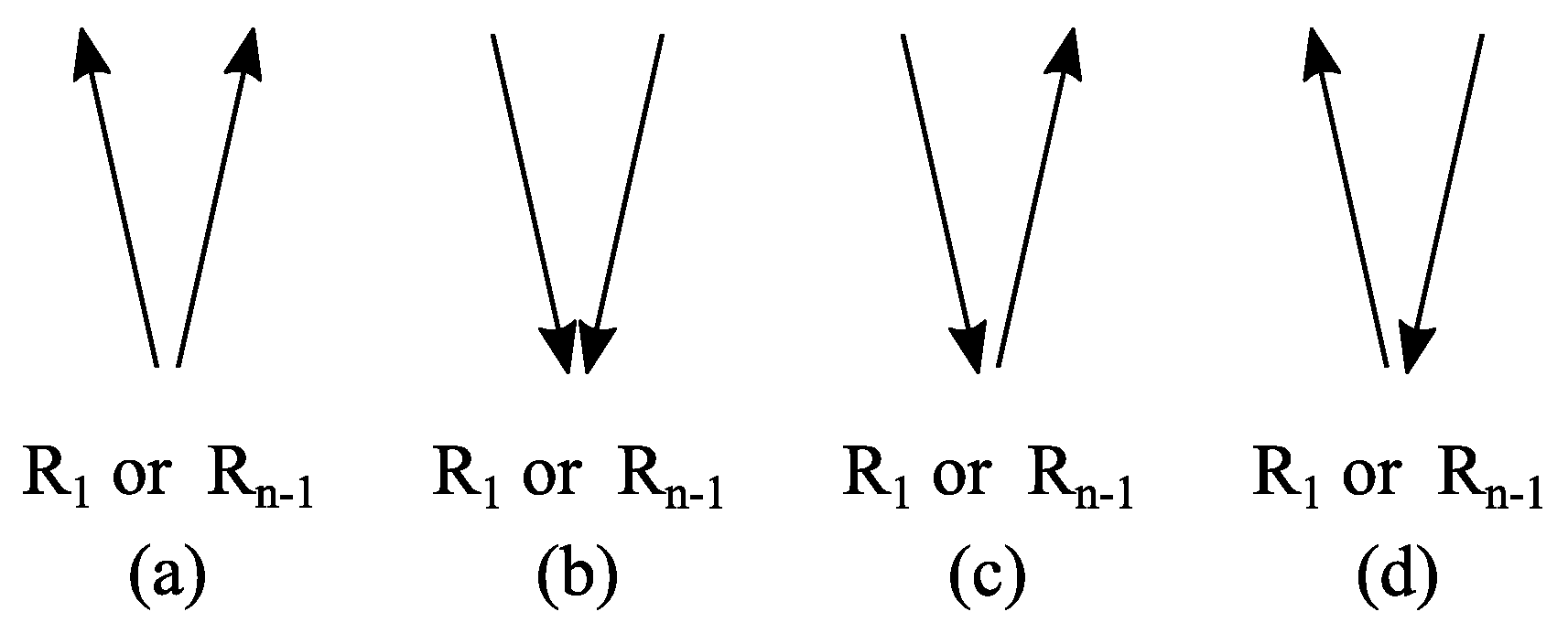





| Sum of Diagonals | Sum of Roots of Unity | Conditions for n |
|---|---|---|
| - | ||
| 3 | 3 | |
| 2 | 2 | - |
| 1 | 1 | - |
| Sum of Diagonals | Sum of Roots of Unity | Conditions for n |
|---|---|---|
| - | ||
| 3 | 3 | - |
| 2 | 2 | - |
| 1 | 1 | - |
| Substitution Rules and Their Edges Have at Least Dihedral Symmetry D1 | Substitution Rules and Their Edges Have Dihedral Symmetry D2 | |
|---|---|---|
| Even edge configuration | Case 1a Case 1b | Case 3a Case 3b |
| Odd edge configuration | Case 2a Case 2b | Case 4a Case 4b |
| n | Minimal Rhomb Edge Sequence | Minimal Inflation Multiplier ηmin |
|---|---|---|
| … | … | … |
| n | Minimal Rhomb Edge Sequence | Minimal Inflation Multiplier ηmin |
|---|---|---|
| … | … | … |
| n | Minimal Rhomb Edge Sequence | Minimal Inflation Multiplier ηmin |
|---|---|---|
| … | … | … |
| n | Minimal Rhomb Edge Sequence | Minimal Inflation Multiplier ηmin |
|---|---|---|
| … | … | … |
| n | Inflation Multiplier | Corresponding Figure |
|---|---|---|
| 7 | Figure 18 | |
| 7 | Figure 19 | |
| 4 | Figure 20 |
| n | Inflation Multiplier | Corresponding Figure |
|---|---|---|
| 4 | Figure 21 | |
| 5 | Figure 22 | |
| 5 | Figure 23 | |
| 7 | Figure 24 |
| n | Name | Inflation Multiplier | Patches with Individual Symmetry | Reference |
|---|---|---|---|---|
| 5 | Penrose | [27,28,29,32] [2] (Chapter 10.3) [3] (Chapter 6.2) | ||
| 7 | Danzer’s 7-fold variant | [33] (Figure 1 and Section 3, 2nd matrix) Herein Figure 3 | ||
| 7 | Danzer’s 7-fold variant (two variants) | [32] (credited to L. Danzer) | ||
| [33] (Figure 11) | ||||
| 7 | Math Pages 7-fold | - | [41] | |
| 9 | Math Pages 9-fold | [41] | ||
| 5 | Lançon-Billard / Binary | - | [32,37,38] [3] (Chapter 6.5.1) | |
| 6 | Shield | - | [32,59,60] [3] (Chapter 6.3.2) | |
| 4 | Ammann-Beenker | [10,32,48,49] [2] (Chapter 10.4) [3] (Chapter 6.1) | ||
| 5 | Tie and Navette / Bowtie-Hexagon 1 | - | [57,58] [22] (Section 8.2, Figure 8.3) [32] [56] (Figure 25) | |
| 5 | Bowtie-Hexagon-Decagon 1 | [32] (credited to L. Andritz) | ||
| 7 | Danzer’s 7-fold (two variants) | [33] (Figure 12) [32] [3] (Chapter 6.5.2) | ||
| 7 | Franco-Ferreira-da-Silva 7-fold | [61] | ||
| 7 | Maloney’s 7-fold | [32] [62] (Figure 9) | ||
| 7 | Cyclotomic Trapezoids | [32,63] | ||
| 9 | ||||
| 11 | ||||
| 4 | Watanabe-Ito-Soma 8-fold | [32,64,65,66] | ||
| 4 | Generalized Goodman-Strauss rhomb | [39] [32] (credited to C. Goodman-Strauss and E. O. Harris) | ||
| 5 | , | |||
| 6 | Watanabe-Soma-Ito 12-fold (variants) | [32,66] | ||
| 6 | Socolar | [10,32,67] | ||
| 6 | Stampfli-Gähler / Ship | [59,68,69] | ||
| 6 | Square Triangle | [70,71,72,73] [32] (credited to M. Schlottmann) [3] (Chapter 6.3.1) | ||
| 5 | Cromwell | [56] (Figures 12 and 13) | ||
| 5 | Topkapi Scroll | Herein Figure 23, derived from [56] (Figures 14 and 15) and patterns shown in the Topkapi Scroll, in detail [53] (Panels 28, 31, 32, 34) | ||
| 5 | Bowtie-Hexagon-Decagon 2 | [32] (credited to L. Andritz) | ||
| 5 | Bowtie-Hexagon-Decagon 3 | [32] (credited to L. Andritz) | ||
| 5 | Darb-i Imam Shrine | [54,55] [56] (Figure 21) | ||
| 7 | Franco’s 7-fold | [74] | ||
| 7 | Gähler-Kwan-Maloney 7-fold | [62] (Figure 10) | ||
| 7 | Socolar’s 7-fold | [32] (credited to J. Socolar) | ||
| 9 | Franco-da-Silva-Inácio 9-fold | [75] | ||
| 11 | Maloney’s 11-fold | [8] |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pautze, S. Cyclotomic Aperiodic Substitution Tilings. Symmetry 2017, 9, 19. https://doi.org/10.3390/sym9020019
Pautze S. Cyclotomic Aperiodic Substitution Tilings. Symmetry. 2017; 9(2):19. https://doi.org/10.3390/sym9020019
Chicago/Turabian StylePautze, Stefan. 2017. "Cyclotomic Aperiodic Substitution Tilings" Symmetry 9, no. 2: 19. https://doi.org/10.3390/sym9020019






