Multi-Class Disease Classification in Brain MRIs Using a Computer-Aided Diagnostic System
Abstract
:1. Introduction
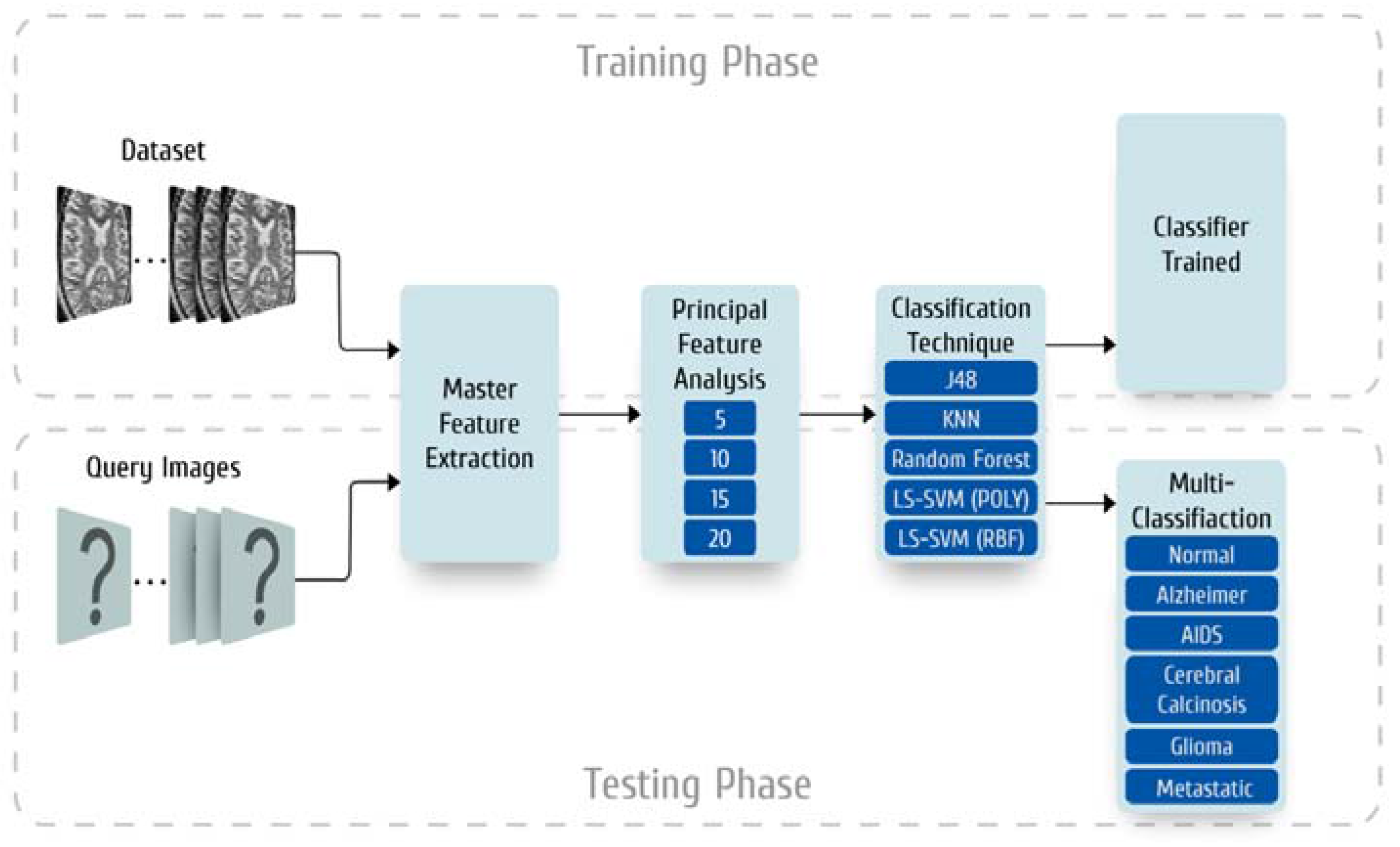
2. Materials and Methods
2.1. Dataset Collection
2.2. Master Feature Extraction
2.3. Preparation of the Principal Feature Vector
2.3.1. Feature Subset Sizes
2.4. Classifier Models
2.4.1. J48 Classifier (J48)
2.4.2. K-Nearest Neighbor (kNN)
2.4.3. Random Forest (RF)
2.4.4. Least Squares-Support Vector Machine (LS-SVM)
2.5. Performance Measures
- TP (True Positive): Number of images correctly diagnosed under any specific class;
- TN (True Negative): Number of images correctly rejected by the classifier;
- FP (False Positive): Number of images incorrectly identified by the classifier;
- FN (False Negative): Number of images incorrectly discarded by the classifier.
- RecallM is the average of the each class recall (i.e., the probability of the test finding the positive cases among all the positive cases of the respective class):
- PrecisionM is the average of the each class precision (i.e., the probability of the test correctly diagnosed as positive cases given that the number of cases labelled by the system as positive):
- F-MeasureM (macro-averaged F-measure) is a weighted combination of the and . Mathematically, it is defined as:
- Average Accuracy is the fraction of test results predicted as correct among all the classes:
- Area under the ROC curve (AUC) is the area occupied by the receiver operating characteristic curve of each class. It is used to analyse how good any classification model predicts the specific class versus all other classes:where C represents the total number of classes. i.e., . M index represents to macro-averaging. was used in this research.
2.6. Experimental Setup
3. Results and Discussion
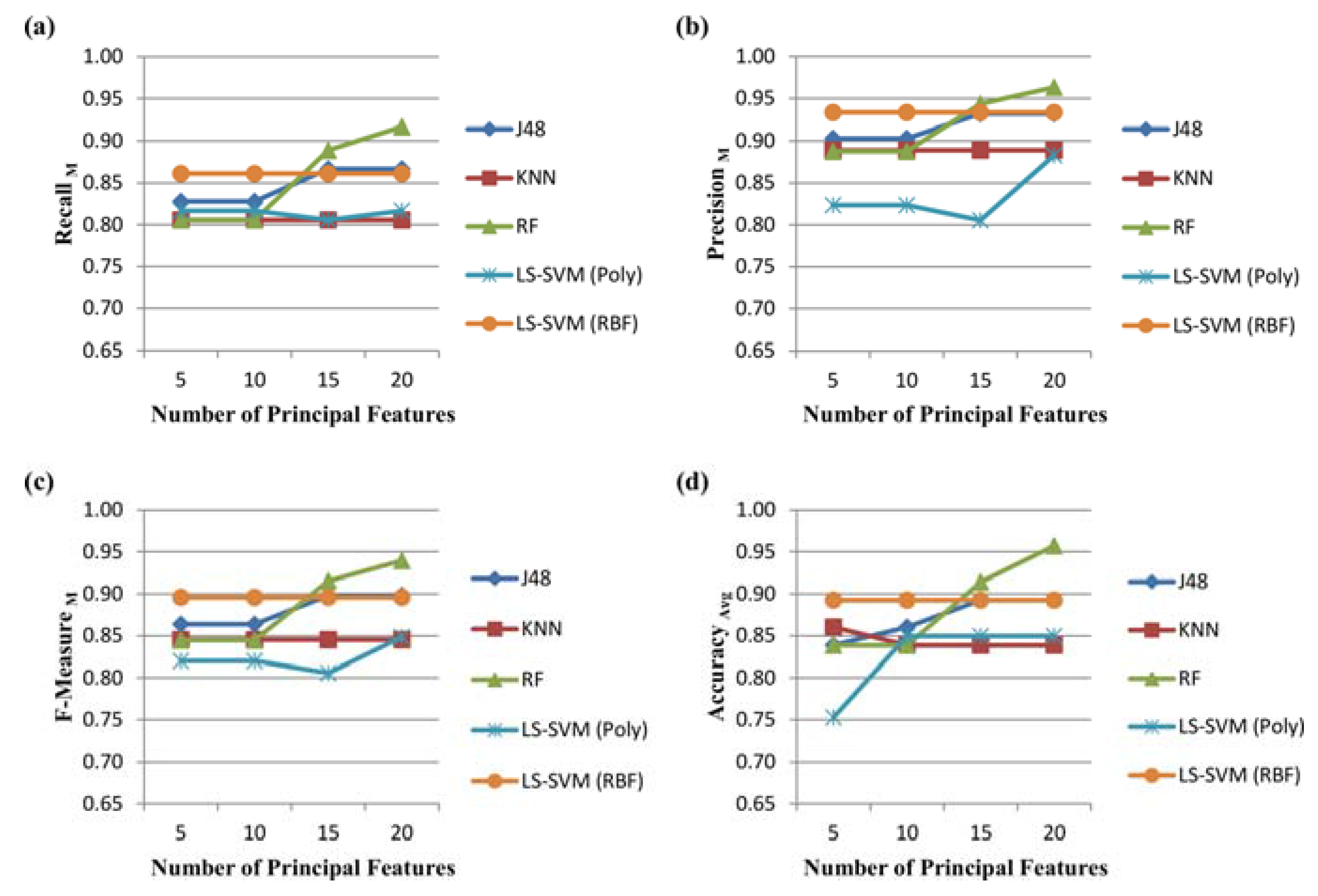
3.1. Feature Reduction
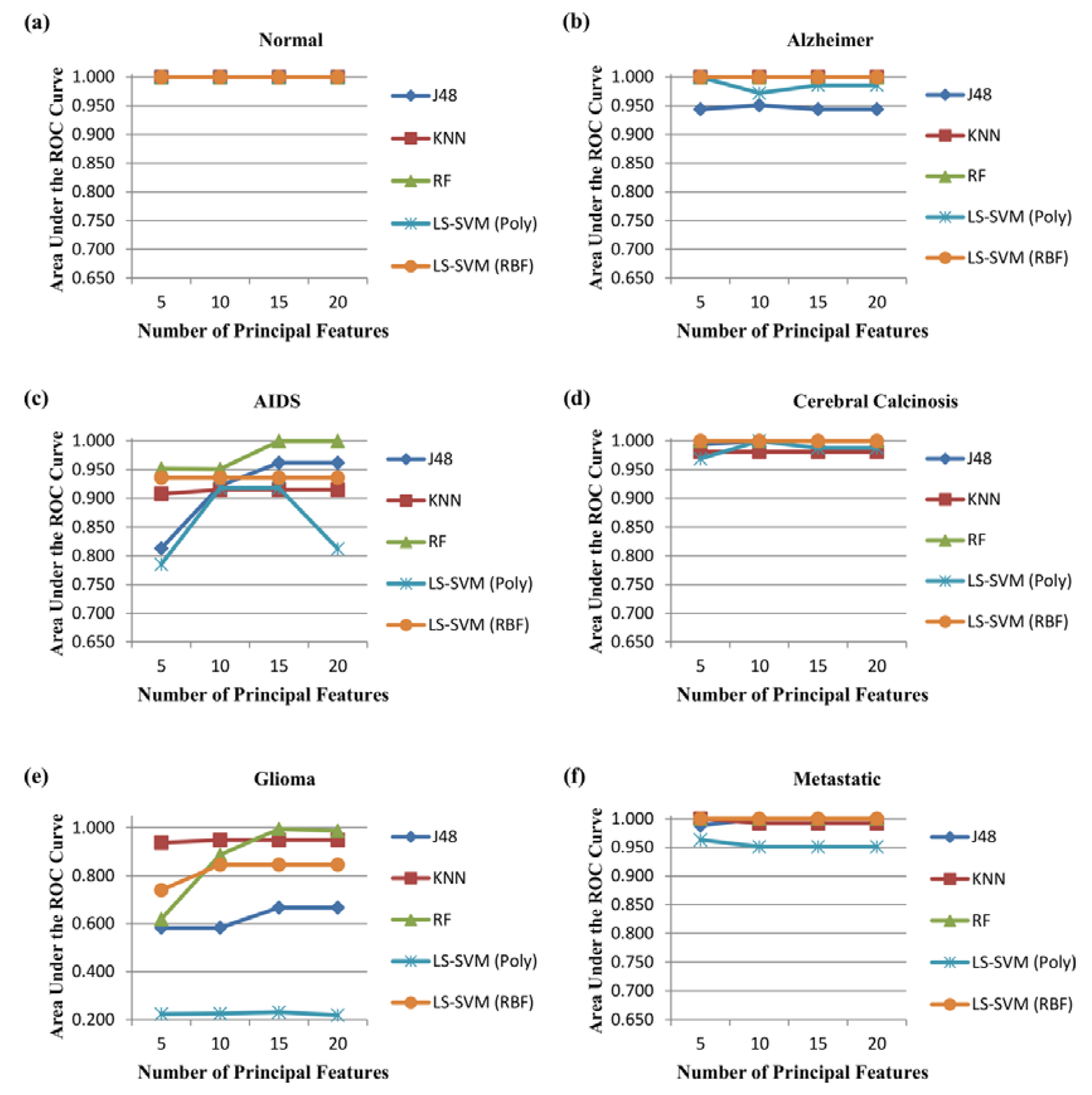
3.2. Performance Evaluation
3.3. Comparison with Existing State-of-the-Art Classification Schemes
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- McKhann, G.; Drachman, D.; Folstein, M.; Katzman, R.; Price, D.; Stadlan, E.M. Clinical diagnosis of Alzheimer’s disease report of the nincds-adrda work group* under the auspices of department of health and human services task force on Alzheimer’s disease. Neurology 1984, 34, 939. [Google Scholar] [CrossRef] [PubMed]
- Sahu, O.; Anand, V.; Kanhangad, V.; Pachori, R.B. Classification of magnetic resonance brain images using bi-dimensional empirical mode decomposition and autoregressive model. Biomed. Eng. Lett. 2015, 5, 311–320. [Google Scholar] [CrossRef]
- Prasad, P.V. Magnetic Resonance Imaging: Methods and Biologic Applications; Springer Science & Business Media: New York, NY, USA, 2006; Volume 124. [Google Scholar]
- Maji, P.; Chanda, B.; Kundu, M.K.; Dasgupta, S. Deformation correction in brain MRI using mutual information and genetic algorithm. In Proceedings of the International Conference on Computing: Theory and Applications, Kolkata, India, 5–7 March 2007; pp. 372–376.
- Scapaticci, R.; Di Donato, L.; Catapano, I.; Crocco, L. A feasibility study on microwave imaging for brain stroke monitoring. Prog. Electromagn. Res. B Pier B 2012, 40, 305–324. [Google Scholar] [CrossRef]
- Siddiqui, M.F.; Reza, A.W.; Kanesan, J. An automated and intelligent medical decision support system for brain MRI scans classification. PLoS ONE 2015, 10, e0135875. [Google Scholar]
- Mujtaba, G.; Shuib, L.; Raj, R.G.; Rajandram, R.; Shaikh, K. Automatic text classification of ICD-10 related CoD from complex and free text forensic autopsy reports. In Proceedings of the 5th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 1055–1058.
- Mujtaba, G.; Shuib, L.; Raj, R.G.; Rajandram, R.; Shaikh, K.; Al-Garadi, M.A. Automatic ICD-10 multi-class classification of cause of death from plaintext autopsy reports through expert-driven feature selection. PLoS ONE 2017, 12, e0170242. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Wee, C.Y.; Shi, F.; Thung, K.H.; Ni, D.; Yap, P.T.; Shen, D. Identification of infants at high-risk for autism spectrum disorder using multiparameter multiscale white matter connectivity networks. Hum. Brain Mapp. 2015, 36, 4880–4896. [Google Scholar] [CrossRef]
- Huang, L.; Jin, Y.; Gao, Y.; Thung, K.-H.; Shen, D.; Initiative, A.S.D.N. Longitudinal clinical score prediction in Alzheimer’s disease with soft-split sparse regression based random forest. Neurobiol. Aging 2016, 46, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Mwangi, B.; Ebmeier, K.P.; Matthews, K.; Steele, J.D. Multi-centre diagnostic classification of individual structural neuroimaging scans from patients with major depressive disorder. Brain 2012, 135, 1508–1521. [Google Scholar] [CrossRef] [PubMed]
- Klöppel, S.; Stonnington, C.M.; Barnes, J.; Chen, F.; Chu, C.; Good, C.D.; Mader, I.; Mitchell, L.A.; Patel, A.C.; Roberts, C.C. Accuracy of dementia diagnosis—A direct comparison between radiologists and a computerized method. Brain 2008, 131, 2969–2974. [Google Scholar] [CrossRef] [PubMed]
- Faisal, A.; Parveen, S.; Badsha, S.; Sarwar, H.; Reza, A.W. Computer assisted diagnostic system in tumor radiography. J. Med. Syst. 2013, 37. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, L.; Wang, S. Magnetic resonance brain image classification by an improved artificial bee colony algorithm. Prog. Electromagn. Res. Pier 2011, 116, 65–79. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Wu, L.; Wang, S. A hybrid method for MRI brain image classification. Expert Syst. Appl. 2011, 38, 10049–10053. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. An MR brain images classifier via principal component analysis and kernel support vector machine. Prog. Electromagn. Res. Pier 2012, 130, 369–388. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G.; Dong, Z. An MR brain images classifier system via particle swarm optimization and kernel support vector machine. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- El-Dahshan, E.-S.A.; Hosny, T.; Salem, A.-B.M. Hybrid intelligent techniques for MRI brain images classification. Digit. Signal Process. 2010, 20, 433–441. [Google Scholar] [CrossRef]
- El-Dahshan, E.-S.A.; Mohsen, H.M.; Revett, K.; Salem, A.-B.M. Computer-aided diagnosis of human brain tumor through MRI: A survey and a new algorithm. Expert Syst. Appl. 2014, 41, 5526–5545. [Google Scholar] [CrossRef]
- Das, S.; Chowdhury, M.; Kundu, M.K. Brain MR image classification using multiscale geometric analysis of Ripplet. Prog. Electromagn. Res. Pier 2013, 137, 1–17. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Wang, S.; Ji, G.; Yang, J. Preclinical diagnosis of magnetic resonance (MR) brain images via discrete wavelet packet transform with Tsallis entropy and generalized eigenvalue proximal support vector machine (GEPSVM). Entropy 2015, 17, 1795–1813. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, S.; Xu, W.; Ji, G.; Phillips, P.; Sun, P.; Zhang, Y. Detection of pathological brain in MRI scanning based on wavelet-entropy and naive Bayes classifier. In Proceedings of the Bioinformatics and Biomedical Engineering, Granada, Spain, 15–17 April 2015; pp. 201–209.
- Wang, S.; Lu, S.; Dong, Z.; Yang, J.; Yang, M.; Zhang, Y. Dual-tree complex wavelet transform and twin support vector machine for pathological brain detection. Appl. Sci. 2016, 6, 169. [Google Scholar] [CrossRef]
- Zacharaki, E.I.; Wang, S.; Chawla, S.; Soo Yoo, D.; Wolf, R.; Melhem, E.R.; Davatzikos, C. Classification of brain tumor type and grade using MRI texture and shape in a machine learning scheme. Magn. Reson. Med. 2009, 62, 1609–1618. [Google Scholar] [CrossRef] [PubMed]
- Chaplot, S.; Patnaik, L.; Jagannathan, N. Classification of magnetic resonance brain images using wavelets as input to support vector machine and neural network. Biomed. Signal Process. Control 2006, 1, 86–92. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Wu, L. A novel method for magnetic resonance brain image classification based on adaptive chaotic pso. Prog. Electromagn. Res. Pier 2010, 109, 325–343. [Google Scholar] [CrossRef]
- Maitra, M.; Chatterjee, A. A slantlet transform based intelligent system for magnetic resonance brain image classification. Biomed. Signal Process. Control 2006, 1, 299–306. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Blum, A.L.; Langley, P. Selection of relevant features and examples in machine learning. Artif. Intell. 1997, 97, 245–271. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Wettschereck, D.; Aha, D.W.; Mohri, T. A review and empirical evaluation of feature weighting methods for a class of lazy learning algorithms. Artif. Intell. Rev. 1997, 11, 273–314. [Google Scholar] [CrossRef]
- Sengur, A. An expert system based on principal component analysis, artificial immune system and fuzzy k-NN for diagnosis of valvular heart diseases. Comput. Biol. Med. 2008, 38, 329–338. [Google Scholar] [CrossRef] [PubMed]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Zhao, Y.; Zhang, Y. Comparison of decision tree methods for finding active objects. Adv. Space Res. 2008, 41, 1955–1959. [Google Scholar] [CrossRef]
- Bao, Y.; Ishii, N.; Du, X. Combining multiple k-nearest neighbor classifiers using different distance functions. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Exeter, UK, 25–27 August 2004; pp. 634–641.
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Academic Press: Salk Lake City, UT, USA, 2013. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by random forest. R News 2002, 2, 18–22. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Patil, N.; Shelokar, P.; Jayaraman, V.; Kulkarni, B. Regression models using pattern search assisted least square support vector machines. Chem. Eng. Res. Des. 2005, 83, 1030–1037. [Google Scholar] [CrossRef]
- Wang, F.-F.; Zhang, Y.-R. The support vector machine for dielectric target detection through a wall. Prog. Electromagn. Res. Pier Lett. 2011, 23, 119–128. [Google Scholar] [CrossRef]
- Chen, G.-C.; Juang, C.-F. Object detection using color entropies and a fuzzy classifier. IEEE Comput. Intell. Mag. 2013, 8, 33–45. [Google Scholar] [CrossRef]
- Magalhães, F.; Sousa, R.; Araújo, F.M.; Correia, M.V. Compressive sensing based face detection without explicit image reconstruction using support vector machines. In Proceedings of the 10th International Conference on Image Analysis and Recognition, Berlin, Germany, 26–28 June 2013; pp. 758–765.
- Dasgupta, J.; Bhattacharya, K.; Chanda, B. A holistic approach for off-line handwritten cursive word recognition using directional feature based on arnold transform. Pattern Recogn. Lett. 2016, 79, 73–79. [Google Scholar] [CrossRef]
- Komiyama, Y.; Banno, M.; Ueki, K.; Saad, G.; Shimizu, K. Automatic generation of bioinformatics tools for predicting protein–ligand binding sites. Bioinformatics 2015, 32, 901–907. [Google Scholar] [CrossRef] [PubMed]
- Cristianini, N.; Shawe-Taylor, J. An introduction to SVM; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Van Gestel, T.; Suykens, J.A.; Baesens, B.; Viaene, S.; Vanthienen, J.; Dedene, G.; De Moor, B.; Vandewalle, J. Benchmarking least squares support vector machine classifiers. Mach. Learn. 2004, 54, 5–32. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
| Class | Total No. of Images | Total No. of Training Images | Total No. of Testing Images | Distribution (%) |
|---|---|---|---|---|
| Normal | 70 | 49 | 21 | 22.58 |
| Alzheimer | 70 | 49 | 21 | 22.58 |
| Aids | 50 | 35 | 15 | 16.13 |
| Cerebral Calcinosis | 40 | 28 | 12 | 12.90 |
| Glioma | 40 | 28 | 12 | 12.90 |
| Metastasis | 40 | 28 | 12 | 12.90 |
| Kernel | Expression |
|---|---|
| Linear | |
| Polynomial | |
| RBF |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddiqui, M.F.; Mujtaba, G.; Reza, A.W.; Shuib, L. Multi-Class Disease Classification in Brain MRIs Using a Computer-Aided Diagnostic System. Symmetry 2017, 9, 37. https://doi.org/10.3390/sym9030037
Siddiqui MF, Mujtaba G, Reza AW, Shuib L. Multi-Class Disease Classification in Brain MRIs Using a Computer-Aided Diagnostic System. Symmetry. 2017; 9(3):37. https://doi.org/10.3390/sym9030037
Chicago/Turabian StyleSiddiqui, Muhammad Faisal, Ghulam Mujtaba, Ahmed Wasif Reza, and Liyana Shuib. 2017. "Multi-Class Disease Classification in Brain MRIs Using a Computer-Aided Diagnostic System" Symmetry 9, no. 3: 37. https://doi.org/10.3390/sym9030037







