1. Introduction
With a 16 kHz sampling rate, the adaptive multi-rate wideband (AMR-WB) speech codec [
1,
2,
3,
4] is one of the speech codecs applied to modern mobile communication systems as a way to remarkably improve the speech quality on handheld devices. The AMR-WB is a speech codec developed on the basis of an algebraic code-excited linear-prediction (ACELP) coding technique [
4,
5], and provides nine coding modes with bitrates of 23.85, 23.05, 19.85, 18.25, 15.85, 14.25, 12.65, 8.85, and 6.6 kbps. The ACELP-based technique is developed as an excellent speech coding technique, having a double advantage of low bit rates and high speech quality, but a price paid is a high computational complexity required in an AMR-WB codec. Using an AMR-WB speech codec, the speech quality of a smartphone can be improved but at the cost of high battery power consumption.
In an AMR-WB encoder, a vector quantization (VQ) of immittance spectral frequency (ISF) coefficients [
6,
7,
8,
9,
10] occupies a significant computational load in various coding modes. The VQ structure in AMR-WB adopts a combination of a split VQ (SVQ) and a multi-stage VQ (MSVQ) techniques, referred to as split-multistage VQ (S-MSVQ), to quantize the 16-order ISF coefficient [
1]. Conventionally, VQ uses a full search to obtain a codeword best matched with an arbitrary input vector, but the full search requires an enormous computational load. Therefore, many studies [
11,
12,
13,
14,
15,
16,
17,
18,
19] have made efforts to simplify the search complexity of an encoding process. These approaches are classified into two types in terms of the manner the complexity is reduced: triangular inequality elimination (TIE)-based approaches [
11,
12,
13,
14] and equal-average equal-variance equal-norm nearest neighbor search (EEENNS)-based algorithms [
15,
16,
17,
18,
19].
As in [
11], a TIE algorithm is proposed to address the computational load issue in a VQ-based image coding. Improved versions of TIE approaches are presented in [
12,
13] to reduce the scope of a search space, giving rise to further reduction in the computational load. However, there exists a high correlation between ISF coefficients of neighboring frames in AMR-WB, that is, ISF coefficients evolve smoothly over successive frames. This feature benefits TIE-based VQ encoding, according to which a considerable computational load reduction is demonstrated. Yet, a moving average (MA) filter is employed to smooth the data in advance of VQ encoding of ISF coefficients. It means that the high correlation feature is gone, resulting in a poor performance in computational load reduction. Recently, a TIE algorithm equipped with a dynamic and an intersection mechanism, named DI-TIE, is proposed to effectively simplify the search load, and this algorithm is validated as the best candidate among the TIE-based approaches so far. On the other hand, an EEENNS algorithm was derived from equal-average nearest neighbor search (ENNS) and equal-average equal-variance nearest neighbor search (EENNS) approaches [
15,
16,
17,
18,
19]. In contrast to TIE-based approaches, the EEENNS algorithm uses three significant features of a vector, i.e., mean, variance, and norm, as a three-level elimination criterion to reject impossible codewords.
Furthermore, a binary search space-structured VQ (BSS-VQ) is presented in [
20] as a simple as well as efficient way to quantize line spectral frequency (LSF) coefficients in the ITU-T G.729 speech codec [
5]. This algorithm demonstrated that a significant computational load reduction is achieved with a well maintained speech quality. In view of this, this paper will apply the BSS-VQ search algorithm to the ISF coefficients quantization in AMR-WB. This work aims to verify whether the performance superiority of the BSS-VQ algorithm remains, for the reason that the VQ structure in AMR-WB is different from that in G.729. On the other hand, another major motivation behind this is to meet the energy saving requirement on handheld devices, e.g. smartphones, for an extended operation time period.
The rest of this paper is outlined as follows.
Section 2 gives the description of ISF coefficients quantization in AMR-WB. The BSS-VQ algorithm for ISF quantization is presented in
Section 3.
Section 4 demonstrates experimental results and discussions. This work is summarized at the end of this paper.
3. BSS-VQ Algorithm for ISF Quantization
The basis of the BSS-VQ algorithm is that an input vector is efficiently assigned to a subspace where a small number of codeword searches is carried out using a combination of a fast locating technique and lookup tables, as a prerequisite of a VQ codebook search. In this manner, a significant computational load reduction can be achieved.
At the start of this algorithm, each dimension is dichotomized into two subspaces, and an input vector is then assigned to a corresponding subspace according to the entries of the input vector. This idea is illustrated in the following example. There are 29 = 512 subspaces for a 9-dimensional subvector r1(n) associated with codebook CB1, and an input vector can then be assigned to one of the 512 subspaces by means of a dichotomy according to each entry of the input vector. Finally, VQ encoding is performed using a prebuilt lookup table containing the statistical information on sought codewords.
In this proposal, the lookup table in each subspace is pre-built in a way that requires lots of data for training purposes. A training as well as an encoding procedure in BSS-VQ is illustrated with the example of a 9-dimensional codebook CB1 with 256 entries in AMR-WB.
3.1. BSS Generation with Dichotomy Splitting
As a preliminary step of a training procedure, each dimension is dichotomized into two subspaces, and a dichotomy position is defined as the mean of all the codewords contained in a codebook, formulated as:
where
represents the
jth component of the
ith codeword
ci,
dp(
j) the mean value of all the
jth components. Taking the codebook CB1 as an instance,
CSize = 256,
Dim = 9. As listed in
Table 3, all the
dp(
j) values are saved and then presented in a tabular form.
Subsequently, for vector quantization on the
nth input vector
xn, a quantity
νn(
j) is defined as:
where
xn(
j) denotes the
jth component of
xn. Then
xn is assigned to subspace
k (
bssk), with
k given as the sum of
νn(
j) over the entire dimensions, formulated as:
In this study, 0 ≤ k < BSize and BSize = 29 = 512 represents the total number of subspaces. Taking an input vector xn = {20.0, 20.1, 20.2, 20.3, 20.4, 20.5, 20.6, 20.7, 20.8} as an instance, νn(j) = {20, 21, 22, 0, 0, 0, 0, 0, 28} for each j, 0 ≤ j ≤ 8, and k = 263 can be obtained by Equations (9) and (10) respectively. Thus, the input vector xn is assigned to the subspace bssk with k = 263.
By means of Equations (9) and (10), it is noted that this algorithm requires a small number of basic operations, i.e., comparison, shift and addition, such that an input vector is assigned to a subspace in a highly efficient manner.
3.2. Training Procedure of BSS-VQ
Following the determination of the dichotomy position for each dimension, a training procedure is performed to build a lookup table in each subspace. The lookup tables give the probability that each codeword serves as the best-matched codeword in each subspace, referred to as the hit probability of a codeword in a subspace for short.
A training procedure is stated below as Algorithm 1. With more than 1.56 GB of memory, a duration longer than 876 min and a total of 2,630,045 speech frames, a large speech database, covering a diversity of contents and multiple speakers, is employed as the training data in a training procedure.
| Algorithm 1: Training procedure of BSS-VQ |
- Step 1.
Initial setting: assign each codeword to all the subspaces, and then set the probability that the codeword ci corresponds to the best-matched codeword in bssk , 1 ≤ i ≤ CSize, 0 ≤ k < BSize. - Step 2.
Referencing Table 3 and through Equations (9) and (10), an input vector can be efficiently assigned to bssk. - Step 3.
A full search is conducted on all the codewords according to the Euclidean distance, given as:
and an optimal codeword copt satisfies:
- Step 4.
Update the statistics on the optimal codeword, that is, . - Step 5.
Repeat Steps 2–4, until the training is performed on all the input vectors.
|
A lookup table is built for each subspace, following the completion of a training procedure. The lookup table gives the hit probability of each codeword in a subspace. For sorting purposes, a quantity , 1 ≤ m ≤ CSize, is defined as the m ranked probability that a codeword hits the best-matched codeword in subspace bssk. Taking m = 1 as an instance, , namely, the highest hit probability in bssk. As it turns out, the lookup table in each subspace gives the ranked hit probability in descending order and the corresponding codeword.
3.3. Encoding Procedure of BSS-VQ
In the encoding procedure of BSS-VQ, the cumulative probability
is firstly defined as the sum of the top
M in
bssk, that is:
Subsequently, given a threshold of quantization accuracy (
TQA), a quantity
Mk(
TQA) represents the minimum value of
M that satisfies the condition
in
bssk, that is:
For a given
TQA, a total of 512
Mk(
TQA)s are evaluated by Equation (14) for all the subspaces, and the mean value is then given as:
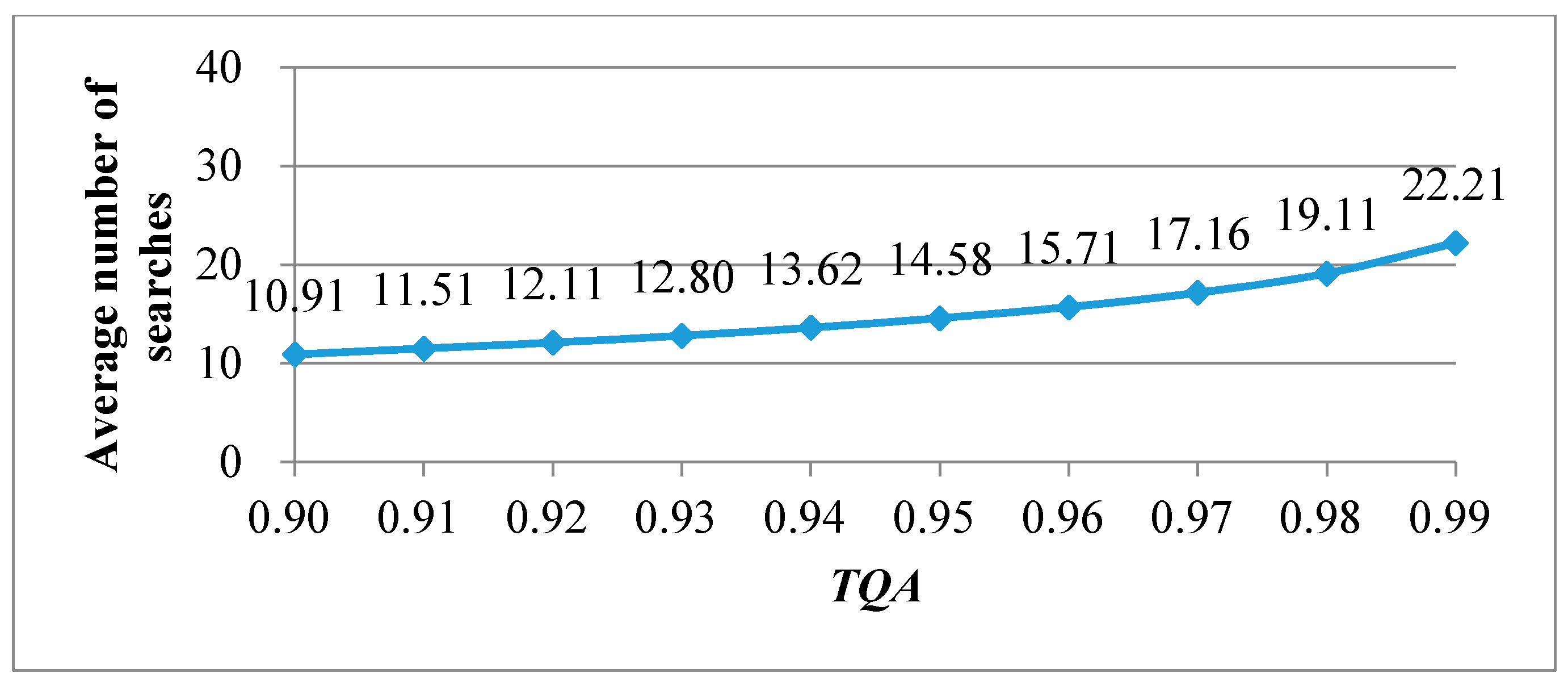
Illustrated in
Figure 1 is a plot of the average number of searches
corresponding to the values of
TQA ranging between 0.90 and 0.99. Given a
TQA = 0.95 as an instance, a mere average of 14.58 codeword searches is required to reach a search accuracy as high as 95%. In simple terms, the search performance can be significantly improved at the cost of a small drop in search accuracy. Furthermore, a trade-off can be made instantly between the quantization accuracy and the search load according to
Figure 1. Hence, a BSS-VQ encoding procedure is described below as Algorithm 2.
| Algorithm 2: Encoding procedure of BSS-VQ |
- Step 1.
Given a TQA, Mk(TQA) satisfying Equation (14) is found directly in the lookup table in bssk. - Step 2.
Referencing Table 3 and by means of Equations (9) and (10), an input vector is assigned to a subspace bssk in an efficient manner. - Step 3.
A full search for the best-matched codeword is performed on the top Mk(TQA) sorted codewords in bssk, and then the output is the index of the found codeword. - Step 4.
Repeat Steps 2 and 3 until all the input vectors are encoded.
|
The BSS-VQ algorithm is briefly summarized as follows.
Table 3 is the outcome by performing Equation (8) and is saved as the first lookup table. Subsequently, the second lookup table concerning
and the corresponding codeword is built for each subspace according to the training procedure. Accordingly, the VQ encoding can be performed using Algorithm 2.
4. Experimental Results
There are three experiments conducted in this work. The first is a search load comparison among various search approaches. The second is a quantization accuracy (QA) comparison among a full search and other search approaches. The third is a performance comparison among various approaches in terms of ITU-T P.862 perceptual evaluation of speech quality (PESQ) [
21] as an objective measure of speech quality. A speech database, completely different from all the training data, is employed for outside testing purposes. With one male and one female speaker, the speech database in total takes up more than 221 MB of memory, occupies more than 120 min, and covers 363,281 speech frames.
Firstly,
Table 4 lists a comparison on the average number of searches among full search, multiple TIE (MTIE) [
13], DI-TIE, and EEENNS, while
Table 5 gives the search load corresponding to
TQA values of the BSS-VQ algorithm. Moreover, with the search load required in the full search algorithm as a benchmark,
Table 6 and
Table 7 present comparisons on the load reduction (LR) with respect to
Table 4 and
Table 5. A high value of LR reflects a high search load reduction.
Table 6 indicates that DI-TIE provides a higher value of LR than MTIE and EEENNS search approaches among all the codebooks. It is also found that most LR values of BSS-VQ are higher than the DI-TIE approach by an observation in
Table 6 and
Table 7. For example, the LR values of BSS-VQ are indeed higher than DI-TIE in case the
TQA is equal to or smaller than 0.99, 0.98, 0.96, and 0.99 in codebooks CB1, CB2, CB21, and CB22, respectively. Accordingly, a remarkable search load reduction is reached by the BSS-VQ search algorithm.
In the QA aspect, a 100% QA is obtained by the MTIE, DI-TIE, and EEENNS algorithms as compared with a full search approach. Thus, only the QA experiment of BSS-VQ is conducted. The QA corresponding to
TQA values of the BSS-VQ algorithm is given in
Table 8. It reveals that QA is an approximation of
TQA in either inside or outside testing cases. Moreover, this algorithm provides an LR between 77.78% and 93.98% at
TQA = 0.90 as well as an LR between 67.23% and 88.39% at
TQA = 0.99, depending on the codebooks. In other words, a trade-off can be made between the quantization accuracy and the search load.
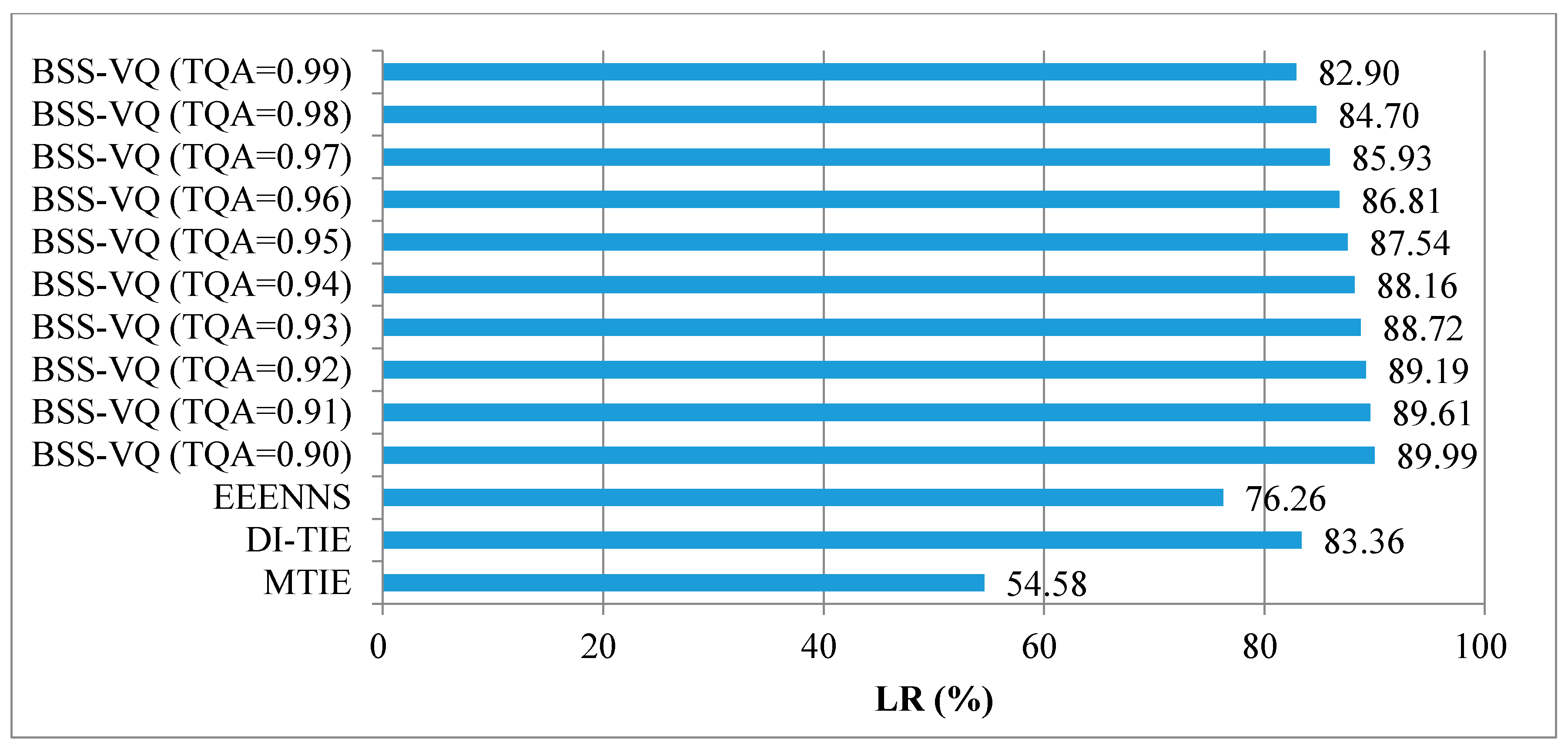
Furthermore, an overall LR is evaluated to observe the total search load of an entire VQ encoding procedure of an input vector. The overall LR refers to the total search load, defined as the sum of the average number of searches multiplied by the vector dimension in each codebook. Thus, an overall LR comparison with the full search as a benchmark is presented as a bar graph in
Figure 2. As clearly indicated in
Figure 2, the overall LR of BSS-VQ is higher than MTIE, DI-TIE, and EEENNS approaches, but at the same time the QA is as high as 0.98. Moreover,
Table 9 gives a PESQ comparison, including the mean and the STD, among various approaches. Since MTIE, DI-TIE, and EEENNS provide a 100% QA, they both share the same PESQ with a full search, meaning that there is no deterioration in the speech quality. A close observation reveals little difference between PESQs obtained in a full search and in this search algorithm, that is, the speech quality is well maintained in BSS-VQ at
TQA not less than 0.90. This BSS-VQ search algorithm is experimentally validated as a superior candidate relative to its counterparts.
5. Conclusions
This paper presents a BSS-VQ codebook search algorithm for ISF vector quantization in the AMR-WB speech codec. Using a combination of a fast locating technique and lookup tables, an input vector is efficiently assigned to a search subspace where a small number of codeword searches is carried out and the aim of remarkable search load reduction is reached consequently. Particularly, a trade-off can be made between the quantization accuracy and the search load to meet a user’s need when performing a VQ encoding. This BSS-VQ search algorithm, providing a considerable search load reduction as well as nearly lossless speech quality, is experimentally validated as superior to MTIE, DI-TIE, and EEENNS approaches. Furthermore, this improved AMR-WB speech codec can be adopted to upgrade the VoIP performance on a smartphone. As a consequence, the energy efficiency requirement is achieved for an extended operation time period due to computational load reduction.