Experimental Tests on a Small-Scale Model of a Mine Stope to Study the Behavior of Waste Rock Barricades during Backfilling
Abstract
:1. Introduction
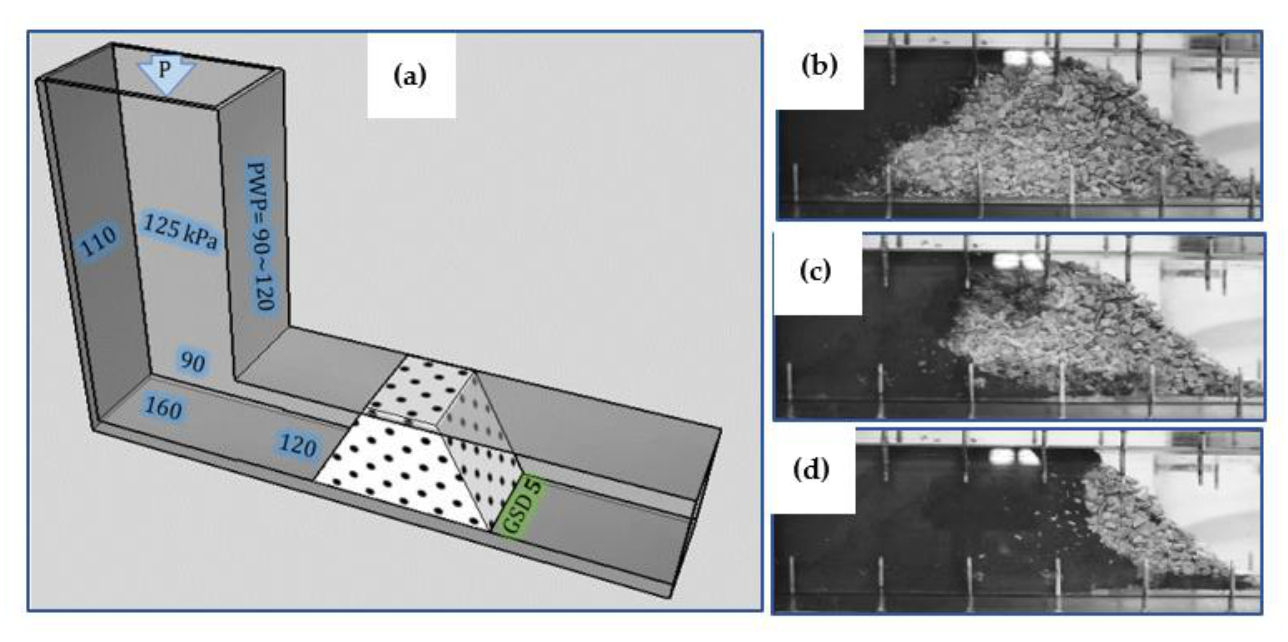
2. Small-Scale Model and Equipment Description
3. Material Characteristics
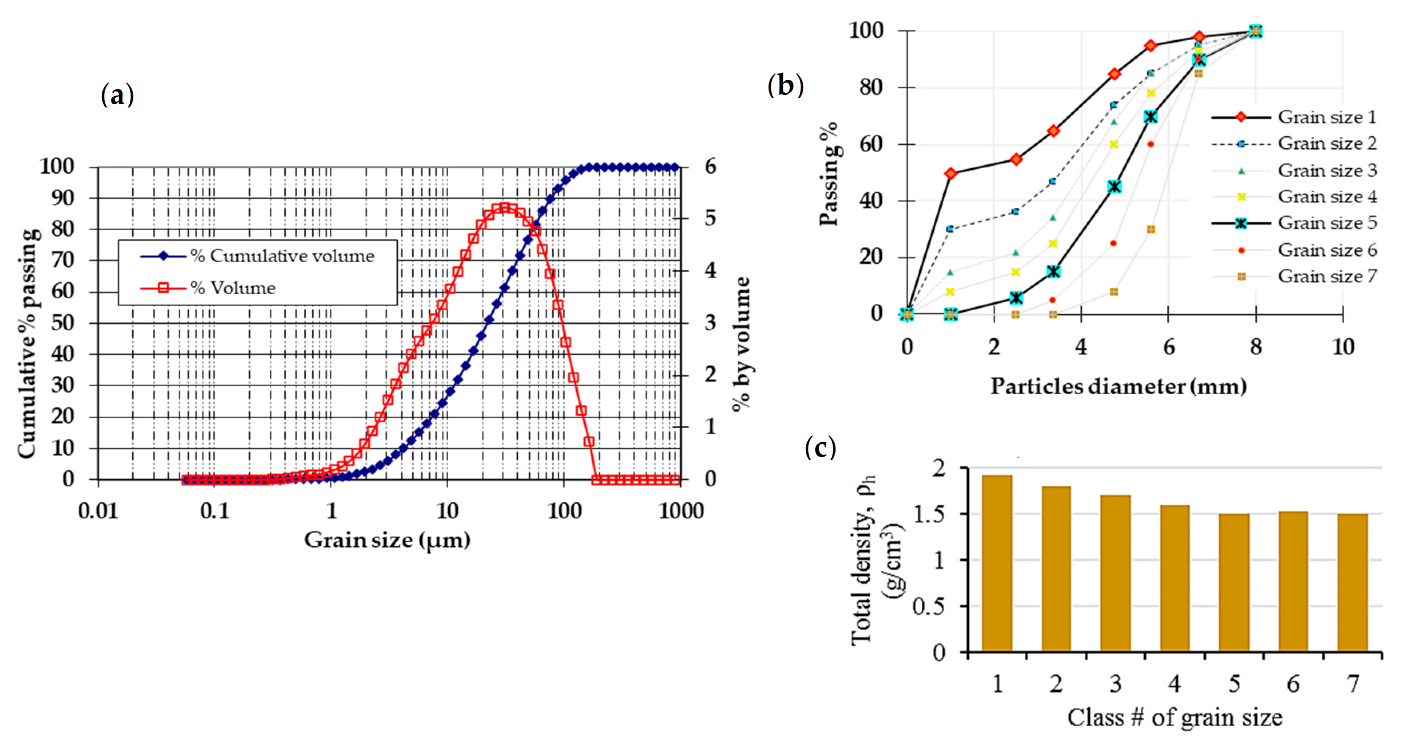
3.1. Mine Tailings
3.2. Waste Rock Barricade
4. Experimental Setup and Program
4.1. Setting Up the Waste Rock Barricade
4.2. CPB Mix Design and Preparation
4.3. Experimental Program
5. Results
5.1. Stress State after the CPB Placement in the Small-Scale Model
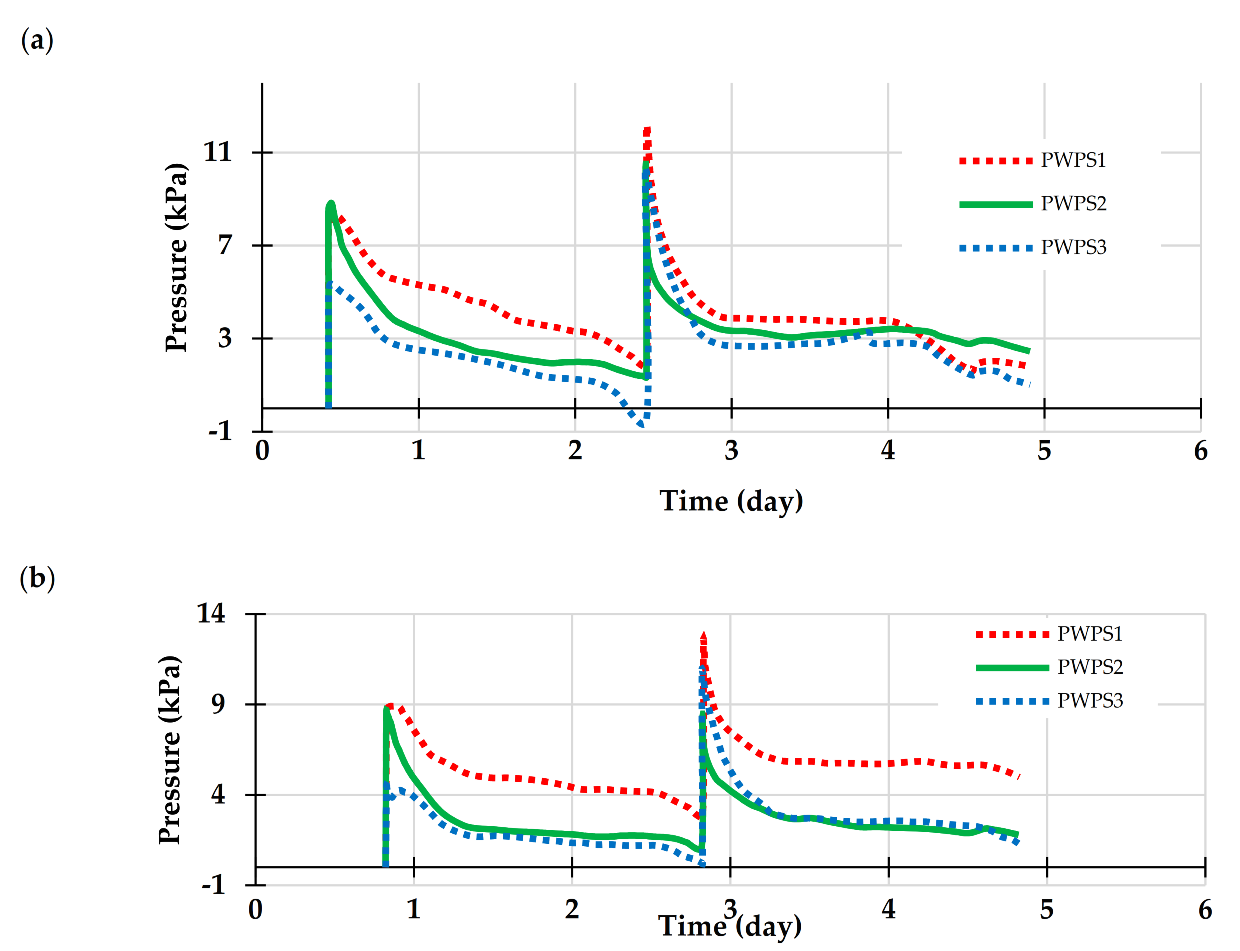
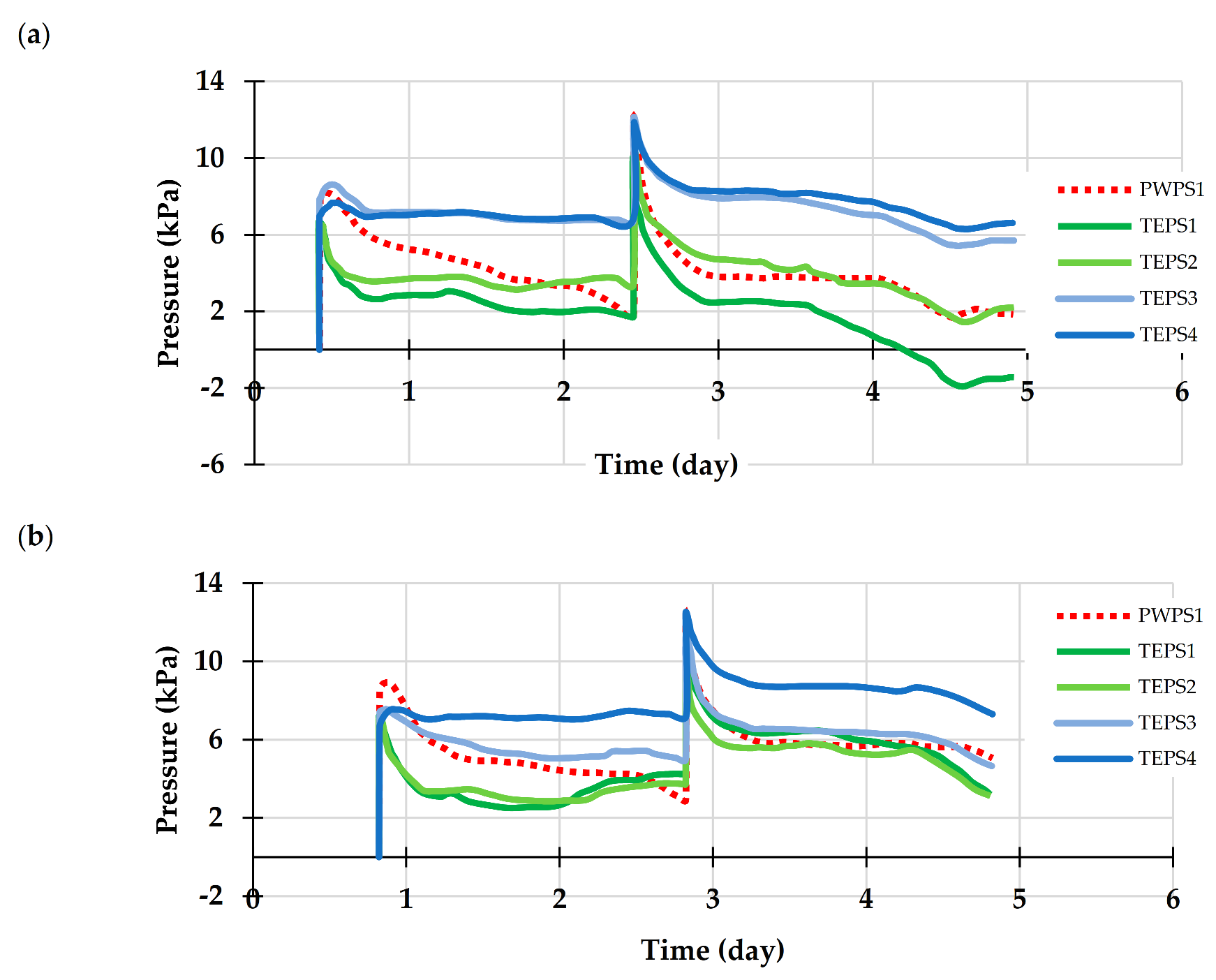
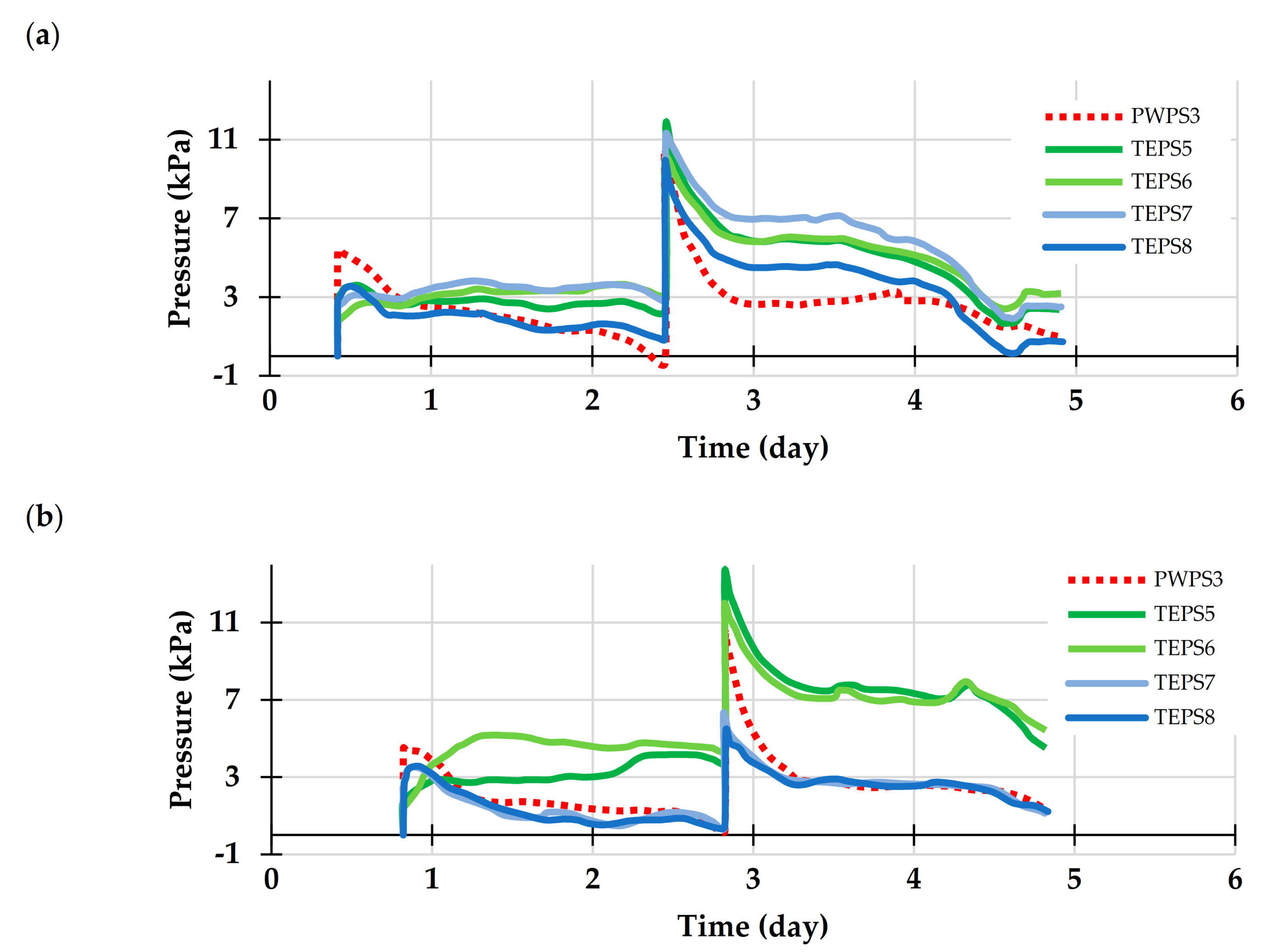
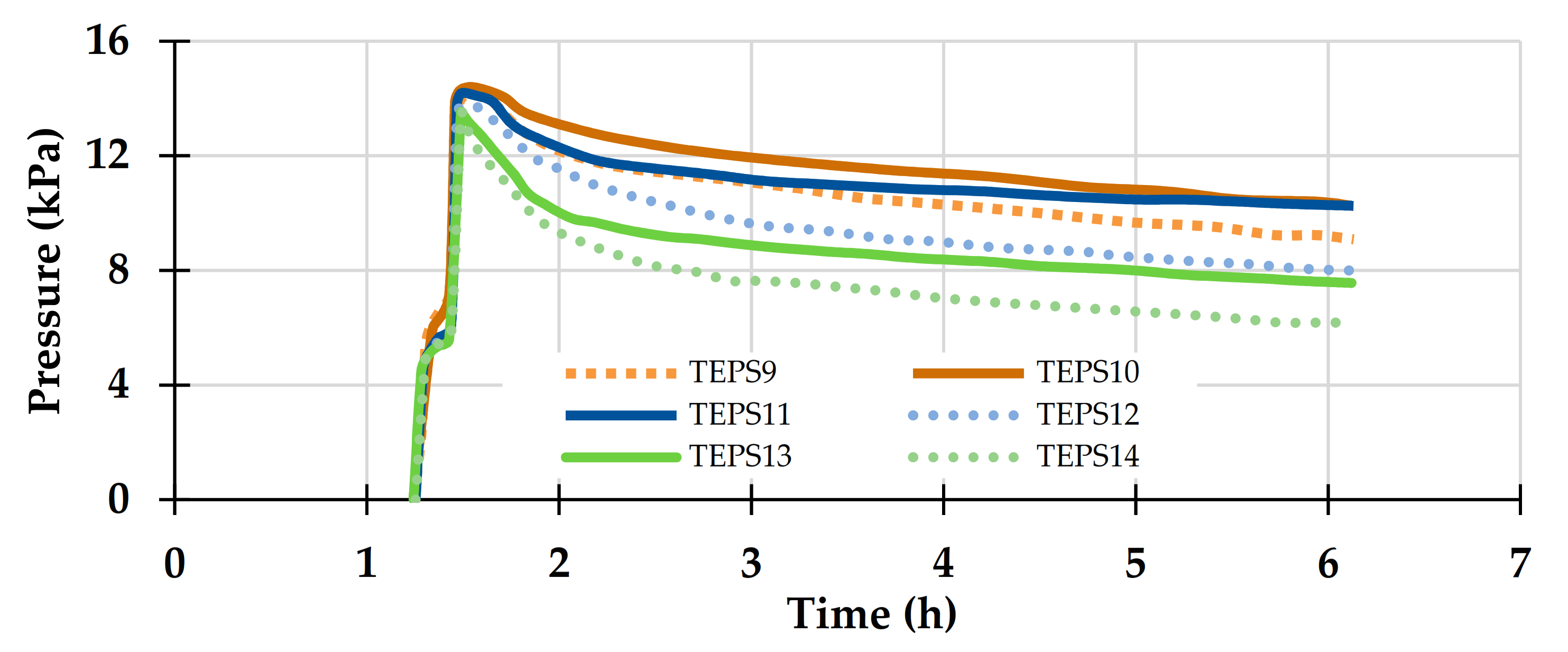
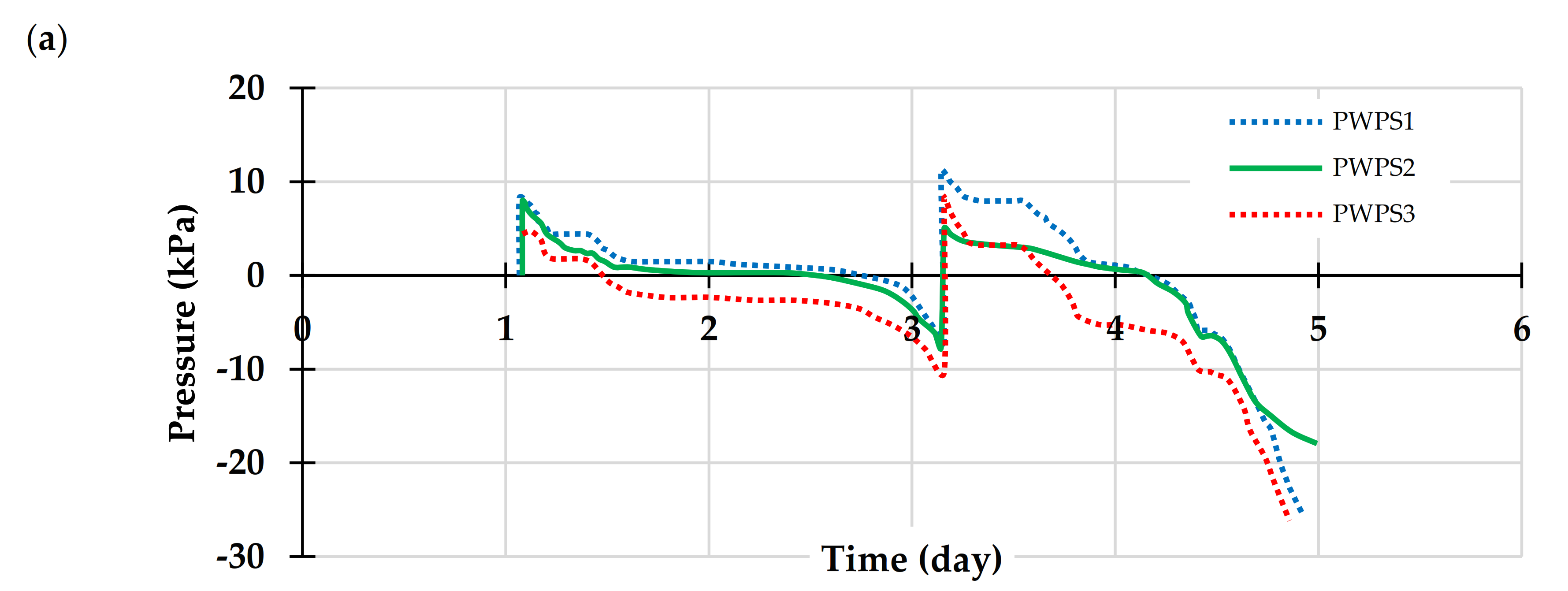
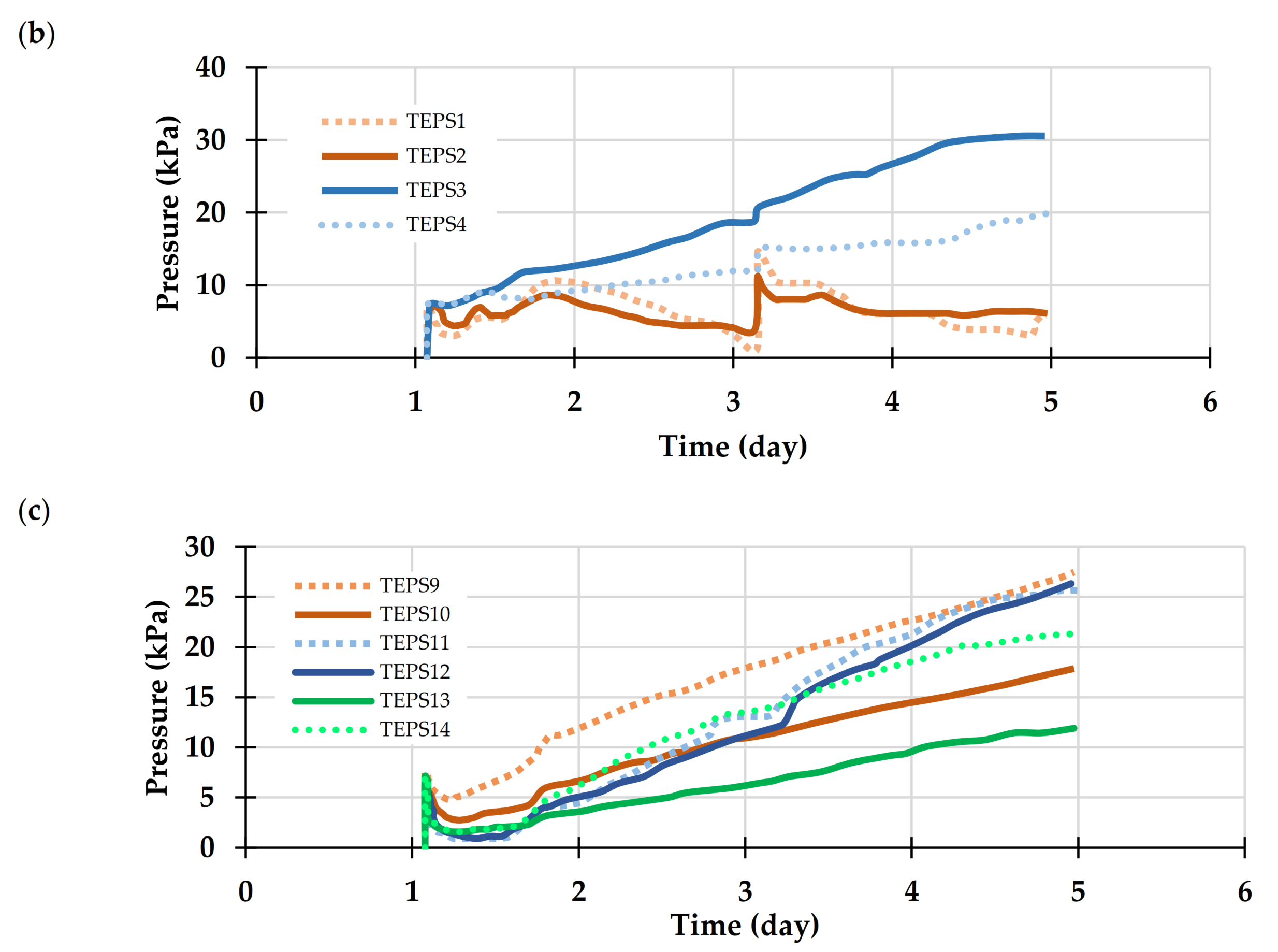
5.1.1. Uncemented Backfill
5.1.2. Cemented Backfill
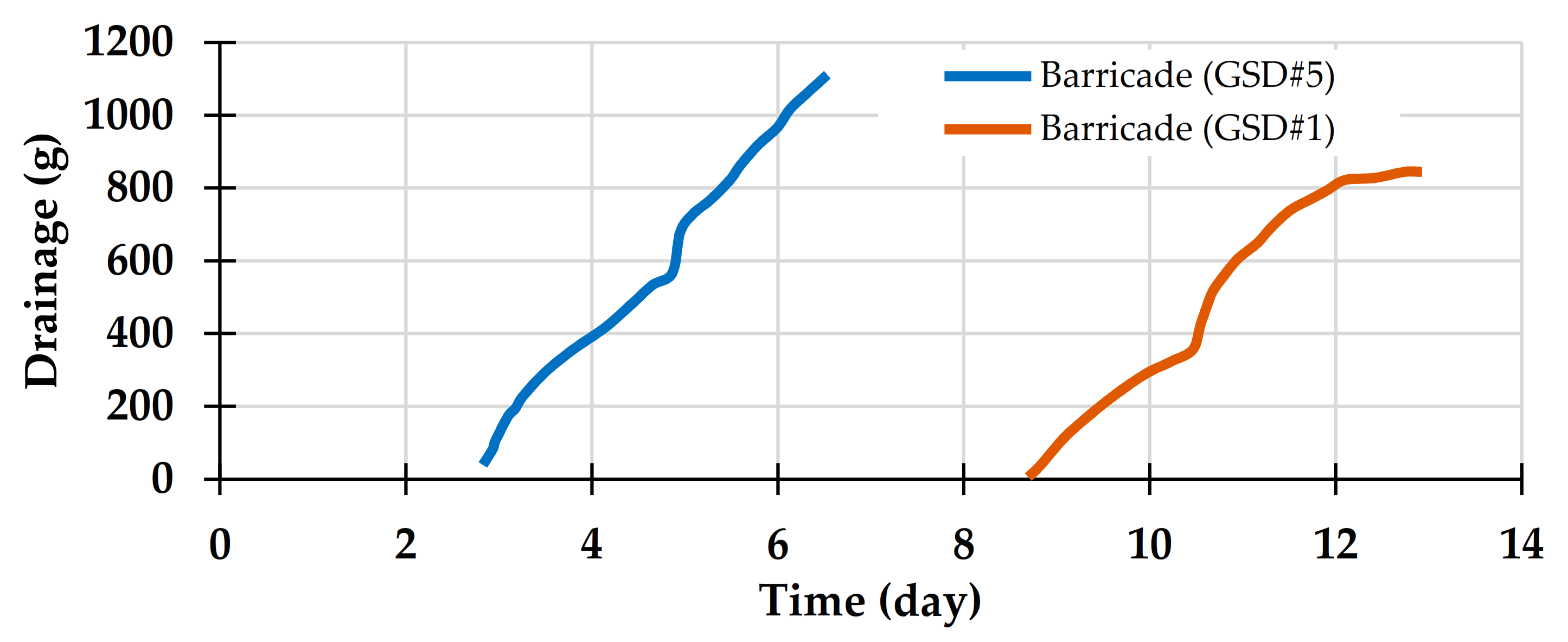
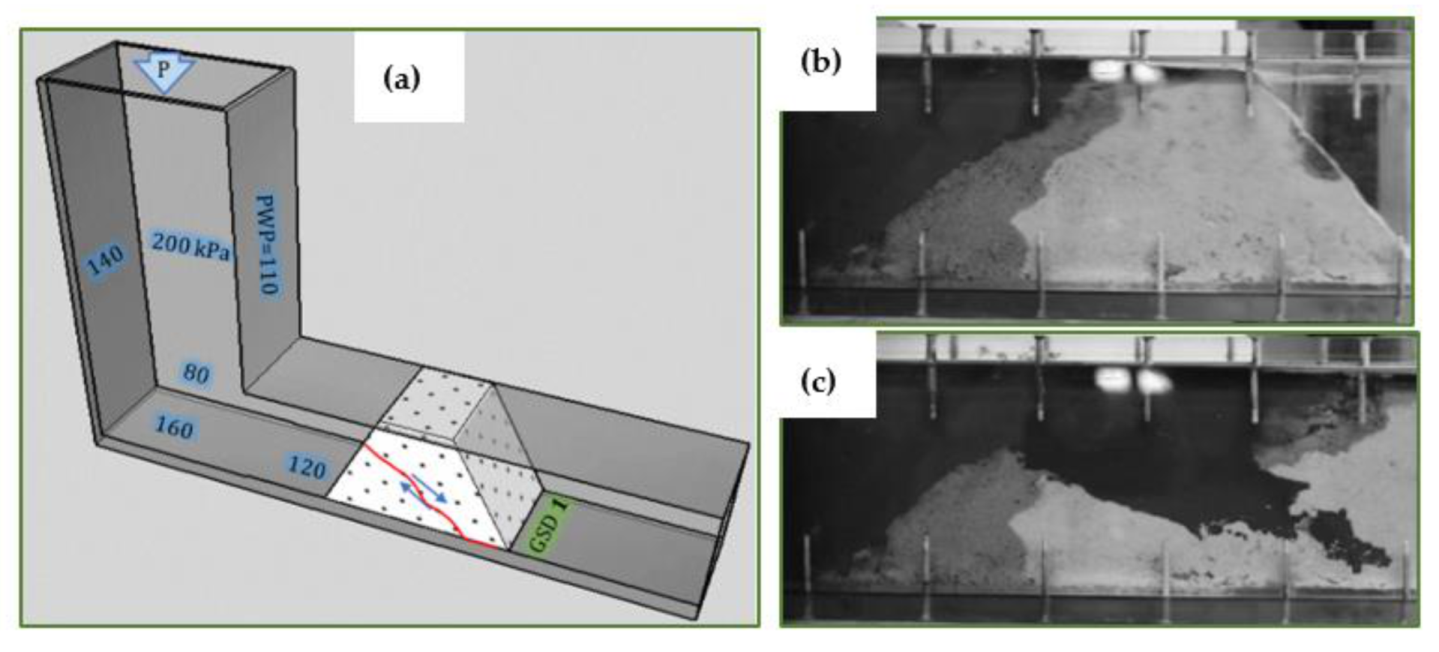
5.2. Stability and Failure Mechanism of the Waste Rock Barricades
6. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Pressure Sensors’ Calibration Using Water
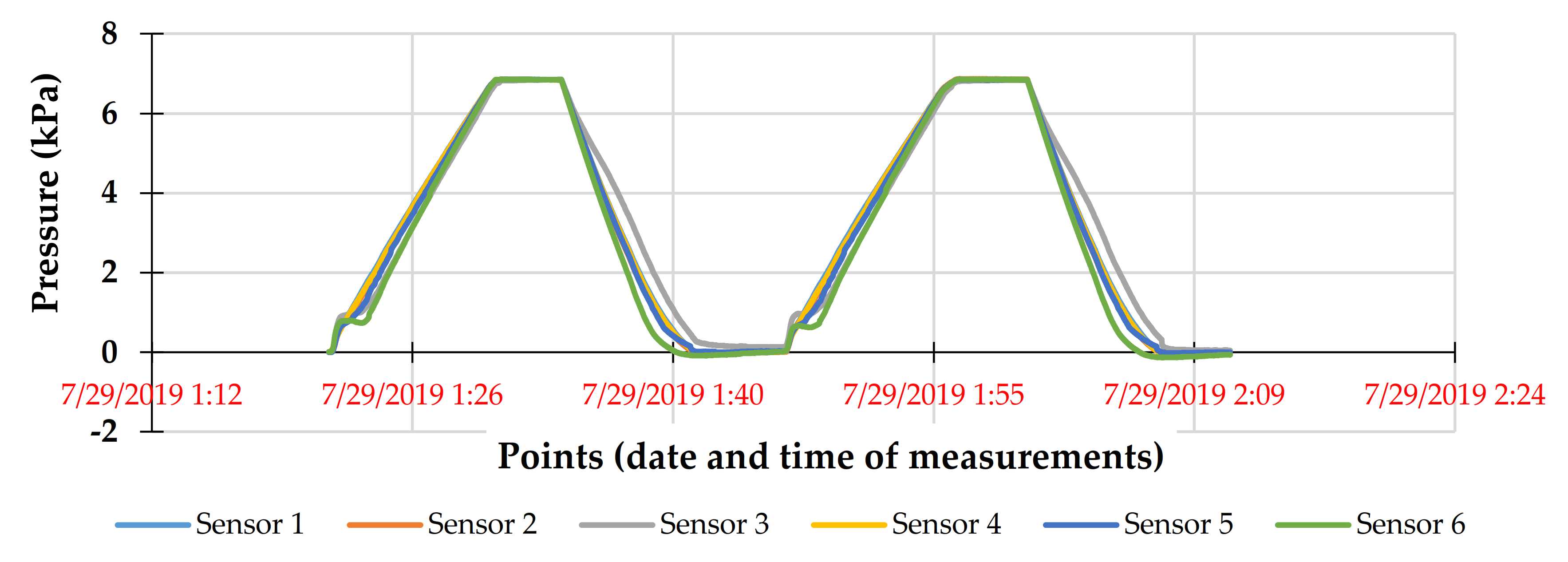

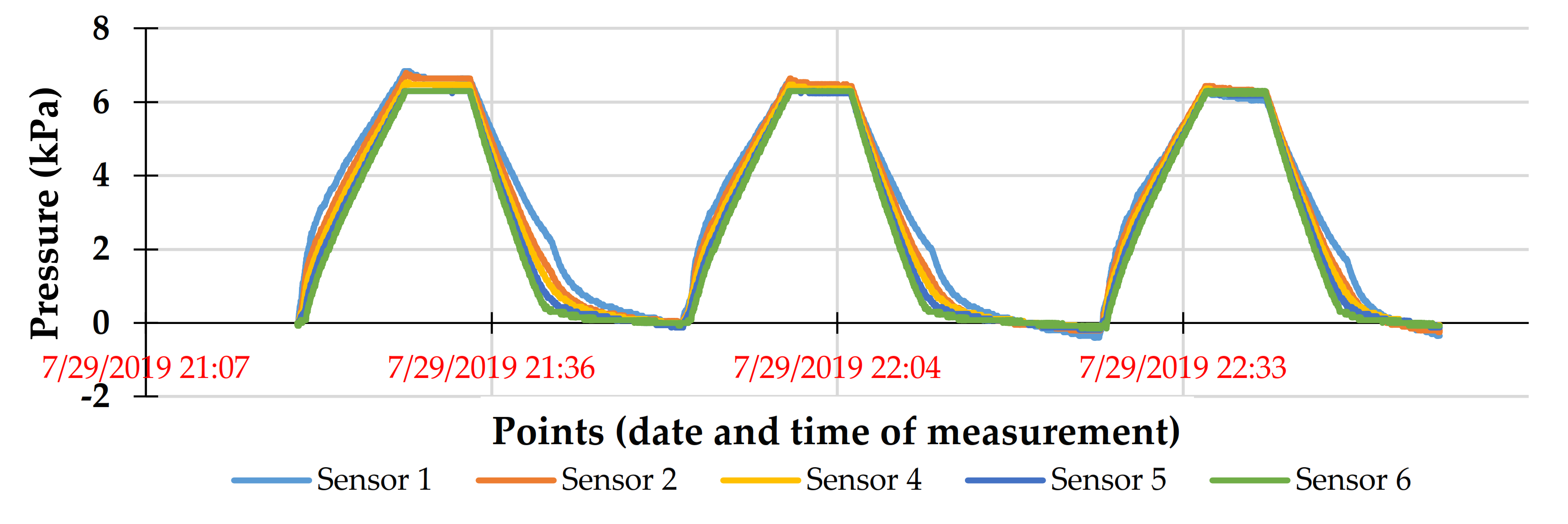
Appendix B. Cemented Paste Backfill Preparation
References
- Thomas, E.G. Fill Technology in Underground Metalliferous Mines; University of British Columbia, Department of Mineral Engineering: Vancouver, BC, Canada, 1979. [Google Scholar]
- Hassani, F.; Archibald, J. Mine Backfill [CD-ROM]; Canadian Institute of Mining, Metallurgy, and Petroleum: Montreal, QC, Canada, 1998. [Google Scholar]
- Potvin, Y.; Thomas, E.; Fourie, A. Handbook on Mine Fill; Australian Centre for Geomechanics: Crawley, Australia, 2005. [Google Scholar]
- Belem, T.; Benzaazoua, M. Design and application of underground mine paste backfill technology. Geotech. Geol. Eng. 2008, 26, 147–174. [Google Scholar] [CrossRef]
- Benzaazoua, M.; Fall, M.; Belem, T. A contribution to understanding the hardening process of cemented pastefill. Miner. Eng. 2004, 17, 141–152. [Google Scholar] [CrossRef]
- Henderson, A.; Revell, M. Basic mine fill materials. In Handbook of Mine Fill; Potvin, Y., Thomas, E.D., Fourie, A., Eds.; Australian Centre for Geomechanics: Perth, Australia, 2005; pp. 13–20. [Google Scholar]
- Belem, T.; Benzaazoua, M.; Bussière, B. Mechanical behaviour of cemented paste backfill. In Proceedings of the 53rd Annual Conference of the Canadian Geotechnical Society, Montréal, QC, Canada, 15–18 October 2000. [Google Scholar]
- Walske, M.L.; McWilliam, H.; Doherty, J.; Fourie, A. Influence of curing temperature and stress conditions on mechanical properties of cementing paste backfill. Can. Geotech. J. 2015, 53, 148–161. [Google Scholar] [CrossRef]
- Sivakugan, N.; Veenstra, R.; Naguleswaran, N. Underground mine backfilling in Australia using paste fills and hydraulic fills. Int. J. Geosynth. Ground Eng. 2015, 1, 18. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Cao, P.; Tian, M. Strength development and microstructure evolution of cemented tailings backfill containing different binder types and contents. Minerals 2018, 8, 167. [Google Scholar] [CrossRef] [Green Version]
- Belem, T.; Mbonimpa, M.; Li, L. Lecture notes GNM1002 Mine Backfill; Université du Québec à en Abitibi-Témiscamingue: Rouyn-Noranda, QC, Canada, 2018. [Google Scholar]
- Yilmaz, E. Investigating the Hydrogeotechnical and Microstructural Properties of Cemented Paste Backfill Using the Cuaps Apparatus. Ph.D. Thesis, Université du Québec à en Abitibi-Témiscamingue, Rouyn-Noranda, QC, Canada, 2010. [Google Scholar]
- Benzaazoua, M.; Belem, T.; Bussière, B. Chemical aspect of sulfurous paste backfill mixtures. Cem. Concr. 2002, 32, 1133–1144. [Google Scholar] [CrossRef]
- Mitchell, R.J.; Olsen, R.S.; Smith, J.D. Model studies on cemented tailings used in mine backfill. Can. Geotech. J. 1982, 19, 14–28. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. Limit equilibrium analysis for the design of backfilled stope barricades made of waste rock. Can. Geotech. J. 2011, 48, 1713–1728. [Google Scholar] [CrossRef]
- Yang, P.; Li, L.; Aubertin, M.; Brochu-Baekelmans, M.; Ouellet, S. Stability analyses of waste rock barricades designed to retain paste backfill. Int. J. Geomech. 2016, 17, 04016079. [Google Scholar] [CrossRef]
- Zheng, J.; Li, L. Experimental study of the “short-term” pressures of uncemented paste backfill with different solid contents for barricade design. J. Clean. Prod. 2020, 275, 123068. [Google Scholar] [CrossRef]
- Belem, T.; El Aatar, O.; Bussière, B.; Benzaazoua, M. Gravity-driven 1-D consolidation of cemented paste backfill in 3-m-high columns. Innov. Infrastruct. Solut. 2016, 1, 37. [Google Scholar] [CrossRef] [Green Version]
- Belem, T.; Harvey, A.; Simon, R.; Aubertin, M. Measurement and prediction of internal stresses in an underground opening during its filling with cemented fill. In Proceedings of the Fifth International Symposium on Ground Support in Mining and Underground Construction, Perth, Australia, 28–30 September 2004; Tayler & Francis Group: London, UK, 2009; pp. 619–630. [Google Scholar]
- Li, L. Vers une Conception de Barricades plus Sécuritaire dans les Mines: Étude de L’interaction Entre le Remblai et les Structures Encaissantes; Institut de Recherche Robert-Sauvé en Santé et en Sécurité du Travail: Montreal, QC, Canada, 2019. [Google Scholar]
- Belem, T.; Benzaazoua, M. An overview on the use of paste backfill technology as a ground support method in cut-and-fill mines. In Ground Support in Mining and Underground Construction: Proceedings of the Fifth International Symposium on Ground Support, Perth, Australia, 28–30 September 2004; Villaescusa, E., Potvin, Y., Eds.; CRC Press: Leiden, The Netherlands, 2004; pp. 637–650. [Google Scholar]
- le Roux, K.; Bawden, W.F.; Grabinsky, M.F. Field properties of cemented paste backfill at the Golden Giant mine. Min. Technol. 2005, 114, 65–80. [Google Scholar] [CrossRef]
- Thompson, B.D.; Grabinsky, M.; Bawden, W.; Counter, D. In-situ measurements of cemented paste backfill in long-hole stopes. In Proceedings of the ROCKENG09: Proceedings of the 3rd CANUS Rock Mechanics Symposium, Toronto, ON, Canada, 9–15 May 2009; p. 199. [Google Scholar]
- Helinski, M.; Fahey, M.; Fourie, A. Behavior of cemented paste backfill in two mine stopes: Measurements and modeling. J. Geotech. Geoenviron. Eng. 2010, 137, 171–182. [Google Scholar] [CrossRef]
- Thompson, B.; Bawden, W.; Grabinsky, M. In situ measurements of cemented paste backfill at the Cayeli Mine. Can. Geotech. J. 2012, 49, 755–772. [Google Scholar] [CrossRef]
- Hasan, A.; Suazo, G.; Doherty, J.; Fourie, A. In situ measurements of cemented paste backfilling in an operating stope at Lanfranchi Mine. In Proceedings of the 11th International Symposium on Mining Backfill, Perth, Australia, 20–22 May 2014; pp. 327–336. [Google Scholar]
- Sivakugan, N.; Widisinghe, S. Stresses within granular materials contained between vertical walls. Indian Geotech. J. 2013, 43, 30–38. [Google Scholar] [CrossRef]
- Widisinghe, S.; Sivakugan, N.; Wang, V.Z. Laboratory investigations of arching in backfilled mine stopes. In Proceedings of the 18th Southeast Asian Geotechnical Conference (18SEAGC) & Inaugural AGSSEA Conference (1AGSSEA), Singapore, 29—31 May 2013. [Google Scholar]
- Widisinghe, S.; Sivakugan, N.; Wang, V. Loads on barricades in hydraulically backfilled underground mine stopes. In Proceedings of the Eleventh International Symposium on Mining with Backfill, Perth, Australia, 20–22 May 2014. [Google Scholar]
- Widisinghe, S.D. Stress Developments within a Backfilled Mine Stope and the Lateral Loading on the Barricade. Ph.D. Thesis, James Cook University, Townsville, Australia, 2014. [Google Scholar]
- Li, L.; Aubertin, M.; Simon, R.; Bussière, B.; Belem, T. Modeling arching effects in narrow backfilled stopes with FLAC. In Proceedings of the 3rd International Symposium on FLAC & FLAC 3D Numerical Modelling in Geomechanics, Sudbury, ON, Canada, 21–24 October 2003; pp. 211–219. [Google Scholar]
- Li, L.; Aubertin, M.; Shirazi, A.; Belem, T.; Simon, R. Stress distribution in inclined backfilled stopes. In Proceedings of the 9th International Symposium in Mining with Backfill, Montreal, QC, Canada, 29 April–2 May 2007. [Google Scholar]
- Pirapakaran, K.; Sivakugan, N. Arching within hydraulic fill stopes. Geotech. Geol. Eng. 2007, 25, 25–35. [Google Scholar] [CrossRef]
- Hassani, F.; Mortazavi, A.; Shabani, M. An investigation of mechanisms involved in backfill-rock mass behaviour in narrow vein mining. J. South. Afr. Inst. Min. Metall. 2008, 108, 463–472. [Google Scholar]
- Li, L.; Aubertin, M. An improved analytical solution to estimate the stress state in subvertical backfilled stopes. Can. Geotech. J. 2008, 45, 1487–1496. [Google Scholar] [CrossRef]
- Fahey, M.; Helinski, M.; Fourie, A. Some aspects of the mechanics of arching in backfilled stopes. Can. Geotech. J. 2009, 46, 1322–1336. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. Numerical investigation of the stress state in inclined backfilled stopes. Int. J. Geomech. 2009, 9, 52–62. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. Horizontal pressure on barricades for backfilled stopes. Part I: Fully drained conditions. Can. Geotech. J. 2009, 46, 37–46. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. Influence of water pressure on the stress state in stopes with cohesionless backfill. Geotech. Geol. Eng. 2009, 27, 1. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. Horizontal pressure on barricades for backfilled stopes. Part II: Submerged conditions. Can. Geotech. J. 2009, 46, 47–56. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. A three-dimensional analysis of the total and effective stresses in submerged backfilled stopes. Geotech. Geol. Eng. 2009, 27, 559–569. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. An analytical solution for the nonlinear distribution of effective and total stresses in vertical backfilled stopes. Geomech. Geoengin. 2010, 5, 237–245. [Google Scholar] [CrossRef]
- El Mkadmi, N. Simulations du Comportement Géotechnique des Remblais dans les Chantiers Miniers: Effets du Drainage et de la Consolidation. Master’s Thesis, Ecole Polytechnique, Montreal, QC, Canada, 2012. [Google Scholar]
- Veenstra, R.L. A design procedure for determining the in situ stresses of early age cemented paste backfill. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]
- Emad, M.Z.; Mitri, H.; Kelly, C. Effect of blast-induced vibrations on fill failure in vertical block mining with delayed backfill. Can. Geotech. J. 2014, 51, 975–983. [Google Scholar] [CrossRef]
- Falaknaz, N. Analysis of the Geomechanical Behavior of Two Adjacent Backfilled Stopes Based on Two and Three Dimensional Numerical Simulations. Ph.D. Thesis, École Polytechnique de Montréal, Montreal, QC, Canada, 2014. [Google Scholar]
- Yang, P. Investigation of the Geomechanical Behavior of Mine Backfill and Its Interaction with Rock Walls and Barricades. Ph.D. Thesis, École Polytechnique de Montréal, Montreal, QC, Canada, 2016. [Google Scholar]
- Lu, H.; Qi, C.; Li, C.; Gan, D.; Du, Y.; Li, S. A light barricade for tailings recycling as cemented paste backfill. J. Clean. Prod. 2020, 247, 119388. [Google Scholar] [CrossRef]
- Suazo, G.; Villavicencio, G. Numerical simulation of the blast response of cemented paste backfilled stopes. Comput. Geotech. 2018, 100, 1–14. [Google Scholar] [CrossRef]
- Cui, L.; Fall, M. Modeling of pressure on retaining structures for underground fill mass. Tunn. Undergr. Space Technol. 2017, 69, 94–107. [Google Scholar] [CrossRef]
- Doherty, J.P. A numerical study into factors affecting stress and pore pressure in free draining mine stopes. Comput. Geotech. 2015, 63, 331–341. [Google Scholar] [CrossRef]
- Pengyu, Y.; Li, L. Investigation of the short-term stress distribution in stopes and drifts backfilled with cemented paste backfill. Int. J. Min. Sci. Technol. 2015, 25, 721–728. [Google Scholar] [CrossRef]
- Corté, J. Model testing-Geotechnical model test. General Report. In Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering, Rio De Janeiro, Brazil, 13–18 August 1989; pp. 2553–2571. [Google Scholar]
- Niemann, H. L’analyse dimensionnelle et son application aux lois de similitude. Modèles Réduits Génie 1995, 155, 3–20. [Google Scholar]
- Garnier, J. Validation des modèles physiques et numériques: Problème des effets d’échelle. In Proceedings of the Compte-Rendus du 14eme Conférence International de Mécanique des Sols et des Travaux de Fondations, Hambourg, Germany, 6–12 September 1997; pp. 659–662. [Google Scholar]
- Garnier, J. Modèles physiques en géotechnique: Etat des connaissance et évolutions récentes. In Proceedings of the 1ère Biennale Coulomb, Paris, France, 3–5 October 2001; p. 67. [Google Scholar]
- Gade, V.K.; Dasaka, S. Calibration of earth pressure sensors. Indian Geotech. J. 2018, 48, 142–152. [Google Scholar] [CrossRef]
- McLemore, V.T.; Fakhimi, A.; van Zyl, D.; Ayakwah, G.F.; Anim, K.; Boakye, K.; Ennin, F.; Felli, P.; Fredlund, D.; Gutierrez, L.A. Literature review of other rock piles: Characterization, weathering, and stability. Questa Rock Pile Weather. Stab. Proj. New Mex. Bur. Geol. Miner. Resour. Rep. 2009, 517, 101. [Google Scholar]
- Barbour, S.; Hendry, M.; Smith, J.; Beckie, R.; Wilson, G. A Research Partnership Program in the Mining Industry for Waste Rock Hydrology; University of Saskatchewan: Saskatoon, SK, Canada, 2001. [Google Scholar]
- Aubertin, M.; Bussière, B.; Bernier, L.; Chapuis, R.; Julien, M.; Belem, T.; Simon, R.; Mbonimpa, M.; Benzaazoua, M.; Li, L. La gestion des rejets miniers dans un contexte de développement durable et de protection de l’environnement. In Proceedings of the Congrès annuel de la société canadienne de génie civil, Montréal, QC, Canada, 5–8 June 2002. [Google Scholar]
- Aubertin, M. Waste rock disposal to improve the geotechnical and geochemical stability of piles. In 23rd World Mining Congress; X-CD Technologies Inc.: Montreal, QC, Canada, 2013. [Google Scholar]
- Maknoon, M. Slope Stability Analyses of Waste Rock Piles Under Unsaturated Conditions Following Large Precipitations. Ph.D. Thesis, École Polytechnique de Montréal, Montreal, QC, Canada, 2016. [Google Scholar]
- Gélinas, L.-P. Caractérisation des propriétés géomécaniques des barricades rocheuses et des chantiers miniers remblayés en vue de leur analyse de stabilité. Master’s Thesis, Université du Québec en Abitibi-Témiscamingue, Rouyn-Noranda, QC, Canada, 2017. [Google Scholar]

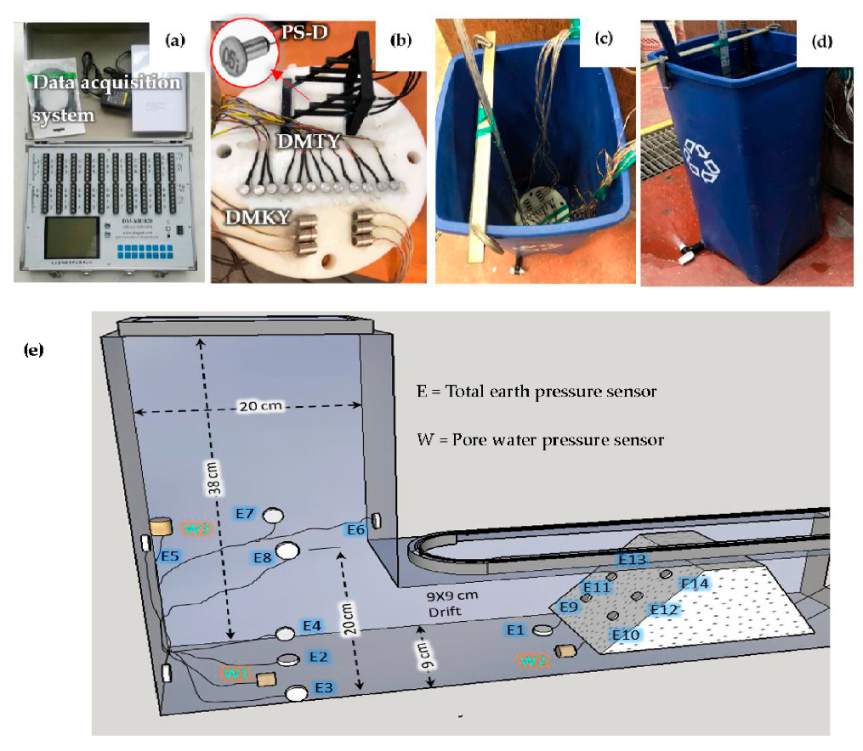






| Sensor | Total Earth Pressure (TEP) Sensors | Pore Water Pressure (PWP) Sensor | |
|---|---|---|---|
| Manufacture (brand) | KYOWA | Dan street Nanjing Electronic Technology Co., | |
| Model Type | PS-D | DMTY | DMKY |
| Capacity | 50 kPa | 100 kPa | 100 kPa |
| Size | 6 × 0.6 | 12 × 4.2 mm | 15.8 × 21 mm |
| Rated Output | 500 × 10−6 strain | 400 × 10−6 strain | 400 × 10−6 strain |
| Overload | 150% | 120% | 120% |
| Input/output resistance | 350 Ω | 350 Ω | 10,000 Ω |
| Exciting voltage | 2 V | 2 V | 2 V |
| Physical Characteristics | Mineralogical Analysis Semi-Quantitative Mineralogical Analysis by X-ray Diffraction | ||
|---|---|---|---|
| Parameter (Units) | Values | Mineral | Values |
| Specific gravity, Gs Ultrafine content P20µm (%) D10, effective particle size (µm) D30, size of 30 % passing (µm) D50, average particle size (µm) D60, size of 60 % passing (µm) D90, size of 90 % passing (µm) CU = D60/D10, coefficient of uniformity CC = D302/(D60 × D10), coefficient of curvature Unified Soil Classification System (USCS) | 3.32 46% 4.16 11.25 21.75 29.18 76.35 7.02 1.04 ML (low plastic silt) | Quartz Pyrite Chamosite 1M Paragonite 1M Albite Muscovite 2M 1 Orthoclase Labradorite An65 Microcline Chalcopyrite Sphalerite Gypsum | 44.84% 25.73% 4.38% 2.98% 2.10% 9.61% 1.56% 3.09% 3.66% 0.45% 0.16% 1.45% |
| Total sulfur analysis and carbon by induction furnace | |||
| Ctotal % p/p (method detection limit, MDL = 0.05) | 0.256 | Stotal % p/p (MDL = 0.009) | 15.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nujaim, M.; Belem, T.; Giraud, A. Experimental Tests on a Small-Scale Model of a Mine Stope to Study the Behavior of Waste Rock Barricades during Backfilling. Minerals 2020, 10, 941. https://doi.org/10.3390/min10110941
Nujaim M, Belem T, Giraud A. Experimental Tests on a Small-Scale Model of a Mine Stope to Study the Behavior of Waste Rock Barricades during Backfilling. Minerals. 2020; 10(11):941. https://doi.org/10.3390/min10110941
Chicago/Turabian StyleNujaim, Mutaz, Tikou Belem, and Albert Giraud. 2020. "Experimental Tests on a Small-Scale Model of a Mine Stope to Study the Behavior of Waste Rock Barricades during Backfilling" Minerals 10, no. 11: 941. https://doi.org/10.3390/min10110941







