Three-Dimensional Prediction and Evaluation of Baiyanghe Uranium Deposit in the Xuemistan Volcanic Belt, Xinjiang
Abstract
:1. Introduction
2. Geological Background of the Study Area
3. 3D Metallogenic Prediction
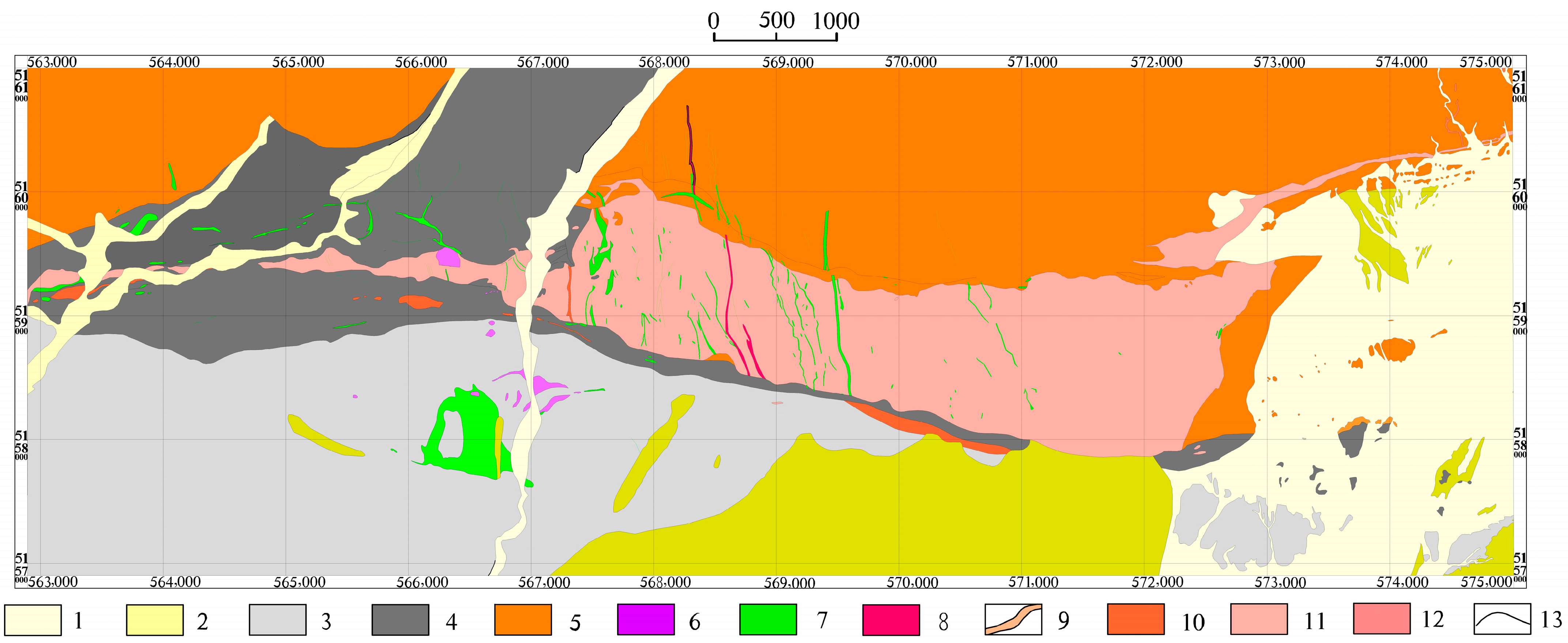
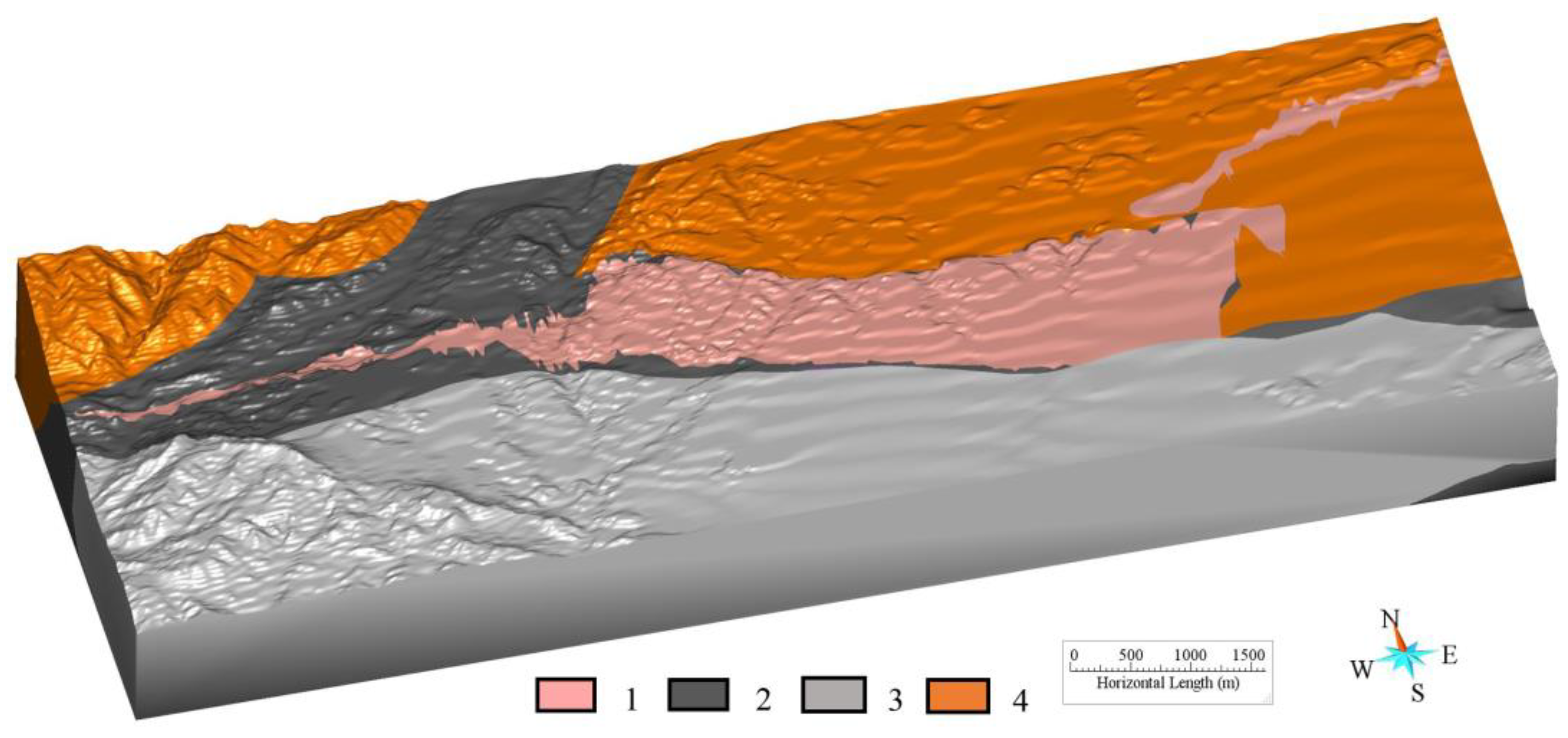
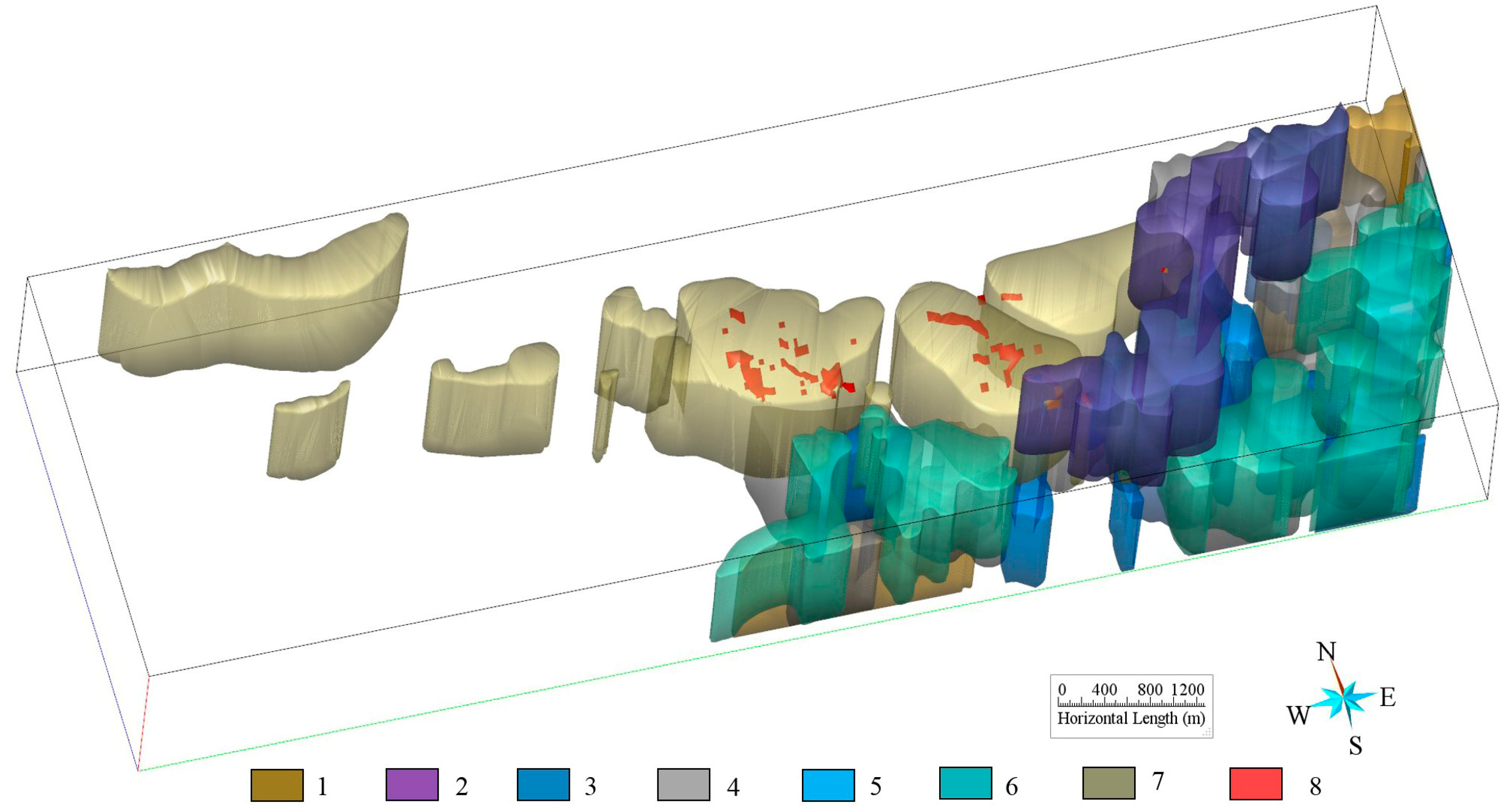
3.1. 3D Geologic Modeling
3.2. Extraction of Favorable Metallogenic Information
3.2.1. Extraction of Information from Ore-Controlling Geologic Elements
- (1)
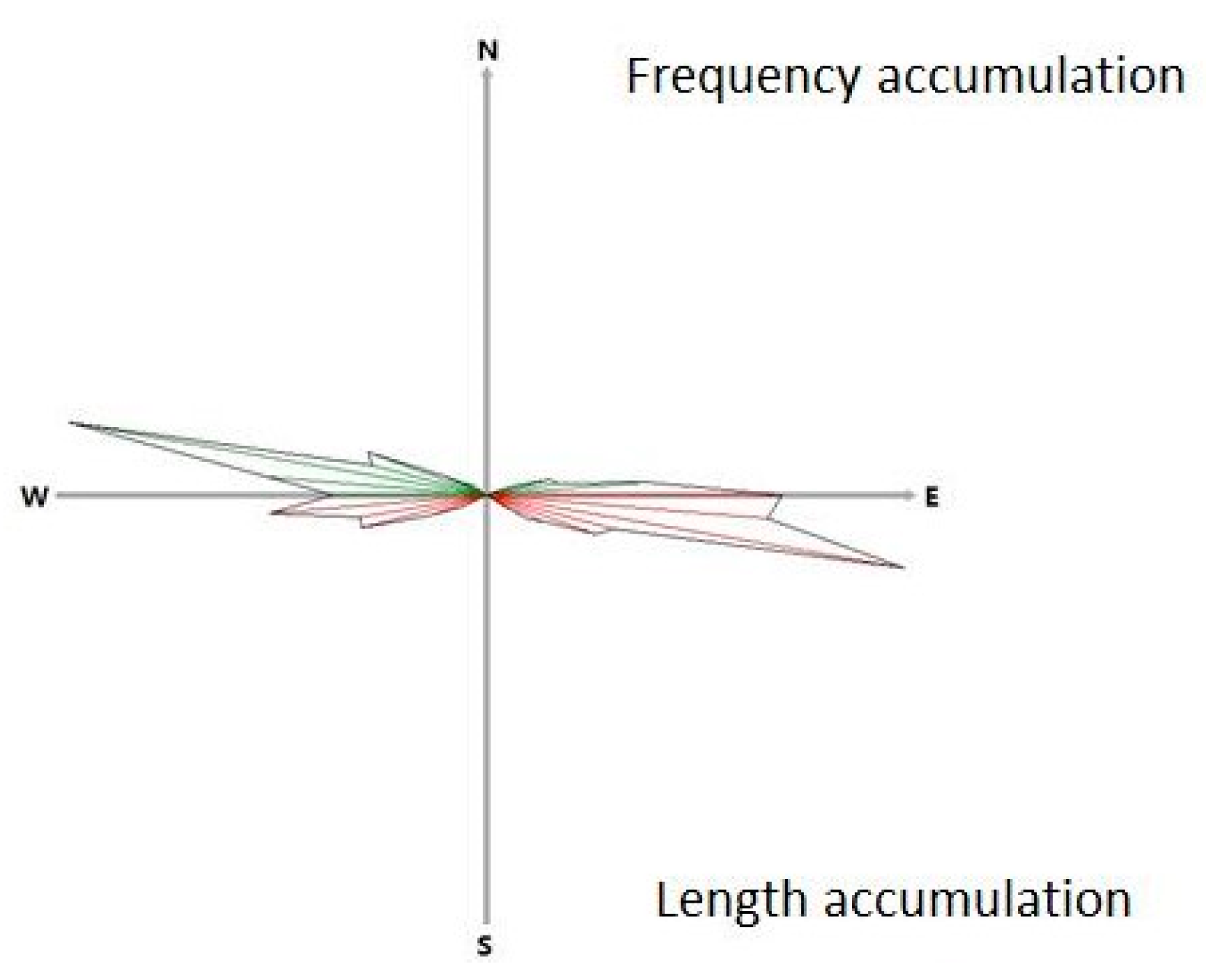
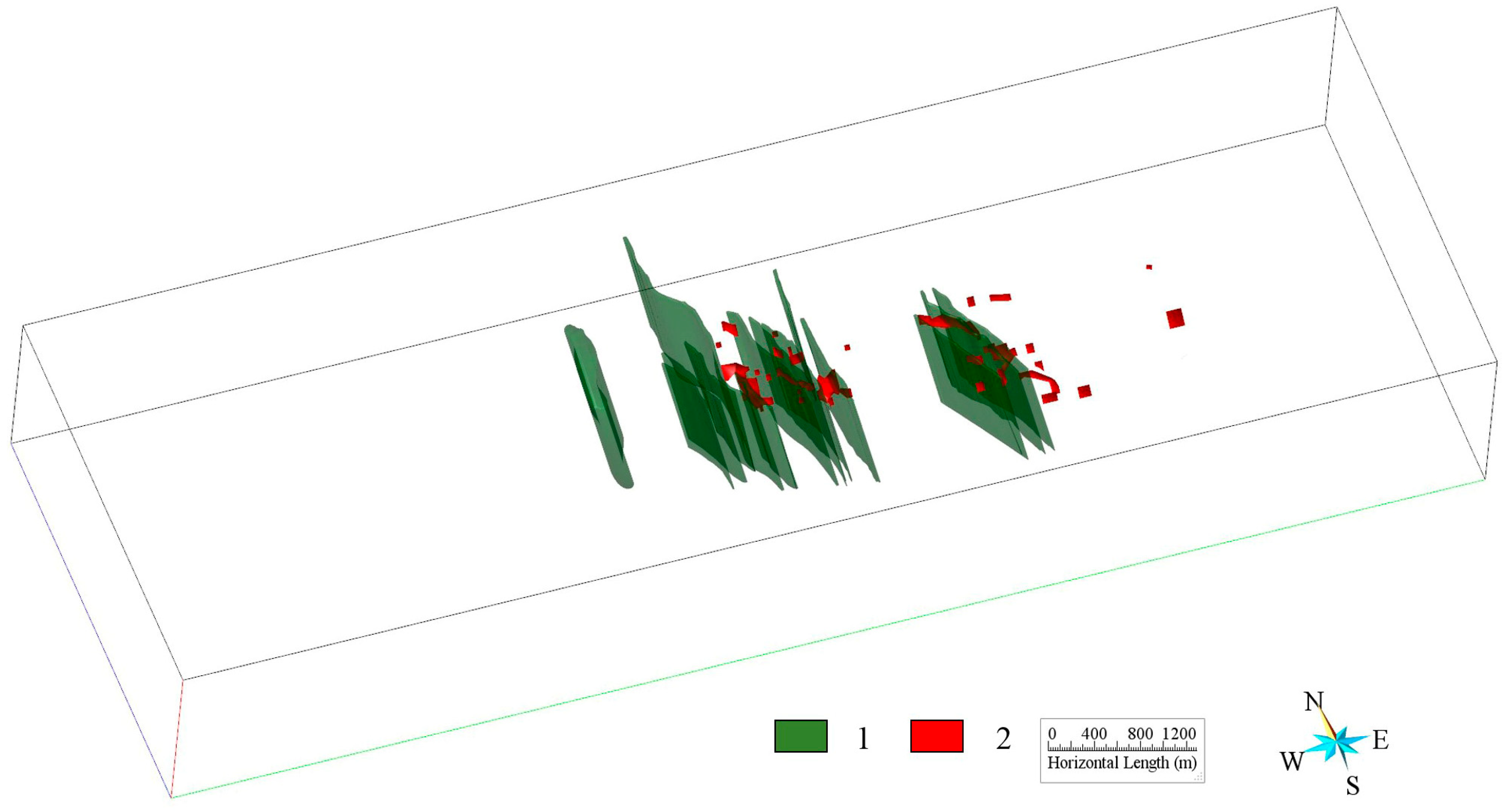
- Extraction of Metallogenic structure information
- (2)
- Extraction of information of rock bottom interface
- (3)
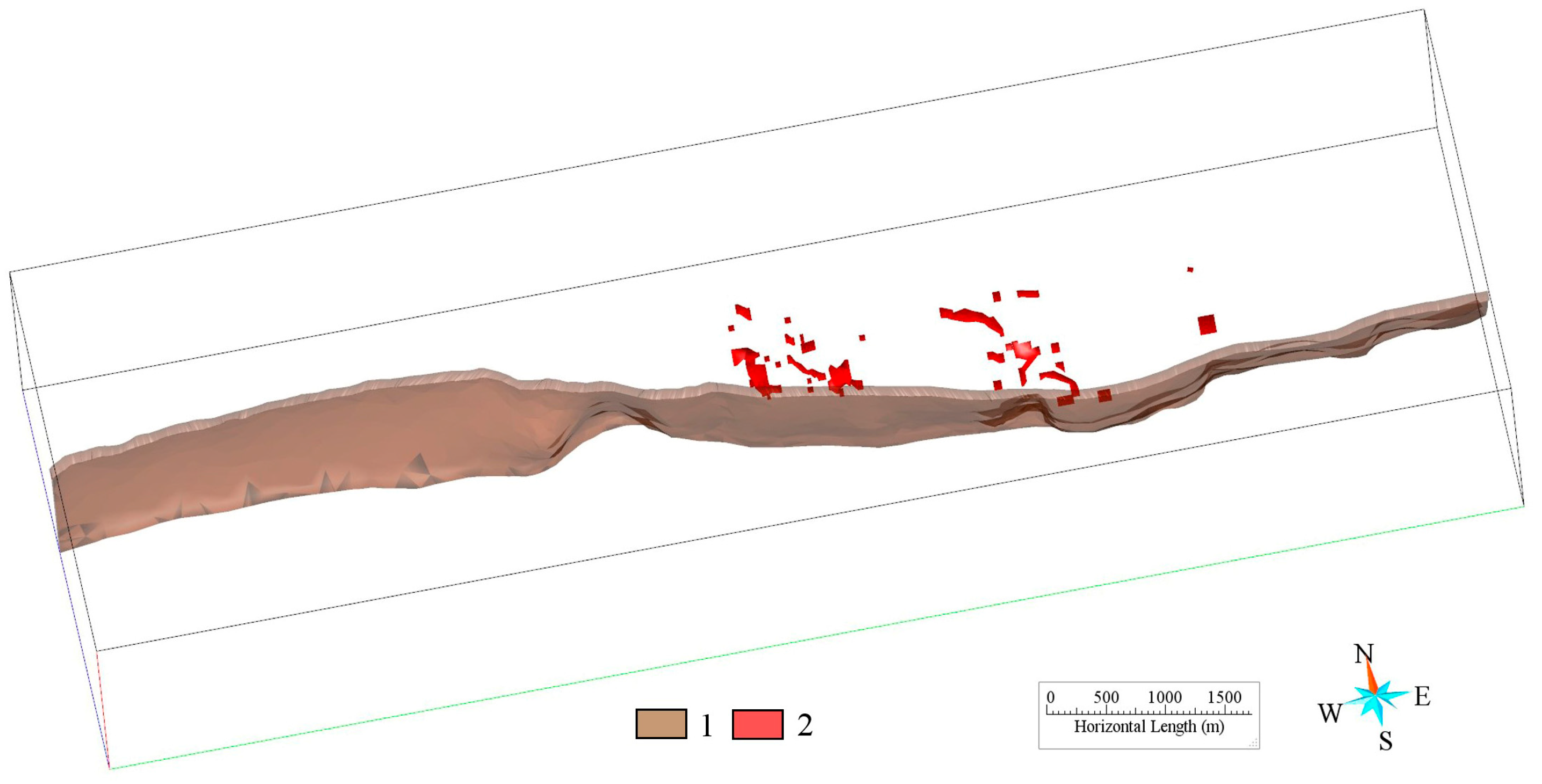
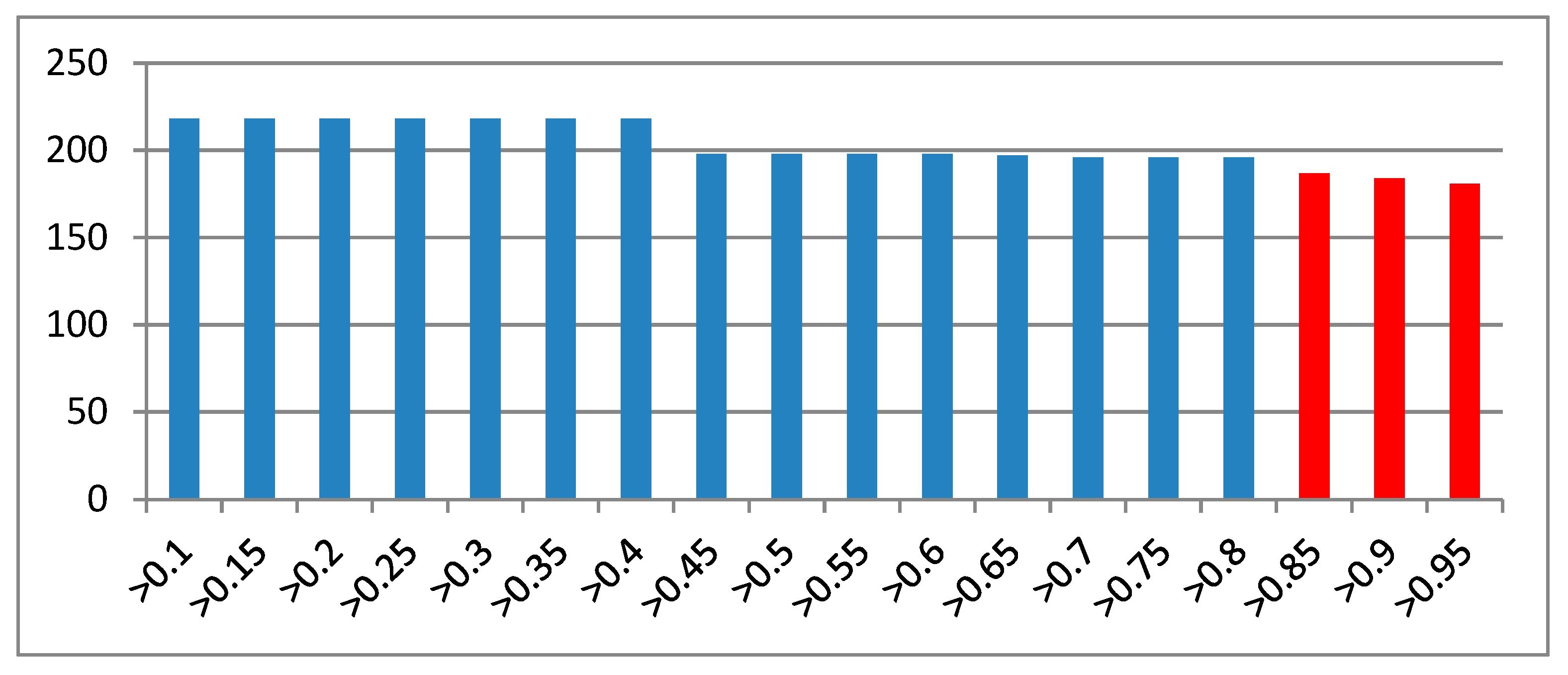
- Extraction of Rock Vein Anomaly Information
3.2.2. Extraction of Geochemical Anomaly Information
3.3. Establishment of the Quantitative Prediction Model
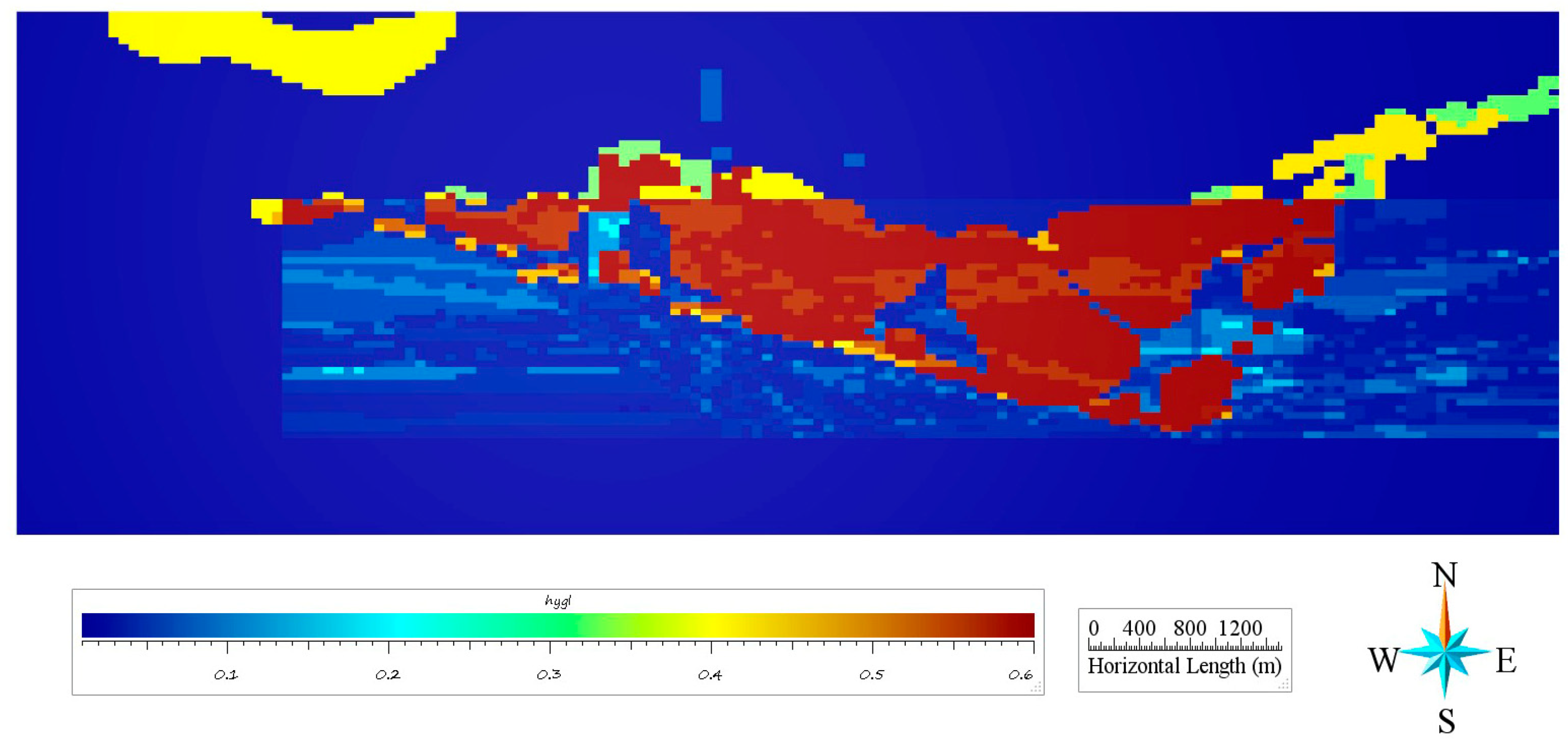
4. Prediction Results
4.1. Weights of Evidence Method
4.2. Informational Prospecting Method
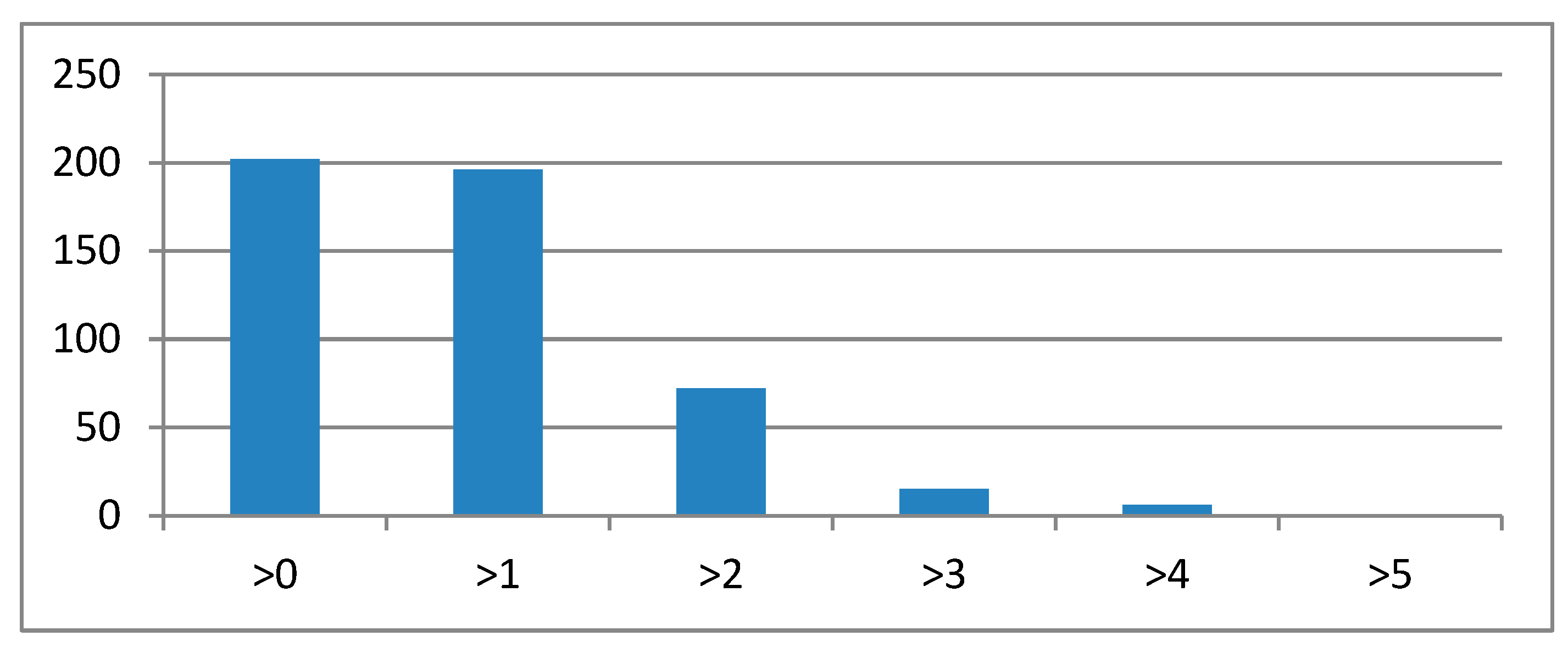
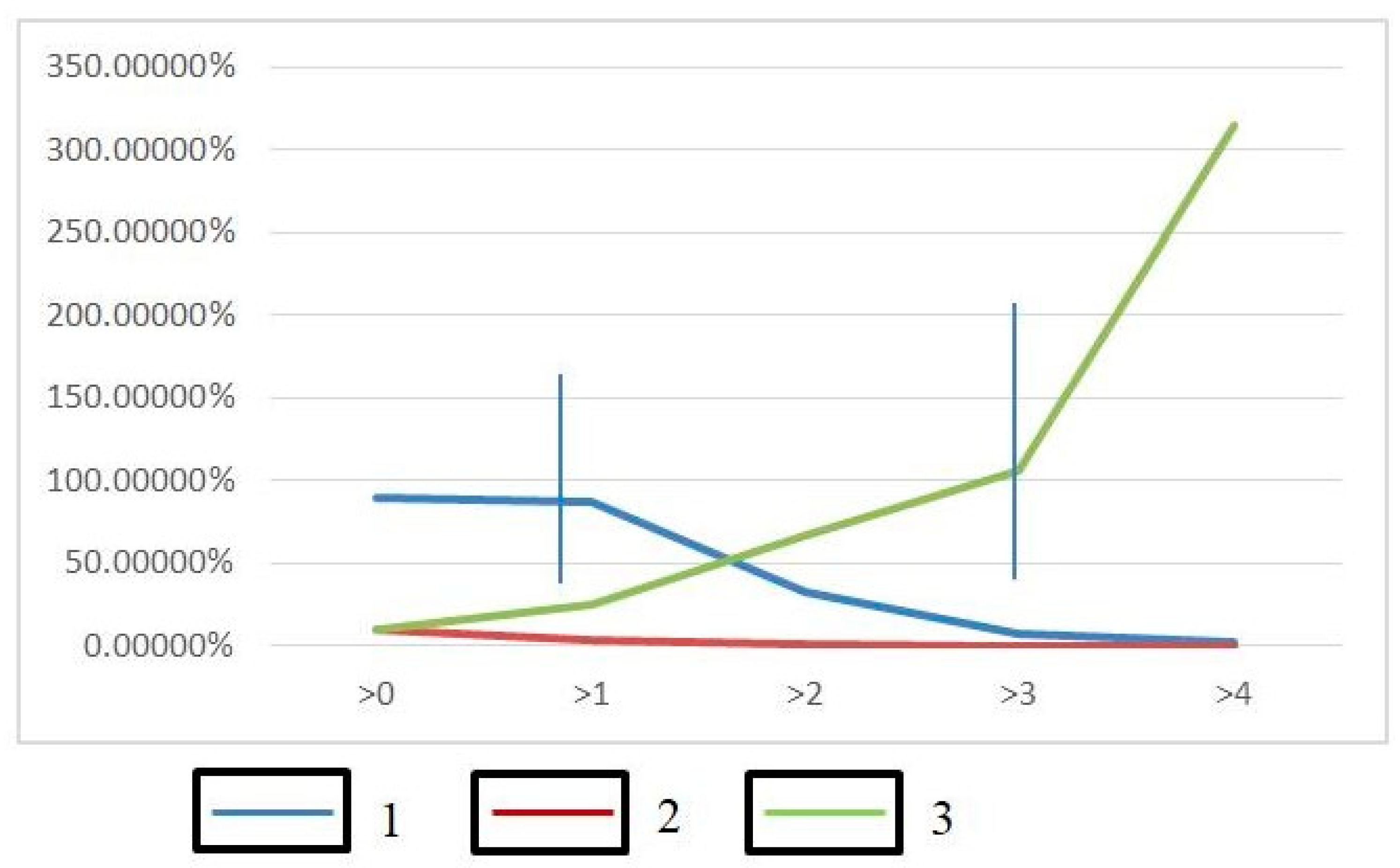
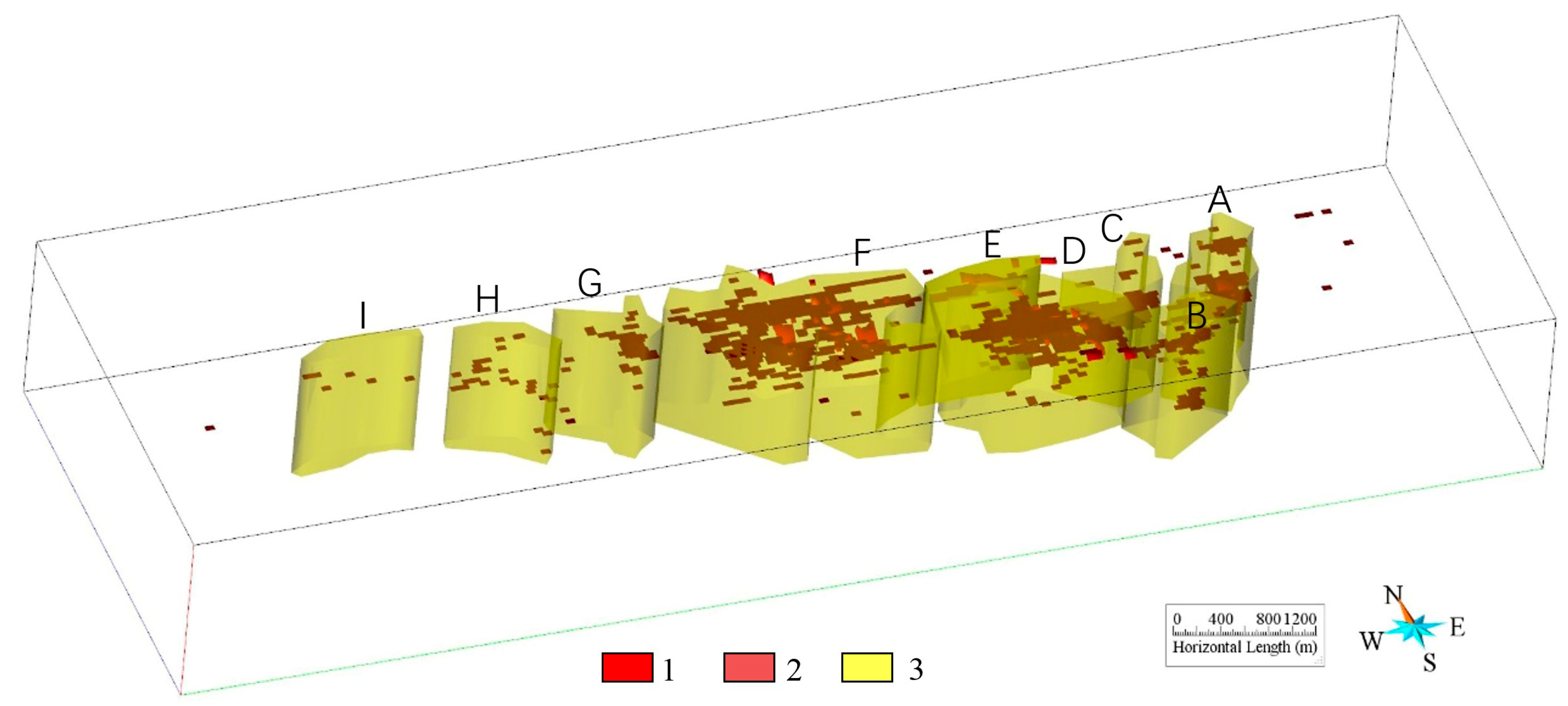
4.3. Analysis of the Prediction Results
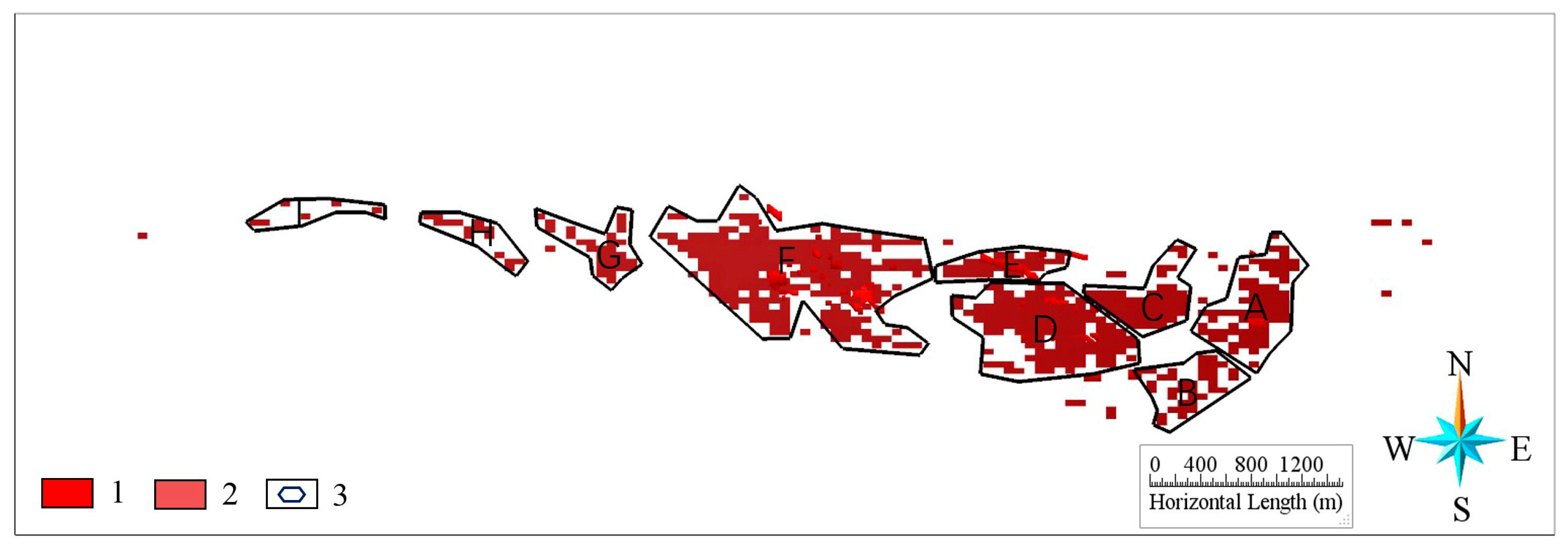
4.4. Delineation of Prospective Plans
4.5. Estimation of Prediction Resources
5. Conclusions
- (1)
- A 3D geological model is established by systematically collecting, arranging, and analyzing the multisource data of geophysical and geochemical exploration, remote sensing, and drilling in the Baiyanghe study area, thus achieving breakthroughs and the application of 3D modeling technology for complex geologic objects. The complex deep geological environment and its controlling effect on uranium mineralization have been comprehensively and intuitively analyzed from the 3D perspective. Therefore, we have obtained a more profound understanding of the uranium mineralization and control rules.
- (2)
- Based on the Baiyanghe uranium deposit model and through the analysis of the metallogenic rule, the prediction model is then established by extraction of elements such as structure, granite bottom interface, rock vein and geochemical anomaly, and the qualitative analysis of 3D correlation of ore-bearing and ore-controlling property. We then performed a quantitative analysis and extraction of elements, and provided element data for 3D quantitative prediction.
- (3)
- To improve the accuracy of 3D quantitative prediction, the 3D weights of the evidence method and the 3D information method are used for the quantitative analysis of the ore deposits. Through the comprehensive application of the prediction and analysis results, the author obtained the favorable high-value area and delineated nine potential areas. It further showcases that the Baiyanghe uranium deposit and its perimeter have a greater prospecting potential.
Author Contributions
Data Availability Statement
Conflicts of Interest
References
- Zhu, Y.S. Introduction to Mineral Resources Evaluation Methodology; Geological Publishing House: Beijing, China, 1984; pp. 120–180. [Google Scholar]
- Houlding, S.W. 3D Geosciences Modeling-Computer Techniques for Geological Characterization; Springer: Berlin, Germany, 1994; pp. 1–309. [Google Scholar]
- Halvorson, L.; Craig, P. Life-history and ecology of a pacific-arctic population of rainbow smelt in coastal waters of the Beaufort Sea. Trans. Am. Fish. Soc. 1984, 113, 33–38. [Google Scholar] [CrossRef]
- Mallet, J.L. Discrete smooth interpolation. ACM Trans. Graph. 1989, 8, 121–144. [Google Scholar] [CrossRef]
- Mallet, J.L. Discrete smooth interpolation in geometric modeling. Comput. Aided Des. 1992, 24, 177–191. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, W.P.; Wu, Z.C.; Guo, F.; Zheng, X. The Development Status f 3D Geological Modeling Technology and Modeling Instances. J. East China Inst. Technol. Soc. Sci. 2013, 32, 403–409. [Google Scholar]
- Allais, M. Method of Appraising Economic Prospects of Mining Exploration over Large Territories: Algerian Sahara Case Study. Manag. Sci. 1957, 3, 285–347. [Google Scholar] [CrossRef]
- Harris, D.P.; Freyman, A.J.; Barry, G.S. Methodology employed to estimate the potential mineral supply of the Canadian Northwest. Dep. Energy Can. Mines Resour. Miner. Resour. Div. Miner. Inform. Bull 1970, 1–56. [Google Scholar]
- Agterberg, F.P. Combining indicator patterns for mineral resource evaluation. In Proceedings of the International Workshop on Statistical Prediction of Mineral Resources, Wuhan, China, 20–25 October 1990; pp. 1–15. [Google Scholar]
- Chen, J.P.; Xiang, J.; Zheng, X. Ten Cases of 3D Quantitative Prediction of Concealed Ore; Science Press: Beijing, China, 2019. [Google Scholar]
- Chen, J.P.; Wang, C.N.; Shang, B.C. 3D metallogenic prediction of concealed ore in Yongmei area of Fujian Province based on digital deposit model. Sci. Technol. Manag. Land Resour. 2012, 29, 14–20. [Google Scholar]
- Wang, M.; Wang, G.; Zhang, X.J. Structural system and metallogenic prediction of Baiyanghe uranium deposit in Xinjiang. Miner. Explor. 2017, 8, 552–558. [Google Scholar]
- Peng, H.L.; An, W.T.; Chen, J.P. Application of 3D quantitative prediction method in South Hongshishan Gold Deposit, Inner Mongolia. J. Geol. 2017, 41, 415–420. [Google Scholar]
- Wang, G.; Zhang, S.; Yan, C.; Song, Y.; Wang, L. 3D geological modeling with multi-source data integration in polymetallic region: A case study of Luanchuan, Henan Province, China. In Proceedings of the 1° World-Y.E.S. Congress 2009, Beijing, China, 25–28 October 2009; pp. 166–167. [Google Scholar]
- Shi, R.; Chen, J.P.; Wang, G. 3D metallogenic prediction and optimal selection of target area of Zhulin ore section in Gejiu, Yunnan province. Geol. Bull. China 2015, 34, 944–952. [Google Scholar]
- He, Z.L.; Zhu, P.F.; Ma, H. 3D geologic modeling of Xiangshan Volcanic Basin based on the combination of multi-source data. Geol. Prospect. 2018, 54, 404–414. [Google Scholar]
- Shi, R.; Chen, J.P.; Chen, Z.P. 3D quantitative prediction of Tongguan section of Xiaoqinling gold mine belt, Shaanxi Province. Geol. Bull. China 2011, 30, 711–721. [Google Scholar]
- Shi, R.; Chen, J.P.; Liu, H.D. 3D prediction model and optimal selection of target area of Jiaojia gold mine belt, Shandong Province. Geoscience 2014, 28, 743–750. [Google Scholar]
- Rong, J.H.; Chen, J.P.; Shang, B.C. 3D prediction of a deep concealed ore body based on a prospecting model in Gejiu, Yunnan province. Geol. Prospect. 2012, 48, 191–198. [Google Scholar]
- Chen, J.P.; Yu, P.P.; Shi, R.; Yu, M.; Zhang, S. Research on 3D quantitative prediction and evaluation method of regional concealed ore body. Earth Sci. Front. 2014, 21, 211–220. [Google Scholar]
- Agterberge, F.P.; Kelly, A.M. Geomathematical methods for use in prospecting. Can. Min. J. 1971, 92, 61–72. [Google Scholar]
- Ma, H. 3D Geological Modeling and Quantitative Prediction of Zoujiashan Area in Xiangshan Uranium Ore Field; University of Geosciences (Beijing): Beijing, China, 2017; pp. 1–75. [Google Scholar]
- Wang, W.J. 3D Modeling and Quantitative Prediction of Julongan Deposit in Xiangshan Uranium Ore Field; China University of Geosciences (Beijing): Beijing, China, 2018; pp. 1–102. [Google Scholar]

| Category | Ore-Controlling Factor | Metallogenic Predictor | Characteristic Variable |
|---|---|---|---|
| Geology | Structure | Fracture buffer zone | 100 m buffer area of fracture crushing zone |
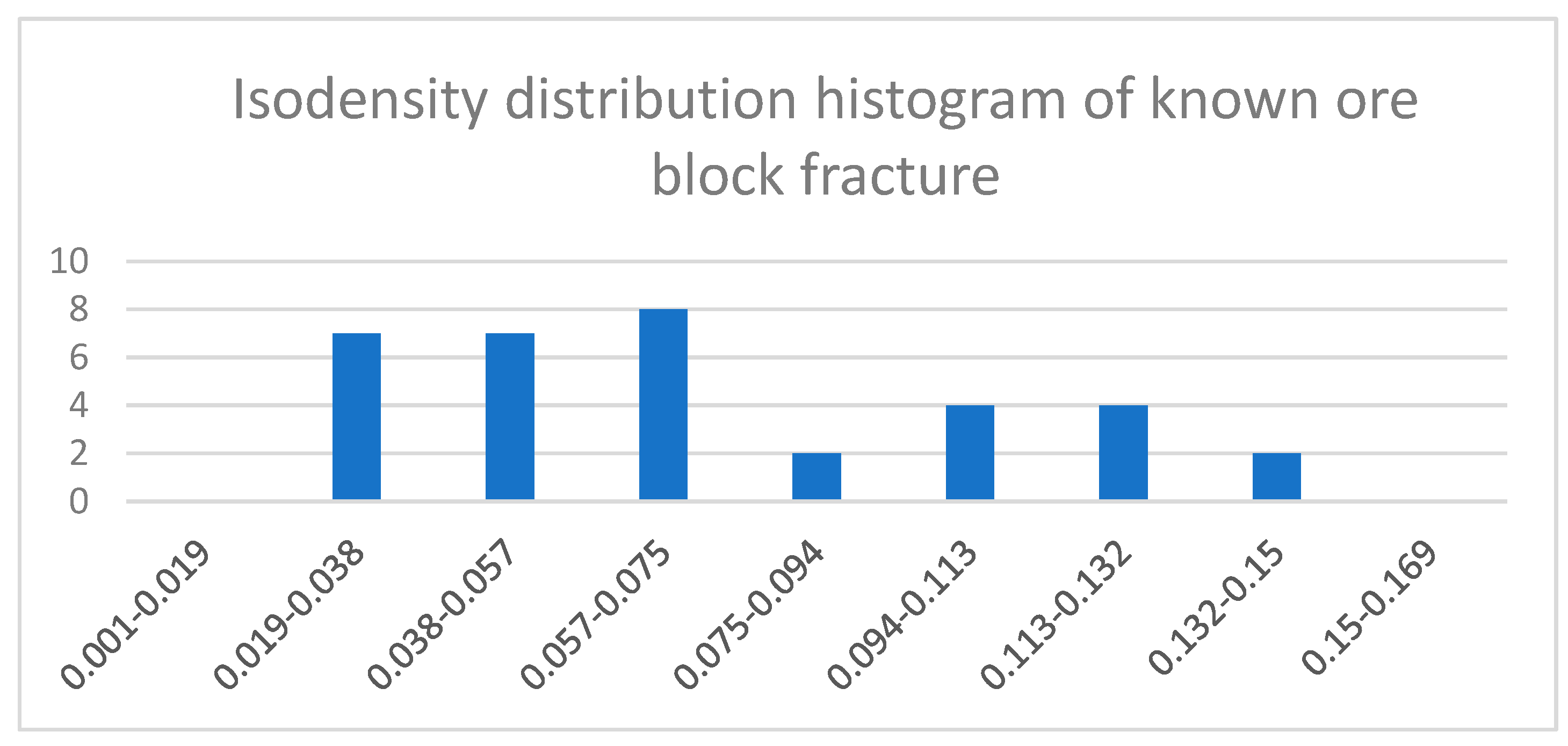
| Structural distribution characteristics | Fracture isodensity (0.019–0.075) | ||
| Fracture frequency (0.52–0.98) | |||
| Fracture anomaly orientation (0.59–0.63, 0.95–1) | |||
| Anomaly level of fracture orientation (0–0.02, 0.09–0.11, 0.19–0.24) | |||
| Main fracture (0.005–117.86) | |||
| Granite’s bottom interface | Favorable metallogenic area | 50 m buffer area around the granite’s bottom interface | |
| Rock veins | Favorable information about rock veins | 5 m buffer zone around the rock vein | |
| Geochemical exploration | Geochemical exploration | Geochemical anomaly information | Seven anomalies of Ba, Mo, Pb, RN, Sr, U component, and U energy spectrum |
| Evidence Item | W+ | S (W+) | W− | S (W−) | C |
|---|---|---|---|---|---|
| Mo anomaly | 0.722296 | 0.217986 | 0.05099 | 0.069839 | 0.77329 |
| Pb anomaly | 0.631068 | 0.300863 | 0.02331 | 0.068196 | 0.654376 |
| U energy spectrum | 2.057473 | 0.067754 | 3.20329 | 0.352455 | 5.260766 |
| Yangzhuang fracture | 0.533274 | 0.288106 | 0.02254 | 0.068355 | 0.555818 |
| Rock veins | 2.666186 | 0.131367 | 0.27826 | 0.077144 | 2.944442 |
| Granite’s bottom interface | 3.221804 | 0.074435 | 1.58029 | 0.14899 | 4.802094 |
| Isodensity | 0.614739 | 0.266816 | 0.02952 | 0.068676 | 0.644255 |
| Anomaly orientation | 2.480429 | 0.223493 | 0.08496 | 0.069669 | 2.565391 |
| Frequency | 1.155135 | 0.223372 | 0.06407 | 0.069669 | 1.219206 |
| Anomaly level of orientation | 1.902034 | 0.266896 | 0.05439 | 0.068676 | 1.956425 |
| Main fracture | 0.812505 | 0.171397 | 0.09358 | 0.072163 | 0.906088 |
| Information Layer | Number of Marker Unit | Number of Information Layer Unit | Information Volume Value |
|---|---|---|---|
| Mo anomaly | 21 | 80,716 | 0.3202219 |
| Pb anomaly | 11 | 46,870 | 0.27545997 |
| U energy spectrum | 213 | 218,865 | 0.89316552 |
| Yangzhuang fracture | 12 | 55,794 | 0.23755598 |
| Rock veins | 56 | 31,996 | 1.14805457 |
| Granite’ bottom interface | 175 | 57,373 | 1.38929272 |
| Isodensity | 14 | 59,756 | 0.27470875 |
| Anomaly orientation | 20 | 13,296 | 1.08227122 |
| Frequency | 19 | 49,727 | 0.48712358 |
| Anomaly level of orientation | 14 | 16,695 | 0.82850385 |
| Main fracture | 34 | 118,596 | 0.36237111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Guo, C.; Zhu, P.; Tian, J.; He, Z. Three-Dimensional Prediction and Evaluation of Baiyanghe Uranium Deposit in the Xuemistan Volcanic Belt, Xinjiang. Minerals 2023, 13, 1408. https://doi.org/10.3390/min13111408
Bai Y, Guo C, Zhu P, Tian J, He Z. Three-Dimensional Prediction and Evaluation of Baiyanghe Uranium Deposit in the Xuemistan Volcanic Belt, Xinjiang. Minerals. 2023; 13(11):1408. https://doi.org/10.3390/min13111408
Chicago/Turabian StyleBai, Yun, Chunying Guo, Pengfei Zhu, Jianji Tian, and Zilan He. 2023. "Three-Dimensional Prediction and Evaluation of Baiyanghe Uranium Deposit in the Xuemistan Volcanic Belt, Xinjiang" Minerals 13, no. 11: 1408. https://doi.org/10.3390/min13111408
APA StyleBai, Y., Guo, C., Zhu, P., Tian, J., & He, Z. (2023). Three-Dimensional Prediction and Evaluation of Baiyanghe Uranium Deposit in the Xuemistan Volcanic Belt, Xinjiang. Minerals, 13(11), 1408. https://doi.org/10.3390/min13111408






