Mine Backfilling in the Permafrost, Part I: Numerical Prediction of Thermal Curing Conditions within the Cemented Paste Backfill Matrix
Abstract
:1. Introduction
2. Governing Equations for Heat Transfer
3. Materials and Testing Methods
3.1. Characteristics of Tailings, Binder, and Mixing Water
3.2. D Heat Transfer Tests on a Physical Model
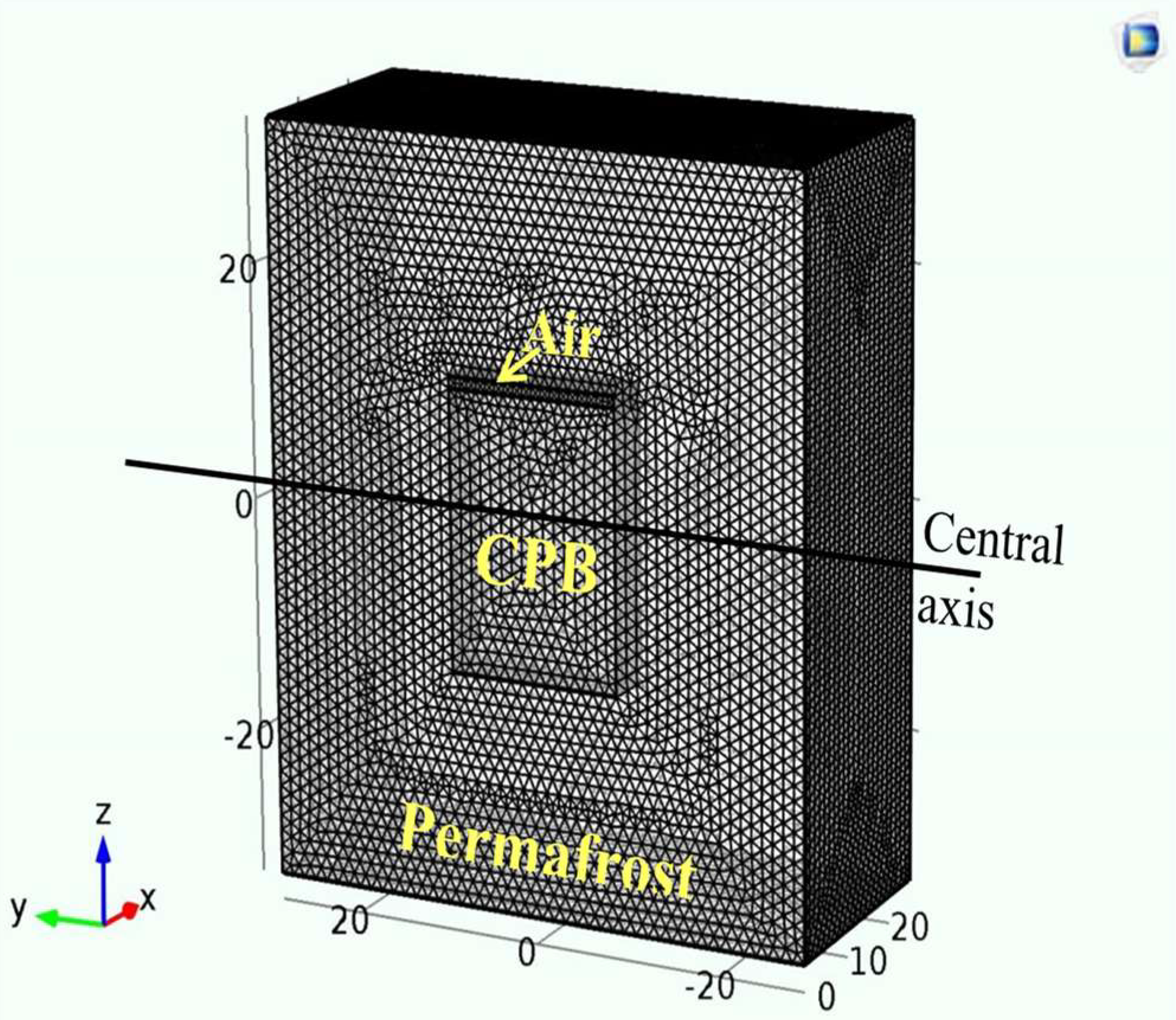
3.3. Numerical Models Using COMSOL Multiphysics®
4. Laboratory Results for the 3D Heat Transfer Test
5. Numerical Modeling Results for Heat Transfer
5.1. Input Parameters and Initial and Boundary Conditions
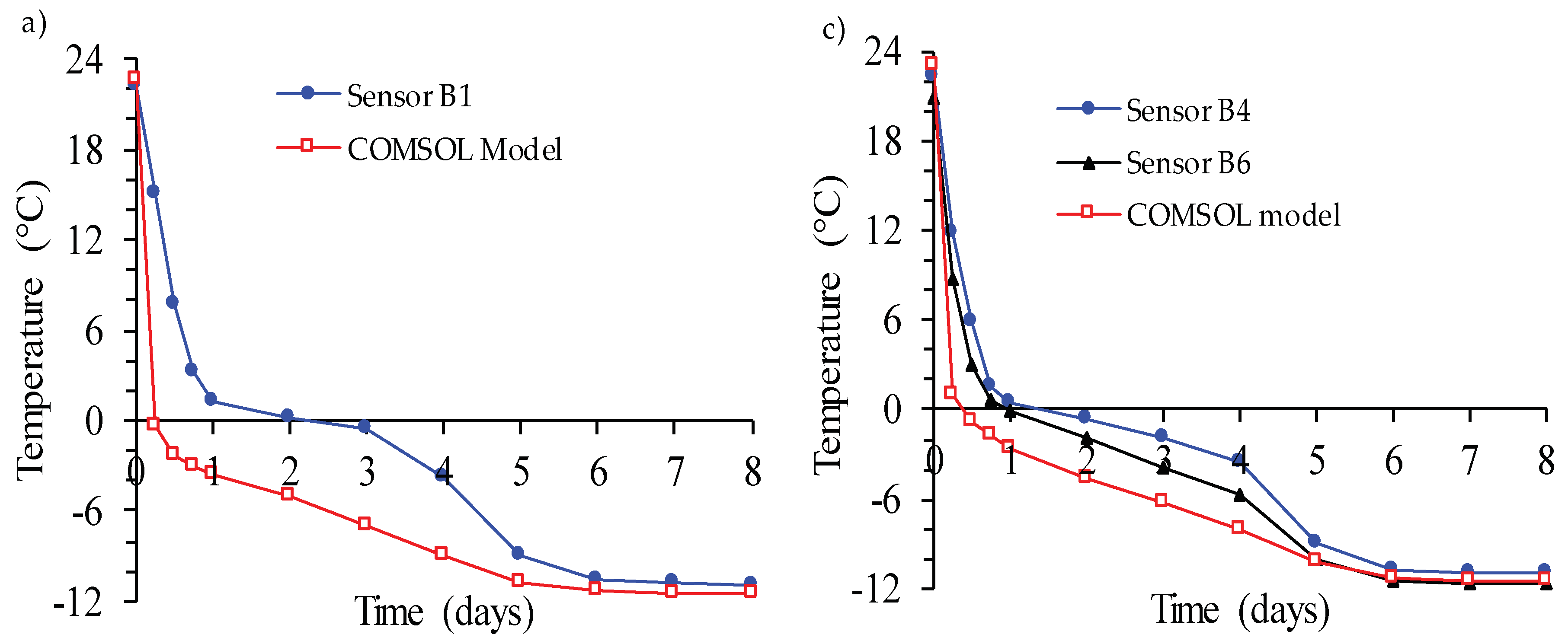
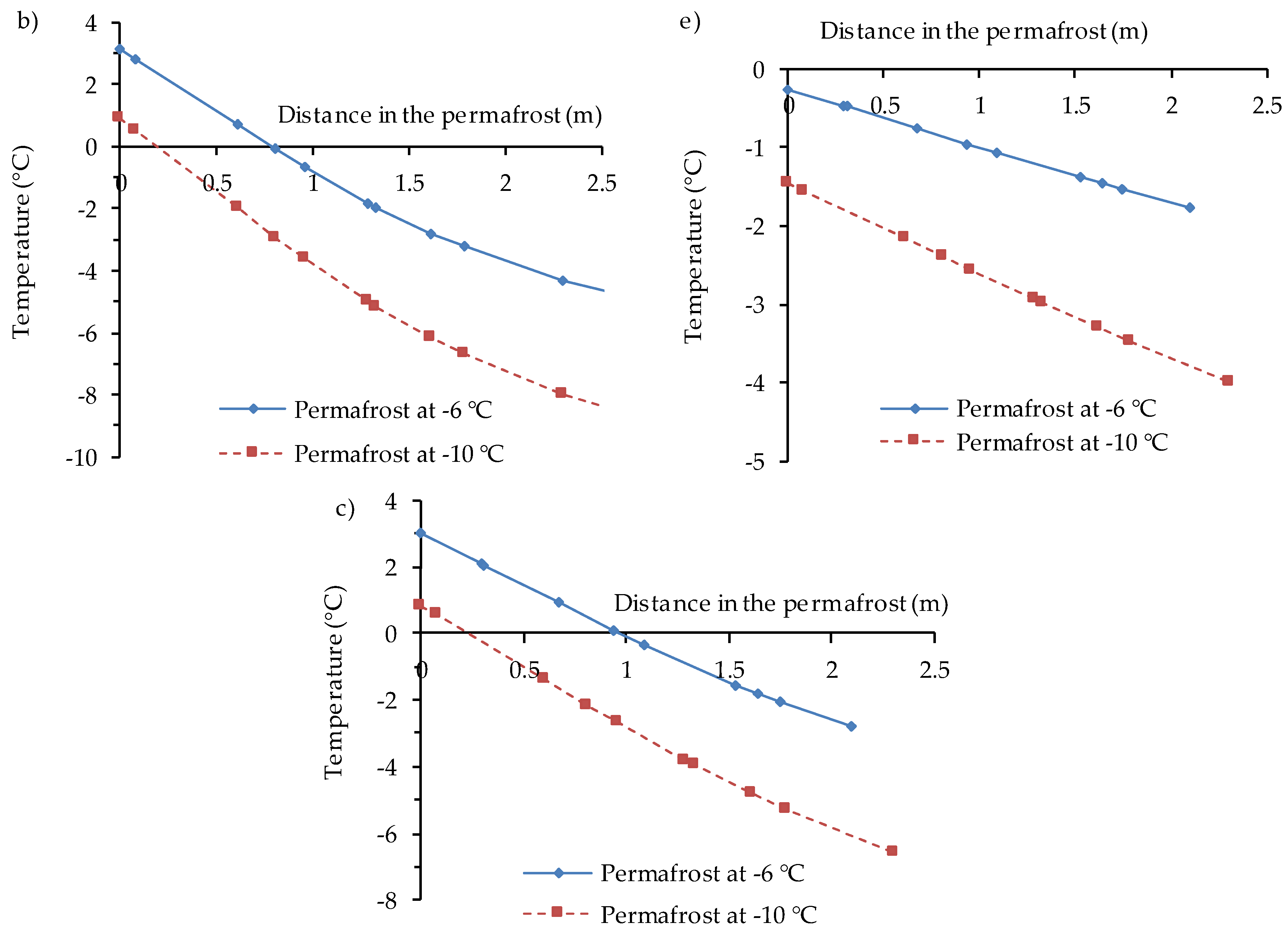
5.2. Model Validation by Comparing Predicted and Experimental Data Obtained from 3D Heat Transfer Tests on CPB Cooled to Freezing
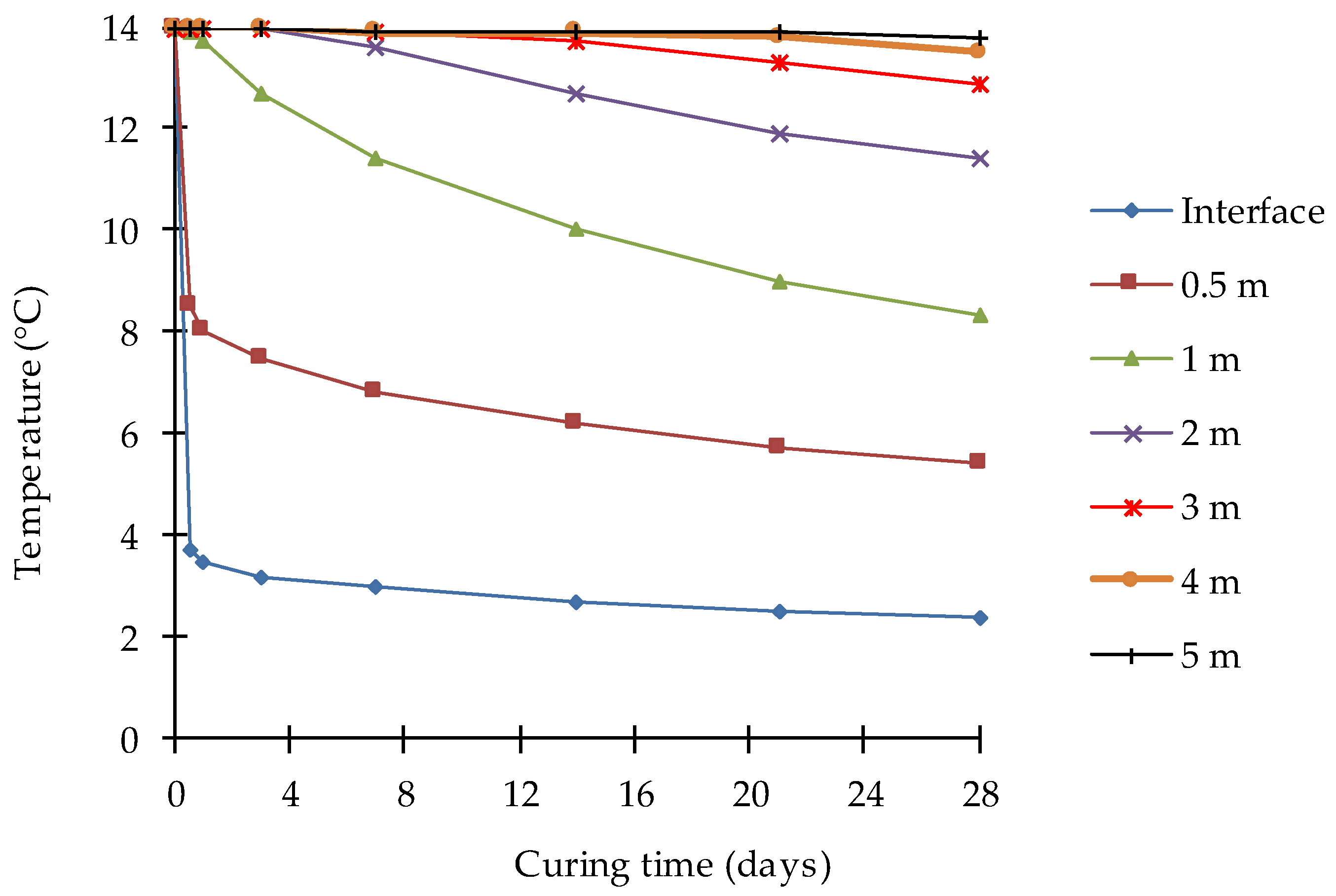
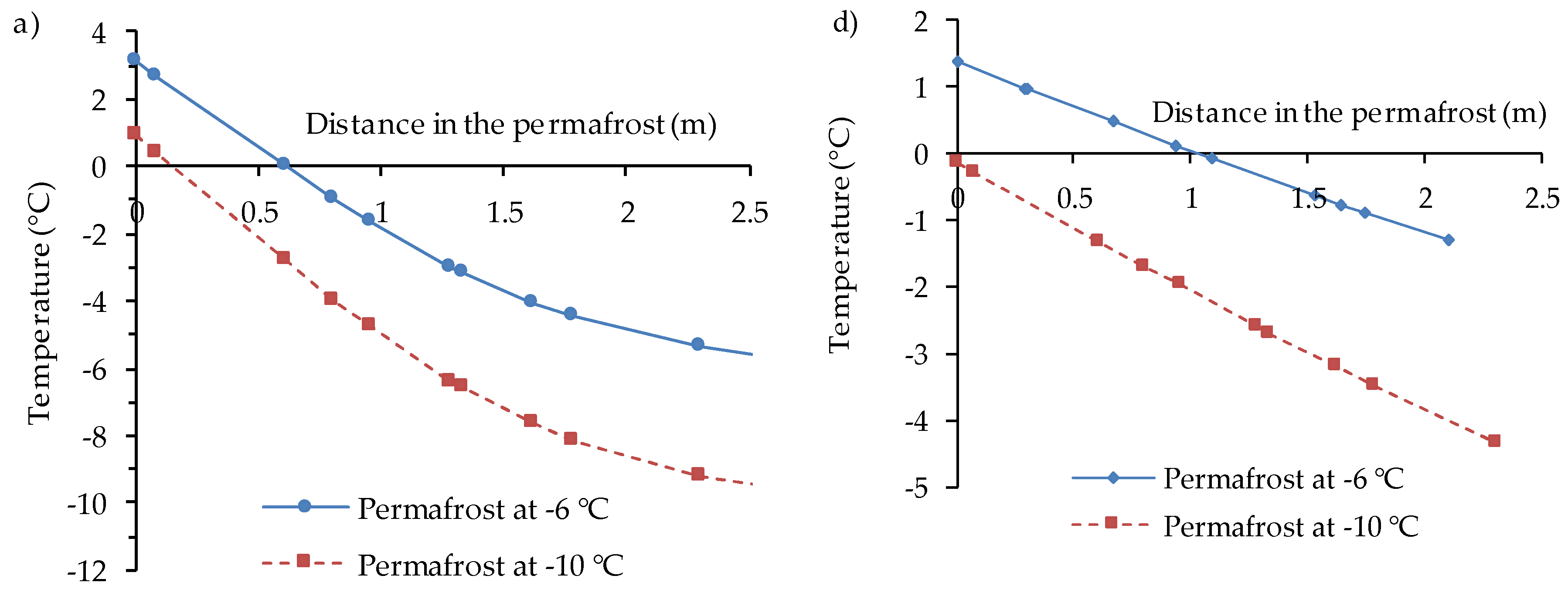
5.3. Application of the Calibrated and Validated Numerical Model to Backfilled Stopes in Permafrost
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Belem, T.; Benzaazoua, M. Design and Application of Underground Mine Paste Backfill Technology. Geotech. Geol. Eng. 2008, 26, 147–174. [Google Scholar] [CrossRef]
- Belem, T.; Benzaazoua, M.; Bussière, B. Mechanical behaviour of cemented paste backfill. In Proceedings of the 53th Annual Conference of the Canadian Geotechnical Society, Montreal, QC, Canada, 15–18 October 2000. [Google Scholar]
- Benzaazoua, M.; Fall, M.; Belem, T. A contribution to understanding the hardening process of cemented pastefill. Miner. Eng. 2004, 17, 141–152. [Google Scholar] [CrossRef]
- Cao, S.; Yilmaz, E.; Song, W. Evaluation of Viscosity, Strength and Microstructural Properties of Cemented Tailings Backfill. Minerals 2018, 8, 352. [Google Scholar] [CrossRef]
- Landriault, D. Paste backfill mix design for Canadian underground hard rock mining. In Proceedings of the 97th Annual General Meeting of CIM, Rock Mechanics and Strata Control Session, Halifax, NS, Canada, 14–18 May 1995; pp. 229–238. [Google Scholar]
- Li, L. Analytical solution for determining the required strength of a side-exposed mine backfill containing a plug. Can. Geotech. J. 2014, 51, 508–519. [Google Scholar] [CrossRef]
- Li, L. Generalized Solution for Mining Backfill Design. Int. J. Geomech. 2014, 14, 04014006. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. A modified solution to assess the required strength of exposed backfill in mine stopes. Can. Geotech. J. 2012, 49, 994–1002. [Google Scholar] [CrossRef]
- Li, L.; Aubertin, M. An improved method to assess the required strength of cemented backfill in underground stopes with an open face. Int. J. Min. Sci. Technol. 2014, 24, 549–558. [Google Scholar] [CrossRef]
- Ouattara, D.; Belem, T.; Mbonimpa, M.; Yahia, A. Effect of superplasticizers on the consistency and unconfined compressive strength of cemented paste backfills. Constr. Buil. Mater. 2018, 181, 59–72. [Google Scholar] [CrossRef]
- Wu, J.; Feng, M.; Xu, J.; Qiu, P.; Wang, Y.; Han, G. Particle Size Distribution of Cemented Rockfill Effects on Strata Stability in Filling Mining. Minerals 2018, 8, 407. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, H.; Taheri, A.; Deng, J.; Ke, B. Effects of Superplasticizer on the Hydration, Consistency, and Strength Development of Cemented Paste Backfill. Minerals 2018, 8, 381. [Google Scholar] [CrossRef]
- Boger, D.; Scales, P.; Sofra, F. Rheological concepts. In Paste and Thickened Tailings-A Guide, 2nd ed.; Jewell, Fourie, Ed.; Australian Centre for Geomechanics: Perth, Australia, 2006; p. 25. [Google Scholar]
- Cooke, R. Backfill pipeline distribution systems-design methodology review. CIM Mag. 2007, 2. [Google Scholar]
- Ouattara, D. Étude des Propriétés Rhéologiques de Résidus Miniers Densifiés. Master’s Thesis, Université du Québec en Abitibi-Témiscamingue, Rouyn-Noranda, QC, Canada, 2011. [Google Scholar]
- Ouattara, D.; Mbonimpa, M.; Belem, T. Rheological properties of thickened tailings and cemented paste tailings and the effects of mixture characteristics on shear behaviour. In Proceedings of the 63rd Canadian Geotechnical Conference, Calgary, AB, Canada, 12 September 2010; pp. 1178–1185. [Google Scholar]
- Ouattara, D.; Mbonimpa, M.; Belem, T. Rheology of cemented paste backfill incorporating superplasticizers. In Proceedings of the 66th Canadian Geotechnical Conference, Montreal, QC, Canada, 7 June 2013. [Google Scholar]
- Ouattara, D.; Mbonimpa, M.; Yahia, A.; Belem, T. Assessment of rheological parameters of high density cemented paste backfill mixtures incorporating superplasticizers. Constr. Build. Mater. 2018, 190, 294–307. [Google Scholar] [CrossRef]
- Ouattara, D.; Yahia, A.; Mbonimpa, M.; Belem, T. Effects of superplasticizer on rheological properties of cemented paste backfills. Int. J. Miner. Process. 2017, 161, 28–40. [Google Scholar] [CrossRef]
- Zhao, Y.; Soltani, A.; Taheri, A.; Karakus, M.; Deng, A. Application of Slag–Cement and Fly Ash for Strength Development in Cemented Paste Backfills. Minerals 2019, 9, 22. [Google Scholar] [CrossRef]
- Belem, T.; Benzaazoua, M.; Bussière, B.; Dagenais, A. Effects of settlement and drainage on strength development within mine paste backfill. In Proceedings of the 9th International Conference, Tailings and Mine Waste, Fort Collins, CO, USA, 27–30 January 2002; Volume 2, pp. 139–148. [Google Scholar]
- Belem, T.; Benzaazoua, M.; El Aatar, O.; Yilmaz, E. Effect of drainage and the pore water pressure dissipation on the backfilling sequencing. In Proceedings of the 23rd World Mining Congress, Montreal, QC, Canada, 10 August 2013; pp. 11–15. [Google Scholar]
- Belem, T.; Bussière, B.; Benzaazoua, M. The effect of microstructural evolution on the physical properties of paste backfill. In Proceedings of the Tailings and Mine Waste, Fort Collins, CO, USA, 16–19 January 2001; Volume 1, p. 5809. [Google Scholar]
- Belem, T.; Effenguet, H.; Mbonimpa, M. Estimation of required minimum binder content by assessing the liquefaction potential of early age cemented mine backfill. In Proceedings of the 66th Canadian Geotechnical Conference, Montreal, QC, Canada, 7 June 2013. [Google Scholar]
- Yilmaz, E.; Belem, T.; Benzaazoua, M.; Bussière, B. Assessment of the modified CUAPS apparatus to estimate in situ properties of cemented paste backfill. Geotech. Test. J. 2010, 33, 351–362. [Google Scholar]
- Benzaazoua, M.; Belem, T.; Bussière, B. Chemical factors that influence the performance of mine sulphidic paste backfill. Cem. Concr. Res. 2002, 32, 1133–1144. [Google Scholar] [CrossRef]
- Benzaazoua, M.; Marion, P.; Picquet, I.; Bussière, B. The use of pastefill as a solidification and stabilization process for the control of acid mine drainage. Miner. Eng. 2004, 17, 233–243. [Google Scholar] [CrossRef]
- Ouellet, S.; Bussière, B.; Mbonimpa, M.; Benzaazoua, M.; Aubertin, M. Reactivity and mineralogical evolution of an underground mine sulphidic cemented paste backfill. Miner. Eng. 2006, 19, 407–419. [Google Scholar] [CrossRef]
- Fall, M.; Wu, D.; Pokharel, M. Effect of deep mine temperature conditions on the heat development in cemented paste backfill and its properties. Deep Min. 2014, 2014, 559–573. [Google Scholar]
- Wu, D.; Fall, M.; Cai, S.-J. Coupled Modeling of Temperature Distribution and Evolution in Cemented Tailings Backfill Structures that Contain Mineral Admixtures. Geotech. Geol. Eng. 2012, 30, 935–961. [Google Scholar] [CrossRef]
- Bandopadhyay, S.; Izaxon, V. Ice-cemented backfill for underground support in arctic mines. In Proceedings of the SME Annual Meeting, Denver, CO, USA, 23–25 February 2004. [Google Scholar]
- Cluff, D.L.; Kazakidis, V. Frozen Baclfill Mix Formulations and Process for Use Thereof in Underground Mining Applications. U.S. Patent US20120114429A1, 10 May 2012. [Google Scholar]
- Kalonji, K. Étude des Propriétés Rhéologiques et du Transport du Remblai Cimenté en Pâte en Conditions Nordiques. Master’s Thesis, Université du Québec en Abitibi-Témiscamingue, Rouyn-Noranda, QC, Canada, 2016. [Google Scholar]
- COMSOL Multiphysics. In Heat Transfer Module User’s Guide, COMSOL version; COMSOL Inc.: Burlington, MA, USA, 2015; Volume 5.2.
- Kalonji, K.; Mbonimpa, M.; Belem, T.; Benzaazoua, M.; Beya, F.; Ouellet, S. Preliminary investigation of the effect of temperature and salinity on the rheological properties of fresh cemented paste backfills. In Proceedings of the 68th Canadian Geotechnical Conference and 7th Canadian Permafrost Conference, Quebec City, QC, Canada, 20–23 September 2015; pp. 20–23. [Google Scholar]
- Kalonji, K.; Mbonimpa, M.; Belem, T.; Benzaazoua, M.; Beya, F.; Ouellet, S. Calage d’un modèle numérique de prédiction de l’évolution de la température pendant le transport du remblai en pâte cimenté. In Proceedings of the 69th Canadian Geotechnical Conference GeoVancouver 2016, Vancouver, BC, Canada, 5 October 2016. [Google Scholar]
- Ghoreishi-Madiseh, S.A.; Hassani, F.; Mohammadian, A.; Abbasy, F. Numerical modeling of thawing in frozen rocks of underground mines caused by backfilling. Int. J. Rock Mech. Min. Sci. 2011, 48, 1068–1076. [Google Scholar] [CrossRef]
- Hivon, E.; Sego, D. Distribution of saline permafrost in the Northwest Territories, Canada. Can. Geotech. J. 1993, 30, 506–514. [Google Scholar] [CrossRef]
- Williams, J.R. Ground Water in the Permafrost Regions of Alaska; US Government Printing Office: Washington, DC, USA, 1970; p. 90. [Google Scholar]
- Abbasy, F. Thermal Conductivity of Mine Backfill. Master’s Thesis, Concordia University, Montreal, QC, USA, 2009. [Google Scholar]
- Abbasy, F.; Hassani, F.P.; Madiseh, S.A.G.; Côté, J.; Nokken, M.R. An Experimental Study on the Effective Parameters of Thermal Conductivity of Mine Backfill. Heat Transf. Eng. 2014, 35, 1209–1224. [Google Scholar] [CrossRef]
- Beya, F.K.; Mbonimpa, M.; Belem, T.; Benzaazoua, M.; Kalonji, K.; Ouellet, S. Preliminary study of the influence of temperature and salinity on the thermal properties of hardening cemented paste backfill. In Proceedings of the 68th Canadian Geotechnical Conference and 7th Canadian Permafrost Conference, Quebec, QC, Canada, 20–23 September 2015. [Google Scholar]
- Célestin, J.C.H.; Fall, M. Thermal conductivity of cemented paste backfill material and factors affecting it. Int. J. Min. Reclam. Environ. 2009, 23, 274–290. [Google Scholar] [CrossRef]
- ASTM. D5334-08 Standard Test Method for Determination of Thermal Conductivity of Soil and Soft Rock by Thermal Needle Probe Procedure; ASTM: West Conshohocken, PA, USA, 2008. [Google Scholar]
- Gobbé, C.; Iserna, S.; Ladevie, B. Hot strip method: Application to thermal characterisation of orthotropic media. Int. J. Therm. Sci. 2004, 43, 951–958. [Google Scholar] [CrossRef]
- Civan, F.; Sliepcevich, C. Limitation in the Apparent Heat Capacity Formulation for Heat Transfer with Phase Change. Proc. Okla. Acad. Sci. 1987, 67, 83–88. [Google Scholar]
- Yao, M.; Chait, A. An Alternative Formulation of The Apparent Heat Capacity Method for Phase-Change Problems. Numer. Heat Transf. Part B Fundam. 1993, 24, 279–300. [Google Scholar] [CrossRef]
- Hwang, C.; Murray, D.; Brooker, E. A thermal analysis for structures on permafrost. Can. Geotech. J. 1972, 9, 33–46. [Google Scholar] [CrossRef]
- Krahn, J. Thermal Modeling with TEMP/W: An Engineering Methodology; GEO-SLOPE: Calgary, AB, Canada, 2004; p. 292. [Google Scholar]
- ASTM. C150-07 Standard Specification for Portland Cement; ASTM: West Conshohocken, PA, USA, 2007. [Google Scholar]
- ASTM. C143/143M-12 Standard Test Method for Slump of Hydraulic-Cement Concrete; ASTM: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Landriault, D.; Verburg, R.; Cincilla, W.; Welch, D. Paste technology for underground backfill and surface tailings disposal applications. In Short Course Notes, Canadian Institute of Mining and Metallurgy, Technical Workshop œ April; Golder Paste Technology Ltd.: Sudbury, ON, Canada, 1997; Volume 27. [Google Scholar]
- Bansal, V.; Misra, R.; Agrawal, G.D.; Mathur, J. Performance analysis of earth–pipe–air heat exchanger for summer cooling. Energy Build. 2010, 42, 645–648. [Google Scholar] [CrossRef]
- Duchaine, F.; Corpron, A.; Pons, L.; Moureau, V.; Nicoud, F.; Poinsot, T. Development and assessment of a coupled strategy for conjugate heat transfer with Large Eddy Simulation: Application to a cooled turbine blade. Int. J. Heat Fluid Flow 2009, 30, 1129–1141. [Google Scholar] [CrossRef]
- Thompson, B.; Bawden, W.; Grabinsky, M. In situ measurements of cemented paste backfill at the Cayeli Mine. Can. Geotech. J. 2012, 49, 755–772. [Google Scholar] [CrossRef]
- Kwizera, P.; Mbonimpa, M.; Belem, T. Mine backfilling in the permafrost, Part II: Effect of reductions in temperature during curing on the unconfined compressive strength of cemented paste backfills. Minerals 2019. under press. [Google Scholar]









| Parameter | D10 | D30 | D60 | P2 | P20 | P80 | CU | CC |
|---|---|---|---|---|---|---|---|---|
| Unit | (µm) | (µm) | (µm) | (%) | (%) | (%) | (-) | (-) |
| Value | 3.5 | 10 | 27.5 | 5.5 | 53 | 89 | 7.9 | 1.0 |
| Mineral | Proportion (wt. %) |
|---|---|
| Quartz | 40.32 |
| Albite | 19.49 |
| Muscovite | 14.65 |
| Ankerite | 8.77 |
| Chlorite | 8.07 |
| Magnetite | 4.58 |
| Calcite | 2.43 |
| Microcline | 1.33 |
| Pyrite | 0.35 |
| Salt | Concentration |
|---|---|
| (g/L) | |
| NaCl | 0.33 |
| MgSO4 | 3.16 |
| MgCl2 | 0.05 |
| Na2S2O5 | 0.36 |
| CaCl2 | 0.32 |
| CuSO4 | 0.69 |
| KCl | 0.09 |
| Input Parameters | Value |
|---|---|
| Volume fraction of solid in the backfill (-) a | 0.52 |
| Thermal conductivity of unfrozen CPB (W/(m K)) b | 1.84 |
| Thermal conductivity of frozen CPB (W/(m K)) b | 2.10 |
| Thermal conductivity of air (W/(m K)) c | 0.0242 |
| Thermal conductivity of steel (W/(m K)) c | 54 |
| Thermal conductivity of PVC (W/(m K)) c | 0.16 |
| Thermal conductivity of plexiglass (W/(m K)) d | 0.184 |
| Thermal conductivity of granite (W/(m K)) e | 2.90 |
| Heat capacity at constant pressure of unfrozen CPB (J/(kg K)) b | 1624 |
| Heat capacity at constant pressure of frozen CPB (J/(kg K)) b | 1681 |
| Heat capacity at constant pressure of air (J/(kg K)) c | 1006 |
| Heat capacity at constant pressure of steel (J/(kg K)) c | 465 |
| Heat capacity at constant pressure of PVC (J/(kg K)) c | 900 |
| Heat capacity at constant pressure of plexiglass (J/(kg K)) d | 1450 |
| Heat capacity at constant pressure of granite (J/(kg K)) e | 995 |
| Density of unfrozen CPB (kg/m3) f | 1924 |
| Density of frozen CPB (kg/m3) f | 1785 |
| Density of air (kg/m3) c | 1.225 |
| Density of steel (kg/m3) c | 7833 |
| Density of PVC (kg/m3) c | 1380 |
| Density of Plexiglas (kg/m3) d | 1190 |
| Density of granite (kg/m3) e | 2650 |
| Latent heat from phase 1 to phase 2: (kJ/kg) g | 220 |
| Phase change temperature from phase 1 to phase 2: (K) g | 271 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beya, F.K.; Mbonimpa, M.; Belem, T.; Li, L.; Marceau, U.; Kalonji, P.K.; Benzaazoua, M.; Ouellet, S. Mine Backfilling in the Permafrost, Part I: Numerical Prediction of Thermal Curing Conditions within the Cemented Paste Backfill Matrix. Minerals 2019, 9, 165. https://doi.org/10.3390/min9030165
Beya FK, Mbonimpa M, Belem T, Li L, Marceau U, Kalonji PK, Benzaazoua M, Ouellet S. Mine Backfilling in the Permafrost, Part I: Numerical Prediction of Thermal Curing Conditions within the Cemented Paste Backfill Matrix. Minerals. 2019; 9(3):165. https://doi.org/10.3390/min9030165
Chicago/Turabian StyleBeya, Fabrice Kazambua, Mamert Mbonimpa, Tikou Belem, Li Li, Ugo Marceau, Patrick Kayumba Kalonji, Mostafa Benzaazoua, and Serge Ouellet. 2019. "Mine Backfilling in the Permafrost, Part I: Numerical Prediction of Thermal Curing Conditions within the Cemented Paste Backfill Matrix" Minerals 9, no. 3: 165. https://doi.org/10.3390/min9030165
APA StyleBeya, F. K., Mbonimpa, M., Belem, T., Li, L., Marceau, U., Kalonji, P. K., Benzaazoua, M., & Ouellet, S. (2019). Mine Backfilling in the Permafrost, Part I: Numerical Prediction of Thermal Curing Conditions within the Cemented Paste Backfill Matrix. Minerals, 9(3), 165. https://doi.org/10.3390/min9030165








