A Method for Ordering of LR-Type Fuzzy Numbers: An Important Decision Criteria
Abstract
:1. Introduction
- (1)
- The method should be consistent with the ranking of real numbers when a real number is considered as a particular situation of a fuzzy number.
- (2)
- The method should avoid evaluating expressions such as or , where a is a real number in the calculus of the ordering.
- (3)
- The method should avoid inconsistencies, such as two different fuzzy numbers with the same ranking.
- (4)
- The method should be based on easy calculation of mathematical expressions.
- (5)
- The method should show consistency with other ordering methods proposed in literature.
2. Elementary Definitions of Fuzzy Theory
3. The Proposal
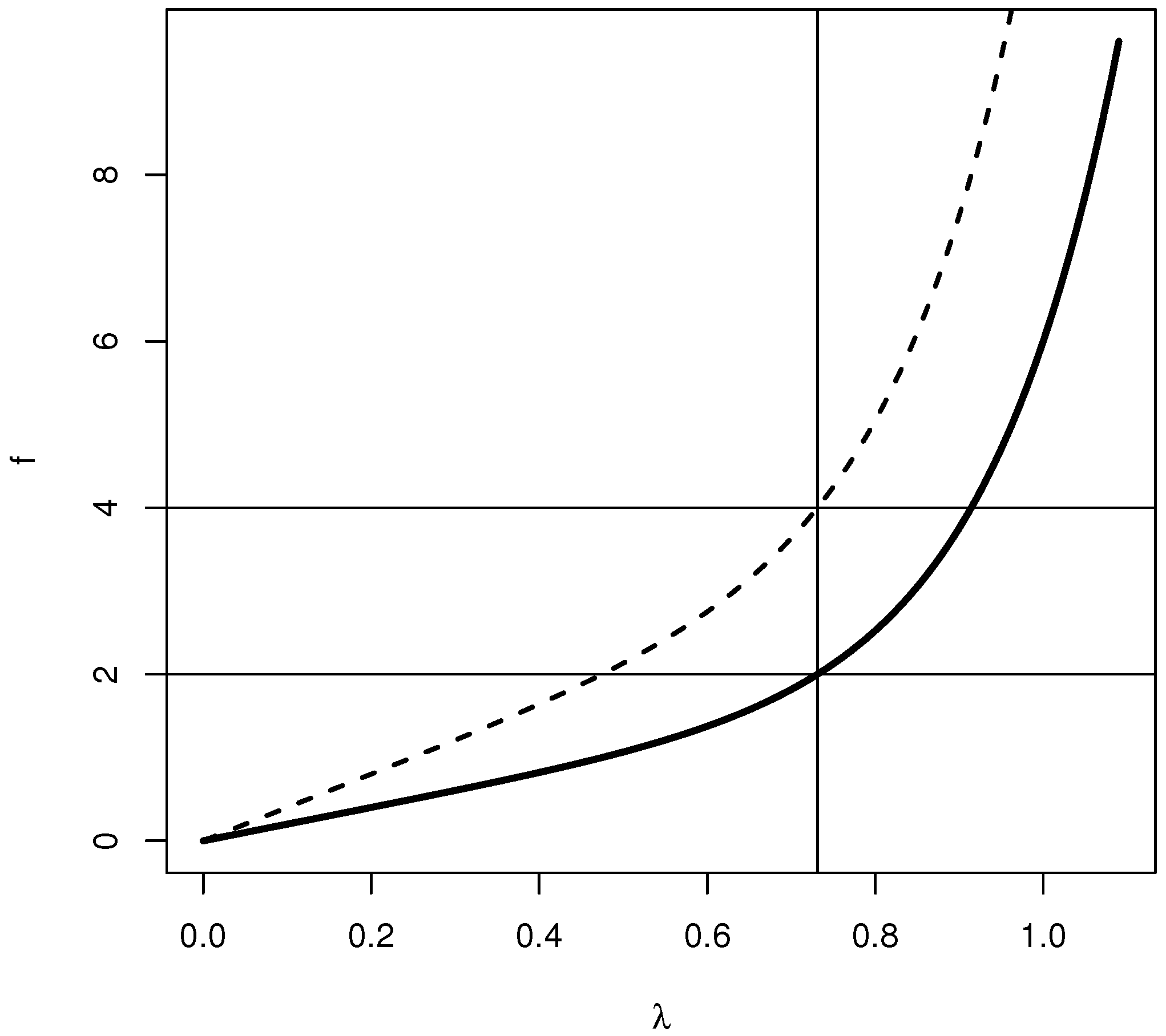
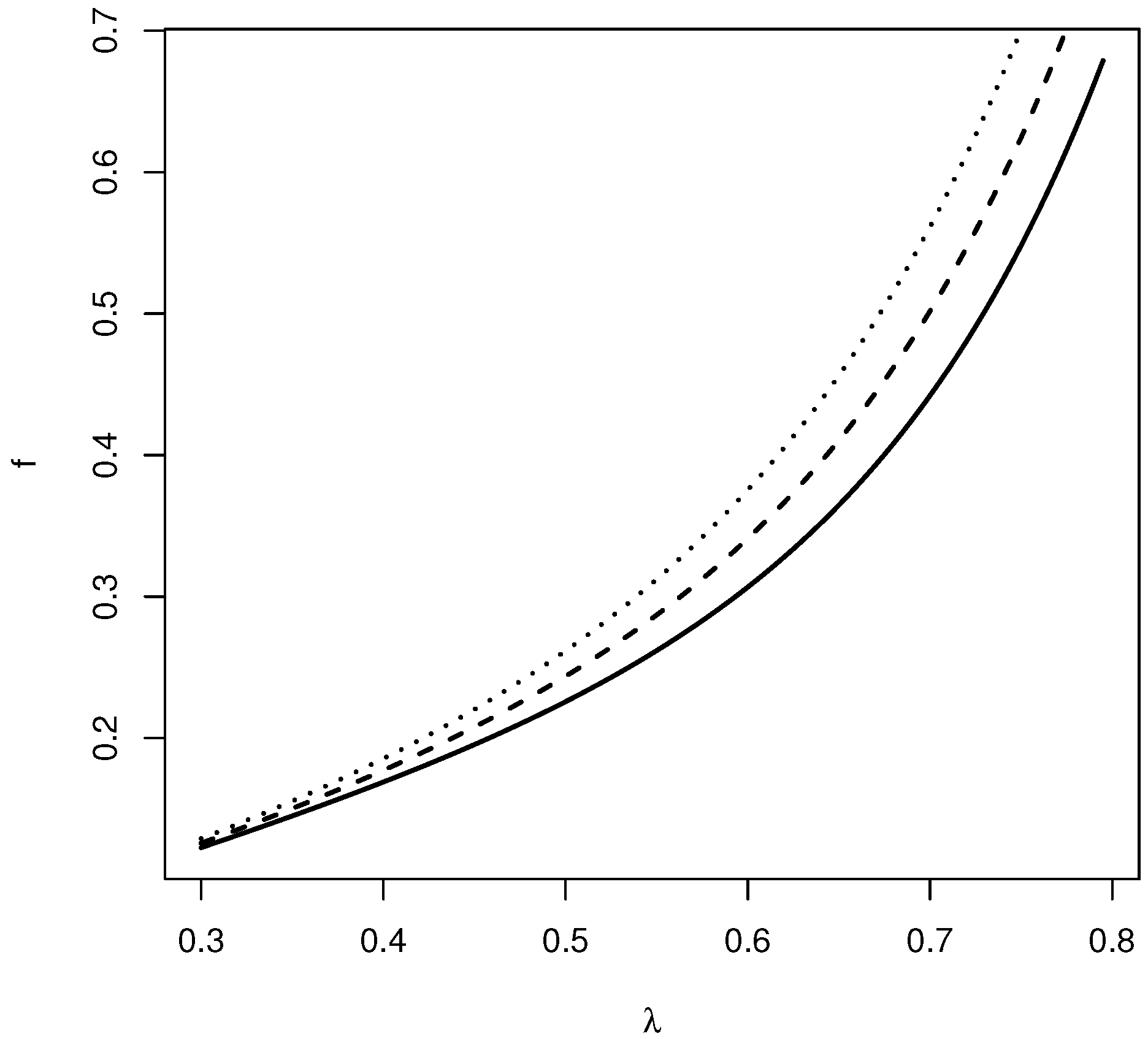
4. Application
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chu, T.C.; Wu, S. A centroid ranking approach based fuzzy mcdm model. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2013, 7, 531–537. [Google Scholar]
- Chen, L.-H.; Lu, H.-W. An approximate approach for ranking fuzzy numbers based on left and right dominance. Comput. Math. Appl. 2001, 41, 1589–1602. [Google Scholar] [CrossRef]
- Chu, T.-C.; Tsao, C.-T. Ranking fuzzy numbers with an area between the centroid point and original point. Comput. Math. Appl. 2002, 43, 111–117. [Google Scholar] [CrossRef]
- Deng, Y.; Zhenfu, Z.; Qi, L. Ranking fuzzy numbers with an area method using radius of gyration. Comput. Math. Appl. 2006, 51, 1127–1136. [Google Scholar] [CrossRef]
- Thorani, Y.; Rao, P.P.B.; Shankar, N.R. Ordering generalized trapezoidal fuzzy numbers. Int. J. Contemp. Math. Sci. 2012, 7, 555–573. [Google Scholar]
- Azman, F.N.; Abdullah, L. A New Centroids Method for Ranking of Trapezoid Fuzzy Numbers. Malays. J. Fundam. Appl. Sci. 2014. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Asady, B. Ranking of fuzzy numbers by sign distance. Inf. Sci. 2006, 176, 2405–2416. [Google Scholar] [CrossRef]
- Tran, L.; Duckstein, L. Comparison of fuzzy numbers using a fuzzy distance measure. Fuzzy Sets Syst. 2002, 130, 331–341. [Google Scholar] [CrossRef]
- Asady, B.; Zendehnam, A. Ranking fuzzy numbers by distance minimization. Appl. Math. Model. 2007, 31, 2589–2598. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Ranking fuzzy numbers in the setting of possibility theory. Inf. Sci. 1983, 30, 183–224. [Google Scholar] [CrossRef]
- Lee, E.; Li, R.-J. Comparison of fuzzy numbers based on the probability measure of fuzzy events. Comput. Math. Appl. 1988, 15, 887–896. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Z. Total ordenings defined on the set of all fuzzy numbers. Fuzzy Sets Syst. 2014, 5, 131–141. [Google Scholar] [CrossRef]
- Cheng, C.-H. A new approach for ranking fuzzy numbers by distance method. Fuzzy Sets Syst. 1998, 95, 307–317. [Google Scholar] [CrossRef]
- Modarres, M.; Sadi-Nezhad, S. Ranking fuzzy numbers by preference ratio. Fuzzy Sets Syst. 2001, 118, 429–436. [Google Scholar] [CrossRef]
- Nasseri, S.; Taleshian, F.; Alizadeh, Z.; Vahidi, J. A new method for ordering lr fuzzy number. J. Math. Comput. Sci. 2012, 4, 283–294. [Google Scholar]
- Wang, Y.-M.; Yang, J.-B.; Xu, D.-L.; Chin, K.-S. On the centroids of fuzzy numbers. Fuzzy Sets Syst. 2006, 157, 919–926. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
- Yang, M.-S.; Ko, C.-H. On a class of fuzzy numbers clustering procedures for fuzzy data. Fuzzy Sets Syst. 1996, 84, 49–60. [Google Scholar] [CrossRef]
- Kelley, C.T. Solving Nonlinear Equations with Newton’s Method; SIAM: Philadelphia, PA, USA, 2003; Volume 1. [Google Scholar]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Wang, X.; Kerre, E. Reasonable properties for the ordering of fuzzy quantities (I). Fuzzy Sets Syst. 2001, 118, 375–385. [Google Scholar]
- Baldwin, J.; Guild, N. Comparison of fuzzy sets on the same decision space. Fuzzy Sets Syst. 1979, 2, 213–231. [Google Scholar] [CrossRef]
- Choobineh, F.; Li, H. An index for ordering fuzzy numbers. Fuzzy Sets Syst. 1993, 54, 287–294. [Google Scholar] [CrossRef]
- Yager, R.R. A procedure for ordering fuzzy subsets of the unit interval. Inf. Sci. 1981, 24, 143–161. [Google Scholar] [CrossRef]
- Yao, J.-S.; Wu, K. Ranking fuzzy numbers based on decomposition principle and signed distance. Fuzzy Sets Syst. 2000, 116, 275–288. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Mon, D.-L. Fuzzy system reliability analysis by interval of confidence. Fuzzy Sets Syst. 1993, 56, 29–35. [Google Scholar] [CrossRef]
- Chen, S.-H. Ranking fuzzy numbers with maximizing set and minimizing set. Fuzzy Sets Syst. 1985, 17, 113–129. [Google Scholar] [CrossRef]
- Lee, A.H.; Chen, W.-C.; Chang, C.-J. A fuzzy ahp and bsc approach for evaluating performance of it department in the manufacturing industry in taiwan. Expert Syst. Appl. 2008, 34, 96–107. [Google Scholar] [CrossRef]

| Fuzzy Number | Set | |
|---|---|---|
| 0.6961 | ||
| Our proposal | 0.7918 | |
| 0.8876 | ||
| 0.333 | ||
| Choobineh and Li [23] | 0.50 | |
| 0.667 | ||
| 0.6 | ||
| Yager [24] | 0.7 | |
| 0.8 | ||
| 0.3375 | ||
| Chen [27] | 0.50 | |
| 0.667 | ||
| 0.3 | ||
| Baldwin and Guild [22] | 0.33 | |
| 0.44 | ||
| 0.299 | ||
| Chu and Tsao [28] | 0.350 | |
| 0.3993 | ||
| 0.6 | ||
| Yao and Wu [25] | 0.7 | |
| 0.8 | ||
| 0.79 | ||
| Cheng distance [13] | 0.8602 | |
| 0.9268 | ||
| 0.0272 | ||
| Cheng CV uniform [13] | 0.0214 | |
| distribution | 0.0225 | |
| Nasseri, Taleshian | ||
| Alizadeh and Vahidi [15] | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González Campos, J.A.; Manríquez Peñafiel, R.A. A Method for Ordering of LR-Type Fuzzy Numbers: An Important Decision Criteria. Axioms 2016, 5, 22. https://doi.org/10.3390/axioms5030022
González Campos JA, Manríquez Peñafiel RA. A Method for Ordering of LR-Type Fuzzy Numbers: An Important Decision Criteria. Axioms. 2016; 5(3):22. https://doi.org/10.3390/axioms5030022
Chicago/Turabian StyleGonzález Campos, José A., and Ronald A. Manríquez Peñafiel. 2016. "A Method for Ordering of LR-Type Fuzzy Numbers: An Important Decision Criteria" Axioms 5, no. 3: 22. https://doi.org/10.3390/axioms5030022






