1. Introduction
Recently, quantum biological studies have gained momentum, which can be judged by the number of recent publications related to this topic [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21]. It has become evident that quantum mechanics has an important role in photosynthesis [
8], magnetoreception [
9], and evolution [
5]. In photosynthesis, the Fenna–Matthews–Olson (FMO) complex supports the coherent transport of electron excitation over a short period of time, upon the photon absorption, to the reaction center where the energy gets converted into sugar. In the second phase of this interaction, the environment decoheres the system, which speeds up the excitation transfer by avoiding the system being trapped into the dark states. Further, the DNA replication and protein synthesis have been described by using Grover’s search algorithm [
15]. Additionally, the quantum mechanical formalism for biological evolution has been established in [
21].
There were also many attempts in an effort to explain the structure of genetic code and transfer of information from DNA to protein by using the concepts of quantum mechanics [
3,
5,
7]. For instance, the general quantum mechanical model to describe the transfer of information from DNA to protein by using the quantum information theory is proposed by Karafyllidis [
3]. However, given the high complexity of the problem [
22], the determination of
quantum biological channel capacity is still an open problem. On the other hand, the classical biological channel capacity has been determined by Yockey [
10]. Yockey developed a discrete memoryless classical biological channel model, and explicitly derived the transitional probabilities among amino acids. Namely, he represented the information transfer from DNA to protein as a communication problem and determined the corresponding classical biological channel capacity by maximizing the mutual information between DNA and protein. Interestingly enough, there are certain papers that question the role of quantum information in biological processes [
12]. The main justification is that the entanglement in living system is limited to a very short time and small regions, and the decoherence is too high for quantum entanglement to be relevant on the molecular level in the ambient conditions. However, in photosynthesis, as indicated above, this decoherence phase is essential to avoid the system being caught in dark states. Moreover, it is possible to represent the genetic coding using the quantum error correction concepts. Even though that decoherence is going to introduce errors, these errors can be corrected by the “quantum decoder,” performing the mRNA to protein translation. Another argument, also known as
kBT-argument, claims that whenever interaction energies are smaller than
kBT at room temperature, the corresponding quantum effect cannot persist. However, the electron clouds of complementary DNA strands experience dipole–dipole interaction, resulting in attractive van der Waals bonding [
14], with interaction frequency
ω being in the optical range, suggesting that
![Life 02 00377 i001]()
Therefore, since the electronic system of DNA is globally in the ground state, the DNA system must be locally in a mixed state. Given the uncertainty principle, it is impossible to distinguish whether a local mixed state is a result of temperature or entanglement.
In this paper, we develop the quantum biological channel model suitable for study of quantum information transfer from DNA to proteins, as well as the quantum DNA error correction. The quantum channel model is derived based on codon transition probabilities. We assume that the quantum genetic noise is introduced by the imperfect transcription process, DNA point mutations, insertions, deletions, and imperfect translation process. By using the Holevo–Schumacher–Westmoreland (HSW) theorem [
11], we adopt the proposed model to determine biological quantum channel capacity. We observe several cases of interest: (i) completely mixed state approach, in which the different codon basekets (basis vectors) representing the same amino acid occur with the same probability; (ii) by representing an amino acid as a superposition of eigenvectors spanning the subspace of DNA Hilbert space, and, (iii) by selecting an eigenvector representing an amino acid from subspace at random. We will show later in the paper that the quantum biological channel capacity is higher than classical channel capacity, suggesting that the quantum mechanics has an important role in biological systems.
2. Quantum Biological Channel Model Suitable for Study of Quantum Information Transfer from DNA to Proteins
In
Figure 1, we describe the generic quantum biological model suitable to study the flow of information from DNA to protein. The process of transcription is interpreted as encoding, the various errors introduced during replication, transcription or translation are considered as a source of genetic noise, while the process of translation is interpreted as decoding. Notice that this interpretation is consistent to the classical model defined by Yockey [
10]. The process of translation is also prone to errors, which can also be contributed to the genetic noise. Therefore, all errors introduced in any stage shown in
Figure 1 are called “genetic noise.” The transcription, DNA point mutations, insertions, deletions, and translation can all be interpreted as the quantum channel. It is assumed that genetic noise introduces random errors, which can be classified into several broad categories. The first types of errors, “storage errors,” occur in DNA itself as it is an imperfect storage of genetic information. The second types of errors are introduced during the DNA replication process. (For instance, the probability of error during replication is ~10
−7 per base pair [
15].) The third types of errors, transcription errors, are introduced during DNA to mRNA transcription process. The fourth type of errors, translation errors, is introduced during the translation process.
Therefore, the key difference with respect to communication systems, where both encoders and decoders are implemented from perfect gates, in biological systems DNA replication, DNA to mRNA transcription, and mRNA to protein translations, are imperfect processes. This difference requires redefining the channel model, as it is done in
Figure 1.
We assume that the problem with the burst of errors, introduced for example by an alpha particle passing through a segment of DNA, have been resolved by duplicate genes. Moreover, the introns may serve as interleavers in eukaryotic genes, suggesting that quantum errors indeed appear in a random fashion. The genome, which represents the ensemble of genetic codewords, is pre-recorded in DNA sequence by using the nucleotide alphabet composed of four symbols: Adenine (A), guanine (G), cytosine (C) and thymine (T). The fourth base is replaced in RNA by uracil (U). The DNA codewords contain the information for protein synthesis. The mRNA consists of three-symbol words known as codons. Multiple codons can correspond to the same amino acid.
Figure 1.
Generic quantum channel model describing the information flow from DNA to protein. It is assumed that quantum genetic noise introduces the random errors. In this model, the classical information, representing the information for a single polypeptide synthesis, is transmitted over the quantum genetic channel. DNA template is also a subject of mutations and, as such, is also represented as a part of biological quantum channel.
Figure 1.
Generic quantum channel model describing the information flow from DNA to protein. It is assumed that quantum genetic noise introduces the random errors. In this model, the classical information, representing the information for a single polypeptide synthesis, is transmitted over the quantum genetic channel. DNA template is also a subject of mutations and, as such, is also represented as a part of biological quantum channel.
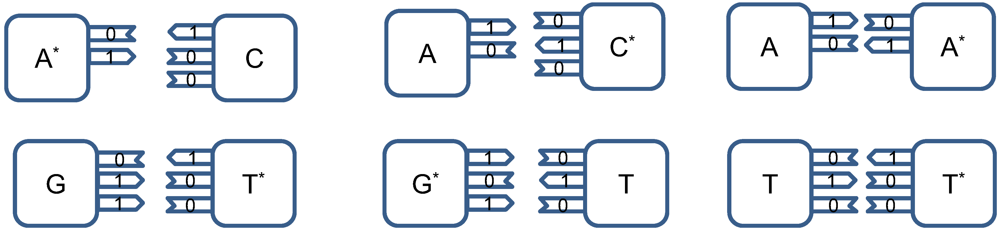
The point mutations are caused by tautomeric forms of nucleic acids [
13,
16]. There exist two main forms of tautomerism: (i)
amino-imino tautomerism given by [
13]
and
keto-enol tautomerism given by [
13]
The amino and keto forms are considered as standard forms. Namely, the pairing of nucleotides is specific to
![Life 02 00377 i005]()
combinations, with
![Life 02 00377 i006]()
representing the hydrogen bond (H-bond), as shown in
Figure 2. In the same figure, we provide the schematic representation in which the “donors” of protons are denoted with symbol 1, while the “acceptors” of protons are denoted with symbol 0. However, in tautomeric forms A
*, G
*, C
* and T
*, a proton involved in H-bond has been moved from one electron lone pair to another, which is illustrated in
Figure 3. During either DNA replication or translation, the tautomeric nucleic acids bind with non-complementary nucleic acids introducing the mutations. For instance, tautomeric A
* binds with C instead of T (U in mRNA), tautomeric C
* binds with A, G
* binds with T (U) and T
* (U
*) with G. It is also possible that both bases in DNA pair to be in the tautomeric forms as illustrated in
Figure 4. Namely, when DNA is used for long-term storage of genetic information, the proton tunneling (tautomeric forms’ creation) can contribute to random errors introduction. The probability of occurrence of tautomeric nucleic acids’ forms is low so that it makes sense to assume that errors introduced by tautomeric forms are random. However, the presence of mutagens, carcinogens, electromagnetic radiation and/or proton bombardment can either increase the probability of occurrence of tautomeric forms or damage the bases, and consequently introduce the storage errors. In addition to increasing the rate of spontaneous mutations, the mutagens can cause the induced mutations due to deamination, oxidation, and alkylation. The DNA is the subject of continuous mutations and damages, and the cell has various mechanisms to deal with damages, including direct reversal (such as photoreactivation) mechanism, various damaged bases excising mechanisms (nucleotide excision repair-NER, base excision repair-BER and nucleotide mismatched repair-NMR), single-strand damage repair, double-strand breaks repair, and translesion synthesis (TLS). In this paper, we assume that only the point induced mutations, transitions or transversions, have remained upon the DNA repair process.
Figure 2.
Standard nucleic acids’ pairing together with schematic representation. In schematic representation the symbol 1 is used to denote the “donor” of a proton, while symbol 0 to denote “acceptor” of a proton.
Figure 2.
Standard nucleic acids’ pairing together with schematic representation. In schematic representation the symbol 1 is used to denote the “donor” of a proton, while symbol 0 to denote “acceptor” of a proton.
Figure 3.
The tautomeric nucleic acids’ pairing.
Figure 3.
The tautomeric nucleic acids’ pairing.
Figure 4.
Tautomeric forms are responsible for random errors introduced within DNA, when DNA is used for long-term storage of genetic information.
Figure 4.
Tautomeric forms are responsible for random errors introduced within DNA, when DNA is used for long-term storage of genetic information.
Even though the probability of occurrence of tautomeric forms in normal ambient conditions is low, we can associate corresponding probability amplitude between normal and tautomeric forms, and represent the nucleic acid states as quantum states. For instance, the superposition states corresponding to T and C can be represented as:
where with
![Life 02 00377 i011]()
we denoted the standard form of T, while
![Life 02 00377 i012]()
the corresponding tautomeric form T
* that occurs with probability
P100, pyr (10
−5–10
−3). We use the notation
![Life 02 00377 i013]()
(
![Life 02 00377 i014]()
) to denote that corresponding base is of pyrimidine (purine) type so that we can uniquely distinguished among different tautomeric forms. Strictly speaking, the probability amplitudes are complex numbers; however, from a quantum information theory point of view, the representation given above is sufficient.
To determine the exact probability of the occurrence of the tautomeric form, we can use the
double-well model and tunneling effect in a fashion similar to that first described in [
13]. By close inspection of
Figure 2, we can see that H-bonds in standard forms are asymmetric. Further, the protons have two equilibrium positions, for instance:
The principles of quantum mechanics indicate that the proton can move between these two equilibrium positions, so that it makes sense to observe the corresponding quantum states as the superposition of these two equilibrium states, with probability amplitude not necessarily 1/√2 (the exact probability amplitude needs to be determined either experimentally or by using double-well model [
13]). The hydrogen bonds are weak bonds; and as it has been shown in [
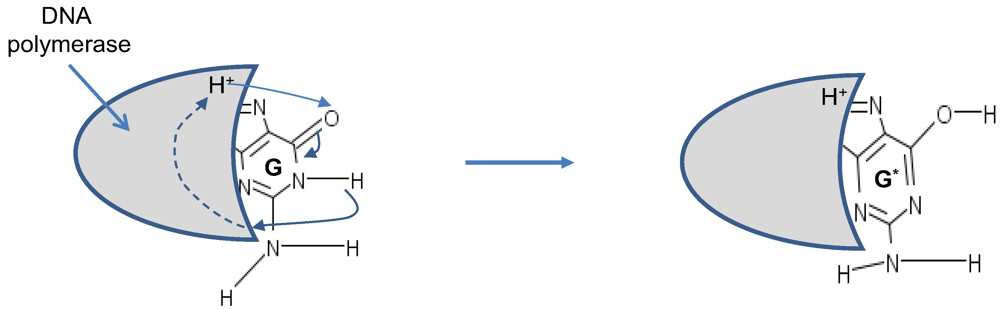
14], the electron clouds of complementary DNA strands experience dipole–dipole interaction, resulting in attractive van der Waals bonding. Therefore, the superposition of basekets can be caused by either van der Waals interaction or thermal fluctuations. When the DNA polymerase reads out the genetic information, it separates two DNA strands, and the nonstandard proton position can cause the error. For instance, the separation of AT in
Figure 2 can result into a nonstandard splitting as shown in
Figure 5. The nonstandard splitting, illustrated in
Figure 5, is responsible for time-shift deletion errors introduced during DNA replication. A nucleotide deletion error causes the amino acids inserted after the deleted nucleotide to be incorrect. The process of recognition of DNA polymerase and corresponding nucleotide can also be responsible for creation of tautomeric forms, which is illustrated in
Figure 6.
Figure 5.
The illustration of nonstandard splitting during the replication process. The superscript + is used to denote the existence of additional proton, while the superscript – is used to denote a missing proton.
Figure 5.
The illustration of nonstandard splitting during the replication process. The superscript + is used to denote the existence of additional proton, while the superscript – is used to denote a missing proton.
Figure 6.
Tautomeric formation of G* by proton transfer between DNA polymerase (active region shown by shaded area) and G.
Figure 6.
Tautomeric formation of G* by proton transfer between DNA polymerase (active region shown by shaded area) and G.
The mutation rates can vary even within the same genome of a single organism, with typical values 10
−9–10
−8, particularly in bacteria. (Interestingly enough, the error-prone polymerase genes in human have the mutation rates 10
−3–10
−2, as shown by Johnson [
17].) In rapidly reproducing bacteria, even the mutation rates of the order 10
−9 accumulate fast over the time, leading to the resistance of bacteria to antibiotics [
18]. Therefore, even though the tautomeric forms occur with low probability (10
−5–10
−3), they introduce the occasional DNA storage and replication errors, which are responsible for mutations, aging and evolution.
The models described above will be used to determine the probability of single and double codon errors (the probability of triple codon errors is so small that can be considered negligible). Notice that here we are concerned with small-scale mutations; such as point mutations, deletions, and insertions; rather than large-scale mutations (amplifications, chromosomal region deletions, chromosomal translocations, heterozygosity loss,
etc.). Therefore, it is of crucial importance to determine how the quantum channel capacity changes with respect to single base error probability
p. (Notice that double-base error probability is proportional to
p2 and can be neglected when the probability
p is low.) It is important to point out that some of the errors introduced during the DNA replication are corrected by various DNA repair processes. Repair enzymes are able to recognize improperly paired nucleotides, remove out the wrong nucleotides and replacing them with the correct ones. Unfortunately, some of the replication errors stay uncorrected during DNA repair and thus represent permanent mutations. We assume that these permanent mutations contribute to the base error probability
p. Given the fact that three bases determine the codon, representing the amino acid in protein synthesis, the single base error does not necessarily result in amino acid error. Since the genetic information is encoded in codons, it makes sense to assume that each codon represents a baseket. Because there exist 64 codons, the corresponding Hilbert code space is 64-dimensional. Similarly to the model due to Karafyllidis [
3], we assume that each codon is a baseket in this Hilbert space. For instance, the basekets (codons) corresponding to Ile are |AUU〉, |AUA〉, and |AUC〉, and they span the subspace of Hilbert code space. In what follows, we describe three interesting scenarios. In scenario (i), we assume that |Ile〉-state is a completely mixed state, a statistical mixture of basekets each occurring with the same probability. The corresponding density state (operator) of an amino acid is given by
![Life 02 00377 i018]()
where
pm describes the probability that a member of the ensemble (codon baseket) has been prepared in state |
m〉. For instance,
m⋴{AUU, AUA, AUC} for Ile, and
m⋴{UUU, UUC} for Phe. In scenario (ii), we assume that |Ile〉-state is a superposition of eignekets of corresponding Hamiltonian [
3]:
where
a,
b and
c are probability amplitudes. (In the lack of experimental data, we assume that
![Life 02 00377 i020]()
) In similar fashion, the |Phe〉-state is a superposition of eigenkets (eigenvectors) |UUC〉+|UUU〉 and |UUC〉-|UUU〉:
where
a and
b are corresponding probability amplitudes. In case (iii), we select one of the eigenkets from equations above at random. The same strategy is applied to other amino acids.
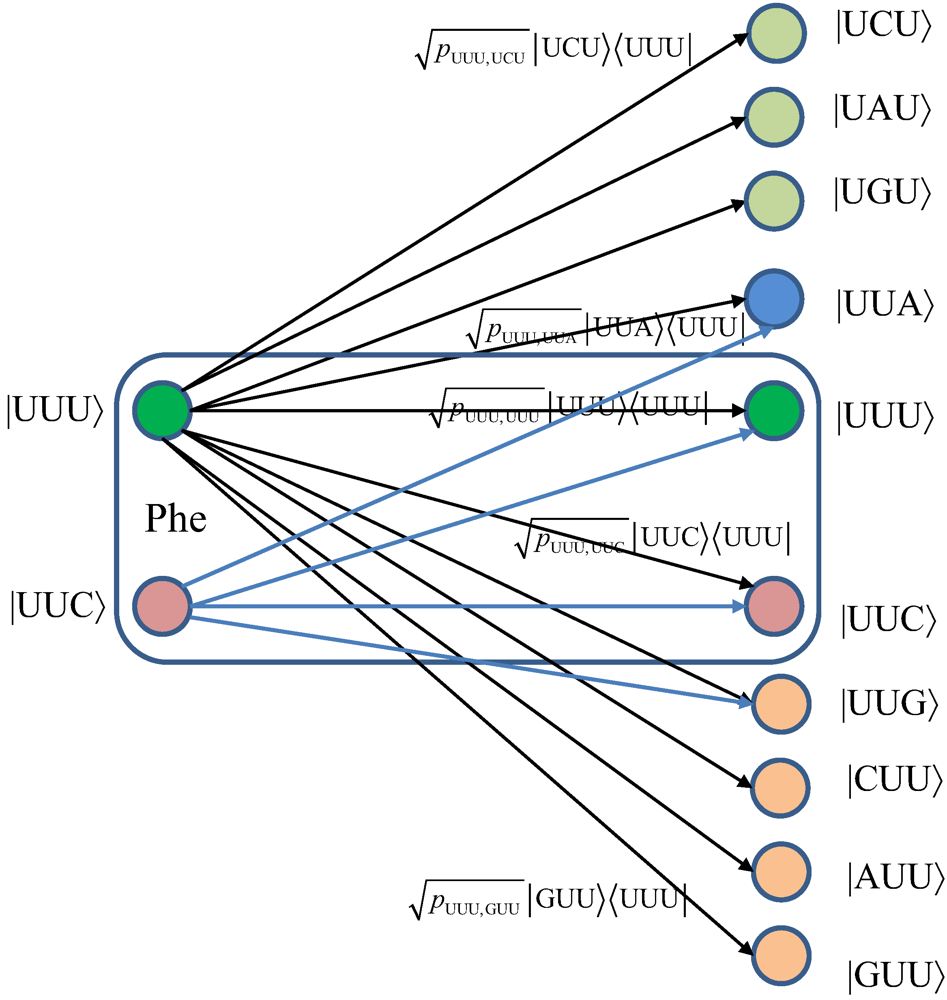
We turn our attention to the quantum channel model, which is applicable to all three scenarios discussed above. When the baseket |
m〉, representing one of codons (
m), is transmitted over the quantum biological channel, it can be detected on the receiver (protein) side as baseket |
n〉 (
n ≠
m) due to the presence of genetic noise. To completely characterize this quantum channel model it is essential to determine baseket transition probabilities. As an illustration, in
Figure 7, we provide the transition diagram corresponding to Ile, while in
Figure 8, we provide the transition diagram corresponding to Phe. For Ile, only transitions caused by single base error in baseket |AUU〉 are shown. On the other hand, for Phe the single base error caused transitions for |UUU〉 have been shown. Other transitions can easily be obtained by following the same strategy. With
pm,n we denoted the transition probability from baseket |
m〉, representing the initial codon, to baseket |
n〉, representing the final codon; while corresponding Kraus operator is given by
![Life 02 00377 i022]()
Notice that certain codon base errors will not result in a different amino acid, as illustrated in
Figure 7 and
Figure 8. As a remark, the model described in
Figure 7 and
Figure 8 is used to describe the collective action of various types of errors (DNA storage errors, DNA replication errors, transcription errors and translation errors) on protein synthesis and the amount of DNA information transfer from DNA to protein.
True transitional probabilities can be obtained either from experimental data or by employing Löwdin’s double-well model, while for illustrative purposes we will assume that single base errors are dominant and independent of each other. The model described above is applicable to both spontaneous mutations and induced mutations (caused by mutagens, be they of chemical origin or introduced by radiation). In induced mutations, the base error probability increases as the concentration of corresponding chemical (NH
2OH, BrdU,
N-ethyl-
N-nitrosourea, Ochratoxin A, EtBr,
etc.) or the radiation level increases. Once the level of induced mutations goes well above the natural level, the quantum channel capacity starts to decrease dramatically as shown later in
Section 4.
Figure 7.
The quantum biological channel transition diagram for basekets corresponding to Ile. Only transitions from baseket |AUU〉 due to the errors in single base of codon are shown. The
pm,n denotes the transition probability from baseket |
m〉 to baseket |
n〉, where
m⋴{AUU,AUC,AUA} and
n could be any of 64 basekets. The Kraus operator
Em,n is obtained as
![Life 02 00377 i023]()
.
Figure 7.
The quantum biological channel transition diagram for basekets corresponding to Ile. Only transitions from baseket |AUU〉 due to the errors in single base of codon are shown. The
pm,n denotes the transition probability from baseket |
m〉 to baseket |
n〉, where
m⋴{AUU,AUC,AUA} and
n could be any of 64 basekets. The Kraus operator
Em,n is obtained as
![Life 02 00377 i023]()
.
Figure 8.
The quantum biological channel transition diagram for basekets corresponding to Phe.
Figure 8.
The quantum biological channel transition diagram for basekets corresponding to Phe.
3. Quantum Biological Channel Capacity
In quantum information theory, developed by Schumacher (see [
11] and references therein), a quantum channel can be described by the transformation of an input density matrix
ρs to the output density matrix
ρs’. This transformation, described by the quantum operation (superoperator)
U, can be represented as the following mapping
![Life 02 00377 i026]()
Clearly, the super-operator
U cannot be unitary due to the decoherence effects. However, the total evolution operator of quantum system and environment (ambient) can be represented by unitary operator
Us,E . Without loss of generality, let us assume that the environment (ambient)
E is initially in a pure state |0
E〉. Hence, the expression for super-operator under this initial condition can be written as Equation 1.
where the partial trace tr
E(·) is taken with respect to the environmental degrees of freedom. Consider equation (1) as a completely positive linear transformation acting on the density matrix, which can be reconstructed as Equation 2.
The corresponding Kraus operators
Ei in (2) must satisfy the completeness relationship such that
For the quantum biological channel, the Kraus operator
Em, n performing the transformation from codon baseket |
m〉 to |
n〉 can be constructed according to the transition probabilities
pm,n, as discussed earlier. Clearly, the generic quantum biological channel model consists of 4,096 Kraus operators. An arbitrary state, |
ψin〉= ∑
m αm|
m〉, represents the amino acid in genome; after transcription, point mutations, translation, and other genetic noise sources can be represented as Equation 3.
while the resulting density matrix can be expressed as Equation 4.
We can rewrite the previous equation in terms of Kraus operators
![Life 02 00377 i032]()
, as Equation 5.
which is consistent with equation (2), after replacing double-indexing with single-indexing. Notice that partial trace over the environment qubit has been omitted due to the fact that a mixing process can be described either with or without a fictitious environment [
11]. In other words,
![Life 02 00377 i034]()
is equivalent to the density operator
![Life 02 00377 i035]()
after tracing out the environment.
The genetic noise introduces uncertainty about the genome, and the amount of information related to initial density state
ρs, which can be expressed as [
11] (Equation 6).
where
S[(
U(
ρs)] denotes the von Neumann entropy. The elements in the
i-th row and the
j-th column of the information matrix
U can be found as Equation 7.
Each element of
U measures the exchangeable amount of information between the system and the environment during its interaction. With initial environment states being the pure states,
S(
U) gives the entropy of the environment. By employing the HSW theorem [
11], the quantum channel capacity can be calculated as Equation 8.
where the maximization is performed over all ensembles {
pj,
ρj} of possible input states
ρj. By choosing
a priori probabilities of codons as
pi= 1/61 and
pi=0 for stop codons (UAA, UAG, and UGA), the maximum information rate can be achieved since the source is discrete.
4. Results
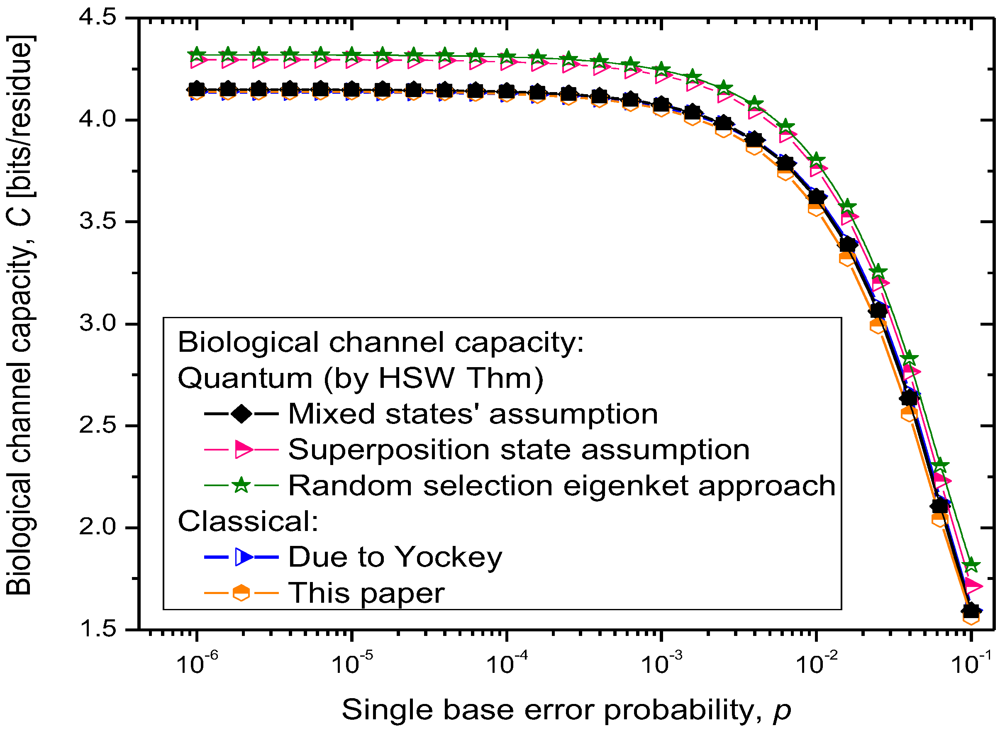
The results of quantum channel capacity with respect to the single base error probability are depicted in
Figure 9. The results of calculations are obtained by using the Equations 6–8.
Figure 9.
Quantum biological channel capacity against the single base error probability.
Figure 9.
Quantum biological channel capacity against the single base error probability.
Clearly, for the scenario (i), the quantum channel capacity is very similar to that of the classical channel, which is expected as the quantum biological information is represented as
statistical (classical) mixture of codon basekets. This case can be considered as a lower bound on quantum biological channel capacity. The use of superposition state assumption, scenario (ii), results in higher quantum channel capacity, as shown in
Figure 9. Finally, the random selection of Hamiltonian eigenkets, spanning the subspace of corresponding amino acid, results in even higher quantum channel capacity, which can be interpreted as an upper bound on the quantum channel capacity. Therefore, the numerical results shown in
Figure 9 suggest that quantum effects could play a role in increasing robustness of information processing in biological systems. Even though the coherent quantum channel model shows small improvements in biological channel capacity than classical channel models, in addition to improved reliability of biological information processing, the quantum coherence could also improve the DNA replication rates as suggested by Patel [
15]. Namely, as it has been advocated by Patel, the enzymes could provide the shielded environment for quantum coherence to be preserved sufficiently long for the completion of the base-paring process. When the base error probability is larger than 10
−2, the quantum biological channel capacity decreases dramatically, as shown in
Figure 9, and in that regime the quantum coherence of biological systems cannot be preserved. We conclude that for the base error probability higher than 10
−2 the classical biological processes might have the same role as quantum processes as the gap between quantum and classical models becomes negligible. For base error probabilities close to 0.1, the biological channel capacity drops dramatically, suggesting that the cell is no longer capable of performing protein synthesis. Notice that in this analysis, different contributors to genetic noise (storage, replication and translation errors) are included in the base error probability
p.
For completeness of presentation, in
Figure 9, we also report the results of classical biological channel capacity obtained by using the model credited to Yockey [
10], which are in excellent agreement with classical channel capacity calculations obtained by developing the equivalent classical model to that shown in
Figure 7 and
Figure 8 (by simply converting codon basekets to classical nonbinary symbols), which is illustrated in
Figure 10. The
pm,n denotes the transition probability from codon
m to codon
n,
pmn=
P(
n|
m), where
m⋴{AUU,AUC,AUA} and
n could be any of 64 codons. The codon transition probabilities are employed to evaluate the classical channel capacity, defined as Equation 9.
where
H(
Y) [
H(
X)] stands for the biological channel output (input) entropy, and
H(
Y|
X) [
H(
X|
Y)] represents the conditional entropy (or the equivocation) of biological channel output (input) given the biological channel input (output)
X (
Y). The entropy of biological channel output and conditional entropy are defined respectively as Equations 10 and 11.
where {
p(
Xi)} denotes the probability of occurrence of codons in DNA, and {
p(
Yj|
Xi)} denotes the conditional probability of the received codons {
Yi} given the transmitted codons {
Xi}. Since the source information encrypted in DNA is discrete, the maximum information rate in (9) is achieved for the uniform distribution of codons; that is
pi=0 for stop codons (UAA, UAG, and UGA) and
pi = 1/61 for other codons. The classical biological channel capacity curve in
Figure 9 (the orange curve) is obtained by using Equations 9–11 and model from
Figure 10, and represents a lower bound on biological channel capacity. The transition probabilities
pmn required in Equations 10 and 11 are obtained numerically by using the model shown in
Figure 10 and the theory of Markov chains. These transition probabilities are also used in the quantum biological channel model, see
Figure 7 and
Figure 8, to determine probability amplitudes needed for calculation of quantum channel capacity by HSW theorem (by using Equation 8).
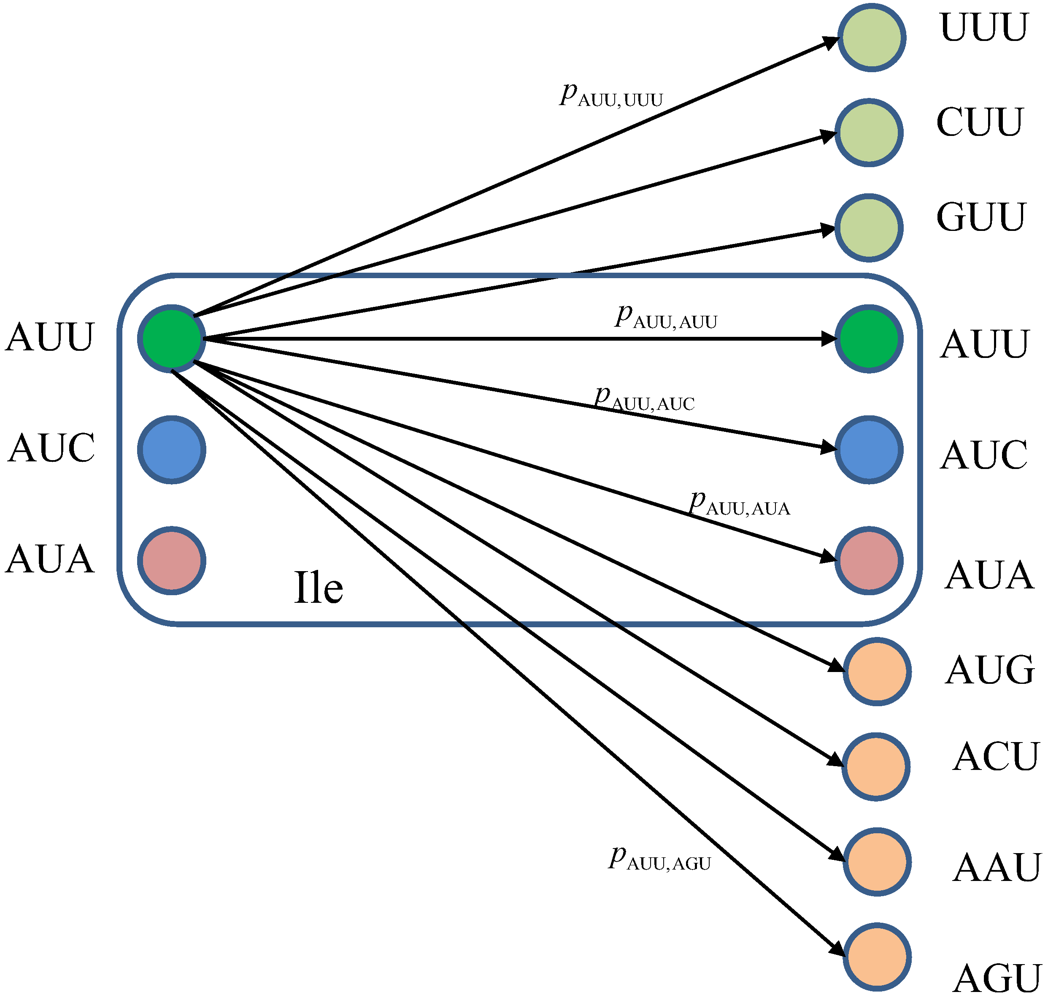
Figure 10.
The classical biological channel transition diagram for codons corresponding to Ile. The pm,n denotes the transition probability from codon m to codon n, where m⋴{AUU,AUC,AUA} and n could be any of 64 codons.
Figure 10.
The classical biological channel transition diagram for codons corresponding to Ile. The pm,n denotes the transition probability from codon m to codon n, where m⋴{AUU,AUC,AUA} and n could be any of 64 codons.
 Therefore, since the electronic system of DNA is globally in the ground state, the DNA system must be locally in a mixed state. Given the uncertainty principle, it is impossible to distinguish whether a local mixed state is a result of temperature or entanglement.
Therefore, since the electronic system of DNA is globally in the ground state, the DNA system must be locally in a mixed state. Given the uncertainty principle, it is impossible to distinguish whether a local mixed state is a result of temperature or entanglement. 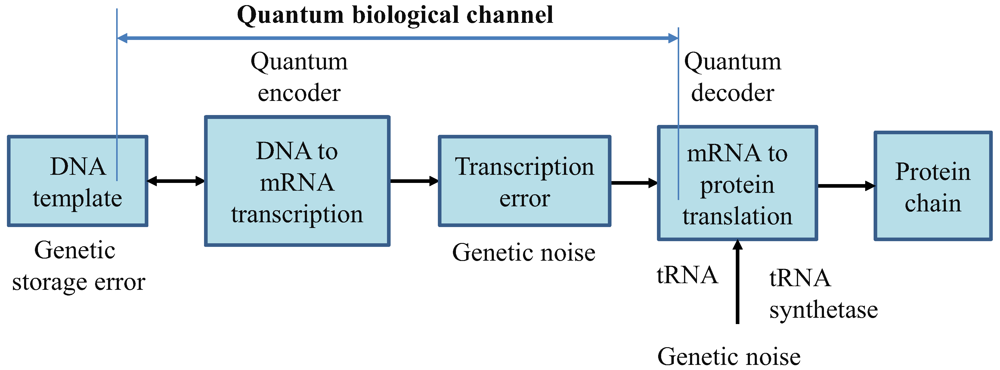


 combinations, with
combinations, with  representing the hydrogen bond (H-bond), as shown in Figure 2. In the same figure, we provide the schematic representation in which the “donors” of protons are denoted with symbol 1, while the “acceptors” of protons are denoted with symbol 0. However, in tautomeric forms A*, G*, C* and T*, a proton involved in H-bond has been moved from one electron lone pair to another, which is illustrated in Figure 3. During either DNA replication or translation, the tautomeric nucleic acids bind with non-complementary nucleic acids introducing the mutations. For instance, tautomeric A* binds with C instead of T (U in mRNA), tautomeric C* binds with A, G* binds with T (U) and T* (U*) with G. It is also possible that both bases in DNA pair to be in the tautomeric forms as illustrated in Figure 4. Namely, when DNA is used for long-term storage of genetic information, the proton tunneling (tautomeric forms’ creation) can contribute to random errors introduction. The probability of occurrence of tautomeric nucleic acids’ forms is low so that it makes sense to assume that errors introduced by tautomeric forms are random. However, the presence of mutagens, carcinogens, electromagnetic radiation and/or proton bombardment can either increase the probability of occurrence of tautomeric forms or damage the bases, and consequently introduce the storage errors. In addition to increasing the rate of spontaneous mutations, the mutagens can cause the induced mutations due to deamination, oxidation, and alkylation. The DNA is the subject of continuous mutations and damages, and the cell has various mechanisms to deal with damages, including direct reversal (such as photoreactivation) mechanism, various damaged bases excising mechanisms (nucleotide excision repair-NER, base excision repair-BER and nucleotide mismatched repair-NMR), single-strand damage repair, double-strand breaks repair, and translesion synthesis (TLS). In this paper, we assume that only the point induced mutations, transitions or transversions, have remained upon the DNA repair process.
representing the hydrogen bond (H-bond), as shown in Figure 2. In the same figure, we provide the schematic representation in which the “donors” of protons are denoted with symbol 1, while the “acceptors” of protons are denoted with symbol 0. However, in tautomeric forms A*, G*, C* and T*, a proton involved in H-bond has been moved from one electron lone pair to another, which is illustrated in Figure 3. During either DNA replication or translation, the tautomeric nucleic acids bind with non-complementary nucleic acids introducing the mutations. For instance, tautomeric A* binds with C instead of T (U in mRNA), tautomeric C* binds with A, G* binds with T (U) and T* (U*) with G. It is also possible that both bases in DNA pair to be in the tautomeric forms as illustrated in Figure 4. Namely, when DNA is used for long-term storage of genetic information, the proton tunneling (tautomeric forms’ creation) can contribute to random errors introduction. The probability of occurrence of tautomeric nucleic acids’ forms is low so that it makes sense to assume that errors introduced by tautomeric forms are random. However, the presence of mutagens, carcinogens, electromagnetic radiation and/or proton bombardment can either increase the probability of occurrence of tautomeric forms or damage the bases, and consequently introduce the storage errors. In addition to increasing the rate of spontaneous mutations, the mutagens can cause the induced mutations due to deamination, oxidation, and alkylation. The DNA is the subject of continuous mutations and damages, and the cell has various mechanisms to deal with damages, including direct reversal (such as photoreactivation) mechanism, various damaged bases excising mechanisms (nucleotide excision repair-NER, base excision repair-BER and nucleotide mismatched repair-NMR), single-strand damage repair, double-strand breaks repair, and translesion synthesis (TLS). In this paper, we assume that only the point induced mutations, transitions or transversions, have remained upon the DNA repair process. 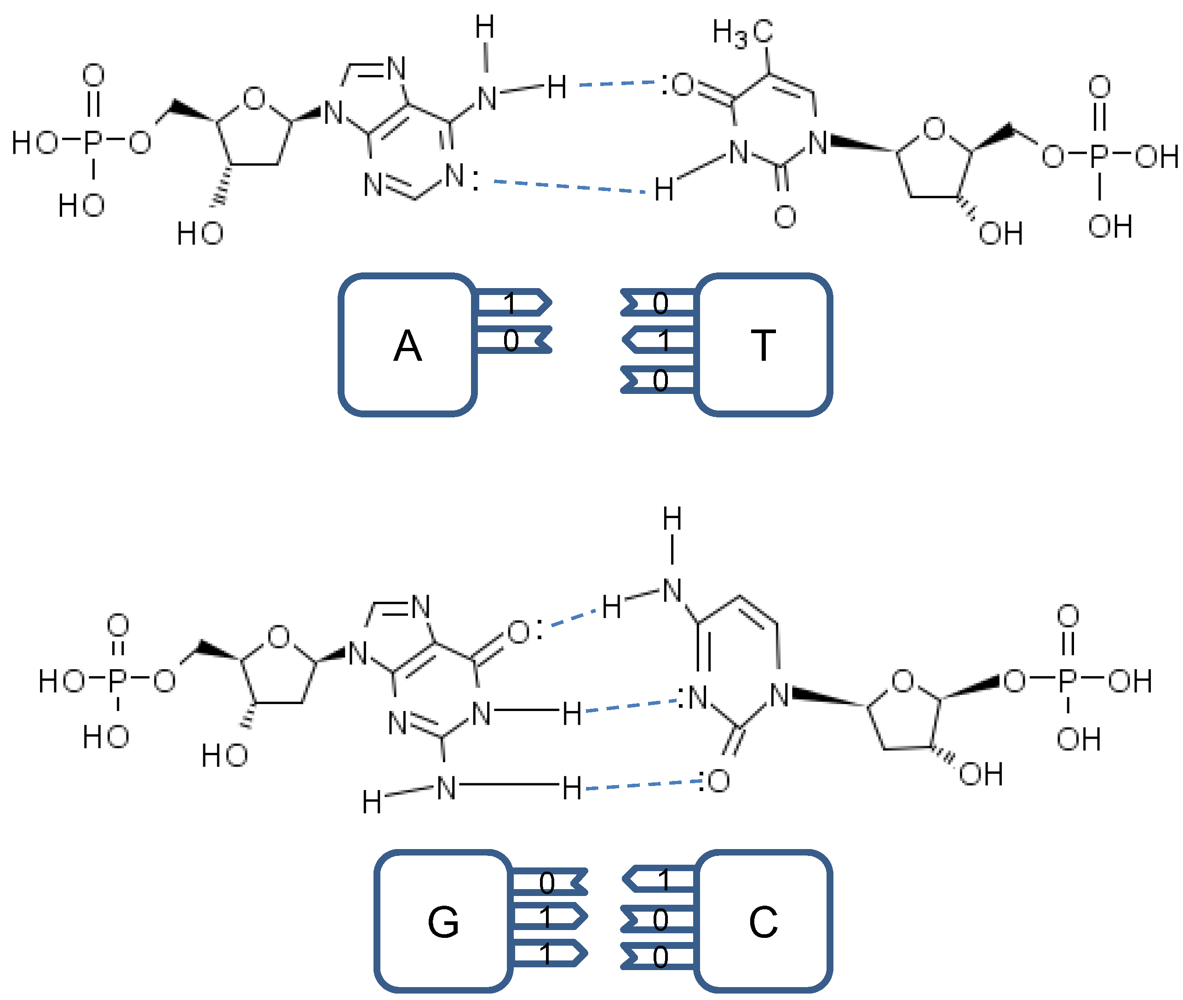


 we denoted the standard form of T, while
we denoted the standard form of T, while  the corresponding tautomeric form T* that occurs with probability P100, pyr (10−5–10−3). We use the notation
the corresponding tautomeric form T* that occurs with probability P100, pyr (10−5–10−3). We use the notation  (
(  ) to denote that corresponding base is of pyrimidine (purine) type so that we can uniquely distinguished among different tautomeric forms. Strictly speaking, the probability amplitudes are complex numbers; however, from a quantum information theory point of view, the representation given above is sufficient.
) to denote that corresponding base is of pyrimidine (purine) type so that we can uniquely distinguished among different tautomeric forms. Strictly speaking, the probability amplitudes are complex numbers; however, from a quantum information theory point of view, the representation given above is sufficient.

 where pm describes the probability that a member of the ensemble (codon baseket) has been prepared in state |m〉. For instance, m⋴{AUU, AUA, AUC} for Ile, and m⋴{UUU, UUC} for Phe. In scenario (ii), we assume that |Ile〉-state is a superposition of eignekets of corresponding Hamiltonian [3]:
where pm describes the probability that a member of the ensemble (codon baseket) has been prepared in state |m〉. For instance, m⋴{AUU, AUA, AUC} for Ile, and m⋴{UUU, UUC} for Phe. In scenario (ii), we assume that |Ile〉-state is a superposition of eignekets of corresponding Hamiltonian [3]:

 ) In similar fashion, the |Phe〉-state is a superposition of eigenkets (eigenvectors) |UUC〉+|UUU〉 and |UUC〉-|UUU〉:
) In similar fashion, the |Phe〉-state is a superposition of eigenkets (eigenvectors) |UUC〉+|UUU〉 and |UUC〉-|UUU〉:

 Notice that certain codon base errors will not result in a different amino acid, as illustrated in Figure 7 and Figure 8. As a remark, the model described in Figure 7 and Figure 8 is used to describe the collective action of various types of errors (DNA storage errors, DNA replication errors, transcription errors and translation errors) on protein synthesis and the amount of DNA information transfer from DNA to protein.
Notice that certain codon base errors will not result in a different amino acid, as illustrated in Figure 7 and Figure 8. As a remark, the model described in Figure 7 and Figure 8 is used to describe the collective action of various types of errors (DNA storage errors, DNA replication errors, transcription errors and translation errors) on protein synthesis and the amount of DNA information transfer from DNA to protein. .
.
 .
.
 Clearly, the super-operator U cannot be unitary due to the decoherence effects. However, the total evolution operator of quantum system and environment (ambient) can be represented by unitary operator Us,E . Without loss of generality, let us assume that the environment (ambient) E is initially in a pure state |0E〉. Hence, the expression for super-operator under this initial condition can be written as Equation 1.
Clearly, the super-operator U cannot be unitary due to the decoherence effects. However, the total evolution operator of quantum system and environment (ambient) can be represented by unitary operator Us,E . Without loss of generality, let us assume that the environment (ambient) E is initially in a pure state |0E〉. Hence, the expression for super-operator under this initial condition can be written as Equation 1.





 , as Equation 5.
, as Equation 5.

 is equivalent to the density operator
is equivalent to the density operator  after tracing out the environment.
after tracing out the environment.